Joint Torques and Tibiofemoral Joint Reaction Force in the Bodyweight “Wall Squat” Therapeutic Exercise

Featured Applications

With the results of this study, therapists can manage the wall squat exercise and its variants to finely modulate the lower-limb joint torques and to minimize the shear component of the tibiofemoral joint reaction force.

Abstract

This study provides a biomechanical analysis of the bodyweight wall-squat exercise considering four exercise variants: knee angle; horizontal hip-ankle distance (d); shift between the rearfoot and forefoot of the centre of pressure (x_GR) of the ground reaction force; back supported via the scapular or pelvic zone. The ankle and hip angles corresponding to a given knee angle can be modulated, changing the distance d, to manage limitation in lumbopelvic and ankle mobility. The knee-extensor muscles can be overloaded (250 Nm muscle torque) with knees flexed at 90°, back supported through the pelvic zone, and feet away from the wall (d = 50 cm). Scapular support, x_GR at forefoot, and d = 50 cm, yield a higher level of muscle-torque for hip-extension (130 Nm) and knee-flexion (65 Nm), with knees at 90° of flexion or near full extension, respectively. Ankle-dorsiflexion (plantarflexion) muscle torque up to 40 Nm is reached with x_GR at the forefoot (rearfoot). This study may aid trainers and therapists to finely modulate the muscle torques (up to the above-mentioned levels) by an appropriate selection of exercise variants for training or rehabilitation purposes. Low levels (60 N) of anterior tibial pull may occur near 25° of knee flexion with $x_{\mathrm{GR}}$ at the rearfoot.

1. Introduction

The bodyweight wall squat is a popular physical exercise frequently included in the early stage of lower limb rehabilitation interventions [1]. It can also be used to promote exercise-induced hypoalgesia [2], increase the thickness of deep abdominal muscles [3], improve posture [4] and lumbar stability [3], and reduce resting blood pressure in home-based training [5]. The support provided by the wall during the wall squat considerably reduces the balance and stability demands, compared to the free squat. For this reason, the wall squat constitutes a functional lower limb exercise that can be included in the early stage of rehabilitation interventions, as soon as the patient can tolerate weight bearing [1]. In the early subacute phase of lower limb rehabilitation, and particularly during the transition from partial to full weight-bearing, squat exercises should necessarily be performed with no external resistance and with the aid of external stabilization supports. A progression involving mini-squat with upper extremity assistance and bodyweight wall squat can be safely employed in this phase [1].

In the starting position, the exerciser stands with the back flat against the wall (any flat vertical surface with negligible friction), knees fully extended, arms straight at the sides of the body, feet flat on the floor about shoulder-width apart. The horizontal distance d of the ankle from the hip (which nearly coincides with the heel-to-wall distance) determines the hip and ankle angle in the starting position and constitutes the main variant of the exercise. From the starting position, the exerciser slowly flexes the knees and slides down the wall until the desired degree of knee flexion is reached. In the isometric wall-squat exercise, this position is held for a selected time before the subject returns back to the starting position. In the dynamic wall-squat exercise, the eccentric (descending) phase of the exercise is followed in a continuous motion by the concentric (ascending) phase. During the entire exercise, the subject should maintain a neutral spine position, the back vertical against the wall, a proper knee alignment (to avoid knee varus/valgus and internal/external rotation), and feet flat on the floor. From a kinematic perspective, the wall-squat exercise has only one degree of freedom: given the distance d and the exerciser’s anthropometry, the configuration of the body in each phase of the exercise is completely determined by only one parameter, e.g., the hip height from the ground or the knee angle ${\mathsf{\theta }}_{\mathrm{knee}}$.

Despite the popularity and importance of the bodyweight wall squat, a quantitative biomechanical analysis of this exercise is lacking. In 1999, Blanpied [6] published an electomyographic (EMG) study for the dynamic bodyweight wall squat performed from full knee extension to 60° of knee flexion, in two different conditions of foot position (foot in line with the hip and foot 50 cm forward) and posterior support location (at hip level and scapular level). In that study, the mean EMG activity of gluteus maximus, semitendinosus, vastus lateralis, and medial gastrocnemius was recorded during three consecutive repetitions. Notably, to date, no study has provided information related to the joint torques, joint reaction forces, and forces acting on specific joint structures during the bodyweight wall-squat exercise. Knowledge and control of the joint torques and forces acting during the execution of a physical exercise is of paramount importance for safe and effective implementation of the exercise in rehabilitation and training programs.

The main aim of this study was to provide an in-depth quantitative biomechanical analysis of the bodyweight wall-squat exercise, in static condition, accounting for all relevant exercise positions and variants. The specific goals were:

To determine the functional relationships among the relevant lower-limb kinematic parameters (joint spatial coordinates and joint angles) for all the possible static wall-squat configurations determined by the different values d and ${\mathsf{\theta }}_{\mathrm{knee}}$;

To determine the torque at the hip, knee, ankle, and lumbosacral joint, and the tibiofemoral (TF) joint reaction force, in any wall-squat configuration, with the use of biomechanical modelling in combination with kinematic and force plate measurements.

Furthermore, during the static wall squat, the exerciser can voluntary shift, between the scapular and the gluteal zone, the centre of pressure $({\mathrm{y}}_{\mathrm{wall}})$ of the supporting force exerted by the wall on the back. Likewise, the centre of pressure of the ground reaction force $(x_{\mathrm{GR}}$) can be voluntary shifted between the rearfoot and forefoot. In the static wall-squat, this can be readily done without compromising the safety of the exercise, that is, maintaining a neutral spine, trunk sustained by the wall and aligned with the vertical, and foot flat on the floor. These voluntary shifts may considerably change the relevant biomechanical quantities related to the exercise. Therefore, a further goal of this study is that of assessing the effect of a change in $x_{\mathrm{GR}}$ and ${\mathrm{y}}_{\mathrm{wall}}$ on the joint torques and on the TF joint reaction force, in the different wall-squat configurations.

2. Materials and Methods

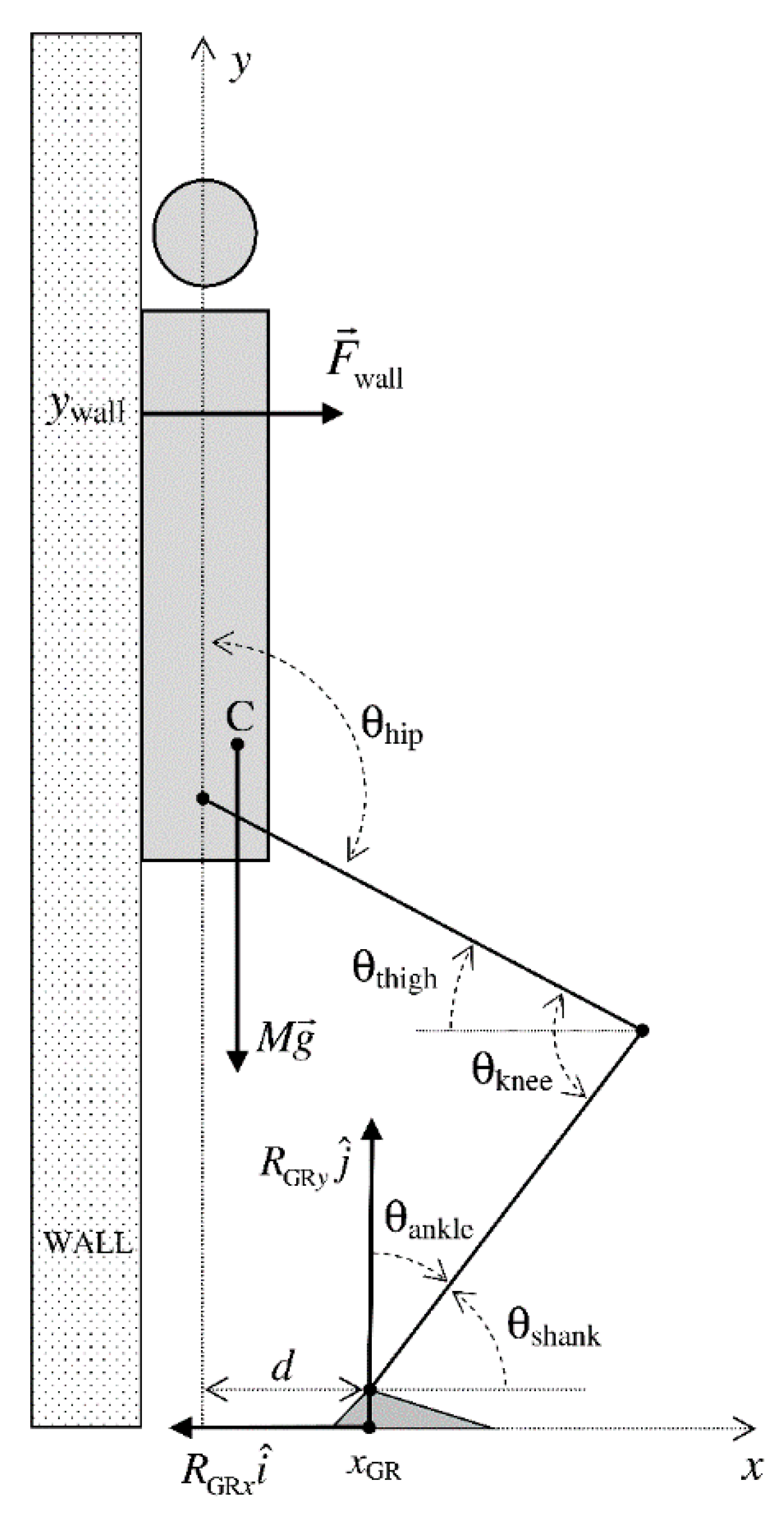
2.1. Biomechanical Modelling

Figure 1 illustrates a mechanical diagram of the bodyweight wall-squat exercise. The human body is modelled by 14 linked rigid segments: head, trunk, upper arms, forearms, hands, thighs, shanks and feet (for the sake of clarity, the upper limbs, straight at the sides of the body and aligned with the vertical, are nor displayed in the figure) [7,8]. The mass, dimension, centre of mass, and moment of inertia of these 14 segments have been deduced from extensive anthropometric studies [9,10]. We adopted a Cartesian frame of reference in the sagittal plane of the body, with the x-axis lying on the ground and directed forward relative to the body, and the y-axis directed vertically upward along the longitudinal axis of the trunk so that

$$x_{\mathrm{hip}}=0$$

(1)

in each wall-squat position. The horizontal ankle-to-hip distance $d=x_{\mathrm{hip}}-x_{\mathrm{ankle}}$ (which nearly coincides with the heel-to-wall distance) then coincides with the x-coordinate of the ankle joint

$$x_{\mathrm{ankle}}=d$$

(2)

The knee and hip coordinates are determined by the ankle position, the shank and the thigh length ($l_{\mathrm{shank}}$ and $l_{\mathrm{thigh}}$), and their inclination (${\mathsf{\theta }}_{\mathrm{shank}}{\mathrm{and}\mathsf{\theta }}_{\mathrm{thigh}}$) relative to the horizontal

$$x_{\mathrm{knee}}=x_{\mathrm{ankle}}+l_{\mathrm{shank}}\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)$$

(3)

$$y_{\mathrm{knee}}=y_{\mathrm{ankle}}+l_{\mathrm{shank}}\sin \left({\mathsf{\theta }}_{\mathrm{shank}}\right)$$

(4)

$$x_{\mathrm{hip}}=x_{\mathrm{ankle}}+l_{\mathrm{shank}}\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)-l_{\mathrm{thigh}}\cos \left({\mathsf{\theta }}_{\mathrm{thigh}}\right)$$

(5)

$$y_{\mathrm{hip}}=y_{\mathrm{ankle}}+l_{\mathrm{shank}}\sin \left({\mathsf{\theta }}_{\mathrm{shank}}\right)+l_{\mathrm{thigh}}\sin \left({\mathsf{\theta }}_{\mathrm{thigh}}\right)$$

(6)

With the use of Equations (1), (2) and (5), the thigh and shank inclination angles (Figure 1) can be expressed one in terms of the other:

$${\mathsf{\theta }}_{\mathrm{shank}}=\arccos \left(\frac{l_{\mathrm{thigh}}}{l_{\mathrm{shank}}}\cos \left({\mathsf{\theta }}_{\mathrm{thigh}}\right)-\frac{d}{l_{\mathrm{shank}}}\right)$$

(7)

$${\mathsf{\theta }}_{\mathrm{thigh}}=\pm \arccos \left(\frac{l_{\mathrm{shank}}}{{\mathrm{l}}_{\mathrm{thigh}}}\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)+\frac{d}{l_{\mathrm{thigh}}}\right)$$

(8)

When d is given, a specific value of ${\mathsf{\theta }}_{\mathrm{thigh}}$ univocally determines the value of ${\mathsf{\theta }}_{\mathrm{shank}}$, whereas two equal and opposite values of ${\mathsf{\theta }}_{\mathrm{thigh}}$ correspond to a specific value of ${\mathsf{\theta }}_{\mathrm{shank}}$. The ankle, knee, and hip angles (Figure 1) are readily expressed as a function of ${\mathsf{\theta }}_{\mathrm{shank}}{\mathrm{and}\mathsf{\theta }}_{\mathrm{thigh}}$:

$${\mathsf{\theta }}_{\mathrm{ankle}}=90°-{\mathsf{\theta }}_{\mathrm{shank}}$$

(9)

$${\mathsf{\theta }}_{\mathrm{knee}}={\mathsf{\theta }}_{\mathrm{shank}}+{\mathsf{\theta }}_{\mathrm{thigh}}$$

(10)

$${\mathsf{\theta }}_{\mathrm{hip}}=90°+{\mathsf{\theta }}_{\mathrm{thigh}}$$

(11)

The maximum ranges of variation of these joint angles are approximately given by $-50°\le {\mathsf{\theta }}_{\mathrm{ankle}}\le 30°$, $30°\le {\mathsf{\theta }}_{\mathrm{knee}}\le 180°$, and $60°\le {\mathsf{\theta }}_{\mathrm{hip}}\le 180°$. Since the mechanical problem has only one degree of freedom, $y_{\mathrm{hip}}$, or any joint or limb inclination angle that changes monotonically with $y_{\mathrm{hip}}$, determines the entire configuration of the body in each wall-squat position.

The external forces acting on the exerciser’s body are (Figure 1): (1) the weight of the body, equivalent to the vector $M\overrightarrow{g}$ (M is the body mass) applied at the centre of mass $\mathrm{C}=(x_{\mathrm{C}},y_{\mathrm{C}})$ of the body; (2) the supporting force exerted by the wall on the exerciser’s back, which, assuming a frictionless wall surface, can be schematized as a horizontal forces ${\overrightarrow{\mathrm{F}}}_{\mathrm{wall}}$ applied at a point with ordinate $y_{\mathrm{wall}}$ ranging between $y_{\mathrm{hip}}$ and $y_{\mathrm{shoulder}}$; (3) the ground reaction forces acting symmetrically on each foot, equivalent to two equal vectors ${\overrightarrow{R}}_{GR}$ applied at a point $(x_{\mathrm{GR}},0)$ within the contact surface between each foot and the ground. The force equilibrium equation applied to the whole body

$$M\overrightarrow{g}+2{\overrightarrow{R}}_{\mathrm{GR}}+{\overrightarrow{F}}_{\mathrm{wall}}=0$$

(12)

is projected onto the x and y axes, to give the following scalar equations

$$R_{\mathrm{GR}x}=-\frac{1}{2}{F}_{\mathrm{wall}}$$

(13)

$$R_{\mathrm{GR}y}=\frac{1}{2}Mg$$

(14)

where $F_{\mathrm{wall}}$ is the magnitude of ${\overrightarrow{F}}_{\mathrm{wall}}$, while $R_{\mathrm{GR}x}$ and $R_{\mathrm{GR}y}$ are the scalar x- and y-component of ${\overrightarrow{R}}_{\mathrm{GR}}$, respectively. The moment equilibrium equation, relative to the medial-lateral axis that passes through the point of application $(x_{\mathrm{GR}},0)$ of the ground reaction force ${\overrightarrow{R}}_{\mathrm{GR}}$, is given by

$$\left(x_{\mathrm{C}}-x_{\mathrm{GR}}\right)Mg+y_{\mathrm{wall}}{F}_{\mathrm{wall}}=0$$

(15)

and determines the value of $F_{\mathrm{wall}}$

$$F_{\mathrm{wall}}=\left(\frac{x_{\mathrm{GR}}-x_{\mathrm{C}}}{y_{\mathrm{wall}}}\right)Mg$$

(16)

Equations (13) and (16) then determine the $R_{\mathrm{GRx}}$ component

$$R_{\mathrm{GR}x}=-\frac{1}{2}\left(\frac{x_{\mathrm{GR}}-x_{\mathrm{C}}}{y_{\mathrm{wall}}}\right)Mg$$

(17)

The torque ${\tau }_{\mathrm{hip}}$ developed by the hip muscles to maintain a static wall-squat position can be derived by applying to the portion of the body above the hip joints the moment equilibrium equation relative to the hip flexion/extension axis

$$2{\mathsf{\tau }}_{\mathrm{hip}}=M_{\mathrm{UH}}g\left(x_{{\mathrm{C}}_{\mathrm{UH}}}-x_{\mathrm{hip}}\right)+F_{\mathrm{wall}}\left(y_{\mathrm{wall}}-y_{\mathrm{hip}}\right)$$

and replacing $F_{\mathrm{wall}}$ with the right-hand side of equation (16)

$$2{\mathsf{\tau }}_{\mathrm{hip}}=-M_{\mathrm{UH}}g\left(x_{\mathrm{hip}}-x_{{\mathrm{C}}_{\mathrm{UH}}}\right)+Mg\left(x_{\mathrm{GR}}-x_{\mathrm{C}}\right)\left(1-\frac{y_{\mathrm{hip}}}{y_{\mathrm{wall}}}\right)$$

(18)

In this equation, $M_{\mathrm{UH}}$ and ${\mathrm{C}}_{\mathrm{UH}}$ are the mass and the center of mass of the portion of the body above the hip joints. The torques developed by the knee muscles and by the ankle muscles are calculated in the same way

$$\begin{array}{c}2{\mathsf{\tau }}_{\mathrm{knee}}=-M_{\mathrm{UK}}g\left(x_{{\mathrm{C}}_{\mathrm{UK}}}-x_{\mathrm{knee}}\right)-F_{\mathrm{wall}}\left({\mathrm{y}}_{\mathrm{wall}}-y_{\mathrm{knee}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=M_{\mathrm{UK}}g\left(x_{\mathrm{knee}}-x_{{\mathrm{C}}_{\mathrm{UK}}}\right)-Mg\left(x_{\mathrm{GR}}-x_{\mathrm{C}}\right)\left(1-\frac{y_{\mathrm{knee}}}{y_{\mathrm{wall}}}\right)\end{array}$$

(19)

$$\begin{array}{c}2{\mathsf{\tau }}_{\mathrm{ankle}}=M_{\mathrm{UA}}g\left(x_{{\mathrm{C}}_{\mathrm{UA}}}-x_{\mathrm{ankle}}\right)+F_{\mathrm{wall}}\left(y_{\mathrm{wall}}-y_{\mathrm{ankle}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-M_{\mathrm{UA}}g\left(x_{\mathrm{ankle}}-x_{{\mathrm{C}}_{\mathrm{UA}}}\right)+Mg\left(x_{\mathrm{GR}}-x_{\mathrm{C}}\right)\left(1-\frac{y_{\mathrm{ankle}}}{y_{\mathrm{wall}}}\right)\end{array}$$

(20)

Here, $M_{\mathrm{UK}}$ and ${\mathrm{C}}_{\mathrm{UK}}$ ($M_{\mathrm{UA}}$ and ${\mathrm{C}}_{\mathrm{UA}}$) are the mass and the center of mass of the portion of the body above the knee (ankle) joints. Positive values of ${\mathsf{\tau }}_{\mathrm{hip}}$, ${\mathsf{\tau }}_{\mathrm{knee}}$, and ${\mathsf{\tau }}_{\mathrm{ankle}}$ reflect an extensor muscle torque, whereas negative values indicate a flexor muscle torque. The value of ${\mathsf{\tau }}_{\mathrm{hip}}$ also gives a reliable estimation of the muscle torque ${\mathsf{\tau }}_{\mathrm{LS}}$ at the lumbosacral joint (${\mathsf{\tau }}_{\mathrm{LS}}~2{\mathsf{\tau }}_{\mathrm{hip}}$) [7].

It is of interest to determine, in the different exercise conditions, the maximum level of TF shear force that yields anterior tibial translation relative to the femur. This anterior tibial pull is mainly restrained by the anterior cruciate ligament (ACL) tension [11]. A given level of knee-extension muscle torque ${\tau }_{\mathrm{knee}}$ (${\mathsf{\tau }}_{\mathrm{knee}}>0$) can be developed with increasing levels of quadriceps and hamstring cocontraction, as long as the difference between the extensor torque developed by the quadriceps and the flexor torque developed the knee flexor muscles is kept constant at ${\mathsf{\tau }}_{\mathrm{knee}}$. However, for a given level of ${\tau }_{\mathrm{knee}}$, the greatest level of anterior tibial pull is produced by a quadriceps activation with negligible hamstring cocontarction [12,13]. In this condition, the quadriceps force $F_{\mathrm{Q}}$ can be approximated by the ratio of ${\tau }_{\mathrm{knee}}$ to the patellar tendon moment arm $a_{\mathrm{PT}}$

$$F_{\mathrm{Q}}\cong \frac{{\tau }_{\mathrm{knee}}}{a_{\mathrm{PT}}}$$

(21)

and the force ${\overrightarrow{\mathsf{\phi }}}_{TF}$ the femur exerts on the tibia (TF joint reaction force) can be deduced by the force equilibrium equation relative to shank-foot system (the mass of this system is denoted by $m_{\mathrm{SF}}$)

$${\overrightarrow{R}}_{\mathrm{GR}}+m_{\mathrm{SF}}\overrightarrow{g}+{\overrightarrow{F}}_{\mathrm{Q}}+{\overrightarrow{\mathsf{\phi }}}_{\mathrm{TF}}=0$$

(22)

Projecting this equation onto a sagittal-plane axis normal to longitudinal tibial axis, one gets the shear component ${\phi }_{\mathrm{TF},\mathrm{shear}}$ of ${\overrightarrow{\mathsf{\phi }}}_{\mathrm{TF}}$

$${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}=R_{\mathrm{GR}y}\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)-R_{\mathrm{GR}x}\sin \left({\mathsf{\theta }}_{\mathrm{shank}}\right)-m_{\mathrm{SF}}g\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)-F_{\mathrm{Q}}\sin \mathsf{\gamma }$$

(23)

where the quadriceps traction angle $\mathsf{\gamma }$ is the acute angle between the patellar tendon and the longitudinal tibial axis. Taking into account Equations (14), (17) and (21), ${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}$ is finally expressed as

$$\begin{array}{c}{\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}=\frac{1}{2}Mg\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)+\frac{1}{2}\left(\frac{x_{\mathrm{GR}}-x_{\mathrm{C}}}{y_{\mathrm{wall}}}\right)Mg\sin \left({\mathsf{\theta }}_{\mathrm{shank}}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-m_{\mathrm{SF}}g\cos \left({\mathsf{\theta }}_{\mathrm{shank}}\right)-\frac{{\tau }_{\mathrm{knee}}}{a_{\mathrm{PT}}}\sin \mathsf{\gamma }\end{array}$$

(24)

Positive values of ${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}$ reflect a posterior tibial pull and a posterior cruciate ligament (PCL) loading. Conversely, negative values correspond to anterior tibial pull and ACL loading.

The joint torques ${\tau }_{\mathrm{hip}}$, ${\tau }_{\mathrm{knee}}$, and ${\tau }_{\mathrm{ankle}}$, and the TF shear force ${\phi }_{\mathrm{TF},\mathrm{shear}}$ directly depend on the point of application of the ground reaction force $\left(x_{\mathrm{GR}}\right)$. For this reason, we followed the experimental procedure outlined in the next sections to assess whether $x_{\mathrm{GR}}$ can be significantly shifted between the rearfoot and forefoot by a voluntary effort of the exerciser in different exercise conditions.

2.2. Participants

Six female and fourteen male participants (mean age 26 ± 5 years, mean height 1.74 ± 0.08 m, mean body mass 71 ± 11 kg), free from musculoskeletal injury and with no previous record of lower limb pathologies, were recruited from local fitness centres. These volunteers were already experienced in resistance training (intermediate level) and specifically with squat exercises. All participants gave informed consent to their inclusion in the study, which was conducted in accordance with the Declaration of Helsinki, and approved by the ethics committee of the University of Perugia (2014-032). The whole testing procedures were conducted at the Department of Experimental Medicine of the University of Perugia.

2.3. Testing Session

Each participant executed a static wall-squat exercise with ${\mathsf{\theta }}_{\mathrm{knee}}=135°$ in 8 different conditions, which result from the combination of two values of d (given by $d_1=0.5·l_{\mathrm{thigh}}$ and $d_2=l_{\mathrm{thigh}}$, which for a subject 175 cm tall result in $d_1=21.5 \mathrm{cm}$ and $d_2=43 \mathrm{cm}$, respectively), two value of $y_{\mathrm{wall}}$ ($y_{wall} \cong y_{\mathrm{shoulder}}$ and $y_{wall} \cong y_{hip}$), and two distributions of body weight on the contact surface between the foot and the ground (body weight intentionally displaced toward the forefoot and toward the rearfoot). The value of ${\mathsf{\theta }}_{\mathrm{knee}}$ was selected for its clinical relevance in knee rehabilitation. In the $y_{\mathrm{wall}} \cong y_{\mathrm{shoulder}}$ ($y_{\mathrm{wall}} \cong y_{\mathrm{hip}}$) condition, participants were asked to lean against the wall with only the scapular (gluteal) zone without resting any weight on the gluteal (scapular) zone, while maintaining a neutral spine and the longitudinal axis of the trunk aligned with the vertical. Likewise, to displace the body weight toward the rearfoot (forefoot), participants were asked to press the ground with the rearfoot (forefoot) without lifting the forefoot (rearfoot) from the ground. During the exercise, the participants wore their training shoes. In fact, with bare feet and feet away from the wall, the soles of the feet are subjected to high shear forces to fulfil an effective grip on the ground and, thereby provide body stability and static execution. This was accounted for by increasing the value of $y_{\mathrm{ankle}}$ (the height of the ankle from the ground) by 2.5 cm.

After a 10 min warm-up, each participant performed the 8 selected static wall-squat trials. Each wall-squat position was held for 8 s. To avoid any bias due to fatigue, the trial sequence was randomized, and a full recovery (of at least 2 min) was allowed between two consecutive trials.

2.4. Data Recording and Processing

The point of application of the ground reaction force ($x_{\mathrm{GR}}$) was recorded during each trial with the use of a time-synchronized apparatus (BTS Bioengineering, Milano, Italy) constituted by two adjacent force plates (P-6000) [12], an eight-camera optoelectronic motion capture system (Smart-DX 7000) [13], and four reflective markers (6-mm diameter) which were attached on the medial and lateral malleoli, following a procedure illustrated in detail in a previous work [8]. The selected knee angle (${\mathsf{\theta }}_{\mathrm{knee}}=135°$) was reached using a twin axis SG150 electrogoniometer (Biometrics, Newport, UK) [14]. Data were recorded at a sampling frequency of 1 kHz. No filtering was applied to the kinematic and kinetic data. For each trail, the recorded values of $x_{\mathrm{GR}}$ were averaged over the duration of the trail, averaged again between the left and right foot, and normalized to foot length ($l_{\mathrm{foot}}$), to get the value that was then used in the statistical analysis.

2.5. Statistical Analysis

Analysis of variance (ANOVA) was applied for data analysis, as the normality of the distribution of the $x_{\mathrm{GR}}$ values was previously confirmed through the Shapiro–Wilk test with statistical significance designated at 0.05. The dependent variable $x_{\mathrm{GR}}$ was analysed with a 3-way repeated measures ANOVA, with $d$ ($d=0.5·l_{\mathrm{thigh}}$ and $d=l_{\mathrm{thigh}}$), $y_{\mathrm{wall}}$ ($y_{\mathrm{wall}}={\mathrm{y}}_{\mathrm{shoulder}}$ and $y_{\mathrm{wall}}=y_{\mathrm{hip}}$) and intentional body weight distribution (at forefoot and at rearfoot) as independent within-subject factors. Post hoc analysis with the Scheffè test was performed for significant main effects and interactions. Statistical significance was designated at $P<0.05$, and all values are reported as mean ±SD.

3. Results

3.1. Kinematics

Within the normal ranges of knee and hip angle $(30° \le {\mathsf{\theta }}_{\mathrm{knee}} \le 180°, 60°\le {\mathsf{\theta }}_{\mathrm{hip}} \le 180°$), the knee angle ${\mathsf{\theta }}_{\mathrm{knee}}$ displays a monotonic change with $y_{\mathrm{hip}}$. Therefore, in the following, ${\mathsf{\theta }}_{\mathrm{knee}}$ is regarded as the parameter that uniquely determines the configuration of the body in each exercise position, when the value of d is given.

With knees fully extended $\left({\mathsf{\theta }}_{\mathrm{knee}}=180°\right)$ and $d>0$, hips are in flexion $({\mathsf{\theta }}_{\mathrm{hip}}<180°)$ and ankles in plantarflexion $({\mathsf{\theta }}_{\mathrm{ankle}}<0)$, and these two conditions are progressively enhanced by a gradual increase in the distance d (Figure 2). A progressive knee flexion yields a concurrent hip flexion, while the ankle displays a movement of dorsiflexion (increase of ${\mathsf{\theta }}_{\mathrm{ankle}}$) followed by plantarfexion (decrease in ${\mathsf{\theta }}_{\mathrm{ankle}}$). The ankle reverses the movement when the thigh is horizontal (${\mathsf{\theta }}_{\mathrm{thigh}}=0$), and this occurs at a knee angle that becomes progressively greater with the distance d. For any given value of ${\mathsf{\theta }}_{\mathrm{knee}}$, the hip and ankle angle are decreasing functions of d.

3.2. Ground Reaction Force

The point of application of the ground reaction force $\left(x_{\mathrm{GR}}\right)$ was not significantly affected by $d$ ($P=0.08$) and $y_{\mathrm{wall}}$ ($P=0.2$). Conversely, $x_{\mathrm{GR}}$ was significantly affected ($P<{10}^{-3}$) by the intentional weight transfer between the rearfoot and forefoot. In the first condition, the mean value of $x_{\mathrm{GR}}$ was not significantly different ($P=0.02$) from $x_{\mathrm{ankle}}$. In the second condition, $x_{\mathrm{GR}}=\left(x_{\mathrm{ankle}}+0.49 l_{\mathrm{foot}}\right)\pm 0.08 {\mathrm{l}}_{\mathrm{foot}}$, which for a subject 175 cm tall ($l_{\mathrm{foot}} \cong 26.6 \mathrm{cm}$) yields $x_{\mathrm{GR}} \cong \left(x_{\mathrm{ankle}}+13 \mathrm{cm}\right)\pm 2\mathrm{cm}$. For this reason, the hip, knee, and ankle torques, given by Equations (18), (19) and (20), respectively, were numerically calculated for $x_{\mathrm{GR}}=x_{\mathrm{ankle}}$ and $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, as reported in the following section.

3.3. Joint Torques and TF Shear Force

The knee-extension muscle torque (${\mathsf{\tau }}_{\mathrm{knee}}>0$) reaches considerably high values (about 250 Nm) when $y_{\mathrm{wall}}=y_{\mathrm{hip}}$ and $d=50 \mathrm{cm}$, at the higher knee flexion angles $({\mathsf{\theta }}_{\mathrm{knee}} ~ 77°)$ that can be reached in this condition (Figure 3). ${\mathsf{\tau }}_{\mathrm{knee}}$ is an increasing function of d for $y_{\mathrm{wall}}=y_{\mathrm{hip}}$, whereas it becomes a decreasing function of d for $y_{\mathrm{wall}}=y_{\mathrm{shoulder}}$. Near full knee extension, a knee-flexion muscle torque $({\mathsf{\tau }}_{\mathrm{knee}}<0)$ has to be developed to hold a static wall-squat position with scapular support ($y_{\mathrm{wall}}=y_{\mathrm{shouler}}$), and even with pelvic support ($y_{\mathrm{wall}}=y_{\mathrm{hip}}$) as long as $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$. The peak value of knee-flexion torque (−65 Nm) is reached for $y_{\mathrm{wall}}=y_{\mathrm{shouler}}$, $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, $d=50 \mathrm{cm}$, and ${\mathsf{\theta }}_{\mathrm{knee}}=180°$.

For $y_{\mathrm{wall}}=y_{\mathrm{hip}}$, the hip-extension muscle torque ${\mathsf{\tau }}_{\mathrm{hip}}$ turns out to be negligible (${\mathsf{\tau }}_{\mathrm{hip}} ~ 0$). However, ${\mathsf{\tau }}_{\mathrm{hip}}$ reaches values of about 130 Nm for $y_{\mathrm{wall}}=y_{\mathrm{shoulder}}$, $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, $d=50 \mathrm{cm}$, and ${\mathsf{\theta }}_{\mathrm{knee}}~ 80°$ (Figure 4). In this condition ${\mathsf{\tau }}_{\mathrm{knee}}$ is as low as 30 Nm.

For $x_{\mathrm{GR}}=x_{\mathrm{ankle}}$, the ankle muscles always develop a dorsiflexion torque $({\mathsf{\tau }}_{\mathrm{ankle}}<0$), and $\left|{\mathsf{\tau }}_{\mathrm{ankle}}\right|$ is an increasing function of d and a decreasing function of ${\mathsf{\theta }}_{\mathrm{knee}}$ and $y_{\mathrm{wall}}$ (Figure 5). Conversely, for $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, ${\mathsf{\tau }}_{\mathrm{ankle}}$ is of plantarflexion type $({\mathsf{\tau }}_{\mathrm{ankle}}>0$), and becomes a decreasing function of d and an increasing function of ${\mathsf{\theta }}_{\mathrm{knee}}$ and $y_{\mathrm{wall}}$. In both cases, $\left|{\mathsf{\tau }}_{\mathrm{ankle}}\right|$ reaches a maximum value of about 40 Nm.

Table 1. Maximum lower-limb joint torques developed during the static wall squat and corresponding exercise conditions. The maximum isokinetic concentric torques developed by males and females are also reported for comparison [15].

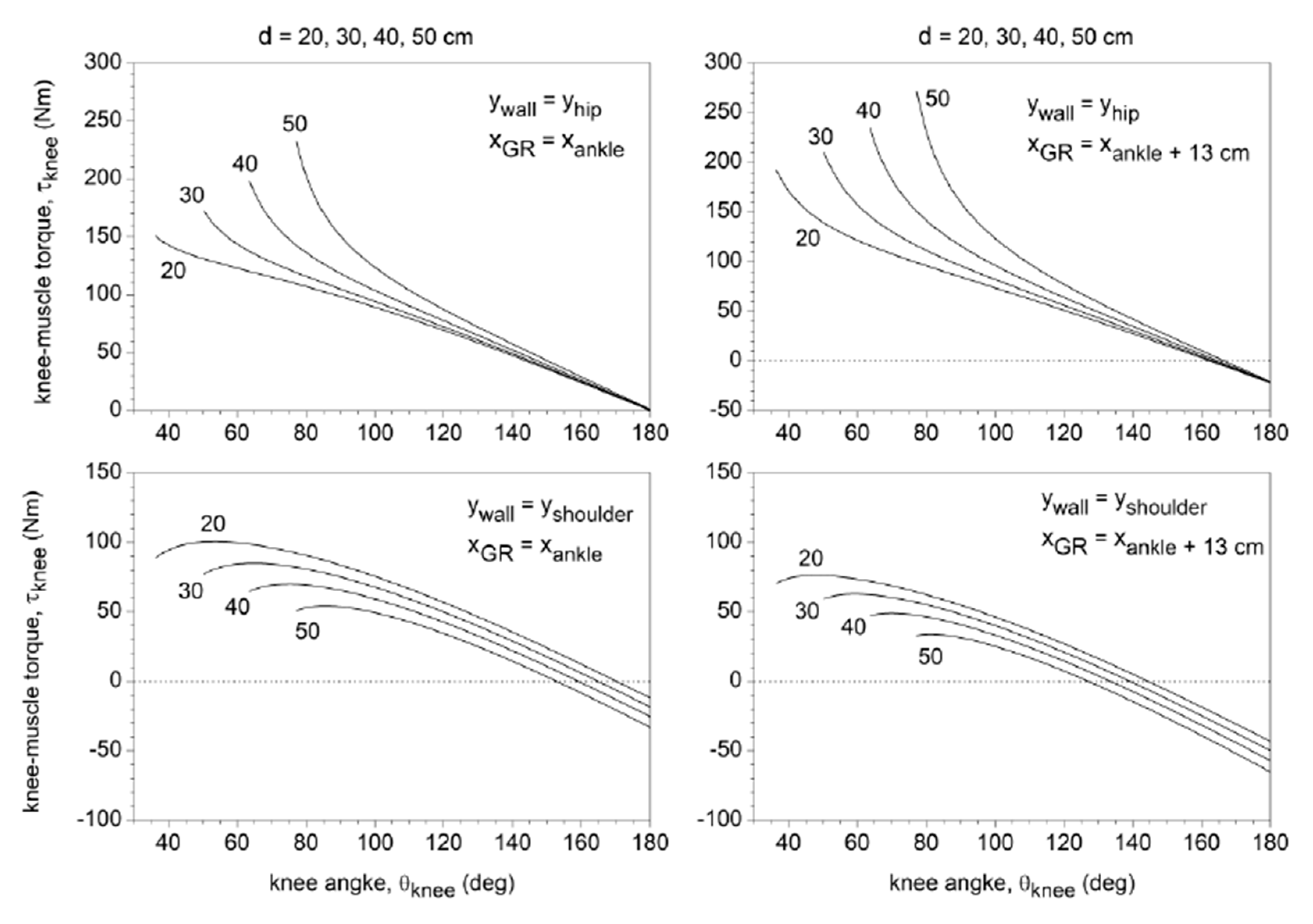
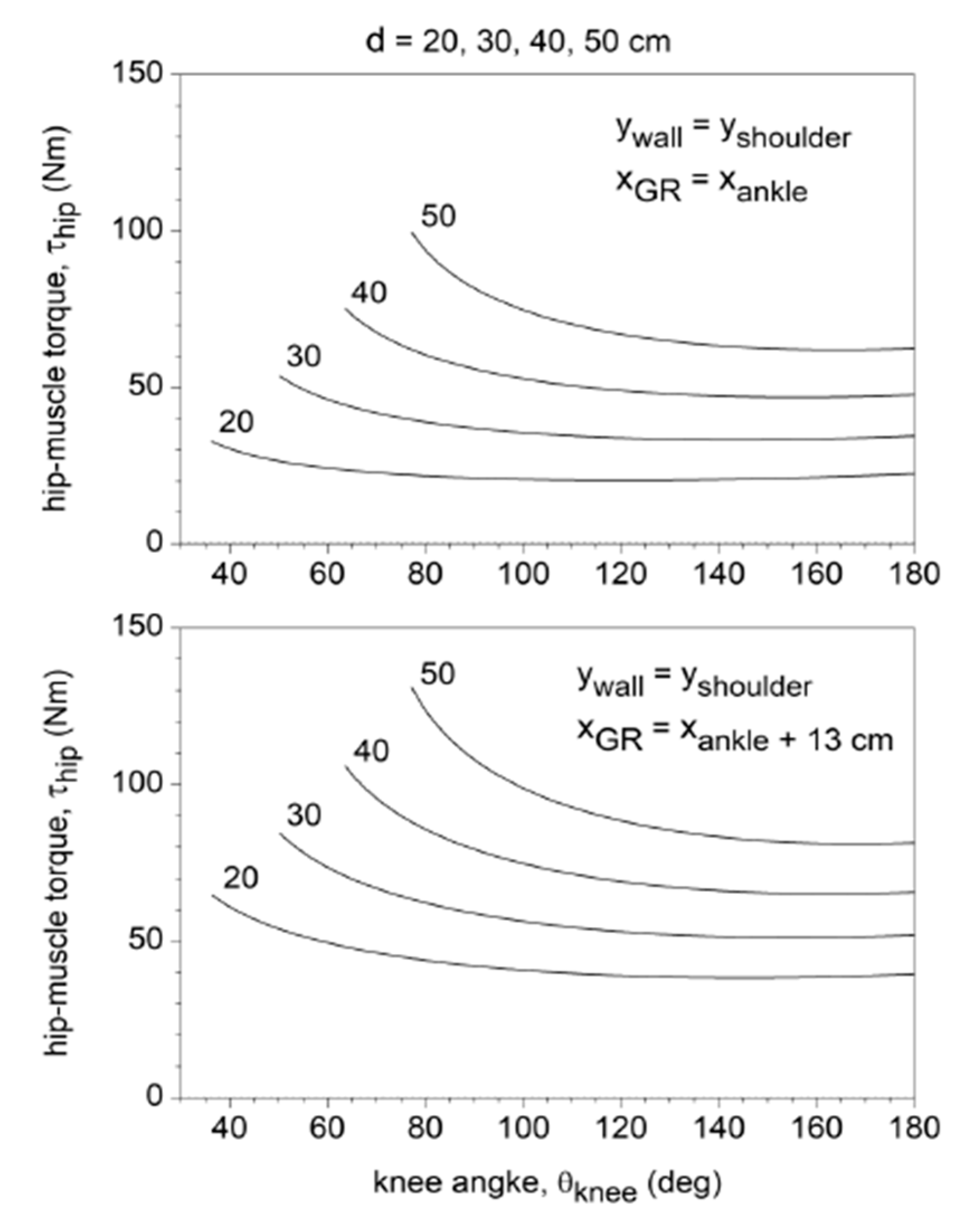
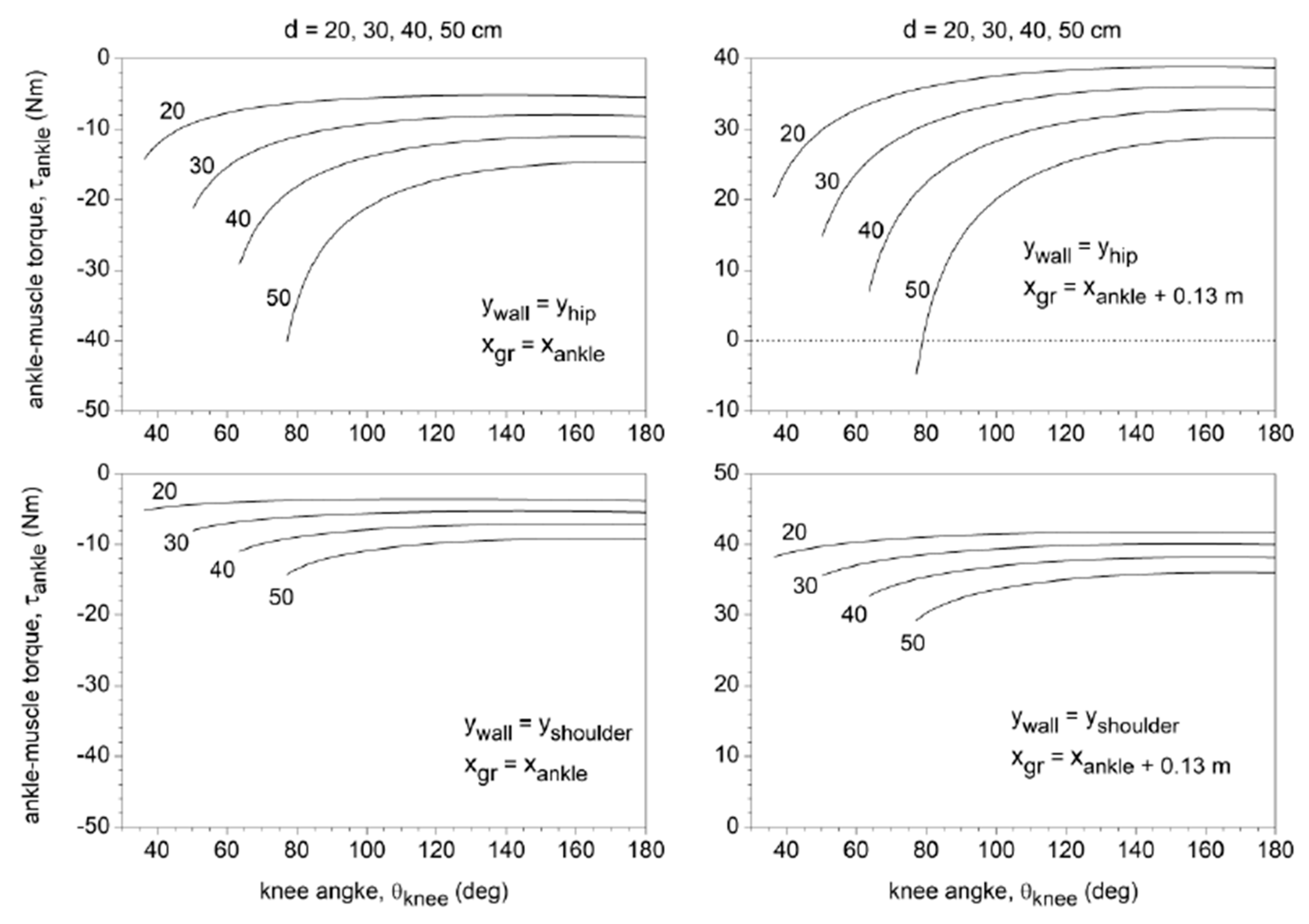
Torque Type	Maximum Torque	Conditions for Maximum Torque				Peak Isokinetic Torque of Males (Females)
		Knee Angle	Distance d	Type of Support	Body Weight at Forefoot/Rearfoot
Hip extension torque	130 Nm	80°	50 cm	scapular	forefoot	177 Nm (110 Nm)
Knee extension torque	250 Nm	80°	50 cm	pelvic	forefoot	268 Nm (176 Nm)
Knee flexion torque	65 Nm	0°	50 cm	scapular	forefoot	171 Nm (110 Nm)
Ankle plantar-flexion torque	40 Nm	0°	50 cm	scapular/pelvic	forefoot	171 Nm (108 Nm)
Ankle dorsi-flexion torque	40 Nm	80°	20 cm	pelvic	rearfoot	33 Nm (26 Nm)

displays the maximum values of the joint torques and the corresponding exercise conditions.

3.4. TF Shear Force

A posterior (PCL-loading) TF shear force (${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}>0$) is developed for $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, in the whole range of knee angles, and for $x_{\mathrm{GR}}=x_{\mathrm{ankle}}$, when ${\mathsf{\theta }}_{\mathrm{knee}} \ge 45°$ (Figure 6). An anterior (ACL-loading) TF shear force (${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}<0$) may only occur for $x_{\mathrm{GR}}=x_{\mathrm{ankle}}$ and ${\mathsf{\theta }}_{\mathrm{knee}}<45°$. However, the peak value of this force (occurring at 25° of knee flexion for $y_{\mathrm{wall}}=y_{\mathrm{hip}}$) is always smaller than 60 N.

4. Discussion

This study provides a quantitative biomechanical analysis of the static wall squat with all relevant exercise variants: (1) the distance of the heels from the wall (more precisely, the horizontal distance d of the ankle from the hip); (2) the whole set of possible body configurations at each distance d, which are determined by the corresponding values of the knee angle ${\mathsf{\theta }}_{\mathrm{knee}}$; (3) a voluntary shift between the rearfoot and forefoot of the centre of pressure $x_{\mathrm{GR}}$ of the ground reaction force; (4) a voluntary shift between the scapular and pelvic zone of the centre of pressure $y_{\mathrm{wall}}$ of the force exerted by the wall on the back.

Figure 2 highlights that the ankle and hip angles corresponding to a given degree of knee flexion can be readily modulated by changing the distance d. For example, placing the feet at progressively greater distance from the wall, while keeping the knee angle unchanged, yields a progressive increase in hip flexion. This information is relevant, because high levels of hip flexion are mechanically linked with posterior pelvic tilt and lumbar spine flexion (hip-lumbo-pelvic rhythm) [16]. Decrease of the lumbar lordosis beyond the neutral zone [17] should be avoided in weight bearing condition. Furthermore, a limitation in ankle dorsiflexion mobility can considerably limit the maximum degree of knee flexion when the feet are placed near the wall due to the mechanical constraint imposed by the wall. Higher values of d are advisable with this limitation.

Figure 3, Figure 4 and Figure 5 highlight that the knee, hip, and ankle muscle torque (${\mathsf{\tau }}_{\mathrm{knee}}$,${\mathsf{\tau }}_{\mathrm{hip}}$, ${\mathsf{\tau }}_{\mathrm{ankle}}$) can be finely modulated by changing the values of $d$,${\mathsf{\theta }}_{\mathrm{knee}}$, $y_{\mathrm{wall}}$, and $x_{\mathrm{GR}}$. Considerable levels of hip-extension muscle torque ${\mathsf{\tau }}_{\mathrm{hip}}$ are only reached by shifting the point of application of the wall force towards the scapular zone and placing the feet at a greater distance from the wall. With the additional conditions ${\mathsf{\theta }}_{\mathrm{knee}} ~ 80°$ and $x_{\mathrm{GR}}=x_{\mathrm{ankle}}+13 \mathrm{cm}$, ${\mathsf{\tau }}_{\mathrm{hip}}$ takes its maximum value of about 130 Nm. This torque level is relevant, given that the average maximal-effort hip extensor torque (measured isokinetically at 30°/s and averaged over the whole range of hip motion) developed by healthy males is about 180 Nm [16]. Notably, the corresponding value of knee-extension muscle torque ${\mathsf{\tau }}_{\mathrm{knee}}$ is about 30 Nm. Thus, the bodyweight wall squat, when adequately managed, may constitute an effective strengthening exercise for the hip (and lumbar spine) extensor muscles with negligible involvement of the knee muscles.

Contrary to the free squat, either an ankle plantarflexion or dorsiflexion torque is needed to hold a static wall-squat position, depending on the point of application of the ground reaction force ($x_{\mathrm{GR}}$ at forefoot or rearfoot). In the free squat, the ankle plantarflexion torque is always need, as the weight of the body should be uniformly distributed between the rearfoot and forefoot ($x_{\mathrm{GR}}$ at midfoot) and the ground reaction is vertical ($R_{\mathrm{GR}x}=0$) [7]. Interestingly, the wall squat constitutes a bodyweight closed-kinetic-chain (CKC) exercise that might enable an effective strengthening of the ankle dorsiflexor muscles. CKC exercises are frequently used in rehabilitation as weight-bearing, which is a typical condition of CKC exercises, stabilizes the joints and protects ligaments [13,14].

The muscle torque at the knee can be of extension or flexion type, depending on the selected variants. Specifically, the wall squat performed in the last 30° of knee extension, leaning against the wall with only the scapular zone ($y_{\mathrm{wall}}=y_{\mathrm{shoulder}}$), and placing the feet away from the wall, constitutes a CKC exercise for strengthening of the knee flexor muscles (${\mathsf{\tau }}_{\mathrm{knee}}<0$). Conversely, the knee-extension muscle torque developed for $y_{\mathrm{wall}}=y_{\mathrm{hip}}$, ${\mathsf{\theta }}_{\mathrm{knee}} ~ 80°$, and $d=50 \mathrm{cm}$ reaches a value as high as 250 Nm, which nearly coincides with the peak torque potential of the knee extensor muscles [15,18]. However, this wall-squat setup entails an extreme body position, with the hips nearly in full flexion (${\mathsf{\theta }}_{\mathrm{hip}}=60°$), 26 cm above the ground, and 22 cm below the level of the knees. In this condition (i.e., hip below the knee level and $y_{\mathrm{wall}}=y_{\mathrm{hip}}$) the quadriceps torque is maximized because the wall force ${\overrightarrow{F}}_{\mathrm{wall}}$ yields a knee-flexion torque, which adds to the knee-flexion torque developed by weight of the body (more precisely, by the weight of the portion of the body above the knee joints).

This study highlights that low levels (about 60 N) of ACL-loading TF shear force (${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}$) may be developed in the final 45° of knee extension when $x_{\mathrm{GR}}=x_{\mathrm{ankle}}$. However, these values of ${\mathsf{\phi }}_{\mathrm{TF},\mathrm{shear}}$ have been calculated assuming that a net knee-extension muscle torque (${\mathsf{\tau }}_{\mathrm{knee}}>0$) is produced only by the quadriceps, in absence of hamstring cocontraction. Thus, as explained in the methods section, they should be considered as the maximum theoretical limit of ACL-loading TF shear force that might occur during the bodyweight wall-squat exercise. Nevertheless, due to the reduced equilibrium and stability demand induced by wall support and absence of external resistance, low cocontraction hamstring activity is expected when ${\tau }_{\mathrm{knee}}>0$ and ${\mathsf{\theta }}_{\mathrm{knee}}<45$.

This study could have important practical applications in training and rehabilitation interventions. With the use of Figure 3, Figure 4 and Figure 5, trainers and physiotherapists might readily manage the wall-squat exercise conditions ($d$,${\mathsf{\theta }}_{\mathrm{knee}}$, $y_{\mathrm{wall}}$, and $x_{\mathrm{GR}}$) to finely modulate the lower-limb joint torques up to the their maximum values reported in Table 1. Interestingly, contrary to the free squat, the joint toques can be regulated, to a large extent, independently from one another. Figure 6 clearly highlights that anterior tibial pull forces can be avoided, even near full knee extension, in specific exercise conditions. Therefore, if adequately managed, then the wall squat exercise can be safely used in rehabilitation interventions after anterior cruciate ligament injury or reconstruction.

The main limitation of this study stems from the lack of information related to the mechanical loading directly acting on the ACL. Advanced 3D models that fully consider the soft tissue structures of the knee and the complex geometry of the articular surfaces are necessary to estimate how the net TF shear force is distributed among the different knee structures, including the ACL [19,20,21]. However, the adopted simplified model may be considered adequate for the specific purpose of the study, which concerns the determination of the joint torques and the overall TF shear force acting in the sagittal plane during all the possible wall-squat positions and variants. Escamilla and co-workers estimated the cruciate ligament and patellafemoral force during the dynamic wall squat performed with a 12-repetition-maximum external resistance provided by a dumbbell weight held in both hands [22,23]. In this loading condition, the wall squat generates negligible ACL tensile force. This result is consistent with the findings of the present study that revealed only low values of maximum theoretical ACL-loading TF shear force in a very limited range of wall-squat conditions. In addition, this limited anterior tibial pull can in part be resisted by knee structures other than the ACL, as well as by the active and passive force developed by the hamstrings [24].

Figure 2, Figure 3, Figure 4 and Figure 5 refer to an ideal subject 175 cm tall, with a body mass of 75 kg, and other anthropometric parameters deduced from extensive anatomic studies [9,10]. The data recorded from the force plates were only used to determine reliable values of the point of application ($x_{\mathrm{GR}}$) of the ground reaction force when the participants were asked to displace the body weight toward the rearfoot or forefoot. These values were rescaled for the adopted ideal subject and used in the simulation. The determination of the joint torques for each of the 20 participants would have required the knowledge of the mass, dimension, and position of centre of mass of each body segment of each individual participant (Equations (18)–(20)). Aside from acknowledging this limitation, one critical key of the provided analytical model is that it may be directly applied to any real subject when their anthropometric data is given.

5. Conclusions

This study provides an in-depth biomechanical analysis of the bodyweight wall-squat exercise, which takes in consideration all the relevant exercise variants. With the results of this study, trainers and therapists might manage the wall squat exercise to finely modulate the lower-limb joint torques and to minimize the shear component of the tibiofemoral joint reaction force.