MViDO: A High Performance Monocular Vision-Based System for Docking A Hovering AUV
Abstract
1. Introduction
- Section 1 contains a survey of the state of the art related to our work; the contributions of our work and the methodology followed for the development of the presented system.
- Section 2 contains the developed system for docking the AUV MARES using a single camera. In particular, the pose estimation method, the developed tracking system and the guidance law,
- Section 3 contains a theoretical characterization of the used set camera-target,
- Section 4 describes the developed guidance law,
- Section 5 describes the experimental setup and presents the experimental results: an experimental validation of the developed algorithms under real conditions such as the sensor noise, lens distortion and the illumination conditions,
- Section 6 contains the results of tests to the guidance law performed in a simulation environment,
- Section 7: a discussion about the results,
- Section 8: conclusions.
1.1. Related Works
- build a target composed by well identifiable visual markers,
- visually detect the target through image processing and estimate the relative pose of the AUV with regard to the target: the success of the docking process relies in accurate and fast target detection and estimation of the target relative pose,
- ensure target tracking: the success of the docking process depends on a robust tracking of the target even in situations of partial target occlusions and the presence of outliers,
- define a strategy to guide the AUV to the station’s cradle without ever losing sight of the target.
1.1.1. Vision-Based Approaches to Autonomous Dock An Auv
1.1.2. Vision-Based Related Works
1.1.3. Approaches Based on Different Sensors
1.1.4. Vision-Based Relative Localization
1.1.5. Tracking: Filtering Approaches
1.1.6. Docking: Guidance Systems
- In [27] a monocular vision guidance system is introduced, considering no distance information. The relative heading is estimated and an AUV is controlled to track a docking station axis line with a constant heading, and a traditional PID control is used for yaw control,
- In another work [28], two phases compose the final approach to the docking station: a crabbed approach where the AUV is supposed to follow the dock centerline path. The cross-track error is computed and fed-backed; and a final alignment to eliminate the contact of the AUV and the docking station.
1.2. Contributions of This Work
- A module for detection and for attitude estimate of an AUV dock station based on a single camera and a 3D target: for this purpose, a target was designed and constructed whose physical characteristics maximize its observability. The developed target is a hybrid target (active/passive) composed by spherical color markers which could be illuminated from the inside allowing to increase the visibility of the markers at a distance or in very poor visibility situations. It was also designed an algorithm for detecting the target that responds to needs of low computational cost and that can be run in low power, low size computers. A new method for estimate the relative attitude was also developed in this work.
- A novel approach for tracking by visual detection in a particle filtering framework. In order to make the pose estimation more resilient to markers occlusions, it was designed and implemented a solution based on Particle Filters that considers geometric constraints of the target and constraints of the markers in the color space. These specific approaches have improved the pose estimator performance, as presented in the results section. The innovation in our proposal for the tracking system consists of the introduction of the geometric restrictions of the target, as well as the restrictions in the color space as a way to improve the filtering performance. Another contribution is the introduction, in each particle filter, of an automatic color adjustment. This allowed not only to reduce the size of the region of interest (ROI), saving processing time, but also to reduce the likelihood of outliers.
- It was developed a method for real-time color adjustments during the target tracking process, which improves the performance of the markers detector through better rejection of outliers.
- It was designed and implemented an experimental process, with Hardware-in-the-loop, to characterize the developed algorithms.
- A guidance law was designed to guide the AUV with the aim of maximizing the target’s observance during the docking process. This law was designed from a generalist perspective and can be adapted to any system that bases its navigation on monocular vision, or another sensor whose field of view is known.
1.3. Requirements
Components Specifications
1.4. Methodology
2. Mvido: A Monocular Vision-Based System for Docking a Hovering Auv
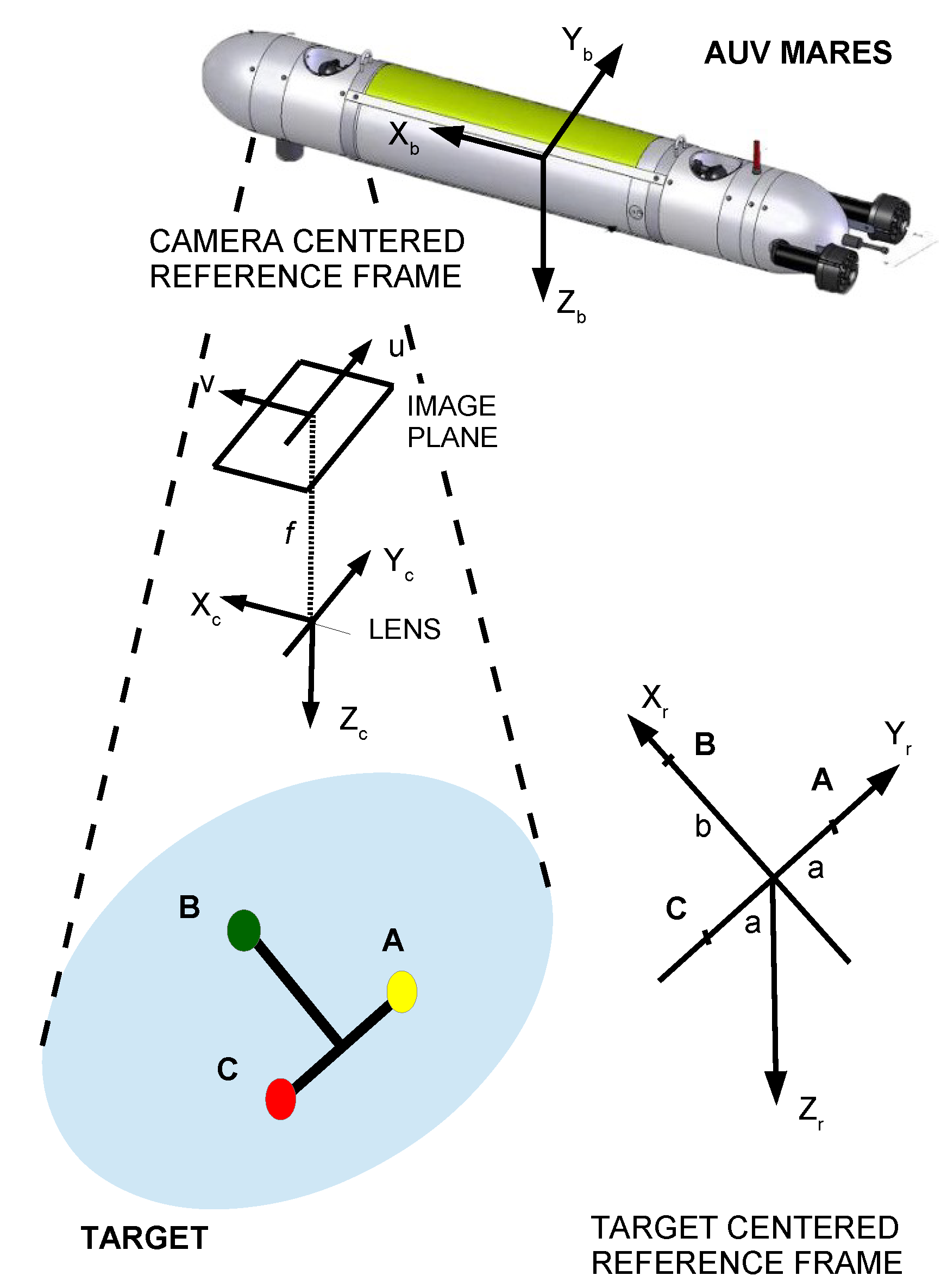
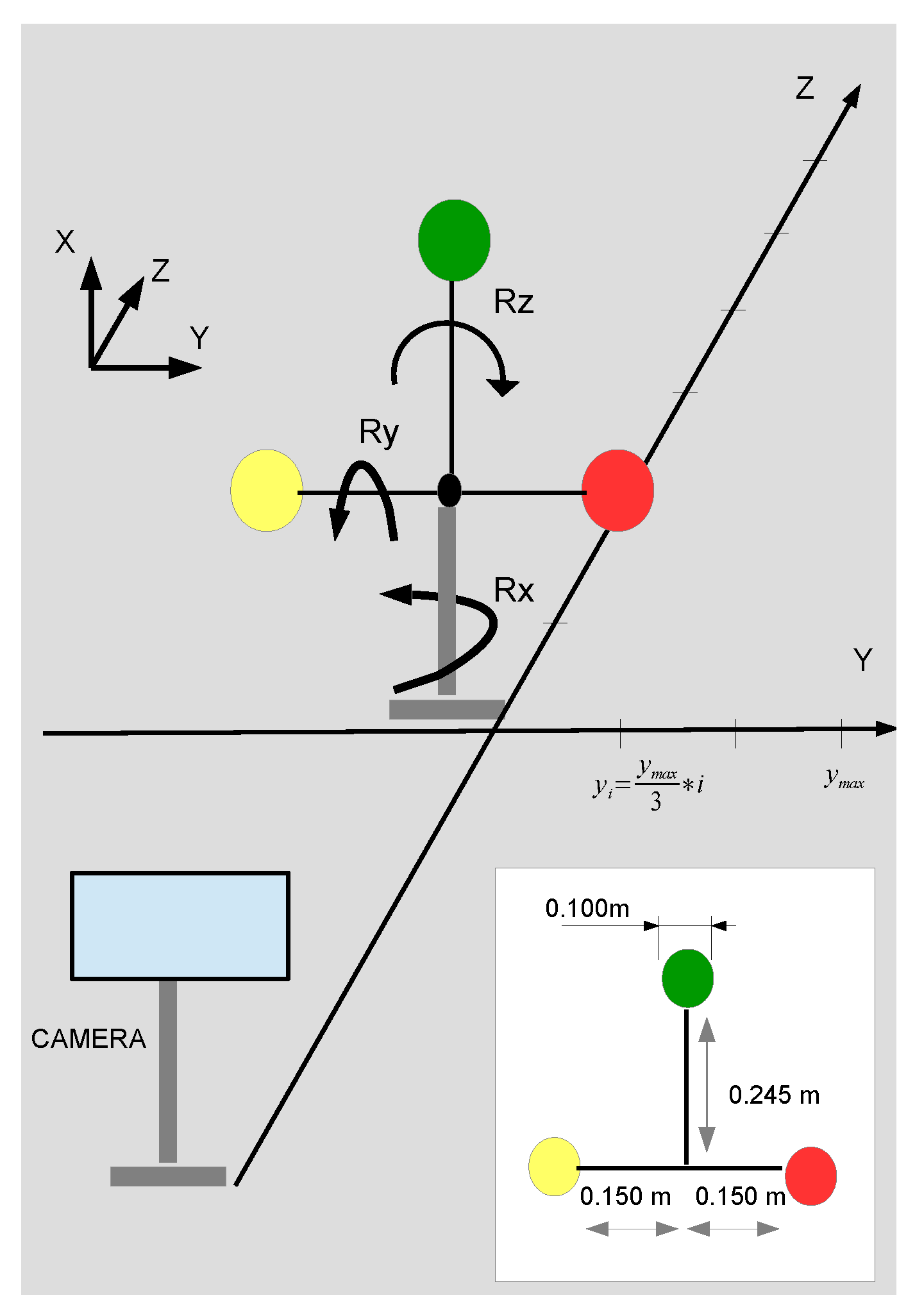
2.1. Target and Markers
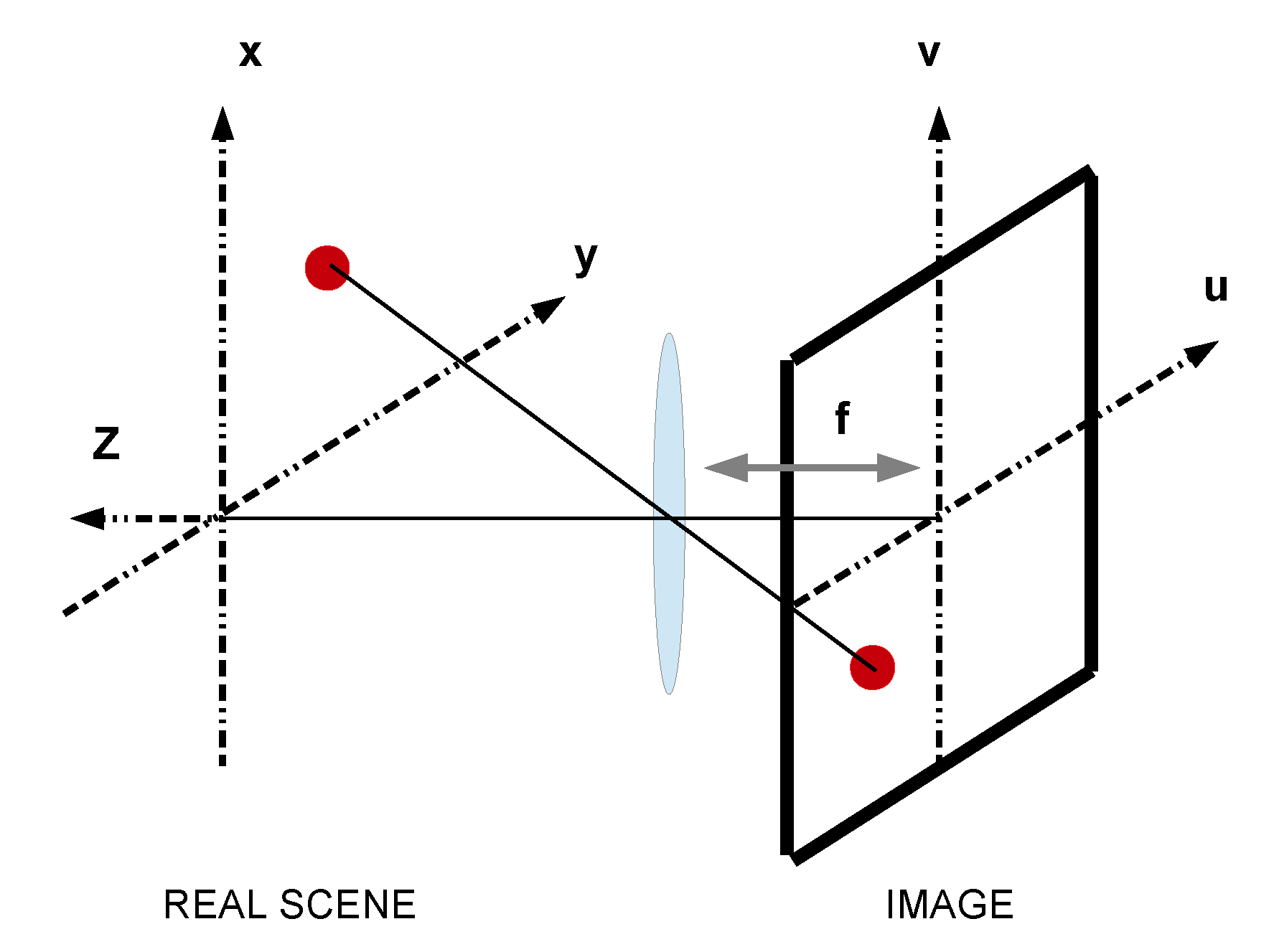
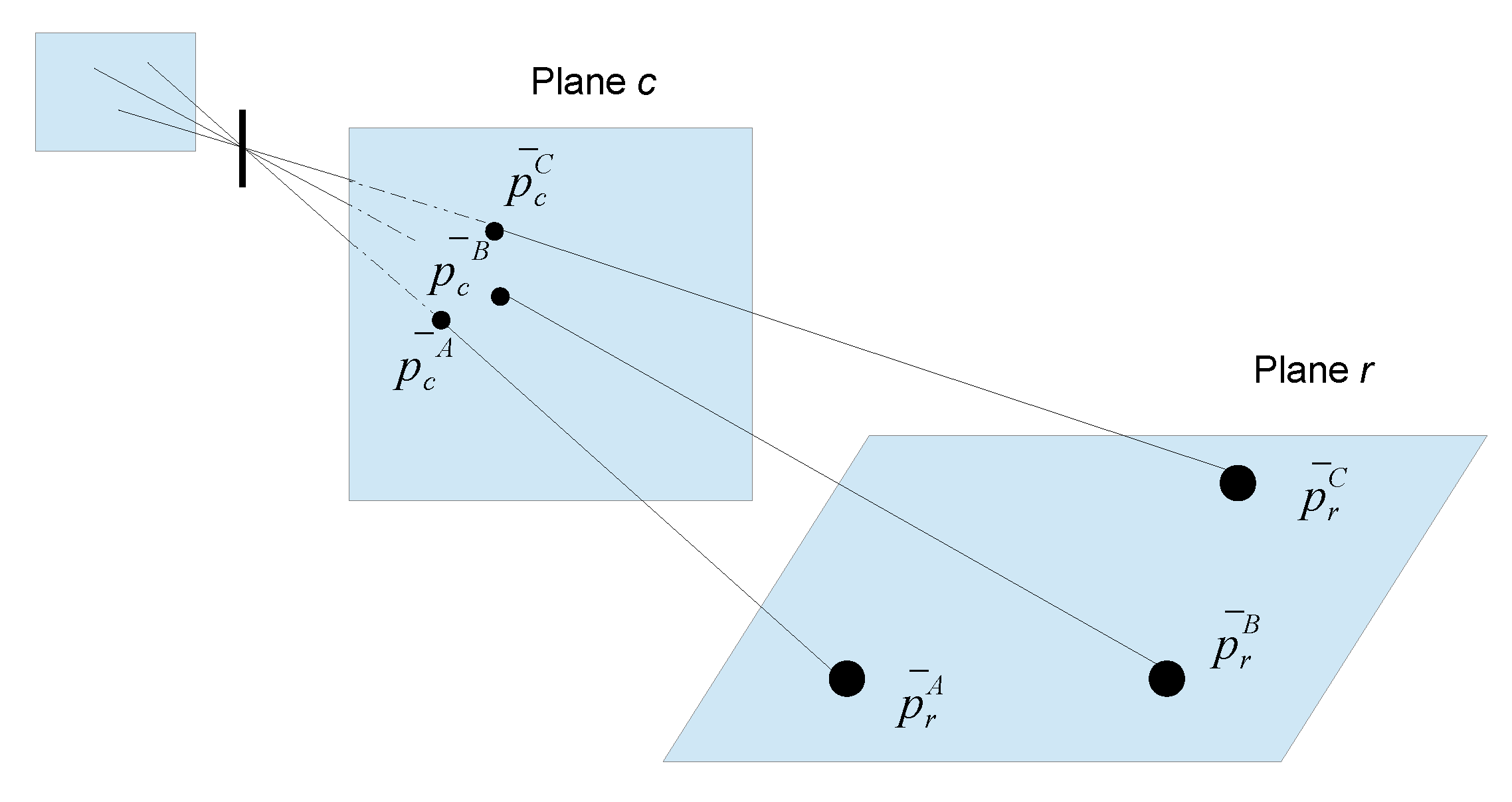
2.2. Attitude Estimator
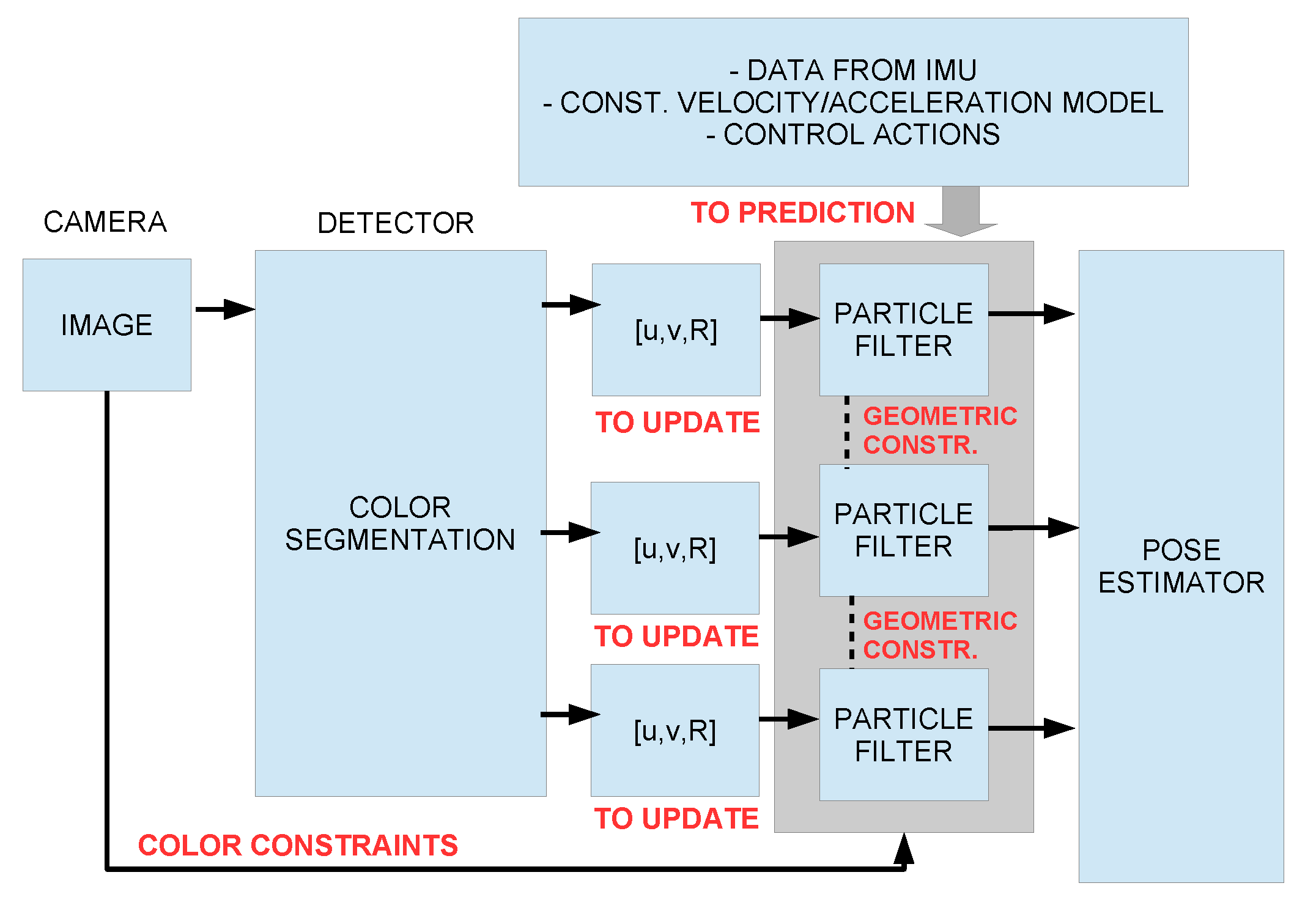
2.3. Resilience to Occlusions and Outliers Rejection
2.3.1. Problem Formulation
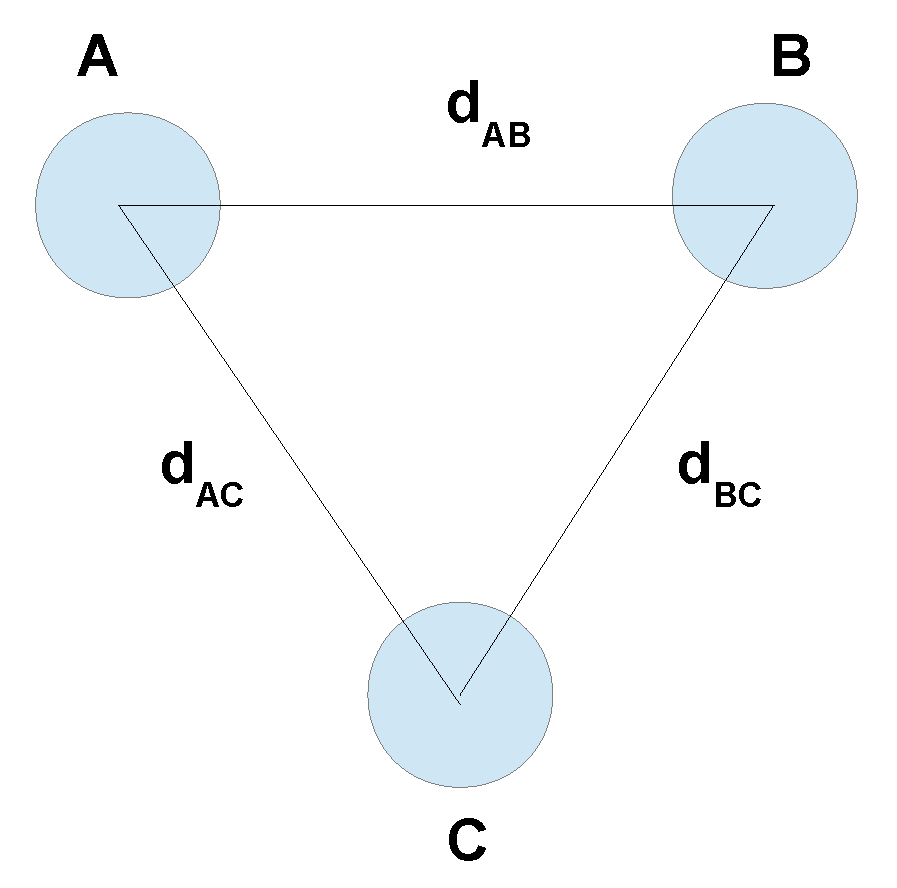
2.3.2. Considering Geometrical Constraints
2.3.3. Considering Constraints in the Color Space
2.3.4. Automatic Color Adjustment
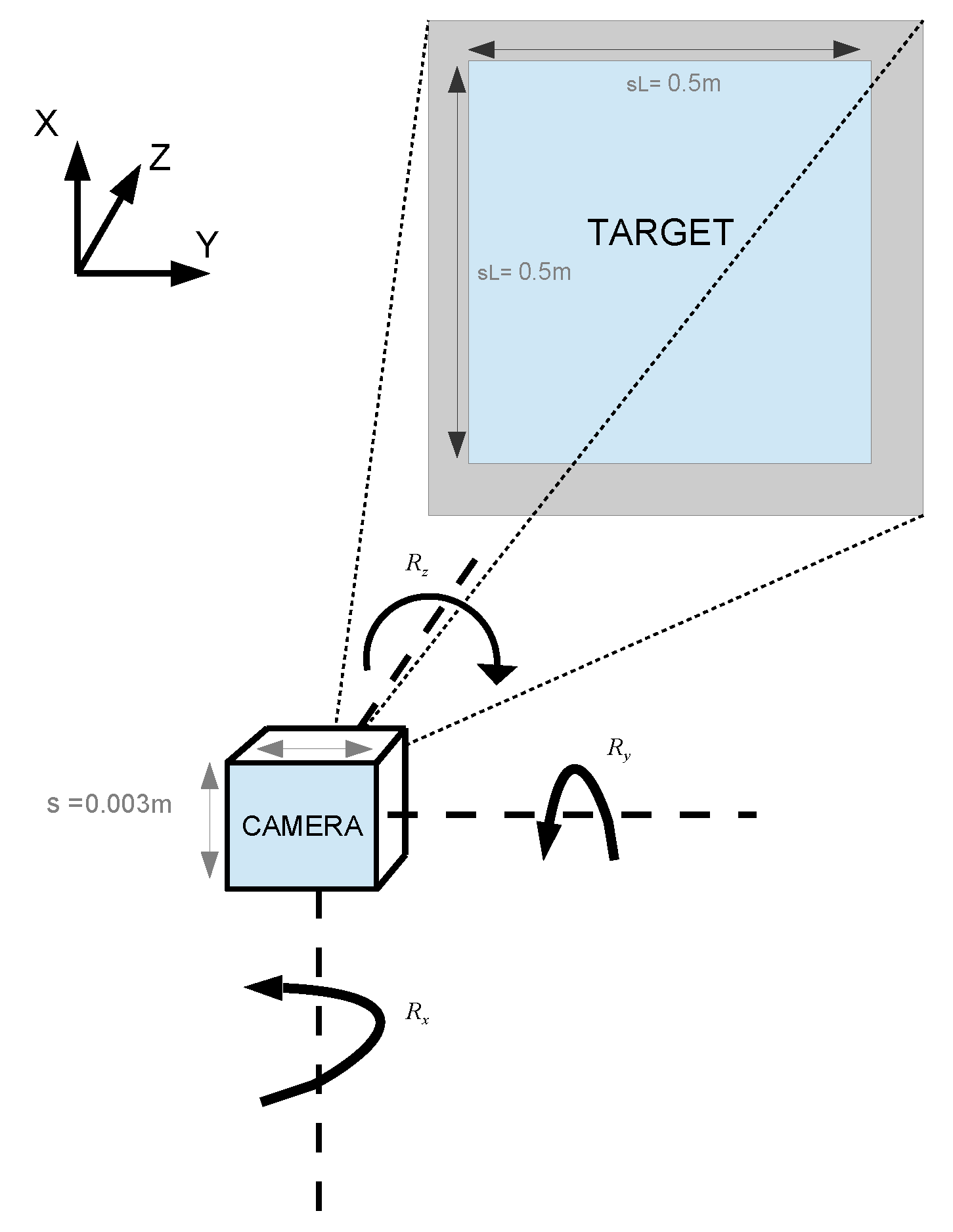
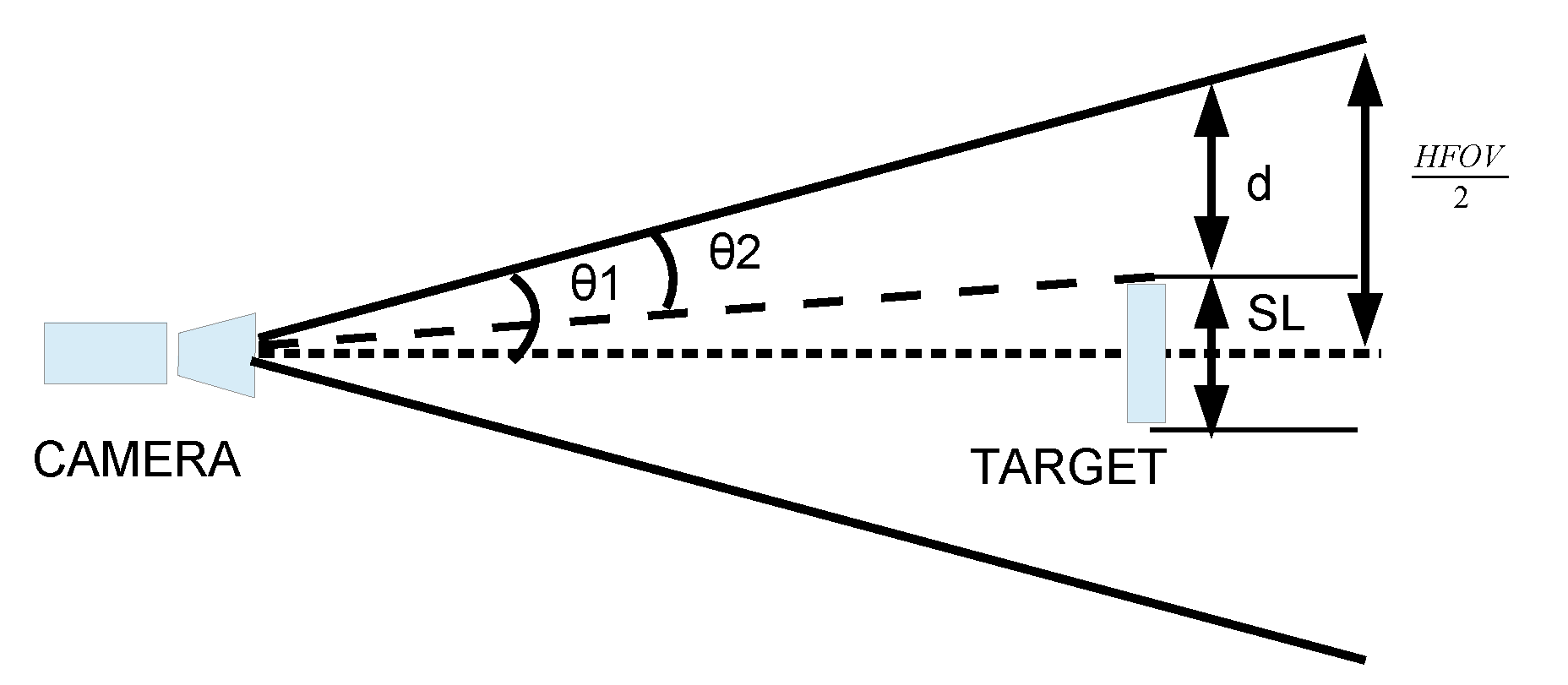
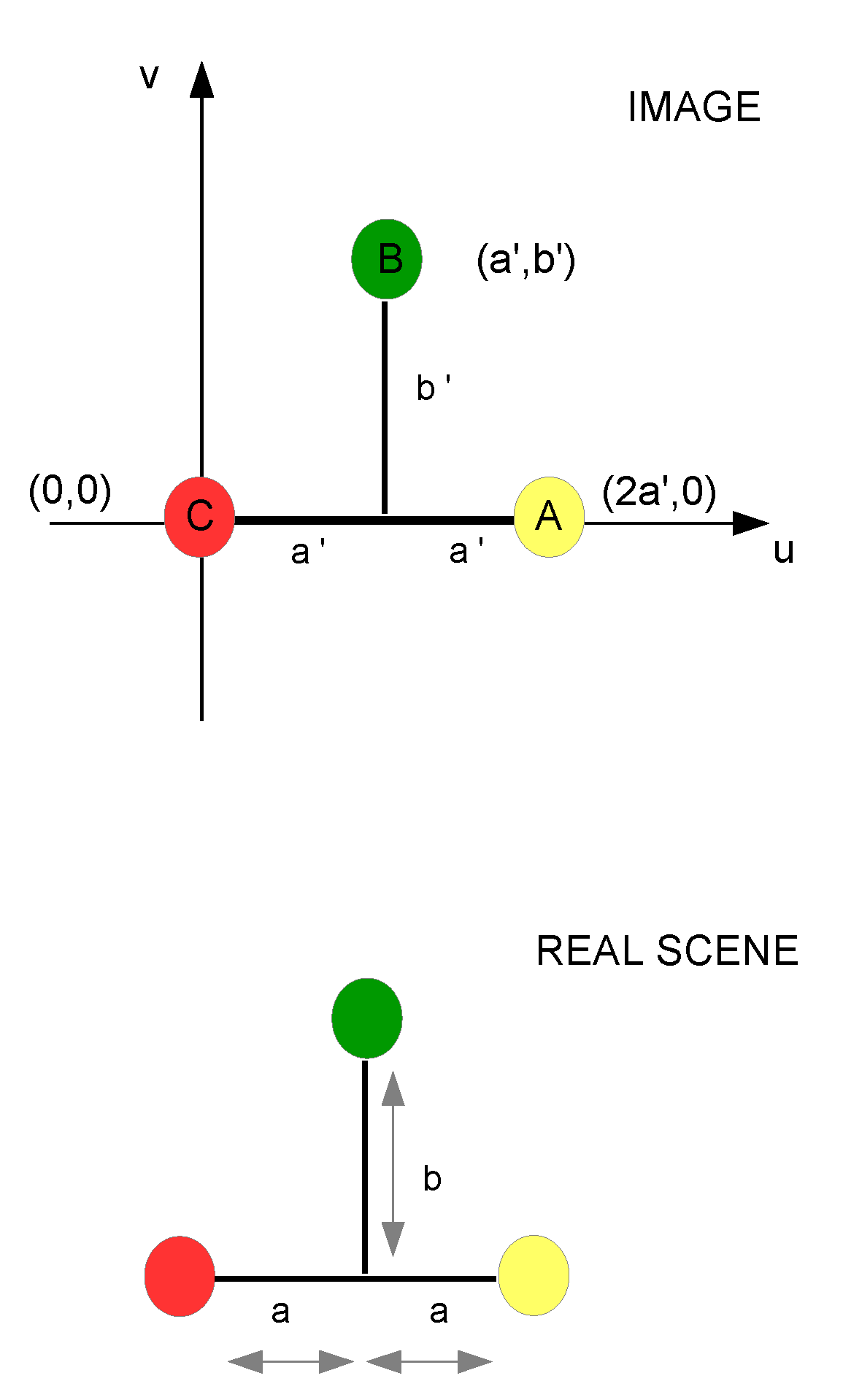
3. Mvido: Theoretical Characterization of the System Camera-Target
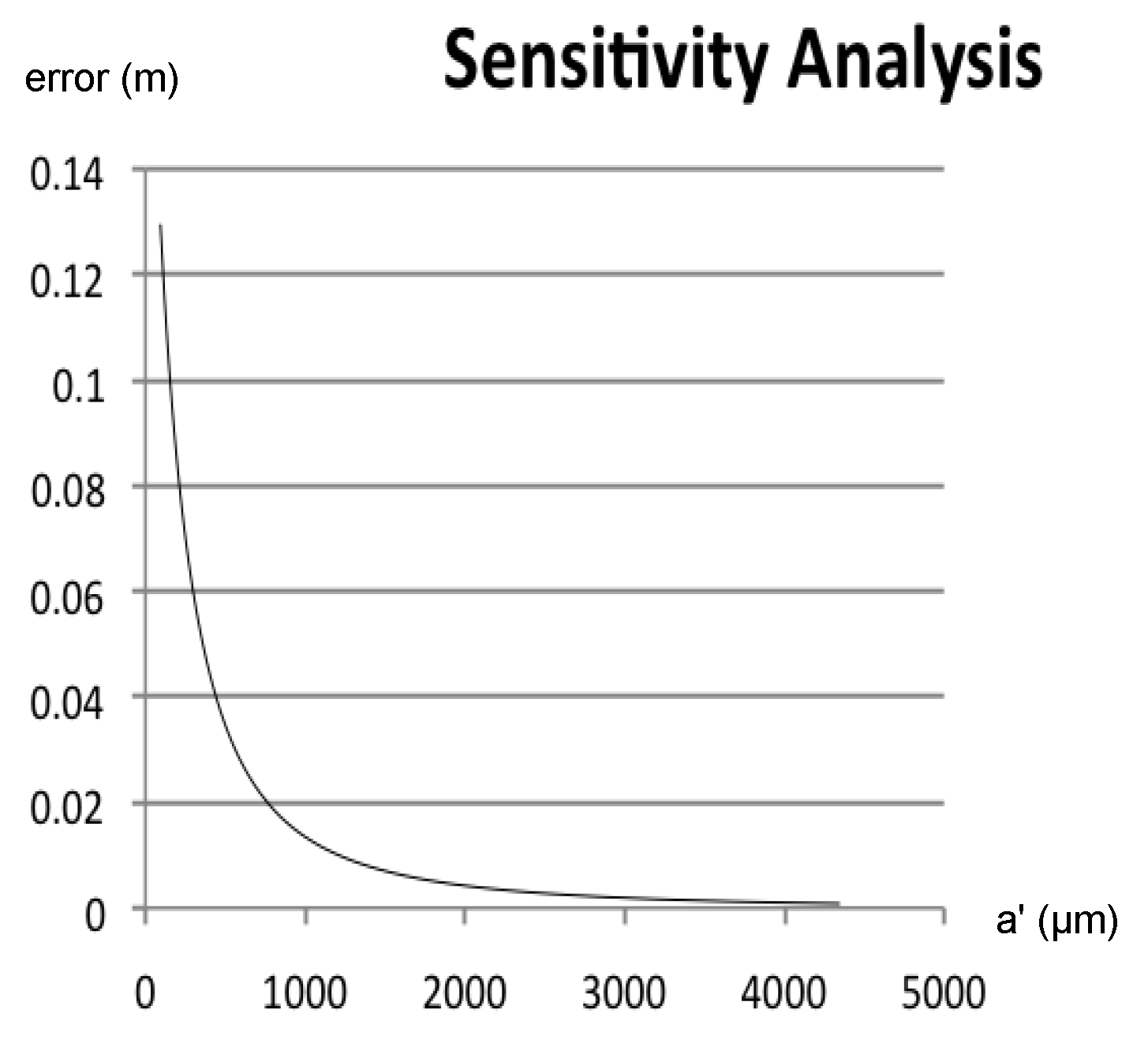
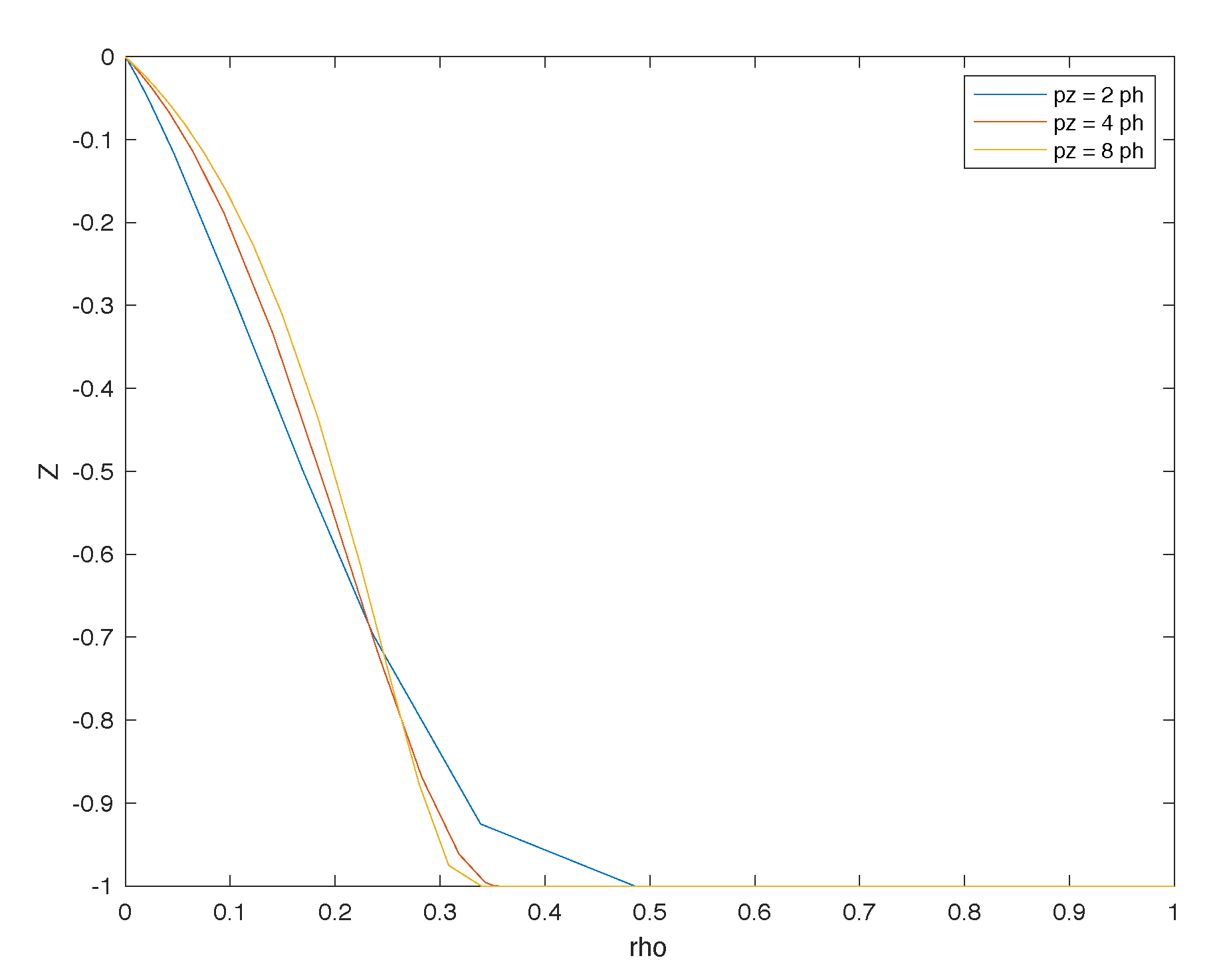
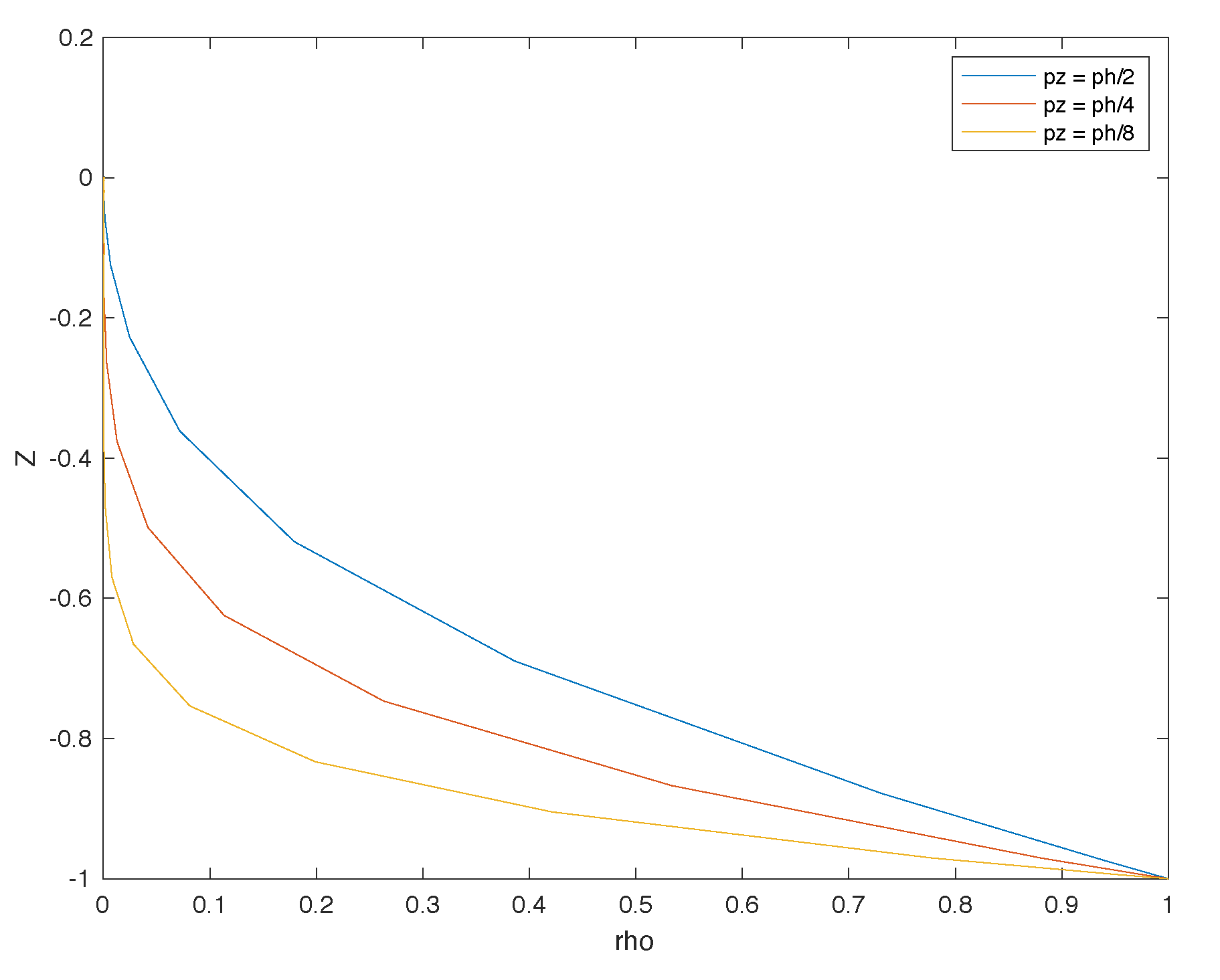
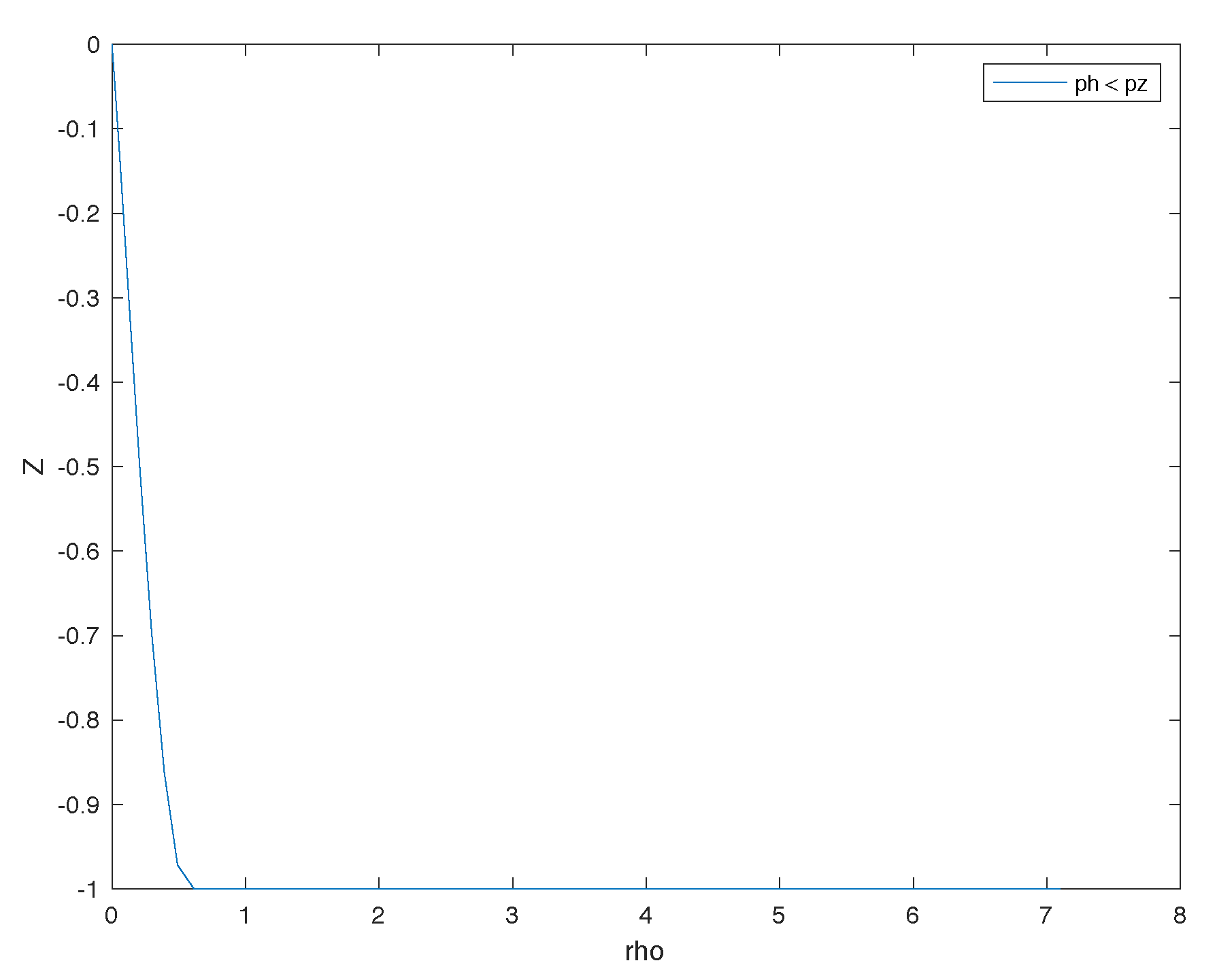
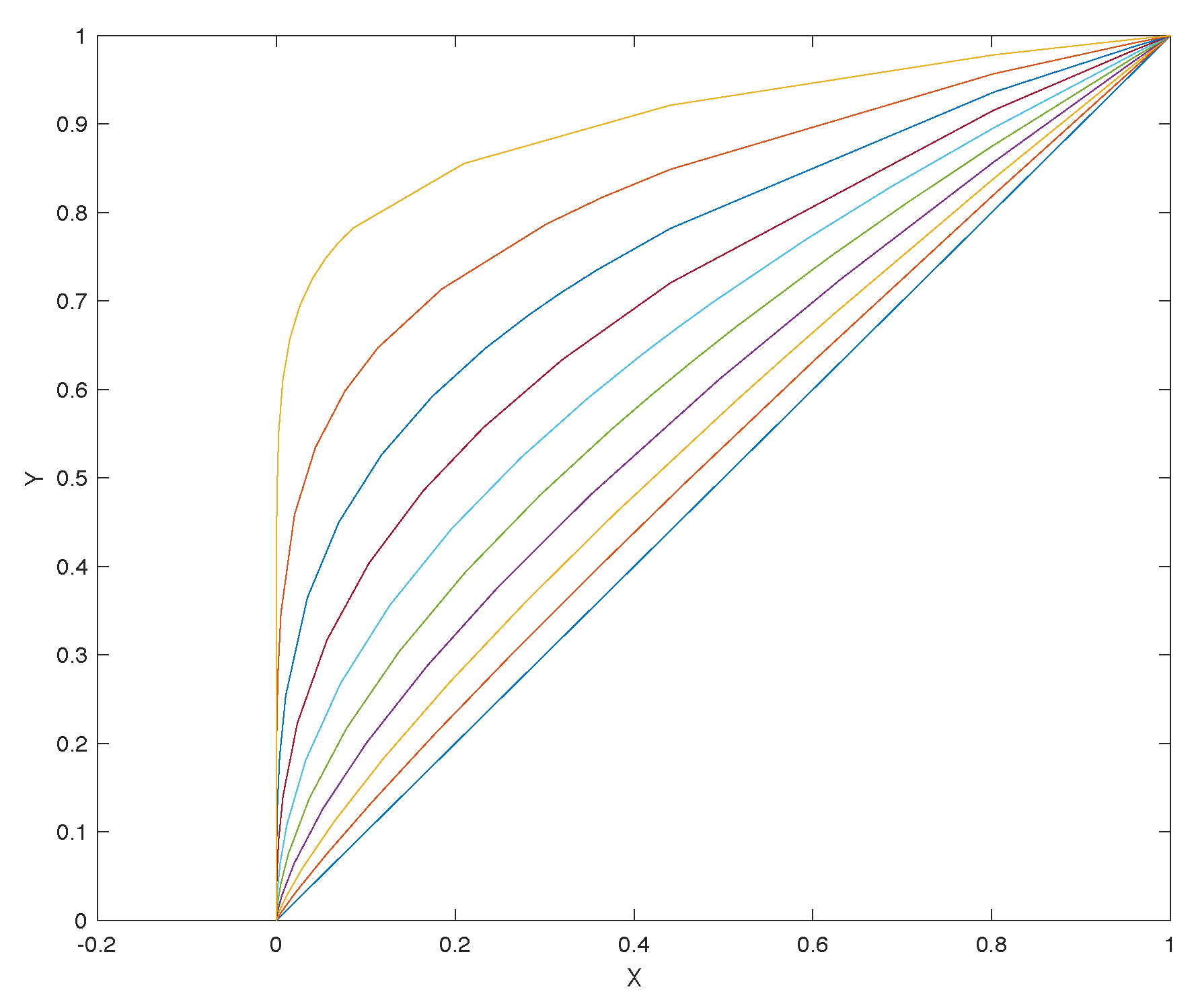
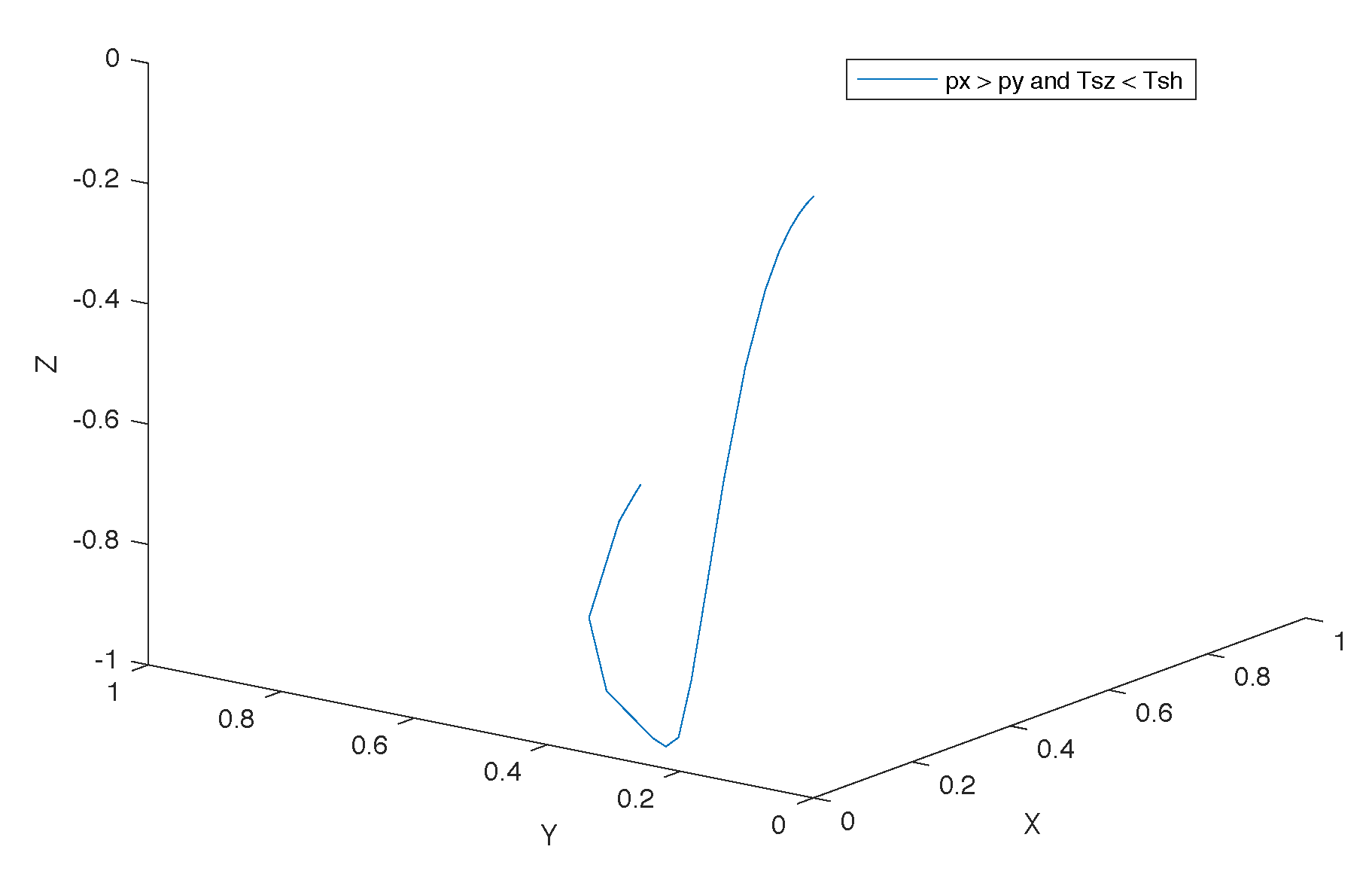
Sensitivity Analysis
4. Mvido: Guidance Law
5. Experimental Results: Pose Estimator and Tracking System
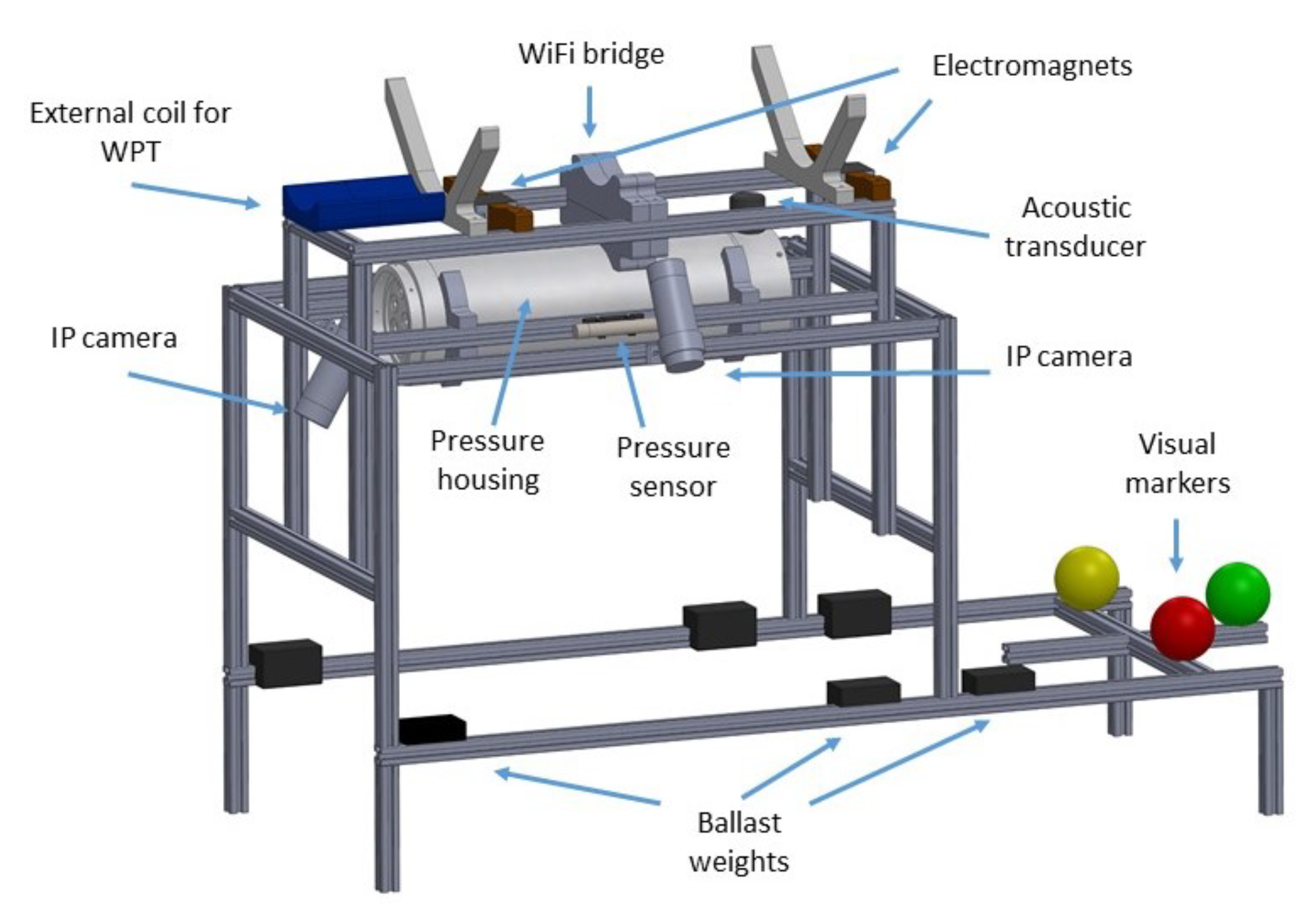
5.1. Experimental Setup
5.1.1. Pose Estimator
5.1.2. Tracking System
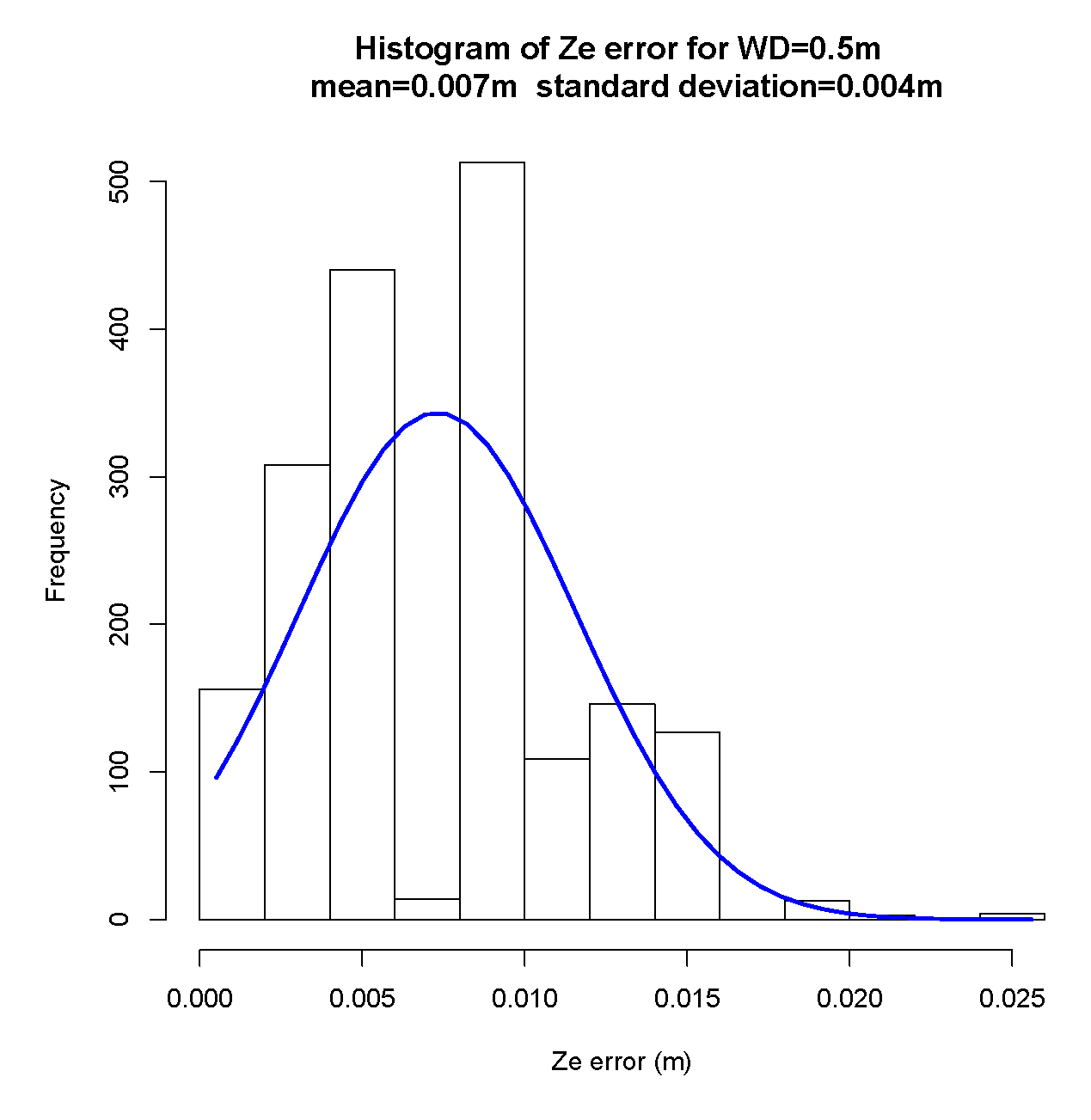
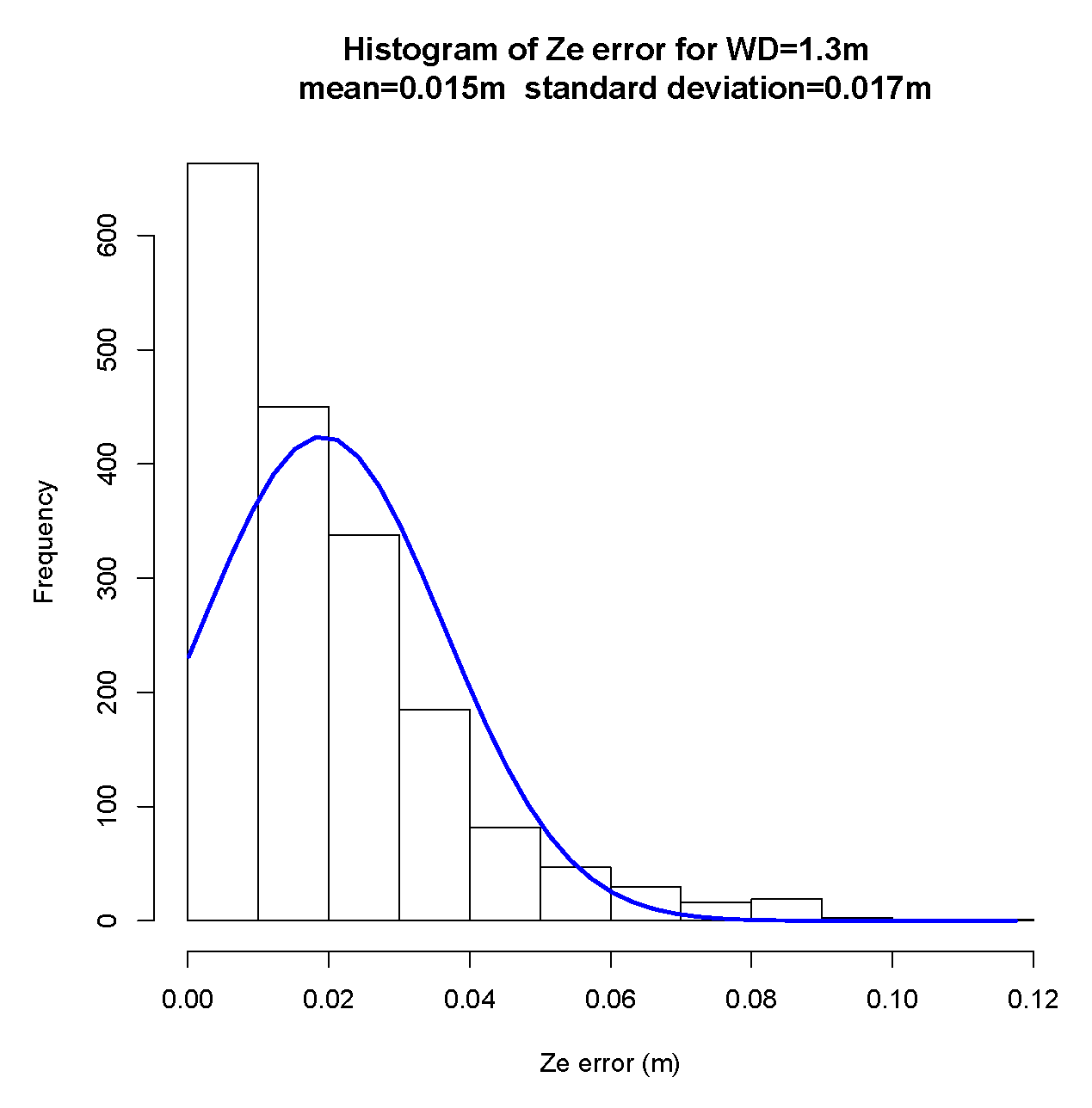
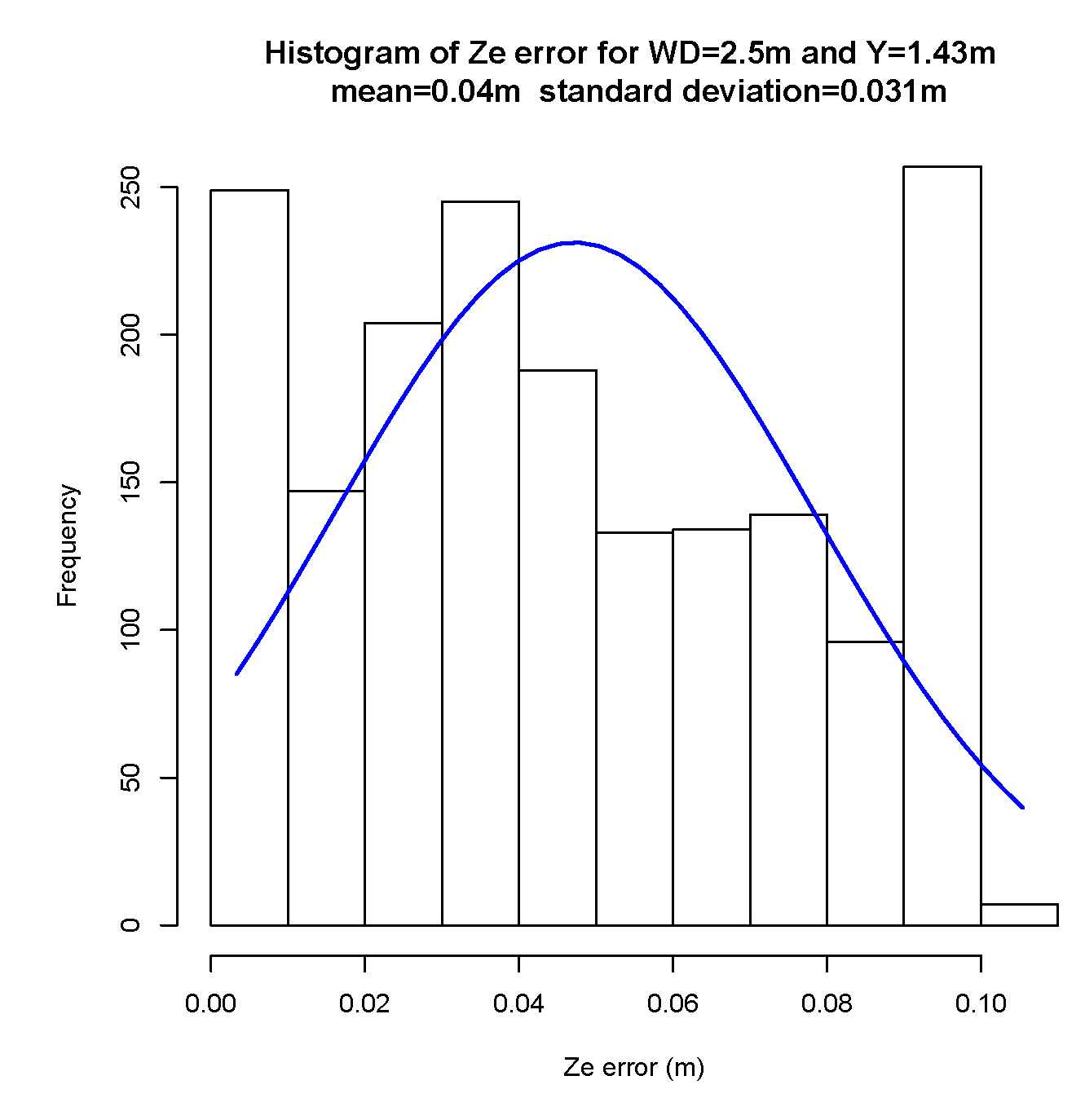
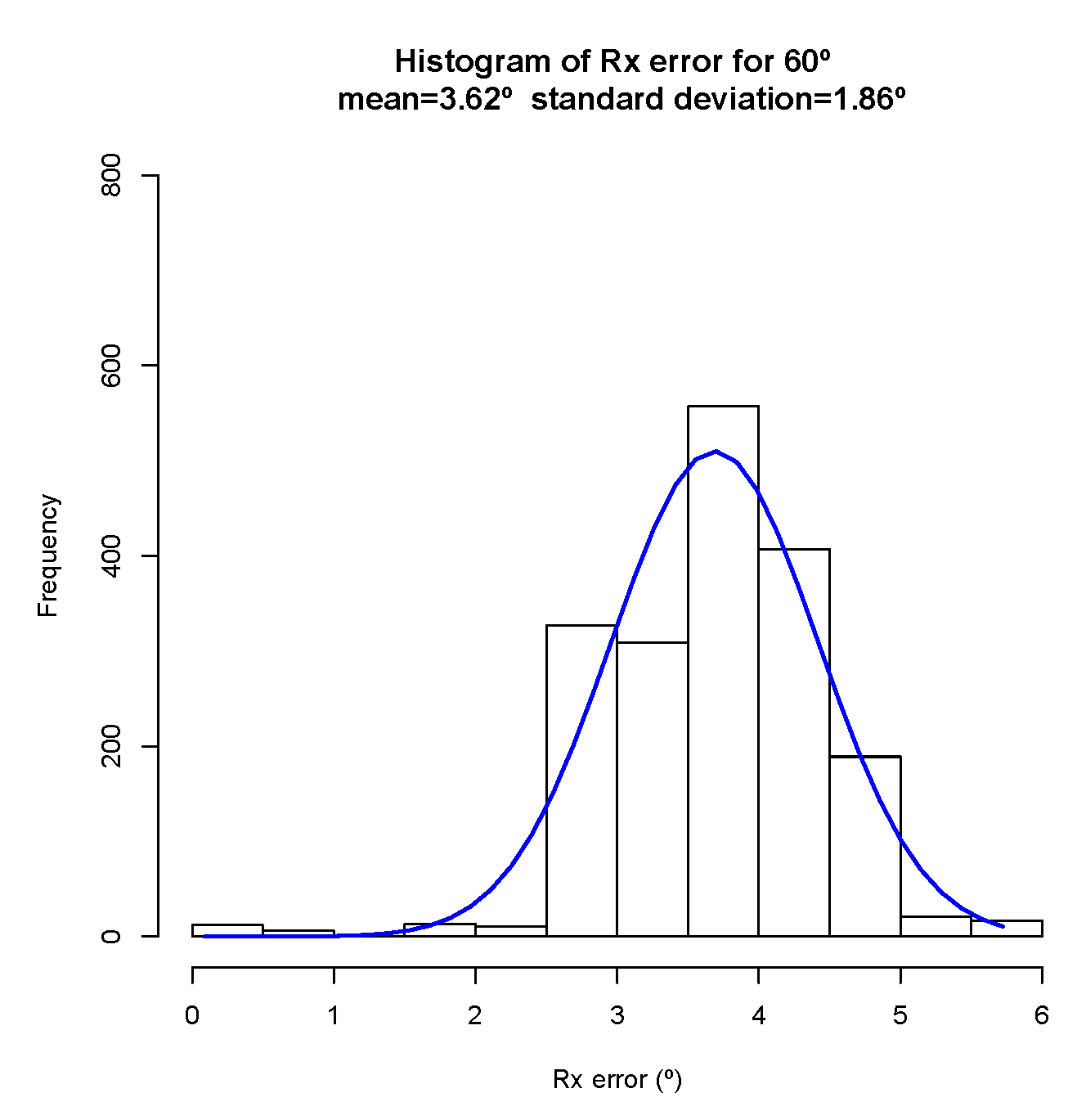
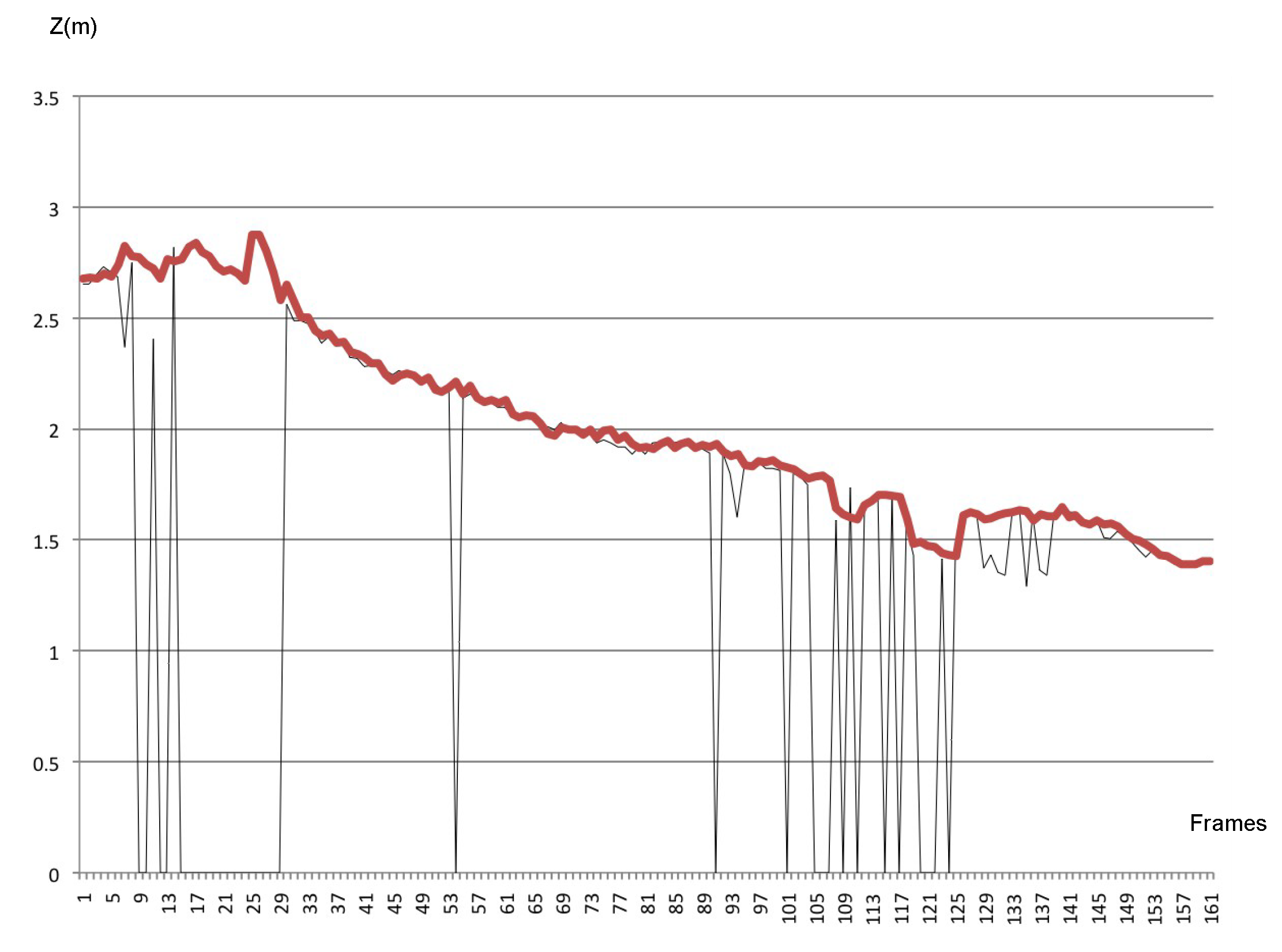
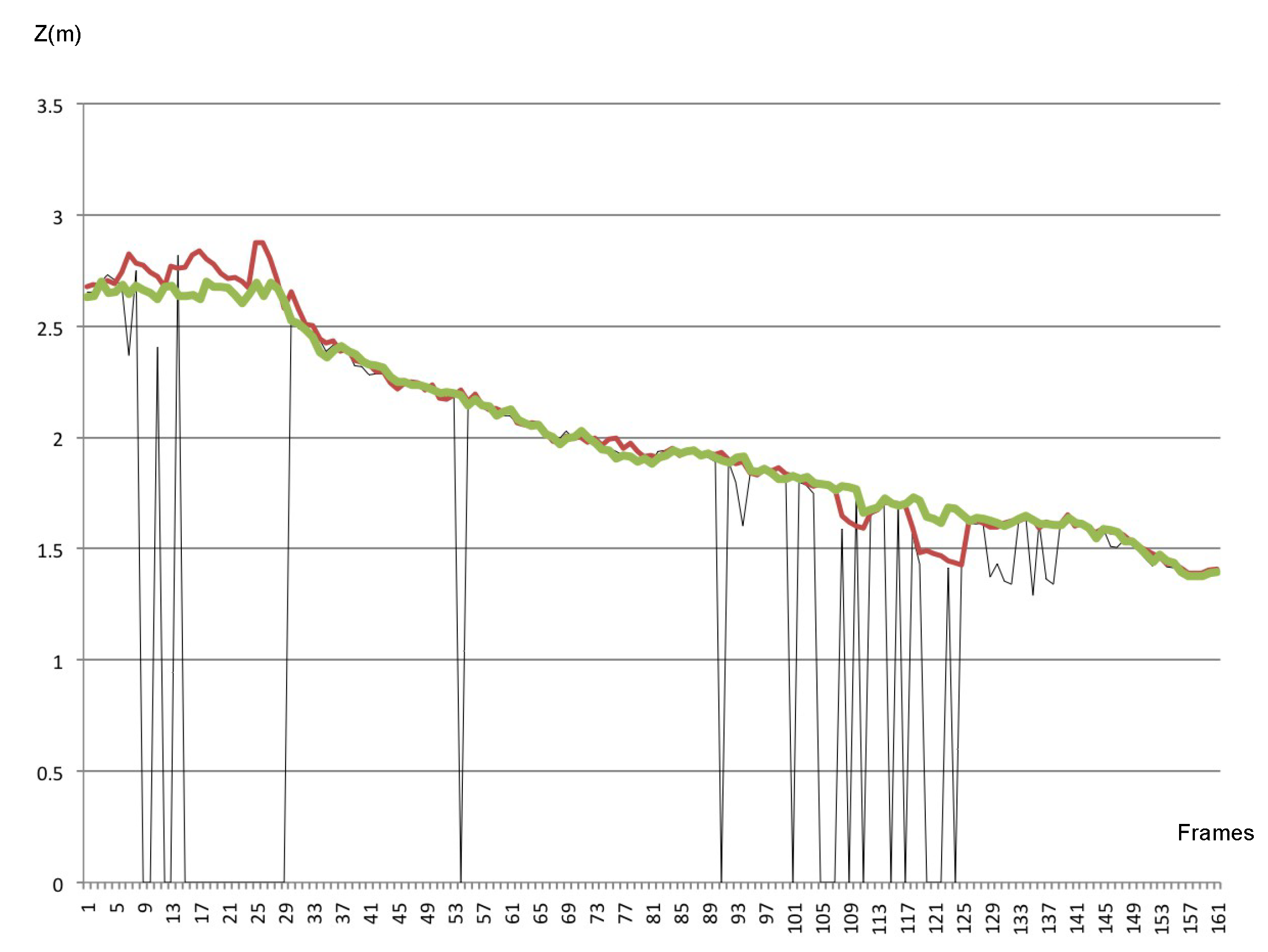
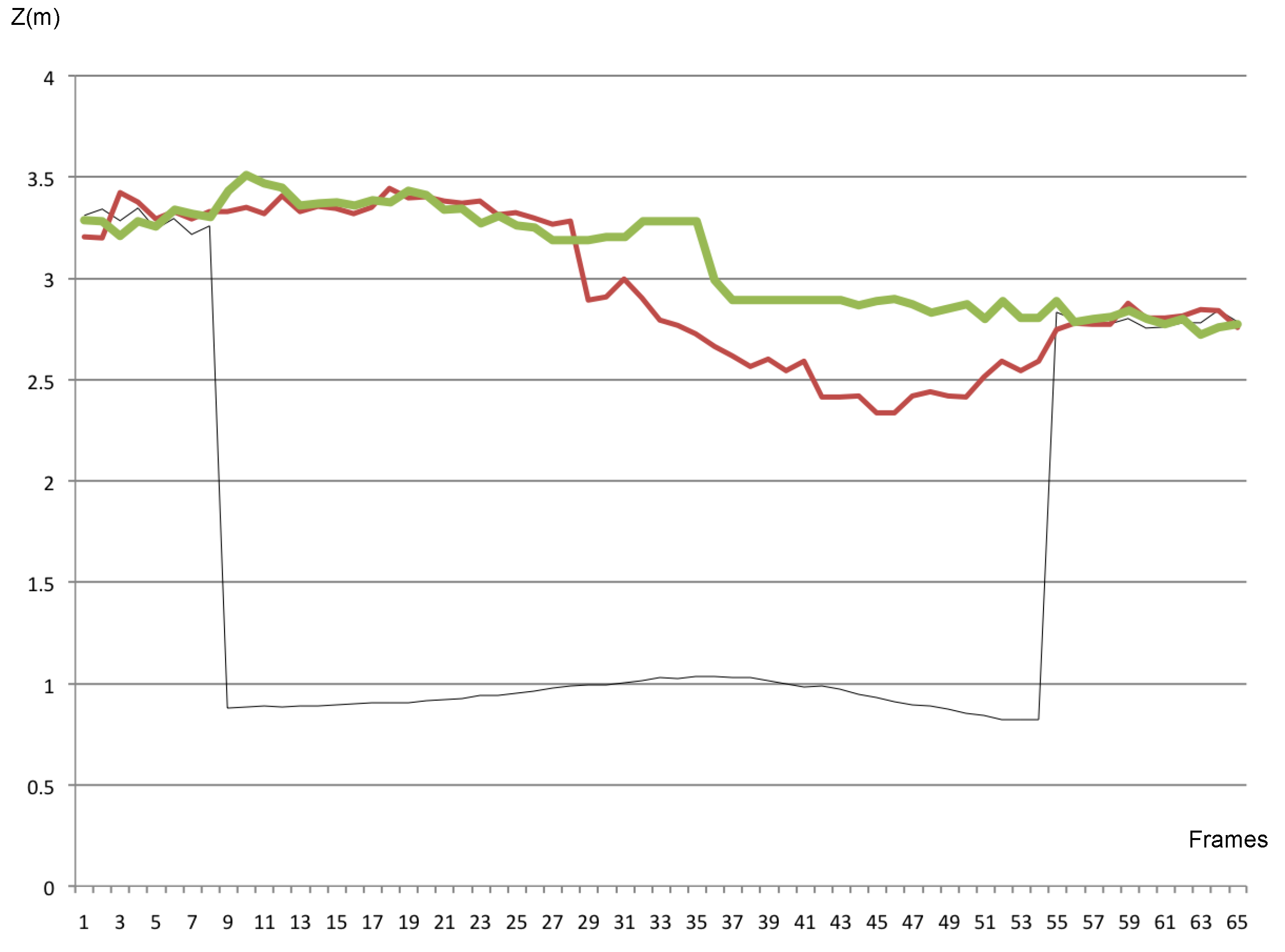
5.2. Results
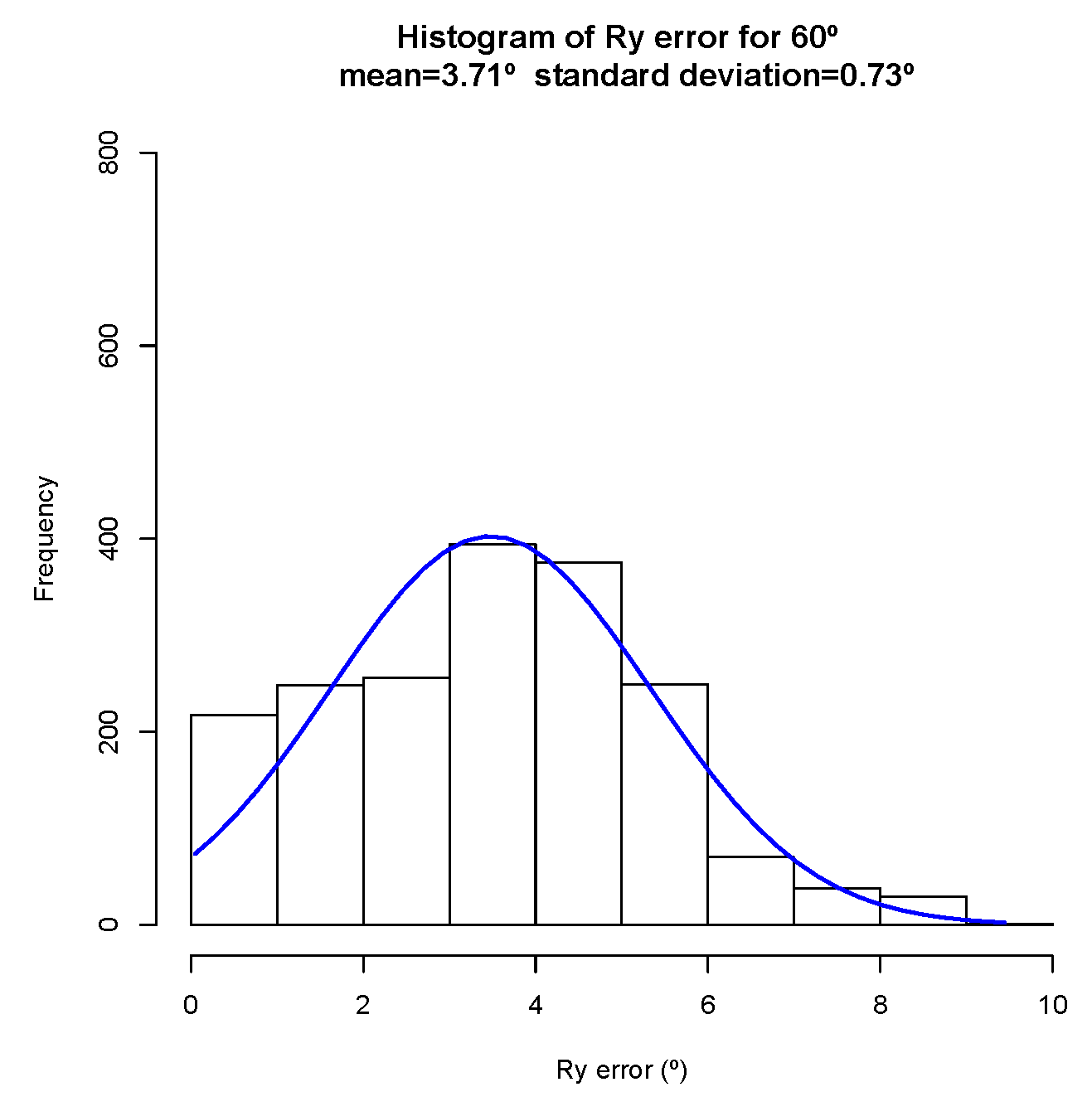
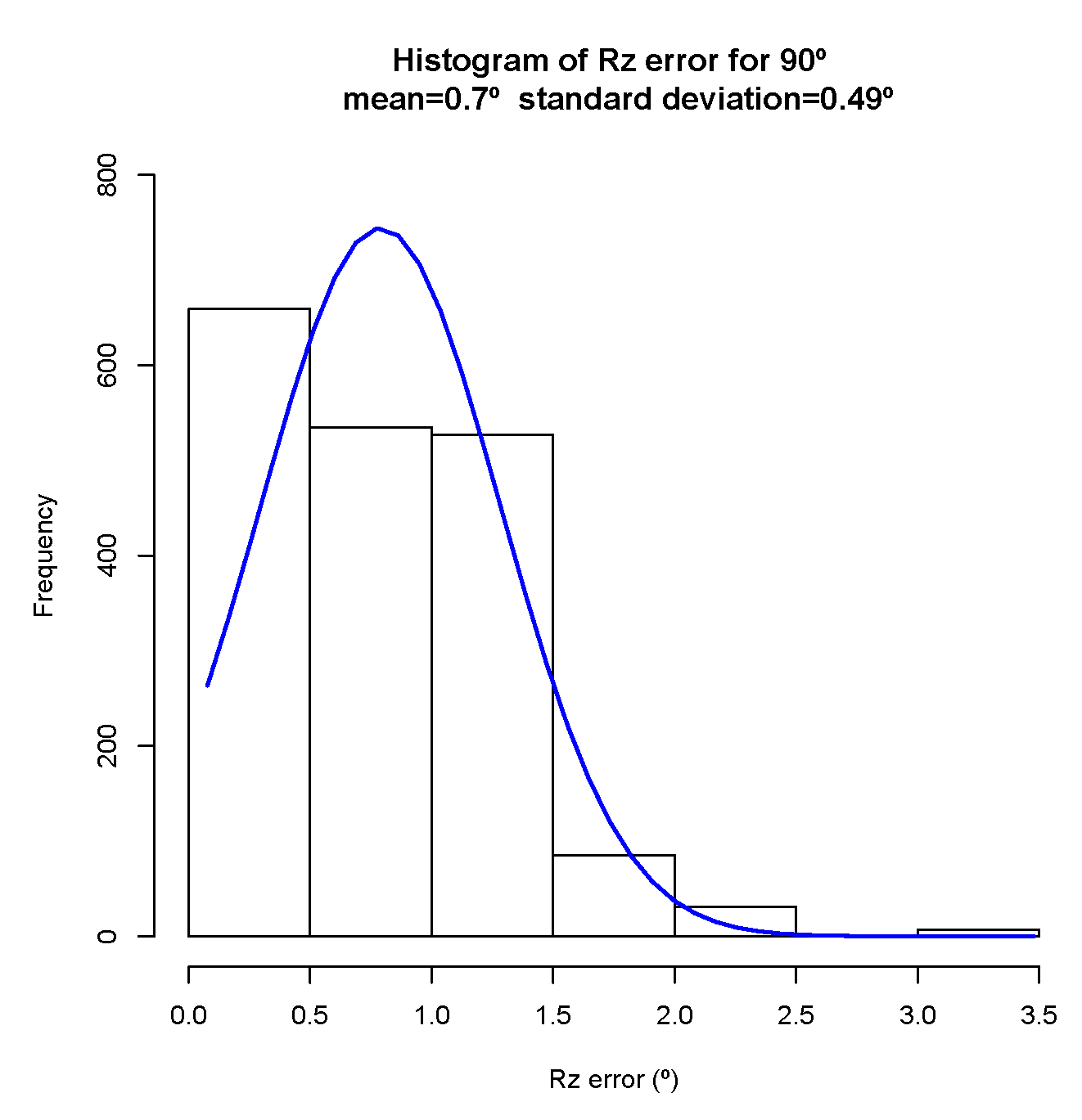
5.2.1. Pose Estimator
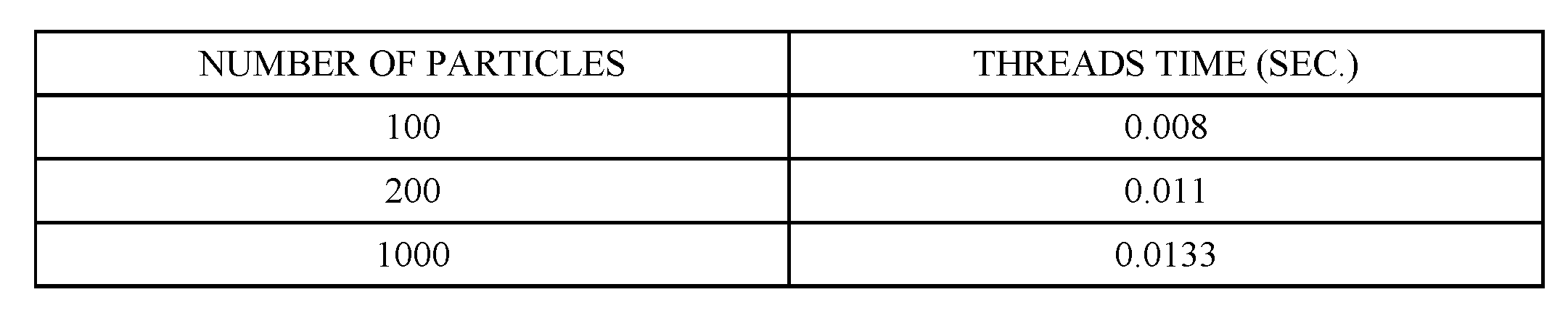
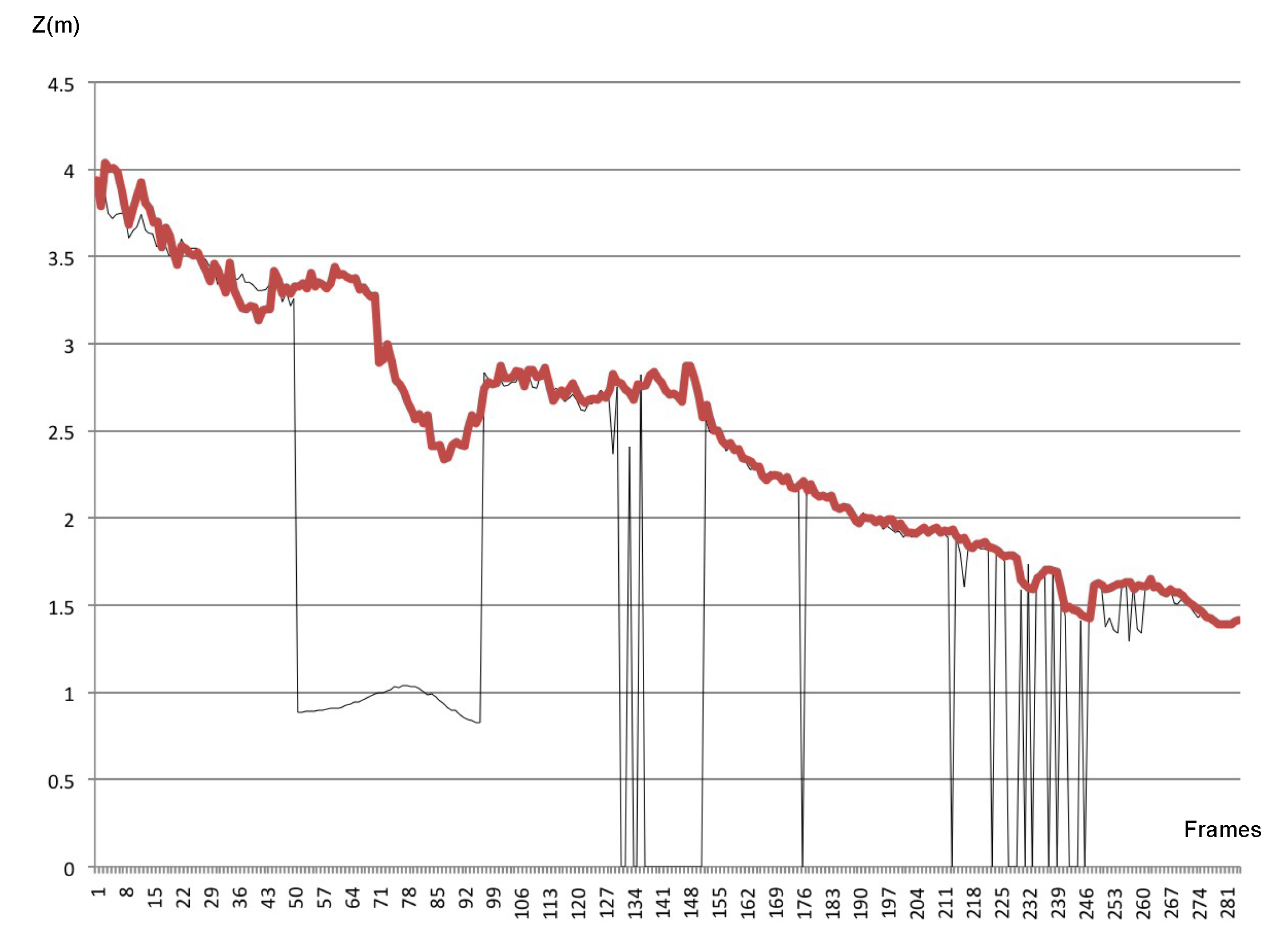
5.2.2. Tracking System
6. Simulation Results: Guidance Law
7. Discussion
7.1. Pose Estimator
- a misalignment of the camera related to the rail: the nonexistence of a mechanical solution that guarantees the correct alignment between the center of the camera to the tube rail. This misalignment has influence especially on the Y axis, which means a yaw rotation of the camera related to the rail,
- the increasing offset along the z-axis is related to the non-calibration of the value of the focal length of the cameras lens,
- small variations in markers illumination that affect the accuracy in detecting the center of mass of each marker in the image,
- the more the target is away from the camera, any small variation in the detection of the blobs in the image will imply a greater error in the pose estimation. The pinhole model shows that as the target moves away (any small variation on the sensor side (IMAGE) implies a greater sensitivity and a greater error on the SCENE side).
7.2. Resilience to Occlusions and Outliers Rejection
7.3. Guidance Law
8. Conclusions
- versatility (active in certain situations and passive in others)
- be easily identifiable even in low visibility situations
- allow to be seen from different points of view.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| ASV | Autonomous Surface Vehicle |
| MARES | Modular Autonomous Robot for Environment Sampling |
| MVO | Monocular Visual Odometry |
| MViDO | Monocular Vision-based Docking Operation aid |
| DOF | degrees of freedom |
| EKF | extended Kalman filter |
| GPS | global positioning system |
| IMU | inertial measurement unit |
| FOV | lens field of view |
| HFOV | horizontal field of view |
| AOV | angle of view |
| Npixels | number of pixels |
References
- Cruz, N.A.; Matos, A.C. The MARES AUV, a Modular Autonomous Robot for Environment Sampling. In Proceedings of the OCEANS 2008, Washington, DC, USA, 15–18 September 2008; pp. 1–6. [Google Scholar]
- Figueiredo, A.; Ferreira, B.; Matos, A. Tracking of an underwater visual target with an autonomous surface vehicle. In Proceedings of the Oceans 2014, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Figueiredo, A.; Ferreira, B.; Matos, A. Vision-based Localization and Positioning of an AUV. In Proceedings of the Oceans 2016, Shangai, China, 10–13 April 2016. [Google Scholar]
- Vallicrosa, G.; Bosch, J.; Palomeras, N.; Ridao, P.; Carreras, M.; Gracias, N. Autonomous homing and docking for AUVs using Range-Only Localization and Light Beacons. IFAC-PapersOnLine 2016, 49, 54–60. [Google Scholar] [CrossRef]
- Maki, T.; Shiroku, R.; Sato, Y.; Matsuda, T.; Sakamaki, T.; Ura, T. Docking method for hovering type AUVs by acoustic and visual positioning. In Proceedings of the 2013 IEEE International Underwater Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Park, J.-Y.; Jun, B.-H.; Lee, P.-M.; Oh, J. Experiments on vision guided docking of an autonomous underwater vehicle using one camera. Ocean Eng. 2009, 36, 48–61. [Google Scholar] [CrossRef]
- Maire, F.D.; Prasser, D.; Dunbabin, M.; Dawson, M. A Vision Based Target Detection System for Docking of an Autonomous Underwater Vehicle. In Proceedings of the 2009 Australasian Conference on Robotics and Automation (ACRA 2009), Sydney, Australia, 2–4 December 2009; University of Sydney: Sydney, Australia, 2009. [Google Scholar]
- Ghosh, S.; Ray, R.; Vadali, S.R.K.; Shome, S.N.; Nandy, S. Reliable pose estimation of underwater dock using single camera: A scene invariant approach. Mach. Vis. Appl. 2016, 27, 221–236. [Google Scholar] [CrossRef]
- Gracias, N.; Bosch, J.; Karim, M.E. Pose Estimation for Underwater Vehicles using Light Beacons. IFAC-PapersOnLine 2015, 48, 70–75. [Google Scholar] [CrossRef]
- Palomeras, N.; Peñalver, A.; Massot-Campos, M.; Negre, P.L.; Fernández, J.J.; Ridao, P.; Sanz, P.J.; Oliver-Codina, G. I-AUV Docking and Panel Intervention at Sea. Sensors 2016, 16, 1673. [Google Scholar] [CrossRef] [PubMed]
- Lwin, K.N.; Mukada, N.; Myint, M.; Yamada, D.; Minami, M.; Matsuno, T.; Saitou, K.; Godou, W. Docking at pool and sea by using active marker in turbid and day/night environment. Artif. Life Robot. 2018. [Google Scholar] [CrossRef]
- Argyros, A.A.; Bekris, K.E.; Orphanoudakis, S.C.; Kavraki, L.E. Robot Homing by Exploiting Panoramic Vision. Auton. Robot. 2005, 19, 7–25. [Google Scholar] [CrossRef]
- Negre, A.; Pradalier, C.; Dunbabin, M. Robust vision-based underwater homing using self-similar landmarks. J. Field Robot. 2008, 25, 360–377. [Google Scholar] [CrossRef]
- Feezor, M.D.; Sorrell, F.Y.; Blankinship, P.R.; Bellingham, J.G. Autonomous underwater vehicle homing/docking via electromagnetic guidance. IEEE J. Ocean. Eng. 2001, 26, 515–521. [Google Scholar] [CrossRef]
- Singh, H.; Bellingham, J.G.; Hover, F.; Lerner, S.; Moran, B.A.; von der Heydt, K.; Yoerger, D. Docking for an autonomous ocean sampling network. IEEE J. Ocean. Eng. 2001, 26, 498–514. [Google Scholar] [CrossRef]
- Bezruchko, F.; Burdinsky, I.; Myagotin, A. Global extremum searching algorithm for the AUV guidance toward an acoustic buoy. In Proceedings of the OCEANS’11-Oceans of Energy for a Sustainable Future, Santander, Spain, 6–9 June 2011. [Google Scholar]
- Jantapremjit, P.; Wilson, P.A. Guidance-control based path following for homing and docking using an Autonomous Underwater Vehicle. In Proceedings of the Oceans’08, Kobe, Japan, 8–11 April 2008. [Google Scholar]
- Wirtz, M.; Hildebrandt, M.; Gaudig, C. Design and test of a robust docking system for hovering AUVs. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Fraundorfer, F. Tutorial: Visual odometry. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Jaegle, A.; Phillips, S.; Daniilidis, K. Fast, robust, continuous monocular egomotion computation. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 773–780. [Google Scholar]
- Aguilar-González, A.; Arias-Estrada, M.; Berry, F.; de Jesús Osuna-Coutiño, J. The fastest visual ego-motion algorithm in the west. Microprocess. Microsyst. 2019, 67, 103–116. [Google Scholar] [CrossRef]
- Li, S.; Xu, C.; Xie, M. A Robust O(n) Solution to the Perspective-n-Point Problem. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34. [Google Scholar] [CrossRef] [PubMed]
- Philip, N.; Ananthasayanam, M. Relative position and attitude estimation and control schemes for the final phase of an autonomous docking mission of spacecraft. Acta Astronaut. 2003, 52, 511–522. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Arulampalam, S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for On-line Non-linear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2001, 50, 174–188. [Google Scholar] [CrossRef]
- Arnaud Doucet, N.d.F.N.G. (Ed.) Sequential Monte Carlo Methods in Practice; Springer: Berlin, Germany, 2001. [Google Scholar]
- Li, B.; Xu, Y.; Liu, C.; Fan, S.; Xu, W. Terminal navigation and control for docking an underactuated autonomous underwater vehicle. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 25–30. [Google Scholar] [CrossRef]
- Park, J.Y.; Jun, B.H.; Lee, P.M.; Oh, J.H.; Lim, Y.K. Underwater docking approach of an under-actuated AUV in the presence of constant ocean current. IFAC Proc. Vol. 2010, 43, 5–10. [Google Scholar] [CrossRef]
- Caron, F.; Davy, M.; Duflos, E.; Vanheeghe, P. Particle Filtering for Multisensor Data Fusion With Switching Observation Models: Application to Land Vehicle Positioning. IEEE Trans. Signal Process. 2007, 55, 2703–2719. [Google Scholar] [CrossRef]
- Andersson, M. Automatic Tuning of Motion Control System for an Autonomous Underwater Vehicle. Master’s Thesis, Linköping University, Linköping, Sweden, 2019. [Google Scholar]
- Yang, R. Modeling and Robust Control Approach for Autonomous Underwater Vehicles. Ph.D. Thesis, Université de Bretagne occidentale-Brest, Brest, France, Ocean University of China, Qingdao, China, 2016. [Google Scholar]


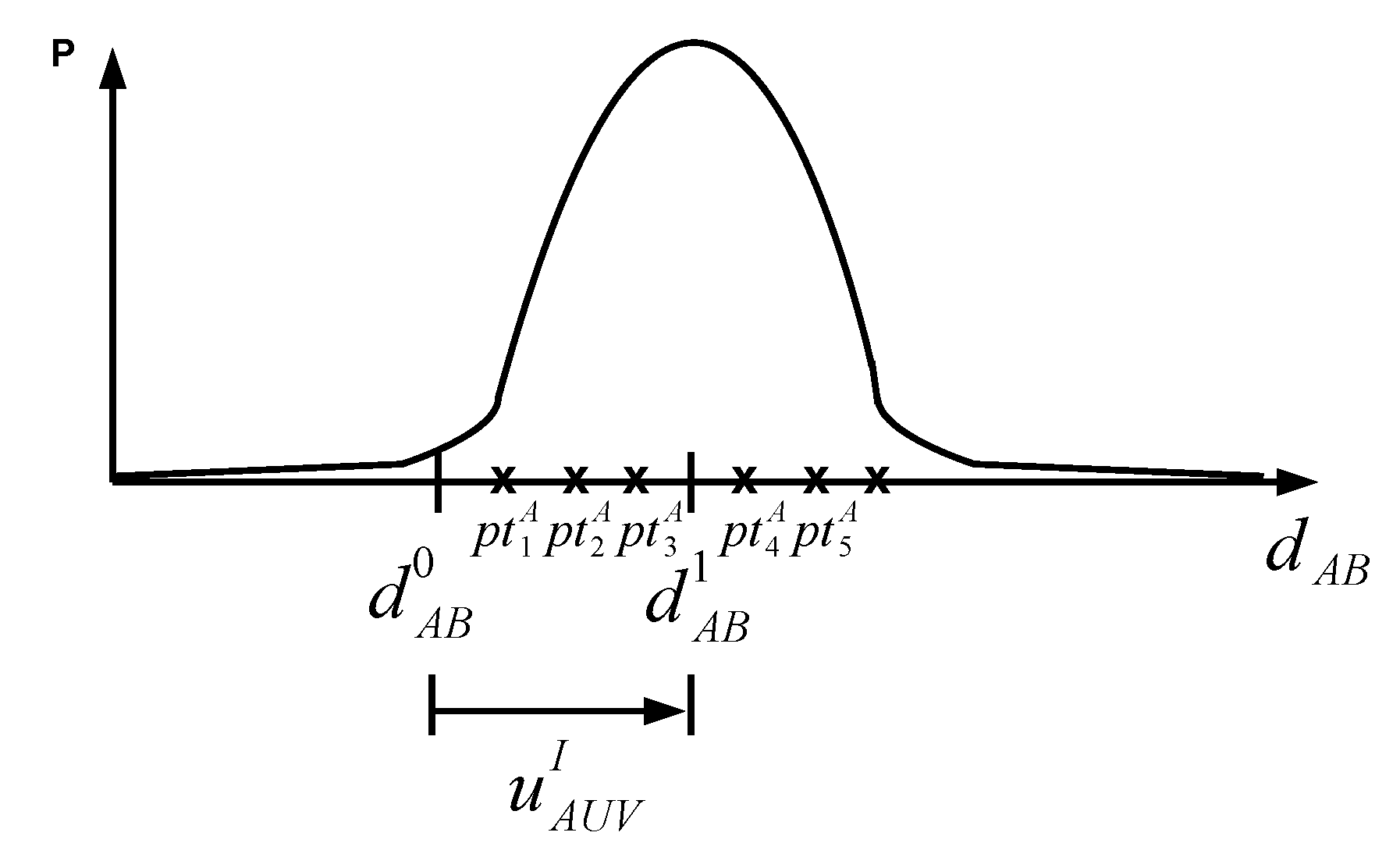











| Sensor Size (mm) | 3.2 × 2.4 |
| Resolution (pixels) | 704 × 576 |
| Pixel Size (m) | 6.5 × 6.25 |
| Focal length (mm) | 3.15 |
| Diagonal Field of View () | 65 |
| Maximum Aperture |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianchi Figueiredo, A.; Coimbra Matos, A. MViDO: A High Performance Monocular Vision-Based System for Docking A Hovering AUV. Appl. Sci. 2020, 10, 2991. https://doi.org/10.3390/app10092991
Bianchi Figueiredo A, Coimbra Matos A. MViDO: A High Performance Monocular Vision-Based System for Docking A Hovering AUV. Applied Sciences. 2020; 10(9):2991. https://doi.org/10.3390/app10092991
Chicago/Turabian StyleBianchi Figueiredo, André, and Aníbal Coimbra Matos. 2020. "MViDO: A High Performance Monocular Vision-Based System for Docking A Hovering AUV" Applied Sciences 10, no. 9: 2991. https://doi.org/10.3390/app10092991
APA StyleBianchi Figueiredo, A., & Coimbra Matos, A. (2020). MViDO: A High Performance Monocular Vision-Based System for Docking A Hovering AUV. Applied Sciences, 10(9), 2991. https://doi.org/10.3390/app10092991





