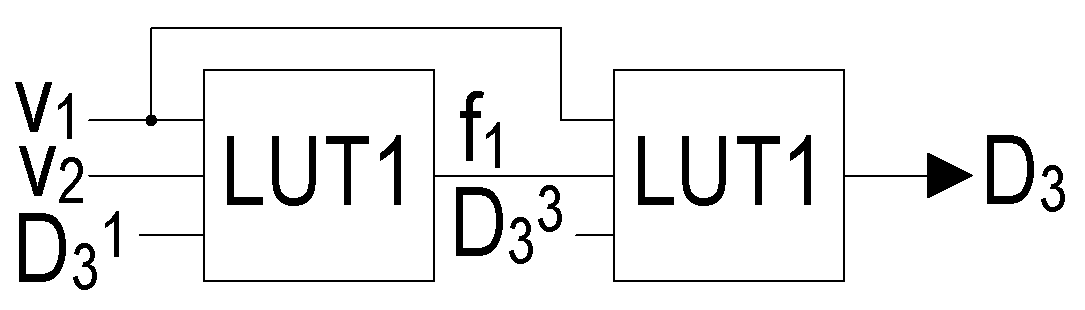Encoding of Terms in EMB-Based Mealy FSMs

Abstract

A method is proposed targeting implementation of FPGA-based Mealy finite state machines. The main goal of the method is a reduction for the number of look-up table (LUT) elements and their levels in FSM logic circuits. To do it, it is necessary to eliminate the direct dependence of input memory functions and FSM output functions on FSM inputs and state variables. The method is based on encoding of the terms corresponding to rows of direct structure tables. In such an approach, only terms depend on FSM inputs and state variables. Other functions depend on variables representing terms. The method belongs to the group of the methods of structural decomposition. The set of terms is divided by classes such that each class corresponds to a single-level LUT-based circuit. An embedded memory block (EMB) generates codes of both classes and terms as elements of these classes. The mutual using LUTs and EMB allows diminishing chip area occupied by FSM circuit (as compared to its LUT-based counterpart). The simple sequential algorithm is proposed for finding the partition of the set of terms by a determined number of classes. The method is based on representation of an FSM by a state transition table. However, it can be used for any known form of FSM specification. The example of synthesis is shown. The efficiency of the proposed method was investigated using a library of standard benchmarks. We compared the proposed with some other known design methods. The investigations show that the proposed method gives better results than other discussed methods. It allows the obtaining of FSM circuits with three levels of logic and regular interconnections.

1. Introduction

The model of Mealy finite state machine (FSM) is used very often in the process of designing control units of modern digital systems [1,2,3]. There are many problems connected with optimization of characteristics of control units [4,5]. One of the most important problems is a problem of hardware reduction [6,7].

Solution of this problem allows reducing the power consumption and increasing the performance (maximizing operating frequency) [8,9]. To solve this problem, it is necessary to take into account the specific features of both an FSM model and logic elements used to implement the circuit of FSM [3,10].

The main specific of Mealy FSM is a dependence of input memory functions and output functions on both input variables and state variables [1,8]. Our investigation of standard benchmarks [11] shows that it could be up to 17 arguments in Boolean functions representing FSM circuits.

Presently, the field-programmable gate array (FPGA) chips are widely used for implementing different digital systems [8,12,13]. Of course, FPGAs also are used to implement control units of these systems. There are three main elements of FPGA which could be used to implement FSM circuits. They are: look-up table (LUT) elements, embedded memory blocks (EMB) and tools of programmable interconnections [14,15,16]. LUTs fit for implementing Boolean functions represented as sum-of-products (SOP) [8]. EMBs implement large truth tables representing systems of Boolean functions (SBF).

A LUT is an array of SRAM cells with $S_L$ inputs ($S_L\le 6)$ [13,14]. Outputs of LUTs are connected with programmable flip-flops which could be bypassed. Therefore, it is possible to implement distributed registers keeping state codes [3].

An EMB is a RAM with $S_A$ address inputs and $t_F$ outputs. The main specific of EMBs is their reconfigurability [3]. It means that the values of $S_A$ and $t_F$ could be changed. Of course, the number of bits (the volume of EMB) is constant. It is determined as

$$V_0=2^{S_A}·t_F.$$

(1)

Due to the reconfigurability, it is possible to tune EMBs to meet the requirements of a particular design. There are the following pairs $<S_A,t_F>$ [13]: $<15,1>$, $<14,2>$, $<13,4>$, $<12,8>$, $<11,16>$, $<10,32>$ and $<9,64>$. It gives $V_0=32K$, bits.

In this article, we propose a method of synthesis leading an FSM circuit to implemented as a network of EMBs and LUTs. The method is based on the structural decomposition [17] of FSM circuit.

2. Background of Mealy FSMs

The logic circuit of Mealy FSM is represented by the following systems of Boolean functions [1]:

$$\Phi =\Phi (T,X);$$

(2)

$$Y=Y(T,X).$$

(3)

In (2) and (3), there are the following sets: $\Phi =\{D_1,\dots D_R\}$ is a set of input memory functions, $T=\{T_1,\dots T_R\}$ is a set of state variables, $X=\{x_1,\dots x_L\}$ is a set of input variables, $Y=\{y_1,\dots y_N\}$ is a set of output functions.

To find systems (2) and (3), it is necessary to specify a behaviour of FSM. In this article, we use a state transition table (STT) to represent a Mealy FSM. An STT contains information about the transitions between internal states $a_m\in A$, where $A=\{a_1,\dots a_M\}$ is a set of states [8]. There are the following columns in an STT: $a_m$ is a current state; $a_s$ is a state of transition; $X_h$ is a conjunction of input variables (or their complements) determining the transition $\langle a_m,a_s\rangle$; $Y_h$ is a collection of output functions (COF) generated during the transition $\langle a_m,a_s\rangle$; h is a number of transition $(h\in \{1,\dots ,H\})$. For example, consider some Mealy FSM $S_1$ represented by STT (

Table 1. State transition table of Mealy FSM $S_1$.

${\mathit{a}}_{\mathit{m}}$	${\mathit{a}}_{\mathit{s}}$	${\mathit{X}}_{\mathit{h}}$	${\mathit{Y}}_{\mathit{h}}$	h
$a_1$	$a_2$	$x_1$	$y_1{y}_2$	1
$a_1$	$a_3$	$\overline{x_1}$	$y_3$	2
$a_2$	$a_3$	$x_2$	$y_2{y}_5$	3
$a_2$	$a_5$	$\overline{x_2}{x}_3$	$y_4{y}_{11}$	4
$a_2$	$a_2$	$\overline{x_2}\overline{x_3}$	$y_6$	5
$a_3$	$a_6$	1	$y_3{y}_8$	6
$a_4$	$a_2$	$x_3$	$y_7$	7
$a_4$	$a_7$	$\overline{x_3}$	$y_2{y}_5$	8
$a_5$	$a_8$	1	$y_6$	9
$a_6$	$a_2$	$x_4$	$y_3{y}_8$	10
$a_6$	$a_{11}$	$\overline{x_4}$	$y_1$	11
$a_7$	$a_1$	1	$y_9{y}_{10}$	12
$a_8$	$a_{19}$	$x_5$	$y_1{y}_7$	13
$a_8$	$a_{10}$	$\overline{x_5}$	$y_4$	14
$a_9$	$a_4$	$x_6$	$y_1{y}_{10}$	15
$a_9$	$a_{11}$	$\overline{x_6}$	$y_9$	16
$a_{10}$	$a_7$	1	$y_3$	17
$a_{11}$	$a_{12}$	1	$y_4{y}_{11}$	18
$a_{12}$	$a_{10}$	$x_7$	$y_7$	19
$a_{12}$	$a_1$	$\overline{x_7}$	–	20

).

The following sets and their parameters could be derived from Table 1: $A=\{a_1,\dots ,a_{12}\}$, $M=12$, $X=\{x_1,\dots ,x_7\}$, $L=7$, $Y=\{y_1,\dots ,y_{11}\}$, $N=11$. There are $H=20$ rows in Table 1. To find the sets $\Phi$ and T, it is necessary to encode the states $a_m\in A$ by binary codes $K\left(a_m\right)$ with R bits. It is a step of state assignment [8]. Let us use minimum number of state variables when there is

$$R=\lceil lo{g}_{2}M\rceil .$$

(4)

In the discussed case, there is $R=4$. It gives the sets $T=\{T_1,\dots ,T_4\}$ and $\Phi =\{D_1,\dots ,D_4\}$. As follows from the set $\Phi$, we use D flip-flops to implement the register$\left(RG\right)$.

To get functions (2) and (3), it is necessary to turn an STT into a direct structure table (DST) [1] of Mealy FSM. To do it, we should add three columns into an STT, namely: $K\left(a_m\right)$ is a code of current state; $K\left(a_s\right)$ is a code of state of transition; ${\Phi }_h$ is a collection of input memory functions equal to 1 to replace $K\left(a_m\right)$ by $K\left(a_s\right)$.

Each row of DST corresponds to a product term $F_h$ $(h\in \{1,\dots ,H\left\}\right)$. The term $F_h$ is the following conjunction:

$$F_h=\left(\underset{r=1}{\overset{R}{\bigwedge }}{T}_r^{l_{mr}}\right)·X_h(h\in \{1,\dots ,H\}).$$

(5)

The first member of (5) is a conjunction $A_m$ of state variables corresponding to the code $K\left(a_m\right)$ of the state $a_m\in A$ from the h-th row of $DST$. There are $l_{mr}\in \{0,1\}$, $T_r^0=\overline{T_r}$, $T_r^1=T_r$ $(r\in \{1,\cdots ,R\left\}\right)$. The symbol $l_{mr}$ stands for the value of the r-th bit of $K\left(a_m\right)$.

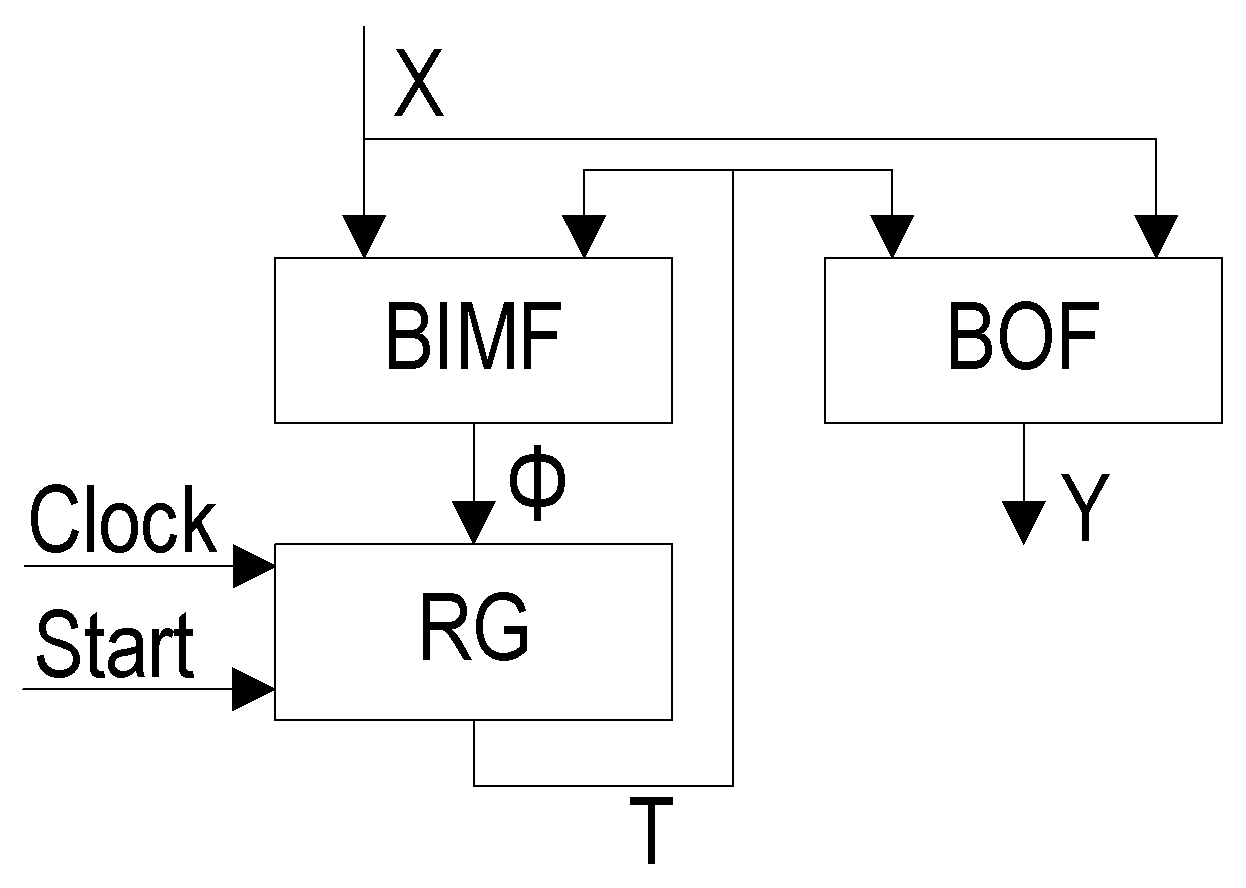
The functions (2) and (3) depend on terms (5). The system (2) determines a block of input memory functions (BIMF), the system (3) the block of output functions (BOF). State codes are kept into $RG$. It determines a Mealy FSM $U_1$ (Figure 1). The pulse $Start$ loads the code $K\left(a_1\right)$ of the initial state $a_1\in A$ into $RG$. The pulse $Clock$ allows changing the content of RG.

3. Implementing Mealy FSMs with FPGAs

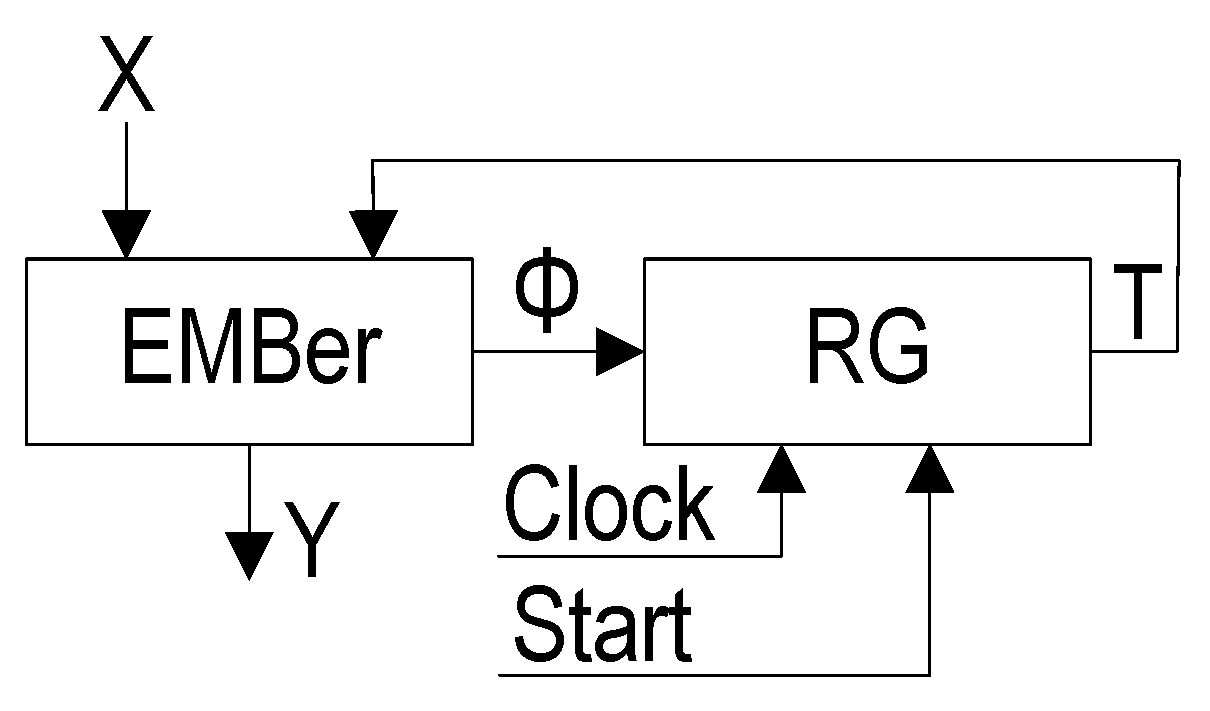
Each block of FSM $U_1$ could be implemented using either LUTs or EMBs. We name the block of LUTs as LUTer, the block of EMBs as EMBer. In the simplest case, we have a LUT-based FSM $U_1$ (Figure 2).

Let an FSM circuit be represented by I Boolean functions. There is $I=R+N$ in the case $U_1$. Let the following condition take place:

$$L\left(f_i\right)\le S_L(i\in \{1,\dots I\}).$$

(6)

In (6), the symbol $L\left(f_i\right)$ stands for the number of literals in a SOP of $f_i$.

In this case, there are exactly I LUTs in the circuit of $U_1$. If the condition (6) is violated, then some functions should be decomposed. To do it, the different methods of functional decomposition are used [18,19,20]. It leads to multi-level circuits with complex interconnections. The multi-level circuits of LUTers consume more energy and have less performance than their single-level counterparts.

It is very important to use EMBs in FSM design. It decreases the chip area occupied by FSM circuit, as well as the number of interconnections [21,22,23]. In turn, it results in decreasing for both the power consumption and propagation time (as compared to LUT-based counterparts). Because of it, there is a lot of EMB-based methods of Mealy FSMs synthesis [10,16].

Let the following condition take place:

$$2^{L+R}(N+R)\le V_0.$$

(7)

In this case, it is enough a single EMB to implement the circuit of $U_1$. It leads to FSM $U_2$ (Figure 3).

If condition (7) is violated, then EMBer is implemented as a network of EMBs. It has sense till the following conditions take places:

$$L+R\le S_A;$$

(8)

$$N+R>t_F.$$

(9)

If condition (8) is violated, then some methods of structural decomposition [16,17] could be used to diminish the values of $L\left(f_i\right)$.

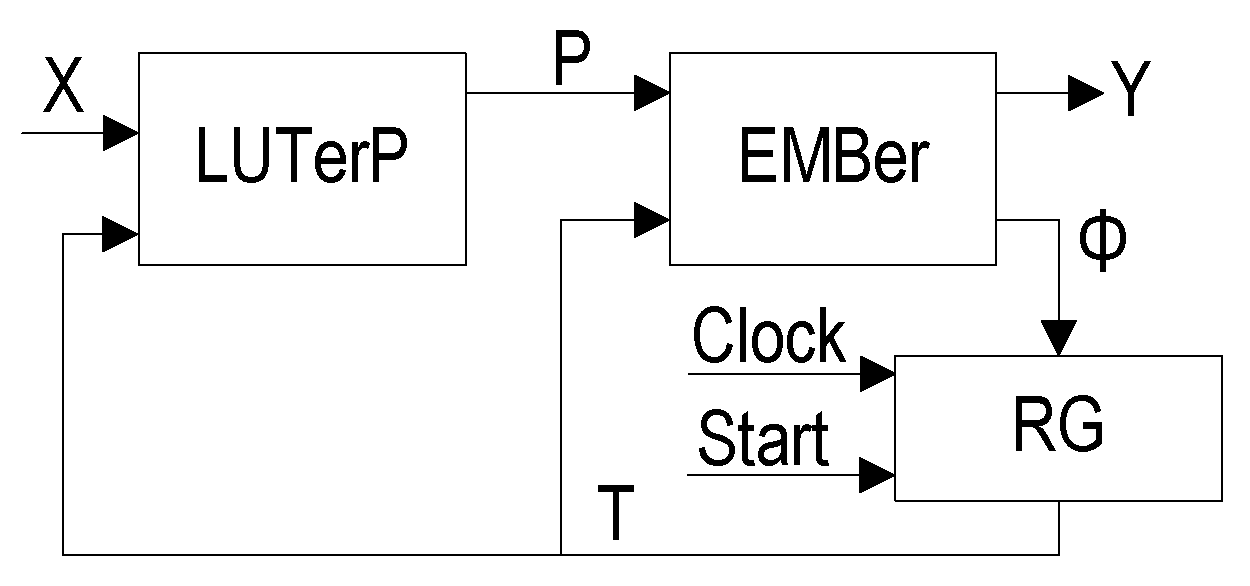
As a rule, the method of replacement of input variables is used [1,10]. In this case, the variables $x_l\in X$ are replaced by variables $p_g\in P=\{p_1,\dots ,p_G\}$. In many practical cases, there is $G\le 3$ [2]. Our analysis of standard benchmarks [16] justifies this statement. In this case, three following SBFs represent the FSM circuit:

$$P=P(T,X);$$

(10)

$$\Phi =\Phi (T,P);$$

(11)

$$Y=Y(T,P).$$

(12)

As a rule, the system (10) is implemented by LUTs [10,21]. The systems (11) and (12) are implemented by EMBs. It leads to Mealy FSM $U_3$ (Figure 4).

To find the system (10) it is necessary: (1) to construct the set P; (2) to execute the replacement of $X\to P$; (3) to encode the states and (4) to construct the table of LUTerP. To find the systems (11) and (12), it is necessary to transform the initial DST of $U_1$. The transformation is reduced to: (1) the replacement $x_l\in X$ by $p_g\in P$ and (2) the replacement of the column $X_h$ by the column $P_h$.

Let us use the symbol $U_i\left(S_j\right)$ to show that the model $U_i$ is used to synthesize an FSM circuit starting from the STT of FSM $S_j$. Let us find the system (10) for FSM $U_3\left(S_1\right)$.

As follows from Table 1, there are transitions depended on a single variable $x_l\in X$ or two variables. Therefore, there is $G=2$. It gives $P=\{p_1,p_2\}$. There is $M=12$, $R=4$. Let us encode the states of $S_1$ in the trivial way: $K\left(a_1\right)=0000,\dots ,K\left(a_{12}\right)=1011$. The replacement $X\to P$ is represented by

Table 2. Table of replacement $X\to P$.

	${\mathit{p}}_{\mathit{g}}$	${\mathit{p}}_1$	${\mathit{p}}_2$	$\mathit{K}\left({\mathit{a}}_{\mathit{m}}\right)$
${\mathit{a}}_{\mathit{m}}$
$a_1$		$x_1$	-	0000
$a_2$		$x_2$	$x_3$	0001
$a_3$		-	-	0010
$a_4$		-	$x_3$	0011
$a_5$		-	-	0100
$a_6$		$x_4$	-	0101
$a_7$		-	-	0110
$a_8$		-	$x_5$	0111
$a_9$		–	$x_6$	1000
$a_{10}$		-	-	1001
$a_{11}$		-	-	0101
$a_{12}$		$x_7$	-	0011

. It is constructed using the rules [1].

After minimizing, we can find the following equations:

$$\begin{array}{ccc}\hfill p_1& =& \overline{T_4}{x}_1\vee \overline{T_1}\overline{T_2}{T}_4{x}_2\vee T_2{x}_4\vee T_1{x}_7;\hfill \\ \hfill p_2& =& \overline{T_1}\overline{T_2}{x}_3\vee T_2{x}_5\vee T_1{x}_6.\hfill \end{array}$$

(13)

Obviously, a proper state assignment could diminish the number of arguments in functions (10). These methods are discussed in [1,10].

Let the following condition take place:

$$2^{G+R}(N+R)\le V_0.$$

(14)

In this case, it is enough a single EMB to implement the circuit of EMBer of FSM $U_3$.

There are other methods of structural decomposition [10]. For example, there are such methods as: (1) the encoding of collections of output functions; (2) the encoding of terms of DST; (3) the transformation of object codes. In this article, we discuss the using the encoding of terms in EMB-based Mealy FSMs. This method was used in FSMs implemented with programmable logic arrays [1]. It has never been used in FPGA-based design.

Let us explain this approach. Let us encode a term $F_h$ by a binary code $K\left(F_h\right)$ with $R_H$ bits, where

$$R_H=\lceil lo{g}_{2}H\rceil .$$

(15)

Let us use variables $z_r\in Z$ for the encoding, where $\left|Z\right|=R_H$. Let us construct the following SBFs:

$$Z=Z(T,X);$$

(16)

$$\Phi =\Phi \left(Z\right);$$

(17)

$$Y=Y\left(Z\right).$$

(18)

Let the following condition take place:

$$2^{L+R}·R_H\le V_0.$$

(19)

Let the condition (7) is violated. In this case, we propose the FSM $U_4$ (Figure 5). In this FSM, the EMB implements the system (16), the LUTer$Phi$ the system (17) and the LUTerY the system (18).

Let the following condition take place:

$$R_H\le S_L.$$

(20)

In this case, there are $R+N$ LUTs in the FSM circuit. Both LUTers have only a single level of LUTs.

However, if the condition (20) is violated, it is necessary to use the functional decomposition of functions (17) and (18). In this article, we discuss a case when the condition (20) is violated. Also, we discuss the additional condition: we could use only a single EMB. This restriction could be connected with the fact that other EMBs are taken for implementing other parts of a digital system.

As a rule, it is very important to choose the state codes leading to minimizing the values of $L\left(f_i\right)$ [8]. There are a lot of methods of state assignment targeting FPGA-based design [17,18,19,20,21,24,25]. There is an opinion that JEDI [8] is the best of them [4]. But in the case of $U_4$ there is no influence of state codes on the hardware amount. Therefore, we do not analyze the state assignment methods in this article.

4. Main Idea of Proposed Method

Let a Mealy FSM be represented by an STT with H rows. Let us possess only a single EMB to implement the FSM circuit. Let us have FPGA chip with LUTs with $S_L$ inputs. Let the terms $F_h$$(h\in \{1,\dots ,F_H\})$ form a set $F=\{F_1,\dots ,F_H\}$. Let us use the encoding of terms $F_h\in F$ to reduce the number of LUTs in the FSM circuit.

Let us find the value of K for given STT and value of $S_L$, where:

$$K=\lceil H/2^{S_L}\rceil .$$

(21)

Let us discuss a case, when $K>1$. It means that $R_H>S_L$. Therefore, both LUTerΦ and LUTerY of $U_4$ are represented by multi-level circuits.

In this article, we propose a method allowing: (1) to diminish the number of LUTs in comparison with equivalent FSM $U_4$ and (2) to regularize the interconnections. The method is based on dividing the initial STT by K sub-tables with up to $2^{S_L}$ rows. Let us illustrate this method using the STT of $S_1$ (Table 1).

Let us use an EMB such that the condition (7) is violated for $S_1$. Let the EMB have the configuration $\langle S_A,t_F\rangle$ such that the following conditions are true:

$$S_A-1<L+R\le S_A;$$

(22)

$$N+R>t_F\ge R_H.$$

(23)

The condition (22) shows that it is enough a single EMB to implement SBF (16). The condition (23) shows that it is not possible to implement an FSM circuit using a single EMB.

Let us find a partition ${\mathsf{\Pi }}_F=\{F^1,\dots ,F^K\}$ of the set F such that the following condition takes place:

$$R_k\le S_L(k\in \{1,\dots ,K\}).$$

(24)

Let it be $H_k$ elements in the set $F^k$. The value of $R_k$ is determined as:

$$R_k=\lceil lo{g}_2{H}_k\rceil (k\in \{1,\dots ,K\}).$$

(25)

Each class $F^k\in {\mathsf{\Pi }}_F$ determines sets $Y^k\subseteq Y$ and $A^k\subseteq A$. The set $A^k$ includes states of transition written in the rows of STT corresponding to the class $F^k\in {\mathsf{\Pi }}_F$. The set $Y^k$ includes output functions written in the rows of STT corresponding to the $F^k\in {\mathsf{\Pi }}_F$. Let us find such a partition ${\mathsf{\Pi }}_F$ that

$$|Y^i\cap Y^j|\to min;$$

(26)

$$|A^i\cap Y^j|\to min.$$

(27)

In (26) and (27), there is $i\ne j$ and $i,j\in \{1,\dots K\}$.

Let us encode the term $F_h\in F^k$ by a binary code $C\left(F_h\right)$ with $R_k$ bits. Let us use variables $z_r\in Z$ for the encoding. These variables are the same for all classes $F^k\in {\mathsf{\Pi }}_F$. To distinguish the classes, let us encode classes $F^k\in {\mathsf{\Pi }}_F$ by binary codes $C\left(F^k\right)$ with $R_C$ bits:

$$R_C=\lceil lo{g}_{2}K\rceil .$$

(28)

Let us use the variables $v_r\in V$ to encode the classes, where $\left|V\right|=R_c$.

Now, the code $K\left(F_h\right)$ is represented as

$$K\left(F_h\right)=C\left(F^k\right)\ast C\left(F_h\right),$$

(29)

where * is a sign of concatenation. Of course there is $R_H=R_k+R_C$.

Let the following condition take place:

$${\Delta }_t=t_F-R_H>0.$$

(30)

In this case, some functions $D_r\in \Phi$ and $y_n\in Y$ could be implemented by EMB. Let they form sets ${\Phi }_E$ and $Y_E$, respectively. Therefore, LUTs should be used for implementing the remained functions. Let it be ${\Phi }_L=\Phi \setminus {\Phi }_E$ and $Y_L=Y\setminus Y_E$. Using these preliminaries, we propose the model of Mealy FSM $U_5$ (Figure 6).

In FSM $U_5$, the EMB generates functions (16) and the following SBFs:

$$V=V(T,X);$$

(31)

$${\Phi }_E={\Phi }_E(T,X);$$

(32)

$$Y_E=Y_E(T,X).$$

(33)

The LUTerk $(k\in \{1,\dots ,K\left\}\right)$ generates functions:

$${\Phi }_L^k={\Phi }_L^k\left(Z\right);$$

(34)

$$Y_L^k=Y_L^k\left(Z\right).$$

(35)

The LUTerΦY implements functions $D_r\in {\Phi }_L$ and $y_n\in Y_L$ where

$$D_r=\underset{k=1}{\overset{k}{\bigvee }}{C}_{rk}{V}_k{D}_r^k;$$

(36)

$$y_n=\underset{k=1}{\overset{k}{\bigvee }}{C}_{nk}{V}_k{y}_n^k.$$

(37)

In (36) and (37) the superscript k means that the corresponding function is generated by LUTerk. The $C_{rk}\left(C_{nk}\right)$ is a Boolean variable equal 1 if and only if $D_r\in {\Phi }_L^k$, $y_n\in Y_L^k$. Also, functions $D_r\in {\Phi }_E$ enter LUTerΦY. Each function requires a flip-flop, so it uses a single LUT. The symbol $V_k$ stands for the conjunction corresponding to $C\left(F^k\right)$:

$$V_k=\underset{r=1}{\overset{R_c}{\bigwedge }}{v}_r^{l_{kr}}(k\in \{1,\dots ,K\}).$$

(38)

In (38), $l_{kr}$ is a value of the r-th bit of $C\left(F^k\right)$, $l_{kr}\in \{0,1\}$, $v_r^0=\overline{v_r}$, $v_r^1=v_r$ $(r\in \{1,\dots ,R_c\})$.

Because the condition (24) is true, there are $|{\Phi }_L^k|+|Y_L^k|$ LUTs in the circuit of LUTerk. If conditions (26) and (27) take places, the number of LUTs in LUTer1-LUTerK is minimized.

Assuming that a Mealy FSM S is represented by an STT, we propose the following design method for FSM $U_5$:

• Creating the partition ${\mathsf{\Pi }}_F$ corresponding to (26) and (27).
• Executing the state assignment.
• Creating the DST of Mealy FSM.
• Creating the sets $Y_E$, ${\Phi }_E$, $Y_L$ and ${\Phi }_L$.
• Encoding of terms and classes of ${\mathsf{\Pi }}_F$.
• Creating the systems (34) and (37).
• Transformation of DST.
• Creating the table of EMB.
• Implementing FSM circuit with particular EMB and LUTs.

The number of LUTs in $U_5$ are mostly determined by the partition ${\mathsf{\Pi }}_F$. Let us discuss how to find the partition ${\mathsf{\Pi }}_F$.

5. Constructing Partition of the Set of Terms

The problem is formulated as the following. It is necessary to find the partition ${\mathsf{\Pi }}_F$ with K blocks such that relations (26) and (27) take places. The value of K is determined by (21).

In this article, we propose a simple sequential algorithm for solution of this problem. We characterize each term $F_h\in F$ by two sets. The set $Y\left(F_h\right)\subseteq Y$ includes output functions written in the h-th row of STT. The set $A\left(F_h\right)\subset A$ includes a state of transition $a_s\in A$ from the h-th row of STT. If $F_h\in F^k$, then $y_n\in Y^k$ and $a_s\in A^k$. Of course, the set ${\Phi }^k$ is determined by the codes $K\left(a_s\right)$ of states $a_s\in A^k$.

We use two evaluations in this algorithm. The evaluation $N(F_h,Y^k)$ determines how many new output functions will be added to $Y^k$ due to including $F_h$ into $F^k$. We determine these evaluations as the following:

$$N(F_h,Y^k)=|Y\left(F_h\right)\setminus Y^k|.$$

(39)

$$N(F_h,A^k)=|A\left(F_h\right)\cap A^k|.$$

(40)

There are ${\Delta }_Z$ insignificant assignments of variables $z_r\in Z$:

$${\Delta }_Z=2^{S_L}·K-H.$$

(41)

They could be used for minimizing function (34) and (35). We propose to distribute terms evenly among K groups. It corresponds to the vector $\Delta =\langle {\Delta }_1,{\Delta }_2,\dots ,{\Delta }_K\rangle$. Therefore, each class $F^k\in {\mathsf{\Pi }}_F$ includes $H_k$ elements, where:

$$H_k=2^{S_L}-{\Delta }_k(k\in \{1,\dots ,K\}).$$

(42)

There are two stages in generating each block $F^k\in {\mathsf{\Pi }}_F$. Let $k-1$ blocks be constructed. At the first stage, we should choose the basic element (BE) $F_h\in F^{*}$, where there is $F^{*}=F\setminus \{F^1\cup ,\dots ,\cup F^{k-1}\}$. The term $F_h$ is a BE of $F^k$ if it satisfies to the following relation:

$$|Y\left(F_h\right)|=max|Y\left(F_j\right)|,F_j\in F^{*}\setminus \left\{F_h\right\}.$$

(43)

If the condition (43) is true for terms $F_i$ and $F_j$, the we choose the term $F_j$ where $i<j$.

The second stage has $H_k-1$ steps. At each step, we should choose the next element of $F^k$. To do it, we use the following approach. Let us form a set $P\left(F^k\right)$ including terms $F_h\in F^{*}$ such that $Y\left(F_h\right)\cap Y^k\ne Ø$. Let us select a term $F_h\in P\left(F^k\right)$ such that

$$N(F_h,F^k)=max\left(\right|Y\left(F^k\right)\cup Y\left(F_h\right)|-N(F_h,Y^k)).$$

(44)

If more than a single term satisfies to (44), then we should choose the term with the following property:

$$N(F_h,A^k)=1,F_h\in P\left(F^k\right).$$

(45)

If there are several terms with the property (45), we choose a term with the less value of h. Next, we should make $P\left(F^k\right)=Ø$ and eliminate the term $F_h$ from $F^{*}$.

The constructing $F^k$ is terminated if: (1) all terms are already distributed $(F^{*}=Ø)$ or (2) there are $H_k$ elements in $F^k\in {\mathsf{\Pi }}_F$.

Let us discuss an example of creating the partition ${\mathsf{\Pi }}_F$ for Mealy FSM $S_1$. Let it be $S_L=3$. Using (21) gives $K=3$. Using (41) gives ${\Delta }_Z=24-20=4$. Let us form the vector $\Delta =\langle 2,1,1\rangle$. It gives $H_1=6$, $H_2=H_3=7$. The process is shown in

Table 3. The constructing the partition ${\mathsf{\Pi }}_F$.

h	$\mathit{N}\left({\mathit{F}}_{\mathit{h}}\right)$	BE1	I/II					BE2	I/II
			1	2	3	4	5		1	2	3	4	5	6
1	2	⊕	–	–	–	–	–	–	–	–	–	–	–	–
2	1		−1	−1	−1	−1	−1		−1	−1	−1/	−1/0	−1	−1
3	2		0	0/0${}^{+}$	–	–	–	–	–	–	–	–	–	–
4	2		−2	−2	−2	−2	−2	⊕	–	–	–	–	–
5	1		−1	−1	−1	−1	−1		−1	−1	−1/	−1/0	−1	−1
6	2		−2	−2	−2	−2	−2		−2	−2	−2	−2/	−2	−2
7	1		−1	−1	−1	−1	−1		−1	−1	−1	−1/0	1${}^{+}$	–
8	2		0	0/0	2${}^{+}$	–	–	–	–	–	–	–	–	–
9	1		−1	−1	−1	−1	−1		−1	−1	−1	−1/0	−1	−1
10	2		−2	−2	−2	−2	−2		−2	−2	−2	−2	−2	−2
11	1		1${}^{+}$	–	–	–	–	–	–	–	–	–	–	–
12	2		−2	−2	−2	−2	0/0${}^{+}$	–	–	–	–	–	–	–
13	2		0	0/0	0	0/0	0/0		−2	−2	−2	−2	0	0${}^{+}$
14	1		−1	−1	−1	−1	−1		1	1${}^{+}$	–	–	–	–
15	2		0	0	0	0/1${}^{+}$	–	–	–	–	–	–	–	–
16	1		−1	−1	−1	−1	−1		−1	−1	−1	−1/0	−1	−1
17	1		−1	−1	−1	−1	−1		−1	−1	−1	−1/0	−1	−1
18	2		−2	−2	−2	−2	−2		2${}^{+}$	–	–	–	–	–
19	1		−1	−1	−1	−1	−1		−1	−1	−1	−1/1${}^{+}$	–	–
20	0		0	0/0	0	0/0	0/0		0	0	0${}^{+}$	–	–	–
$F^k$		$F_1$	$F_{11}$	$F_3$	$F_8$	$F_{15}$	$F_{12}$	$F_4$	$F_{18}$	$F_{14}$	$F_{20}$	$F_{19}$	$F_7$	$F_{13}$
$Y^k$		$y_1,y_2,y_5,y_9,y_{10}$						$y_1,y_4,y_7,y_{11}$
$A^k$		$a_1,a_2,a_3,a_4,a_7{a}_{11}$						$a_2,a_5,a_{10},a_{12}$

.

Let us explain columns of Table 3. There are terms $F_h$ in the column h. The column $N\left(F_h\right)$ contains the numbers of output functions in terms $F_h$. There are basic elements of $F^1$ and $F^2$ shown in columns BE1 and BE2, respectively. The symbol I stands for (39), the symbol $II$ for (40). The sign ⊕ means that a particular term is chosen as a basic element. The sign “−” means than $F_h\notin F^{*}$. The sign “+” means that the corresponding term is included into the class $F^k$. There are terms $F_h\in F^k$ in the row $F^k$. They are shown in the order of their selection. There are output functions $y_n\in Y^k$ in the row $Y^k$, the states $a_s\in A^k$ in the row $A^k$. We determine the evaluation (40) only for terms with equal values of (39).

As follows from Table 3, there are $H_1+H_2=13$ steps in the process of selection. The class $F^3$ includes terms $F_h\notin F^1\cup F^2$. Our approach allows constructing the partition ${\mathsf{\Pi }}_F=\{F^1,F^2,F^3\}$ with the following classes: $F^1=\{F_1,F_3,F_8,F_{11},F_{12},F_{15}\}$, $F^2=\{F_4,F_7,F_{13},F_{14},F_{18},F_{19},F_{20}\}$ and $F^3=\{F_2,F_5,F_6,F_9,F_{10},F_{16},F_{17}\}$. It gives the following sets: $X^1=\{x_1,x_2,x_3,x_4,x_6\}$, $X^2=\{x_2,x_3,x_5,x_7\}$ and $X^3=\{x_1,x_2,x_3,x_4,x_6\}$, $Y^1=\{y_1,y_2,y_5,y_9,y_{10}\}$, $Y^2=\{y_1,y_4,y_7,y_{11}\}$, $Y^3=\{y_3,y_6,y_8,y_9\}$, $A^1=\{a_1,a_2,a_3,a_4,a_7,a_{11}\}$, $A^2=\{a_2,a_5,a_9,a_{10},a_{12}\}$, $A^3=\{a_2,a_3,a_6,a_8,a_{10},a_{11}\}$. Therefore, there are the following results for (26) and (27): $|Y^1\cap Y^2|=1$, $|Y^1\cap Y^3|=1$, $|Y^2\cap Y^3|=0$, $|A^1\cap A^2|=1$, $|A^1\cap A^3|=2$, $|A^2\cap A^3|=2$.

6. Example of Synthesis

In Section 5, we found the partition ${\mathsf{\Pi }}_F$ for the discussed example. Let us use an EMB including the configuration $\langle 11,7\rangle$. Therefore, there is $S_A=11$ and $t_F=7$. There is $L+R=11$ for FSM $S_1$. The condition (22) takes place. There is $H=20$ and $S_L=3$. Using (21) gives $K=3$: so, there is $R_C=2$ and $V=\{v_1,v_2\}$ obviously, $R_1=R_2=R_3=3$. Also, there is $R_H=5$. Because $N+R=15$, the condition (23) takes place. Therefore, it is possible to use the model $U_5$ for FSM $S_1$. Therefore, let us design the FSM $U_5\left(S_1\right)$.

Let us execute the state assignment allowing a reduction to the numbers of elements in the sets ${\Phi }^k\subseteq \Phi$. One of the possible solutions is shown in Figure 7.

Using Figure 7 and sets $A^1-A^3$ gives the sets ${\Phi }^1-{\Phi }^3$. They are the following: ${\Phi }^1=\{D_2,D_3,D_4\}$, ${\Phi }^2=\{D_1,D_2,D_4\}$ and ${\Phi }^3=\Phi$.

Using Table 1 and codes form Figure 7, we can construct the direct structure table of FSM $U_5\left(S_1\right)$. It is

Table 4. DST of Mealy FSM $U_5\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{K}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{a}}_{\mathit{s}}$	$\mathit{K}\left({\mathit{a}}_{\mathit{s}}\right)$	${\mathit{X}}_{\mathit{h}}$	${\mathit{Y}}_{\mathit{h}}$	${\mathsf{\Phi }}_{\mathit{h}}$	h
$a_1$	0000	$a_2$	0100	$x_1$	$y_1{y}_2$	$D_2$	1
		$a_3$	0001	$\overline{x_1}$	$y_3$	$D_4$	2
$a_2$	0100	$a_3$	0001	$x_2$	$y_2{y}_5$	$D_4$	3
		$a_5$	1100	$\overline{x_2}{x}_3$	$y_4{y}_{11}$	$D_1{D}_2$	4
		$a_2$	0100	$\overline{x_2}\overline{x_3}$	$y_6$	$D_2$	5
$a_3$	0001	$a_6$	1110	1	$y_3{y}_8$	$D_1{D}_2{D}_3$	6
$a_4$	0101	$a_2$	0100	$x_3$	$y_7$	$D_2$	7
		$a_7$	0010	$\overline{x_3}$	$y_2{y}_5$	$D_3$	8
$a_5$	1100	$a_8$	1010	1	$y_6$	$D_1{D}_3$	9
$a_6$	1110	$a_2$	0100	$x_4$	$y_3{y}_8$	$D_2$	10
		$a_{11}$	0110	$\overline{x_4}$	$y_1$	$D_2{D}_3$	11
$a_7$	0010	$a_1$	0000	1	$y_9{y}_{10}$	–	12
$a_8$	1010	$a_9$	1101	$x_5$	$y_1{y}_7$	$D_1{D}_2{D}_4$	13
		$a_{10}$	1000	$\overline{x_5}$	$y_4$	$D_1$	14
$a_9$	1101	$a_4$	0101	$x_6$	$y_1{y}_{10}$	$D_2{D}_4$	15
		$a_{11}$	0110	$\overline{x_6}$	$y_9$	$D_2{D}_3$	16
$a_{10}$	1000	$a_7$	0010	1	$y_3$	$D_3$	17
$a_{11}$	0110	$a_{12}$	1001	1	$y_4{y}_{11}$	$D_1{D}_4$	18
$a_{12}$	1001	$a_{10}$	1000	$x_7$	$y_7$	$D_1$	19
		$a_1$	0000	$\overline{x_7}$	–	–	20

. To construct the transformed DST, it is necessary to find codes $C\left(F_h\right)$ and $C\left(F^k\right)$.

Let us construct the sets $Y_E$, ${\varphi }_E$, $Y_L$ and ${\Phi }_L$. To do it, we should find the value of ${\Delta }_t$. There are $R_H=5$ and $t_F=7$. Using (30) gives ${\Delta }_t=2$. We should eliminate functions $D_r\in \Phi$ and $y_n\in Y$ which belong to K corresponding sets. In the discuss case, there is $D_2,D_4\in {\Phi }^1\cup {\Phi }^2\cup {\Phi }^3$. Therefore, let us form the sets ${\Phi }_E=\{D_2,D_4\}$ and ${\Phi }_L=\{D_1,D_3\}$. Obviously, there are $Y_E=Ø$ and $Y_L=Y$. Now, we have the sets ${\Phi }_L^1=\left\{D_3\right\}$, ${\Phi }_L^2=\left\{D_1\right\}$ and ${\Phi }_L^3=\{D_1,D_3\}$. Of course, there are the sets $Y_L^1=Y^1$, $Y_L^2=Y^2$ and $Y_L^3=Y^3$.

Let us construct the systems of Boolean functions shoving dependence of functions $D_r^k\in {\Phi }_L^k$ and $y_n^k\in Y_L^k$ on the terms $F_h\in F^k$ $(k\in \{1,\dots ,K\left\}\right)$. To do it, we use the DST (Table 4) and classes $F^k\in {\mathsf{\Pi }}_F$. We could find the following systems:

$$\begin{array}{ccc}\hfill D_3^1& =& F_8\vee F_{11};\hfill \\ \hfill y_1^1& =& F_1\vee F_{11}\vee F_{15};\hfill \\ \hfill y_2^1& =& F_1\vee F_3\vee F_8;\hfill \\ \hfill y_5^1& =& F_{13}\vee F_8;\hfill \\ \hfill y_9^1& =& F_{12};\hfill \\ \hfill y_{10}^1& =& F_{12}\vee F_{15}.\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill D_1^2& =& F_4\vee F_{13}\vee F_{14},F_{18},F_{19};\hfill \\ \hfill y_1^2& =& F_{13};\hfill \\ \hfill y_4^2& =& F_4\vee F_{14}\vee F_{18};\hfill \\ \hfill y_7^2& =& F_7\vee F_{13}\vee F_{19};\hfill \\ \hfill y_{11}^2& =& F_4\vee F_{18}.\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill D_1^3& =& F_{6}vee{F}_9;\hfill \\ \hfill D_3^3& =& F_6\vee F_9\vee F_{16}\vee F17\hfill \\ \hfill y_3^3& =& F_2\vee F_6\vee F_{10}\vee F_{17};\hfill \\ \hfill y_6^3& =& F_5\vee F_9;\hfill \\ \hfill y_8^3& =& F_6\vee F_{10};\hfill \\ \hfill y_9^3& =& F_{16}.\hfill \end{array}$$

(48)

Let us encode the terms $F_h\in F^k$ in such a manner that there is minimum number of literals in systems (46) and (48). We could get codes shown in Figure 8.

Using the system (46) and Karnaugh map (Figure 8a), we could form the following system:

$$\begin{array}{ccc}\hfill D_3^1& =& \overline{z_2}\overline{z_3};y_1^1=z_1;y_2^1=\overline{z_1}\overline{z_3}\vee z_2;\hfill \\ \hfill y_5^1& =& \overline{z_1}\overline{z_3};y_9^1=\overline{z_1}{z}_3;y_{10}^1=z_3.\hfill \end{array}$$

(49)

The system (49) represents the circuit of LUTer1. It includes 4 LUTs and has 9 interconnections with the EMB.

Using the system (47) and Karnaugh map (Figure 8b), we could form the following system:

$$\begin{array}{ccc}\hfill D_1^2& =& z_3\vee z_2\overline{z_3};y_1^2=z_1{z}_2;y_4^2=z_3;\hfill \\ \hfill y_7^2& =& \overline{z_1}\overline{z_3}\vee z_1{z}_2;y_{11}^2=\overline{z_1}{z}_3.\hfill \end{array}$$

(50)

The system (50) represents the circuit of LUTer2. It includes 4 LUTs and has 9 interconnections with the EMB.

Using the system (49) and Karnaugh map (Figure 8c), we could form the following system:

$$\begin{array}{ccc}\hfill D_1^3& =& \overline{z_1}{z}_3;D_3^3=z_3;y_3^3=\overline{z_2};\hfill \\ \hfill y_6^3& =& \overline{z_1}{z}_2;y_8^3=\overline{z_1}\overline{z_2}{z}_3\vee z_1\overline{z_3};y_9^3=z_1{z}_2.\hfill \end{array}$$

(51)

The system (51) represents the circuit of LUTer3. It includes 5 LUTs and has 10 interconnections with the EMB.

Let us encode the classes $F^k\in {\mathsf{\Pi }}_F$ as the following: $C\left(F^1\right)=00$, $C\left(F^2\right)=*1$ and $C\left(F^3\right)=1*$. It gives the conjunctions $V_1=\overline{v_1}\overline{v_2}$, $V_2=v_2$ and $V_3=v_1$. Using these codes and Equations (49) and (51), we could find the systems (36) and (37). They are the following:

$$\begin{array}{ccc}\hfill D_1& =& v_2{D}_1^2\vee v_1{D}_1^3;L\left(D_1\right)=4;\hfill \\ \hfill D_2& =& EMB\left[6\right];L\left(D_2\right)=1;\hfill \\ \hfill D_3& =& \overline{v_1}\overline{v_2}{D}_3^1\vee v_1{D}_3^3;L\left(D_3\right)=4;\hfill \\ \hfill D_4& =& EMB\left[7\right];L\left(D_4\right)=1.\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill y_1& =& \overline{v_1}\overline{v_2}{y}_1^1\vee v_2{y}_1^2;L\left(y_1\right)=4\hfill \\ \hfill y_2& =& \overline{v_1}\overline{v_2}{y}_2^1;L\left(y_2\right)=3;\hfill \\ \hfill y_3& =& v_1{y}_3^3;L\left(y_3\right)=2;y_4=v_1{y}_3^3;L\left(y_4\right)=2;\hfill \\ \hfill y_5& =& \overline{v_1}\overline{v_2}{y}_5^1;L\left(y_5\right)=3;y_6=v_1{y}_6^3;L\left(y_6\right)=2;\hfill \\ \hfill y_7& =& v_2{y}_7^2;L\left(y_7\right)=2;y_8=v_1{y}_8^3;L\left(y_8\right)=2;\hfill \\ \hfill y_9& =& \overline{v_1}\overline{v_2}{y}_9^1\vee v_1{y}_9^3;L\left(y_9\right)=4;\hfill \\ \hfill y_{10}& =& \overline{v_1}\overline{v_2}{y}_{10}^1;L\left(y_{10}\right)=3;y_{11}=v_2{y}_{11}^2;L\left(y_{11}\right)=2.\hfill \end{array}$$

(53)

As follows from the system (52), it is necessary to transform the equations for $D_1$ and $D_3$. But we can escape it using the following approach. There is $L\left(D_1^2\right)=2$. Let us multiply it by $v_2$. It gives $D_1=v_2(z_2\vee z_2\overline{z_3})$. Now, we could represent $D_1$ as $D_1=D_1^2\vee v_1{D}_1^3$ with $L\left(D_1\right)=3$. So, now it is enough a single LUT for implementing the function $D_1$. The same could be done for $y_1$. But it is necessary to apply the rules of functional decomposition for functions $D_3$ and $y_9$. For example, there are two LUTs in the circuit for $D_3$ (Figure 9).

The equation $D_3$ is represented as $f_1\vee v_1$$D_3^3$, where $f_1=\overline{v_1}\overline{v_2}{D}_3^1$. The equation for $y_9$ will be the following: $f_2\vee v_1{y}_9^3$. Here $f_2=\overline{v_1}{v}_2{y}_9^1$. Therefore, there are two LUTs in the circuit of $y_9$.

To find the systems (16) and (31), it is necessary to transform the DST of Mealy FSM $U_5$. To transform the DST, it is necessary to delete the column $a_s$, $K\left(a_s\right)$, $Y_h$ and ${\Phi }_h$. They are replaced by the following columns: $C\left(F^k\right)$, $C\left(F_h\right)$, $V_h$, $Z_h$, $Y_{Eh}$ and ${\Phi }_{E_h}$. The column $V_h$ includes the variables $v_r\in V$ equal to 1 in the code $C\left(F^k\right)$ from the h-th row of transformed DST. The column $Z_h$ includes the variables $z_r\in Z$ equal 1 in the code $C\left(F_h\right)$ of the term $F_h$ $h\in \{1,\dots ,H\}$. The column $Y_{Eh}$ includes the functions $y_n\in Y_E$ generated during the h-th transition of FSM. The column ${\Phi }_{Eh}$ contains the variables $D_r\in {\Phi }_E$ equal to 1 in the h-row of initial DST. In the discussed case, there is $Y_E=Ø$. So, the column $Y_{Eh}$ is absent in the transformed table of Mealy FSM $U_5\left(S_1\right)$ (

Table 5. Transformed DST of Mealy FSM $U_5\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{K}\left({\mathit{a}}_{\mathit{m}}\right)$	$\mathit{C}\left({\mathit{F}}^{\mathit{k}}\right)$	$\mathit{C}\left({\mathit{F}}_{\mathit{h}}\right)$	${\mathit{V}}_{\mathit{h}}$	${\mathit{Z}}_{\mathit{h}}$	${\mathsf{\Phi }}_{\mathit{E}\mathit{h}}$	h	${\mathit{X}}_{\mathit{h}}$
$a_1$	0000	00	110	–	$z_1{z}_2$	$D_2$	1	$x_1$
		*1	000	$v_2$	–	$D_4$	2	$\overline{x_1}$
$a_2$	0100	00	010	–	$z_2$	$D_4$	3	$x_2$
		1*	001	$v_1$	$z_3$	$D_2$	4	$\overline{x_2}{x}_3$
		*1	010	$v_2$	$z_2$	$D_2$	5	$\overline{x_2}\overline{x_3}$
$a_3$	0001	*1	001	$v_2$	$z_3$	$D_2$	6	1
$a_4$	0101	1*	000	$v_1$	–	$D_2$	7	$x_3$
		00	011	–	$z_2{z}_3$	–	8	$\overline{x_3}$
$a_5$	1100	*1	011	$v_2$	$z_2{z}_3$	–	9	1
$a_6$	1110	*1	100	$v_2$	$z_1$	$D_2$	10	$x_4$
		00	100	–	$z_1$	$D_2$	11	$\overline{x_4}$
$a_7$	0010	00	001	–	$z_3$	–	12	1
$a_8$	1010	1*	110	$v_1$	$z_1{z}_2$	$D_2{D}_4$	13	$x_5$
		1*	101	$v_1$	$z_1{z}_3$	–	14	$\overline{x_5}$
$a_9$	1101	00	101	–	$z_1{z}_3$	$D_2{D}_4$	15	$x_6$
		*1	111	$v_2$	$z_1{z}_2{z}_3$	$D-2$	16	$\overline{x_6}$
$a_{10}$	1000	*1	101	$v_2$	$z_1{z}_{3}3$	–	17	1
$a_{11}$	0110	1*	011	$v_1$	$z_2{z}_3$	$D_4$	18	1
$a_{12}$	1001	1*	010	$v_1$	$z_2$	–	19	$x_7$
		1*	100	$v_1$	$z_1$	–	20	$\overline{x_7}$

).

To implement the functions $Z(T,X)$, $V(T,X)$, ${\Phi }_{E}T,X$ and $Y_E(T,X)$, it is necessary to construct the table of EMB. It contains the following columns: $K\left(a_m\right)$, X, Z, V, ${\Phi }_E$, $Y_E$, q. The addresses of cells are determined by concatenations of $K\left(a_m\right)$ and X. The table includes $H_E$ rows:

$$H_E=2^{L+R}.$$

(54)

It is necessary $H\left(a_m\right)$ rows to represent transitions from a state $a_m\in A$, where

$$H\left(a_m\right)=2^L.$$

(55)

Using (54) and (55) gives $H_E=2048$ and $H\left(a_m\right)=128$ for $U_5\left(S_1\right)$. The first 8 rows of table of EMB is shown in

Table 6. Part of table of EMB of Mealy FSM $U_5\left(S_1\right)$

$\mathit{K}\left({\mathit{a}}_{\mathit{m}}\right)$	X	Z	V	${\mathsf{\Phi }}_{\mathit{E}}$	q
${\mathit{T}}_{\mathbf{1}}{\mathit{T}}_{\mathbf{2}}{\mathit{T}}_{\mathbf{3}}{\mathit{T}}_{\mathbf{4}}$	${\mathit{x}}_{\mathbf{1}}{\mathit{x}}_{\mathbf{2}}{\mathit{x}}_{\mathbf{3}}{\mathit{x}}_{\mathbf{4}}{\mathit{x}}_{\mathbf{5}}{\mathit{x}}_{\mathbf{6}}{\mathit{x}}_{\mathbf{7}}$	${\mathit{z}}_{\mathit{1}}{\mathit{z}}_{\mathbf{2}}{\mathit{z}}_{\mathbf{3}}$	${\mathit{v}}_{\mathbf{1}}{\mathit{v}}_{\mathbf{2}}$	${\mathit{D}}_{\mathbf{2}}{\mathit{D}}_{\mathbf{4}}$
0000	0000000	000	01	01	1
0000	0000001	000	01	01	2
0000	0000010	000	01	01	3
0000	0000011	000	01	01	4
0000	0000100	000	01	01	5
0000	0000101	000	01	01	6
0000	0000110	000	01	01	7
0000	0000111	000	01	01	8

. These rows represent transitions from the state $a_1$. There is $x_1=0$ for these rows. Therefore, these 8 rows correspond to $h=2$ from Table 5. Due to $Y_e=Ø$, we do not show the column $Y_E$ in Table 5.

7. Experimental Results

To investigate the efficiency of proposed method, we use standard benchmarks from the library [11]. The library includes 48 benchmarks taken from the design practice. The benchmarks are rather simple, but they are very often used by different studies to compare new and known results [26]. The benchmarks are represented in KISS2 format. The characteristics of benchmarks are shown in

Table 7. Characteristics of Mealy FSM benchmarks.

Benchmark	L	N	H/${\mathit{R}}_{\mathit{H}}$	M/R	EMB
bbara	4	2	60/6	10/4	+
bbsse	7	7	56/6	16/4	+
bbtas	2	2	24/5	6/3	+
beecount	3	4	28/5	7/3	+
cse	7	7	91/7	16/4	+
dk14	3	5	56/6	7/3	+
dk15	3	5	32/5	4/2	+
dk16	2	3	108/7	27/5	+
dk17	2	3	32/5	8/3	+
dk27	1	2	14/4	7/3	+
dk512	1	3	15/4	15/4	+
donfile	2	1	96/7	24/5	+
ex1	9	19	138/8	20/5	<14, 19>
ex2	2	2	72/7	19/5	+
ex3	2	2	36/6	10/4	+
ex4	6	9	21/5	14/4	+
ex5	2	2	32/5	9/4	+
ex6	5	8	34/6	8/3	+
ex7	2	2	36/6	10/4	+
keyb	7	7	170/8	19/5	+
kirkman	12	6	370/9	16/4	<16,6>
lion	2	1	11/4	4/2	+
lion9	2	1	25/5	9/4	+
mark1	5	16	22/5	15/4	+
mc	3	5	10/4	4/2	+
modulo12	1	1	24/5	12/4	+
opus	5	6	22/5	10/4	+
planet	7	19	115/7	48/6	<13,19>
planet1	7	19	115/7	48/6	<13,19>
pma	8	8	73/7	24/5	<13,8>
s1	8	7	106/7	20/5	<13,7>
s1488	8	19	251/8	48/6	<14,19>
s1494	8	19	250/8	48/6	<14,19>
s1a	8	4	107/7	20/5	+
s208	11	2	153/8	18/5	<16,2>
s27	4	1	34/6	6/3	+
s298	3	6	1096/11	218/8	+
s386	7	7	64/6	13/4	+
s420	19	2	137/8	18/5	<24,2>
s510	19	7	77/7	47/6	<25,7>
s8	4	1	20/5	5/3	+
s820	18	19	232/8	25/5	<23,19>
s832	18	19	245/8	25/5	<23,19>
sand	11	9	184/8	32/5	<16, 9>
shiftreg	1	1	16/4	8/3	+
sse	7	7	56/6	16/4	+
styr	9	10	166/8	30/5	<14,10>
tma	7	8	44/6	20/5	+

.

We used our CAD tool K2F [26] to translate KISS2 –based files into VHDL-based FSM models. Next, the Active-HDL environment was used to synthesize and simulate FSMs. To get FSM circuits, we used Xilinx CAD tool Vivado [27]. The FPGA chip XC7VX690TFFG1761-2 by Vertex-7 [28] was used as a target platform. The chip includes LUTs with 6 inputs and EMBs with configurations from $\langle 15,1\rangle$ till $\langle 9,64\rangle$.

We presume that only a single EMB is available to implement an FSM circuit. As follows from Table 7, the condition (7) takes place for 33 benchmark FSMs (it is around 68% from all benchmarks). Therefore, it is necessary only a single EMB to implement an FSM circuit for these benchmarks. We mark this situation by the sign “+” in the column “EMB” of Table 7. Also, we show in this column pairs $\langle S_A,t_F\rangle$ corresponding to the configuration required to implement the circuit with a single EMB. The further research was conducted for these 15 benchmarks.

Three discussed methods ($U_1$, $U_3$ and $U_4$) were taken to compare with our approach ($U_5$). The results are shown in

Table 8. Results of experiments (the number of LUTs).

Benchmark	${\mathit{U}}_1$	${\mathit{U}}_3$	${\mathit{U}}_4$	${\mathit{U}}_5$
ex1	22	19	48	36
kirkman	30	26	27	11
planet	21	16	51	38
planet1	21	16	51	38
pma	28	23	27	14
s1	26	23	24	12
s1488	24	21	52	37
s1494	28	24	50	39
s208	29	23	8	7
s420	38	36	8	7
s510	39	36	22	15
s820	40	34	47	36
s832	41	34	47	35
sand	27	23	29	16
styr	26	20	31	18
Total	440	374	522	359
Percentage	123%	104%	145%	100%

(the number of LUTs in FSM circuits),

Table 9. Results of experiments (the operating frequency, MHz).

Benchmark	${\mathit{U}}_1$	${\mathit{U}}_3$	${\mathit{U}}_4$	${\mathit{U}}_5$
ex1	141.43	105.78	158.28	212.93
kirkman	125.78	107.81	155.11	174.73
planet	122.01	105.41	124.31	187.95
planet1	122.01	105.41	124.31	187.95
pma	115.41	114.49	127.65	186.22
s1	124.49	117.80	132.85	178.84
s1488	127.80	112.79	131.77	186.37
s1494	122.79	124.92	135.73	181.62
s208	144.92	128.04	144.05	209.36
s420	148.04	112.66	152.65	192.14
s510	122.66	111.42	138.75	192.87
s820	121.42	88.65	133.36	163.18
s832	98.65	115.57	100.53	184.69
sand	135.57	104.68	146.78	178.65
styr	114.68	116.47	115.69	181.22
Total	1887.66	1671.90	2021.82	2798.72
Percentage	67.4%	59.7%	72.2%	100%

(the operating frequency) and

Table 10. Results of experiments (the consumed energy, Watts).

Benchmark	${\mathit{U}}_1$	${\mathit{U}}_3$	${\mathit{U}}_4$	${\mathit{U}}_5$
ex1	3.560	3.290	3.014	2.918
kirkman	4.922	3.562	2.811	2.476
planet	3.222	3.756	1.727	1.527
planet1	3.222	3.756	1.727	1.527
pma	4.778	4.915	4.257	3.683
s1	3.694	3.813	3.578	3.058
s1488	1.586	2.412	1.449	1.785
s1494	1.730	2.398	1.453	1.302
s208	3.005	3.544	2.574	2.248
s420	1.604	3.384	1.543	1.292
s510	1.883	1.996	1.878	1.682
s820	2.465	2.161	1.756	1.843
s832	2.515	2.504	2.193	1.732
sand	2.579	2.578	2.385	2.017
styr	1.467	1.556	1.307	1.112
Total	42.232	45.625	33.652	30.202
Percentage	139.8%	151%	111.4%	100%

(the consumed energy). To design FSM $U_1$, a single EMB was used to implement a part of FSM circuit. We do not know which part of a circuit was implemented as an EMB. It is up to Vivado and cannot be directly specified by a designer.

Table 8, Table 9 and Table 10 are organized in the same order. The rows are marked by the names of benchmarks, the columns by design methods. The rows “Total” include results of summation for values from corresponding columns. The summarized characteristics of $U_5$-based FSMs are taken as 100%. The rows “Percentage” show the percentage of summarized characteristics respectively to $U_5$-based benchmarks. To design all circuits, we use the mode AUTO of Vivado.

As follows from Table 8, the $U_5$-based FSMs require fewer LUTs than their counterparts based on other FSM models. There is the following economy: (1) 23% regarding $U_1$; (2) 4% regarding $U_3$; (3) 45% regarding $U_4$. Therefore, for these benchmarks the $U_4$-based FSMs require the largest number of LUTs. It is connected with the fact that the condition (20) is violated for all considered $U_4$-based benchmarks. It results in multi-level circuits implementing functions (17) and (18).

As follows from Table 9, the $U_5$-based FSMs have the highest operating frequency as compared to other investigated FSMs. We think that this is due to the smaller number of logic levels and inter-level connections compared to other investigated FSMs. But we cannot prove this statement because Vivado does not show these details about implemented circuits. There is the following gain in operating frequency: (1) 32.6% regarding $U_1$; (2) 44.3% regarding $U_3$; (3) 27.8% regarding $U_4$. The lowest frequency takes place for $U_3$ –-based FSMs. It is connected with rather big amount of inputs. Because $L+R>>SL$, the circuit of LUTerP is multi-level. For discussed benchmarks, the number of logic levels in $U_3$-based FSMs is higher than it is for FSMs produced by other investigated methods.

As follows from Table 10, the $U_5$-based FSMs consume less energy than their counterparts based on other FSM models. There is the following economy: (1) 39.8% regarding $U_1$; (2) 51% regarding $U_3$; (3) 11.4% regarding $U_4$. It is connected with the fact that $U_5$-based FSM circuits have fewer LUTs and, therefore, interconnections compared to other investigated FSMs. Interconnections are known to be responsible for up to 70% of energy losses in FPGA-based circuits [26]. The results shown in Table 10 include the total power value in Watts. It should be noted that the total power consists of individual powers such as: static power, I/O, signals, LUT as Logic, F7/F8 Muxes, BUFG, registers and others. Furthermore, the frequency has a very strong impact to the power consumption.

Therefore, our approach produces better results for FSMs whose circuits cannot be implemented as a single EMB. Of course, this conclusion is true only for the benchmarks [11] and the device XC7VX690TFFG1761-2. It is almost impossible to make similar conclusion for the general case.

8. Conclusions

Contemporary FPGA devices include a lot of look-up table elements. It allows the implementation of very complex digital system using only a single chip. But LUTs have rather small amount of inputs ($S_L$ does not exceeds 6). This value is considered to be optimal [6]. Such a limitation leads multi-level circuits representing, for example, sequential blocks of digital systems. To design multi-level circuits, the methods of functional decomposition are used. But these blocks can be synthesized using different methods of structural decomposition. As our studies [26] show, the structural decomposition can lead to FSM circuits with better characteristics than their counterparts based on functional decomposition.

The aim of this article is a presentation of a novel method of logic synthesis targeting Mealy FSMs implemented with LUTs and a configurable EMB. It is the method of structural decomposition based on encoding of product terms of Boolean functions representing FSM logic circuits. The essence of our approach is a splitting of the set of terms in a way minimizing the number of LUTs in FSM circuits. The proposed method is technology depended because it takes into account the number of inputs of LUT elements.

The experiments conducted using the Xilinx CAD tool Vivado 2019.1 clearly show that the proposed approach leads to reduction for such values as the number of LUTs, propagation time and consumed energy in comparison with FSM circuits based on known methods of terms encoding.

There are three directions in our future research. The first is connected with development design methods targeting FPGA chips of Intel (Altera). The second direction is connected with using our approach in real devices such as PDMS micro-optofluidic chip [29,30]. The last direction targets sequential blocs represented by Moore FSMs.