Some Algorithms to Solve a Bi-Objectives Problem for Team Selection
Abstract
1. Introduction
1.1. Background
1.2. Compromise Solution
1.3. Contribution of the Paper
2. DC Programming and DCA for MDSB
2.1. A Brief Introduction of DC Programming and DCA
- Let , Choose in , and ϵ is small enough.
- Calculate in .
- Calculate
- If come back to step 2.
- A vector y is called a subgradient of a convex function f at a point ifThe set of all subgradients of f at is called the subdifferential of f at and is denoted by .
- The modulus of convex function f denoted byIf then f is strongly convex.
- A point is called a critical point of if it verifies the generalized Kuhn–Tucker condition
- (i)
- The sequences are decreasing and iff and . Moreover, if g or h are strongly convex on C, then = . In such case, DCA terminates at kth iteration (finite convergence of DCA).
- (ii)
- If or are strongly convex, then the series converges.
- (iii)
- If the optimal value α of DC program is finite and the infinite sequences and are bounded, then every limit point of sequence is a critical point of , i.e., .
- (iv)
- DCA has a linear convergence for DC programs.
2.2. DC Decomposition and DCA for MDSB-PMDSB
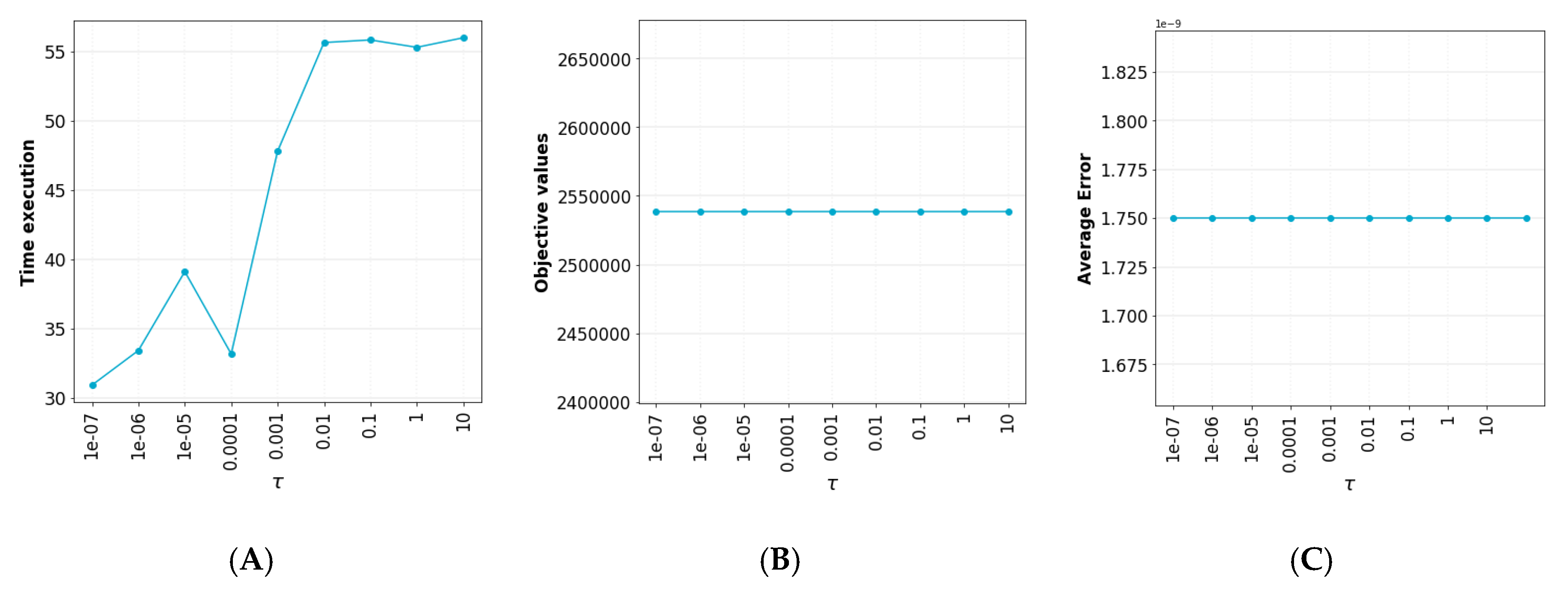
- Randomly select , and ϵ is small enough and a suitable value of τ.
- Calculate the approximation of at .
- Compute by solving the sub-problem:subject to:It is possible to solve the problem with several solvers such as CPLEX.
- If , come back to step 2.
2.3. The Convergence of DCA for PMDSB
- (i)
- The sequence is decreasing.
- (ii)
- The sequence is convergent.
- (iii)
- Every limit point of the sequence is a critical point of i.e.,
- (iv)
- .
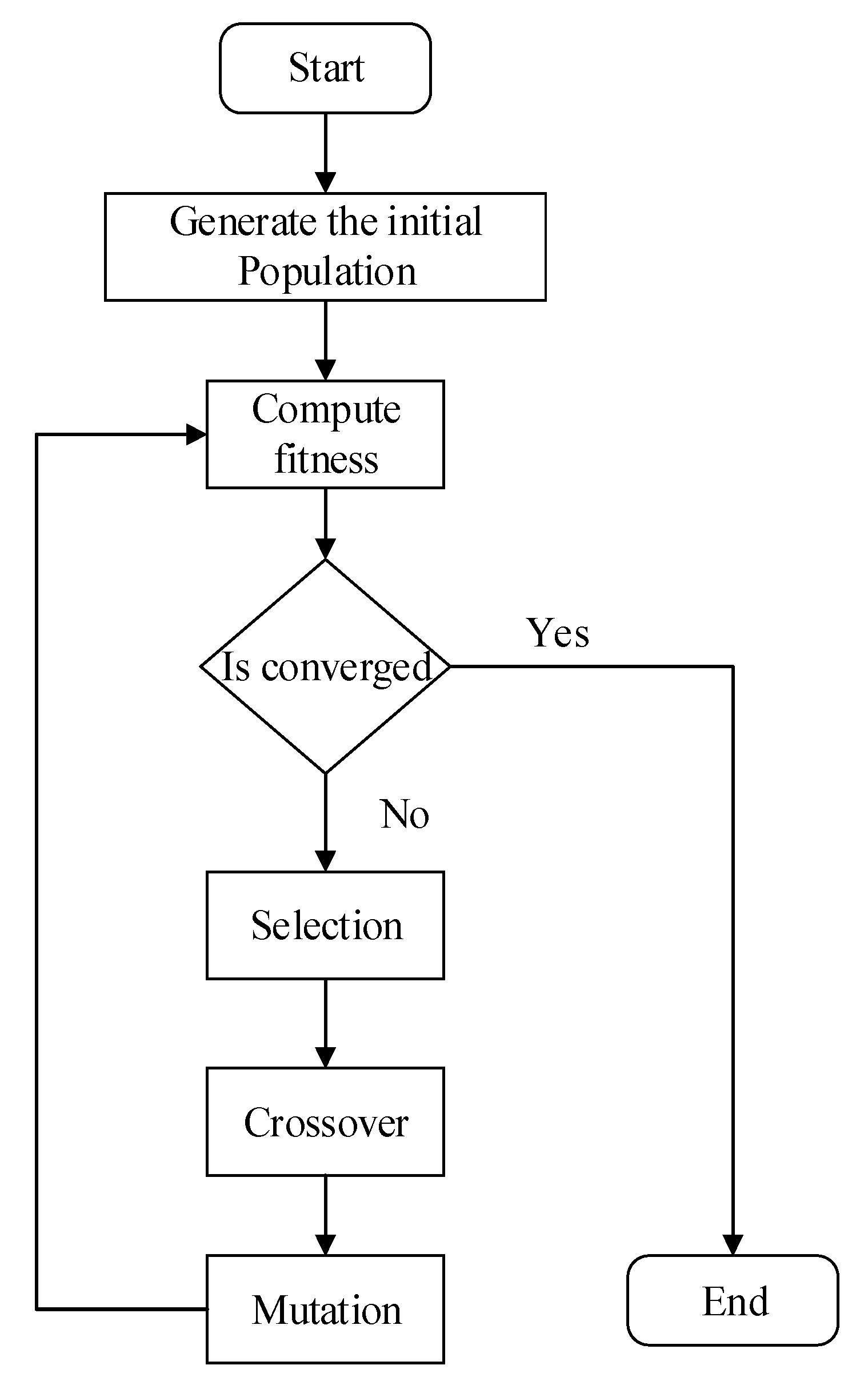
3. Genetic Algorithm for MDSB
3.1. Introduction to Genetic Algorithm
3.2. Genetic Algorithm Scheme for MDSB
- Randomly initialize the populations of k individuals from T.
- Elitism Selection: keep γ as the elitism rate among D individuals that return the best fitness for next-generation. Denote the best fitness value of the generation as .
- Crossover: Denote the ω as crossover rate of the D individuals that return the best fitness as K. Randomly select and from K. We generate the next generation as follows:
- Set is the probability that the candidate dominant selected for the position in the
- Set is the probability that the candidate recessive selected for the position in the .
- Let denote the probability that a random selected candidate in set T chosen for the position in the . This probability represents the rate of mutation.
where and is the function that rolls the dice and returns the corresponding user based on the parameters that are the probabilities passed; - Constraint validation checking: If there is an individual that violates any constraints of the MDSB, then it is removed from the set of results.
- Repeat 2, 3, and 4 until .
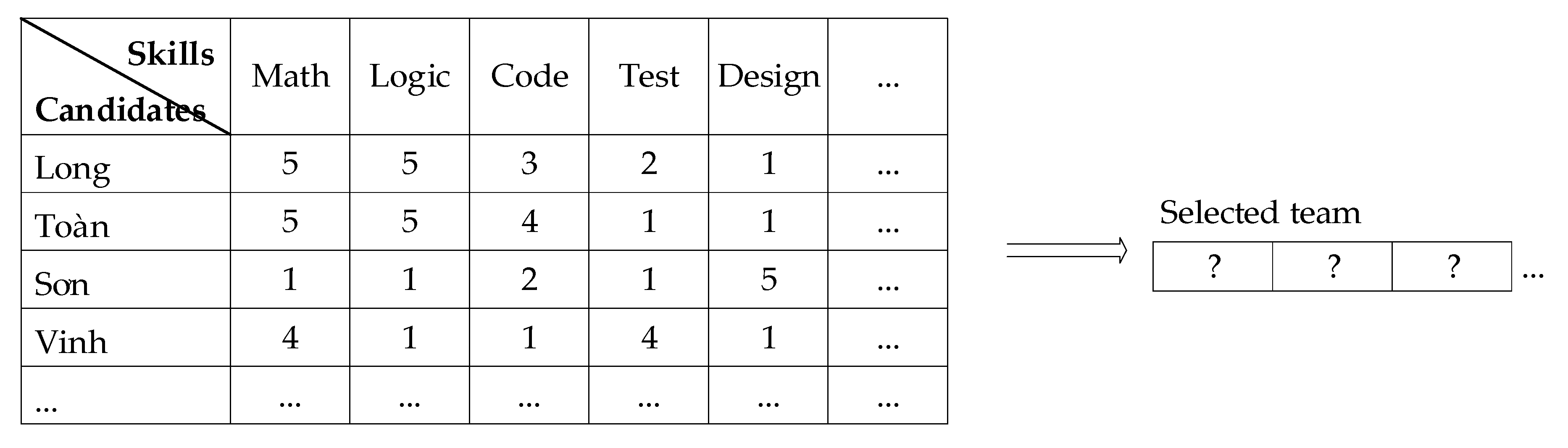
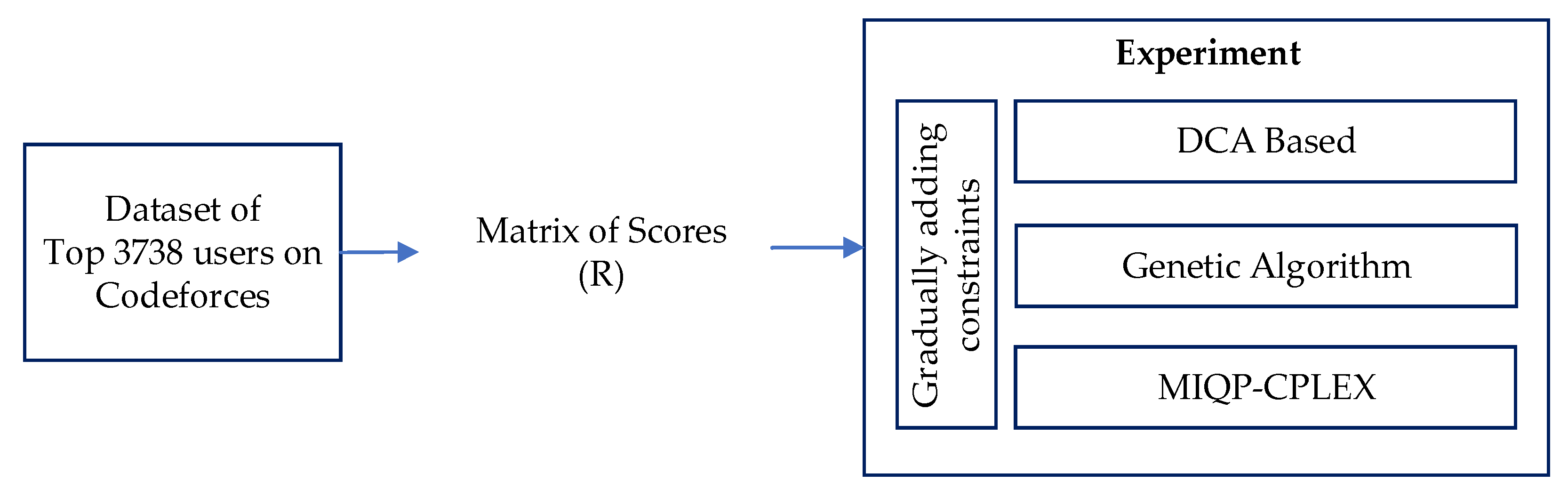
4. Experimental Design
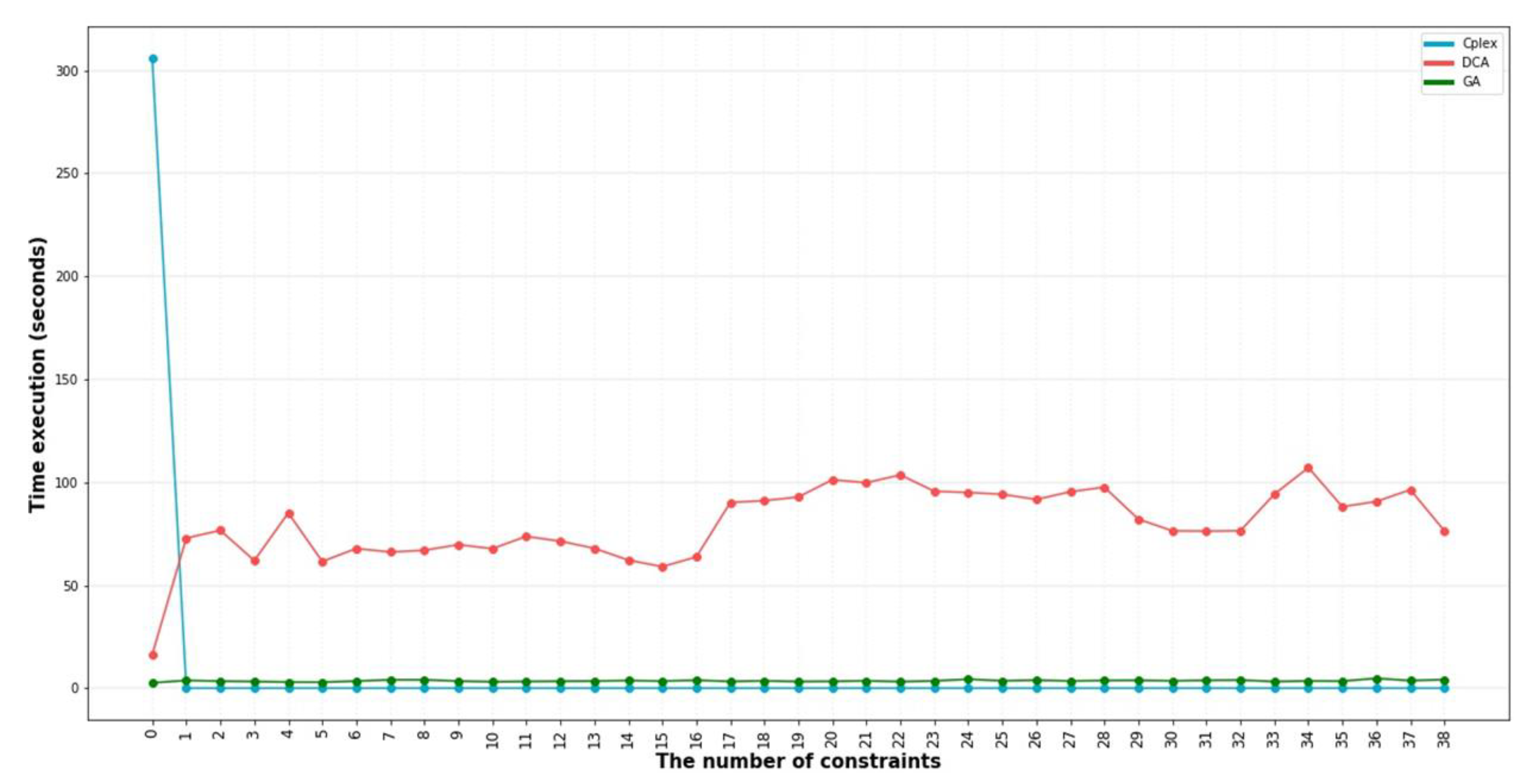
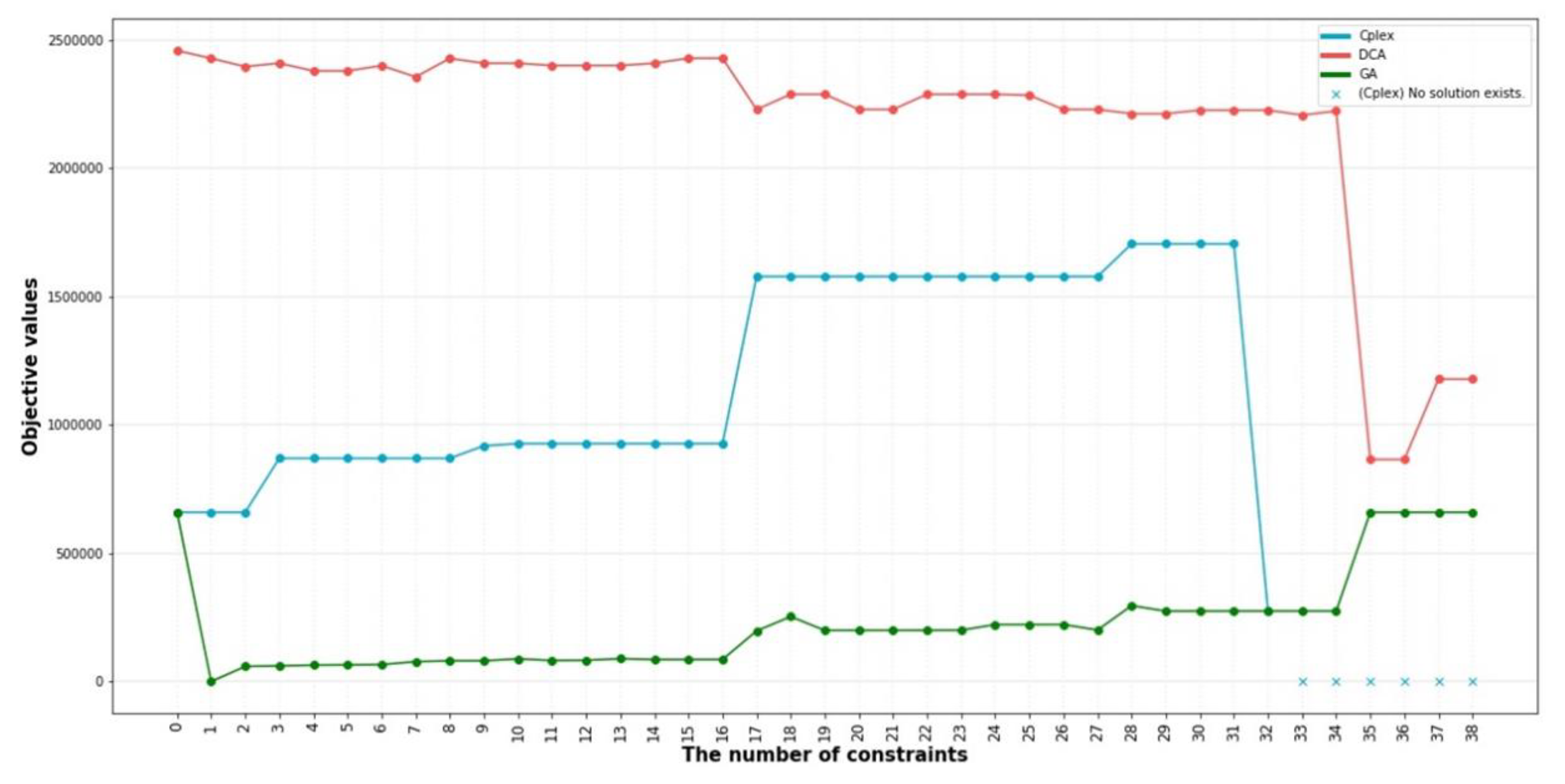
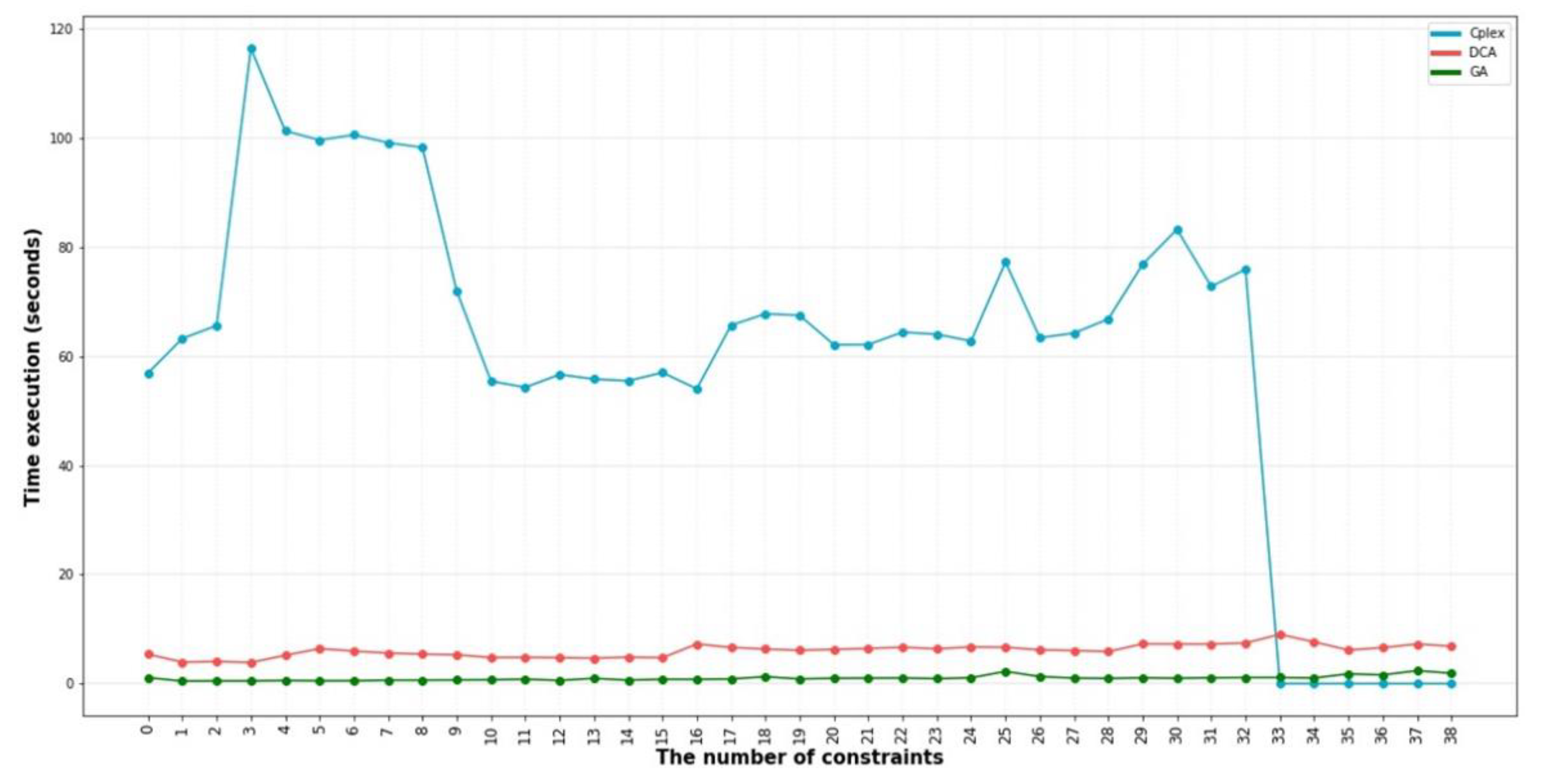
5. Result
5.1. Init Parameter
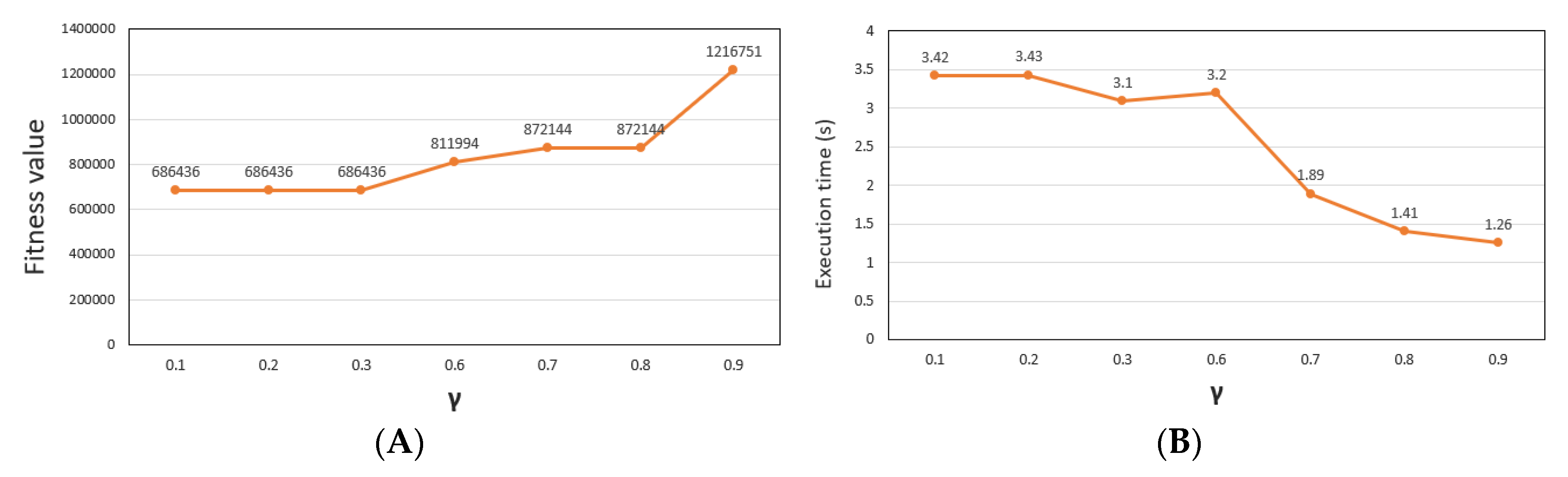
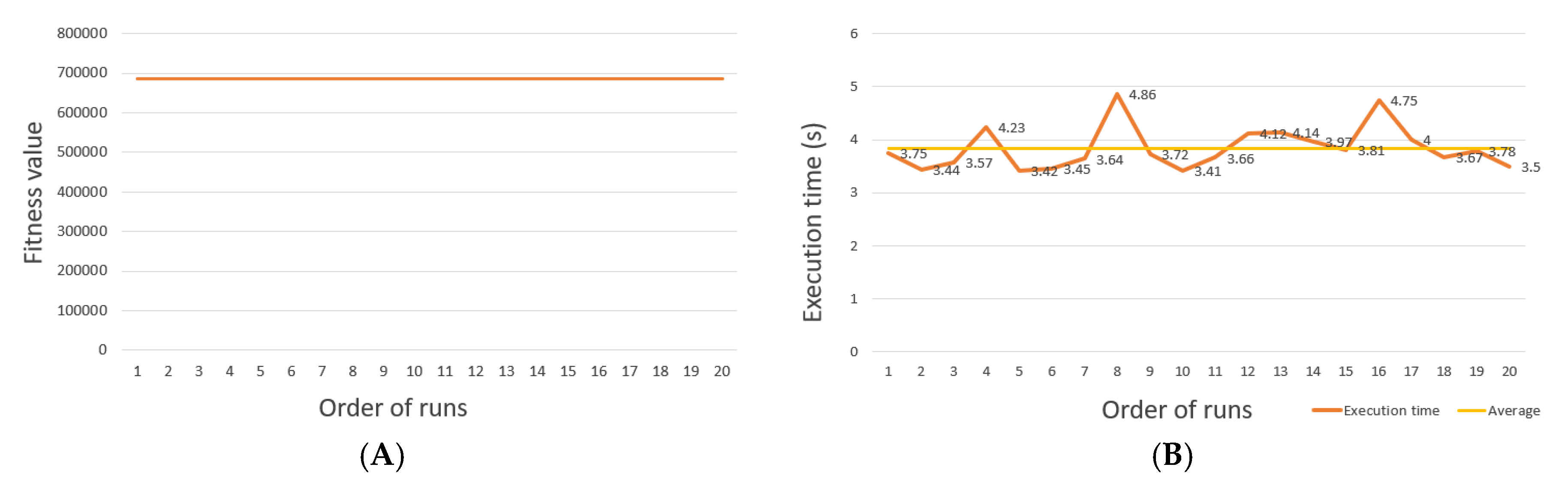
- γ: defined as the rate of individuals remains the same for the next generation. γ = 0.4 to 0.9, the algorithm is fast convergence but generates a not good fitness value. In addition, γ = 0.1 to 0.3 makes the algorithm to have stable convergence, while creating a fitness value. Figure 10 displays the execution and fitness values over generations corresponding to different amounts of γ.
- D: defined as the rate of population size to the whole candidates. The execution time is proportional to the magnitude of D (not significant gap). D takes too small values generating unstable fitness values. D = 0.7 to 0.9 generates more stable fitness values.
- ω: represents the crossover rate. The execution time is proportional to the magnitude of ω (not a significant gap). ω = 0.2 to 0.5 provides relatively stable fitness values. However, there is still a possibility that fitness is not functional because the number of individuals to choose for crossovers shrinks quickly through each generation, leading to a loss of diversity, ultimately making the results worse. ω = 0.6 to 0.9 generates unstable fitness. Because the pool of the crossover is large, it is not good for the improvement of the individuals over generations, which occurs more often when generations > 10.
- : denote the rates of the selection of recessive, dominant, and mutant genes during the crossover. These parameters are interdependent. Table 1 shows some performance results relative to the value pairs.
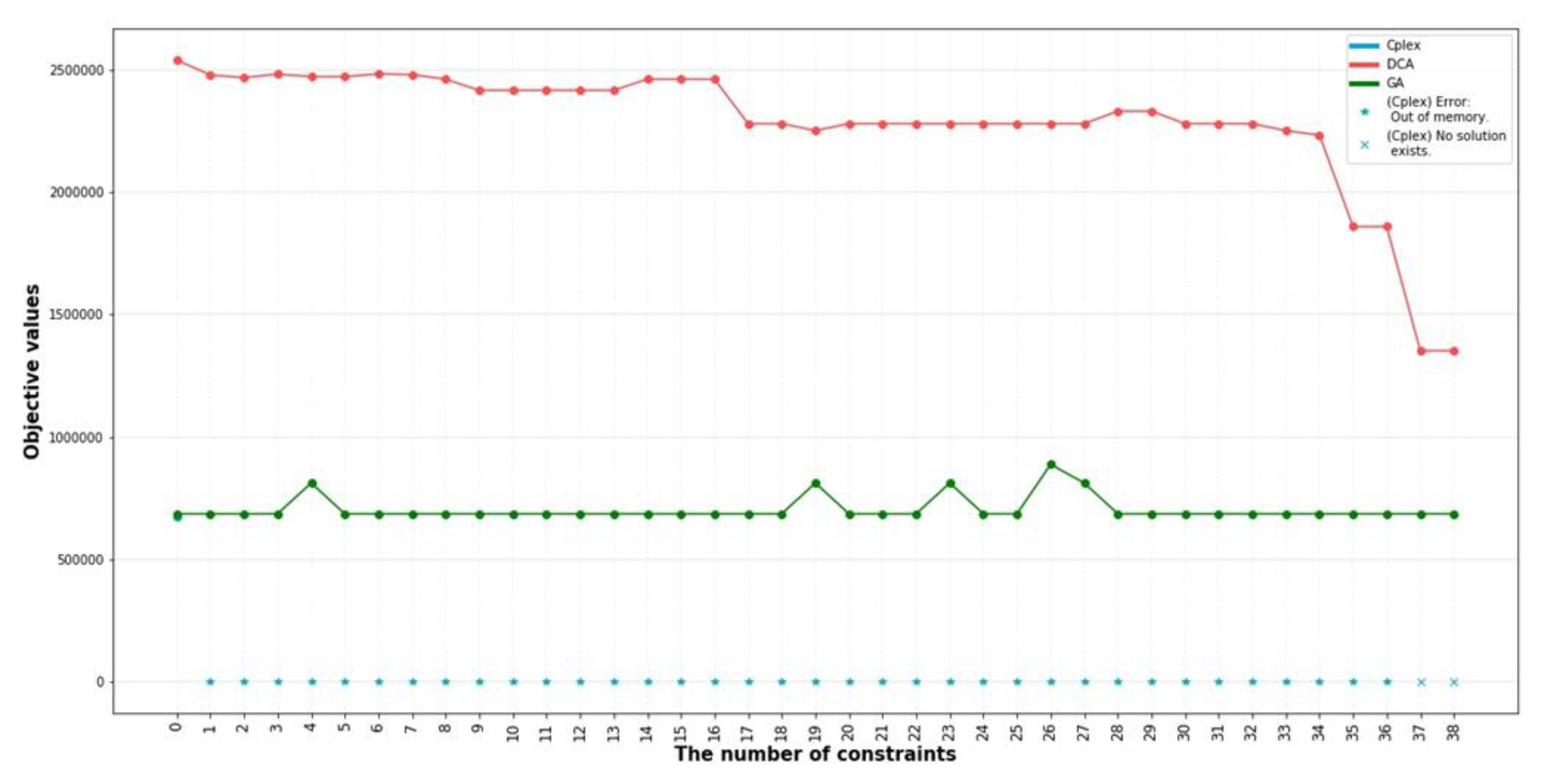
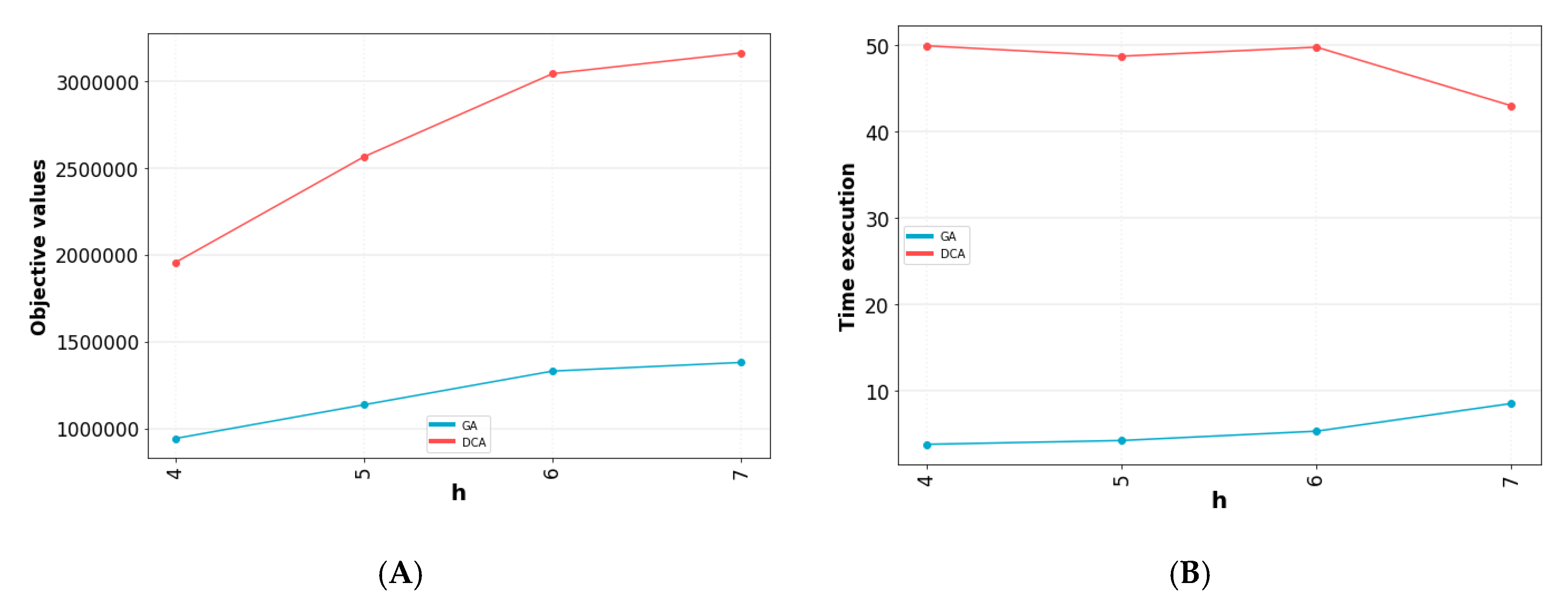
5.2. Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Son, N.T.; Thanh, L.V.; Duong, T.B.; Anh, B.N. A decision support tool for cross-functional team selection: Case study in ACM-ICPC team selection. In Proceedings of the 2018 International Conference on Information Management & Management Science (IMMS ’18), Chengdu, China, 25–27 August 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 133–138. [Google Scholar] [CrossRef]
- Son, N.T.; Thu, T.T.; Anh, B.N.; Dinh, T.V. DCA-Based Algorithm for Cross-Functional Team Selection. In Proceedings of the 2019 8th International Conference on Software and Computer Applications (ICSCA ’19), Penang, Malaysia, 19–22 February 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 125–129. [Google Scholar] [CrossRef]
- Keller, R.T. Cross-functional Project Groups in Research and New Product Development: Diversity, Communication, Job Stress and Outcomes. Acad. Manag. J. 2001, 44, 547–555. [Google Scholar]
- Parker, G. Cross Functional Teams: Working with Allies, Enemies and Other Strangers; Jossey Bass, A Wiley Imprint: San Francisco, CA, USA, 2003; pp. 4–15. Available online: www.josseybass.com (accessed on 12 November 2019).
- Wang, Z.; Yan, H.S.; Ma, X.D. A quantitative approach to the organization of cross-functional teams in concurrent engineering. Int. J. Adv. Manuf. Technol. 2003, 21, 879–888. [Google Scholar] [CrossRef]
- Das, D. Moneyballer: An Integer Optimization Framework for Fantasy Cricket League Selection and Substitution. 2014. Available online: http://debarghyadas.com/files/IPLpaper.pdf (accessed on 12 November 2019).
- Bhattacharjee, D.; Saikia, H. An objective approach of balanced cricket team selection using binary integer programming method. OPSEARCH 2016, 53, 225–247. [Google Scholar] [CrossRef]
- Sandhya, S.; Garg, R.; Garg, R. Implementation of multi-criteria decision making approach for the team leader selection in IT sector. J. Proj. Manag. 2016, 1, 67–75. [Google Scholar] [CrossRef]
- Feng, B.; Jiang, Z.-Z.; Fan, Z.-P.; Fu, N. A method for member selection of cross-functional teams using the individual and collaborative performances. Eur. J. Oper. Res. 2010, 203, 652–661. [Google Scholar] [CrossRef]
- Fan, Z.-P.; Feng, B.; Jiang, Z.-Z.; Fu, N. A method for member selection of R&D teams using the individual and collaborative information. Expert Syst. Appl. 2009, 36, 8313–8323. [Google Scholar] [CrossRef]
- Su, J.; Yang, Y.; Zhang, X. A Member Selection Model of Collaboration New Product Development Teams Considering Knowledge and Collaboration. J. Intell. Syst. 2016, 27, 213–229. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective Evolutionary Algorithms: Analyzing the State-of-the-Art. Evol. Comput. 2000. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.-L.; Masud, A.S.M. Multiple Objective Decision Making, Methods and Applications: A State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1979; ISBN 978-0-387-09111-2. [Google Scholar]
- Zeleny, M. Compromise Programming. In Multiple Criteria Decision Making; Cochrane, J.L., Zeleny, M., Eds.; University of South Carolina Press: Columbia, SC, USA, 1973; pp. 262–301. [Google Scholar]
- Edmondson, A.C.; Harvey, J. Cross-boundary teaming for innovation: Integrating research on teams and knowledge in organizations. Hum. Resour. Manag. Rev. 2018, 28, 347–360. [Google Scholar] [CrossRef]
- Lazimy, R. Mixed-integer quadratic programming. Math. Program. 1982, 22, 332. [Google Scholar] [CrossRef]
- Le Thi, H.A.; Pham Dinh, T. DC programming and DCA: Thirty years of developments. Math. Program. 2018, 169, 5–68. [Google Scholar] [CrossRef]
- Duy, N.T.; Thuy, T.T.; Chung, L.T.; Son, N.T.; Dinh, T.V. DC programming and DCA for Secure Guarantee with Null Space Beamforming in Two-Way Relay Networks. In Proceedings of the 2019 8th International Conference on Software and Computer Applications (ICSCA’19), Penang, Malaysia, 19–21 February 2019; ACM: New York, NY, USA, 2019; pp. 529–532. [Google Scholar] [CrossRef]
- Thuy, T.T.; Nam, N.V.; Son, N.T.; Dinh, T.V. DC Programming and DCA for Power Minimization Problem in Multi-User Beamforming Networks. In Proceedings of the 2019 8th International Conference on Software and Computer Applications (ICSCA’19), Penang, Malaysia, 19–21 February 2019; ACM: New York, NY, USA, 2019; pp. 564–568. [Google Scholar] [CrossRef]
- Phan, D.N.; le Thi, H.A. Group variable selection via lp,0 regularization and application to optimal scoring. Neural Netw. 2019, 118, 220–234. [Google Scholar] [CrossRef] [PubMed]
- Le Thi, H.A.; Ho, V.T. Online Learning based on Online DCA and Application to Online Classification. Neural Comput. 2020, 32, 1–35. [Google Scholar] [CrossRef] [PubMed]
- An, L.T.H.; Tao, P.D.; Muu, L.D. Exact Penalty in D.C. Programming. Vietnam J. Math. 1999, 27, 169–178. [Google Scholar]
- Thede, S.M. An Introduction to Genetic Algorithms. J. Comput. Sci. Coll. 2004, 20, 115–123. [Google Scholar]
- Sharp, G.D.; Brettenny, W.J.; Gonsalves, J.W.; Lourens, M.; Stretch, R.A. Article: Integer optimisation for the selection of a Twenty 20 cricket team. J. Oper. Res. Soc. 2011, 62, 1688–1694. [Google Scholar] [CrossRef]
- Burney, A.S.M.; Mahmood, N.; Rizwan, K.; Amjad, U. Article: A Generic Approach for Team Selection in Multi-player Games using Genetic Algorithm. Int. J. Comput. Appl. 2012, 40, 11–17. [Google Scholar]
- Codeforce API. Available online: https://codeforces.com/apiHelp (accessed on 2 February 2020).
- IBM ILOG CPLEX Optimization Studio. CPLEX User’s Manual. Version 12 Release 8. Available online: https://www.ibm.com/support/knowledgecenter/SSSA5P_12.7.0/ilog.odms.studio.help/pdf/usrcplex.pdf (accessed on 2 February 2020).
- Muthuraman, S.; Venkatesan, V.P. A Comprehensive Study on Hybrid Meta-Heuristic Approaches Used for Solving Combinatorial Optimization Problems. In Proceedings of the 2017 World Congress on Computing and Communication Technologies (WCCCT), Tiruchirappalli, India, 2–4 February 2017. [Google Scholar]
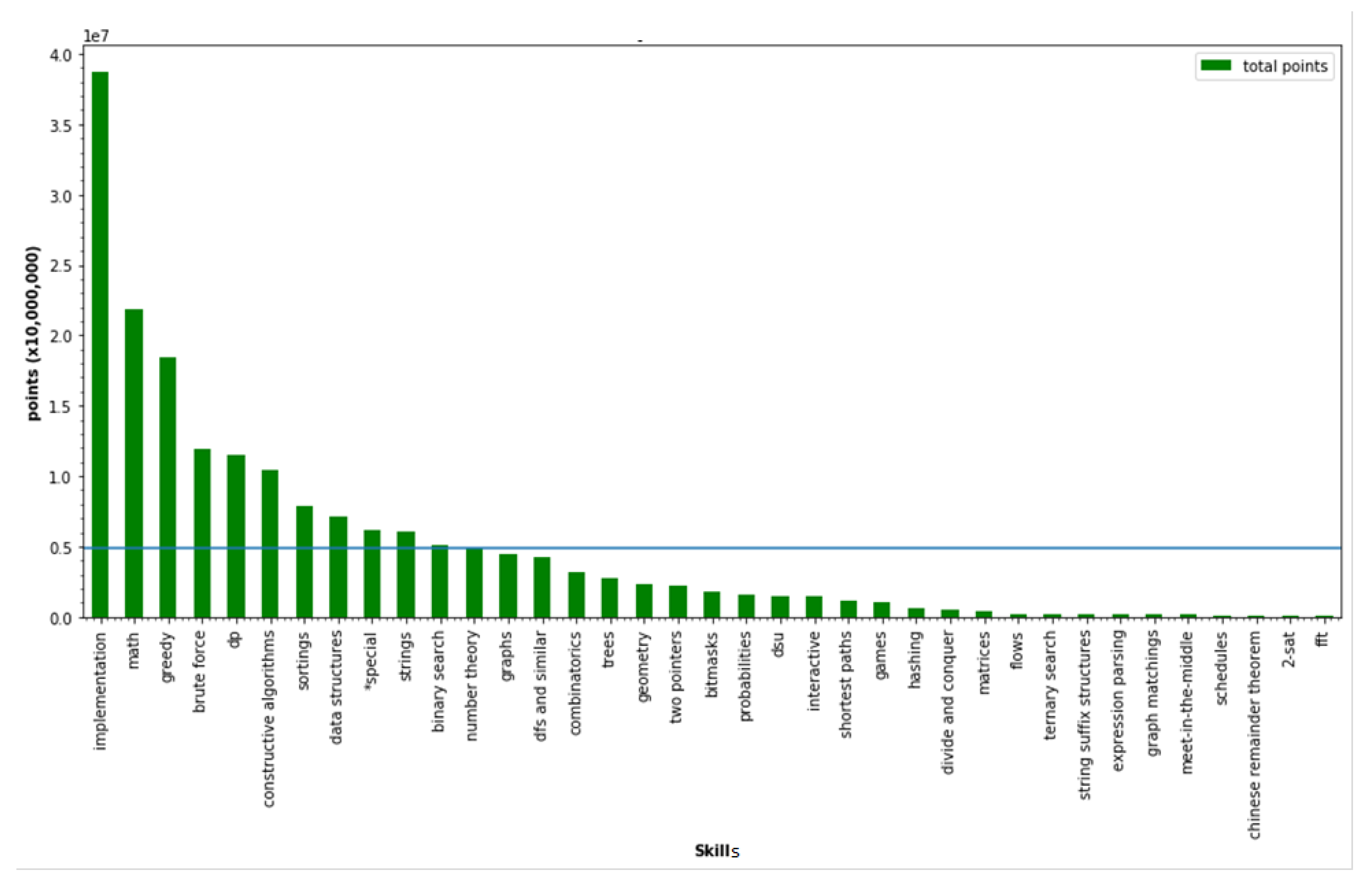
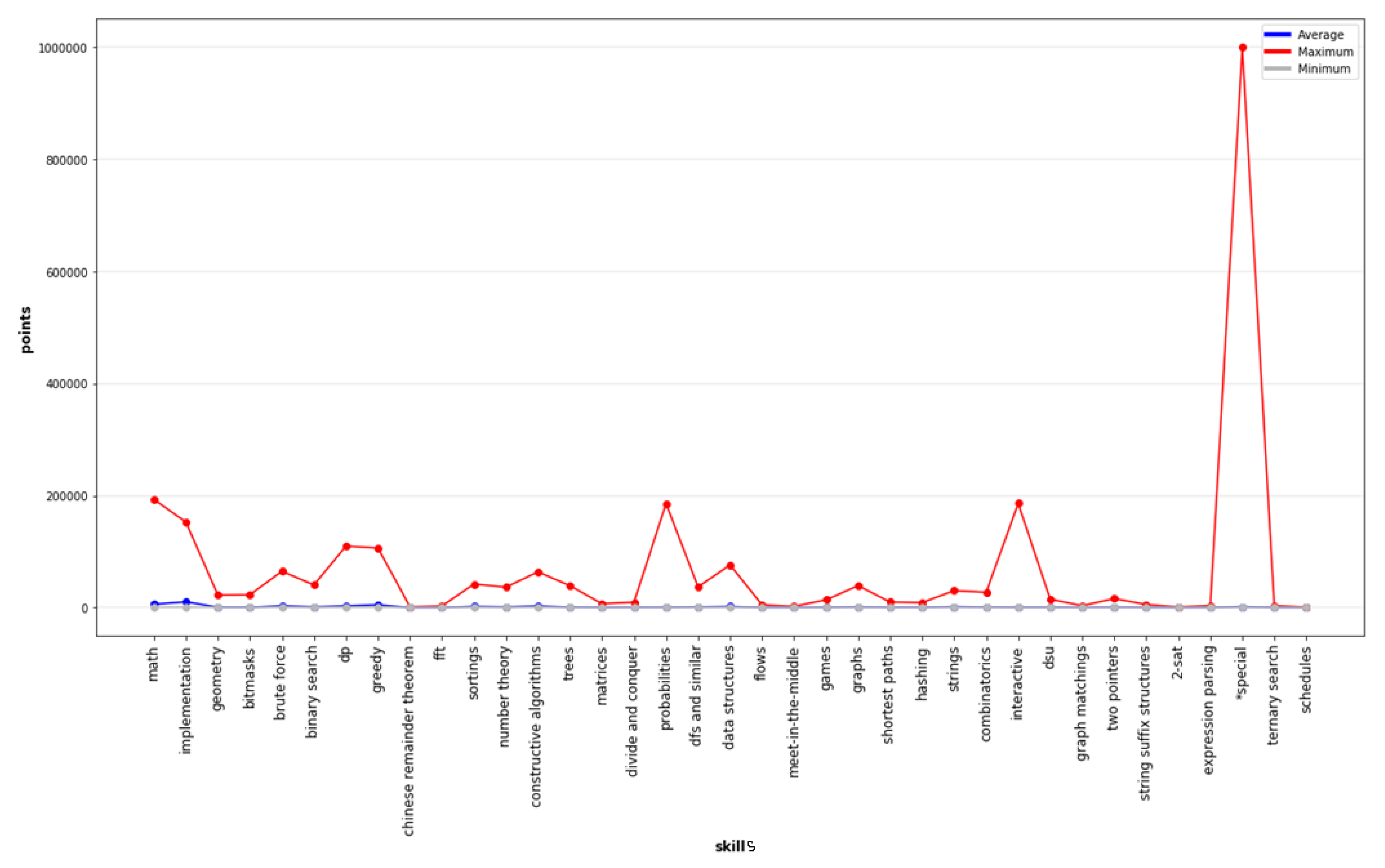
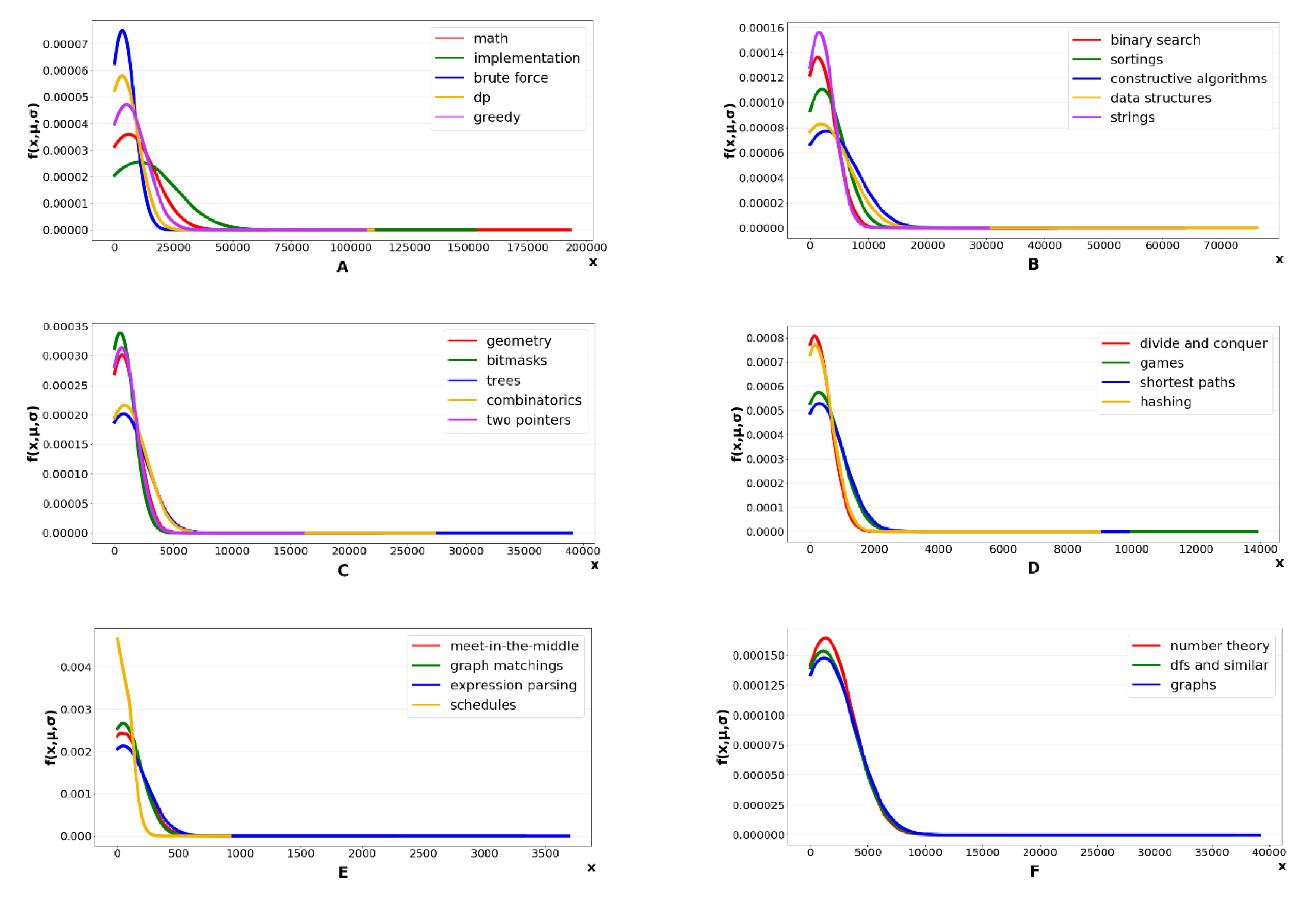
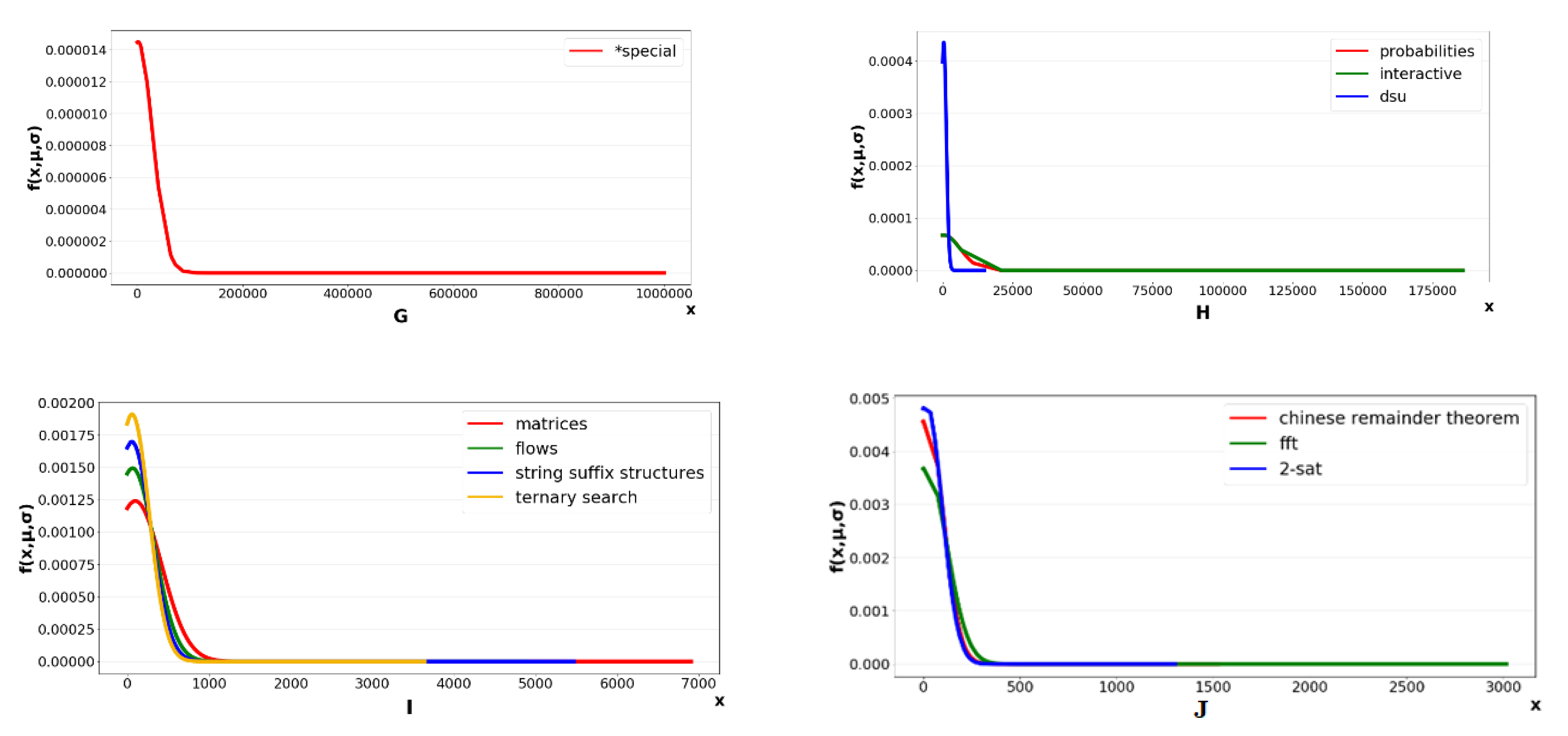
| ID | dom | rec | mut | Observation Results |
|---|---|---|---|---|
| 1 | 0.7 | 0.2 | 0.1 | Fast convergence, good, and stable fitness values. |
| 2 | 0.6 | 0.3 | 0.1 | Fast convergence, good and stable fitness values. More stable than pair 1. |
| 3 | 0.4 | 0.4 | 0.2 | Slow convergence, good, and stable fitness values. |
| 4 | 0.2 | 0.7 | 0.1 | Slow convergence, worse, and unstable fitness values. |
| Parameter | G | D | γ | ω | mut | dom | rec |
|---|---|---|---|---|---|---|---|
| Value | 5 | 0.9 | 0.1 | 0.5 | 0.1 | 0.6 | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngo, T.S.; Bui, N.A.; Tran, T.T.; Le, P.C.; Bui, D.C.; Nguyen, T.D.; Phan, L.D.; Kieu, Q.T.; Nguyen, B.S.; Tran, S.N. Some Algorithms to Solve a Bi-Objectives Problem for Team Selection. Appl. Sci. 2020, 10, 2700. https://doi.org/10.3390/app10082700
Ngo TS, Bui NA, Tran TT, Le PC, Bui DC, Nguyen TD, Phan LD, Kieu QT, Nguyen BS, Tran SN. Some Algorithms to Solve a Bi-Objectives Problem for Team Selection. Applied Sciences. 2020; 10(8):2700. https://doi.org/10.3390/app10082700
Chicago/Turabian StyleNgo, Tung Son, Ngoc Anh Bui, Thi Thuy Tran, Phuong Chi Le, Dinh Chien Bui, The Duy Nguyen, Lac Duong Phan, Quoc Tuan Kieu, Ba Son Nguyen, and Son N. Tran. 2020. "Some Algorithms to Solve a Bi-Objectives Problem for Team Selection" Applied Sciences 10, no. 8: 2700. https://doi.org/10.3390/app10082700
APA StyleNgo, T. S., Bui, N. A., Tran, T. T., Le, P. C., Bui, D. C., Nguyen, T. D., Phan, L. D., Kieu, Q. T., Nguyen, B. S., & Tran, S. N. (2020). Some Algorithms to Solve a Bi-Objectives Problem for Team Selection. Applied Sciences, 10(8), 2700. https://doi.org/10.3390/app10082700






