Influence of Imperfect Position of a Striker and Input Bar on Wave Propagation in a Split Hopkinson Pressure Bar (SHPB) Setup with a Pulse-Shape Technique
Abstract
1. Introduction
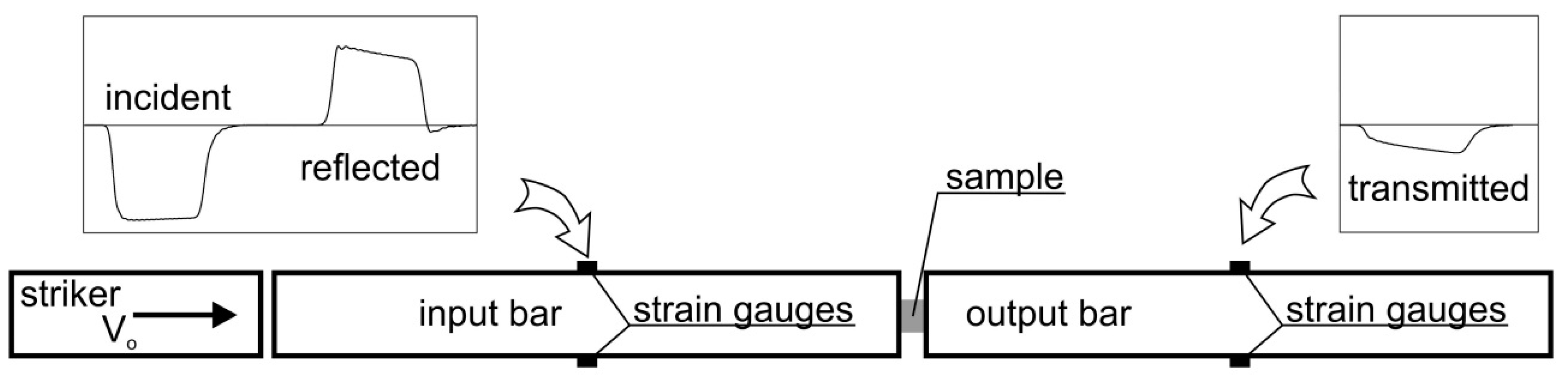
2. Split Hopkinson Pressure Bar Theory
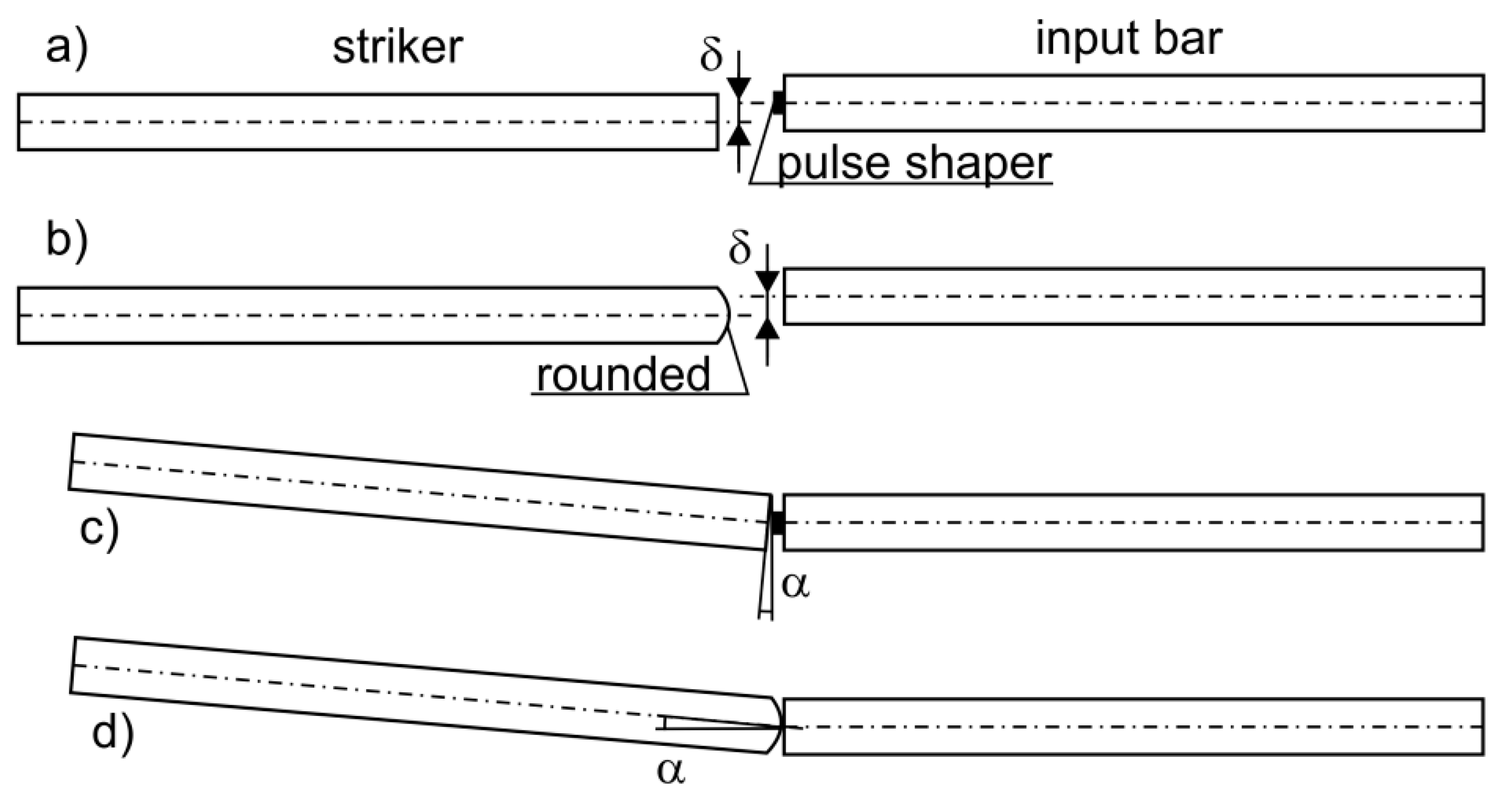
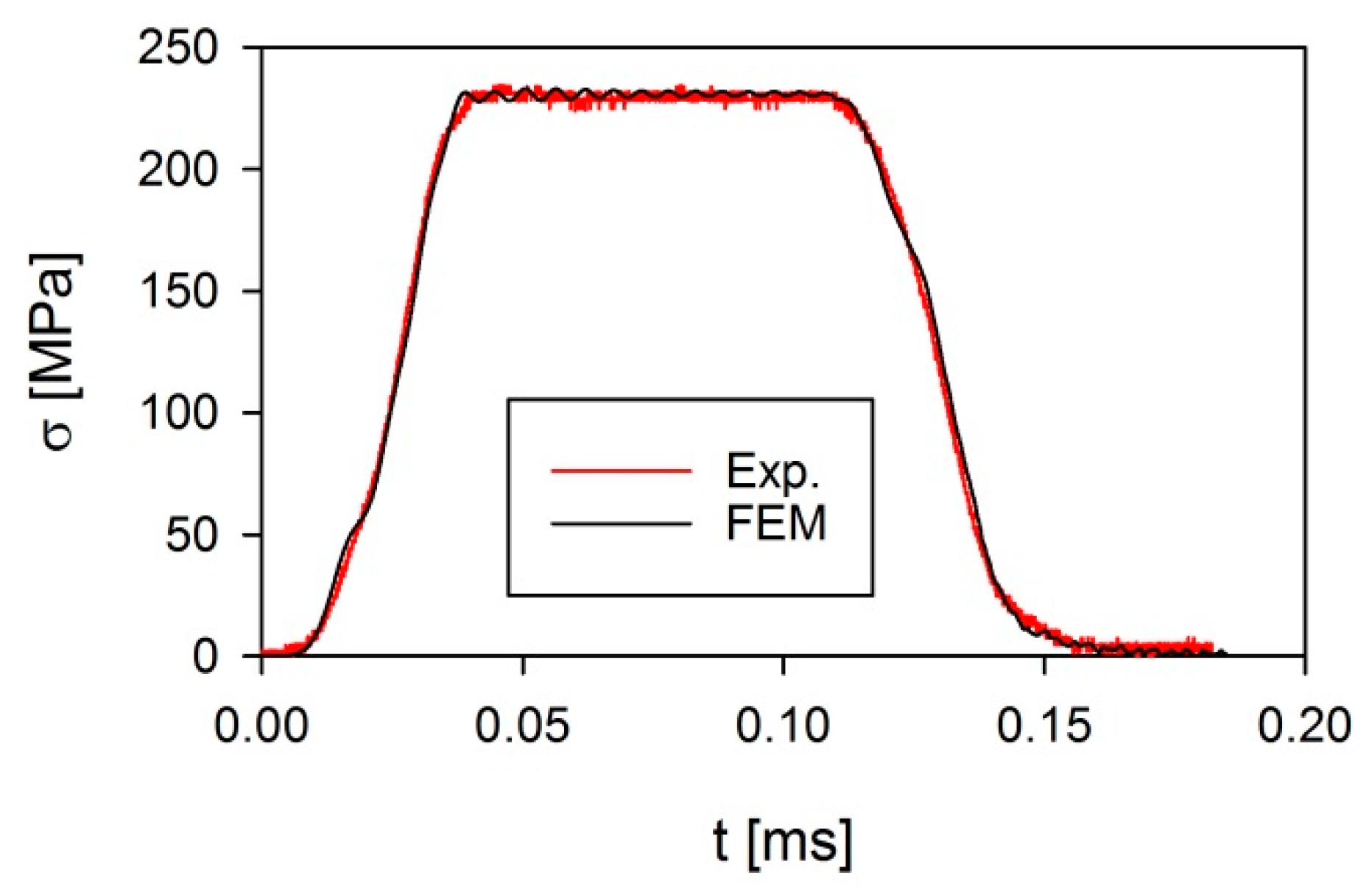
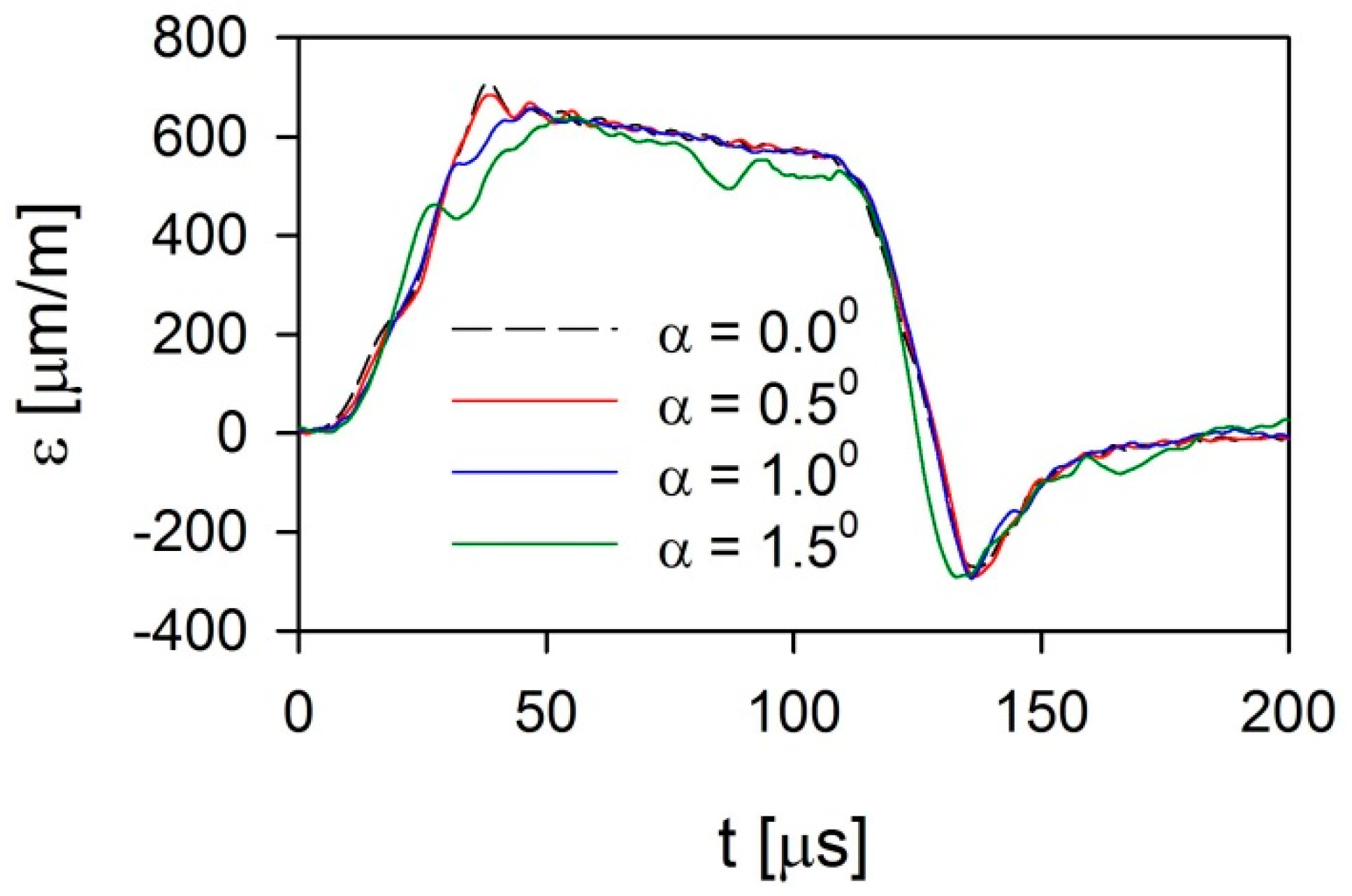
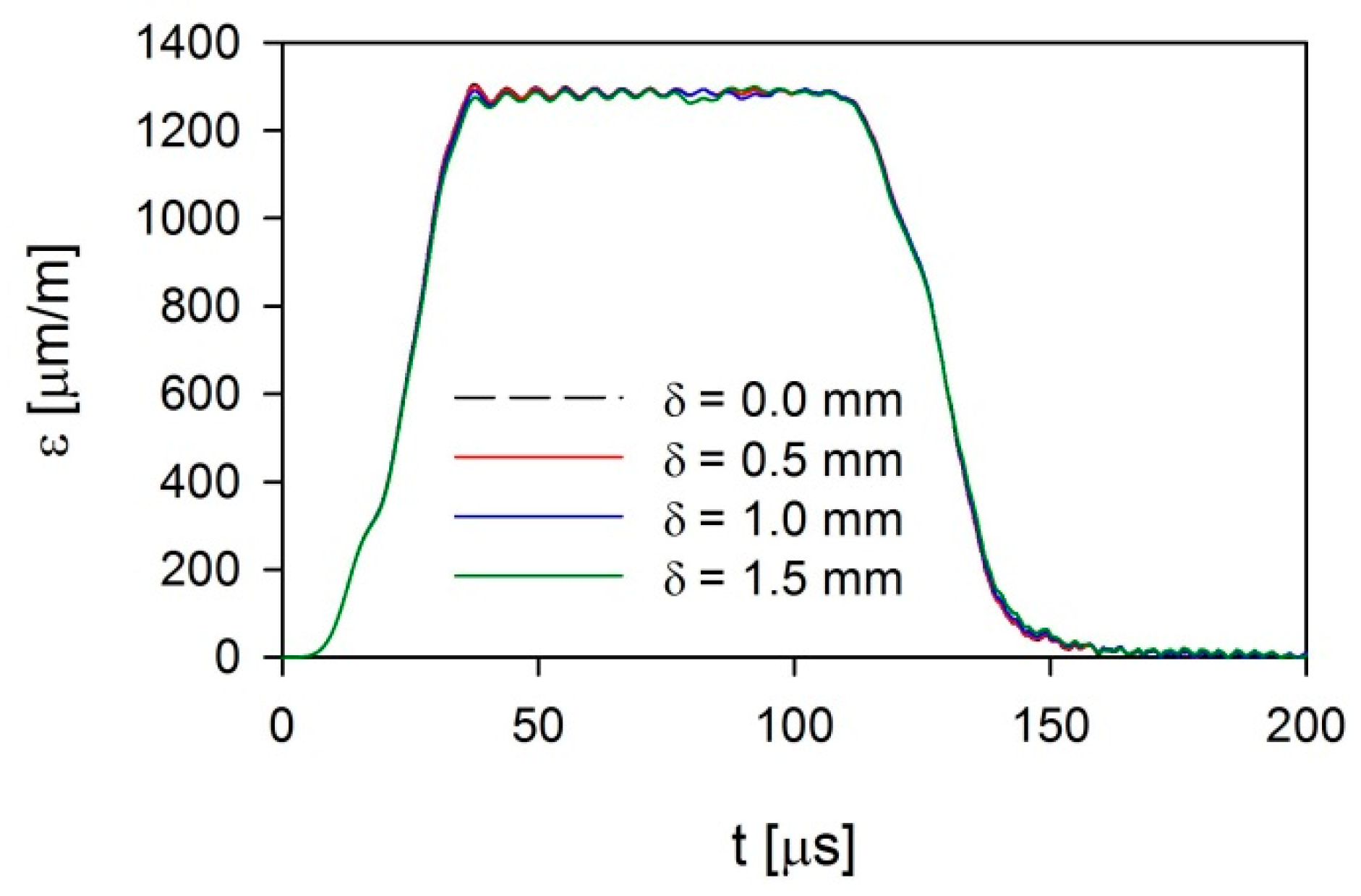
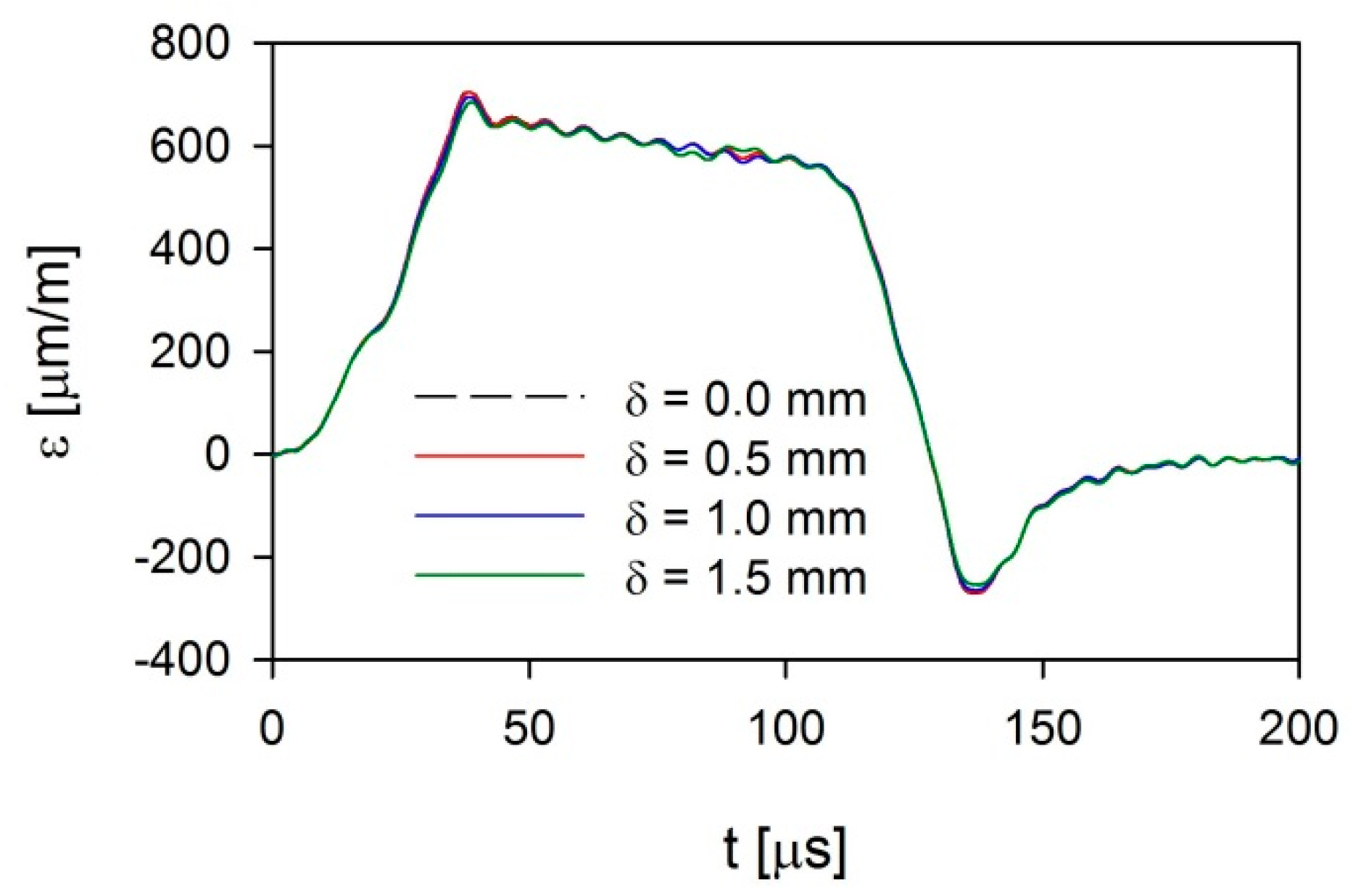
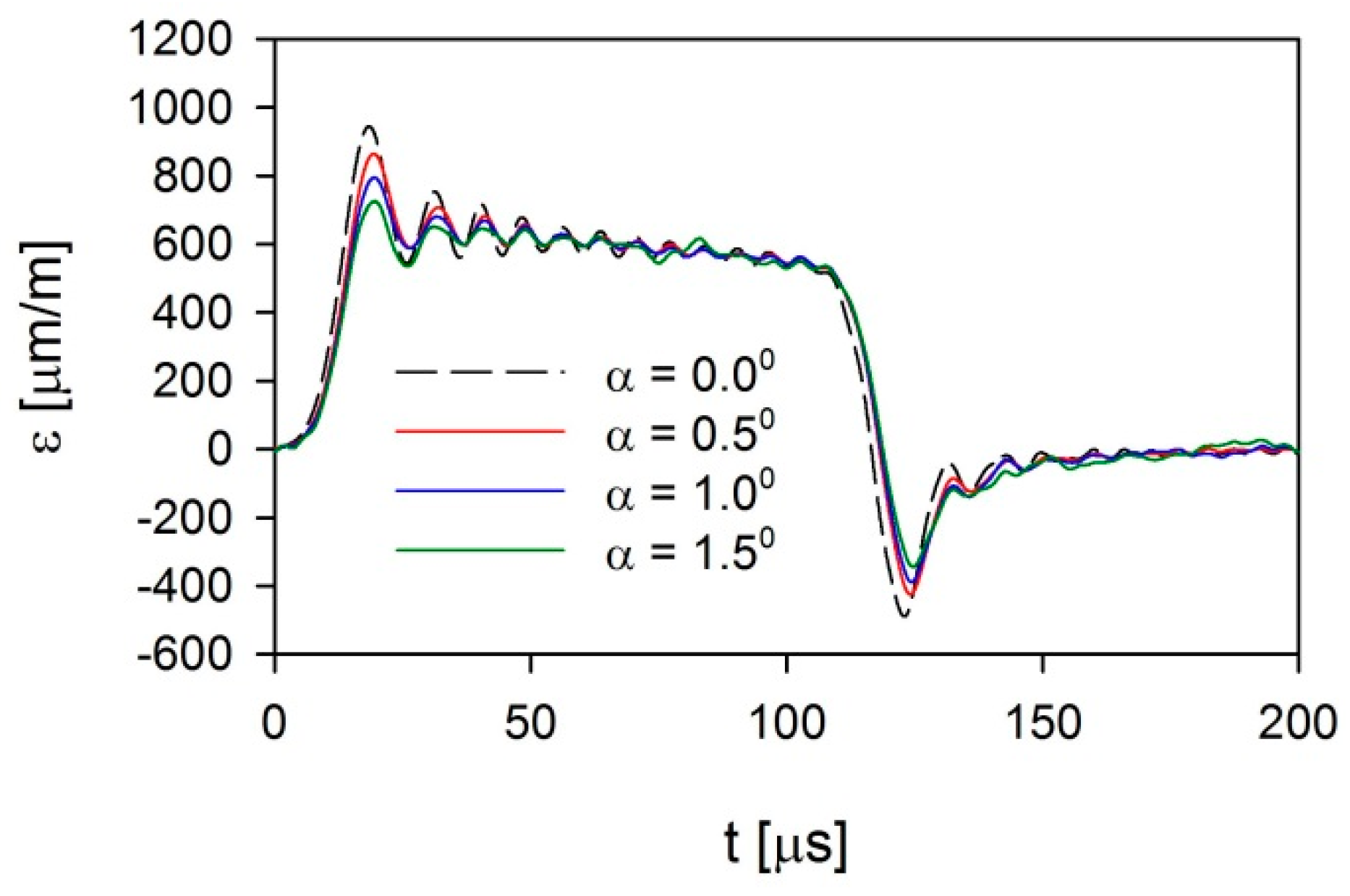
3. Methodology of Numerical Investigations
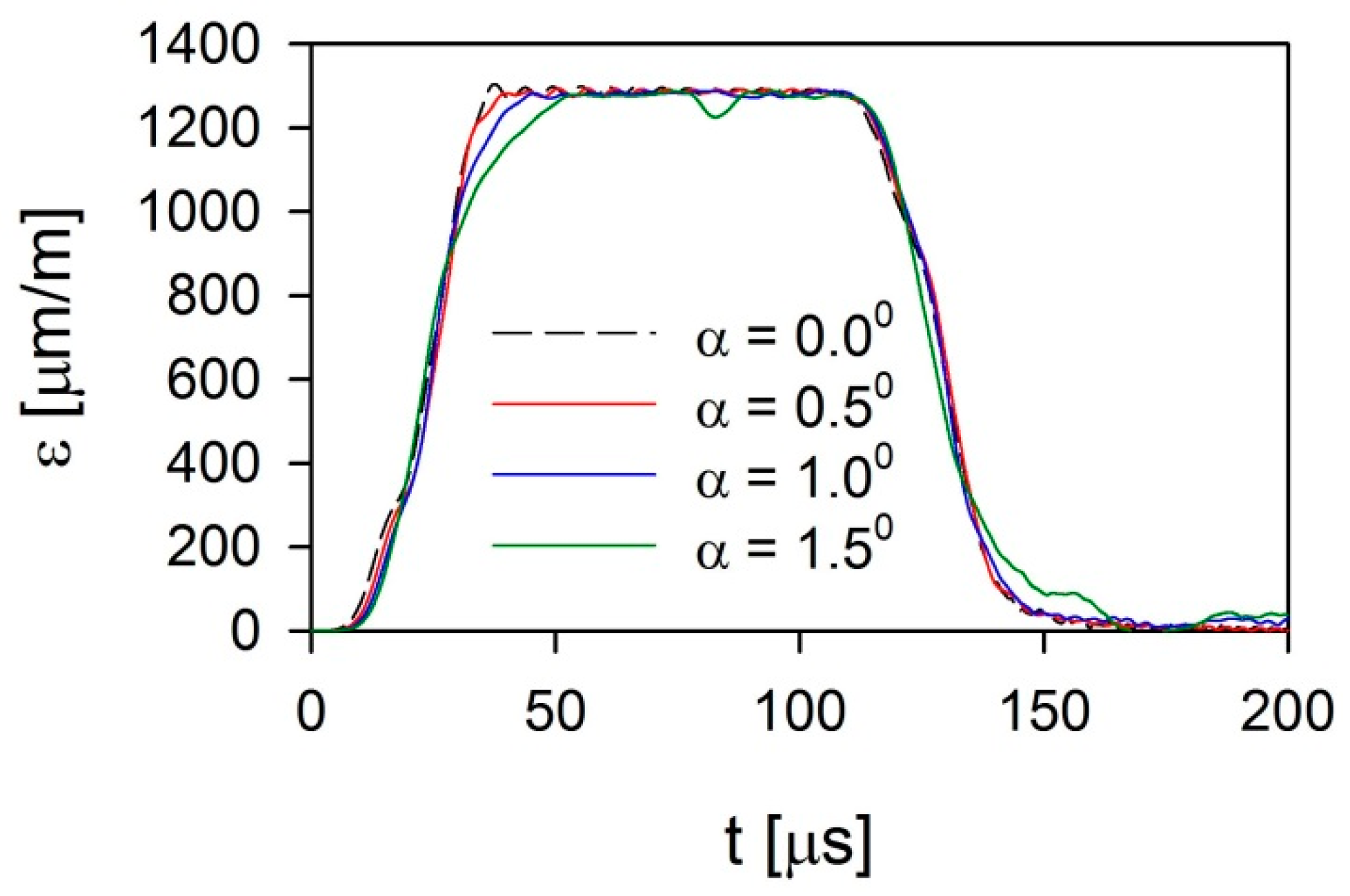
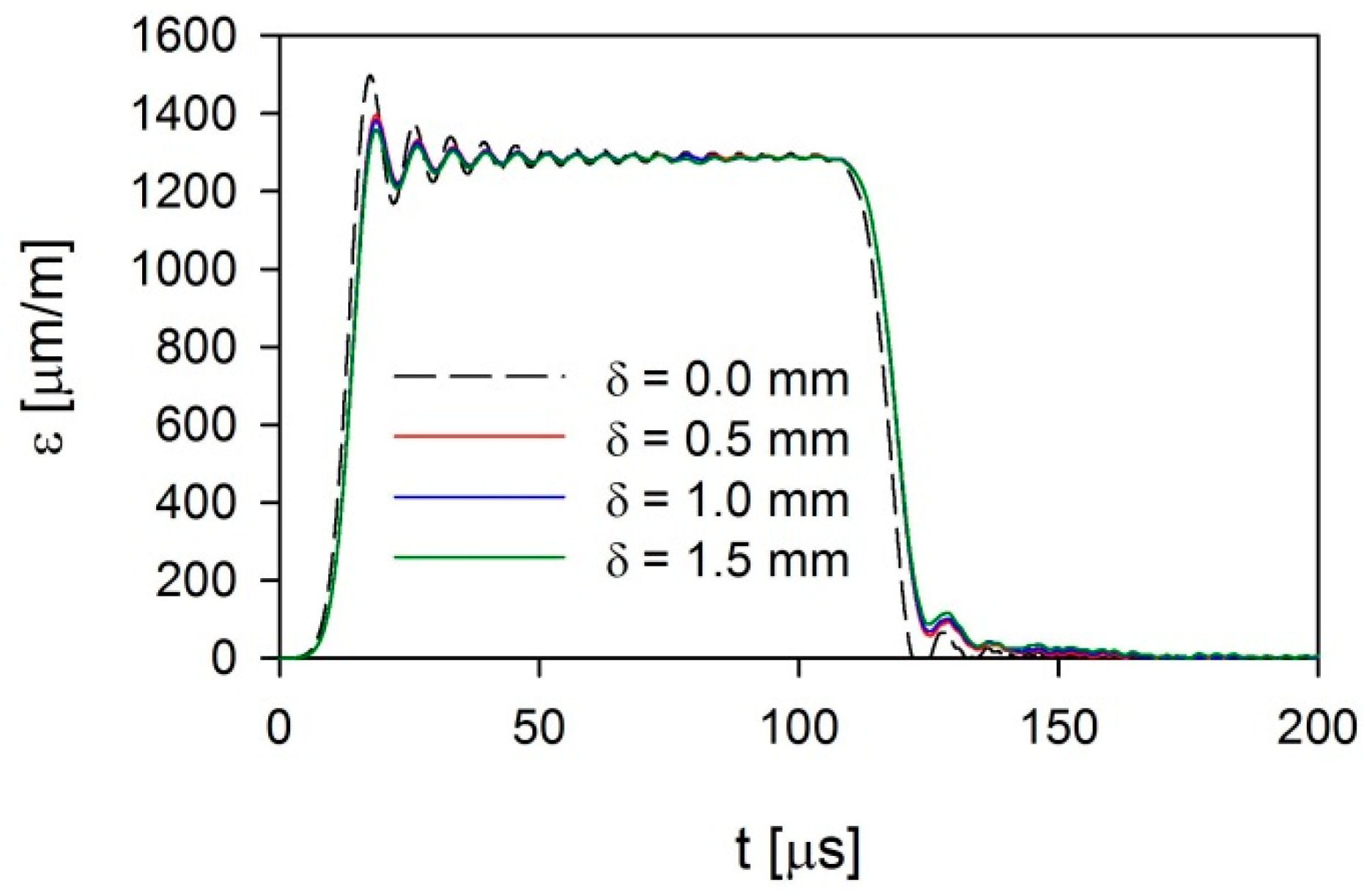
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, W.; Song, B. Split Hopkinson (Kolsky) Bar: Design, Testing and Applications; Springer Science and Business Media: Heidelberg, Germany, 2011. [Google Scholar]
- Chen, W.; Luo, H. Dynamic compressive responses of intact and damaged ceramics from a single split Hopkinson pressure bar experiment. Exp. Mech. 2004, 44, 295–299. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Q. Appraisal of Pulse-Shaping Technique in Split Hopkinson Pressure Bar Tests for Brittle Materials. Int. J. Prot. Struct. 2010, 1, 363–390. [Google Scholar] [CrossRef]
- Cloete, T.; Van Der Westhuizen, A.; Kok, S.; Nurick, G.N. A tapered striker pulse shaping technique for uniform strain rate dynamic compression of bovine bone. In DYMAT—International Conference on the Mechanical and Physical Behaviour of Materials under Dynamic Loading, Brussels, Belgium, 7–11 September 2009; Song, B., Casem, D., Kimberley, J., Eds.; Springer Science Business Media: Heidelberg, Germany, 2009; Volume 1, pp. 901–907. [Google Scholar]
- Bekker, A.; Cloete, T.; Chinsamy-Turan, A.; Nurick, G.; Kok, S. Constant strain rate compression of bovine cortical bone on the Split-Hopkinson Pressure Bar. Mater. Sci. Eng. C 2015, 46, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Baranowski, P.; Małachowski, J.; Gieleta, R.; Damaziak, K.; Mazurkiewicz, Ł.; Kolodziejczyk, D. Numerical study for determination of pulse shaping design variables in SHPB apparatus. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 61, 459–466. [Google Scholar] [CrossRef]
- Ellwood, S.; Griffiths, L.J.; Parry, D.J. Materials testing at high constant strain rates. J. Phys. E Sci. Instrum. 1982, 15, 280–282. [Google Scholar] [CrossRef]
- Jankowiak, T.; Rusinek, A.; Łodygowski, T. Validation of the Klepaczko–Malinowski model for friction correction and recommendations on Split Hopkinson Pressure Bar. Finite Elem. Anal. Des. 2011, 47, 1191–1208. [Google Scholar] [CrossRef]
- Moćko, W. Analysis of the Impact of the Frequency Range of the Tensometer Bridge and Projectile Geometry on the Results of Measurements by the Split Hopkinson Pressure Bar Method. Metrol. Meas. Syst. 2013, 20, 555–564. [Google Scholar] [CrossRef]
- Pochhammer, L. On the propagation velocities of small oscillations in an unlimited isotropic circular cylinder. J. Reine Angew. Math. 1876, 81, 324–326. [Google Scholar]
- Chree, C. The equations of an isotropic elastic solid in polar and cylindrical coordinates, their solutions and applications. Trans. Camb. Philos. Soc. 1889, 14, 250–369. [Google Scholar]
- Kariem, M.A.; Beynon, J.; Ruan, D. Misalignment effect in the split Hopkinson pressure bar technique. Int. J. Impact Eng. 2012, 47, 60–70. [Google Scholar] [CrossRef]
- Wu, X.; Yin, Q.; Wei, Y.; Huang, C. Effects of imperfect experimental conditions on stress waves in SHPB experiments. Acta Mech. Sin. 2015, 31, 827–836. [Google Scholar] [CrossRef][Green Version]
- Panowicz, R.; Janiszewski, J.; Kochanowski, K. The non-axisymmetric pulse shaper position influence on SHPB experiment data. J. Theor. App. Mech. 2018, 56, 873–886. [Google Scholar] [CrossRef]
- Hallquist, J.O. Ls-Dyna, Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006. [Google Scholar]
- Malinowski, J.Z.; Klepaczko, J.R. A unified analytic and numerical approach to specimen behaviour in the Split-Hopkinson pressure bar. Int. J. Mech. Sci. 1986, 28, 381–391. [Google Scholar] [CrossRef]
- Gorham, D. An effect of specimen size in the high strain rate compression test. J. Phys.IV Colloq. 1991, 1, 411–418. [Google Scholar] [CrossRef]
- Gray, G.T. Classic split-Hopkinson pressure bar testing. In Mechanical Testing and Evaluation; Kuhn, H., Medlin, D., Eds.; ASM International: Materials Park, OH, USA, 2000; Volume 8, pp. 462–476. [Google Scholar]
- Forrestal, M.J.; Wright, T.W.; Chen, W. The effect of radial inertia on brittle samples during the split Hopkinson pressure bar test. Int. J. Impact Eng. 2007, 34, 405–411. [Google Scholar] [CrossRef]
- Davies, E.D.H.; Hunter, S.C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar. J. Mech. Phys. Solids 1963, 11, 155–179. [Google Scholar] [CrossRef]
- Panowicz, R. Analysis of selected contact algorithms types in terms of their parameters selection. J. KONES 2013, 20, 263–268. [Google Scholar] [CrossRef]
- Konyukhov, A.; Schweizerhof, K. Computational Contact Mechanics—Geometrically Exact Theory for Arbitrary Shaped Bodies; Springer Science Business Media: Heidelberg, Germany, 2013. [Google Scholar]
- Fischer, K.A.; Wriggers, P. Mortar based frictional contact formulation for higher order interpolations using the moving friction cone. Comput. Methods Appl. Mech. Eng. 2006, 195, 5020–5036. [Google Scholar] [CrossRef]
- Wang, Z.; Li, P. Characterisation of dynamic behaviour of alumina ceramics: Evaluation of stress uniformity. AIP Adv. 2015, 5, 107224. [Google Scholar] [CrossRef]
- Tasdemirci, A.; Ergönenç, Ç.; Guden, M. Split Hopkinson pressure bar multiple reloading and modeling of a 316 L stainless steel metallic hollow sphere structure. Int. J. Impact Eng. 2010, 37, 250–259. [Google Scholar] [CrossRef]
- Liu, P.; Hu, D.; Wu, Q.; Liu, X. Sensitivity and uncertainty analysis of interfacial effect in SHPB tests for concrete-like materials. Constr. Build. Mater. 2018, 163, 414–427. [Google Scholar] [CrossRef]
- Hartley, R.; Cloete, T.; Nurick, G. An experimental assessment of friction effects in the split Hopkinson pressure bar using the ring compression test. Int. J. Impact Eng. 2007, 34, 1705–1728. [Google Scholar] [CrossRef]
- Panowicz, R.; Janiszewski, J. Tensile Split Hopkinson Bar Technique: Numerical Analysis of the Problem of Wave Disturbance and Specimen Geometry Selection. Metrol. Meas. Syst. 2016, 23, 425–436. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Nederland, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Steinberg, D.J. Equation of State and Strength Properties of Selected Materials. LLNL Report UCRL-MA-106439; Lawrence Livermore National Laboratory: Livermore, OH, USA, 1996. [Google Scholar]
- Srivastava, A.K.; Ozel, T.; Sima, M. Finite element simulation of high speed machining Ti-6Al-4V alloy using modified material models. In Proceedings of the Transactions of the North American Manufacturing Research Institution of SME, Kingston, ON, Canada, 26–28 May 2010; Volume 38, pp. 49–56. [Google Scholar]
- Grazka, M.; Janiszewski, J. Identification of Johnson-Cook equation constants using finite element method. Eng. Trans. 2012, 60, 215–223. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]




| Physical Parameters | Cu | Ti-6Al-4V 3 |
|---|---|---|
| ρ [kg/m3] | 8940 | 4430 |
| E [GPa] | 100 | 114 |
| ν [-] | 0.31 | 0.3 |
| Tm [K] | 1338 | 1953 |
| cp [J/(kg K)] | 385 | 546 |
| JC Constants | Cu | Ti-6Al-4V 3 |
|---|---|---|
| A [MPa] | 99.7 | 862.5 |
| B [MPa] | 262.8 | 331.2 |
| ν [-] | 0.23 | 0.34 |
| C [-] | 0.029 | 0.012 |
| m [-] | 0.98 | 0.8 |
| Physical Parameters | Cu | Ti-6Al-4V 3 | Physical Parameters | Cu | Ti-6Al-4V 3 |
|---|---|---|---|---|---|
| c0 [m/s] | 3940 | 5130 | γ0 [-] | 2.02 | 1.23 |
| S1 [-] | 1.489 | 1.028 | a [-] | 0.47 | 0.17 |
| S2 [-] | 0.0 | 0.0 | S3 [-] | 0.0 | 0.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panowicz, R.; Konarzewski, M. Influence of Imperfect Position of a Striker and Input Bar on Wave Propagation in a Split Hopkinson Pressure Bar (SHPB) Setup with a Pulse-Shape Technique. Appl. Sci. 2020, 10, 2423. https://doi.org/10.3390/app10072423
Panowicz R, Konarzewski M. Influence of Imperfect Position of a Striker and Input Bar on Wave Propagation in a Split Hopkinson Pressure Bar (SHPB) Setup with a Pulse-Shape Technique. Applied Sciences. 2020; 10(7):2423. https://doi.org/10.3390/app10072423
Chicago/Turabian StylePanowicz, Robert, and Marcin Konarzewski. 2020. "Influence of Imperfect Position of a Striker and Input Bar on Wave Propagation in a Split Hopkinson Pressure Bar (SHPB) Setup with a Pulse-Shape Technique" Applied Sciences 10, no. 7: 2423. https://doi.org/10.3390/app10072423
APA StylePanowicz, R., & Konarzewski, M. (2020). Influence of Imperfect Position of a Striker and Input Bar on Wave Propagation in a Split Hopkinson Pressure Bar (SHPB) Setup with a Pulse-Shape Technique. Applied Sciences, 10(7), 2423. https://doi.org/10.3390/app10072423





