Optimal Control Approach to Lambert’s Problem and Gibbs’ Method
Abstract
1. Introduction
2. Optimal Control Approach to Lambert’s Problem
2.1. Lambert’s Problem
2.2. Optimal Control Approach
3. Extended Lambert’s Problem
3.1. The Energy-Specified Lambert’s Problem
3.2. The Velocity-Specified Lambert’s Problem
3.3. Lambert’s Problem under J2 Perturbation
4. Optimal Control Approach to Gibbs’ Method
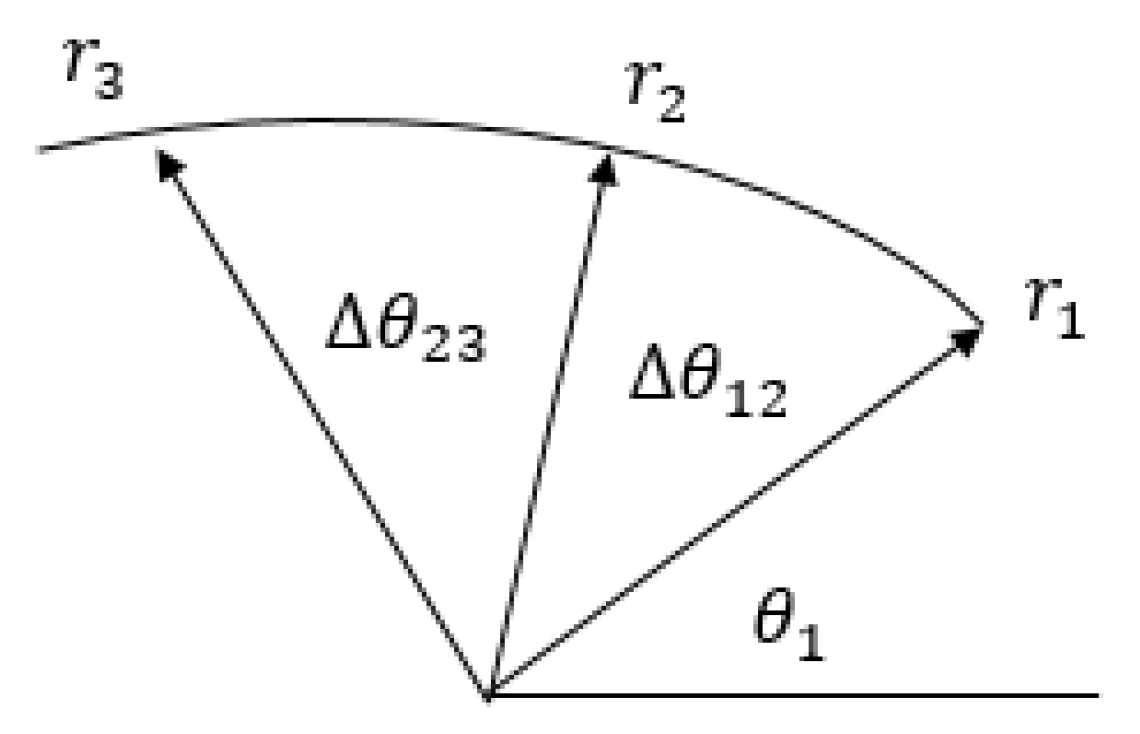
4.1. Gibbs’ Method
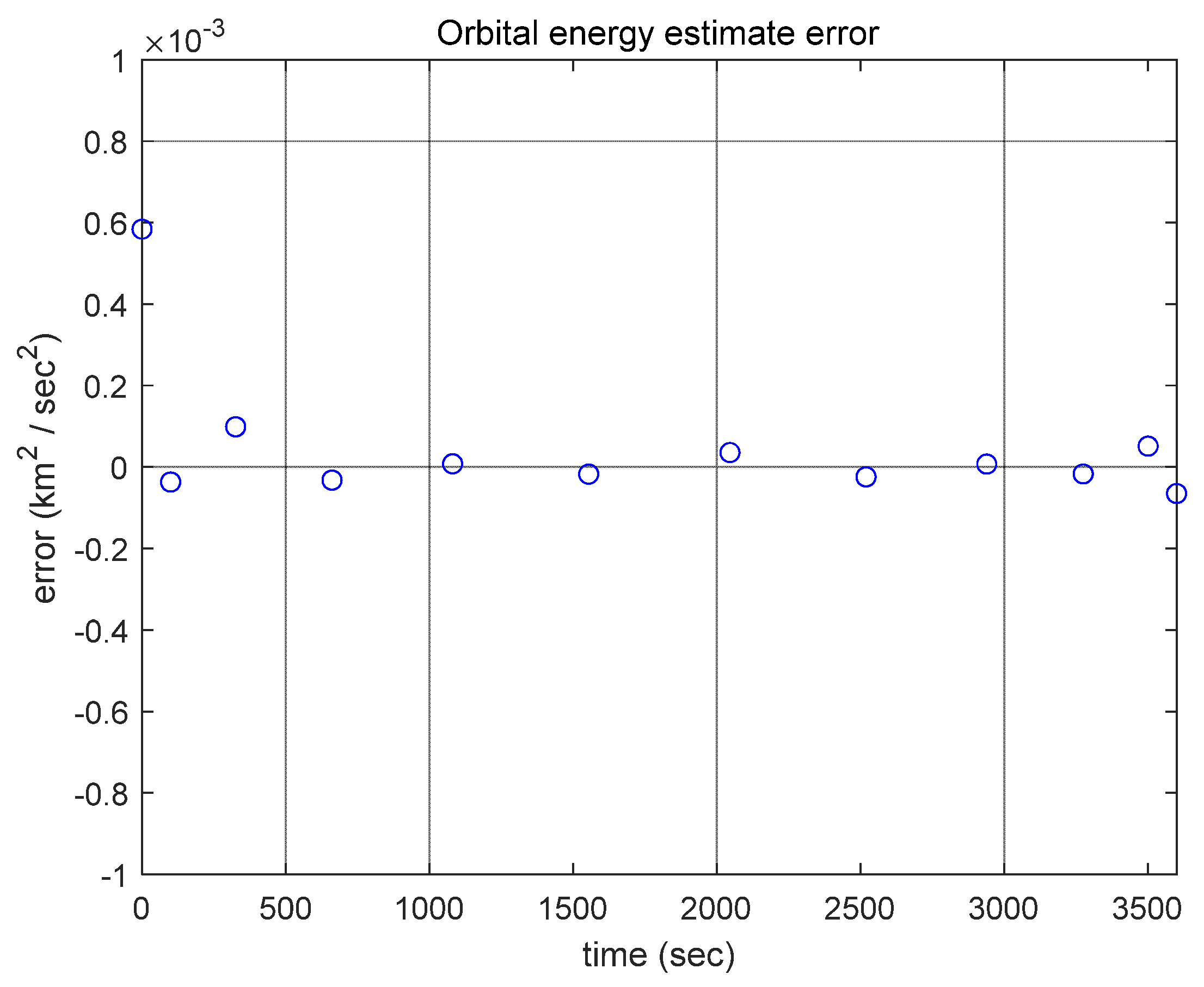
4.2. Orbital Energy Computation
5. Numerical Simulations
5.1. Lobatto Pseudospectral Method
5.2. Extended Lambert’s Problem
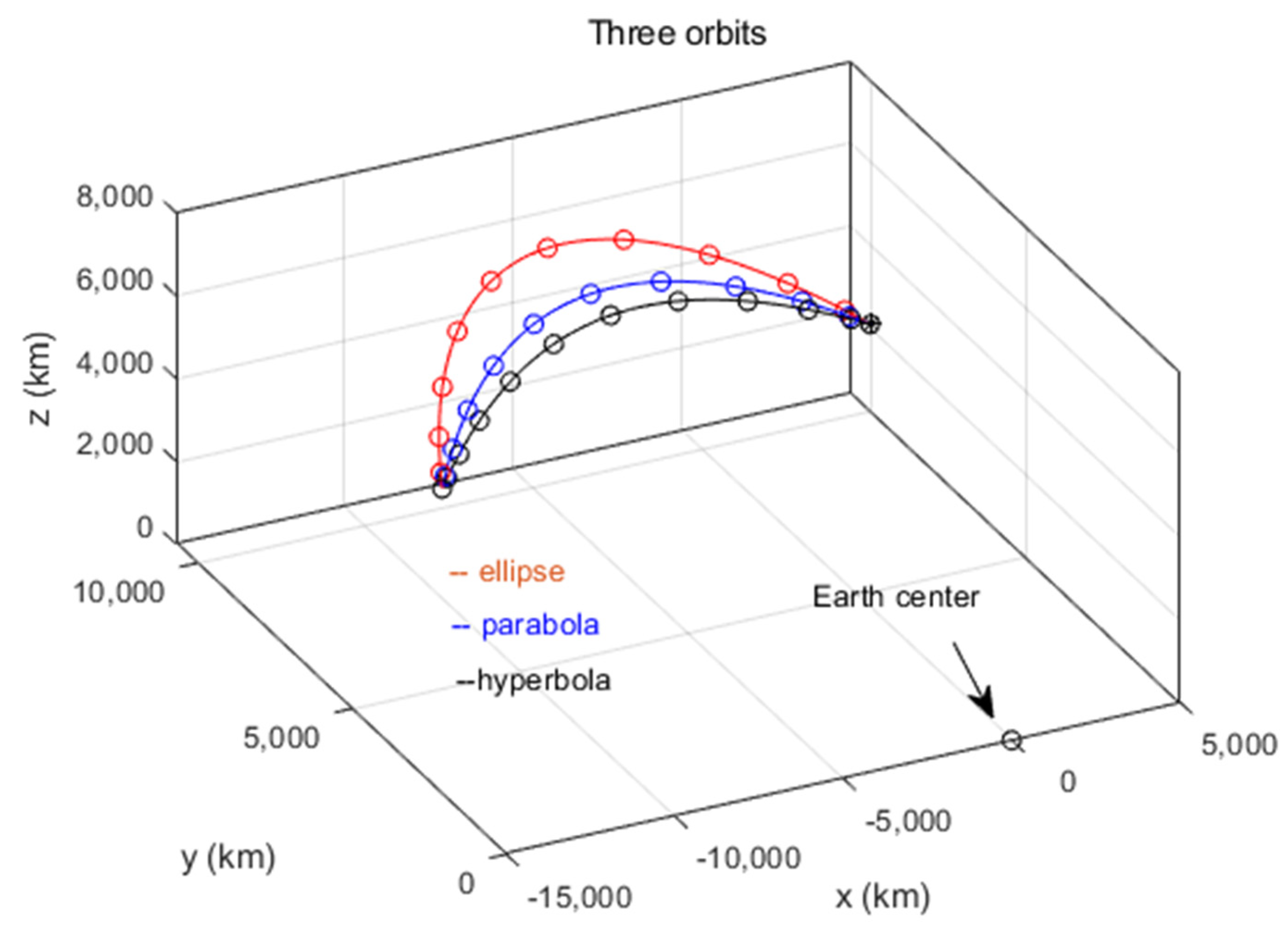
5.3. Gibbs’ Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, H.; Tsiotras, P. Using Battin’s Method to Obtain Multiple-Revolution Lambert’s Solutions. Adv. Astronaut. Sci. 2003, 116, 1067–1084. [Google Scholar]
- Guibout, V.M.; Scheeres, D.J. Solving Two-Point Boundary Value Problems using the Hamiltonian-Jacobi Theory. In Proceedings of the 2th WSEAS International Conference Applied and Theoretical Mechanics, Venice, Italy, 20–22 November 2006; pp. 174–182. [Google Scholar]
- Izzo, D. Revisiting Lambert’s Problem. J. Celest. Mech. Dyn. Astron. 2004, 121, 1–15. [Google Scholar] [CrossRef]
- Avanzini, G. A Simple Lambert Algorithm. J. Guid. Control Dyn. 2008, 31, 1587–1594. [Google Scholar] [CrossRef]
- Bando, M.; Yamakawa, H. New Lambert Algorithm using the Hamilton-Jacobi-Bellman Equation. J. Guid. Control Dyn. 2010, 33, 1000–1008. [Google Scholar] [CrossRef]
- Curtis, A.D. Orbital Mechanics for Engineering Students; Elsevier Butterworth Heinemann: London, UK, 2005. [Google Scholar]
- Kaushik, A.S. A Statistical Comparison between Gibbs and Herrick-Gibbs Orbital Determination Methods. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2016. [Google Scholar]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Microcosm Press: Torrance, CA, USA, 2001. [Google Scholar]
- Lewis, F.; Vrabie, D.; Syrmos, V. Optimal Control; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kirk, D. Optimal Control Theory; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Garcia-Heras, J.; Soler, M.; Saez, F. A Comparison of Optimal Control Methods for Minimum Fuel Cruise at Constant Altitude and Course with Fixed Arrival Time. J. Procedia Eng. 2014, 80, 231–244. [Google Scholar] [CrossRef]
- Garg, D.; Patterson, M.; Hager, W.; Rao, A.; Benson, D. A Unified Framework for The Numerical Solution of Optimal Control Problems using Pseudospectral Methods. J. Autom. 2010, 33, 1843–1851. [Google Scholar] [CrossRef]

| 1 | |
| 2 | , , |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Park, S. Optimal Control Approach to Lambert’s Problem and Gibbs’ Method. Appl. Sci. 2020, 10, 2419. https://doi.org/10.3390/app10072419
Kim M, Park S. Optimal Control Approach to Lambert’s Problem and Gibbs’ Method. Applied Sciences. 2020; 10(7):2419. https://doi.org/10.3390/app10072419
Chicago/Turabian StyleKim, Minjeong, and Sungsu Park. 2020. "Optimal Control Approach to Lambert’s Problem and Gibbs’ Method" Applied Sciences 10, no. 7: 2419. https://doi.org/10.3390/app10072419
APA StyleKim, M., & Park, S. (2020). Optimal Control Approach to Lambert’s Problem and Gibbs’ Method. Applied Sciences, 10(7), 2419. https://doi.org/10.3390/app10072419






