Estimation of Thermal Resistance Field in Layered Materials by Analytical Asymptotic Method
Abstract
1. Introduction
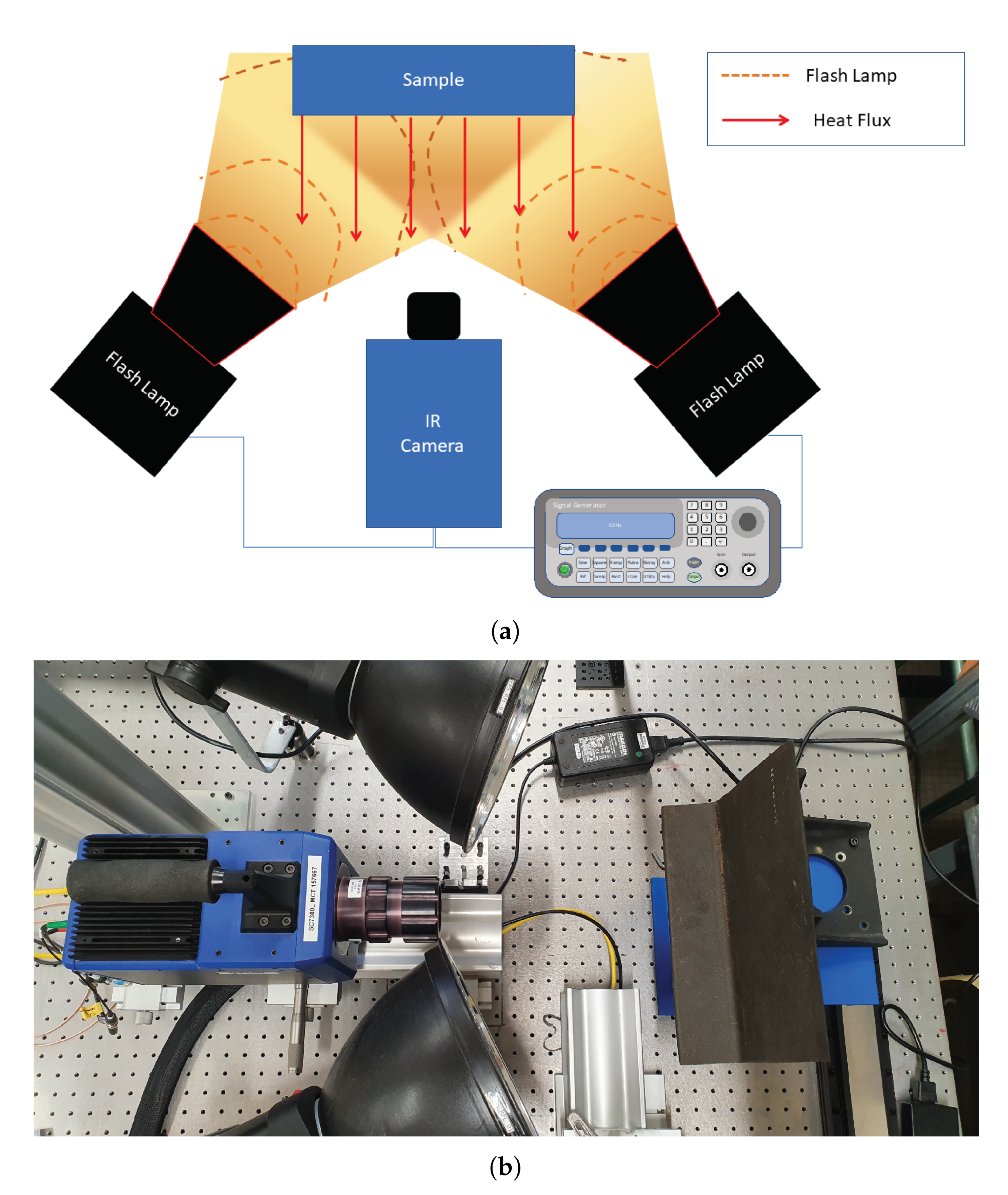
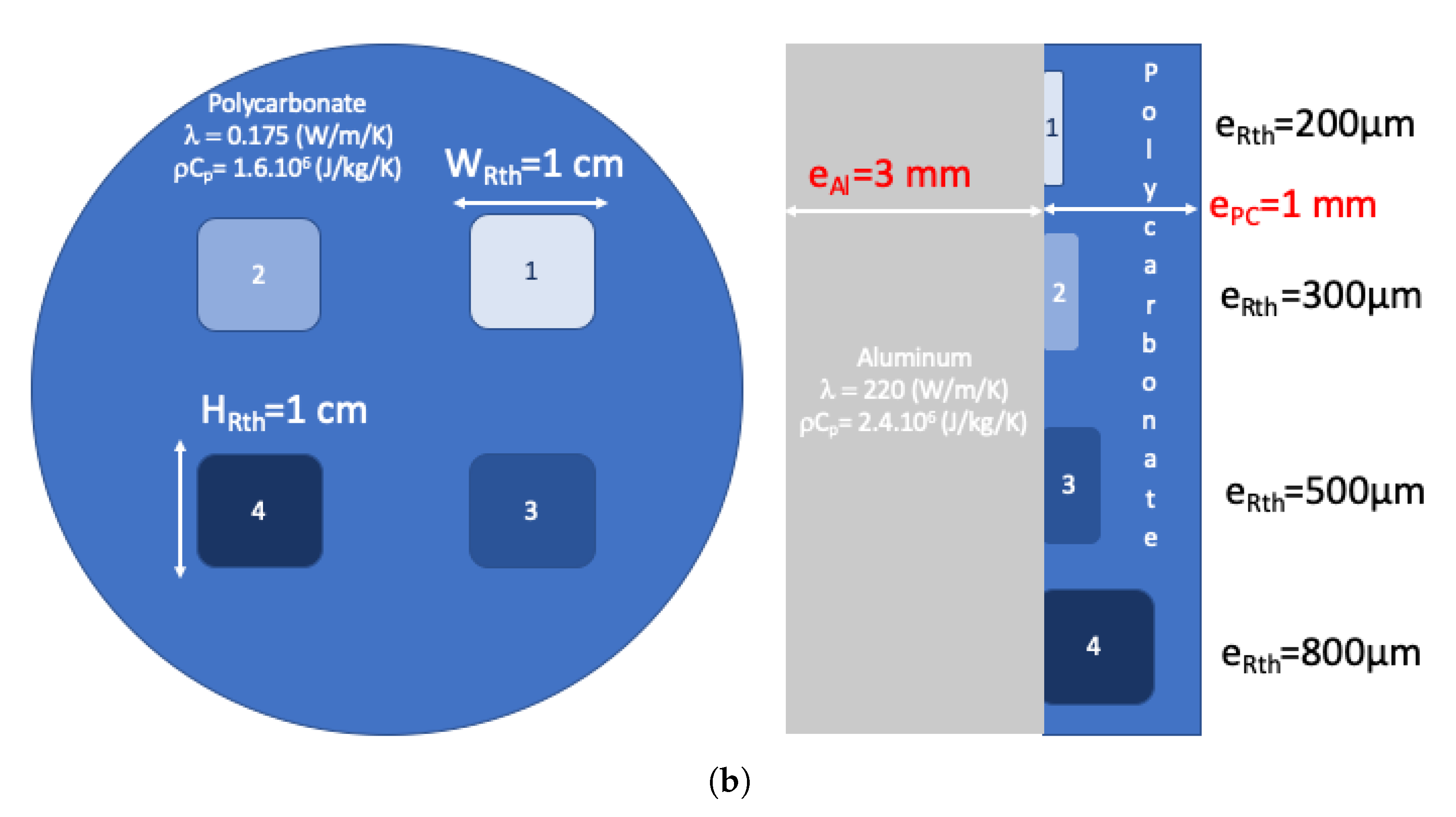
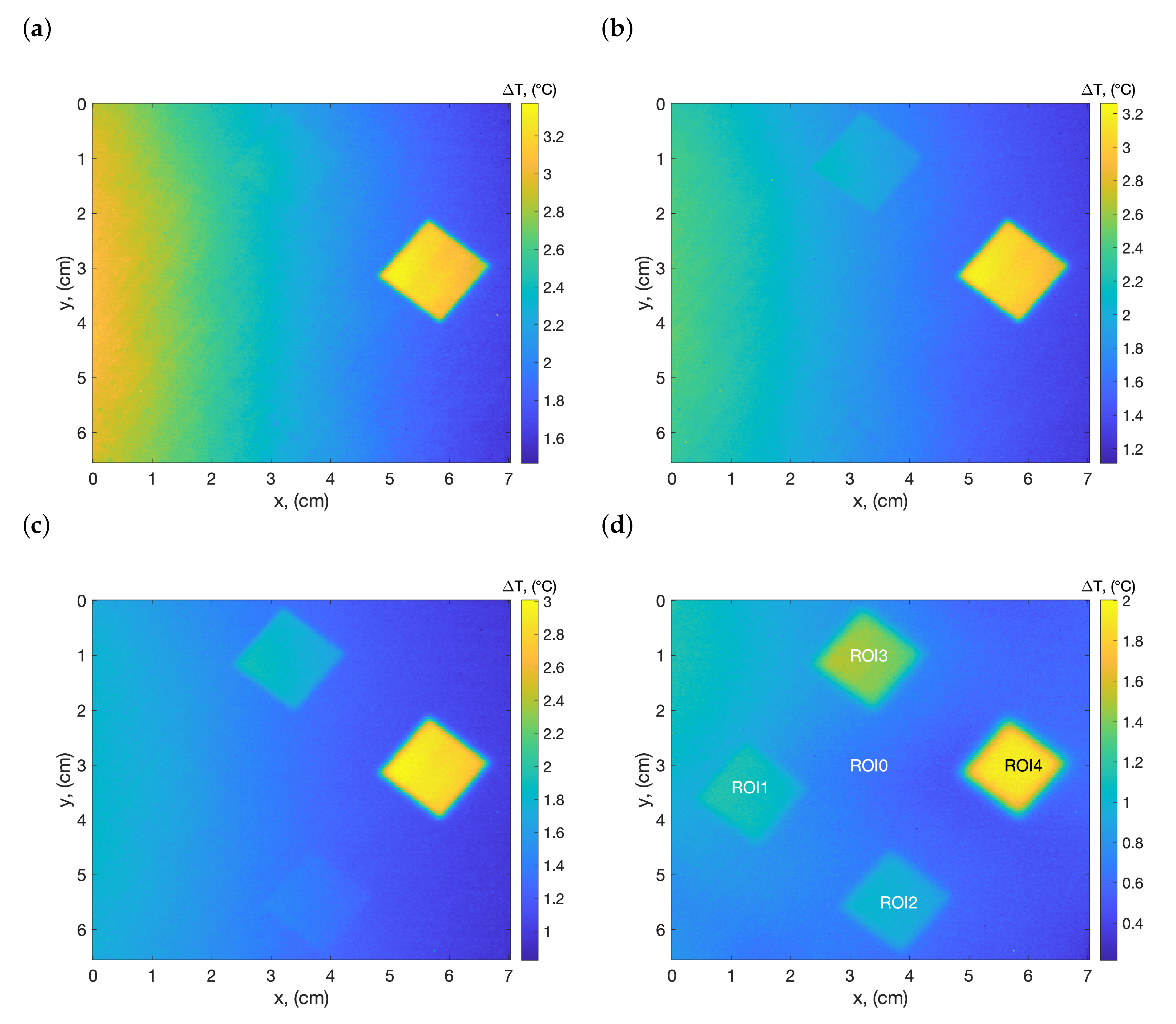
2. Experimental Setup and Materials
3. Methods
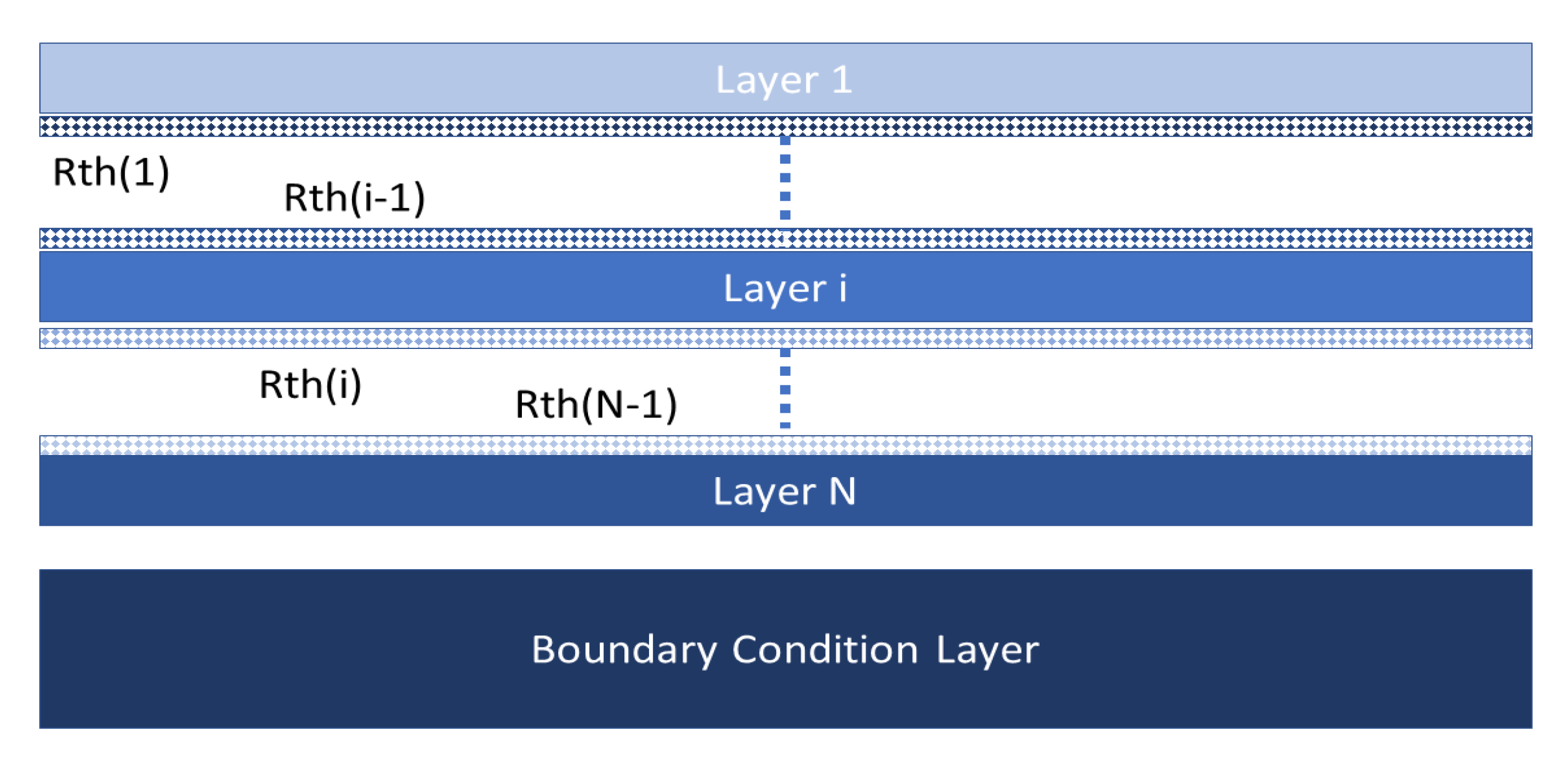
3.1. Direct Problem
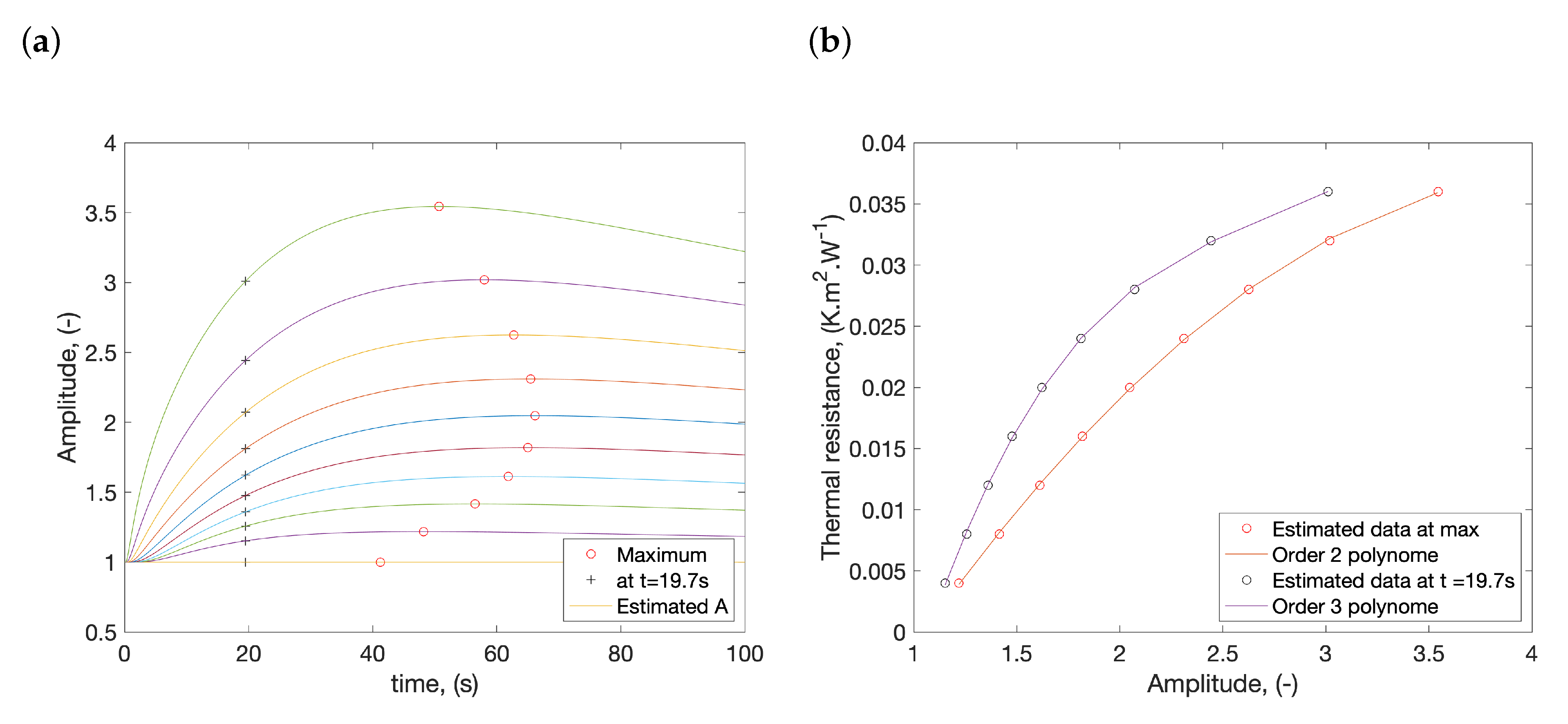
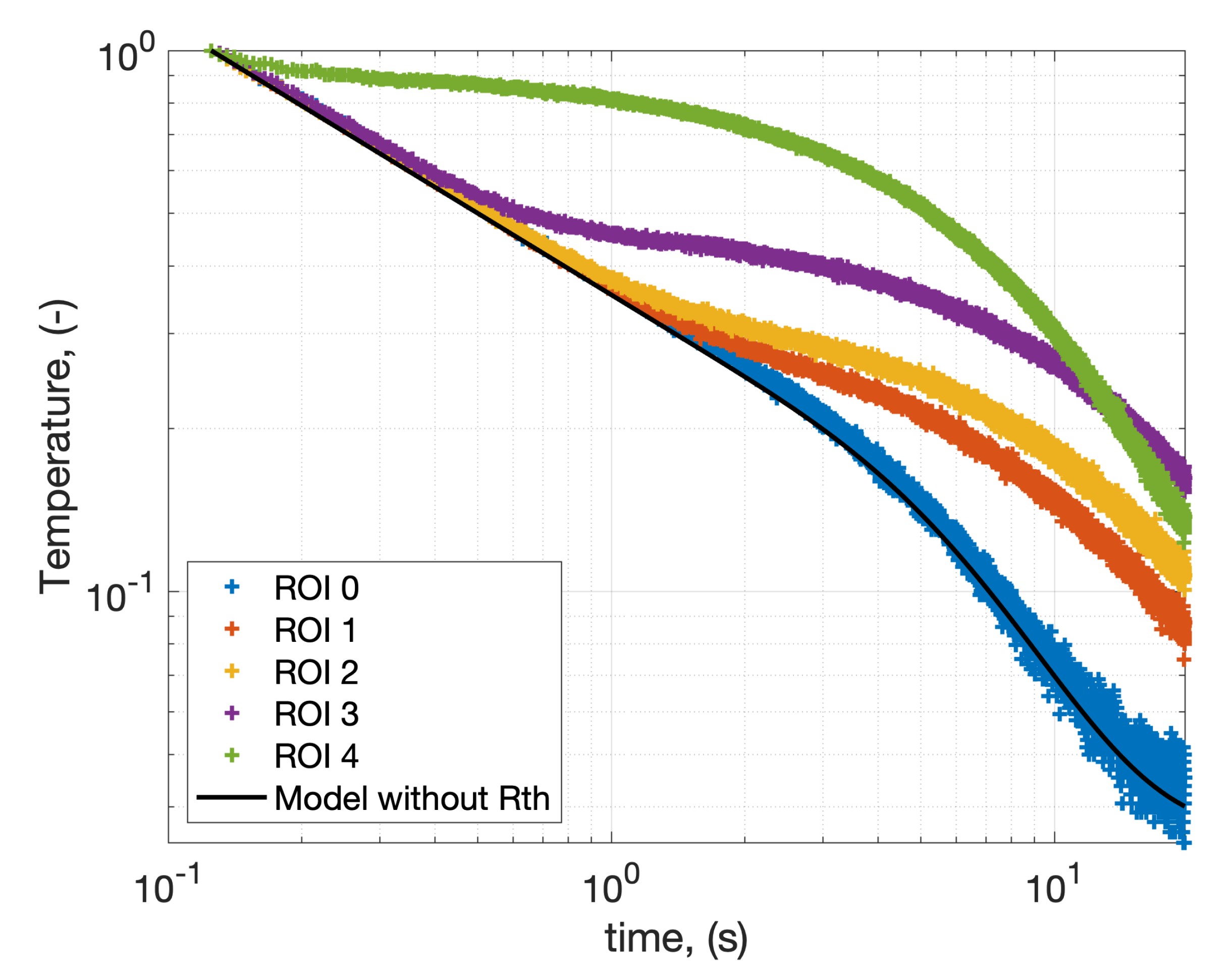
3.2. Autoregressive Asymptotic Method
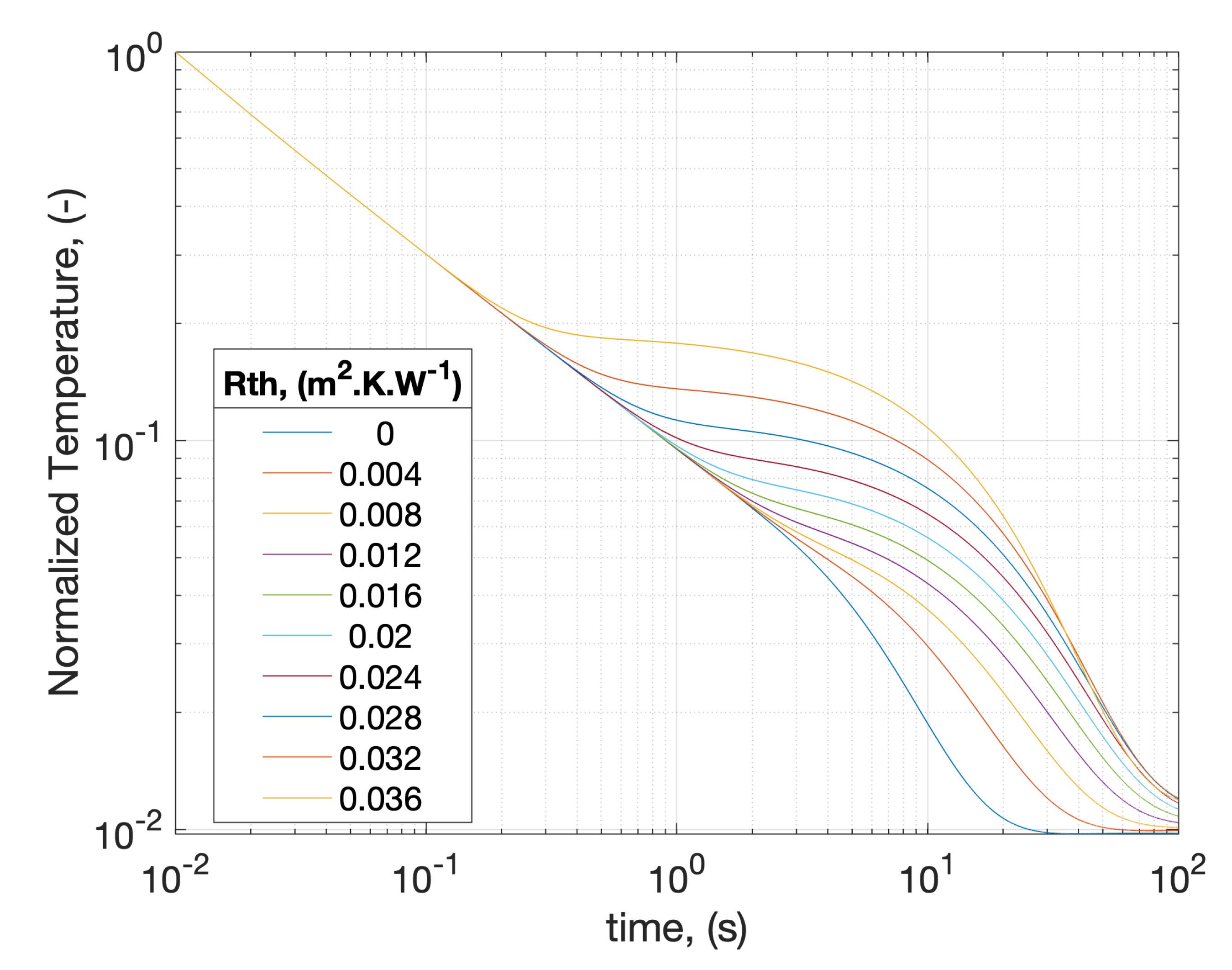
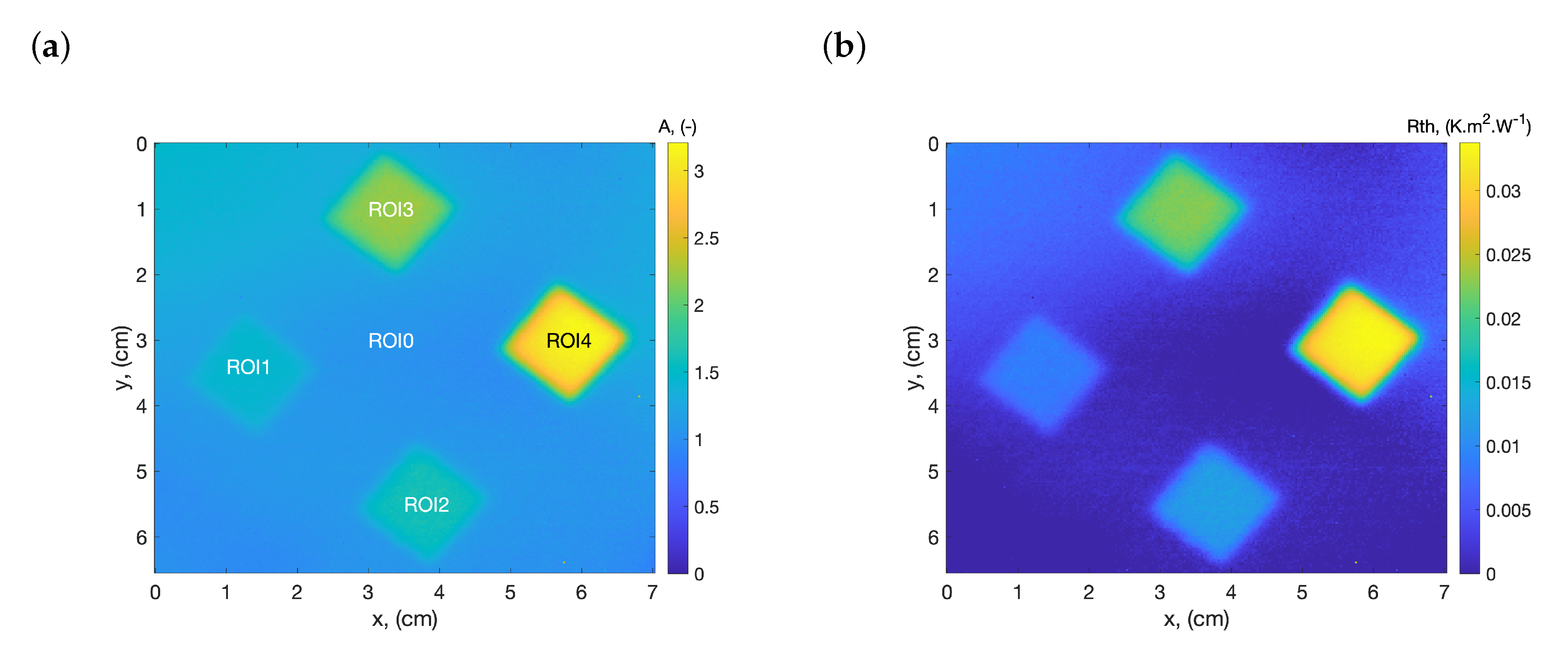
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cahill, D.G. Thermal conductivity measurement from 30 to 750 K: The 3ω method. Rev. Sci. Instrum. 1990, 61, 802–808. [Google Scholar] [CrossRef]
- Dilhaire, S.; Pernot, G.; Calbris, G.; Rampnoux, J.M.; Grauby, S. Heterodyne picosecond thermoreflectance applied to nanoscale thermal metrology. J. Appl. Phys. 2011, 110, 114314. [Google Scholar] [CrossRef]
- Baba, T.; Ishikawa, K.; Yagi, T.; Taketoshi, N. Measurements of thermophysical property of thin films by light pulse heating thermoreflectance methods. arXiv 2007, arXiv:0709.1845. [Google Scholar]
- Horny, N.; Chirtoc, M.; Fleming, A.; Hamaoui, G.; Ban, H. Kapitza thermal resistance studied by high-frequency photothermal radiometry. Appl. Phys. Lett. 2016, 109, 033103. [Google Scholar] [CrossRef]
- Depriester, M.; Hus, P.; Delenclos, S.; Sahraoui, A.H. New methodology for thermal parameter measurements in solids using photothermal radiometry. Rev. Sci. Instrum. 2005, 76, 074902. [Google Scholar] [CrossRef]
- Kusiak, A.; Battaglia, J.L.; Noe, P.; Sousa, V.; Fillot, F. Thermal conductivity of carbon doped GeTe thin films in amorphous and crystalline state measured by modulated photo thermal radiometry. J. Phys. Conf. Ser. 2016, 745, 032104. [Google Scholar] [CrossRef]
- Shepard, S.M. Flash thermography of aerospace composites. 2007. Available online: https://www.ndt.net/article/panndt2007/papers/132.pdf (accessed on 29 January 2020).
- Balageas, D.; Chapuis, B.; Deban, G.; Passilly, F. Improvement of the detection of defects by pulse thermography thanks to the TSR approach in the case of a smart composite repair patch. Quant. InfraRed Thermogr. J. 2010, 7, 167–187. [Google Scholar] [CrossRef]
- Karpen, W.; Wu, D.; Steegmuller, R.; Busse, G. Depth profiling of orientation in laminates with local lockin thermography. Proc. QIRT 1994, 94, 23–26. [Google Scholar]
- Oswald-Tranta, B.; Maier, A.; Schledjewski, R. Defect depth determination in a CFRP structure using TSR technique. In Proceedings of the 12th International Conference on Quantitative Infrared Thermography (QIRT 2014), Bordeaux, France, 7–11 July 2014. [Google Scholar]
- Roche, J.M.; Balageas, D. Imagerie quantitative TSR-RVB: De la détection de défauts au D-scan thermique. Available online: https://www.sft.asso.fr/Local/sft/dir/user-3775/documents/actes/Congres_2015/Communications/41753-fichier4.pdf (accessed on 29 January 2020).
- Ibarra-Castanedo, C.; Maldague, X. Pulsed phase thermography reviewed. Quant. Infrared Thermogr. J. 2004, 1, 47–70. [Google Scholar] [CrossRef]
- Shepard, S.M.; Lhota, J.R.; Rubadeux, B.A.; Wang, D.; Ahmed, T. Reconstruction and enhancement of active thermographic image sequences. Opt. Eng. 2003, 42, 1337–1343. [Google Scholar] [CrossRef]
- Müller, J.P.; Krankenhagen, R. Optimizing thermographic testing of thick GFRP plates by assessing the real energy absorbed within the material. Compos. Struct. 2019, 215, 60–68. [Google Scholar] [CrossRef]
- Maillet, D. Thermal Quadrupoles: Solving the Heat Equation Through Integral Transforms; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Bendada, A.; Erchiqui, F.; Lamontagne, M. Pulsed thermography in the evaluation of an aircraft composite using 3D thermal quadrupoles and mathematical perturbations. Inverse Probl. 2005, 21, 857. [Google Scholar] [CrossRef]
- Winfree, W.P.; Zalameda, J.N.; Howell, P.A.; Cramer, K.E. Simulation of thermographic responses of delaminations in composites with quadrupole method. Thermosense Ther. Infrared Appl. XXXVIII Int. Soc. Opt. Photonics 2016, 9861, 98610N. [Google Scholar]
- Bernegger, R.; Altenburg, S.J.; Roellig, M.; Maierhofer, C. Applicability of a 1D analytical model for pulse thermography of laterally heterogeneous semitransparent materials. Int. J. Thermophys. 2018, 39, 39. [Google Scholar] [CrossRef]
- Feuillet, V.; Ibos, L.; Fois, M.; Dumoulin, J.; Candau, Y. Defect detection and characterization in composite materials using square pulse thermography coupled with singular value decomposition analysis and thermal quadrupole modeling. NDT E Int. 2012, 51, 58–67. [Google Scholar] [CrossRef]
- Stewart, G.W. On the early history of the singular value decomposition. SIAM Rev. 1993, 35, 551–566. [Google Scholar] [CrossRef]
- Jordan, C. Sur la réduction des formes bilinéaires. Comptes Rendus De l’Académie Des Sciences 1874, 78, 614–617. [Google Scholar]
- Beltrami, E. Sulle funzioni bilineari. Giornale di Matematiche ad Uso degli Studenti Delle Universita 1873, 11, 98–106. [Google Scholar]
- Sylvester, J.J. Sur la reduction biorthogonale d’une forme lineo-linéaire a sa forme canonique. Comptes Rendus 1889, 108, 651–653. [Google Scholar]
- Dean, J.A. Lange’s Handbook of Chemistry; Mcgraw-Hill, Inc.: New York, NY, USA; London, UK, 1999. [Google Scholar]
- Touloukian, Y.S.; Powell, R.W.; Ho, C.Y.; Klemens, P.G. Thermophysical Properties of Matter-the tprc Data Series. Volume 1. Thermal Conductivity-Metallic Elements and Alloys; Thermophysical and Electronic Properties Information Analysis Center: Lafayette, IN, USA, 1970. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Zheng, W.X. A least-squares based method for autoregressive signals in the presence of noise. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1999, 46, 81–85. [Google Scholar] [CrossRef]
- Moore, E.H. On the reciprocal of the general algebraic matrix. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
- Penrose, R. A generalized inverse for matrices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1955; Volume 51, pp. 406–413. [Google Scholar]

| Error *** | |||||
|---|---|---|---|---|---|
| (m) | (W.m.K) | (m.K.W) | (m.K.W) | (%) | |
| * ROI 1 | [200–250] ** | 0.025 | [0.008–0.01] | 0.0087 | 3.4 |
| * ROI 2 | [300–350] ** | 0.025 | [0.012–0.014] | 0.0126 | 3.1 |
| * ROI 3 | [500–550] ** | 0.025 | [0.02–0.022] | 0.0221 | 5.2 |
| * ROI 4 | [800–850] ** | 0.025 | [0.032–0.034] | 0.0328 | 0.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groz, M.-M.; Bensalem, M.; Sommier, A.; Abisset-Chavanne, E.; Chevalier, S.; Chulkov, A.; Battaglia, J.-L.; Batsale, J.-C.; Pradere, C. Estimation of Thermal Resistance Field in Layered Materials by Analytical Asymptotic Method. Appl. Sci. 2020, 10, 2351. https://doi.org/10.3390/app10072351
Groz M-M, Bensalem M, Sommier A, Abisset-Chavanne E, Chevalier S, Chulkov A, Battaglia J-L, Batsale J-C, Pradere C. Estimation of Thermal Resistance Field in Layered Materials by Analytical Asymptotic Method. Applied Sciences. 2020; 10(7):2351. https://doi.org/10.3390/app10072351
Chicago/Turabian StyleGroz, Marie-Marthe, Mohamed Bensalem, Alain Sommier, Emmanuelle Abisset-Chavanne, Stéphane Chevalier, Arsenii Chulkov, Jean-Luc Battaglia, Jean-Christophe Batsale, and Christophe Pradere. 2020. "Estimation of Thermal Resistance Field in Layered Materials by Analytical Asymptotic Method" Applied Sciences 10, no. 7: 2351. https://doi.org/10.3390/app10072351
APA StyleGroz, M.-M., Bensalem, M., Sommier, A., Abisset-Chavanne, E., Chevalier, S., Chulkov, A., Battaglia, J.-L., Batsale, J.-C., & Pradere, C. (2020). Estimation of Thermal Resistance Field in Layered Materials by Analytical Asymptotic Method. Applied Sciences, 10(7), 2351. https://doi.org/10.3390/app10072351





