Exploring Geometric Feature Hyper-Space in Data to Learn Representations of Abstract Concepts
Abstract
1. Introduction
2. Related Work
3. Background
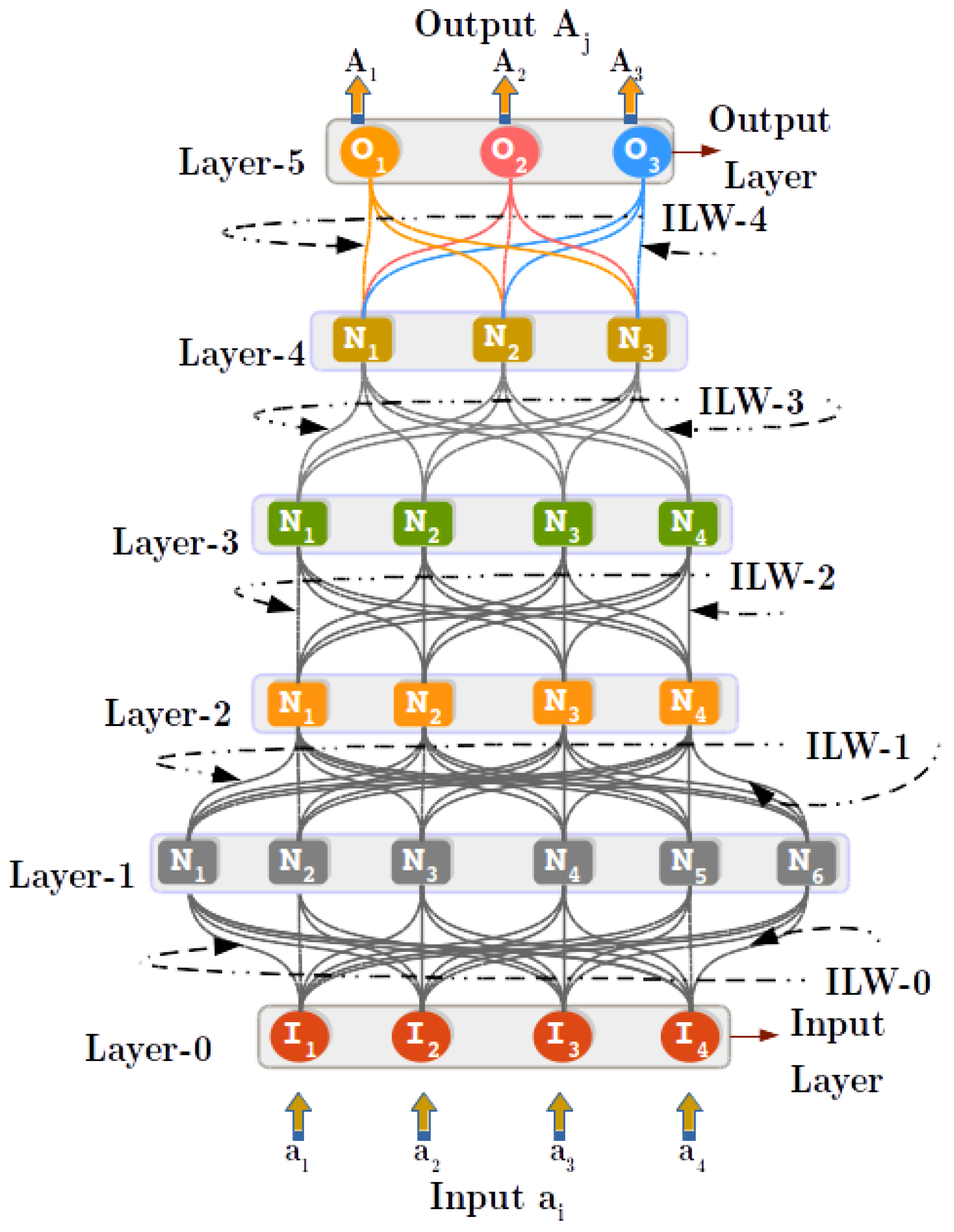
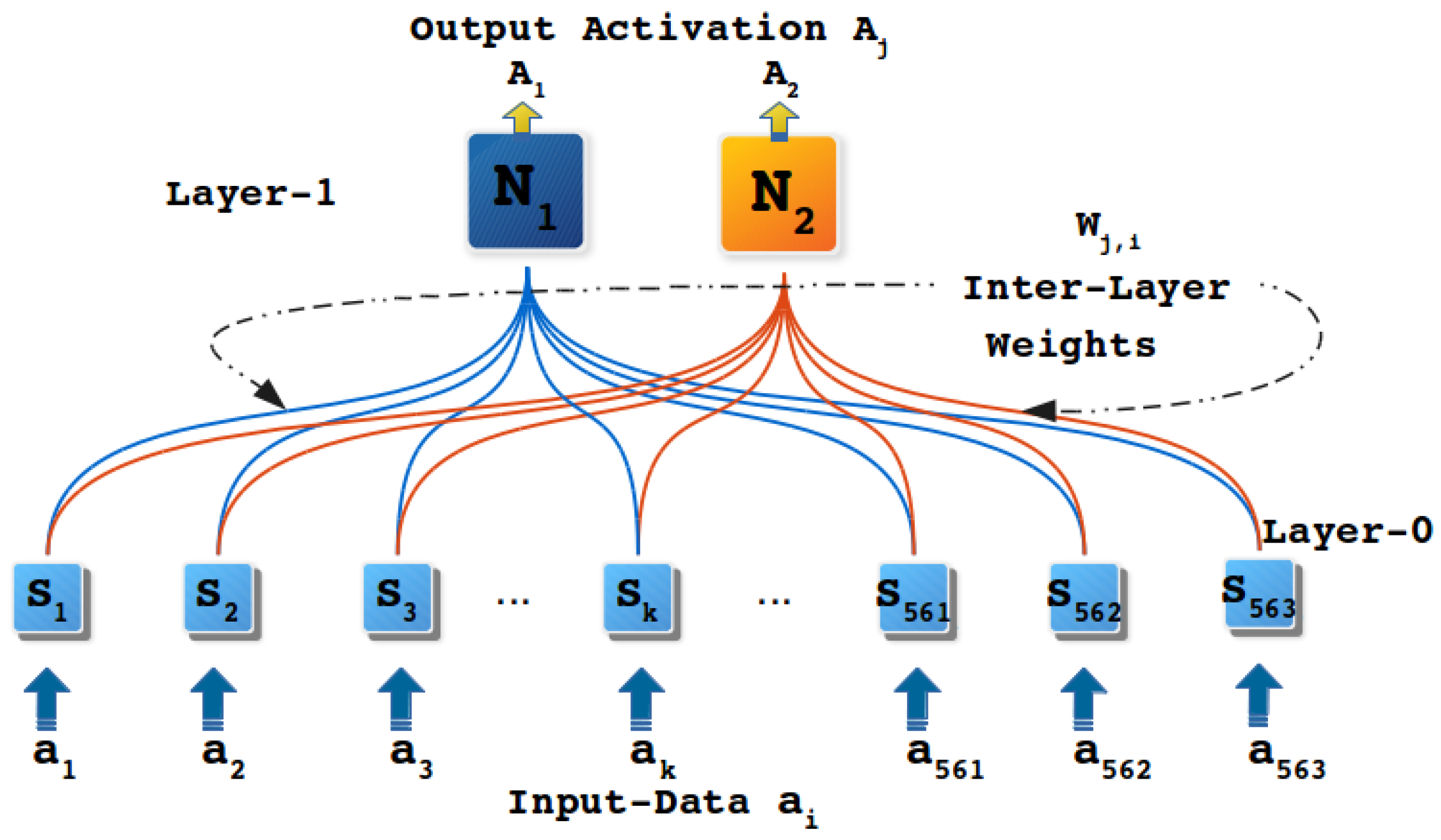
3.1. Principles of Regulated Activation Networks
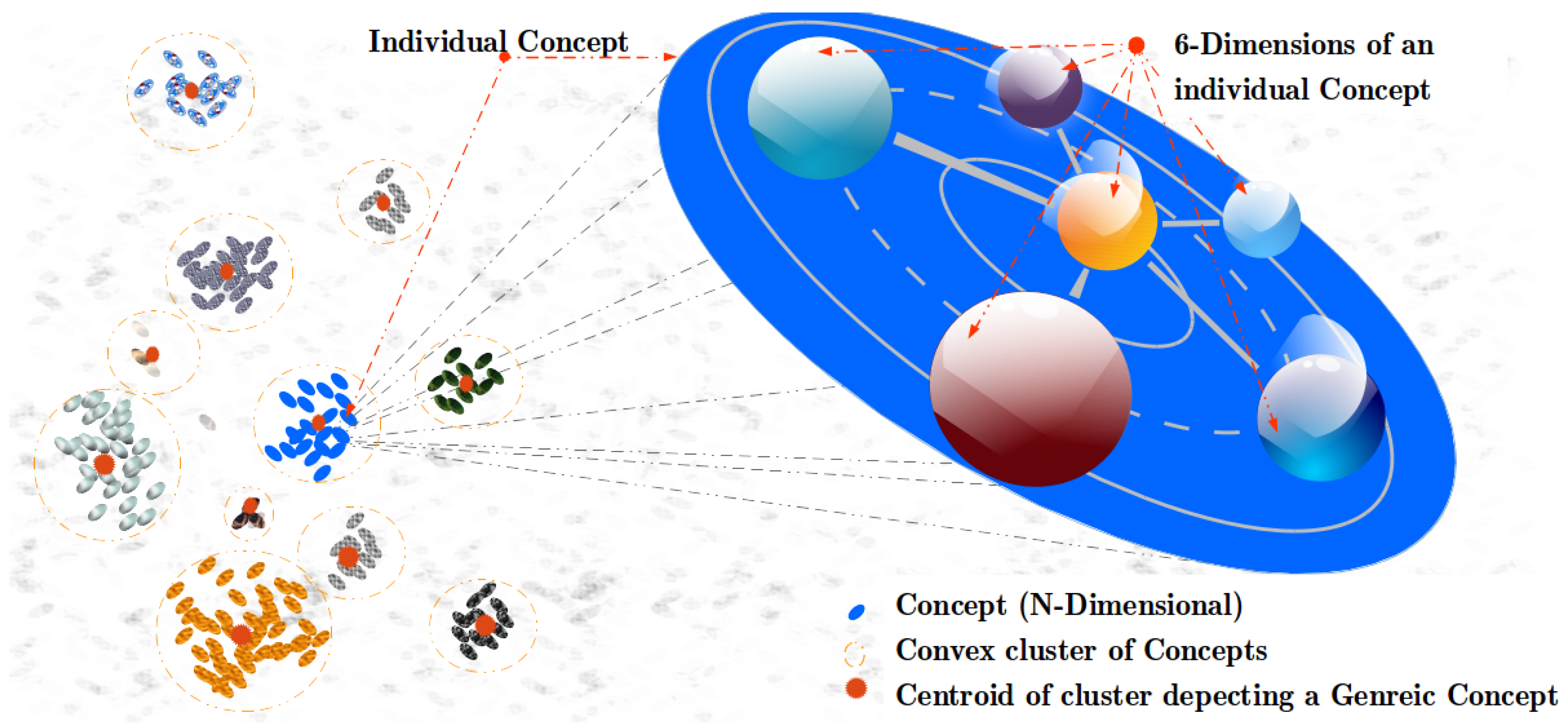
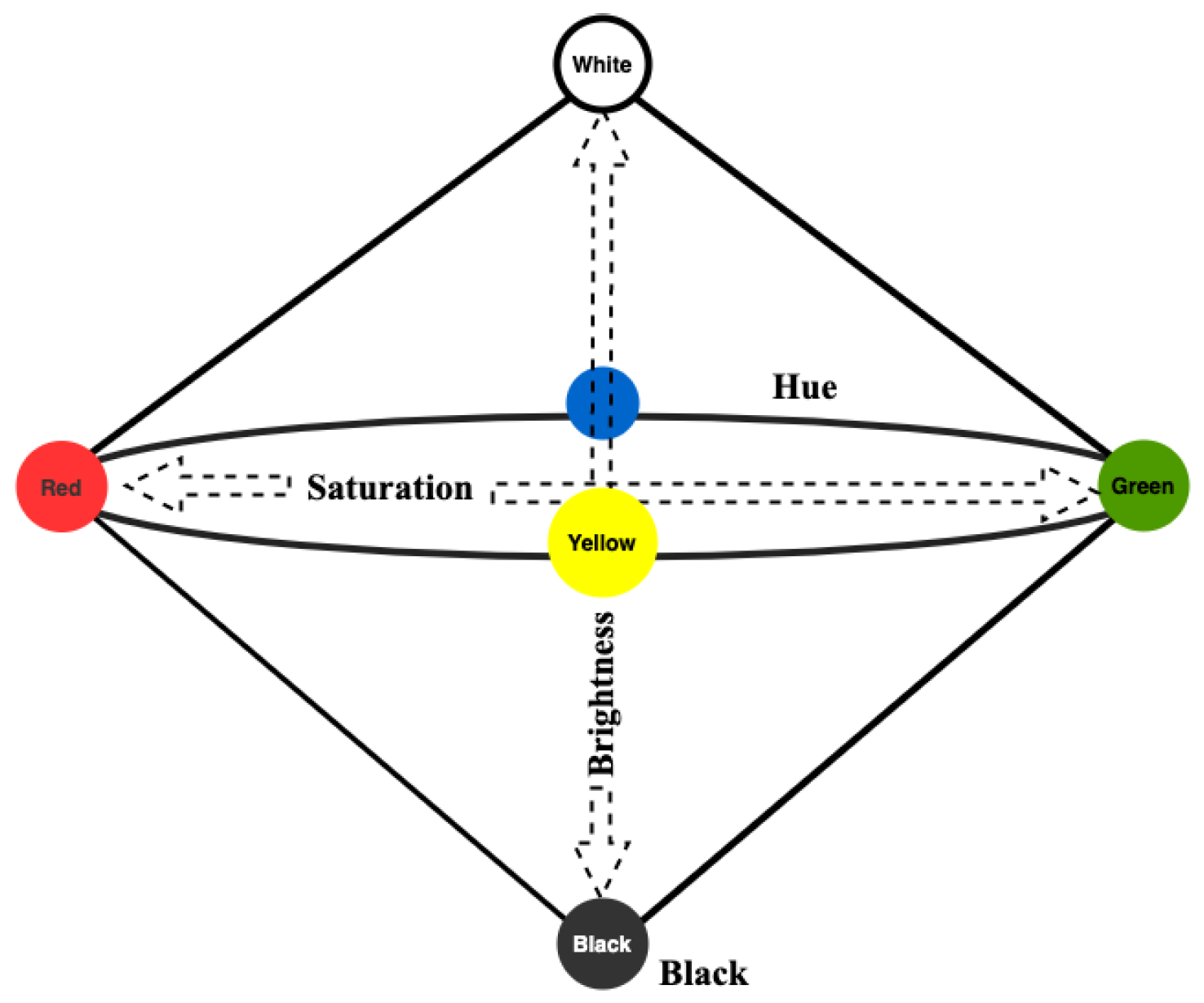
3.2. Conceptual Spaces
3.3. Spreading Activation
4. Abstract Concept Modeling with RANs
4.1. Assumptions and Boundaries
- If a variable in the input data is categorical, e.g., ; ; , transform the data using One Hot Coding technique.
- If a variable in the input data is numerical, bounded within a minimum and a maximum value it can be normalized into , e.g., via ;
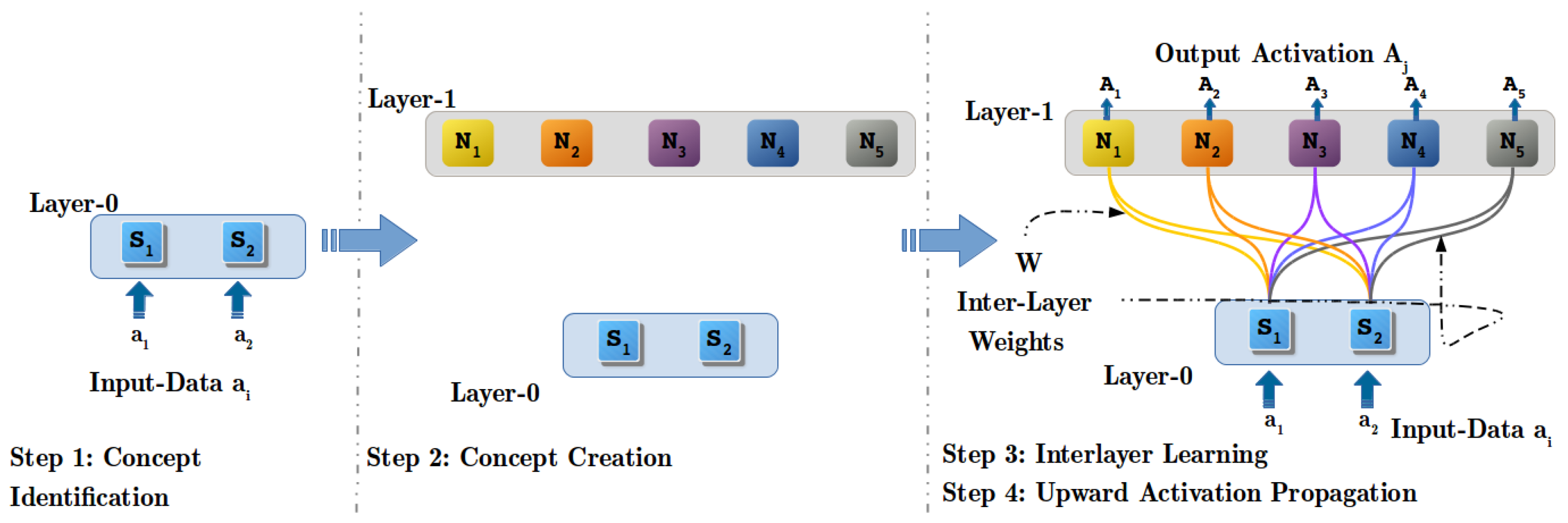
4.2. Step 1: Concept Identification (CI) Process
4.3. Step 2: Concept Creation (CC) Process
4.4. Step 3: Inter-Layer Learning (ILL) Process
4.5. Step 4: Upwards Activation Propagation (UAP) Process
4.5.1. Geometric Distance Function (GDF)—Stage 1
4.5.2. Similarity Translation Function (STF)—Stage 2
- , i.e., when distance is 0 similarity is 100%.
- i.e., when distance is 1 similarity is 0%.
- is continuous, monotonous, and differentiable in the interval.
4.6. RANs Proof of Hypothesis and Complexity
| Algorithm 1 Upwards Activation Propagation algorithm |
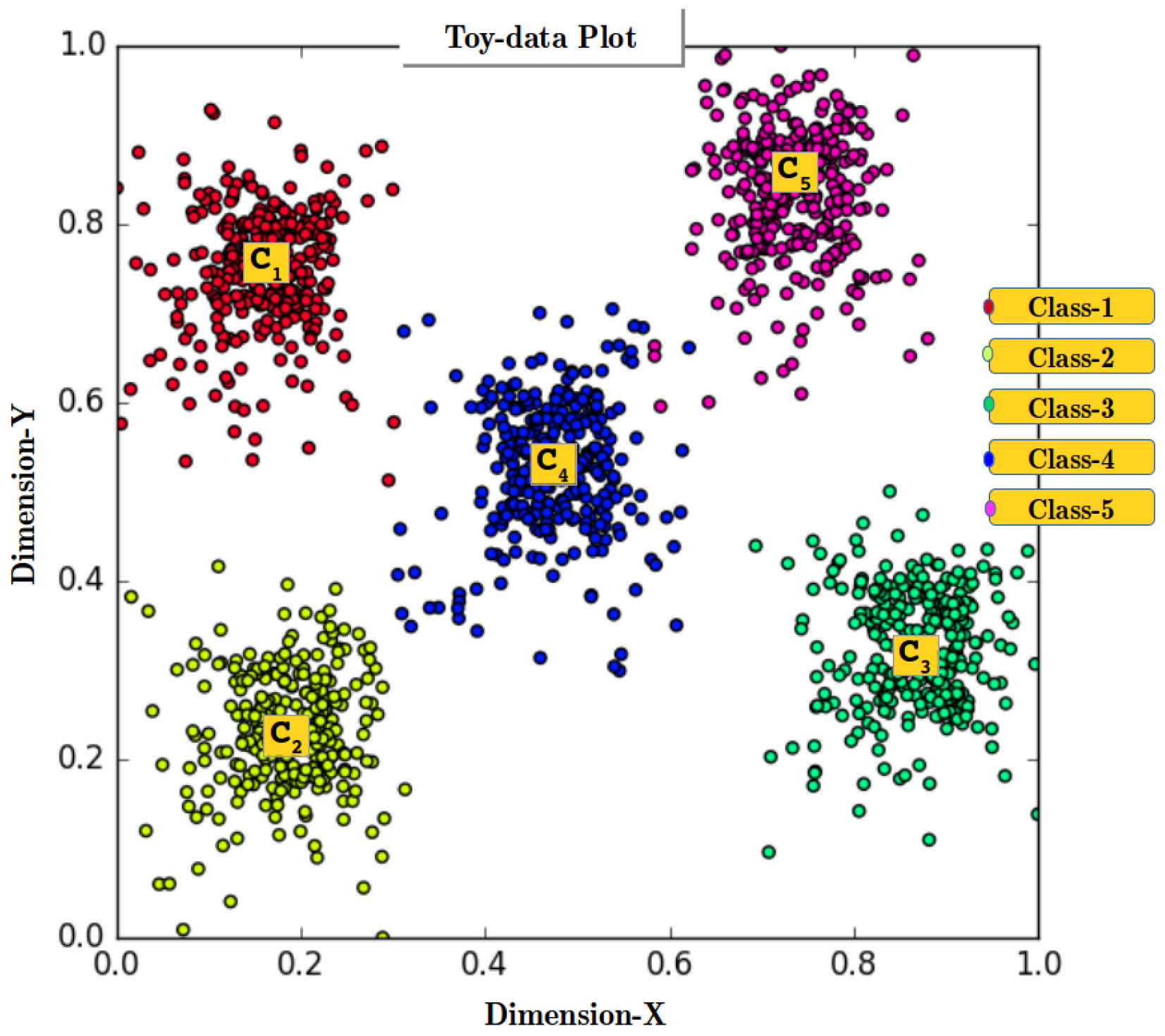
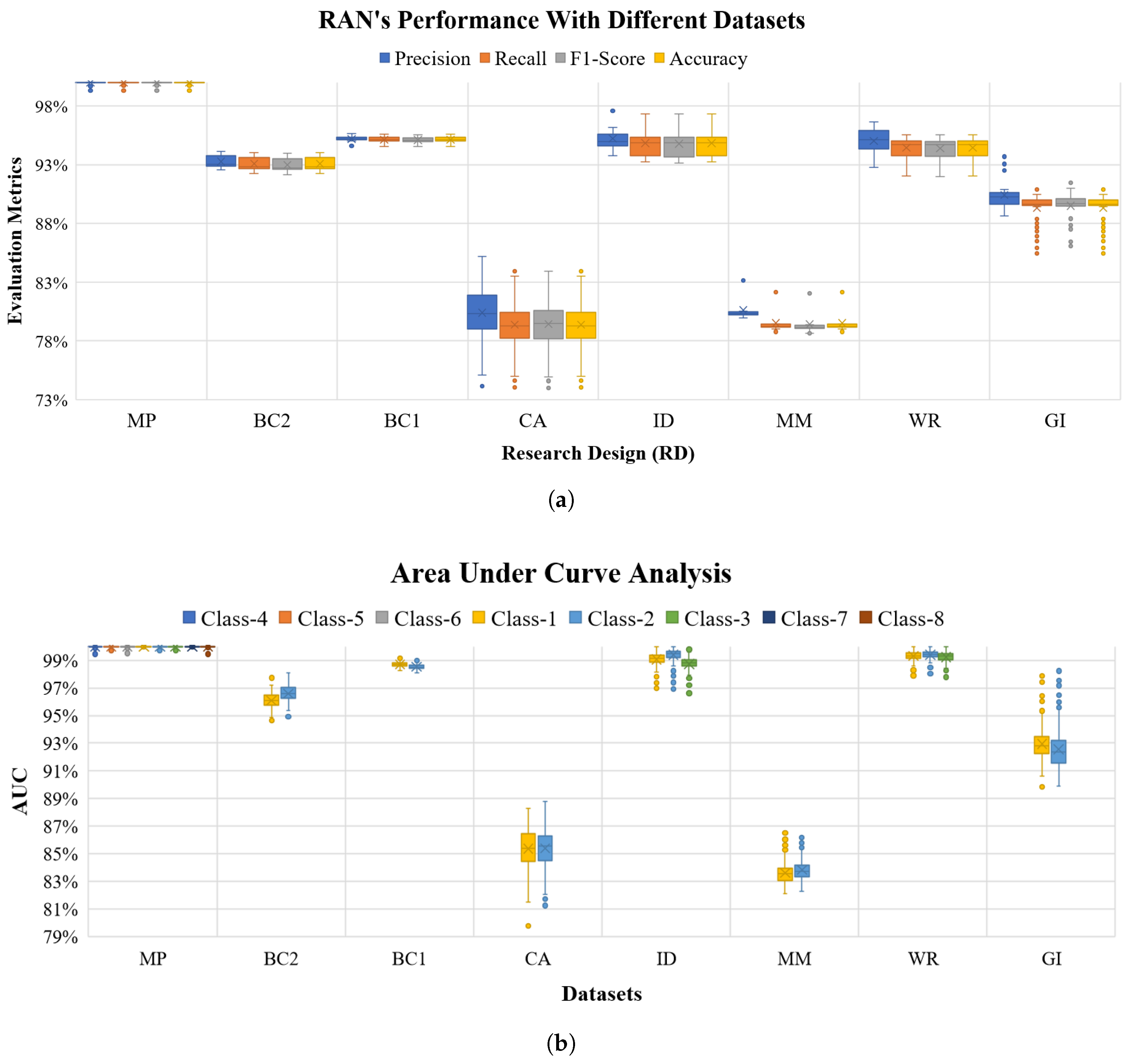
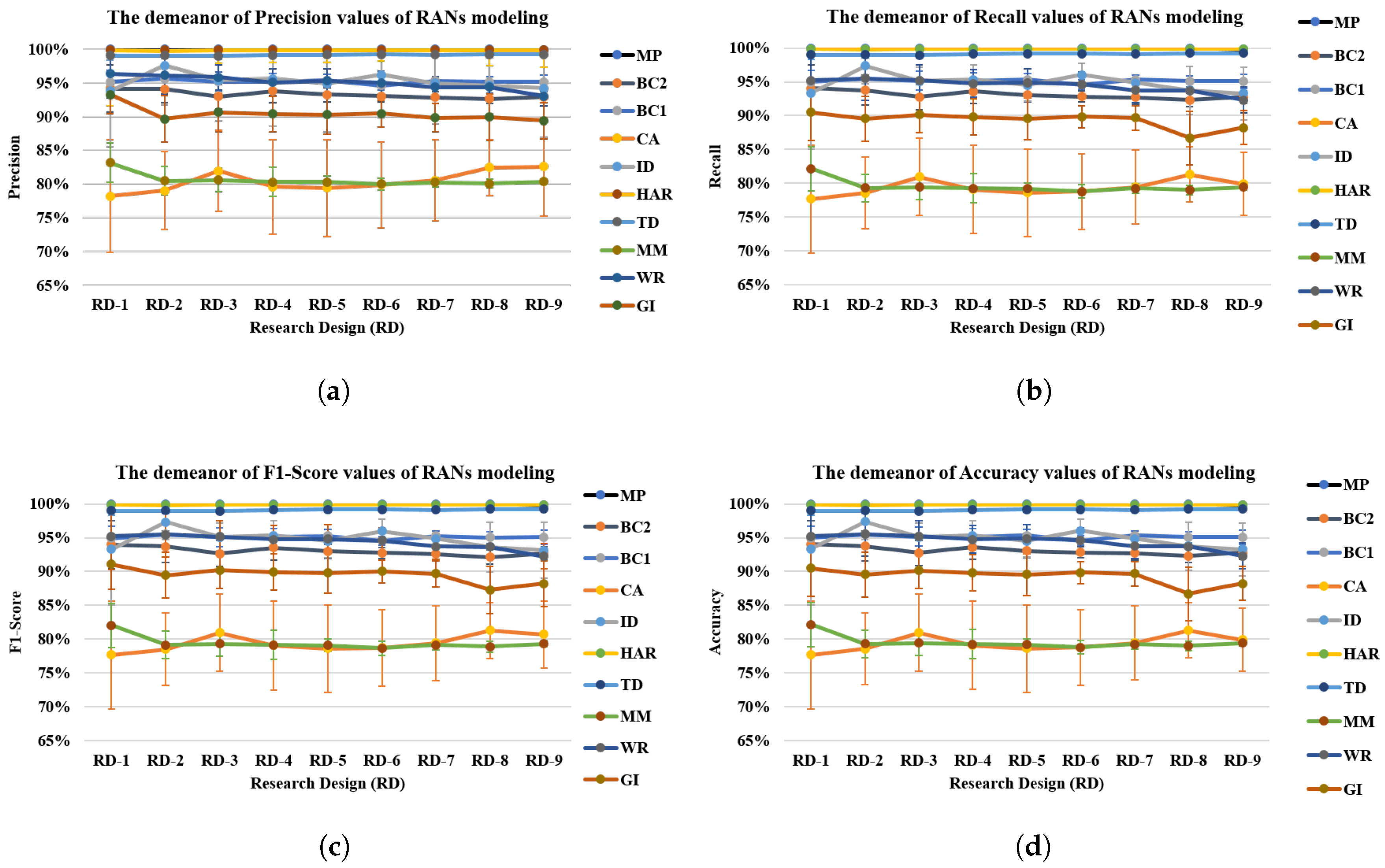
5. Behavioral Demonstration of RANs
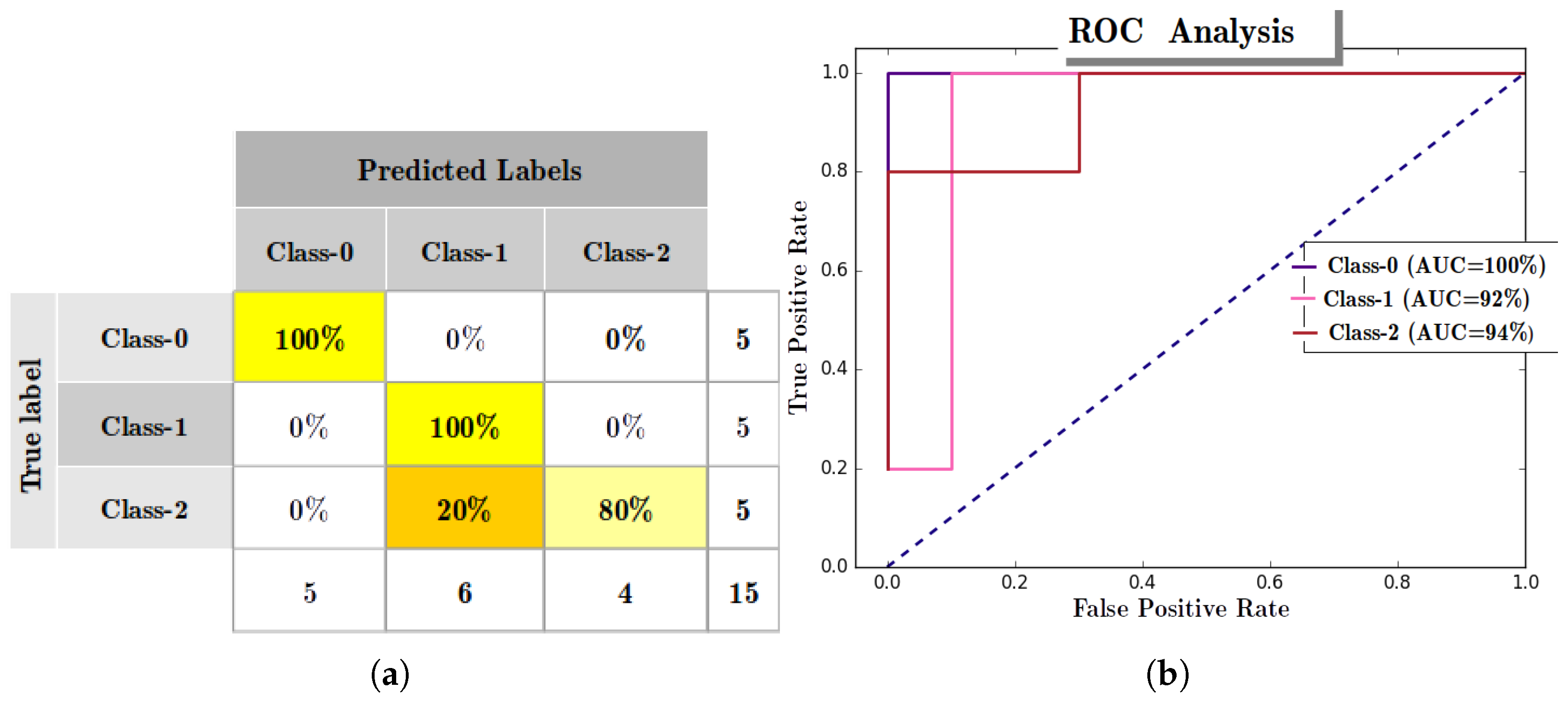
5.1. Experiment with IRIS Dataset
| Algorithm 2 Concept Hierarchy Creation algorithm |
|
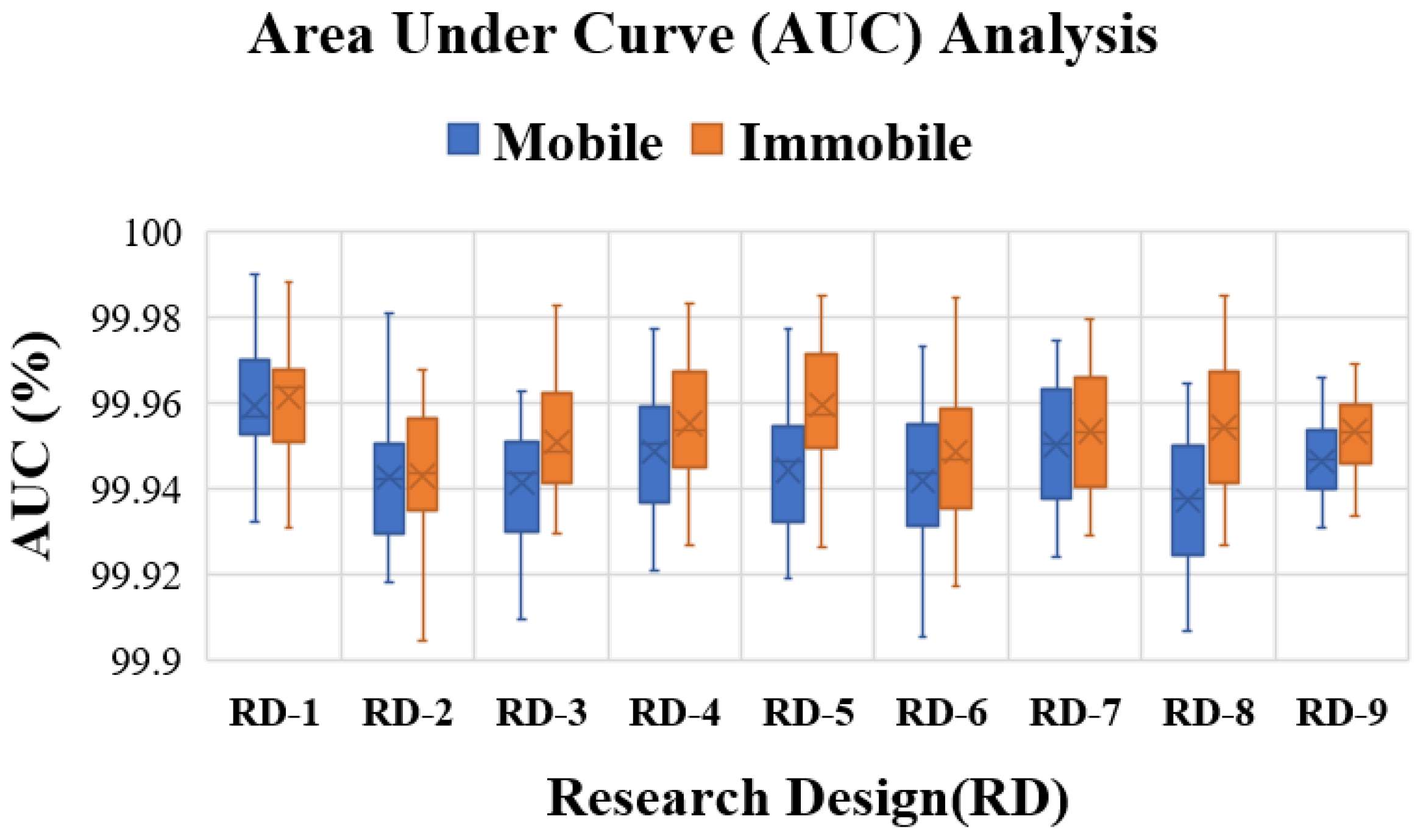
5.2. Experiment with Human Activity Recognition Data
6. RANs Applicability and Observations
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACL | Abstract Concept Labeling |
| AUC | Area Under Curve |
| BC1 | Breast Cancer 669 Dataset |
| BC2 | Breast Cancer 569 Dataset |
| CA | Credit Approval Dataset |
| CHC | Concept Hierarchy Creation |
| CI | Concept Identification |
| CLS | Current Layer Size |
| CRDP | Cluster Representative Data Point |
| DoC | Degree of Confidence |
| GDF | Geometric Distance Function |
| GI | Glass Identification Dataset |
| HAR | Human Activity Recognition Data |
| ID | IRIS Dataset |
| ILL | Inter Layer Learning |
| ILW | Inter Layer Weights |
| K-NN | K Nearest Neighbor |
| MLP | Multilayer Perceptron |
| MM | Mammography Mass Dataset |
| MP | Mice Protein Dataset |
| MRI | Magnetic Resonance Imaging |
| RANs | Regulated Activation Networks |
| RBM | Restricted Boltzmann Machine |
| RBM+ | RBM pipe-lined with Logistic Regression |
| ROC | Receiver Operating Characteristic |
| SGD | Stochastic Gradient Descent |
| STF | Similarity Translation Function |
| UAP | Upward Activation Propagation |
Appendix A
Appendix A.1. Data and Scripts
| Type | Description | File-path |
|---|---|---|
| Data | Download link | https://www.dropbox.com/sh/3410ozeru3o5opm/AAA24aUGtUS1i7xHKp9kyzRKa?dl=0 |
| IRIS Data | data/iris_with_label.csv | |
| Mice Protein data | data/Data_cortex_Nuclear/mice_with_class_label.csv | |
| Glass Identification data | data/newDataToExplore/new/GlassIdentificationDatabase/RANsform.csv | |
| Wine Recognition data | data/newDataToExplore/new/WineRecognitionData/RansForm.csv | |
| Breast cancer 669 data | data/newDataToExplore/new/breastCancerDatabases/699RansForm.csv | |
| Breast Cancer 559 data | data/newDataToExplore/new/breastCancerDatabases/569RansForm.csv | |
| UCIHAR data | data/UCI_HAR_Dataset.csv | |
| Mamographic Mass data | data/newDataToExplore/new/MammographicMassData/RansForm1 | |
| Credit Approval data | data/newDataToExplore/new/CreditApproval/RansForm.csv | |
| Toy-data data | data/toydata5clustersRAN.csv | |
| Script | Download Link | https://www.dropbox.com/sh/rcw1cj4ce1f3zic/AAAm6wVTj2qsLZ1lbc3kn4MPa?dl=0 |
| RANs classes and methods | RAN_V2-0/RAN/RAN_kfold.py | |
| Methods | RAN_V2-0/RAN/Layer.py | |
| Utilities like Labeling and plotting | RAN_V2-0/RAN/UtilsRAN.py | |
| Python Script for using RANs | RAN_V2-0/RAN/RAN_input_T1.py |
| Header | H-1 | H-2 | .............. | H-n | ||||
|---|---|---|---|---|---|---|---|---|
| Data Instances | D-1 | D-2 | .............. | D-n | ||||
| D-1 | D-2 | ............... | D-n | |||||
| . | . | .............. | . | |||||
| . | . | ............... | . | |||||
| . | . | ............... | . | |||||
| D-1 | D-2 | .............. | D-n | |||||
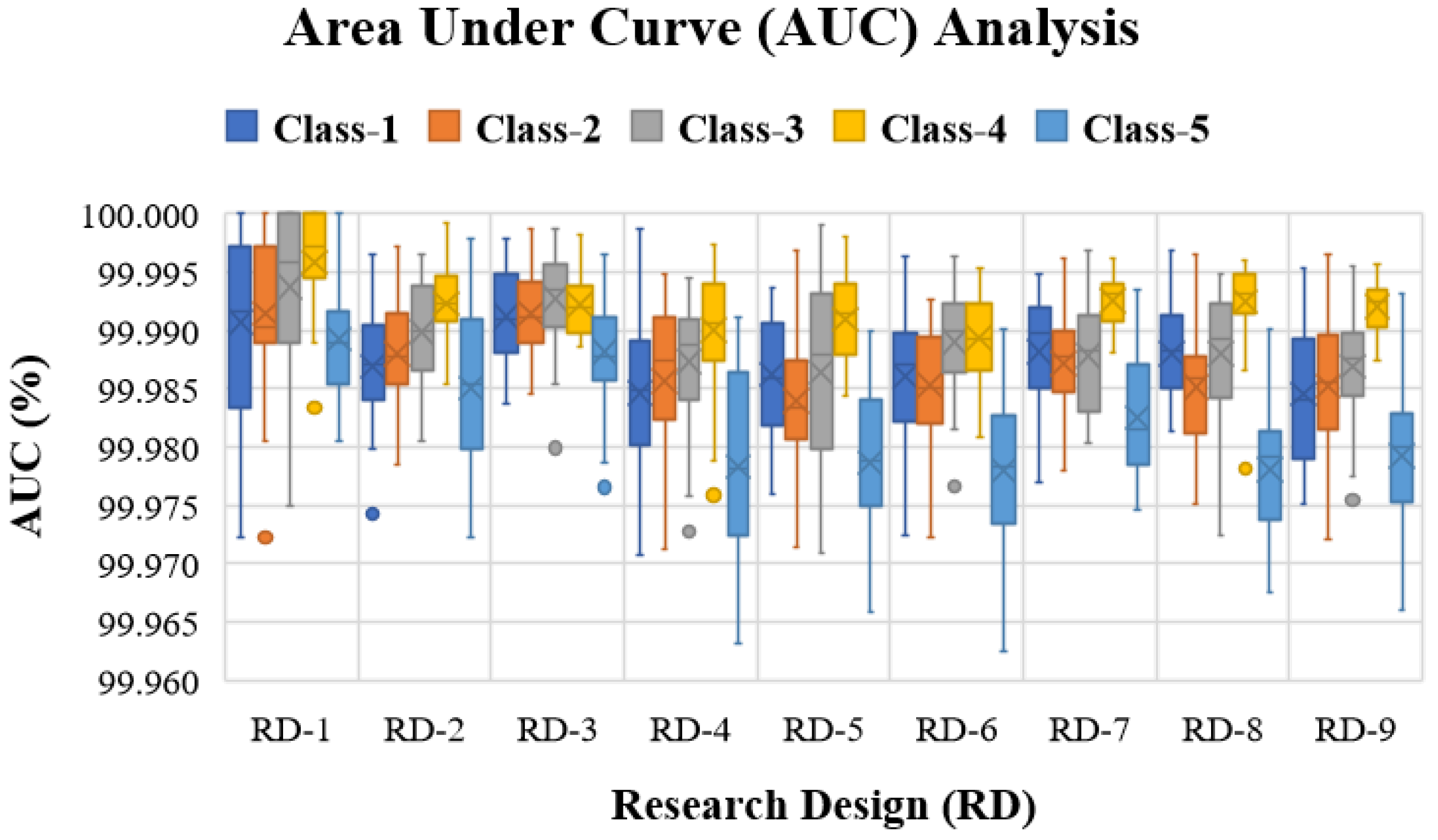
Appendix A.2. Model Configurations and Research Design
| RD-1 | RD-2 | RD-3 | RD-4 | RD-5 | |||||
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test |
| 90% | 10% | 80% | 20% | 70% | 30% | 60% | 40% | 50% | 50% |
| RD-1 | RD-7 | RD-8 | RD-9 | ||||||
| Train | Test | Train | Test | Train | Test | Train | Test | ||
| 40% | 60% | 30% | 70% | 20% | 80% | 10% | 90% | ||
Appendix A.3. Abstract Concept Labeling (ACL)
Appendix A.4. Dataset Description
| Dataset | Attribute | Class | Source | ||||
|---|---|---|---|---|---|---|---|
| Name | Type | Size | Balanced | Type | Size | # | Name |
| Mice Protein | Multivariate | 1080 | yes | Real | 82 | 8 | UCI |
| Breast Cancer 569 | Multivariate | 569 | yes | Real | 32 | 2 | UCI |
| Breast Cancer 669 | Multivariate | 669 | yes | Integer | 10 | 2 | UCI |
| Credit Approval | Multivariate | 690 | yes | Mixed | 15 | 2 | UCI |
| Glass Identification | Multivariate | 214 | yes | Real | 10 | 7 | UCI |
| Mammographic mass | Multivariate | 961 | yes | Integer | 6 | 2 | UCI |
| IRIS | Multivariate | 150 | yes | Real | 4 | 3 | UCI |
| Wine Recognition | Multivariate | 178 | yes | Mixed | 13 | 3 | UCI |
| Human Activity Recognition | Multivariate, Time-Series | 10299 | yes | Real | 561 | 6 | UCI |
| Toy-data | Multivariate | 1500 | yes | Real | 2 | 5 | Self |
| UCI- University of California Irvine’s Machine Learning Repository; Self- Artificially generated dataset | |||||||
Appendix A.5. Multi-Class ROC Analysis with RANs Modeling
- 1
- Node-wise binary transformation of True-Labels: For example, suppose there are three classes (c1, c2, c3) represented by three abstract nodes (n1, n2, and n3) in RANs model at Layer-1, and let true-label be [c1, c2, c2, c1, c2, c3, c3] for 7 test instances, then for node n1 label will be [1, 0, 0, 1, 0, 0, 0] where 1 represents class c1, and 0 depicts others (i.e., c2, and c3).
- 2
- Node-wise confidence-score calculation: This is calculated by averaging activation-value and confidence-indicator of activation for an input instance at an Abstract node. Activation-value is an individual activation of an activation vector obtained by propagating up the data using UAP mechanism of RANs whereas, confidence-indicator is calculated by min-max normalization operation of activation vector. For example, after UAP operation each node (n1, n2, and n3) receives activation [0.89, 0.34, 0.11] (a vector of activation), and confidence-indicator is min-max ([0.89, 0.34, 0.11]) = [1.0, 0.29, 0.0]. and the confidence-score for nodes n1 = (0.89 + 1.0)/2.0 = 0.95, n2 = (0.34 + 0.29)/2.0 = 0.32, and n3 = (0.11 + 0.11)/2.0 = 0.05.
| Data | Algo | Configurations | Data | Algo | Configurations |
|---|---|---|---|---|---|
| Toy-data | RBM + LR | Lr = 0.000001, iter = 500, comp = 20 max_iter = 30, C = 70 | UCIHAR | RBM + LR | Lr = 0.06, iter = 500, comp = 10 max_iter = 10, C = 1 |
| K-NN | n_neighbors = 30 | K-NN | n_neighbors = 15 | ||
| LR | max_iter = 10, C = 1 | LR | max_iter = 30, C = 1 | ||
| MLP | Rs = 1, hls = 10, iter = 250 | MLP | Rs = 1, hls = 10, iter = 400 | ||
| RANs | CLS = 5, Desired_depth = 1 | RANs | CLS = 2, Desired_depth = 1 | ||
| SGD | alpha = 0.0001, n_iter = 5, epsilon = 0.25 | SGD | alpha = 0.1, n_iter = 10, epsilon = 0.25 | ||
| Mice Protein | RBM + LR | Lr = 0.1, iter = 500, comp = 20 max_iter = 30, C = 30 | Breast Cancer 569 | RBM + LR | Lr = 0.006, iter = 100, comp = 10 max_iter = 30, C = 1 |
| K-NN | n_neighbors = 15 | K-NN | n_neighbors = 30 | ||
| LR | max_iter = 4, C = 0.00001 | LR | max_iter = 10, C = 0.001 | ||
| MLP | Rs = 1, hls = 10, iter = 300 | MLP | Rs = 1, hls = 10, iter = 200 | ||
| RANs | CLS = 8, Desired_depth = 1 | RANs | CLS = 2, Desired_depth = 1 | ||
| SGD | alpha = 0.1, n_iter = 10, epsilon = 0.25 | SGD | alpha = 0.0001, n_iter = 5, epsilon = 0.25 | ||
| Breast Cancer 669 | RBM + LR | Lr = 0.001, iter = 100, comp = 10 max_iter = 30, C = 1 | Credit Approval | RBM + LR | Lr = 0.006, iter = 100, comp = 10 max_iter = 30, C = 1 |
| K-NN | n_neighbors = 10 | K-NN | n_neighbors = 30 | ||
| LR | max_iter = 10, C = 0.001 | LR | max_iter = 10, C = 0.001 | ||
| MLP | Rs = 1, hls = 10, iter = 200 | MLP | Rs = 1, hls = 10, iter = 200 | ||
| RANs | CLS = 2, Desired_depth = 1 | RANs | CLS = 2, Desired_depth = 1 | ||
| SGD | alpha = 0.0001, n_iter = 5, epsilon = 0.25 | SGD | alpha = 0.0001, n_iter = 5, epsilon = 0.25 | ||
| Glass Identification | RBM + LR | Lr = 0.001, iter = 400, comp = 10 max_iter = 30, C = 5 | Mamographic Mass | RBM + LR | Lr = 0.01, iter = 500, comp = 20 max_iter = 30, C = 5 |
| K-NN | n_neighbors = 15 | K-NN | n_neighbors = 30 | ||
| LR | max_iter = 5, C = 0.00001 | LR | max_iter = 5, C = 1 | ||
| MLP | Rs = 1, hls = 10, iter = 200 | MLP | Rs = 1, hls = 10, iter = 250 | ||
| RANs | CLS = 2, Desired_depth = 1 | RANs | CLS = 2, Desired_depth = 1 | ||
| SGD | alpha = 0.01, n_iter = 10, epsilon = 0.25 | SGD | alpha = 0.0001, n_iter = 5, epsilon = 0.25 | ||
| IRIS | RBM + LR | Lr = 0.01, iter = 1000, comp = 20 max_iter = 30, C = 5 | Wine Recognition | RBM + LR | Lr = 0.01, iter = 500, comp = 20 max_iter = 30, C = 50 |
| K-NN | n_neighbors = 15 | K-NN | n_neighbors = 15 | ||
| LR | max_iter = 10, C = 1 | LR | max_iter = 10, C = 0.01 | ||
| MLP | Rs = 1, hls = 10, iter = 400 | MLP | Rs = 1, hls = 10, iter = 300 | ||
| RANs | CLS = 3, Desired_depth = 1 | RANs | CLS = 3, Desired_depth = 1 | ||
| SGD | alpha = 0.01, n_iter = 10, epsilon = 0.25 | SGD | alpha = 0.01, n_iter = 10, epsilon = 0.25 |
References
- Kiefer, M.; Pulvermüller, F. Conceptual representations in mind and brain: Theoretical developments, current evidence and future directions. Cortex 2012, 48, 805–825. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Toivonen, H.; Gross, O.; Cardoso, A.; Correia, J.A.; Machado, P.; Martins, P.; Oliveira, H.G.; Sharma, R.; Pinto, A.M.; et al. Conceptual representations for computational concept creation. ACM Comput. Surv. 2019, 52, 1–33. [Google Scholar] [CrossRef]
- Hill, F.; Korhonen, A. Learning abstract concept embeddings from multi-modal data: Since you probably can’t see what I mean. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 255–265. [Google Scholar]
- Braver, T.; Barch, D.; Cohen, J. Cognition and control in schizophrenia: A computational model of dopamine and prefrontal function. Biol. Psychiatry 1999, 46, 312–328. [Google Scholar] [CrossRef]
- O’Reilly, R.C. Biologically based computational models of high-level cognition. Science 2006, 314, 91–94. [Google Scholar] [CrossRef]
- Rolls, E.; Loh, M.; Deco, G.; Winterer, G. Computational models of schizophrenia and dopamine modulation in the prefrontal cortex. Nat. Rev. Neurosci. 2008, 9, 696–709. [Google Scholar] [CrossRef]
- Kyaga, S.; Landén, M.; Boman, M.; Hultman, C.M.; Långström, N.; Lichtenstein, P. Mental illness, suicide and creativity: 40-Year prospective total population study. J. Psychiatr. Res. 2013, 47, 83–90. [Google Scholar] [CrossRef]
- Anderson, J.R.; Matessa, M.; Lebiere, C. ACT-R: A theory of higher level cognition and its relation to visual attention. Hum. Comput. Interact. 1997, 12, 439–462. [Google Scholar] [CrossRef]
- Hinton, G. A practical guide to training restricted boltzmann machines. Momentum 2010, 9, 926. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 160–167. [Google Scholar]
- Sun, R.; Peterson, T. Learning in reactive sequential decision tasks: The CLARION model. In Proceedings of the IEEE International Conference on Neural Networks, Washington, DC, USA, 3–6 June 1996; Volume 2, pp. 1073–1078. [Google Scholar]
- Gruau, F. Automatic definition of modular neural networks. Adapt. Behav. 1994, 3, 151–183. [Google Scholar] [CrossRef]
- Gärdenfors, P. Conceptual Spaces: The Geometry of Thought; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report; California Univ San Diego La Jolla Inst for Cognitive Science: San Diego, CA, USA, 1985. [Google Scholar]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009; Chapter 7. [Google Scholar]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Zhang, T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; ACM: New York, NY, USA, 2004; p. 116. [Google Scholar]
- Binder, J.R.; Westbury, C.F.; McKiernan, K.A.; Possing, E.T.; Medler, D.A. Distinct brain systems for processing concrete and abstract concepts. J. Cogn. Neurosci. 2005, 17, 905–917. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Baucom, L.B.; Kim, J.; Wang, J.; Wedell, D.H.; Shinkareva, S.V. Distinguishing abstract from concrete concepts in supramodal brain begions. Neuropsychologia 2019, 131, 102–110. [Google Scholar] [CrossRef] [PubMed]
- Kousta, S.T.; Vigliocco, G.; Vinson, D.P.; Andrews, M.; Del Campo, E. The representation of abstract words: Why emotion matters. J. Exp. Psychology Gen. 2011, 140, 14. [Google Scholar] [CrossRef]
- Barsalou, L.W.; Wiemer-Hastings, K. Situating abstract concepts. In Grounding Cognition: The Role of Perception and Action in Memory, Language, and Thought; Cambridge University Press: New York, NY, USA, 2005; pp. 129–163. [Google Scholar]
- Löhr, G. Embodied cognition and abstract concepts: Do concept empiricists leave anything out? Philos. Psychol. 2019, 32, 161–185. [Google Scholar] [CrossRef]
- Gibbs, R.W., Jr. Why many concepts are metaphorical. Cognition 1996, 61, 309–319. [Google Scholar] [CrossRef]
- Iosif, E.; Potamianos, A.; Giannoudaki, M.; Zervanou, K. Semantic similarity computation for abstract and concrete nouns using network-based distributional semantic models. In Proceedings of the 10th International Conference on Computational Semantics, Potsdam, Germany, 19–22 March 2013; pp. 328–334. [Google Scholar]
- Iosif, E. Network-Based Distributional Semantic Models. Ph.D. Thesis, Technical University of Crete, Chania, Greece, 2013. [Google Scholar]
- Maniezzo, V. Genetic evolution of the topology and weight distribution of neural networks. IEEE Trans. Neural Netw. 1994, 5, 39–53. [Google Scholar] [CrossRef]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Liang, J.; Meyerson, E.; Rawal, A.; Fink, D.; Francon, O.; Raju, B.; Shahrzad, H.; Navruzyan, A.; Duffy, N.; et al. Evolving deep neural networks. In Artificial Intelligence in the Age of Neural Networks and Brain Computing; Elsevier: Amsterdam, The Netherlands, 2019; pp. 293–312. [Google Scholar]
- Hintze, A.; Edlund, J.A.; Olson, R.S.; Knoester, D.B.; Schossau, J.; Albantakis, L.; Tehrani-Saleh, A.; Kvam, P.; Sheneman, L.; Goldsby, H.; et al. Markov Brains: A technical introduction. arXiv 2017, arXiv:1709.05601. [Google Scholar]
- Pinto, A.M.; Barroso, L. Principles of Regulated Activation Networks. In Graph-Based Representation and Reasoning; Springer: Berlin/Heidelberg, Germany, 2014; pp. 231–244. [Google Scholar]
- Jacoby, L. Perceptual enhancement: Persistent effects of an experience. J. Exp. Psychol. Learn. Mem. Cogn. 1983, 9, 21–38. [Google Scholar] [CrossRef]
- Roediger, H.; Blaxton, T. Effects of varying modality, surface features, and retention interval on priming in word-fragment completion. Mem. Cogn. 1987, 15, 379–388. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Roediger, H.; Mcdermott, K. Creating false memories: Remembering words not presented in lists. J. Exp. Psychol. Learn. Mem. Cogn. 1995, 21, 803–814. [Google Scholar] [CrossRef]
- Gärdenfors, P. Conceptual spaces as a framework for knowledge representation. Mind Matter 2004, 2, 9–27. [Google Scholar]
- Sivik, L.; Taft, C. Color naming: A mapping in the IMCS of common color terms. Scandi. J. Psychol. 1994, 35, 144–164. [Google Scholar] [CrossRef]
- Rosch, E. Cognitive representations of semantic categories. J. Exp. Psychol. Gen. 1975, 104, 192. [Google Scholar] [CrossRef]
- Mervis, C.B.; Rosch, E. Categorization of natural objects. Ann. Rev. Psychol. 1981, 32, 89–115. [Google Scholar] [CrossRef]
- Rosch, E. Prototype classification and logical classification: The two systems. In New Trends in Conceptual Representation: Challenges to Piaget’s Theory; Lawrence Erlbaum Associates: New Jersey, NJ, USA, 1983; pp. 73–86. [Google Scholar]
- Parsons, L. Evaluating subspace clustering algorithms. In Proceedings of the Workshop on Clustering High Dimensional Data and its Applications, SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 24 April 2004; pp. 48–56. [Google Scholar]
- Livingstone, D. Unsupervised Learning; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009; pp. 119–144. [Google Scholar]
- Yoon, J.; Raghavan, V.; Chakilam, V. BitCube: Clustering and statistical analysis for XML documents. J. Intell. Inf. Syst. 2001, 17, 241–254. [Google Scholar] [CrossRef]
- Van Deursen, A.; Kuipers, T. Identifying objects using cluster and concept analysis. In Proceedings of the 21st International Conference on Software Engineering, Los Angeles, CA, USA, 21–28 May 1999; ACM: Piscataway, NJ, USA, 1999; pp. 246–255. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Eigen, D.; Rolfe, J.; Fergus, R.; LeCun, Y. Understanding deep architectures using a recursive convolutional network. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Patt. Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J. A spreading activation theory of memory. J. Verb. Learn. Verb. Behav. 1983, 22, 261–295. [Google Scholar] [CrossRef]
- Collins, A.; Quillian, M. Retrieval time from semantic memory. J. Verb. Learn. Verb. Behav. 1969, 8, 240–247. [Google Scholar] [CrossRef]
- Crestani, F. Application of spreading activation techniques in information retrieval. Artif. Intell. Rev. 1997, 11, 453–482. [Google Scholar] [CrossRef]
- McNamara, T.; Altarriba, J. Depth of spreading activation revisited: Semantic mediated priming occurs in lexical decisions. J. Mem. Lang. 1988, 27, 545–559. [Google Scholar] [CrossRef]
- Roediger, H.; Balota, D.; Watson, J. Spreading activation and arousal of false memories. In The Nature of Remembering: Essays in Honor of Robert G. Crowder; American Psychological Association: Washington, DC, USA, 2001; pp. 95–115. [Google Scholar]
- Kavukcuoglu, K.; Sermanet, P.; Boureau, Y.; Gregor, K.; Mathieu, M.; LeCun, Y. Learning Convolutional Feature Hierachies for Visual Recognition. In Advances in Neural Information Processing Systems (NIPS 2010); Neural Information Processing Systems Foundation, Inc.: South Lake Tahoe, NV, USA, 2010; Volume 23. [Google Scholar]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. OverFeat: Integrated recognition, localization and detection using convolutional networks. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Sharma, R.; Ribeiro, B.; Pinto, A.M.; Cardoso, F.A. Perceiving abstract concepts via evolving computational cognitive modeling. In Proceedings of the IEEE 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brasil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lichman, M. UCI Machine Learning Repository. 2013. Available online: http://archive.ics.uci.edu/ml (accessed on 13 March 2020).
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. In Proceedings of the 21th International European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 24–26 April 2013; pp. 437–442. [Google Scholar]
- Higuera, C.; Gardiner, K.J.; Cios, K.J. Self-organizing feature maps identify proteins critical to learning in a mouse model of down syndrome. PLoS ONE 2015, 10, e0129126. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Street, W.N.; Wolberg, W.H.; Mangasarian, O.L. Nuclear feature extraction for breast tumor diagnosis. In Biomedical Image Processing and Biomedical Visualization; International Society for Optics and Photonics: Bellingham, WA, USA, 1993; Volume 1905, pp. 861–871. [Google Scholar]
- Bennett, K.P.; Mangasarian, O.L. Robust linear programming discrimination of two linearly inseparable sets. Optim. Methods Softw. 1992, 1, 23–34. [Google Scholar] [CrossRef]
- Evett, I.W.; Spiehler, E.J. Rule Induction in Forensic Science; Technical Report; Central Research Establishment, Home Office Forensic Science Service: Birmingham, UK, 1987. [Google Scholar]
- Quinlan, J.R. Simplifying decision trees. Int. J. Hum. Comput. Stud. 1999, 51, 497–510. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Hum. Gen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Forina, M.; Leardi, R.; Armanino, C.; Lanteri, S.; Conti, P.; Princi, P. PARVUS: An extendable package of programs for data exploration, classification and correlation. J. Chemom. 1988, 4, 191–193. [Google Scholar]
Sample Availability: Samples of the compounds, …, are available from the authors. |

| Notation | Description |
|---|---|
| W | Inter-Layer weight matrix |
| A | Output Activation |
| a | Input Activation |
| Number of elements in input vector at Layer l | |
| Number of elements in output vector at Layer | |
| l | l’th Layer representative |
| d | Normalized Euclidean distance |
| C | Cluster center or Centroids |
| Variables to represent node index for input-level, abstract-level, and arbitrary node index in either of the levels, respectively | |
| t | Iterator variable |
| Transfer function to obtain similarity relation |
| Model | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) |
|---|---|---|---|---|
| RBM | 90.87 ± 01.26 | 85.25 ± 2.61 | 82.34 ± 3.85 | 85.25 ± 2.61 |
| K-NN | 99.96 ± 00.08 | 99.95 ± 0.11 | 99.94 ± 0.12 | 99.95 ± 0.11 |
| LR | 99.65 ± 00.07 | 99.64 ± 0.07 | 99.64 ± 0.07 | 99.64 ± 0.07 |
| MLP | 95.62 ± 11.18 | 96.82 ± 7.56 | 96.02 ± 9.95 | 96.82 ± 7.56 |
| RANs | 99.12 ± 00.09 | 99.12 ± 0.09 | 99.12 ± 0.09 | 99.12 ± 0.09 |
| SGD | 96.00 ± 02.81 | 95.25 ± 2.86 | 94.57 ±3.76 | 95.25 ± 2.86 |
| Algorithm | Time Complexity | Description | Source |
|---|---|---|---|
| K-means | n: n_samples; k: n_clusters; p: n_features | [59] | |
| Affinity Propagation | n: n_samples | [59] | |
| MLP | n: n_samples; m: features; k: no. of hidden layers; h: number of hidden neurons o: output neuron; i: no. of iterations | [59] | |
| RBM | d: max(n_components, n_features) | [59] | |
| KNN | m: n_components; n: n_samples; i: min(m, n) | [59] | |
| LR | n: n_samples; m: n_features | [59] | |
| SGD | n: n_samples; k: n_iterations; : the average number of non-zero attributes per sample | [59] |
| Class | Precision (%) | Recall (%) | F1-Score (%) | Support |
|---|---|---|---|---|
| Setosa | 100 | 100 | 100 | 5 |
| Versicolour | 83.33 | 100 | 90.91 | 5 |
| Virginica | 100 | 80 | 88.89 | 5 |
| Avg/Total | 94.44 | 93.33 | 93.26 | 15 |
| Model | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) |
|---|---|---|---|---|
| RBM | 99.68 ± 0.14 | 99.68 ± 0.14 | 99.68 ±0.14 | 99.68 ± 0.14 |
| K-NN | 99.96 ± 0.02 | 99.96 ± 0.02 | 99.96 ± 0.02 | 99.96 ± 0.02 |
| LR | 99.97 ± 0.02 | 99.97 ± 0.02 | 99.97 ± 0.02 | 99.97 ± 0.02 |
| MLP | 99.96 ± 0.02 | 99.96 ± 0.02 | 99.96 ± 0.02 | 99.96 ± 0.02 |
| RANs | 99.85 ± 0.01 | 99.85 ± 0.01 | 99.85 ± 0.01 | 99.85 ± 0.01 |
| SGD | 99.98 ± 0.01 | 99.98 ± 0.01 | 99.98 ± 0.01 | 99.98 ± 0.01 |
| Data | Algo | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) | Data | Algo | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mice Protein | RBM+ | 43.45 ±44.07 | 53.50 ± 38.23 | 45.46 ± 43.36 | 53.50 ± 38.23 | Breast Cancer 569 | RBM+ | 93.60 ± 2.69 | 93.51 ± 2.77 | 93.46 ± 2.86 | 93.51 ± 2.77 |
| KNN | 98.63 ± 3.97 | 98.34 ± 4.84 | 98.07 ± 5.65 | 98.34 ± 4.84 | KNN | 99.80 ± 0.59 | 99.79 ± 0.62 | 99.78 ± 0.63 | 99.79 ± 0.62 | ||
| LR | 98.99 ± 1.94 | 98.28 ± 3.38 | 98.14 ± 3.71 | 98.28 ± 3.38 | LR | 99.89 ± 0.07 | 99.89 ± 0.07 | 99.89 ± 0.07 | 99.89 ± 0.07 | ||
| MLP | 98.54 ± 2.19 | 98.23 ± 2.71 | 97.83 ± 3.34 | 98.23 ± 2.71 | MLP | 98.67 ± 0.94 | 98.65 ± 0.96 | 98.64 ± 0.96 | 99.89 ± 0.07 | ||
| RAN | 99.98 ± 0.06 | 99.97 ± 0.06 | 99.89 ± 0.06 | 99.97 ± 0.06 | RAN | 93.17 ± 0.36 | 92.97 ± 0.36 | 92.87 ± 0.42 | 92.97 ± 0.36 | ||
| SGD | 99.11 ± 1.84 | 98.84 ± 2.46 | 98.68 ± 2.81 | 98.84 ± 2.46 | SGD | 99.87 ± 0.13 | 99.85 ± 0.18 | 99.83 ± 0.20 | 99.85 ± 0.18 | ||
| Breast Cancer 669 | RBM+ | 95.72 ± 3.62 | 95.34 ± 4.60 | 95.13 ± 5.16 | 95.34 ± 4.60 | Credit Approval | RBM+ | 76.44 ±12.50 | 75.63 ±12.98 | 74.04 ±14.59 | 75.63 ±12.98 |
| KNN | 99.46 ± 0.88 | 99.44 ± 0.93 | 99.43 ± 0.94 | 99.44 ± 0.93 | KNN | 95.48 ± 0.16 | 95.46 ± 0.17 | 95.46 ± 0.17 | 95.46 ± 0.17 | ||
| LR | 99.16 ± 0.17 | 99.14 ± 0.17 | 99.15 ± 0.17 | 99.14 ± 0.17 | LR | 95.06 ± 0.38 | 95.04 ± 0.39 | 95.04 ± 0.39 | 95.04 ± 0.39 | ||
| MLP | 98.96 ± 0.76 | 98.95 ± 0.76 | 98.95 ± 0.77 | 98.95 ± 0.76 | MLP | 98.02 ± 1.32 | 98.00 ± 1.34 | 97.99 ± 1.34 | 98.00 ± 1.34 | ||
| RAN | 95.18 ± 0.25 | 95.15 ± 0.24 | 95.11 ± 0.25 | 95.15 ± 0.24 | RAN | 80.67 ± 1.37 | 79.58 ± 1.05 | 79.66 ± 1.13 | 79.58 ± 1.05 | ||
| SGD | 99.88 ± 0.16 | 99.88 ± 0.16 | 99.18 ± 0.16 | 99.88 ± 0.16 | SGD | 99.77 ± 0.39 | 99.75 ± 0.40 | 99.75 ± 0.40 | 99.75 ± 0.40 | ||
| Glass Identification | RBM+ | 82.58 ±10.29 | 84.19 ± 4.90 | 80.61 ± 8.42 | 84.19 ± 4.90 | Mamographic Mass | RBM+ | 84.85 ±16.54 | 85.18 ±14.98 | 82.42 ±20.30 | 85.18 ±14.98 |
| KNN | 94.08 ±12.12 | 95.97 ± 7.32 | 94.82 ±10.59 | 95.97 ± 7.32 | KNN | 99.65 ± 0.88 | 99.64 ± 0.89 | 99.64 ± 0.89 | 99.64 ± 0.89 | ||
| LR | 99.52 ± 0.18 | 99.49 ± 0.18 | 99.49 ± 0.18 | 99.49 ± 0.18 | LR | 99.41 ± 0.30 | 99.40 ± 0.30 | 99.40 ± 0.30 | 99.40 ± 0.30 | ||
| MLP | 93.78 ± 1.40 | 93.28 ± 1.52 | 92.85 ± 1.64 | 93.28 ± 1.52 | MLP | 98.91 ± 2.11 | 98.79 ± 2.35 | 98.79 ± 2.35 | 98.79 ± 2.35 | ||
| RAN | 90.07 ± 0.43 | 89.18 ± 1.23 | 89.32 ± 1.10 | 89.18 ± 1.23 | RAN | 80.28 ± 0.18 | 79.20 ± 0.23 | 79.08 ± 0.24 | 79.20 ± 0.23 | ||
| SGD | 97.95 ± 0.66 | 97.87 ± 0.69 | 97.82 ± 0.70 | 97.87 ± 0.69 | SGD | 99.96 ± 0.03 | 99.94 ± 0.07 | 99.93 ± 0.09 | 99.94 ± 0.07 | ||
| IRIS | RBM+ | 79.81 ±11.91 | 77.41 ±11.88 | 70.66 ±16.28 | 77.41 ±11.88 | Wine Recognition | RBM+ | 56.00 ±25.66 | 67.05 ±16.91 | 59.07 ±21.91 | 67.05 ±16.91 |
| KNN | 90.41 ±28.77 | 92.80 ±21.61 | 91.00 ±27.01 | 92.80 ±21.61 | KNN | 90.74 ±26.00 | 92.88 ±19.48 | 91.14 ±24.70 | 92.88 ±19.48 | ||
| LR | 97.38 ± 4.15 | 96.64 ± 5.65 | 96.45 ± 6.12 | 96.64 ± 5.65 | LR | 94.14 ± 1.55 | 93.13 ± 1.82 | 93.00 ± 1.92 | 93.13 ± 1.82 | ||
| MLP | 97.31 ± 0.71 | 96.86 ± 1.13 | 96.81 ± 1.21 | 96.86 ± 1.13 | MLP | 97.44 ± 0.51 | 97.33 ± 0.59 | 97.32 ± 0.59 | 97.33 ± 0.59 | ||
| RAN | 95.43 ± 0.67 | 95.02 ± 0.94 | 94.98 ± 0.98 | 95.02 ± 0.94 | RAN | 94.87 ± 0.91 | 94.34 ± 1.00 | 94.29 ± 1.01 | 94.34 ± 1.00 | ||
| SGD | 94.47 ± 6.40 | 94.46 ± 5.20 | 93.31 ± 6.78 | 94.46 ± 5.20 | SGD | 98.13 ± 0.70 | 97.91 ± 0.75 | 97.91 ± 0.76 | 97.91 ± 0.75 |
| Features\Models | RBM | K-NN | LR | MLP | RANs | SGD |
|---|---|---|---|---|---|---|
| Graph-Based | Yes | No | No | Yes | Yes | No |
| Dynamic Topology | No | No | No | No | Yes | No |
| Dimension Reduction | Yes | Yes | No | Yes | Yes | No |
| Dimension Expansion | May be | No | No | May be | Yes | No |
| Unisupervised | Yes | No | No | No | Yes | No |
| Supports Classification | Yes | Yes | Yes | Yes | Yes | Yes |
| Bio-inspired | Yes | No | No | Yes | Yes | No |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, R.; Ribeiro, B.; Miguel Pinto, A.; Cardoso, F.A. Exploring Geometric Feature Hyper-Space in Data to Learn Representations of Abstract Concepts. Appl. Sci. 2020, 10, 1994. https://doi.org/10.3390/app10061994
Sharma R, Ribeiro B, Miguel Pinto A, Cardoso FA. Exploring Geometric Feature Hyper-Space in Data to Learn Representations of Abstract Concepts. Applied Sciences. 2020; 10(6):1994. https://doi.org/10.3390/app10061994
Chicago/Turabian StyleSharma, Rahul, Bernardete Ribeiro, Alexandre Miguel Pinto, and F. Amílcar Cardoso. 2020. "Exploring Geometric Feature Hyper-Space in Data to Learn Representations of Abstract Concepts" Applied Sciences 10, no. 6: 1994. https://doi.org/10.3390/app10061994
APA StyleSharma, R., Ribeiro, B., Miguel Pinto, A., & Cardoso, F. A. (2020). Exploring Geometric Feature Hyper-Space in Data to Learn Representations of Abstract Concepts. Applied Sciences, 10(6), 1994. https://doi.org/10.3390/app10061994







