SAHA: A String Adaptive Hash Table for Analytical Databases
Abstract
1. Introduction
1.1. Background
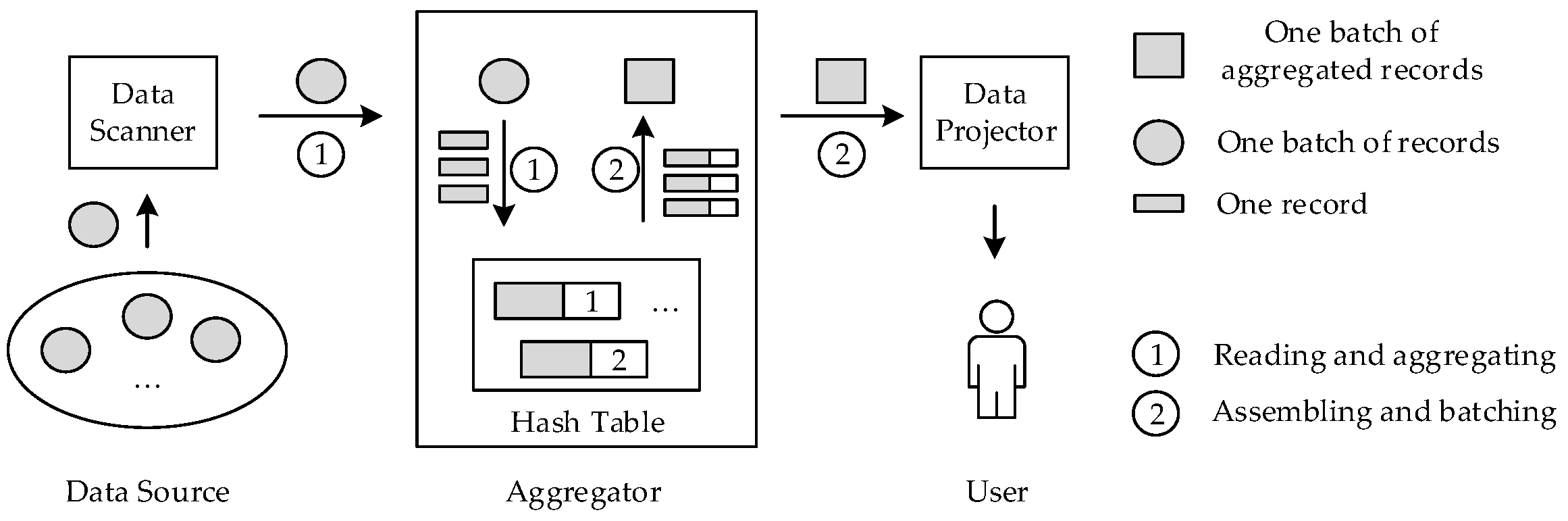
1.1.1. Group Operator
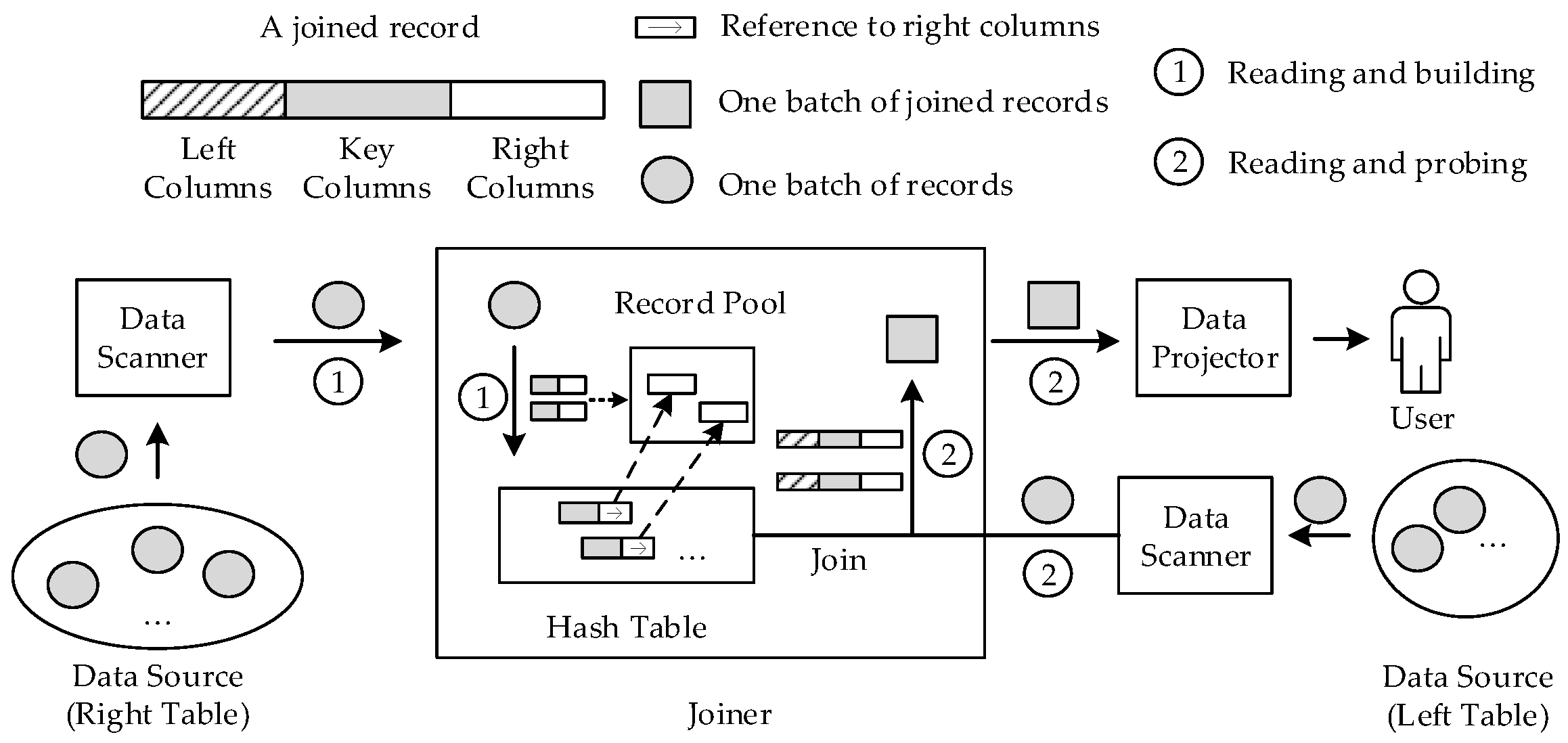
1.1.2. Join Operator
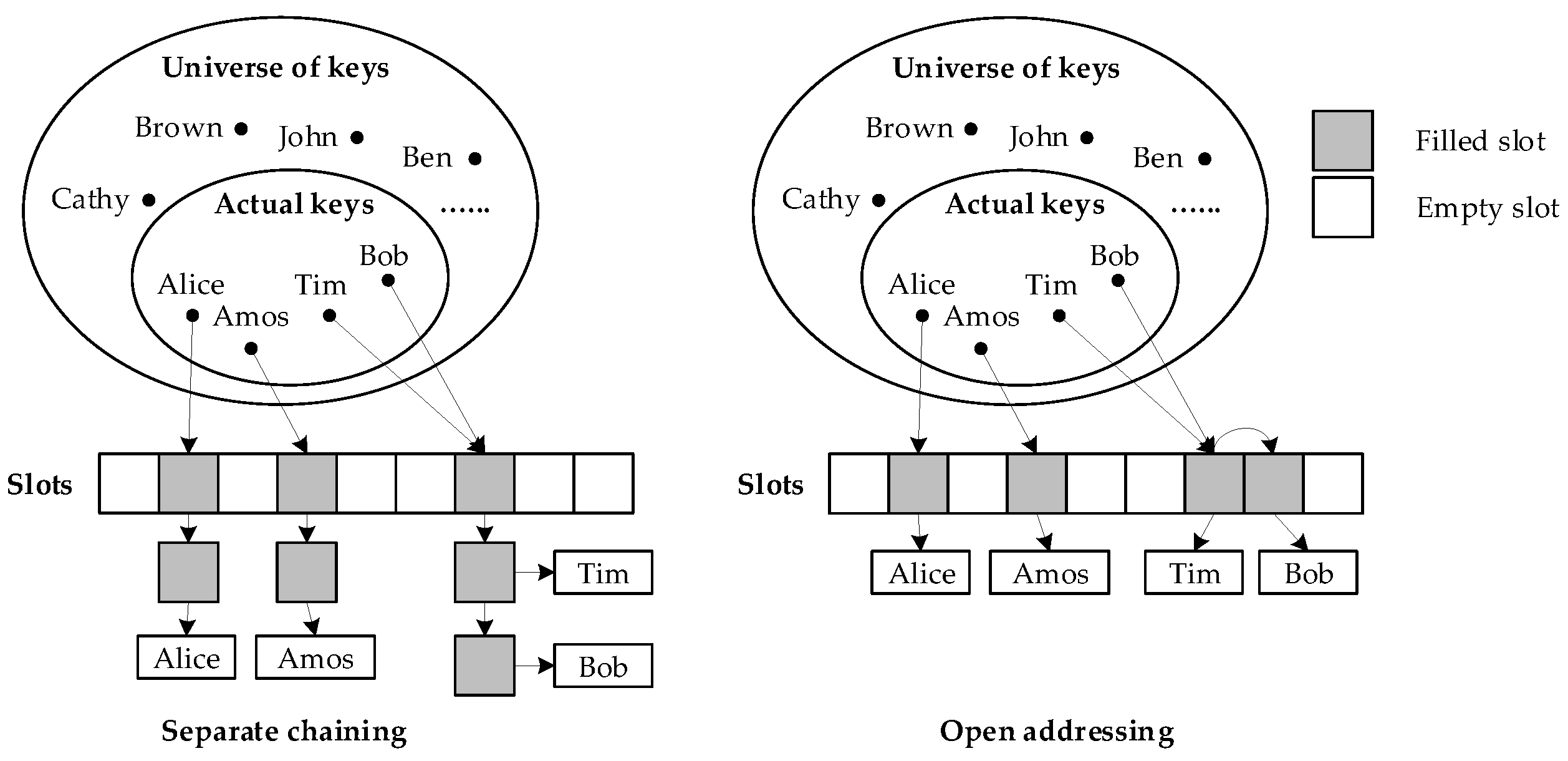
1.1.3. Hash Table
1.2. Problems
- When processing string datasets, different optimizations should be applied based on the distribution of string length. There is no single hash table that can fit all cases of string data.
- Short strings are cost-ineffective when stored with pointers, and it is a waste of space to store saved hash values for short strings.
- Hashing long strings while doing insertion or lookup in hash tables is cache unfriendly.
1.3. Our Solutions and Contributions
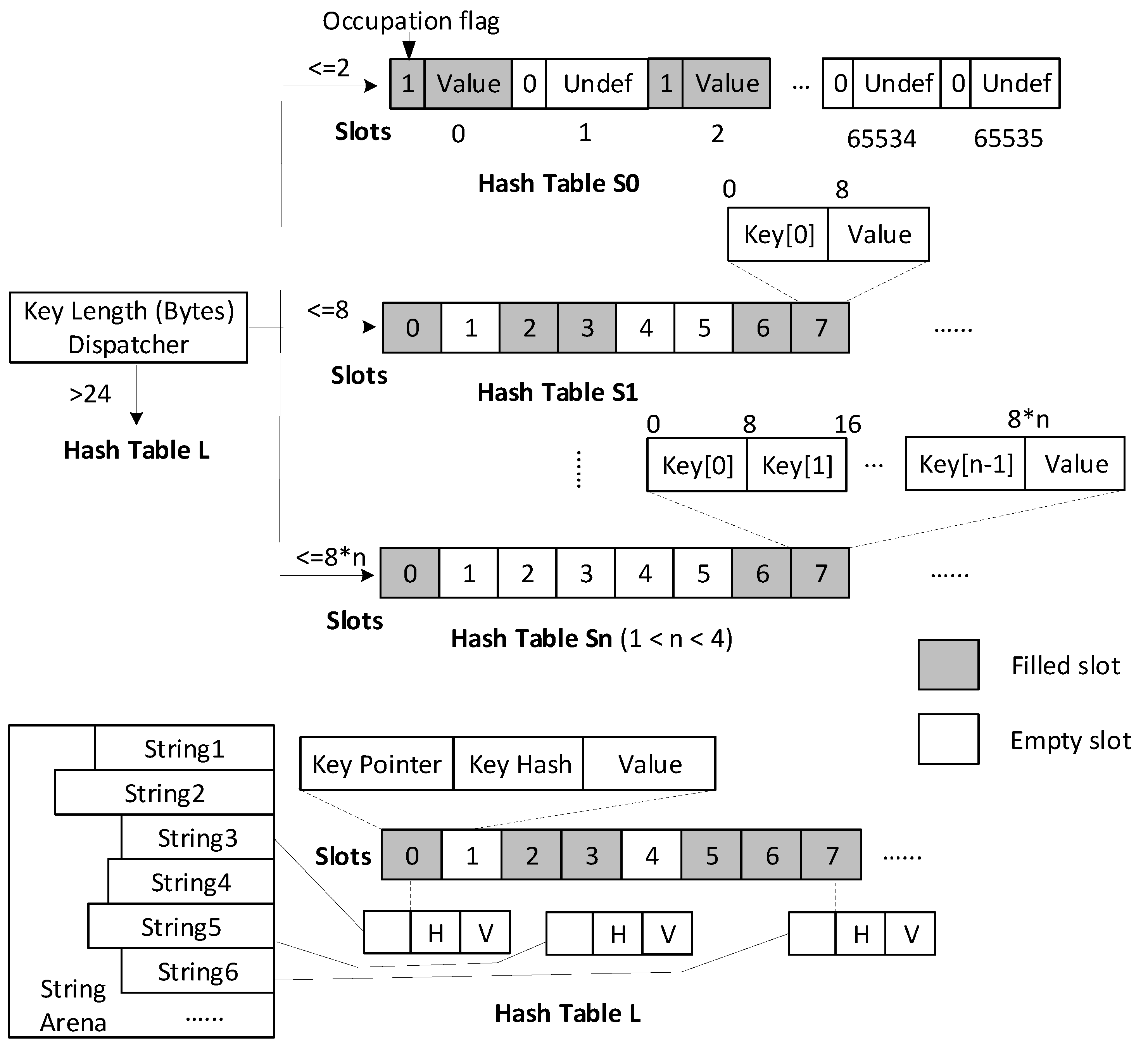
- Optimized String Dispatcher. We implement a string key dispatcher based on the length of a string. It is used to categorize string datasets into subsets with predefined string length distributions. The dispatcher is optimized with special memory loading techniques so that it does not introduce performance regressions to the underlying hash table.
- Hybrid String Hash Tables. We design five implementations of hash tables for strings with different lengths. Each implementation is optimized for one distribution of string length. All implementations are united as one hash table with the standard hash table interface but can adapt to string data. It has the benefit of low peak memory usage because the sub hash tables grow independently, which is smoother than growing as a whole.
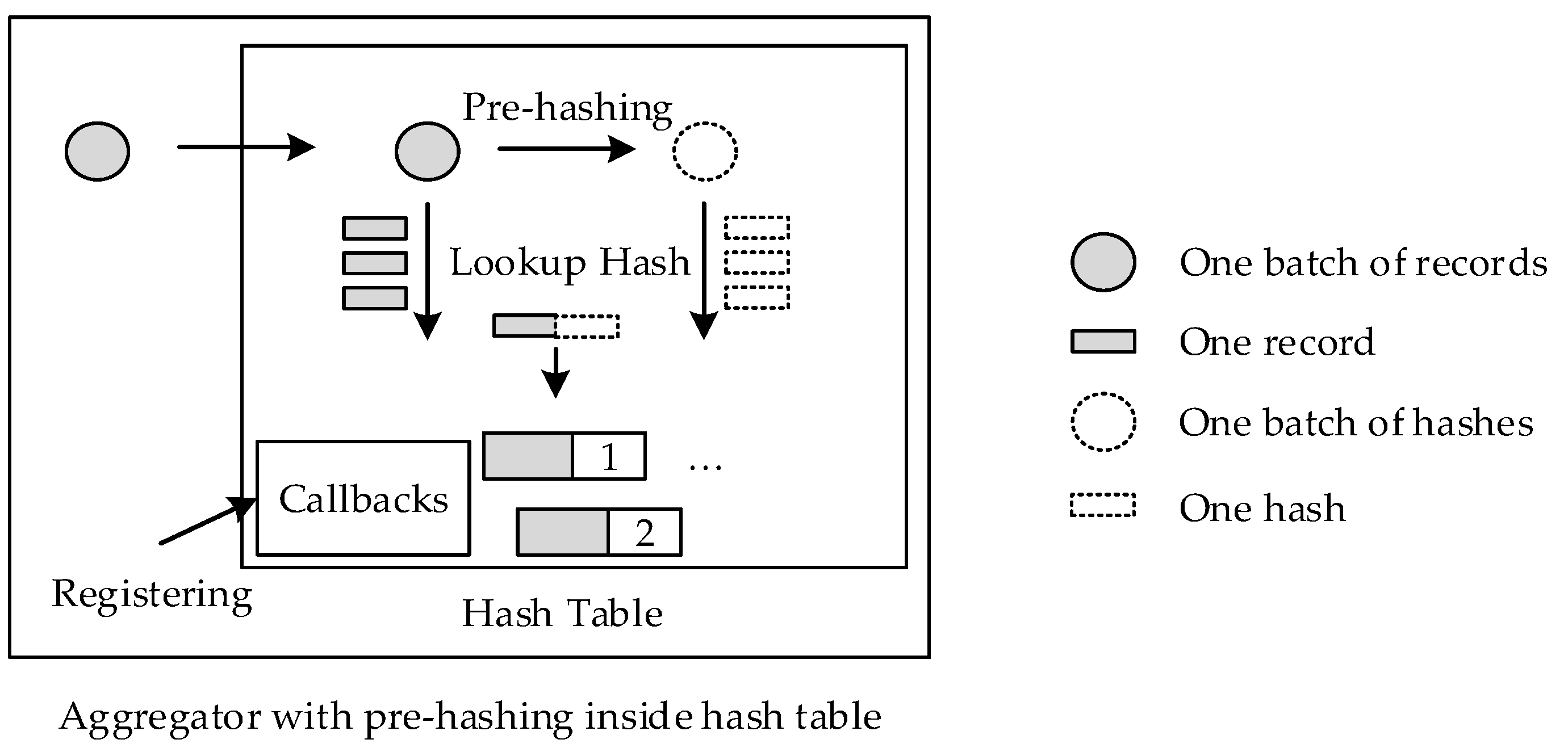
- Pre-hashing and Vectorized Programming Interface. We identify the chance of precomputing the hash values of records before doing vectorized processing in the hash table. This optimizes the cache utilization when the current batch is filled with long strings. We propose a new programming interface accepting callbacks to insertion and lookup functions so that additional information such as the precomputed hash values can be calculated inside the hash table.
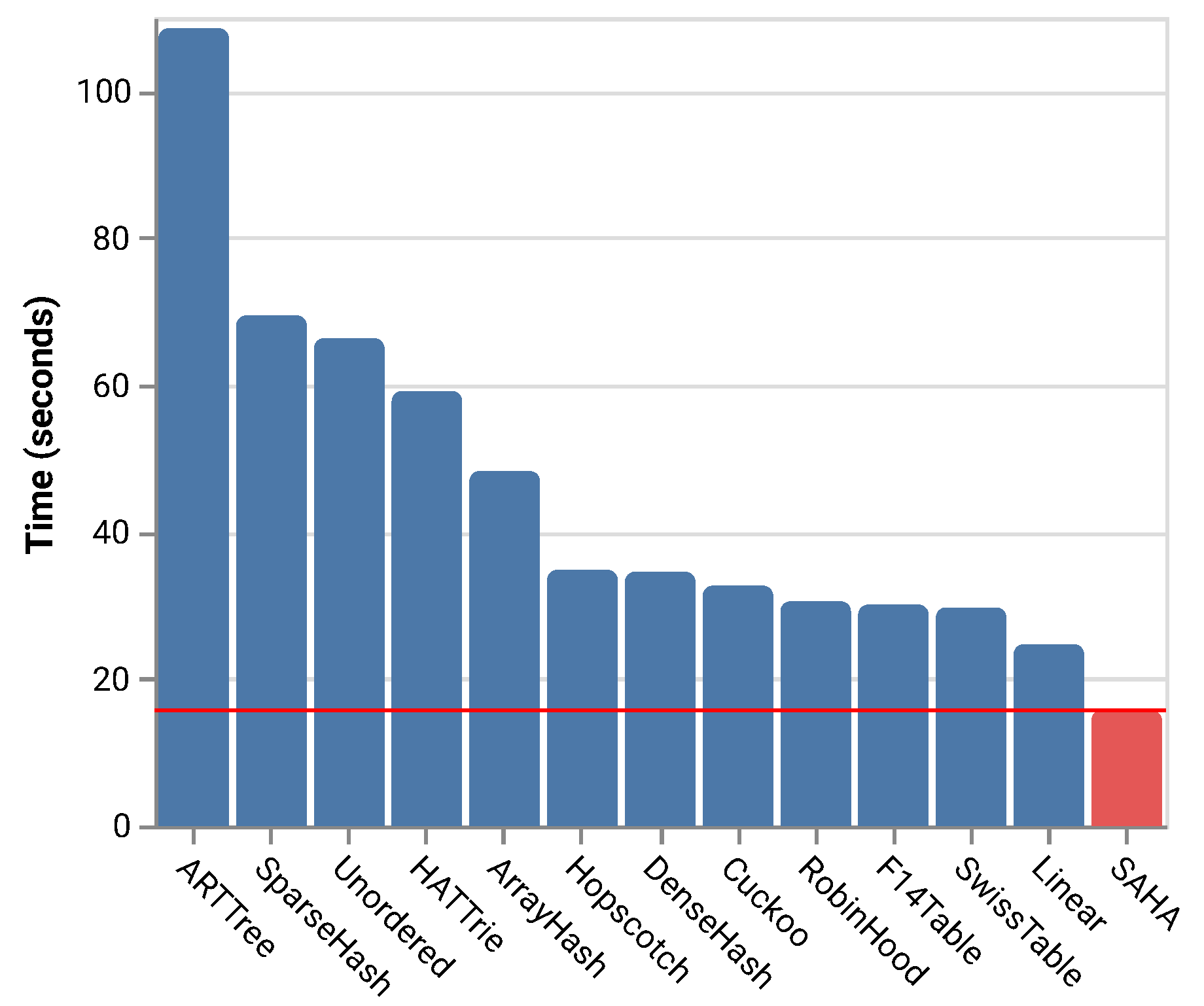
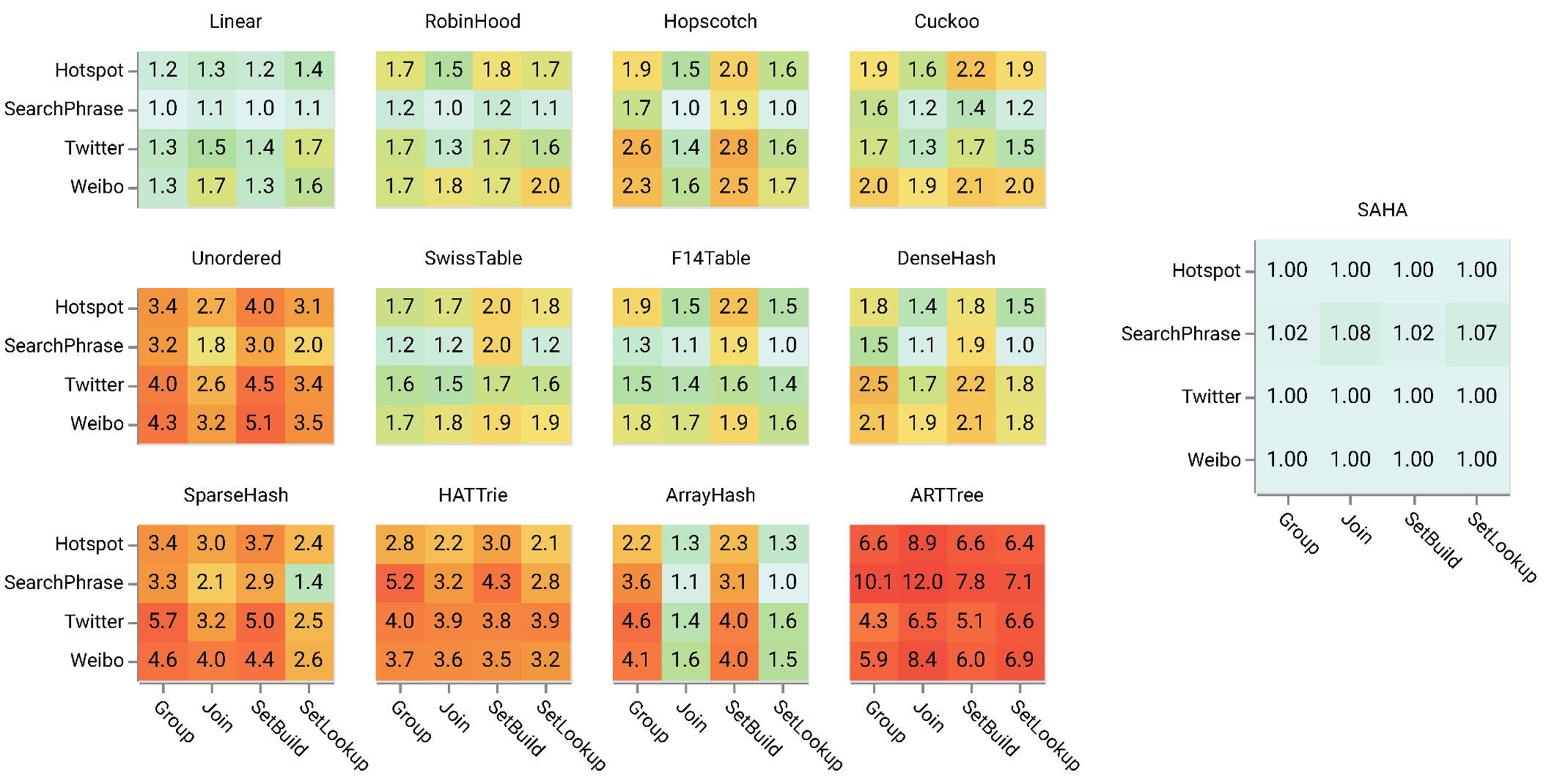
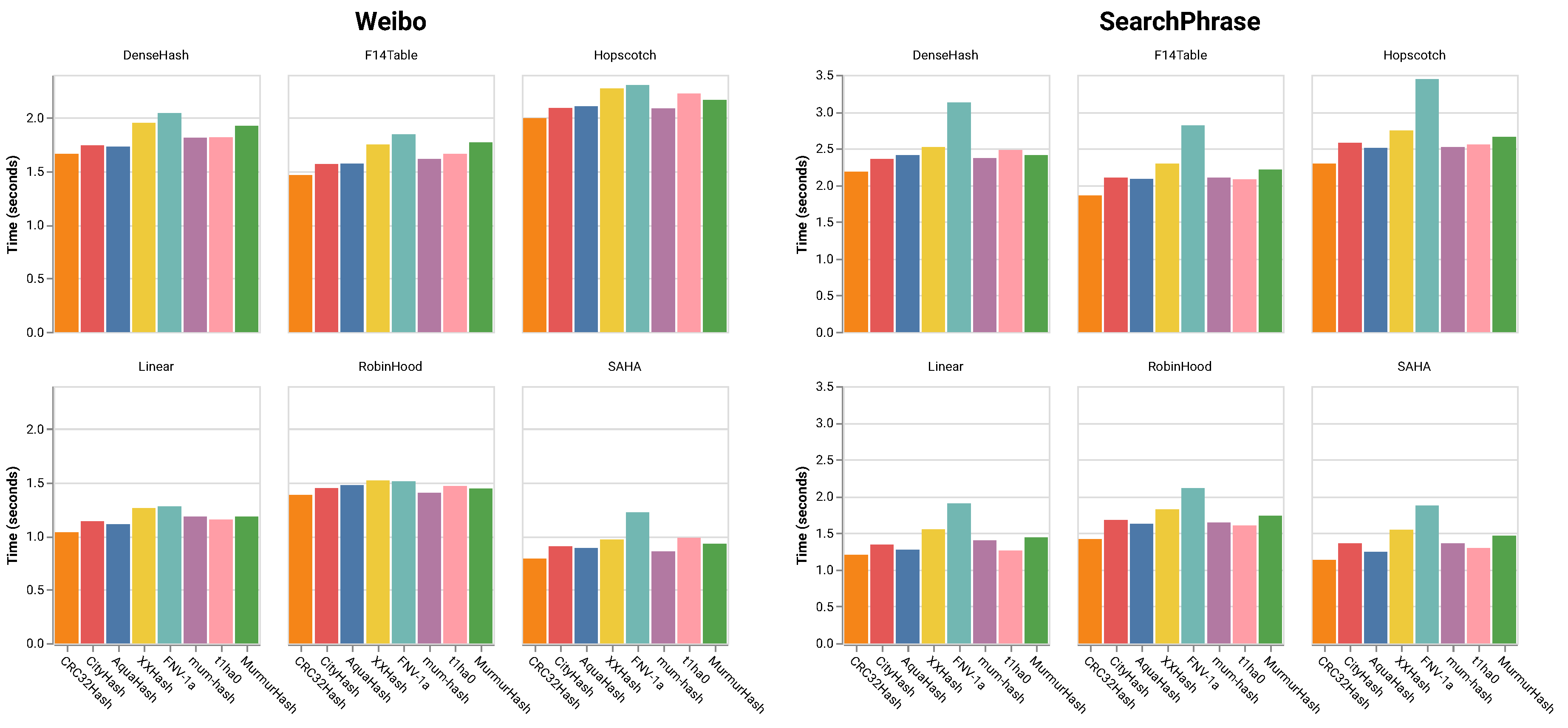
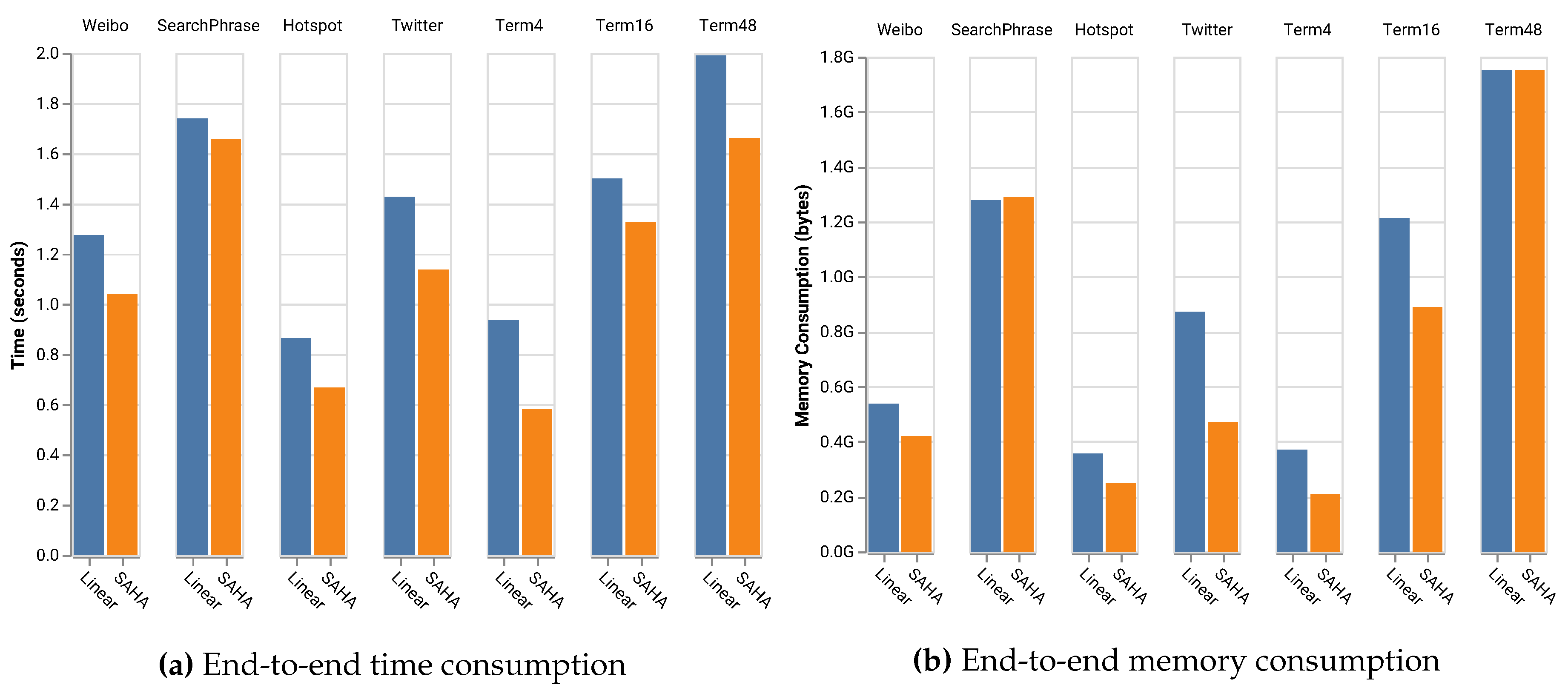
- Extensive Experiments. We carry out extensive experiments using both real-world and synthetic datasets to validate the performance of SAHA. Our experiments look into the key performance factors of a hash table, including the hashing functions, the computational time and the effectiveness of main memory utilization. The results reveal that SAHA outperforms the state-of-the-art hash tables in all cases by one to five times, as shown in Figure 4.
2. Related Works
2.1. Hash Tables
2.2. Data Structures and Optimizations for Strings
2.3. Summary
- Inline string. Whether the hash table has stored the string data directly without holding string pointers.
- Saved hash. Whether the computed hash value of a string is stored together with the string in the hash table.
- Compact. Whether the hash table has high load factors (we consider tries to have 100% load factor).
3. Constructs
- Slot empty check for Hash Table Sn. As the string length is not stored in Hash Table Sn, one way to check if a given slot is empty is to verify that all the integers in the slot’s key array are equal to zero. However, since the zero byte in UTF8 is code point 0, NUL character. There is no other Unicode code point that will be encoded in UTF8 with a zero byte anywhere within it. We only need to check the first integer, that is key[0] == 0 in Figure 5. This gives considerable improvements, especially for Hash Table S3, which contains three integers per key.
- Automatic ownership handling for Hash Table L. For long strings, we copy the string data into String Arena to hold the ownership of string key when successfully inserted. This requires the insertion method to return the reference of the inserted string key in order to modify the string pointer to the new location in String Arena. However, it is expensive to return the key reference, since strings are also stored as integers in SAHA; returning references universally would require constructing temporary strings. To address this, we augment the string key with an optional memory pool reference and allow the hash table to decide when the string key needs to be parsed into the memory pool. It is used in Hash Table L that automatically parses strings when newly inserted.
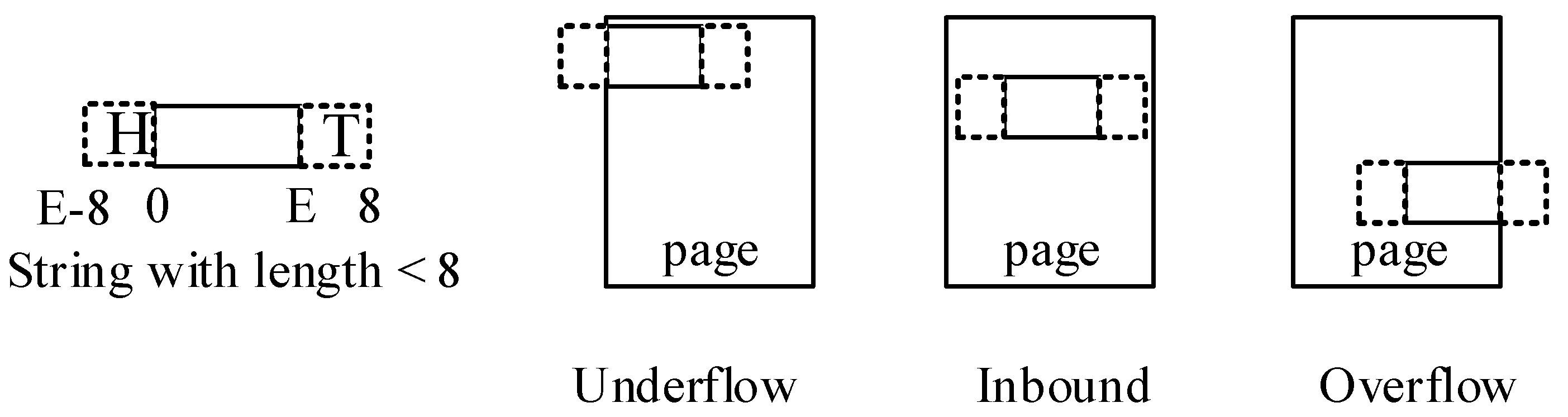
- CRC32 hashing with memory loading optimization. Cyclic redundancy check (CRC) is an error-detecting code. It hashes a stream of bytes with as few collisions as possible, which makes it a good candidate as a hash function. Modern CPUs provide CRC32 native instructions that compute the CRC value of eight bytes in a few cycles. As a result, we can use the memory loading technique in the string dispatcher to do CRC32 hashing efficiently.
| Listing 1. Implementatation of string dispatcher for the emplace routine in pseudo C++. |
| void dispatchEmplace (StringRef key, Slot∗& slot) { |
| int tail = (-key.size & 7) * 8; |
| union { StringKey8 k8; StringKey16 k16; StringKey24 k24; uint64_t n [3]; }; |
| switch (key.size) { |
| case 0: |
| Hash_Table_S0.emplace(0, slot); |
| case 1..8: |
| if (key.pointer & 2048) == 0) |
| { memcpy(&n [0], key.pointer, 8); n [0] &= -1 >> tail;} |
| else { memcpy(&n [0], key.pointer + key.size - 8, 8); n [0] >>= tail; } |
| if (n [0] < 65536) Hash_Table_S0.emplace(k8, slot); |
| else Hash_Table_S1.emplace(k8, slot); |
| case 9..16: |
| memcpy(&n [0], key.pointer, 8); |
| memcpy(&n [1], key.pointer + key.size - 8, 8); |
| n [1] >>= s; |
| Hash_Table_S2.emplace(k16, slot); |
| case 17..24: |
| memcpy(&n [0], key.pointer, 16); |
| memcpy(&n [2], key.pointer + key.size - 8, 8); |
| n [2] >>= s; |
| Hash_Table_S3.emplace(k24, slot); |
| default: |
| Hash_Table_L.emplace(key, slot); |
| } |
| } |
4. Pre-Hashing and Vectorized Programming Interface
| Listing 2. Comparison of the emplace routine with and without vectorization in pseudo C++. | |
| // vanilla emplace void emplace( StringRef key, Slot∗& slot) { uint64_t hash = hashing(key); slot = HashTable.probing(hash); } // Aggregating for (StringRef& key : keys) { Slot∗ slot; emplace(key, slot); if (slot == nullptr) slot->value = 1; else ++ slot->value; } | // vectorized emplace with pre-hashing void emplaceBatch( vector<StringRef>& keys, Callback func) { vector<uint64_t> hashes(keys.size()); for (int i=0; i<keys.size(); ++i) hashes[i] = hashing(keys[i]); for (int i=0; i<keys.size(); ++i) func(HashTable.probing(hash[i])); } void callback(Slot∗ slot) { if (slot == nullptr) slot->value = 1; else ++ slot->value; } // Aggregating emplaceBatch(keys, callback); |
5. Evaluation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wikipedia Contributors. SIMD—Wikipedia, The Free Encyclopedia, 2020. Available online: https://en.wikipedia.org/w/index.php?title=SQL&oldid=938477808 (accessed on 1 February 2020).
- Nambiar, R.O.; Poess, M. The Making of TPC-DS. VLDB 2006, 6, 1049–1058. [Google Scholar]
- ClickHouse Contributors. ClickHouse: Open Source Distributed Column-Oriented DBMS, 2020. Available online: https://clickhouse.tech (accessed on 1 February 2020).
- Bittorf, M.K.A.B.V.; Bobrovytsky, T.; Erickson, C.C.A.C.J.; Hecht, M.G.D.; Kuff, M.J.I.J.L.; Leblang, D.K.A.; Robinson, N.L.I.P.H.; Rus, D.R.S.; Wanderman, J.R.D.T.S.; Yoder, M.M. Impala: A Modern, Open-Source SQL Engine for Hadoop; CIDR: Asilomar, CA, USA, 2015. [Google Scholar]
- Thusoo, A.; Sarma, J.S.; Jain, N.; Shao, Z.; Chakka, P.; Anthony, S.; Liu, H.; Wyckoff, P.; Murthy, R. Hive: A Warehousing Solution over a Map-reduce Framework. Proc. VLDB Endow. 2009, 2, 1626–1629. [Google Scholar] [CrossRef]
- Wikipedia Contributors. SQL—Wikipedia, The Free Encyclopedia, 2020. Available online: https://en.wikipedia.org/w/index.php?title=SIMD&oldid=936265376 (accessed on 1 February 2020).
- Celis, P.; Larson, P.A.; Munro, J.I. Robin hood hashing. In Proceedings of the IEEE 26th Annual Symposium on Foundations of Computer Science (sfcs 1985), Washington, DC, USA, 21–23 October 1985; pp. 281–288. [Google Scholar]
- Herlihy, M.; Shavit, N.; Tzafrir, M. Hopscotch Hashing. In Distributed Computing; Taubenfeld, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 350–364. [Google Scholar]
- Richter, S.; Alvarez, V.; Dittrich, J. A seven-dimensional analysis of hashing methods and its implications on query processing. Proc. VLDB Endow. 2015, 9, 96–107. [Google Scholar] [CrossRef]
- Pagh, R.; Rodler, F.F. Cuckoo hashing. In European Symposium on Algorithms; Springer: Berlin/Heidelberg, Germany, 2001; pp. 121–133. [Google Scholar]
- Kirsch, A.; Mitzenmacher, M.; Wieder, U. More robust hashing: Cuckoo hashing with a stash. SIAM J. Comput. 2010, 39, 1543–1561. [Google Scholar] [CrossRef]
- Breslow, A.D.; Zhang, D.P.; Greathouse, J.L.; Jayasena, N.; Tullsen, D.M. Horton tables: Fast hash tables for in-memory data-intensive computing. In Proceedings of the 2016 USENIX Annual Technical Conference (USENIX ATC 16), Denver, CO, USA, 22–24 June 2016; pp. 281–294. [Google Scholar]
- Scouarnec, N.L. Cuckoo++ hash tables: High-performance hash tables for networking applications. In Proceedings of the 2018 Symposium on Architectures for Networking and Communications Systems, Ithaca, NY, USA, 23–24 July 2018; pp. 41–54. [Google Scholar]
- google sparsehash@googlegroups.com. Google Sparse Hash, 2020. Available online: https://github.com/sparsehash/sparsehash (accessed on 1 February 2020).
- Barber, R.; Lohman, G.; Pandis, I.; Raman, V.; Sidle, R.; Attaluri, G.; Chainani, N.; Lightstone, S.; Sharpe, D. Memory-efficient hash joins. Proc. VLDB Endow. 2014, 8, 353–364. [Google Scholar] [CrossRef]
- Benzaquen, S.; Evlogimenos, A.; Kulukundis, M.; Perepelitsa, R. Swiss Tables and absl::Hash, 2020. Available online: https://abseil.io/blog/20180927-swisstables (accessed on 1 February 2020).
- Bronson, N.; Shi, X. Open-Sourcing F14 for Faster, More Memory-Efficient Hash Tables, 2020. Available online: https://engineering.fb.com/developer-tools/f14/ (accessed on 1 February 2020).
- Wikipedia Contributors. Trie—Wikipedia, The Free Encyclopedia, 2020. Available online: https://en.wikipedia.org/w/index.php?title=Trie&oldid=934327931 (accessed on 1 February 2020).
- Aoe, J.I.; Morimoto, K.; Sato, T. An efficient implementation of trie structures. Softw. Pract. Exp. 1992, 22, 695–721. [Google Scholar] [CrossRef]
- Heinz, S.; Zobel, J.; Williams, H.E. Burst tries: A fast, efficient data structure for string keys. ACM Trans. Inf. Syst. (Tois) 2002, 20, 192–223. [Google Scholar] [CrossRef]
- Askitis, N.; Sinha, R. HAT-trie: A cache-conscious trie-based data structure for strings. In Proceedings of the Thirtieth Australasian Conference on Computer Science, Ballarat, VIC, Australia, 30 January–2 February2007; Australian Computer Society, Inc.: Mountain View, CA, USA, 2007; Volume 62, pp. 97–105. [Google Scholar]
- Leis, V.; Kemper, A.; Neumann, T. The adaptive radix tree: ARTful indexing for main-memory databases. In Proceedings of the 2013 IEEE 29th International Conference on Data Engineering (ICDE), Brisbane, QLD, Australia, 8–12 April 2013; pp. 38–49. [Google Scholar] [CrossRef]
- Alvarez, V.; Richter, S.; Chen, X.; Dittrich, J. A comparison of adaptive radix trees and hash tables. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea, 13–17 April 2015; pp. 1227–1238. [Google Scholar]
- Askitis, N.; Zobel, J. Cache-conscious collision resolution in string hash tables. In International Symposium on String Processing and Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2005; pp. 91–102. [Google Scholar]
- Lamb, A.; Fuller, M.; Varadarajan, R.; Tran, N.; Vandiver, B.; Doshi, L.; Bear, C. The Vertica Analytic Database: C-store 7 Years Later. Proc. VLDB Endow. 2012, 5, 1790–1801. [Google Scholar] [CrossRef]
- Färber, F.; Cha, S.K.; Primsch, J.; Bornhövd, C.; Sigg, S.; Lehner, W. SAP HANA Database: Data Management for Modern Business Applications. SIGMOD Rec. 2012, 40, 45–51. [Google Scholar] [CrossRef]
- Stonebraker, M.; Abadi, D.J.; Batkin, A.; Chen, X.; Cherniack, M.; Ferreira, M.; Lau, E.; Lin, A.; Madden, S.; O’Neil, E.; et al. C-store: A column-oriented DBMS. In Making Databases Work: The Pragmatic Wisdom of Michael Stonebraker; ACM: New York, NY, USA, 2018; pp. 491–518. [Google Scholar]
- Amos Bird (Tianqi Zheng). Add StringHashMap to Optimize String Aggregation, 2019. Available online: https://github.com/ClickHouse/ClickHouse/pull/5417 (accessed on 1 February 2020).

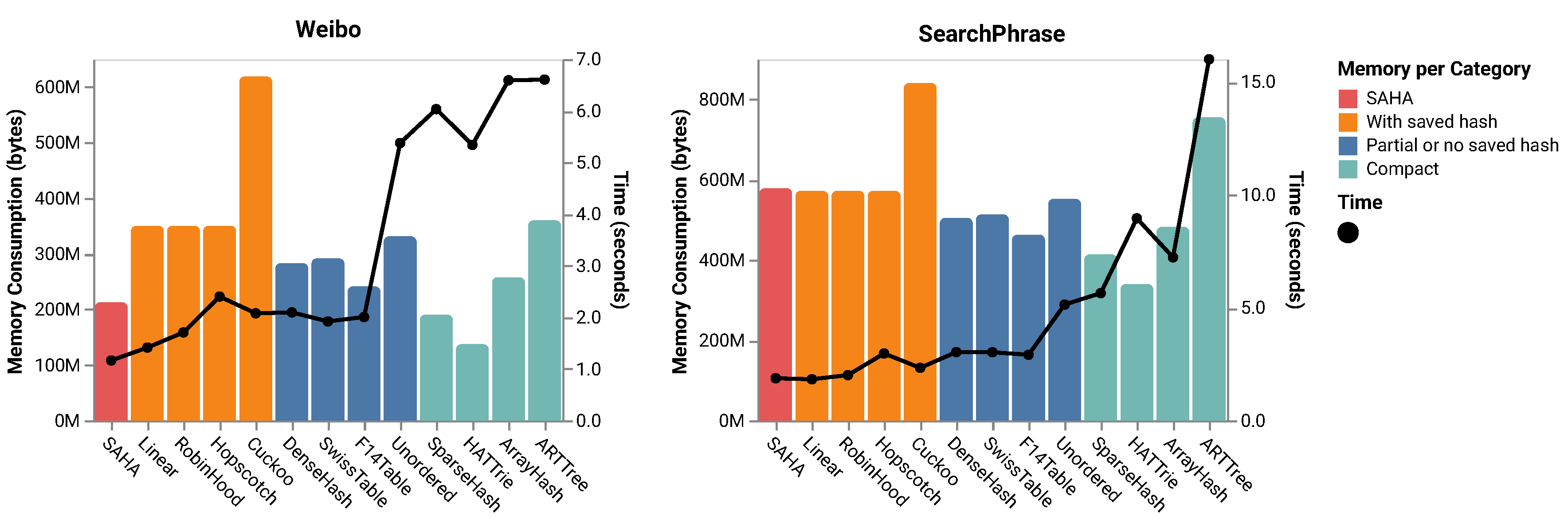
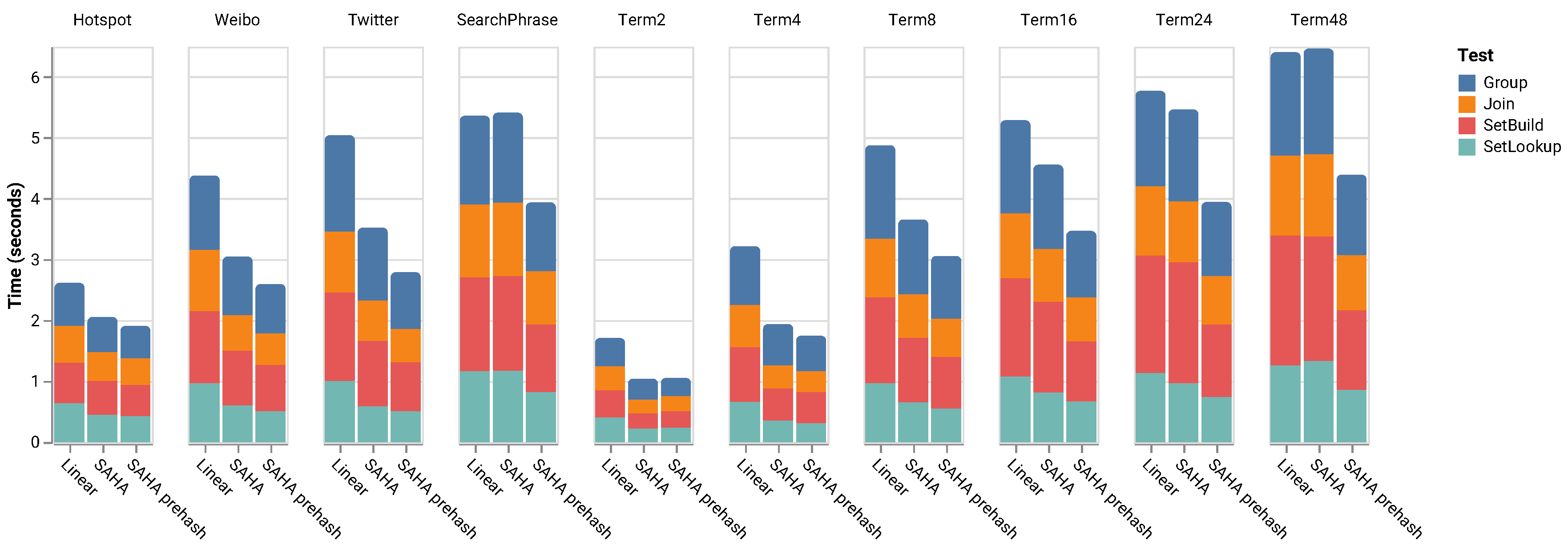
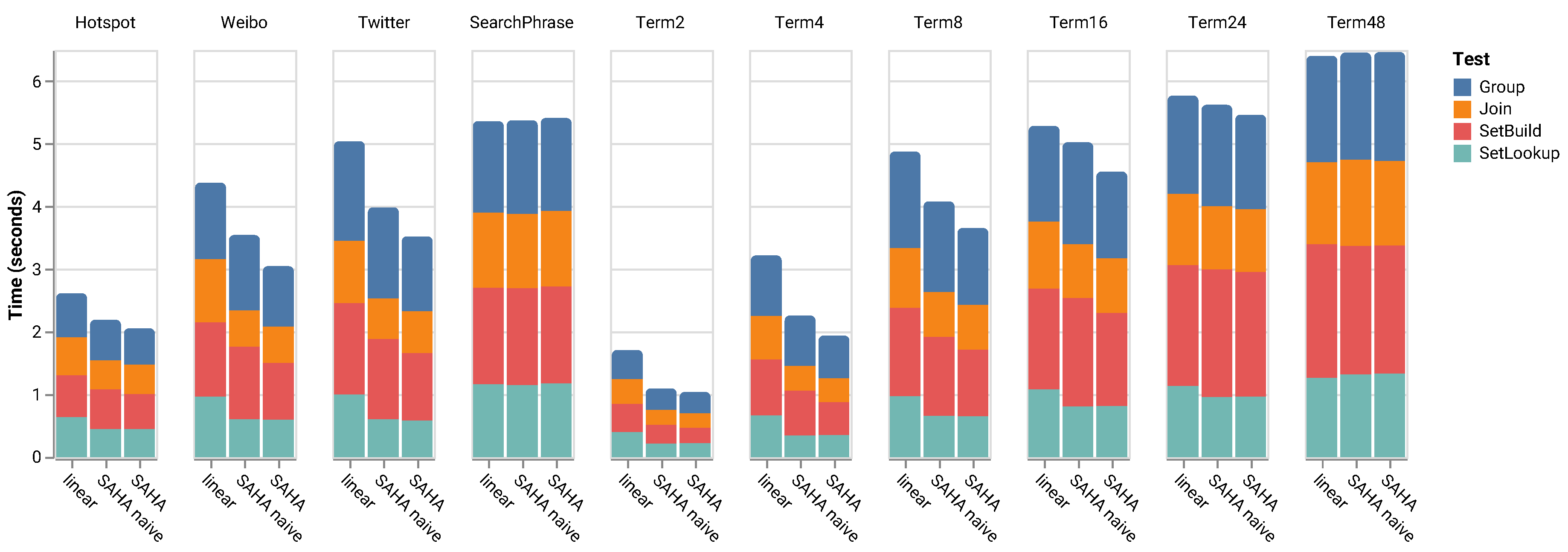
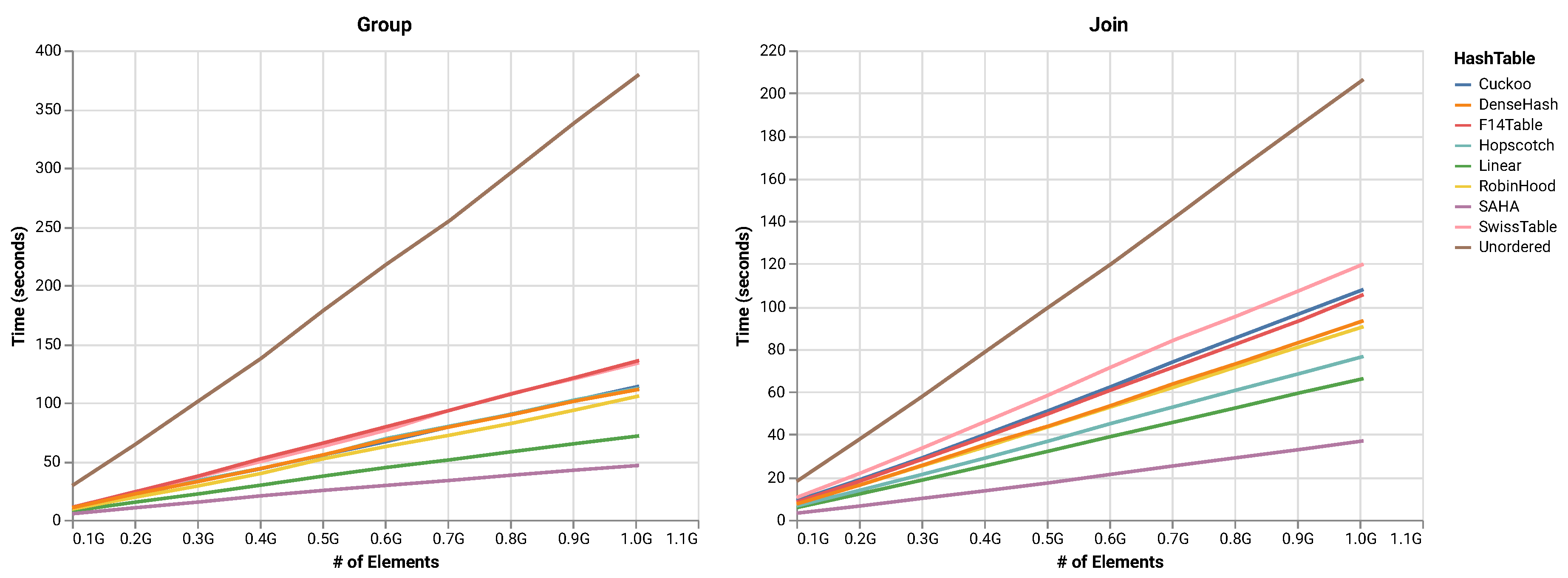
| Name | Inline String | Saved Hash | Compact | Description |
|---|---|---|---|---|
| SAHA | Hybrid | Hybrid | No | Linear probing after dispatching by length |
| Linear [3] | No | Yes | No | Linear probing |
| RobinHood [7] | No | Yes | No | Linear probing within limited distance |
| Hopscotch [8] | No | Yes | No | Neighborhood probing |
| Cuckoo [10] | No | Yes | No | Alternatively probing between two tables |
| Unordered | No | No | No | Chaining (GNU stdlibc++’s implementation) |
| SwissTable [16] | No | Partial | No | Quadratic probing with separated metadata |
| F14Table [17] | No | Partial | No | Quadratic probing with inlined metadata |
| DenseHash [14] | No | No | No | Quadratic probing |
| SparseHash [14] | No | No | Yes | Quadratic probing over sparse table |
| HATTrie [21] | Yes | No | Yes | Trie tree with ArrayHash as leaf nodes |
| ArrayHash [24] | Yes | No | Yes | Chaining with compacted array |
| ARTTree [22] | Yes | No | Yes | Trie tree with hybrid nodes |
| Parameter | Baseline | SAHA | Optimizations |
|---|---|---|---|
| H | 33 | 22 | Memory loading optimization |
| 56 | 37 | String inlining and slot empty check optimization | |
| 34 | 6 | String dispatching and automatic ownership handling | |
| 16 | 14 | Selective hash saving | |
| Unit | Cycles per key | Cycles per key |
| Name | Description | # Strings | # Distinct | String Length Quantiles | ||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | ||||
| Real World Datasets | ||||||||
| Hotspot | Weibo’s hot topics | 8,974,818 | 1,590,098 | 12 | 15 | 18 | 24 | 837 |
| Weibo’s user nicknames | 8,993,849 | 4,381,094 | 10 | 12 | 16 | 21 | 45 | |
| Twitter’s user nicknames | 8,982,748 | 7,998,096 | 8 | 9 | 11 | 13 | 20 | |
| SearchPhrase | Yandex’s web search phrases | 8,928,475 | 4,440,301 | 29 | 44 | 57 | 77 | 2025 |
| Synthetic Datasets (with Binomial Distributions) | ||||||||
| Term2 | Mean length 2 | 8,758,194 | 835,147 | 1 | 1 | 2 | 3 | 14 |
| Term4 | Mean length 4 | 8,758,194 | 3,634,680 | 2 | 3 | 4 | 6 | 17 |
| Term8 | Mean length 8 | 8,758,194 | 8,247,994 | 6 | 7 | 9 | 10 | 25 |
| Term16 | Mean length 16 | 8,758,194 | 8,758,189 | 13 | 15 | 17 | 19 | 40 |
| Term24 | Mean length 24 | 8,758,194 | 8,758,194 | 20 | 23 | 25 | 28 | 47 |
| Term48 | Mean length 48 | 8,758,194 | 8,758,194 | 44 | 47 | 49 | 52 | 73 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, T.; Zhang, Z.; Cheng, X. SAHA: A String Adaptive Hash Table for Analytical Databases. Appl. Sci. 2020, 10, 1915. https://doi.org/10.3390/app10061915
Zheng T, Zhang Z, Cheng X. SAHA: A String Adaptive Hash Table for Analytical Databases. Applied Sciences. 2020; 10(6):1915. https://doi.org/10.3390/app10061915
Chicago/Turabian StyleZheng, Tianqi, Zhibin Zhang, and Xueqi Cheng. 2020. "SAHA: A String Adaptive Hash Table for Analytical Databases" Applied Sciences 10, no. 6: 1915. https://doi.org/10.3390/app10061915
APA StyleZheng, T., Zhang, Z., & Cheng, X. (2020). SAHA: A String Adaptive Hash Table for Analytical Databases. Applied Sciences, 10(6), 1915. https://doi.org/10.3390/app10061915





