Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest
Abstract
1. Introduction
2. Significance of the Research Study
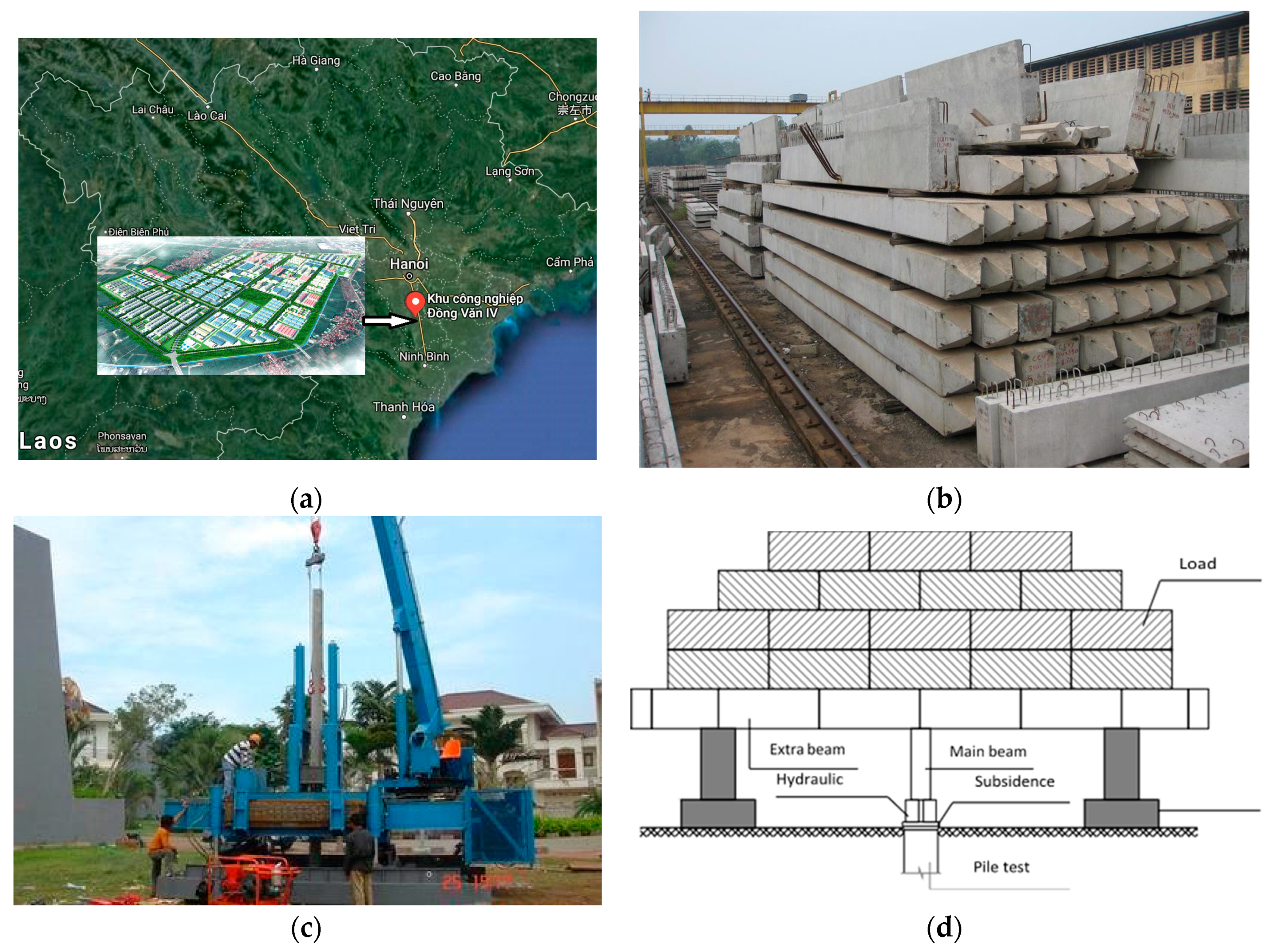
3. Data Collection and Preparation
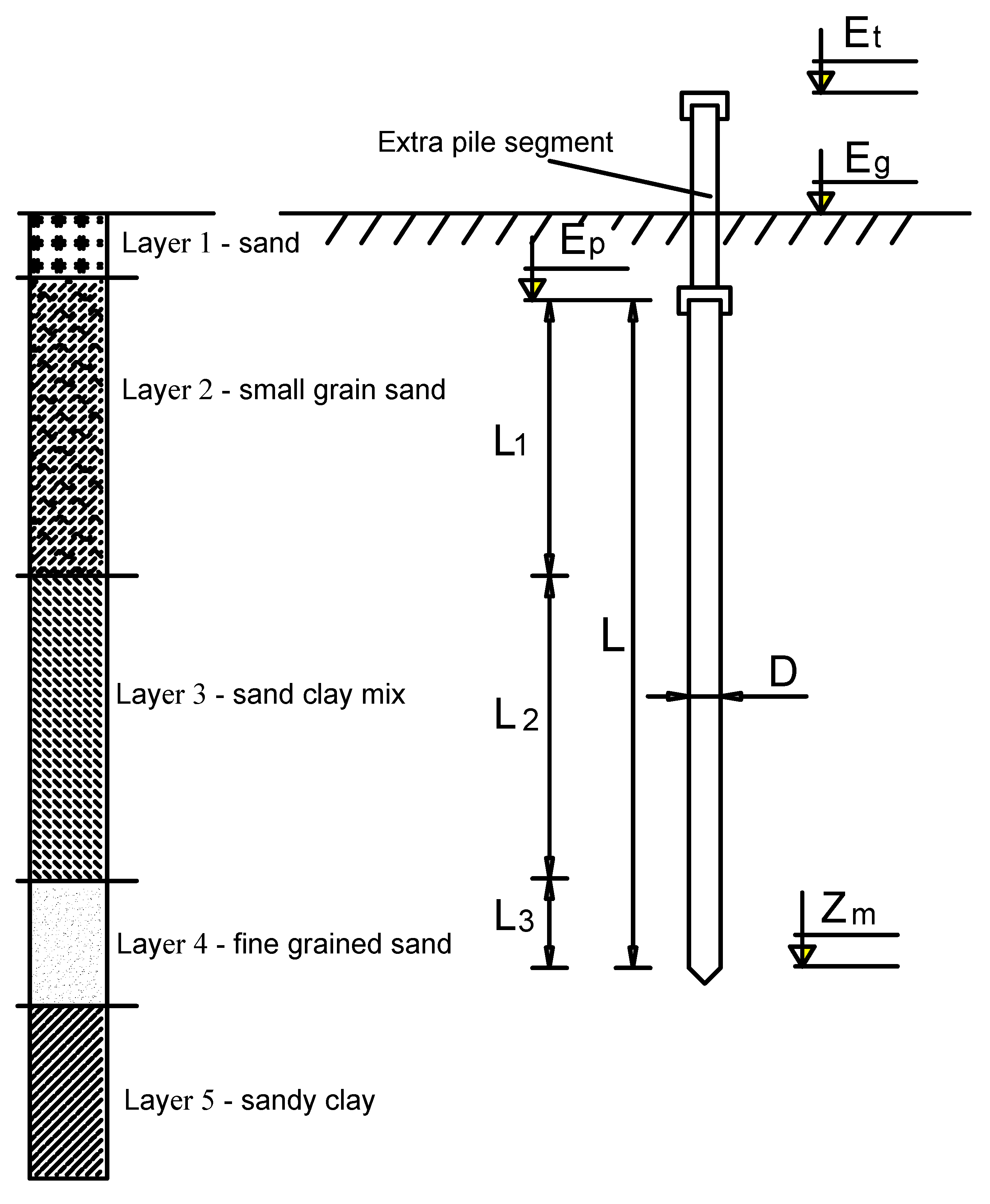
3.1. Experimental Measurement of Bearing Capacity
- (i)
- (i) If the settlement of pile top at a given load level was 5 times higher than the settlement of pile top at the previous load level, or the settlement of the pile top at a given load level increased continuously while the load did not increase, the pile bearing capacity was determined based on that given failure load. The number of piles corresponded to this situation was 688, representing about 30% of the samples. An example of this situation is given in Appendix A (Figure A1).
- (ii)
- When the pile load capacity was too large to be able to test by the destructive load, the load curve (P)– settlement (S) was plotted in log(P)–log(S). The intersection point of two lines was considered as a result of failure and taken as the pile bearing capacity, according to De Beer (1968) [47]. The number of piles corresponded to this situation was 1225 piles (accounting for more than 50% of the samples). An example of this situation is given in Appendix A (Figure A2 and Figure A3).
- (iii)
- For the remaining samples, when the log(P)–log(S) relationship is linear, which could not find the intersection point compared with the previous case. The determination of the pile bearing capacity was taken at the load level when the settlement of the pile top exceeded 10% of the pile diameter.
3.2. Data Preparation
4. Machine Learning Methods
4.1. Random Forest (RF)
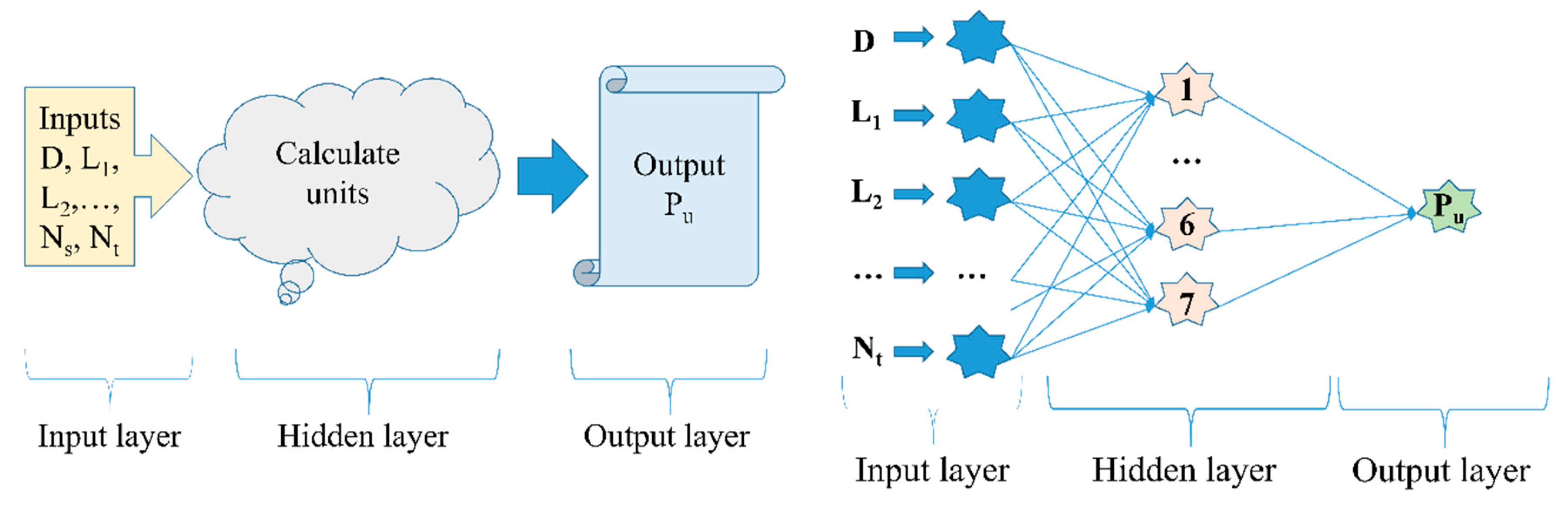
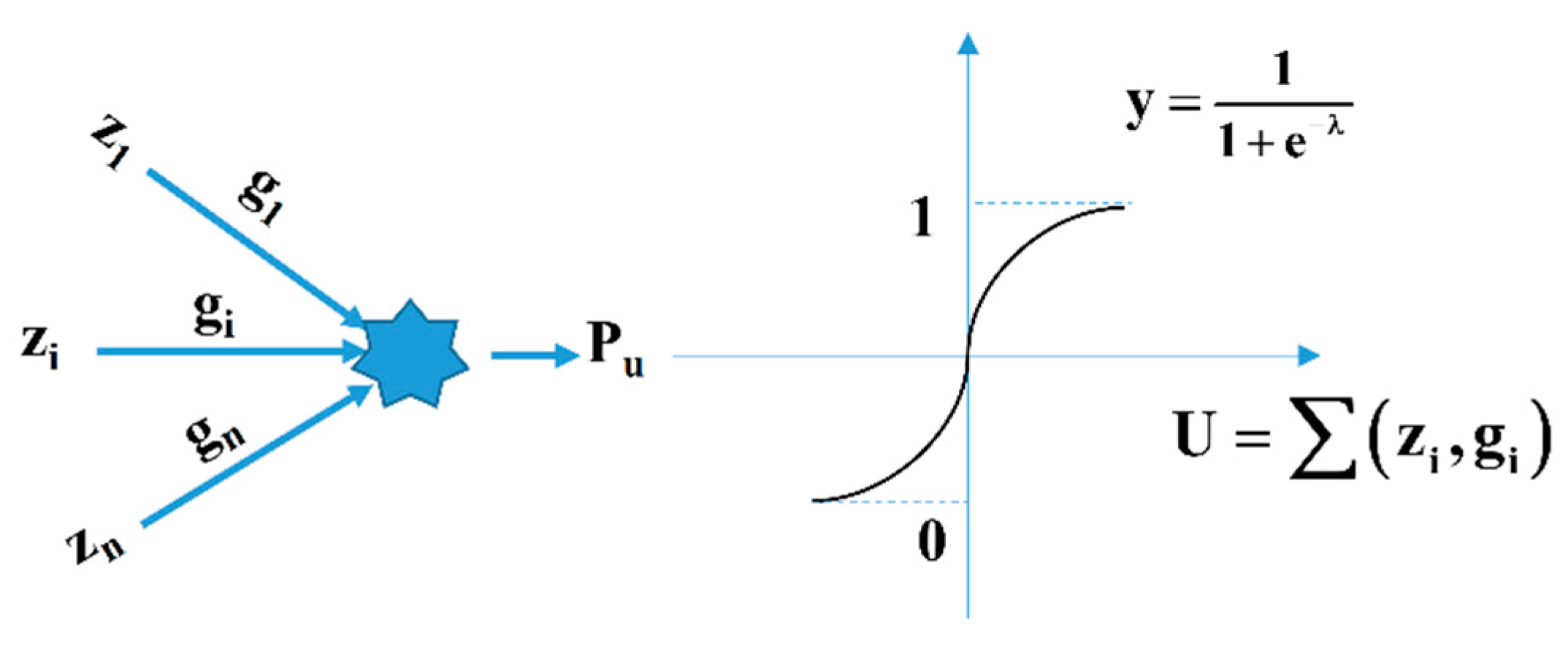
4.2. Artificial Neural Network (ANN)
4.3. Performance Evaluation
5. Results and Discussion
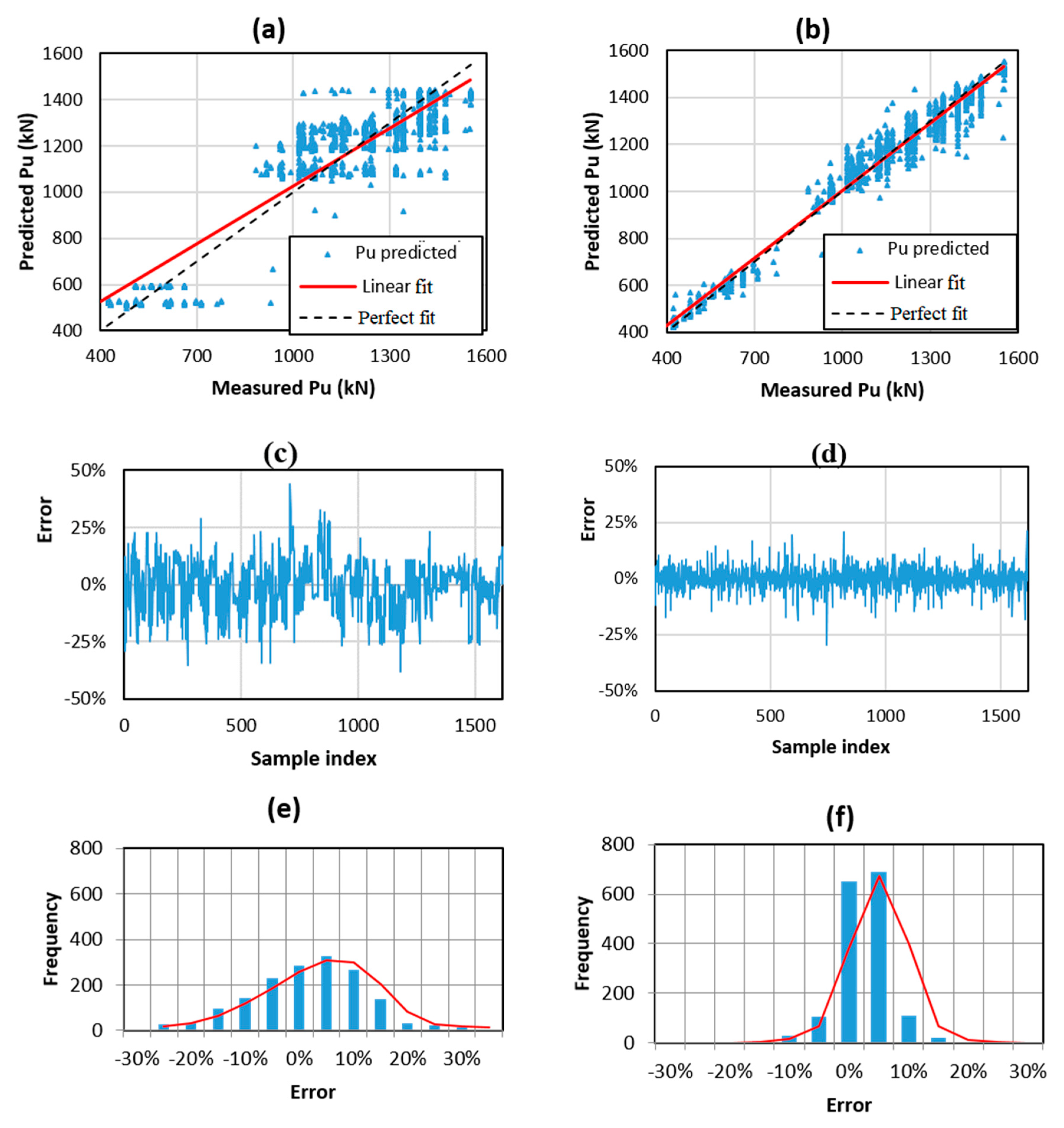
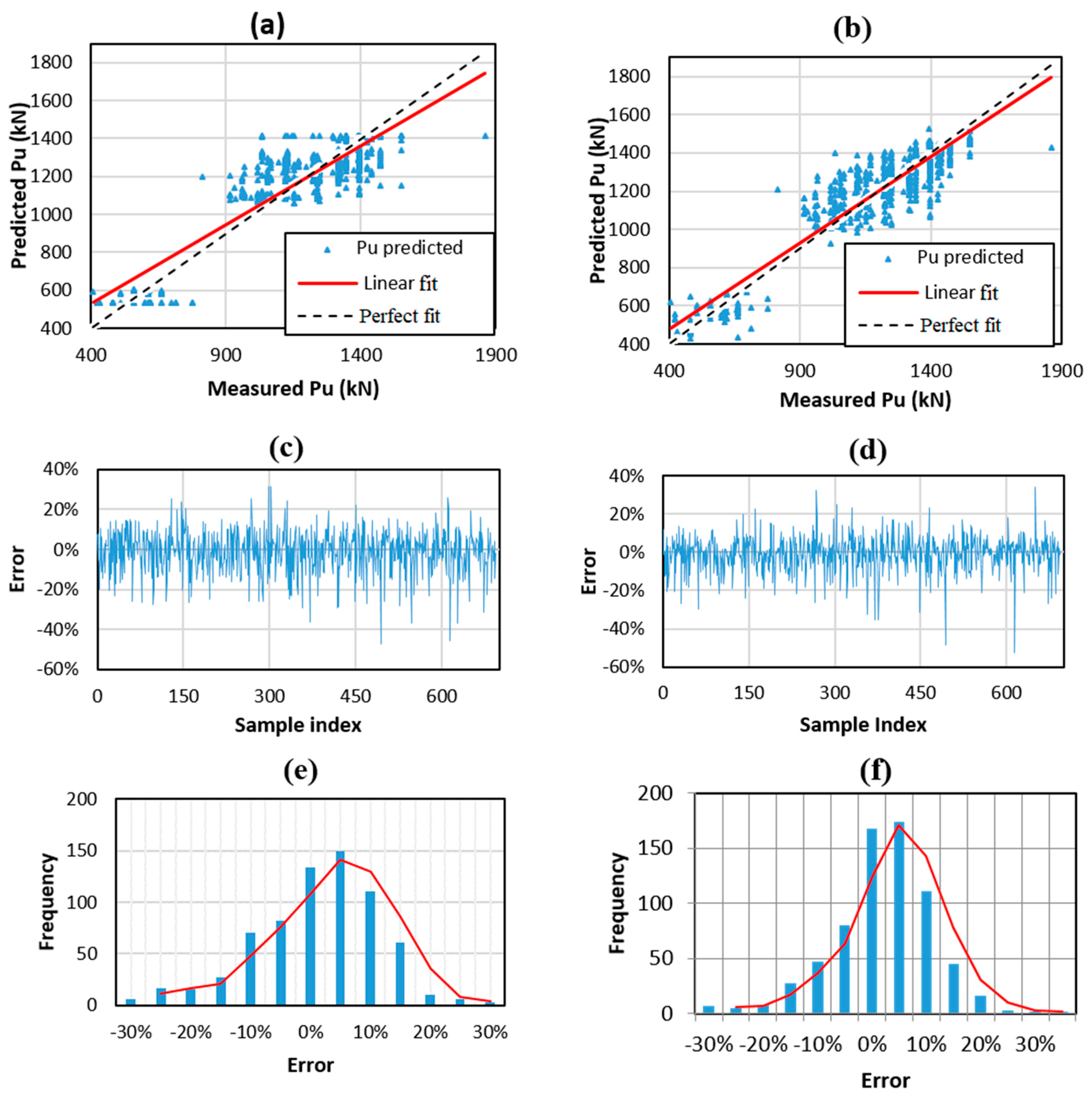
5.1. Comparison of RF and ANN
5.2. Comparison with Empirical Equations and Multi-Variable Regression
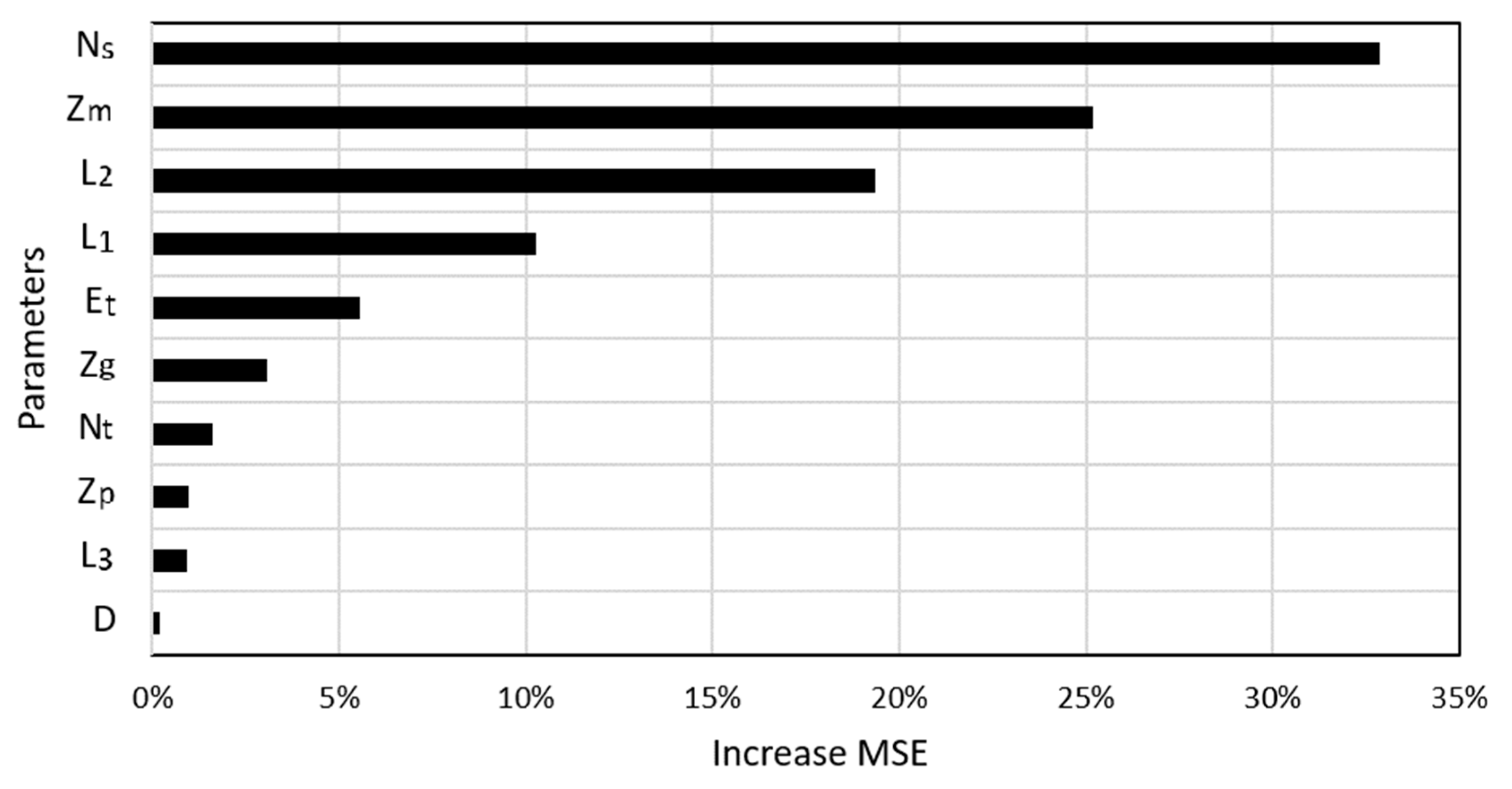
5.3. Feature Importance Analysis Using RF
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A



References
- Shooshpasha, I.; Hasanzadeh, A.; Taghavi, A. Prediction of the axial bearing capacity of piles by SPT-based and numerical design methods. Int. J. GEOMATE 2013, 4, 560–564. [Google Scholar] [CrossRef]
- Bond, A.J.; Schuppener, B.; Scarpelli, G.; Orr, T.L.L.; Dimova, S.; Nikolova, B.; Pinto, A.V.; European Commission; Joint Research Centre; Institute for the Protection and the Security of the Citizen. Eurocode 7: Geotechnical Design Worked Examples; Publications Office: Luxembourg, 2013; ISBN 978-92-79-33759-8. [Google Scholar]
- Bouafia, A.; Derbala, A. Assessment of SPT-based method of pile bearing capacity–analysis of a database. In Proceedings of the International Workshop on Foundation Design Codes and Soil Investigation in View of International Harmonization and Performance-Based Design, IWS Kamakura 2002, Tokyo, Japan, 10–12 April 2002; pp. 369–374. [Google Scholar]
- Meyerhof, G.G. Bearing Capacity and Settlement of Pile Foundations. J. Geotech. Eng. Div. 1976, 102, 197–228. [Google Scholar]
- Bazaraa, A.R.; Kurkur, M.M. N-values used to predict settlements of piles in Egypt. In Proceedings of In Situ ’86; New York, American Society of Civil Engineers: New York, NY, USA, 1986; pp. 462–474. [Google Scholar]
- Robert, Y. A few comments on pile design. Can. Geotech. J. 1997, 34, 560–567. [Google Scholar] [CrossRef]
- Shioi, Y.; Fukui, J. Application of N-value to design of foundations in Japan. In Proceedings of the Second European Symposium on Penetration Testing, ESOPT II, Amsterdam, The Netherlands, 24–27 May 1982; pp. 159–164. [Google Scholar]
- Shariatmadari, N.; Eslami, A.A.; Karim, P.F.M. Bearing capacity of driven piles in sands from SPT–applied to 60 case histories. Iran. J. Sci. Technol. Trans. B Eng. 2008, 32, 125–140. [Google Scholar]
- Lopes, R.F.; Laprovitera, H. On the prediction of the bearing capacity of bored piles from dynamic penetration tests. In Proceedings of the Deep Foundations on Bored and Auger Piles BAP III, Ghent, Belgium, 19–21 October 1998; A.A. Balkema: Rotterdam, The Netherlands; pp. 537–540. [Google Scholar]
- Decourt, L. Prediction of load-settlement relationships for foundations on the basis of the SPT. In Ciclo de Conferencias Internationale “Leonardo Zeevaert”; UNAM: Mexico City, Mexico, 1995; pp. 85–104. [Google Scholar]
- Architectural Institute of Japan. Recommendations for Design of Building Foundation; Architectural Institute of Japan: Tokyo, Japan, 2004. [Google Scholar]
- Asteris, P.G.; Ashrafian, A.; Rezaie-Balf, M. Prediction of the compressive strength of self-compacting concrete using surrogate models. Computers and Concrete. 2019, 24, 137–150. [Google Scholar]
- Asteris, P.G.; Moropoulou, A.; Skentou, A.D.; Apostolopoulou, M.; Mohebkhah, A.; Cavaleri, L.; Rodrigues, H.; Varum, H. Stochastic Vulnerability Assessment of Masonry Structures: Concepts, Modeling and Restoration Aspects. Appl. Sci. 2019, 9, 243. [Google Scholar] [CrossRef]
- Hajihassani, M.; Abdullah, S.S.; Asteris, P.G.; Armaghani, D.J. A gene expression programming model for predicting tunnel convergence. Appl. Sci. 2019, 9, 4650. [Google Scholar] [CrossRef]
- Huang, L.; Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M.M. Invasive Weed Optimization Technique-Based ANN to the Prediction of Rock Tensile Strength. Appl. Sci. 2019, 9, 5372. [Google Scholar] [CrossRef]
- Le, L.M.; Ly, H.-B.; Pham, B.T.; Le, V.M.; Pham, T.A.; Nguyen, D.-H.; Tran, X.-T.; Le, T.-T. Hybrid Artificial Intelligence Approaches for Predicting Buckling Damage of Steel Columns Under Axial Compression. Materials 2019, 12, 1670. [Google Scholar] [CrossRef]
- Ly, H.-B.; Pham, B.T.; Dao, D.V.; Le, V.M.; Le, L.M.; Le, T.-T. Improvement of ANFIS Model for Prediction of Compressive Strength of Manufactured Sand Concrete. Appl. Sci. 2019, 9, 3841. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, L.M.; Duong, H.T.; Nguyen, T.C.; Pham, T.A.; Le, T.-T.; Le, V.M.; Nguyen-Ngoc, L.; Pham, B.T. Hybrid Artificial Intelligence Approaches for Predicting Critical Buckling Load of Structural Members under Compression Considering the Influence of Initial Geometric Imperfections. Appl. Sci. 2019, 9, 2258. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, T.-T.; Le, L.M.; Tran, V.Q.; Le, V.M.; Vu, H.-L.T.; Nguyen, Q.H.; Pham, B.T. Development of Hybrid Machine Learning Models for Predicting the Critical Buckling Load of I-Shaped Cellular Beams. Appl. Sci. 2019, 9, 5458. [Google Scholar] [CrossRef]
- Ly, H.-B.; Le, L.M.; Phi, L.V.; Phan, V.-H.; Tran, V.Q.; Pham, B.T.; Le, T.-T.; Derrible, S. Development of an AI Model to Measure Traffic Air Pollution from Multisensor and Weather Data. Sensors 2019, 19, 4941. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhou, J.; Asteris, P.G.; Jahed Armaghani, D.; Tahir, M.M. Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate. Appl. Sci. 2019, 9, 3715. [Google Scholar] [CrossRef]
- Ly, H.-B.; Monteiro, E.; Le, T.-T.; Le, V.M.; Dal, M.; Regnier, G.; Pham, B.T. Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees. Materials 2019, 12, 1544. [Google Scholar] [CrossRef]
- Chen, H.; Asteris, P.G.; Jahed Armaghani, D.; Gordan, B.; Pham, B.T. Assessing Dynamic Conditions of the Retaining Wall: Developing Two Hybrid Intelligent Models. Appl. Sci. 2019, 9, 1042. [Google Scholar] [CrossRef]
- Nguyen, H.-L.; Le, T.-H.; Pham, C.-T.; Le, T.-T.; Ho, L.S.; Le, V.M.; Pham, B.T.; Ly, H.-B. Development of Hybrid Artificial Intelligence Approaches and a Support Vector Machine Algorithm for Predicting the Marshall Parameters of Stone Matrix Asphalt. Appl. Sci. 2019, 9, 3172. [Google Scholar] [CrossRef]
- Nguyen, H.-L.; Pham, B.T.; Son, L.H.; Thang, N.T.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Le, T.-H.; Tien Bui, D. Adaptive Network Based Fuzzy Inference System with Meta-Heuristic Optimizations for International Roughness Index Prediction. Appl. Sci. 2019, 9, 4715. [Google Scholar] [CrossRef]
- Asteris, P.G.; Nozhati, S.; Nikoo, M.; Cavaleri, L.; Nikoo, M. Krill herd algorithm-based neural network in structural seismic reliability evaluation. Mech. Adv. Mater. Struct. 2019, 26, 1146–1153. [Google Scholar] [CrossRef]
- Asteris, P.G.; Armaghani, D.J.; Hatzigeorgiou, G.D.; Karayannis, C.G.; Pilakoutas, K. Predicting the shear strength of reinforced concrete beams using Artificial Neural Networks. Comput. Concr. 2019, 24, 469–488. [Google Scholar]
- Asteris, P.G.; Apostolopoulou, M.; Skentou, A.D.; Moropoulou, A. Application of artificial neural networks for the prediction of the compressive strength of cement-based mortars. Comput. Concr. 2019, 24, 329–345. [Google Scholar]
- Asteris, P.G.; Kolovos, K.G. Self-compacting concrete strength prediction using surrogate models. Neural Comput. Appl. 2019, 31, 409–424. [Google Scholar] [CrossRef]
- Asteris, P.G.; Mokos, V.G. Concrete compressive strength using artificial neural networks. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Trinh, S.H.; Le, T.-T.; Pham, B.T. Artificial Intelligence Approaches for Prediction of Compressive Strength of Geopolymer Concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef] [PubMed]
- Dao, D.V.; Trinh, S.H.; Ly, H.-B.; Pham, B.T. Prediction of Compressive Strength of Geopolymer Concrete Using Entirely Steel Slag Aggregates: Novel Hybrid Artificial Intelligence Approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
- Qi, C.; Ly, H.-B.; Chen, Q.; Le, T.-T.; Le, V.M.; Pham, B.T. Flocculation-dewatering prediction of fine mineral tailings using a hybrid machine learning approach. Chemosphere 2020, 244, 125450. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Nguyen, M.D.; Dao, D.V.; Prakash, I.; Ly, H.-B.; Le, T.-T.; Ho, L.S.; Nguyen, K.T.; Ngo, T.Q.; Hoang, V.; et al. Development of artificial intelligence models for the prediction of Compression Coefficient of soil: An application of Monte Carlo sensitivity analysis. Sci. Total Environ. 2019, 679, 172–184. [Google Scholar] [CrossRef]
- Kumar, B.M.; Kumar, K.A.; Bharathi, A. Improved Soil Data Prediction Model Base Bioinspired K-Nearest Neighbor Techniques for Spatial Data Analysis in Coimbatore Region. Int. J. Future Revolut. Comput. Sci. Commun. Eng. 2017, 3, 345–349. [Google Scholar]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Kulhawy, F.H.; Chua, C.G. Bayesian Neural Network Analysis of Undrained Side Resistance of Drilled Shafts. J. Geotech. Geoenviron. Eng. 2005, 131, 84–93. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B. Neural network prediction of pullout capacity of marquee ground anchors. Comput. Geotech. 2005, 32, 153–163. [Google Scholar] [CrossRef]
- Shahin, M.A. Load–settlement modeling of axially loaded steel driven piles using CPT-based recurrent neural networks. Soils Found. 2014, 54, 515–522. [Google Scholar] [CrossRef]
- Shahin, M.A. State-of-the-art review of some artificial intelligence applications in pile foundations. Geosci. Front. 2016, 7, 33–44. [Google Scholar] [CrossRef]
- Shahin, M.A. Intelligent computing for modeling axial capacity of pile foundations. Can. Geotech. J. 2010, 47, 230–243. [Google Scholar] [CrossRef]
- Nawari, N.O.; Liang, R.; Nusairat, J. Artificial intelligence techniques for the design and analysis of deep foundations. Electr. J. Geotech. Eng. 1999, 4, 1–21. [Google Scholar]
- Pooya Nejad, F.; Jaksa, M.B.; Kakhi, M.; McCabe, B.A. Prediction of pile settlement using artificial neural networks based on standard penetration test data. Comput. Geotech. 2009, 36, 1125–1133. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Armaghani, D.J.; Maizir, H. Application of Artificial Neural Network for Predicting Shaft and Tip Resistances of Concrete Piles. Earth Sci. Res. J. 2015, 19, 85–93. [Google Scholar] [CrossRef]
- Bagińska, M.; Srokosz, P.E. The Optimal ANN Model for Predicting Bearing Capacity of Shallow Foundations trained on Scarce Data. KSCE J. Civ. Eng. 2019, 23, 130–137. [Google Scholar] [CrossRef]
- Teh, C.I.; Wong, K.S.; Goh, A.T.C.; Jaritngam, S. Prediction of Pile Capacity Using Neural Networks. J. Comput. Civil Eng. 1997, 11, 129–138. [Google Scholar] [CrossRef]
- De Beer, E.E. Proefondervindlijkebijdrage tot de studie van het grensdraagvermogen van zandonderfunderingen op staal; Tijdshift der OpenbarVerken van Belgie, No.6; NICI: Gent, Belgium, 1968. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Oxfordshire, UK, 1984; ISBN 978-0-412-04841-8. [Google Scholar]
- Latinne, P.; Debeir, O.; Decaestecker, C. Limiting the Number of Trees in Random Forests. In Proceedings of the Second International Workshop on Multiple Classifier Systems, Cambridge, UK, 2–4 July 2001; pp. 178–187. [Google Scholar]
- Bernard, S.; Adam, S.; Heutte, L. Using Random Forests for Handwritten Digit Recognition. In Proceedings of the Ninth International Conference on Document Analysis and Recognition (ICDAR 2007), Curitiba, Parana, Brazil, 23–26 September 2007; pp. 1043–1047. [Google Scholar]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput. Aided Civil Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Tarawneh, B. Pipe pile setup: Database and prediction model using artificial neural network. Soils Found. 2013, 53, 607–615. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Armaghani, D.J.; Maizir, H. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement 2014, 57, 122–131. [Google Scholar] [CrossRef]
- Zaabab, A.H.; Zhang, Q.-J.; Nakhla, M. A neural network modeling approach to circuit optimization and statistical design. IEEE Trans. Microw. Theory Tech. 1995, 43, 1349–1358. [Google Scholar] [CrossRef]
- Das, S.K.; Basudhar, P.K. Undrained lateral load capacity of piles in clay using artificial neural network. Comput. Geotech. 2006, 33, 454–459. [Google Scholar] [CrossRef]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Dao, D.V.; Adeli, H.; Ly, H.-B.; Le, L.M.; Le, V.M.; Le, T.-T.; Pham, B.T. A Sensitivity and Robustness Analysis of GPR and ANN for High-Performance Concrete Compressive Strength Prediction Using a Monte Carlo Simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Maizir, H.; Kassim, K.A. Neural network application in prediction of axial bearing capacity of driven piles. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 14–16 March 2013; Volume 2202, pp. 51–55. [Google Scholar]
- Pal, M.; Deswal, S. Modeling pile capacity using support vector machines and generalized regression neural network. J. Geotech. Geoenviron. Eng. 2008, 134, 1021–1024. [Google Scholar] [CrossRef]
- Benali, A.; Nechnech, A. Prediction of the pile capacity in purely coherent soils using the approach of the artificial neural networks. In Proceedings of the International Seminar, Innovation and Valorization in Civil Engineering and Construction Materials, Rabat, Morocco, 23–25 November 2011; pp. 23–25. [Google Scholar]
- Nehdi, M.; Djebbar, Y.; Khan, A. Neural network model for preformed-foam cellular concrete. Mater. J. 2001, 98, 402–409. [Google Scholar]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Phong, T.V.; Ly, H.-B.; Le, T.-T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. CATENA 2020, 188, 104451. [Google Scholar] [CrossRef]
- Le, T.-T.; Pham, B.T.; Ly, H.-B.; Shirzadi, A.; Le, L.M. Development of 48-h Precipitation Forecasting Model using Nonlinear Autoregressive Neural Network. In CIGOS 2019, Innovation for Sustainable Infrastructure: Proceedings of the 5th International Conference on Geotechnics, Civil Engineering Works and Structures; Springer: Singapore, 2020; pp. 1191–1196. [Google Scholar]
- Pham, B.T.; Nguyen, M.D.; Ly, H.-B.; Pham, T.A.; Hoang, V.; Van Le, H.; Le, T.-T.; Nguyen, H.Q.; Bui, G.L. Development of Artificial Neural Networks for Prediction of Compression Coefficient of Soft Soil. In CIGOS 2019, Innovation for Sustainable Infrastructure: Proceedings of the 5th International Conference on Geotechnics, Civil Engineering Works and Structures; Springer: Singapore, 2020; pp. 1167–1172. [Google Scholar]
- Pham, B.T.; Le, L.M.; Le, T.-T.; Bui, K.-T.T.; Le, V.M.; Ly, H.-B.; Prakash, I. Development of advanced artificial intelligence models for daily rainfall prediction. Atmos. Res. 2020, 237, 104845. [Google Scholar] [CrossRef]
- Thanh, T.T.M.; Ly, H.-B.; Pham, B.T. A Possibility of AI Application on Mode-choice Prediction of Transport Users in Hanoi. In CIGOS 2019, Innovation for Sustainable Infrastructure: Proceedings of the 5th International Conference on Geotechnics, Civil Engineering Works and Structures; Springer: Singapore, 2020; pp. 1179–1184. [Google Scholar]
- Ly, H.-B.; Desceliers, C.; Le, L.M.; Le, T.-T.; Pham, B.T.; Nguyen-Ngoc, L.; Doan, V.T.; Le, M. Quantification of Uncertainties on the Critical Buckling Load of Columns under Axial Compression with Uncertain Random Materials. Materials 2019, 12, 1828. [Google Scholar] [CrossRef] [PubMed]
- Egbe, J.G.; Ewa, D.E.; Ubi, S.E.; Ikwa, G.B.; Tumenayo, O.O. Application of multilinear regression analysis in modeling of soil properties for geotechnical civil engineering works in Calabar South. Nig. J. Tech. 2018, 36, 1059. [Google Scholar] [CrossRef]
- Silva, S.H.G.; Teixeira, A.F.D.S.; Menezes, M.D.D.; Guilherme, L.R.G.; Moreira, F.M.D.S.; Curi, N. Multiple linear regression and random forest to predict and map soil properties using data from portable X-ray fluorescence spectrometer (pXRF). Ciênc. Agrotec. 2017, 41, 648–664. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R. News 2002, 2, 18–22. [Google Scholar]
- Zhang, B.; MacLean, D.; Johns, R.; Eveleigh, E. Effects of Hardwood Content on Balsam Fir Defoliation during the Building Phase of a Spruce Budworm Outbreak. Forests 2018, 9, 530. [Google Scholar] [CrossRef]
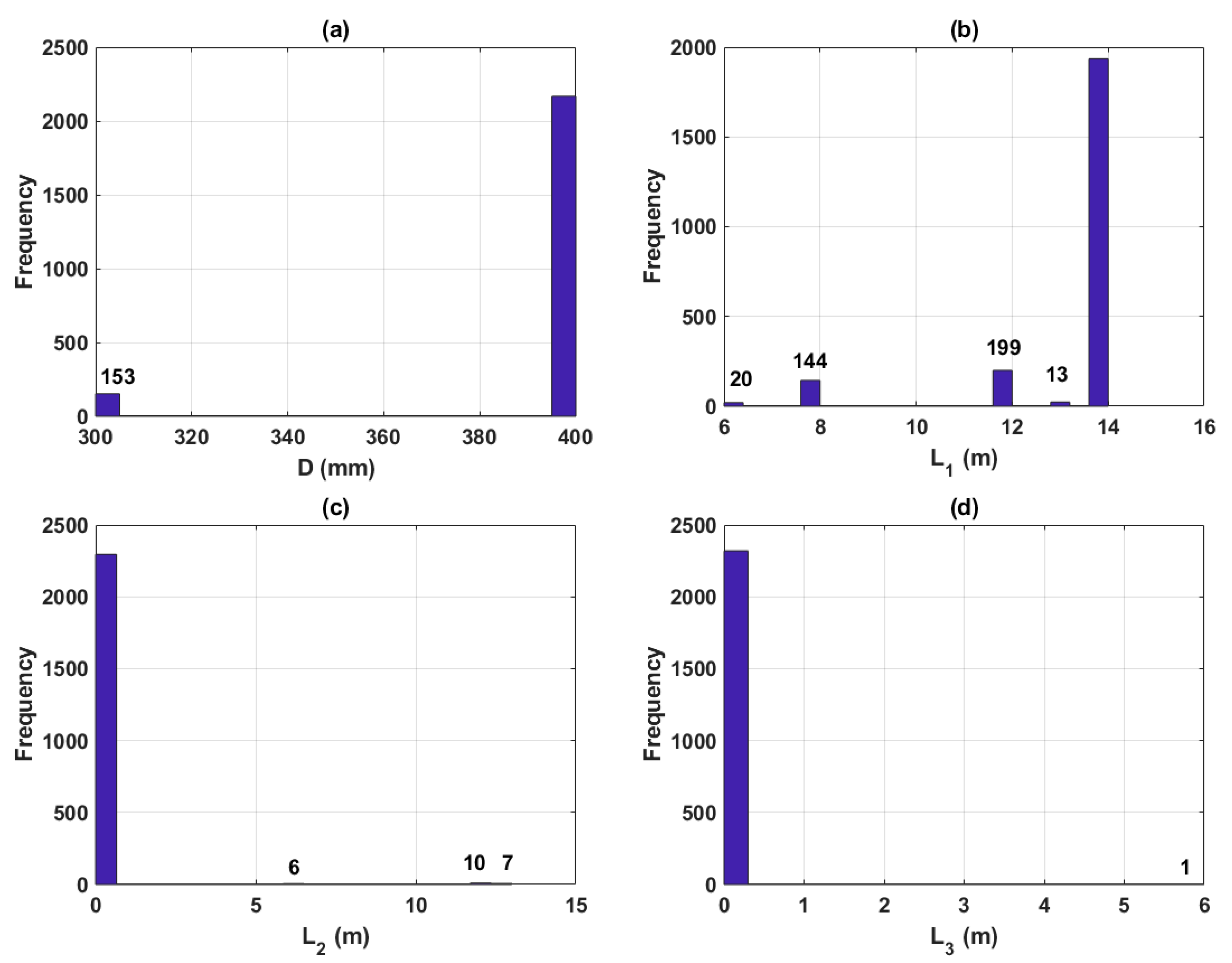
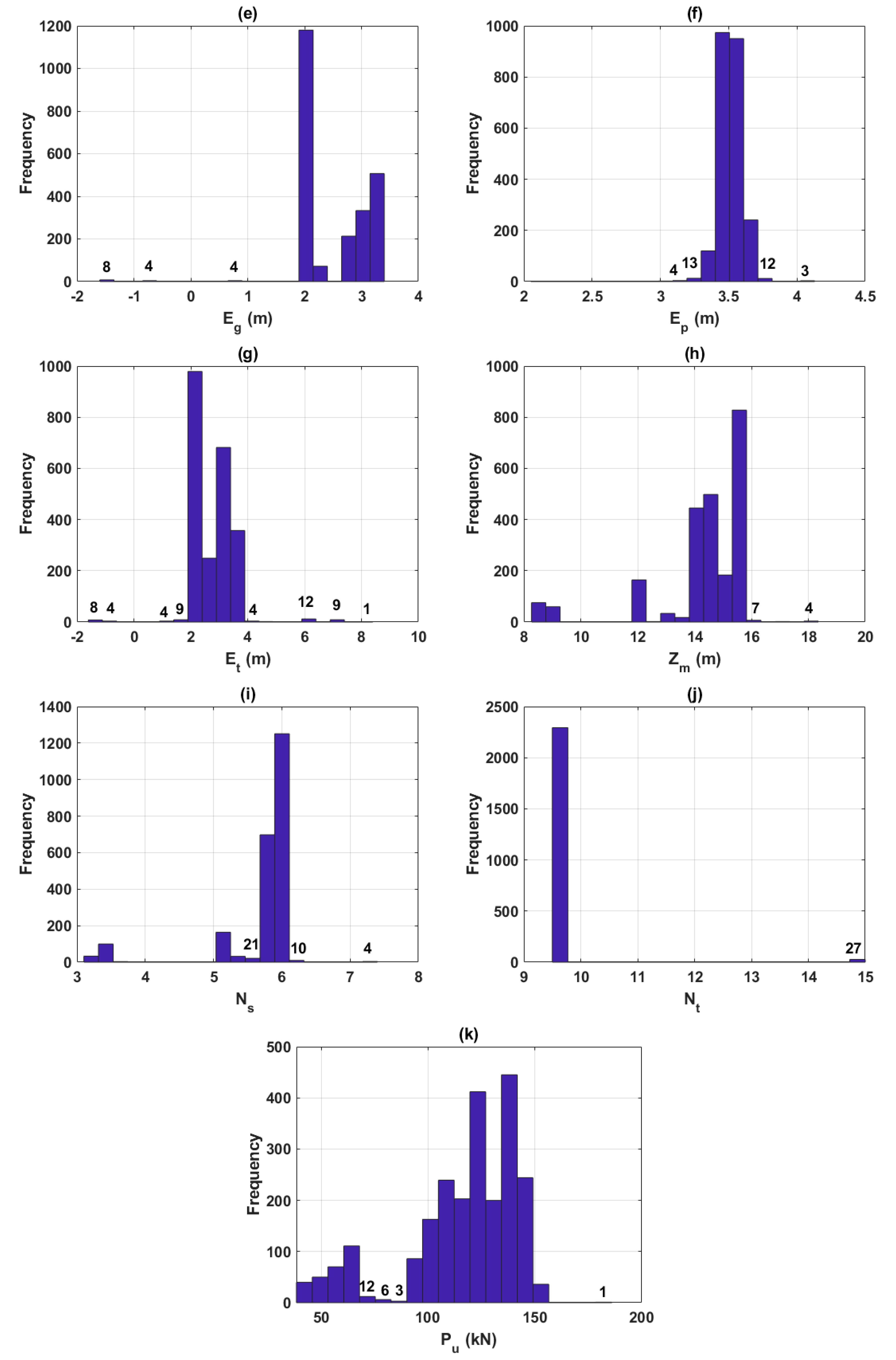
| N° | D | L1 | L2 | L3 | Eg | Ep | Et | Zm | Ns | Nt | Pu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit | mm | m | m | m | m | m | m | m | - | - | kN |
| 1 | 400 | 3.45 | 8 | 0.07 | 2.95 | 3.42 | 2.95 | 14.47 | 11.52 | 7.44 | 1163 |
| 2 | 400 | 3.4 | 7.29 | 0 | 3.4 | 3.49 | 3.4 | 14.09 | 10.69 | 7.27 | 1240 |
| 3 | 400 | 4.35 | 8 | 1.2 | 2.05 | 3.4 | 5.8 | 15.6 | 13.55 | 7.74 | 1297.8 |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . | . | . | . | . |
| 2312 | 400 | 5.72 | 8 | 1.67 | 0.68 | 4.13 | 1.06 | 16.07 | 15.39 | 7.50 | 1344 |
| 2313 | 400 | 4.1 | 2.19 | 0 | 2.7 | 3.72 | 2.73 | 8.99 | 6.29 | 4.94 | 480 |
| 2314 | 400 | 4.05 | 8 | 0.7 | 2.35 | 3.5 | 2.4 | 15.1 | 12.75 | 7.58 | 1318 |
| Min | 300 | 3.00 | 1.47 | 0.00 | −1.60 | 2.05 | −1.60 | 8.27 | 5.57 | 4.35 | 384 |
| Average | 393.3 | 4.02 | 7.27 | 0.49 | 2.53 | 3.52 | 2.70 | 14.30 | 11.78 | 7.24 | 1164.5 |
| Max | 400 | 8.40 | 8.00 | 3.95 | 3.40 | 4.13 | 8.40 | 18.35 | 19.20 | 8.47 | 1860 |
| SD | 24.85 | 0.55 | 1.53 | 0.50 | 0.63 | 0.09 | 0.75 | 1.68 | 2.02 | 0.71 | 268.63 |
| D | L1 | L2 | L3 | Eg | Ep | Et | Zm | Ns | Nt | |
|---|---|---|---|---|---|---|---|---|---|---|
| Min | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 | −1.0 |
| Average | 0.868 | 0.845 | −0.983 | −0.999 | 0.651 | 0.410 | −0.139 | 0.197 | 0.401 | 0.284 |
| Max | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| SD | 0.497 | 0.413 | 0.172 | 0.042 | 0.253 | 0.084 | 0.150 | 0.333 | 0.342 | 0.959 |
| Parameters | Value and Description |
|---|---|
| Number of neurons in the input layer | 10 |
| Number of hidden layers | 1 |
| Number of neurons in the hidden layer | 7 |
| Number of neurons in the output layer | 1 |
| Activation function for the hidden layer | Logistic |
| Activation function for the output layer | Linear |
| Training algorithm | Quasi-Newton methods |
| Cost function | Mean Square Error (MSE) |
| Parameters | Value and Description |
|---|---|
| Number of trees | 15 |
| Number of features to consider when looking for the best split | 10 |
| Minimum number of samples required to split an internal node | 2 |
| Minimum number of samples required to be at a leaf node | 1e-7 |
| Cost function | Mean Square Error (MSE) |
| Maximum depth of the tree | None |
| Part | Method | R2 | MAE (kN) | RMSE (kN) | merror (%) | StDerror (%) |
|---|---|---|---|---|---|---|
| Training | ANN | 0.818 | 1.050 | 114.882 | 0.884% | 10.605% |
| RF | 0.969 | 2.178 | 47.333 | 0.069% | 4.223% | |
| Testing | ANN | 0.809 | 3.190 | 116.366 | 1.202% | 10.786% |
| RF | 0.866 | 2.924 | 98.161 | 0.573% | 9.461% |
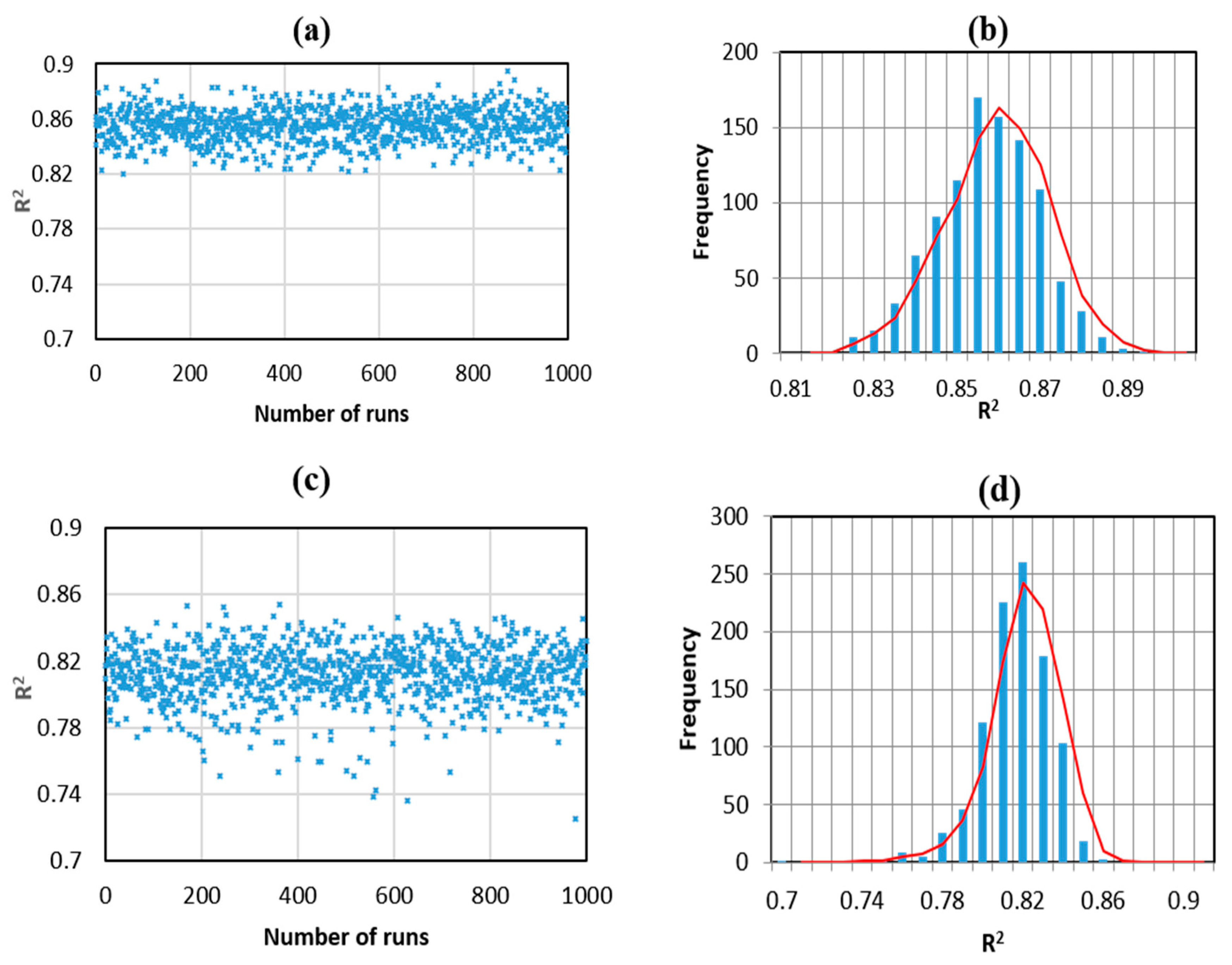
| Part | Method | Avr. R2 | StD. R2 |
|---|---|---|---|
| Testing | ANN | 0.811 | 0.318 |
| RF | 0.861 | 0.277 |
| Ground Type | Sandy Ground | Clayey Ground |
|---|---|---|
| Meyerhof (1976) [4] | ||
| Shioi and Fukui (1982) [7] | ||
| Decourt (1995) [10] | ||
| Shariatmadari (2008) [8] | ||
| AIJ (2004) [11] | ||
| Variable | Intercept | D | L1 | L2 | L3 | Zp | Zg | Et | Zm | Ns | Nt |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Coefficients | −611.39 | 2.33 | 86.29 | 142.11 | 0 | 0 | −54.05 | 62.09 | 31.85 | 23.16 | −169.43 |
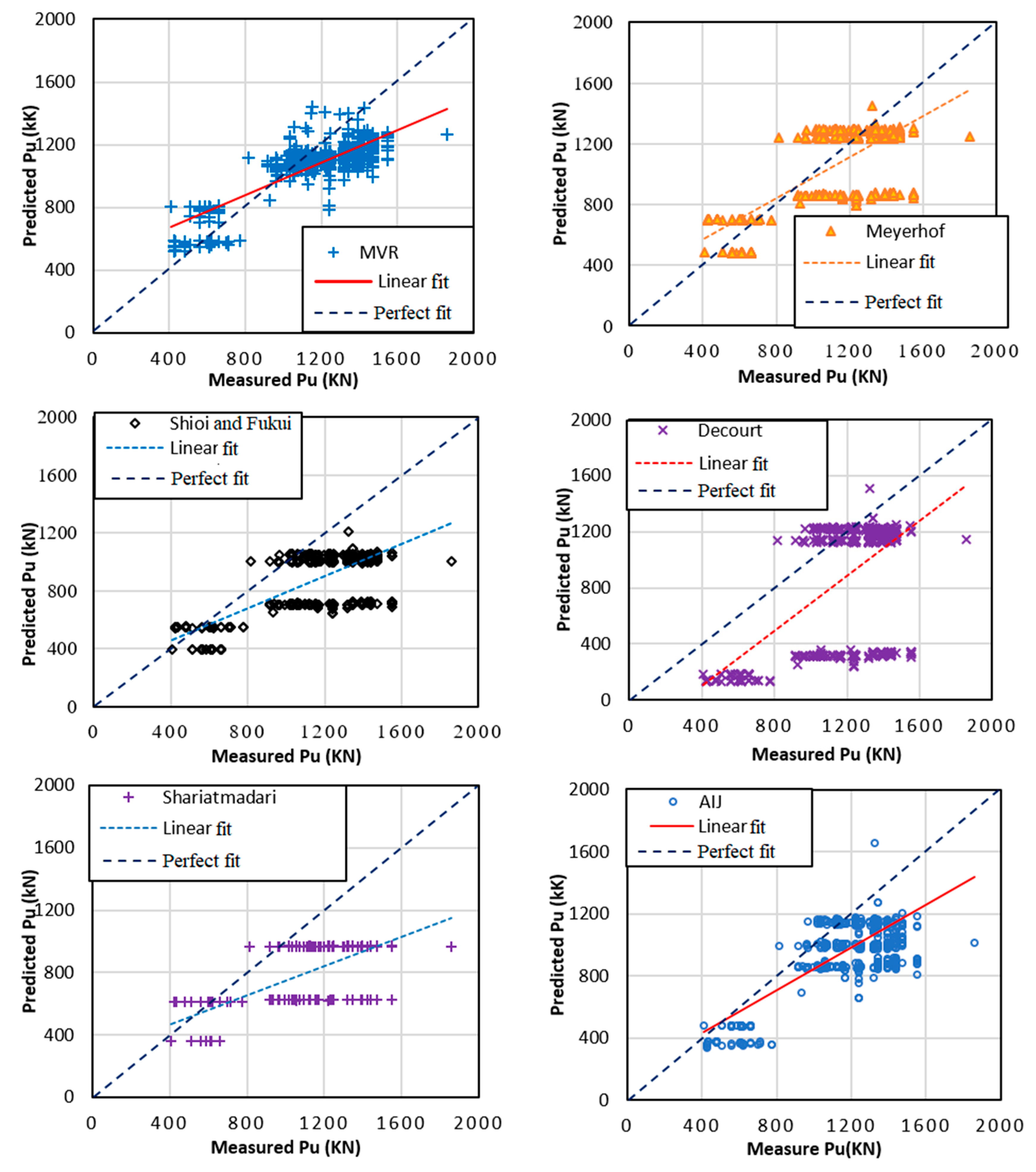
| RF Model | MVR | Meyerhof (1976) | Shioi and Fukui (1982) | Decourt (1995) | Shariatmadari (2008) | AIJ (2004) | |
|---|---|---|---|---|---|---|---|
| R2 | 0.866 | 0.702 | 0.467 | 0.485 | 0.334 | 0.391 | 0.611 |
| MAE (kN) | 2.924 | 94.267 | 77.830 | 280.727 | 312.297 | 340.668 | 205.721 |
| RMSE(kN) | 98.161 | 183.046 | 224.500 | 340.606 | 483.335 | 400.470 | 265.531 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.A.; Ly, H.-B.; Tran, V.Q.; Giap, L.V.; Vu, H.-L.T.; Duong, H.-A.T. Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest. Appl. Sci. 2020, 10, 1871. https://doi.org/10.3390/app10051871
Pham TA, Ly H-B, Tran VQ, Giap LV, Vu H-LT, Duong H-AT. Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest. Applied Sciences. 2020; 10(5):1871. https://doi.org/10.3390/app10051871
Chicago/Turabian StylePham, Tuan Anh, Hai-Bang Ly, Van Quan Tran, Loi Van Giap, Huong-Lan Thi Vu, and Hong-Anh Thi Duong. 2020. "Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest" Applied Sciences 10, no. 5: 1871. https://doi.org/10.3390/app10051871
APA StylePham, T. A., Ly, H.-B., Tran, V. Q., Giap, L. V., Vu, H.-L. T., & Duong, H.-A. T. (2020). Prediction of Pile Axial Bearing Capacity Using Artificial Neural Network and Random Forest. Applied Sciences, 10(5), 1871. https://doi.org/10.3390/app10051871






