Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon
Abstract
1. Introduction
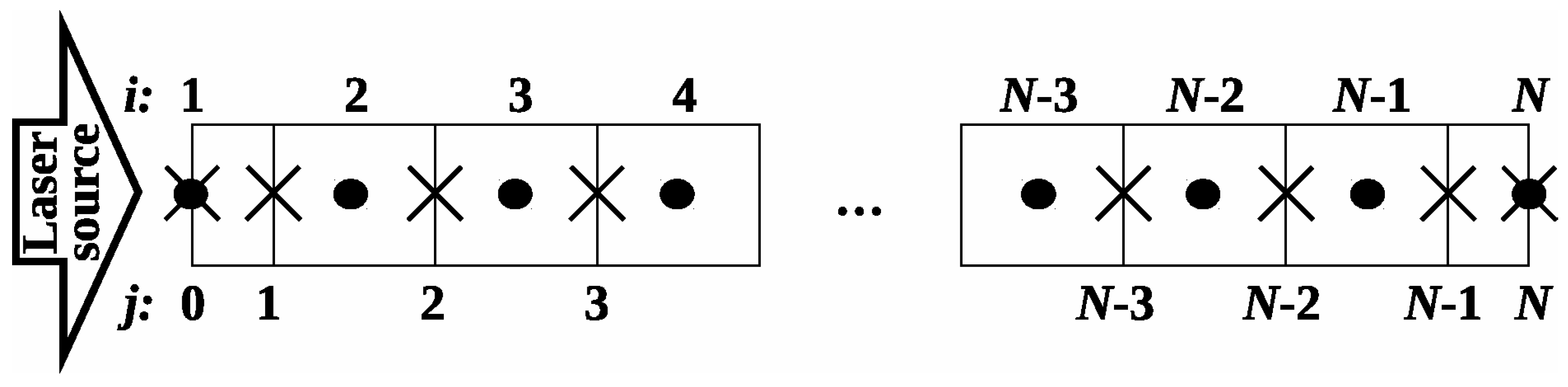
2. Model Description
3. Numerical Solution Scheme
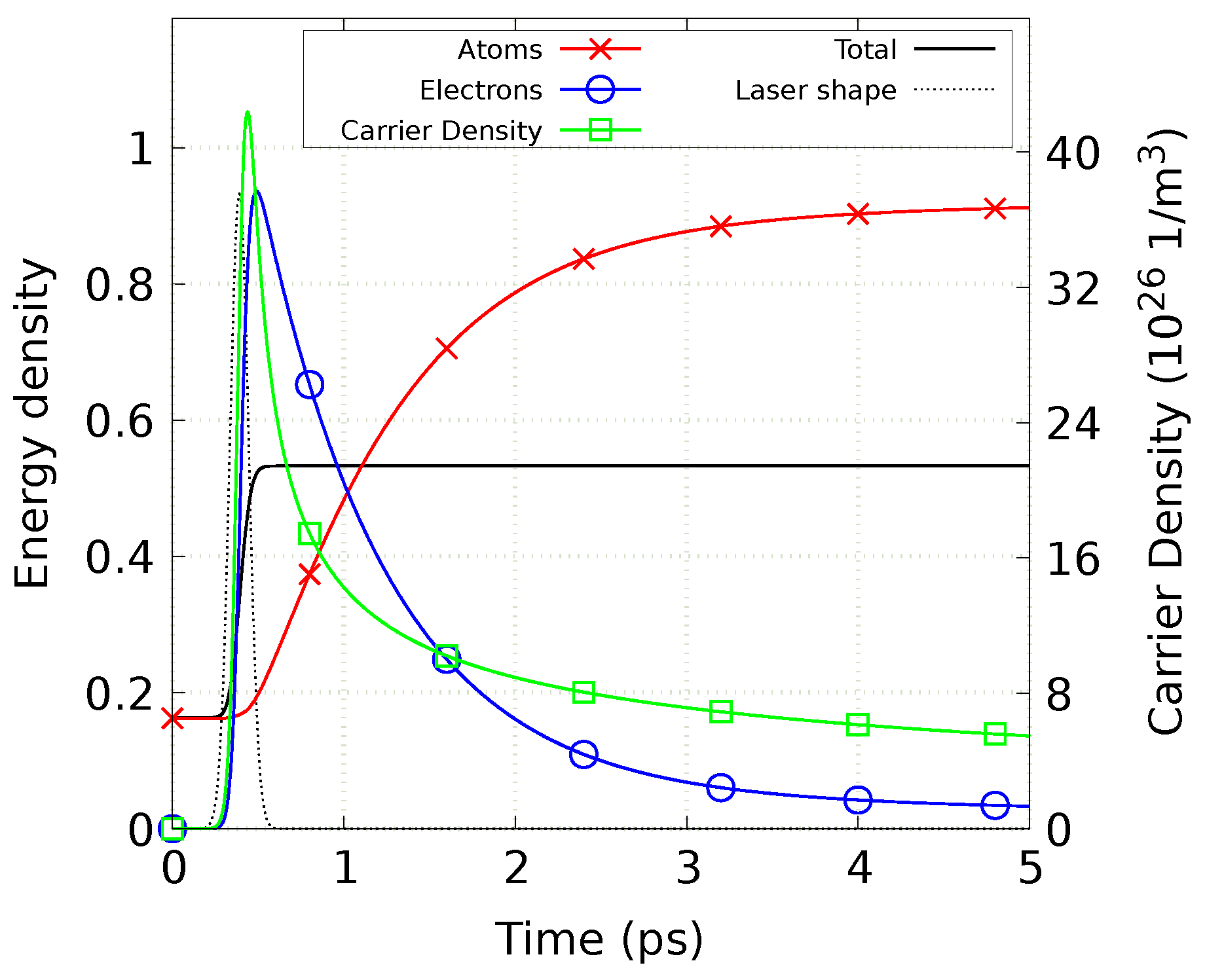
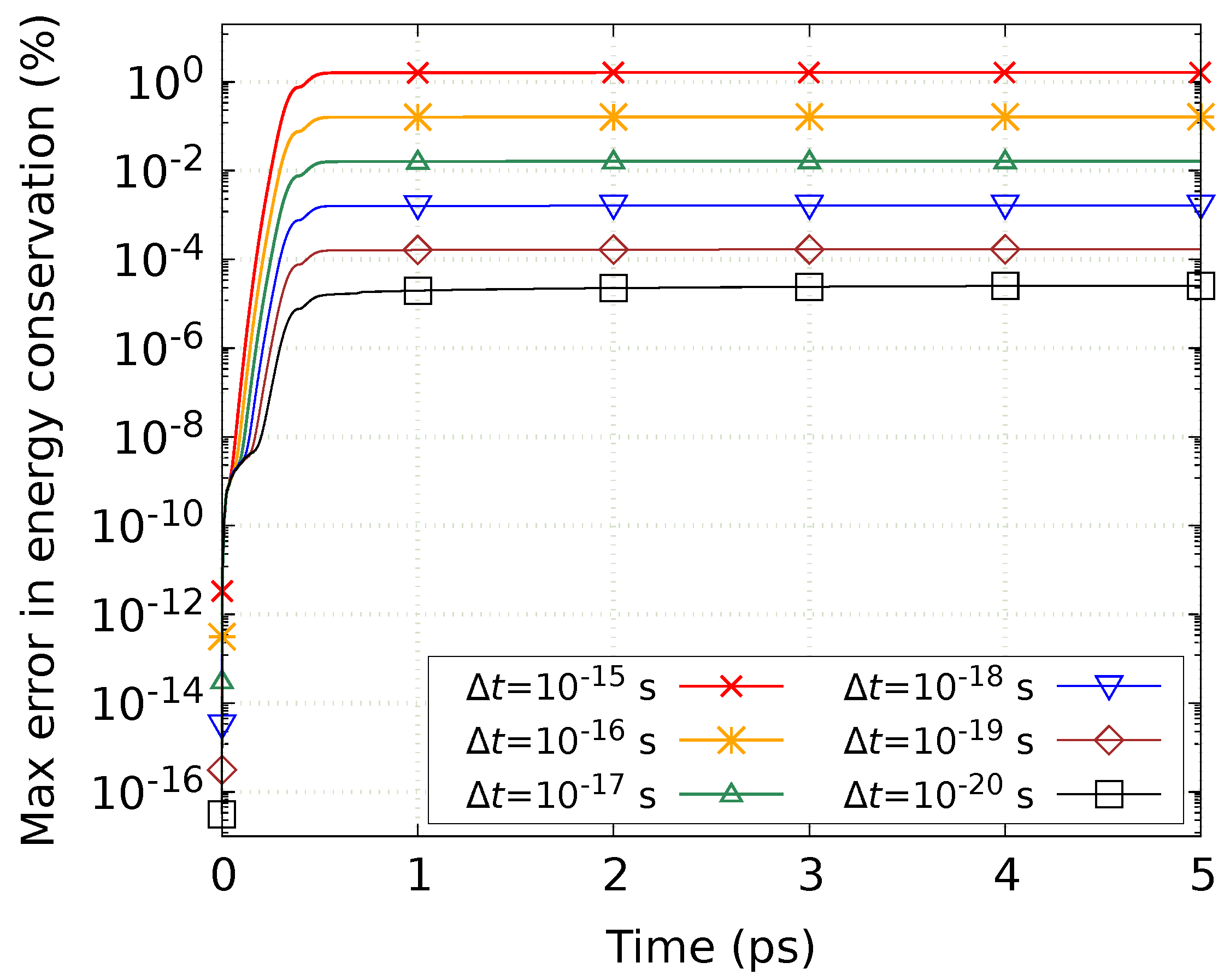
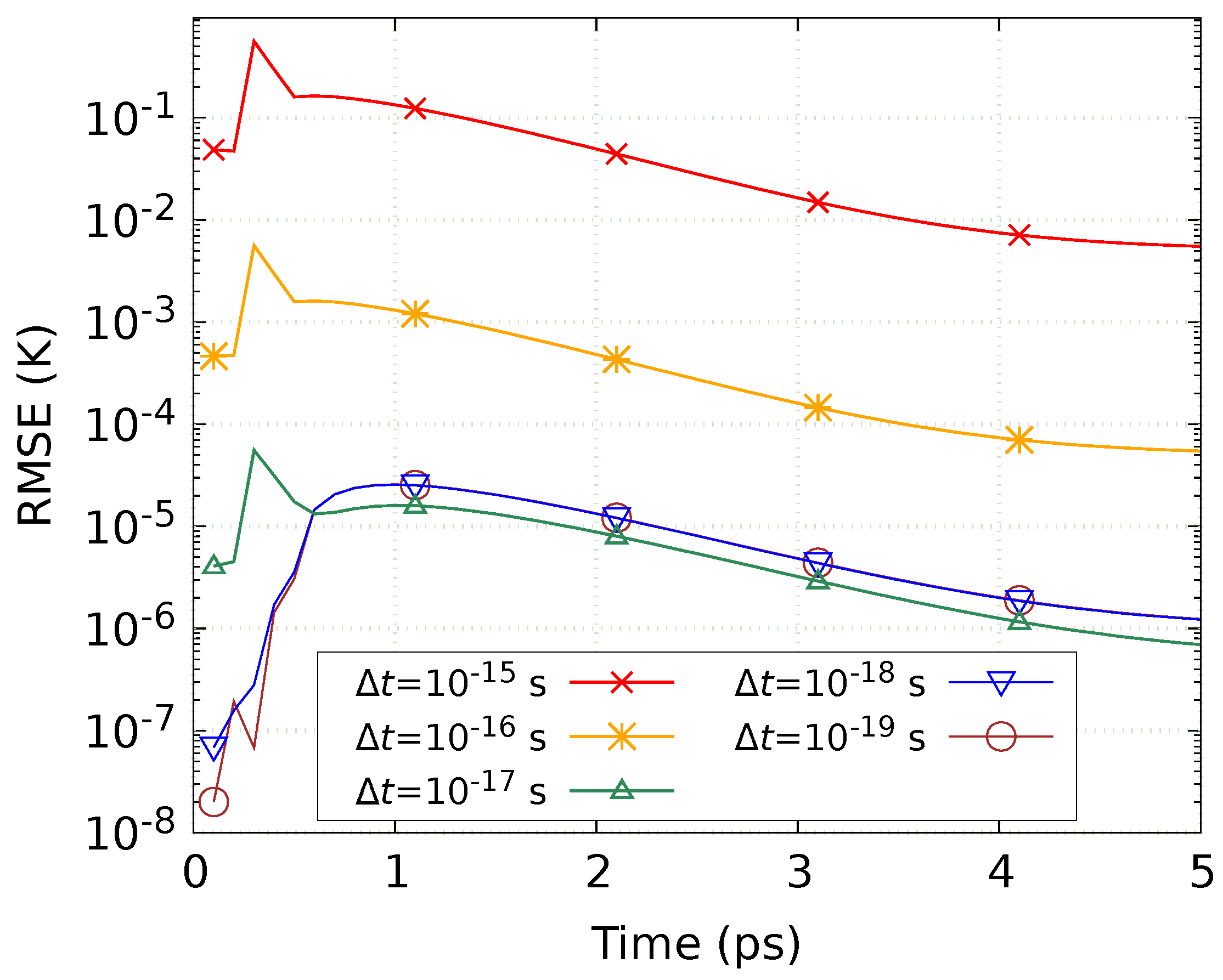
4. Calculation Example
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, Z.; Zhao, J.; Yin, J.; Li, H. Nonlinear Diffusion Equations; World Scientific: Singapore, 2001. [Google Scholar]
- McKane, A.; Waxman, D. Singular solutions of the diffusion equation of population genetics. J. Theor. Biol. 2007, 247, 849–858. [Google Scholar] [CrossRef]
- Bower, J.M.; Bolouri, H. Computational Modeling of Genetic and Biochemical Networks; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Aubert, G.; Kornprobst, P. Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations; Springer Science & Business Media: New York, NY, USA, 2006; Volume 147. [Google Scholar]
- Nagasawa, M. Schrödinger Equations and Diffusion Theory; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Bäuerle, D.W. Laser Processing and Chemistry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Liu, X.; Du, D.; Mourou, G. Laser ablation and micromachining with ultrashort laser pulses. Quantum Electron. IEEE J. 1997, 33, 1706–1716. [Google Scholar] [CrossRef]
- Chichkov, B.N.; Momma, C.; Nolte, S.; Von Alvensleben, F.; Tünnermann, A. Femtosecond, picosecond and nanosecond laser ablation of solids. Appl. Phys. A 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Gattass, R.R.; Mazur, E. Femtosecond laser micromachining in transparent materials. Nat. Photonics 2008, 2, 219–225. [Google Scholar] [CrossRef]
- Chou, S.Y.; Keimel, C.; Gu, J. Ultrafast and direct imprint of nanostructures in silicon. Nature 2002, 417, 835–837. [Google Scholar] [CrossRef] [PubMed]
- Le Harzic, R.; Dörr, D.; Sauer, D.; Stracke, F.; Zimmermann, H. Generation of high spatial frequency ripples on silicon under ultrashort laser pulses irradiation. Appl. Phys. Lett. 2011, 98, 211905. [Google Scholar] [CrossRef]
- Huang, P.H.; Lai, H.Y. Nucleation and propagation of dislocations during nanopore lattice mending by laser annealing: Modified continuum-atomistic modeling. Phys. Rev. B 2008, 77, 125408. [Google Scholar] [CrossRef]
- Stratakis, E.; Ranella, A.; Fotakis, C. Biomimetic micro/nanostructured functional surfaces for microfluidic and tissue engineering applications. Biomicrofluidics 2011, 5, 013411. [Google Scholar] [CrossRef]
- Mathis, A.; Courvoisier, F.; Froehly, L.; Furfaro, L.; Jacquot, M.; Lacourt, P.A.; Dudley, J.M. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Phys. Lett. 2012, 101, 071110. [Google Scholar] [CrossRef]
- Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 081102. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perel’Man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zh. Eksp. Teor. Fiz 1974, 66, 375–377. [Google Scholar]
- Van Driel, H.M. Kinetics of high-density plasmas generated in Si by 1.06-and 0.53-mkm picosecond laser pulses. Phys. Rev. B 1987, 35, 8166. [Google Scholar] [CrossRef]
- Ivanov, D.S.; Zhigilei, L.V. Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films. Phys. Rev. B 2003, 68, 064114. [Google Scholar] [CrossRef]
- Chen, J.K.; Tzou, D.Y.; Beraun, J.E. Numerical investigation of ultrashort laser damage in semiconductors. Int. J. Heat Mass Transf. 2005, 48, 501–509. [Google Scholar] [CrossRef]
- Isaacson, E.; Keller, H.B. Analysis of Numerical Methods; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Cebeci, T. Convective Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2002; Volume 1. [Google Scholar]
- Ivanov, D.; Lipp, V.; Veiko, V.; Yakovlev, E.; Rethfeld, B.; Garcia, M. Molecular dynamics study of the short laser pulse ablation: Quality and efficiency in production. Appl. Phys. A 2014, 117, 2133–2141. [Google Scholar] [CrossRef]
- Rämer, A.; Osmani, O.; Rethfeld, B. Laser damage in silicon: Energy absorption, relaxation, and transport. J. Appl. Phys. 2014, 116, 053508. [Google Scholar] [CrossRef]
- Lipp, V.P.; Rethfeld, B.; Garcia, M.E.; Ivanov, D.S. Atomistic-continuum modeling of short laser pulse melting of Si targets. Phys. Rev. B 2014, 90, 245306. [Google Scholar] [CrossRef]
- Rathore, R.; Singhal, H.; Chakera, J. Temporal evolution of photoinduced thermal strain in InSb probed by ultra-short laser produced Cu Kα x-rays. J. Appl. Phys. 2019, 126, 105706. [Google Scholar] [CrossRef]
- Young, J.F.; Van Driel, H. Ambipolar diffusion of high-density electrons and holes in Ge, Si, and GaAs: Many-body effects. Phys. Rev. B 1982, 26, 2147. [Google Scholar] [CrossRef]
- Lietoila, A.; Gibbons, J.F. Computer modeling of the temperature rise and carrier concentration induced in silicon by nanosecond laser pulses. J. Appl. Phys. 1982, 53, 3207–3213. [Google Scholar] [CrossRef]
- Sproul, A.B.; Green, M.A. Improved value for the silicon intrinsic carrier concentration from 275 to 375 K. J. Appl. Phys. 1991, 70, 846–854. [Google Scholar] [CrossRef]
- Wood, R.F.; Giles, G.E. Macroscopic theory of pulsed-laser annealing. I. Thermal transport and melting. Phys. Rev. B 1981, 23, 2923. [Google Scholar] [CrossRef]
- Agassi, D. Phenomenological model for pisosecond-pulse laser annealing of semiconductors. J. Appl. Phys. 1984, 55, 4376–4383. [Google Scholar] [CrossRef]
- Thurmond, C.D. The standard thermodynamic functions for the formation of electrons and holes in Ge, Si, GaAs, and GaP. J. Electrochem. Soc. 1975, 122, 1133–1141. [Google Scholar] [CrossRef]
- Vankemmel, R.; Schoenmaker, W.; De Meyer, K. A unified wide temperature range model for the energy gap, the effective carrier mass and intrinsic concentration in silicon. Solid-State Electron. 1993, 36, 1379–1384. [Google Scholar] [CrossRef]
- Jellison, G.E., Jr.; Modine, F.A. Optical absorption of silicon between 1.6 and 4.7 eV at elevated temperatures. Appl. Phys. Lett. 1982, 41, 180–182. [Google Scholar] [CrossRef]
- Jellison, G.E., Jr.; Modine, F.A. Optical functions of silicon between 1.7 and 4.7 eV at elevated temperatures. Phys. Rev. B 1983, 27, 7466. [Google Scholar] [CrossRef]
- Dziewior, J.; Schmid, W. Auger coefficients for highly doped and highly excited silicon. Appl. Phys. Lett. 1977, 31, 346–348. [Google Scholar] [CrossRef]
- Geist, J.; Gladden, W.K. Transition rate for impact ionization in the approximation of a parabolic band structure. Phys. Rev. B 1983, 27, 4833. [Google Scholar] [CrossRef]
- Meyer, J.R.; Kruer, M.R.; Bartoli, F.J. Optical heating in semiconductors: Laser damage in Ge, Si, InSb, and GaAs. J. Appl. Phys. 1980, 51, 5513–5522. [Google Scholar] [CrossRef]
- Ioffe Physical-Technical Institute. Electronic Archive “New Semiconductor Materials. Characteristics and Properties”; Silicon Properties. Available online: http://www.ioffe.rssi.ru/SVA/NSM/Semicond/Si/ (accessed on 10 November 2019).
- Free Software Foundation. The GNU Scientific Library (gsl-1.15). Available online: https://www.gnu.org/software/gsl (accessed on 10 November 2019).
- Thomas, L. Elliptic Problems in Linear Differential Equations over a Network: Watson Scientific Computing Laboratory; Columbia Univ.: Columbia, NY, USA, 1949. [Google Scholar]
- Bonse, J.; Brzezinka, K.W.; Meixner, A.J. Modifying single-crystalline silicon by femtosecond laser pulses: An analysis by micro Raman spectroscopy, scanning laser microscopy and atomic force microscopy. Appl. Surf. Sci. 2004, 221, 215–230. [Google Scholar] [CrossRef]
- Lipp, V.P. Atomistic-Continuum Modeling of Ultrafast Laser-Induced Melting of Silicon Targets. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2015. [Google Scholar]
- Wang, T.Y.; Lee, Y.M.; Chen, C.C.P. 3D thermal-ADI: An efficient chip-level transient thermal simulator. In Proceedings of the 2003 International Symposium on Physical Design, Monterey, CA, USA, 6–9 April 2003; ACM: New York, NY, USA, 2003; pp. 10–17. [Google Scholar]
- Peaceman, D.W.; Rachford, H.H., Jr. The numerical solution of parabolic and elliptic differential equations. J. Soc. Ind. Appl. Math. 1955, 3, 28–41. [Google Scholar] [CrossRef]
| Parameter Name | Value | Citation |
|---|---|---|
| Initial carrier density | [29] | |
| Initial lattice and carrier temperature | 300 K | |
| Lattice specific heat | ( in K) | [30] |
| Lattice thermal conductivity | , W/(mK) ( in K) | [30] |
| Carrier thermal conductivity | , eV/(s m K) | [31] |
| Indirect band gap | if and 0 otherwise, eV ( in K, n in m) | [32] [33] |
| Interband absorption (taken from 694 laser) | , m | [34] |
| Two-photon absorption | cm/GW | [25] |
| Reflectivity | ( in K) | [35] |
| Auger recombination coefficient | , m/s | [36] |
| Impact ionization coefficient | , s | [37] |
| Free-carrier absorption cross section | , m ( in K) | [38] |
| Electron-phonon relaxation time | , s (n in m) | [31] |
| Electron effective mass | [39] | |
| Hole effective mass | [39] | |
| Mobility of electrons (taken at 1000 K) | m2/V s | [38] |
| Mobility of holes (taken at 1000 K) | m2/V s | [38] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lipp, V.; Rethfeld, B.; Garcia, M.; Ivanov, D. Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon. Appl. Sci. 2020, 10, 1853. https://doi.org/10.3390/app10051853
Lipp V, Rethfeld B, Garcia M, Ivanov D. Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon. Applied Sciences. 2020; 10(5):1853. https://doi.org/10.3390/app10051853
Chicago/Turabian StyleLipp, Vladimir, Baerbel Rethfeld, Martin Garcia, and Dmitry Ivanov. 2020. "Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon" Applied Sciences 10, no. 5: 1853. https://doi.org/10.3390/app10051853
APA StyleLipp, V., Rethfeld, B., Garcia, M., & Ivanov, D. (2020). Solving a System of Differential Equations Containing a Diffusion Equation with Nonlinear Terms on the Example of Laser Heating in Silicon. Applied Sciences, 10(5), 1853. https://doi.org/10.3390/app10051853





