Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls
Abstract
1. Introduction
2. The Sound Transmission Loss Curve
3. Double Panel Air Cavity, Sandwich and Composite Structures
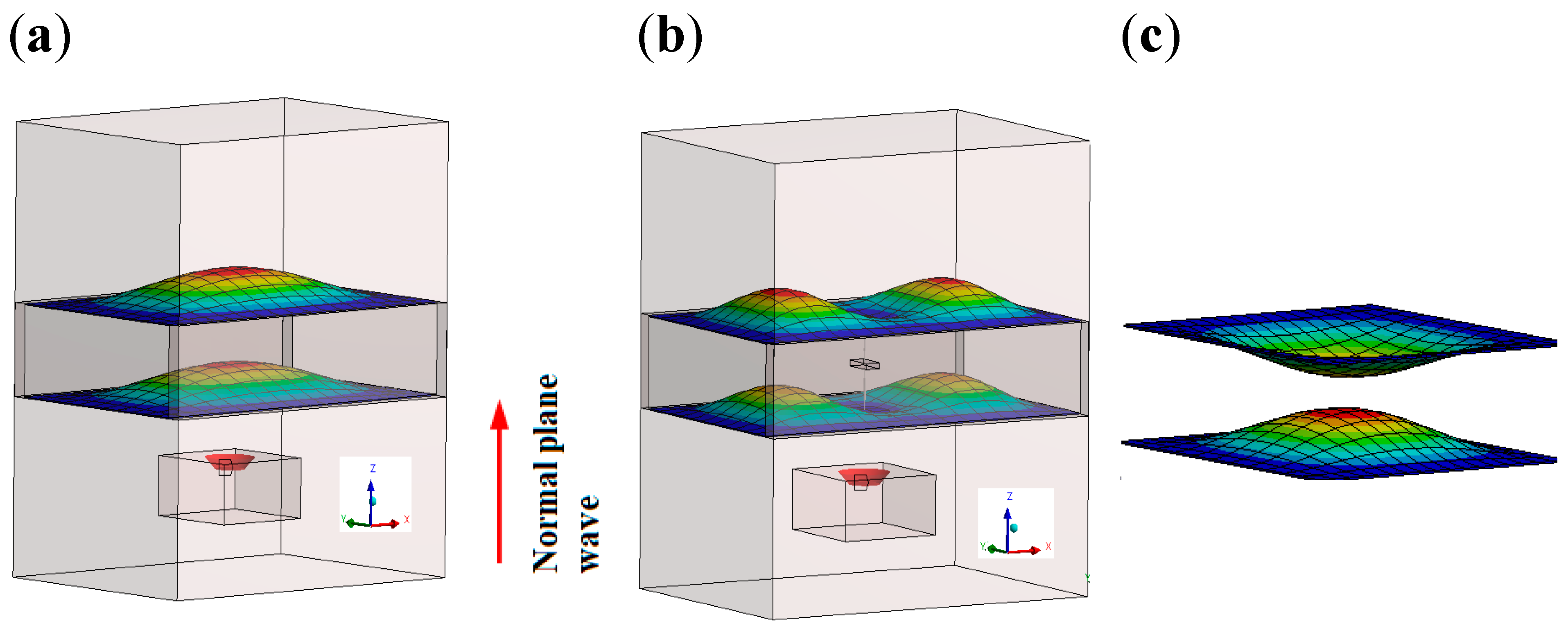
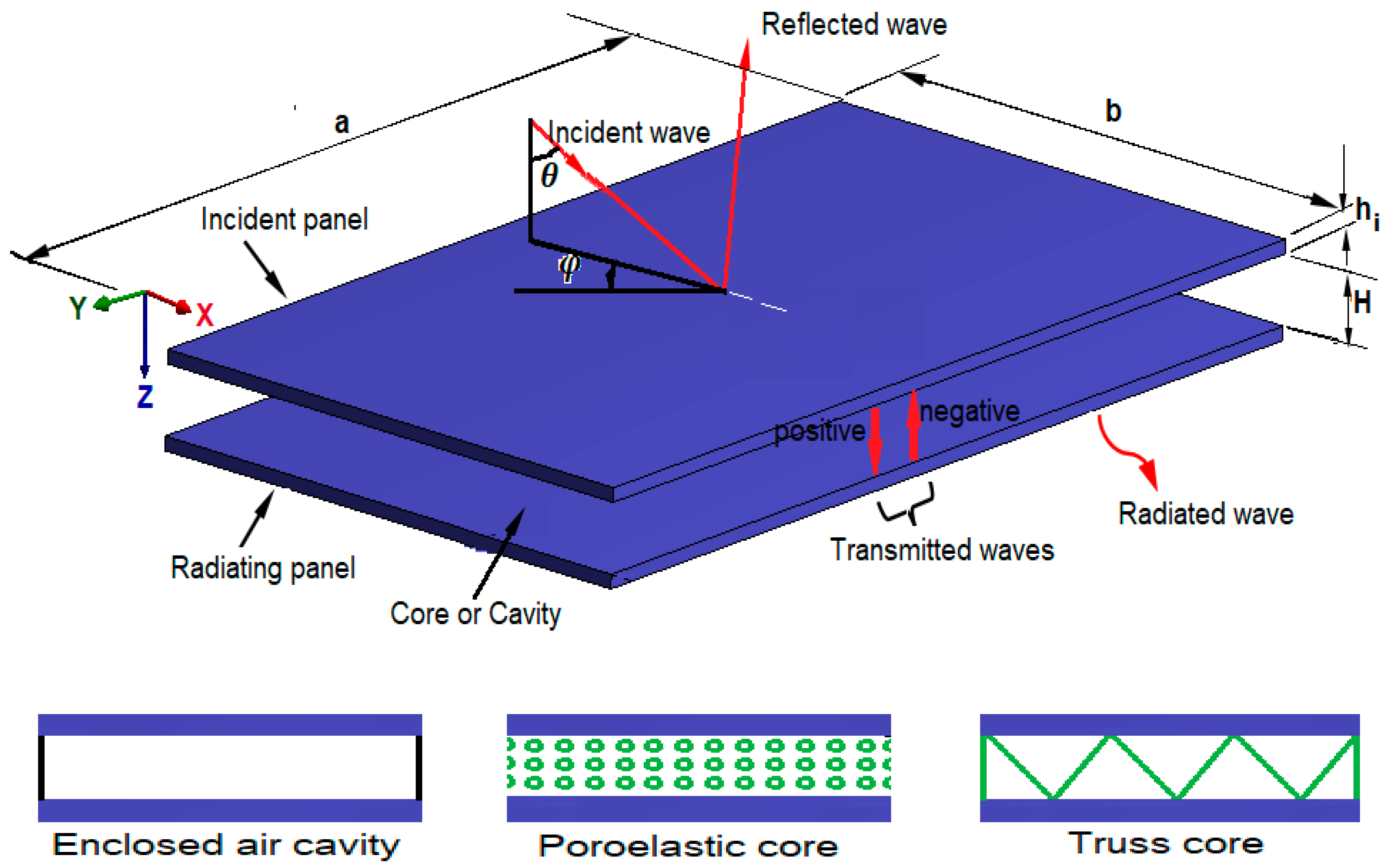
3.1. Double Panel Air Cavity Structures
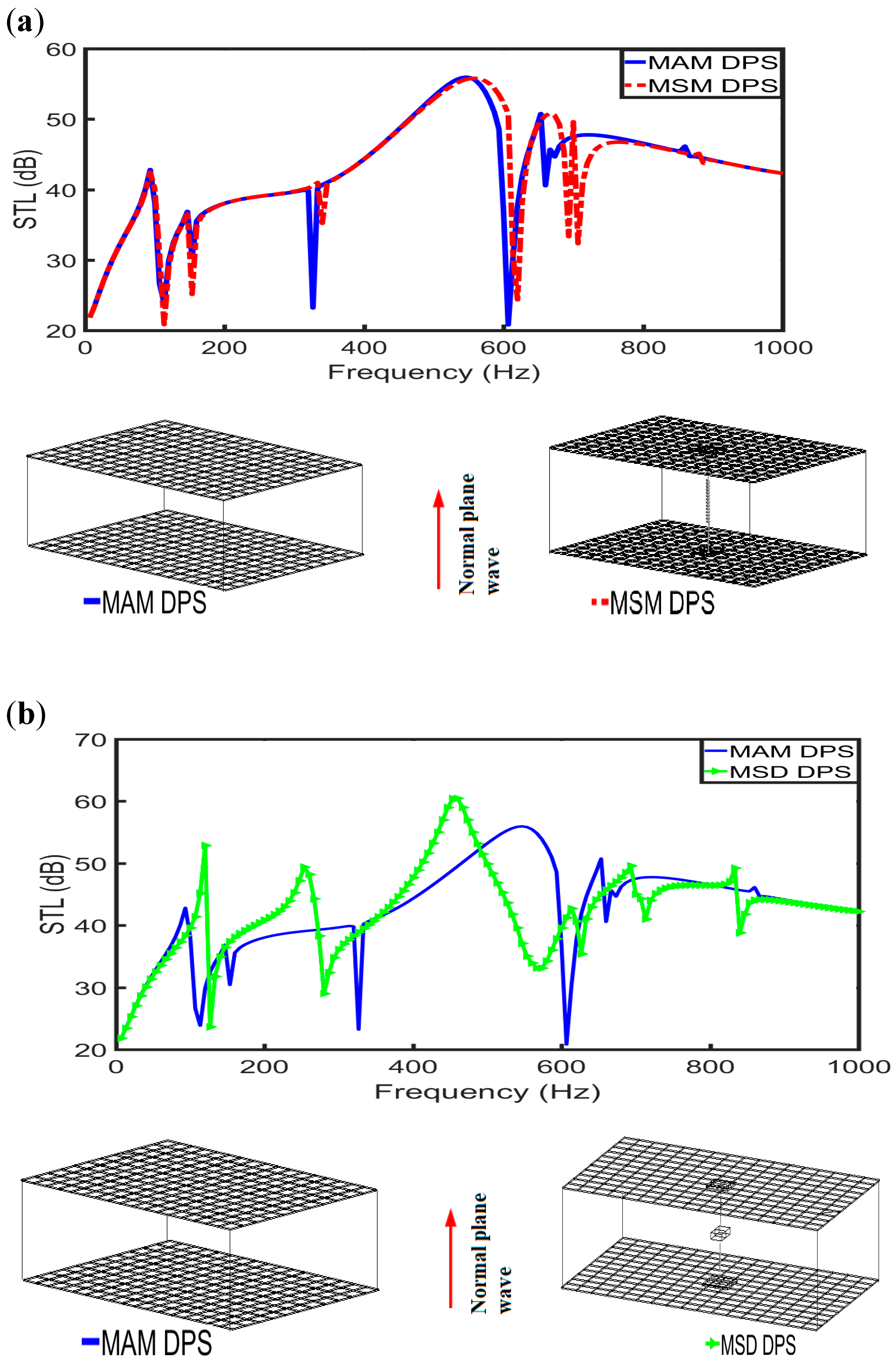
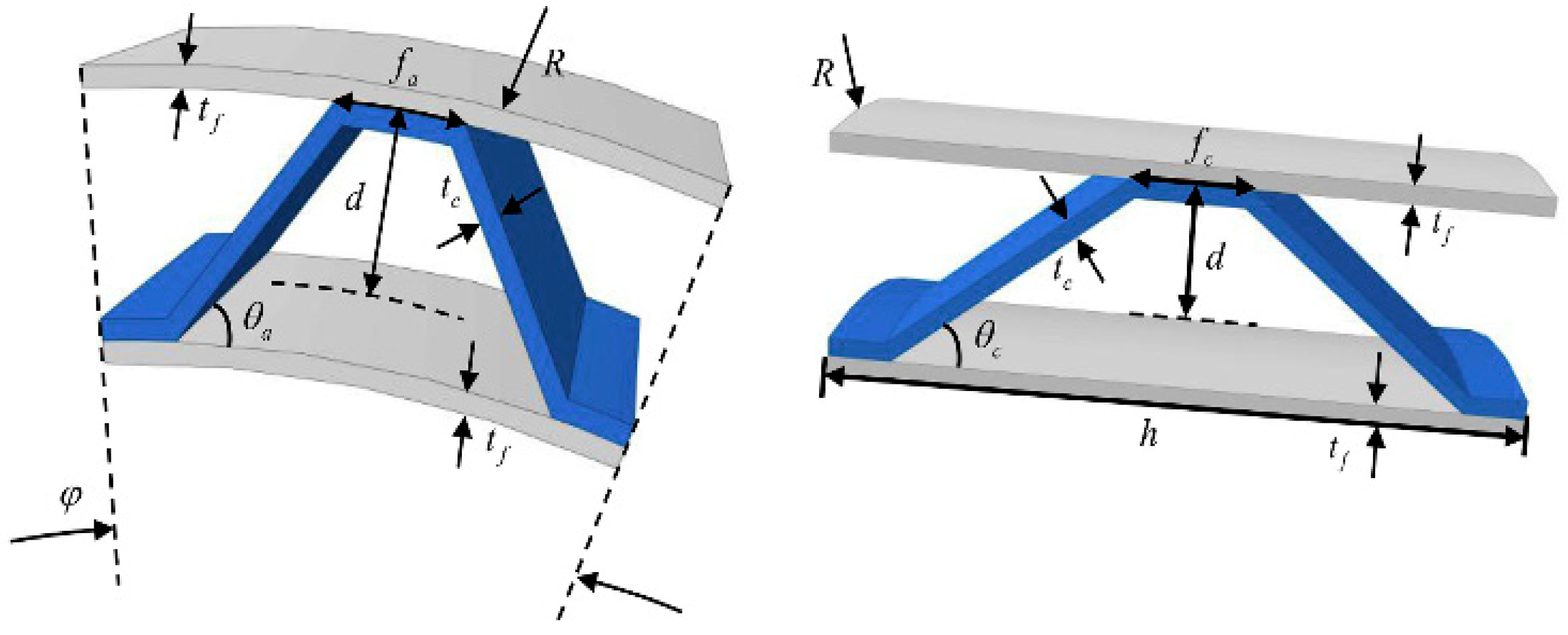
3.2. Sandwich Core Support Structures
3.3. Sandwich Composite Structures
3.3.1. Composite Flat Panels
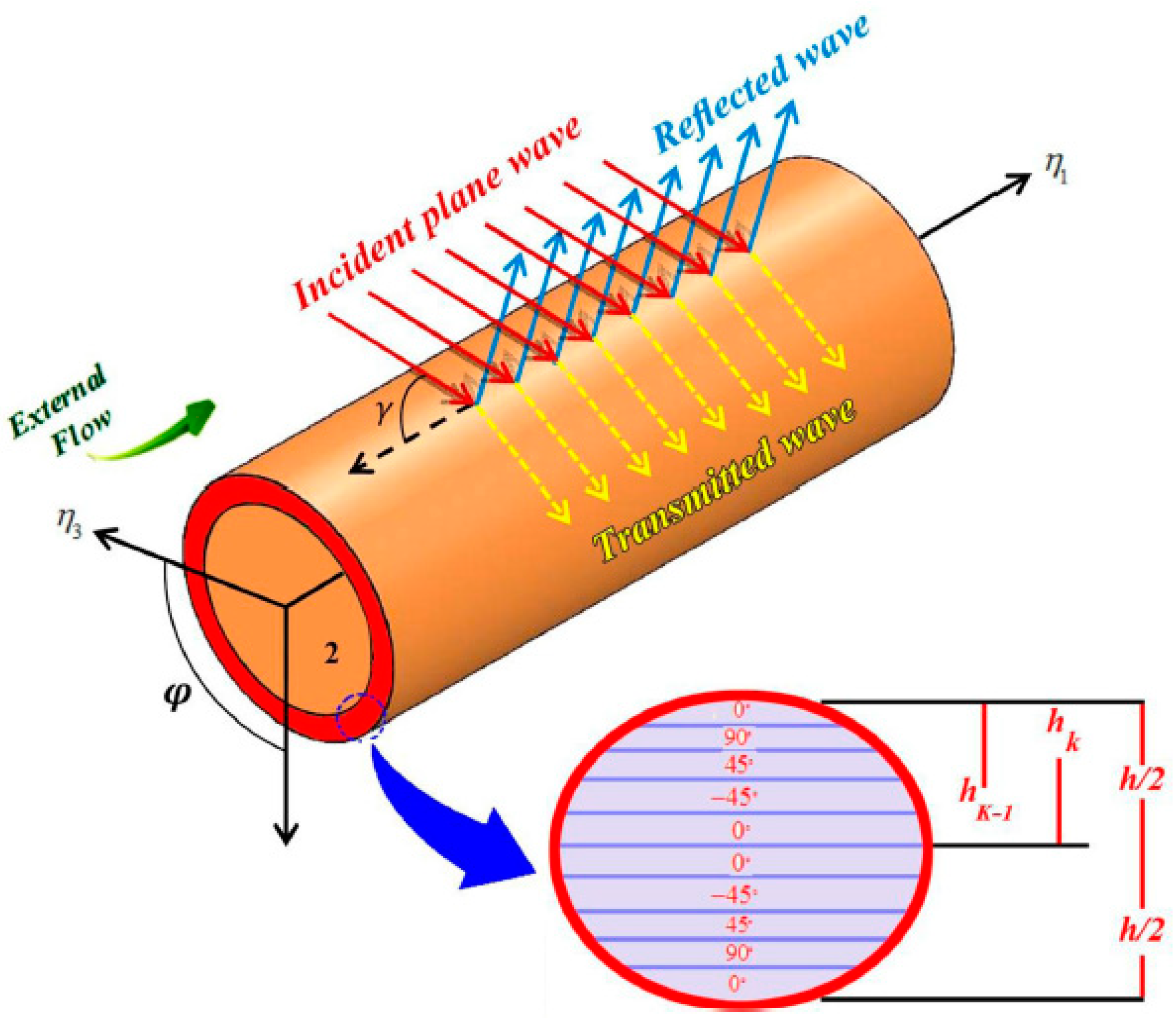
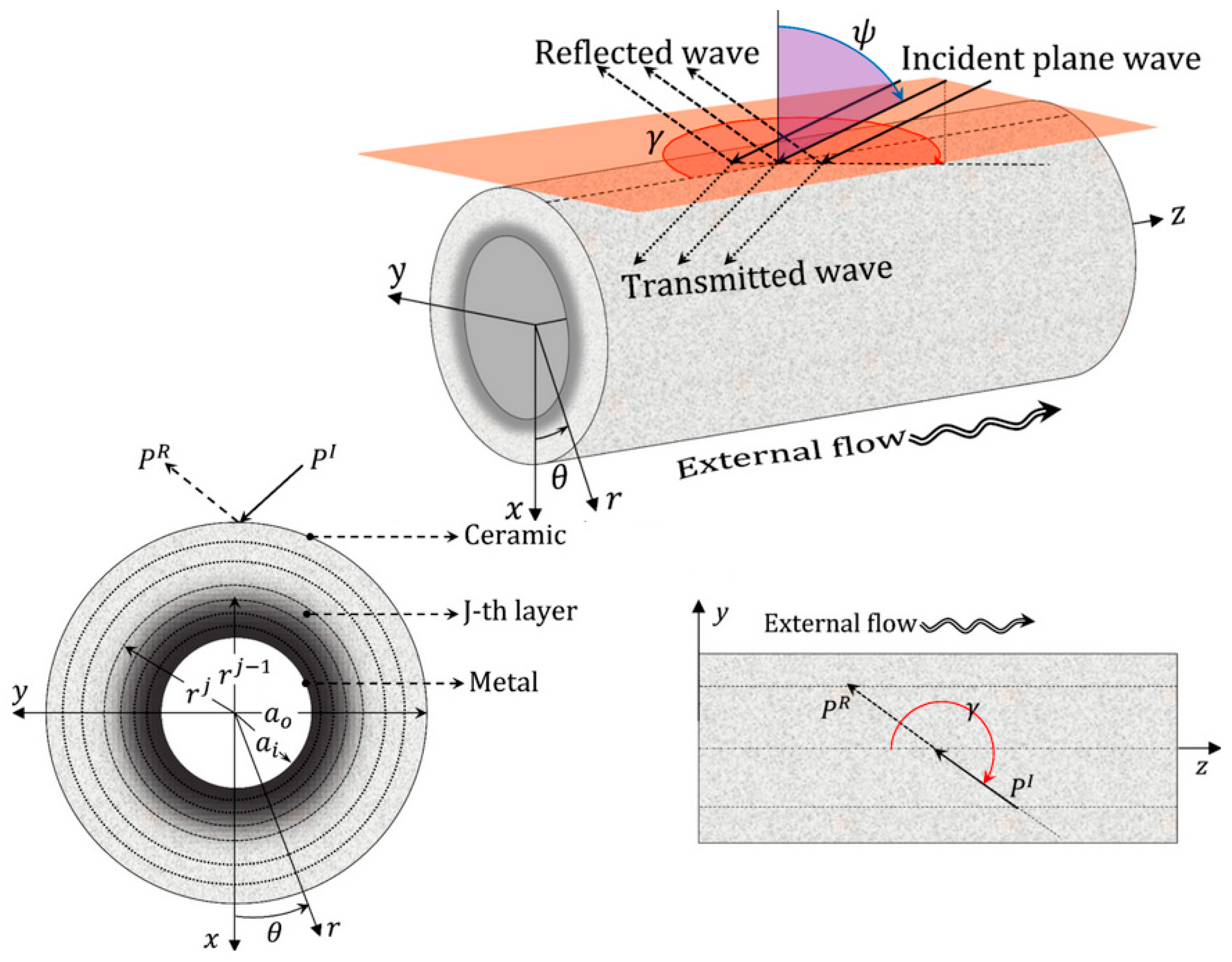
3.3.2. Composite Cylindrical and Curved Shells
3.4. Functionally Graded Materials of Sandwich Structures
4. Methodologies and Models for Obtaining Sound Transmission Loss of Double Panel Walls
4.1. Models and Methods for Sound Transmission Loss Calculation
4.1.1. Statistical Energy Analysis
4.1.2. Transfer Matrix Method
4.1.3. Discrete Laminate Model
4.1.4. Wave Spectral Finite Element Model
4.1.5. Wave Finite Element Method
4.1.6. Biot’s Theory and Equivalent Fluid Method
4.1.7. Hybridization Models
4.2. Numerical Methods and Tools for Simulating STL
4.3. Numerical Vs. Analytical Verification
4.4. Numerical Vs. Experimental Validation
4.5. Analytical Vs. Experimental Validation
5. Parameter Effects and Optimization Strategy on the Sound Transmission Loss of Double Panel Walls
5.1. Influence of Various Parameters on the Sound Transmission Loss of Double Wall Structures
5.2. Optimization of Sound Transmission Loss of Double Panel Structures
- finding the design vector
- that minimizes the objective function
- subject to: constraint 1 (inequality), constraint 2 (equality)
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cherif, R.; Wareing, A.; Atalla, N. Evaluation of a hybrid TMM-SEA method for prediction of sound transmission loss through mechanically coupled aircraft double-walls. Appl. Acoust. 2017, 117, 132–140. [Google Scholar] [CrossRef]
- Omrani, A.; Tawfiq, I. Vibro-acoustic analysis of micro-perforated sandwich structure used in space craft industry. Mech. Syst. Signal Process. 2011, 25, 657–666. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, R.; Li, Y.; Li, M.; Wen, Z.; Xiao, X. Study on sound transmission loss of windows on high speed trains. J. Mech. Eng. 2018, 54, 212–221. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, W.; Zhou, G.; Wang, C. Analysis and parametric optimization of a novel sandwich panel with double-V auxetic structure core under air blast loading. Int. J. Mech. Sci. 2018, 142, 245–254. [Google Scholar] [CrossRef]
- Lai, J.C.; Burgess, M. Application of the sound intensity technique to measurement of field sound transmission loss. Appl. Acoust. 1991, 34, 77–87. [Google Scholar] [CrossRef]
- Chen, K.T.; Chiang, K.T.; Huang, S.M.; Tsai, B.C. Active vibration control for the improvement of sound transmission loss through a square plate. Build Acoust. 2002, 9, 289–301. [Google Scholar] [CrossRef]
- Marulo, F.; Polito, T. Probabilistic analysis and experimental results of sound transmission loss of composite panels. Polym. Eng. Sci. 2017, 57, 722–730. [Google Scholar] [CrossRef]
- Oliazadeh, P.; Farshidianfar, A.; Crocker, M.J. Study of sound transmission through single-and double-walled plates with absorbing material: Experimental and analytical investigation. Appl. Acoust. 2019, 145, 7–24. [Google Scholar] [CrossRef]
- Koutsawa, Y.; Azoti, W.L.; Belouettar, S.; Martin, R.; Barkanov, E. Loss behavior of viscoelastic sandwich structures: A statistical-continuum multi-scale approach. Compos. Struct. 2012, 94, 1391–1397. [Google Scholar] [CrossRef]
- Wareing, R.R.; Davy, J.L.; Pearse, J.R. Variations in measured sound transmission loss due to sample size and construction parameters. Appl. Acoust. 2015, 89, 166–177. [Google Scholar] [CrossRef]
- Mejdi, A.; Legault, J.; Atalla, N. Transmission loss of periodically stiffened laminate composite panels: Shear deformation and in-plane interaction effects. J. Acoust. Soc. Am. 2012, 131, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, S.; Huang, Q. Low-frequency sound radiation of infinite orthogonally rib-stiffened sandwich structure with periodic subwavelength arrays of shunted piezoelectric patches. Compos. Struct. 2018, 187, 144–156. [Google Scholar] [CrossRef]
- Xin, F.X.; Lu, T.J. Analytical and experimental investigation on transmission loss of clamped double panels: Implication of boundary effects. J. Acoust. Soc. Am. 2009, 125, 1506–1517. [Google Scholar] [CrossRef] [PubMed]
- Isaac, C.W. Crushing response of circular thin-walled tube with non-propagating crack subjected to dynamic oblique impact loading. Int. J. Protect. Struct. 2020, 11, 41–68. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; Wiley-VCH: New York, NY, USA, 1999. [Google Scholar]
- Xin, F.X.; Lu, T.J.; Chen, C.Q. External mean flow influence on noise transmission through double-leaf aeroelastic plates. AIAA J. 2009, 47, 1939–1951. [Google Scholar] [CrossRef]
- Du, S.; An, F.; Liu, B. On the sound transmission loss of finite plates with constrained viscoelastic layer. Appl. Acoust. 2019, 149, 32–38. [Google Scholar] [CrossRef]
- Liu, Y. Sound transmission through triple-panel structures lined with poroelastic materials. J. Sound Vib. 2015, 339, 376–395. [Google Scholar] [CrossRef]
- Kim, Y.J.; Han, J.H. Identification of acoustic characteristics of honeycomb sandwich composite panels using hybrid analytical/finite element method. J. Vib. Acoust. 2013, 135, 011006. [Google Scholar] [CrossRef]
- Thamburaj, P.; Sun, J.Q. Effect of material anisotropy on the sound and vibration transmission loss of sandwich aircraft structures. J. Sandw. Struct. Mater. 1999, 1, 76–92. [Google Scholar] [CrossRef]
- Yang, Z.; Dai, H.M.; Chan, N.H.; Ma, G.C.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 Hz regime. Appl. Phys. Lett. 2010, 96, 041906. [Google Scholar] [CrossRef]
- Idrisi, K.; Johnson, M.E.; Toso, A.; Carneal, J.P. Increase in transmission loss of a double panel system by addition of mass inclusions to a poro-elastic layer: A comparison between theory and experiment. J. Sound Vib. 2009, 323, 51–66. [Google Scholar] [CrossRef]
- Varanasi, S.; Bolton, J.S.; Siegmund, T.H.; Cipra, R.J. The low frequency performance of metamaterial barriers based on cellular structures. Appl. Acoust. 2013, 74, 485–495. [Google Scholar] [CrossRef]
- Li, J.; Li, S. Sound transmission through metamaterial-based double-panel structures with poroelastic cores. Acta Acust. Unit. Acust. 2017, 103, 869–884. [Google Scholar] [CrossRef]
- Sui, N.; Yan, X.; Huang, T.Y.; Xu, J.; Yuan, F.G.; Jing, Y. A lightweight yet sound-proof honeycomb acoustic metamaterial. Appl. Phys. Lett. 2015, 106, 171905. [Google Scholar] [CrossRef]
- Blaise, A.; Lesueur, C.; Gotteland, M.; Barbe, M. On sound transmission into an orthotropic infinite shell: Comparison with Koval’s results and understanding of phenomena. J. Sound Vib. 1991, 150, 233–243. [Google Scholar] [CrossRef]
- Manconi, E.; Mace, B.R. Wave characterization of cylindrical and curved panels using a finite element method. J. Acoust. Soc. Am. 2009, 125, 154–163. [Google Scholar] [CrossRef]
- Lu, T.; Xin, F. Vibroacoustics of Uniform Structures in Mean Flow. In Vibro-Acoustics of Lightweight Sandwich Structures; Springer: Berlin/Heidelberg, Germany, 2014; pp. 87–157. [Google Scholar]
- Talebitooti, R.; Ahmadi, R.; Shojaeefard, M.H. Three-Dimensional wave propagation on orthotropic cylindrical shells with arbitrary thickness considering state space method. Compos. Struct. 2015, 132, 239–254. [Google Scholar] [CrossRef]
- Talebitooti, R.; Daneshjou, K.; Tarkashvand, A. Incorporating the Havriliak–Negami model in wave propagation through polymeric viscoelastic core in a laminated sandwich cylinder. Thin Wall. Struct. 2019, 134, 460–474. [Google Scholar] [CrossRef]
- Wang, D.W.; Ma, L.; Wen, Z.H. Sound transmission through a sandwich structure with two-layered pyramidal core and cavity absorption. J. Sound Vib. 2019, 459, 114853. [Google Scholar] [CrossRef]
- Larbi, W.; Deü, J.F.; Ohayon, R. Vibroacoustic analysis of double-wall sandwich panels with viscoelastic core. Comput. Struct. 2016, 174, 92–103. [Google Scholar] [CrossRef]
- Daneshjou, K.; Talebitooti, R.; Tarkashvand, A. An exact solution of three-dimensional elasticity for sound transmission loss through FG cylinder in presence of subsonic external flow. Int. J. Mech. Sci. 2017, 120, 105–119. [Google Scholar] [CrossRef]
- Talebitooti, R.; Gohari, H.D.; Zarastvand, M.R. Multi objective optimization of sound transmission across laminated composite cylindrical shell lined with porous core investigating Non-Dominated Sorting Genetic Algorithm. Aerosp. Sci. Technol. 2017, 69, 269–280. [Google Scholar] [CrossRef]
- Li, D.; Vipperman, J.S. On the noise transmission and control for a cylindrical chamber core composite structure. J. Sound Vib. 2005, 288, 235–254. [Google Scholar] [CrossRef]
- Zhou, J.; Bhaskar, A.; Zhang, X. The effect of external mean flow on sound transmission through double-walled cylindrical shells lined with poroelastic material. J. Sound Vib. 2014, 333, 1972–1990. [Google Scholar] [CrossRef]
- Lee, C.M.; Xu, Y. A modified transfer matrix method for prediction of transmission loss of multilayer acoustic materials. J. Sound Vib. 2009, 326, 290–301. [Google Scholar] [CrossRef]
- Cai, J.; Fu, Q.; Long, M.; Liao, G.; Xu, Z. The sound insulation property of composite from waste printed circuit board and unsaturated polyester. Compos. Sci. Technol. 2017, 145, 132–137. [Google Scholar] [CrossRef]
- Sabet, S.M.; Ohadi, A. Experimental and theoretical investigation of sound transmission loss for polycarbonate, poly (methyl methacrylate), and glass. J. Appl. Polym. Sci. 2016, 133. [Google Scholar] [CrossRef]
- Miskinis, K.; Dikavicius, V.; Buska, A.; Banionis, K. Influence of EPS, mineral wool and plaster layers on sound and thermal insulation of a wall: A case study. Appl. Acoust. 2018, 137, 62–68. [Google Scholar] [CrossRef]
- Liu, Z.; Rumpler, R.; Feng, L. Broadband locally resonant metamaterial sandwich plate for improved noise insulation in the coincidence region. Compos. Struct. 2018, 200, 165–172. [Google Scholar] [CrossRef]
- Wang, X.; You, F.; Zhang, F.S.; Li, J.; Guo, S. Experimental and theoretic studies on sound transmission loss of laminated mica-filled poly (vinyl chloride) composites. J. Appl. Polym. Sci. 2011, 122, 1427–1433. [Google Scholar] [CrossRef]
- Lu, T.; Xin, F. Sound Propagation in Rib-Stiffened Sandwich Structures with Cavity Absorption. In Vibro-Acoustics of Lightweight Sandwich Structures; Springer: Berlin/Heidelberg, Germany, 2014; pp. 289–339. [Google Scholar]
- Shen, C.; Xin, F.; Lu, T. Transmission loss of orthogonally stiffened laminated composite plates. J. Mech. Sci. Technol. 2015, 29, 59–66. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, Y. Sound insulation analysis and optimization of anti-symmetrical carbon fiber reinforced polymer composite materials. Appl. Acoust. 2017, 120, 34–44. [Google Scholar] [CrossRef]
- Oliazadeh, P.; Farshidianfar, A. Analysis of different techniques to improve sound transmission loss in cylindrical shells. J. Sound Vib. 2017, 389, 276–291. [Google Scholar] [CrossRef]
- Li, Q.; Yang, D. Vibration and sound transmission performance of sandwich panels with uniform and gradient auxetic double arrowhead honeycomb cores. Shock Vib. 2019. [Google Scholar] [CrossRef]
- Yang, J.S.; Ma, L.; Schröder, K.U.; Chen, Y.L.; Li, S.; Wu, L.Z.; Schmidt, R. Experimental and numerical study on the modal characteristics of hybrid carbon fiber composite foam filled corrugated sandwich cylindrical panels. Polym. Test 2018, 68, 8–18. [Google Scholar] [CrossRef]
- Mao, Q.; Shen, H. Improvement on sound transmission loss through a double-plate structure by connected with a mass–spring–damper system. Adv. Mech. Eng. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Sadri, M.; Younesian, D. Vibroacoustic analysis of a sandwich panel coupled with an enclosure cavity. Compos. Struct. 2016, 146, 159–175. [Google Scholar] [CrossRef]
- Shen, C.; Xin, F.X.; Lu, T.J. Theoretical model for sound transmission through finite sandwich structures with corrugated core. Int. J. Nonlinear Mech. 2012, 47, 1066–1072. [Google Scholar] [CrossRef]
- Meng, H.; Galland, M.A.; Ichchou, M.; Bareille, O.; Xin, F.X.; Lu, T.J. Small perforations in corrugated sandwich panel significantly enhance low frequency sound absorption and transmission loss. Compos. Struct. 2017, 182, 1–11. [Google Scholar] [CrossRef]
- Kumar, S.; Renji, K. Estimation of strains in composite honeycomb sandwich panels subjected to low frequency diffused acoustic field. J. Sound Vib. 2019, 449, 84–97. [Google Scholar] [CrossRef]
- Tang, Y.; He, W.; Xin, F.; Lu, T.J. Nonlinear sound absorption of ultralight hybrid-cored sandwich panels. Mech. Syst. Signal Process. 2020, 135, 106428. [Google Scholar] [CrossRef]
- Obeid, H.H.; NadhimMohammed, H. Investigation of sound transmission loss through sandwich panel with foam core. J. Univ. Babylon 2018, 26, 101–116. [Google Scholar] [CrossRef][Green Version]
- Petrone, G.; D’Alessandro, V.; Franco, F.; De Rosa, S. Numerical and experimental investigations on the acoustic power radiated by aluminium foam sandwich panels. Compos. Struct. 2014, 118, 170–177. [Google Scholar] [CrossRef]
- Tang, Y.; Xin, F.; Lu, T.J. Sound absorption of micro-perforated sandwich panel with honeycomb-corrugation hybrid core at high temperatures. Compos. Struct. 2019, 226, 111285. [Google Scholar] [CrossRef]
- Wang, D.W.; Ma, L. Sound transmission through composite sandwich plate with pyramidal truss cores. Compos. Struct. 2017, 164, 104–117. [Google Scholar] [CrossRef]
- Orrenius, U.; Wareing, A.; Kumar, S. Prediction and Control of Sound Transmission through Honeycomb Sandwich Panels for Aircraft Fuselage and Train Floors. In Proceedings of the 17th International Congress on Sound and Vibration, Cairo, Egypt, 5–9 October 2010; pp. 117–124. [Google Scholar]
- Arunkumar, M.P.; Jagadeesh, M.; Pitchaimani, J.; Gangadharan, K.V.; Babu, M.L. Sound radiation and transmission loss characteristics of a honeycomb sandwich panel with composite facings: Effect of inherent material damping. J. Sound Vib. 2016, 383, 221–232. [Google Scholar] [CrossRef]
- Radestock, M.; Haase, T.; Monner, H.P. Experimental Transmission Loss Investigation of Sandwich Panels with Different Honeycomb Core Geometries (16.09). In Proceedings of the International Congress and Exposition on Noise Control Engineering 2019, InterNoise19. Institute of Noise Control Engineering, Madrid, Spain, 17–19 June 2019. [Google Scholar]
- Yang, Y.; Li, B.; Chen, Z.; Sui, N.; Chen, Z.; Saeed, M.U.; Li, Y.; Fu, R.; Wu, C.; Jing, Y. Acoustic properties of glass fiber assembly-filled honeycomb sandwich panels. Compos. Part B Eng. 2016, 96, 281–286. [Google Scholar] [CrossRef]
- Wen, Z.H.; Wang, D.W.; Ma, L. Sound transmission loss of sandwich panel with closed octahedral core. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Fu, T.; Chen, Z.; Yu, H.; Zhu, X.; Zhao, Y. Sound transmission loss behavior of sandwich panel with different truss cores under external mean airflow. Aerosp. Sci. Technol. 2019, 86, 714–723. [Google Scholar] [CrossRef]
- Wang, D.W.; Ma, L.; Wang, X.T.; Qi, G. Sound transmission loss of sandwich plate with pyramidal truss cores. J. Sandw. Struct. Mater. 2018. [Google Scholar] [CrossRef]
- Thamburaj, P.; Sun, J.Q. Optimization of anisotropic sandwich beams for higher sound transmission loss. J. Sound Vib. 2002, 254, 23–36. [Google Scholar] [CrossRef]
- Errico, F.; Ichchou, M.; Franco, F.; De Rosa, S.; Bareille, O.; Droz, C. Schemes for the sound transmission of flat, curved and axisymmetric structures excited by aerodynamic and acoustic sources. J. Sound Vib. 2019, 456, 221–238. [Google Scholar] [CrossRef]
- Daneshjou, K.; Nouri, A.; Talebitooti, R. Analytical model of sound transmission through laminated composite cylindrical shells considering transverse shear deformation. Appl. Math. Mech. 2008, 29, 1165–1177. [Google Scholar] [CrossRef]
- Talebitooti, R.; Zarastvand, M.R.; Gheibi, M.R. Acoustic transmission through laminated composite cylindrical shell employing third order shear deformation theory in the presence of subsonic flow. Compos. Struct. 2016, 157, 95–110. [Google Scholar] [CrossRef]
- Arunkumar, M.P.; Pitchaimani, J.; Gangadharan, K.V.; Leninbabu, M.C. Vibro-acoustic response and sound transmission loss characteristics of truss core sandwich panel filled with foam. Aerosp. Sci. Technol. 2018, 78, 1–11. [Google Scholar] [CrossRef]
- Yuan, C.; Bergsma, O.; Beukers, A. Sound transmission loss prediction of the composite fuselage with different methods. Appl. Compos. Mater. 2012, 19, 865–883. [Google Scholar] [CrossRef]
- Li, X.; Yu, K.; Zhao, R.; Han, J.; Song, H. Sound transmission loss of composite and sandwich panels in thermal environment. Compos. Part B Eng. 2018, 133, 1–14. [Google Scholar] [CrossRef]
- Wang, D.W.; Ma, L.; Wang, X.T.; Wen, Z.H.; Glorieux, C. Sound transmission loss of laminated composite sandwich structures with pyramidal truss cores. Compos. Struct. 2019, 220, 19–30. [Google Scholar] [CrossRef]
- Cherif, R.; Atalla, N. Experimental investigation of the accuracy of a vibroacoustic model for sandwich-composite panels. J. Acoust. Soc. Am. 2015, 137, 1541–1550. [Google Scholar] [CrossRef]
- Shen, C.; Xin, F.X.; Lu, T.J. Sound transmission across composite laminate sandwiches: Influence of orthogonal stiffeners and laminate layup. Compos. Struct. 2016, 143, 310–316. [Google Scholar] [CrossRef]
- Qiao, H.; He, Z.; Jiang, W.; Peng, W. Sound transmission of periodic composite structure lined with porous core: Rib-stiffened double panel case. J. Sound Vib. 2019, 440, 256–276. [Google Scholar] [CrossRef]
- Van Der Wal, H.M.; Nilsson, A.C. Sound-Transmission Measurements on Composite and Metal Fuselage Panels for Different Boundary Conditions. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005; p. 3033. [Google Scholar]
- Daneshjou, K.; Nouri, A.; Talebitooti, R. Sound transmission through laminated composite cylindrical shells using analytical model. Arch. Appl. Mech. 2007, 77, 363–379. [Google Scholar] [CrossRef]
- Ghinet, S.; Atalla, N.; Osman, H. The transmission loss of curved laminates and sandwich composite panels. J. Acoust. Soc. Am. 2005, 118, 774–790. [Google Scholar] [CrossRef]
- Talebitooti, R.; Zarastvand, M.; Darvishgohari, H. Multi-objective optimization approach on diffuse sound transmission through poroelastic composite sandwich structure. J. Sandw. Struct. Mater. 2019. [Google Scholar] [CrossRef]
- Errico, F.; Tufano, G.; Robin, O.; Guenfoud, N.; Ichchou, M.; Atalla, N. Simulating the sound transmission loss of complex curved panels with attached noise control materials using periodic cell wavemodes. Appl. Acoust. 2019, 156, 21–28. [Google Scholar] [CrossRef]
- Droz, C.; Robin, O.; Ichchou, M.; Atalla, N. Improving sound transmission loss at ring frequency of a curved panel using tunable 3D-printed small-scale resonators. J. Acoust. Soc. Am. 2019, 145, EL72–EL78. [Google Scholar] [CrossRef]
- Vatanabe, S.L.; Rubio, W.M.; Silva, E.C. Modeling of functionally graded materials. Compr. Mater. Process. 2014, 261–282. [Google Scholar]
- Chandra, N.; Raja, S.; Gopal, K.N. Vibro-acoustic response and sound transmission loss analysis of functionally graded plates. J. Sound Vib. 2014, 333, 5786–5802. [Google Scholar] [CrossRef]
- Daneshjou, K.; Talebitooti, R.; Tarkashvand, A. Analysis of sound transmission loss through thick-walled cylindrical shell using three-dimensional elasticity theory. Int. J. Mech. Sci. 2016, 106, 286–296. [Google Scholar] [CrossRef]
- Danesh, M.; Ghadami, A. Sound transmission loss of double-wall piezoelectric plate made of functionally graded materials via third-order shear deformation theory. Compos. Struct. 2019, 219, 17–30. [Google Scholar] [CrossRef]
- Chandra, N.; Gopal, K.N.; Raja, S. Vibro-acoustic response of sandwich plates with functionally graded core. Acta Mech. 2017, 228, 2775–2789. [Google Scholar] [CrossRef]
- Huang, C.; Nutt, S. An analytical study of sound transmission through unbounded panels of functionally graded materials. J. Sound Vib. 2011, 330, 1153–1165. [Google Scholar] [CrossRef]
- Daneshjou, K.; Talebitooti, R.; Kornokar, M. Vibroacoustic study on a multilayered functionally graded cylindrical shell with poroelastic core and bonded-unbonded configuration. J. Sound Vib. 2017, 393, 157–175. [Google Scholar] [CrossRef]
- Fu, T.; Chen, Z.; Yu, H.; Wang, Z.; Liu, X. An analytical study of sound transmission through corrugated core FGM sandwich plates filled with porous material. Compos. Part B Eng. 2018, 151, 161–172. [Google Scholar] [CrossRef]
- Kumar, B.R.; Ganesan, N.; Sethuraman, R. Vibro-acoustic analysis of functionally graded elliptic disc under thermal environment. Mech. Adv. Mater. Struct. 2009, 16, 160–172. [Google Scholar] [CrossRef]
- Yang, T.; Zheng, W.; Huang, Q.; Li, S. Sound radiation of functionally graded materials plates in thermal environment. Compos. Struct. 2016, 144, 165–176. [Google Scholar] [CrossRef]
- Bartolozzi, G.; Pierini, M.; Orrenius, U.L.; Baldanzini, N. An equivalent material formulation for sinusoidal corrugated cores of structural sandwich panels. Compos. Struct. 2013, 100, 173–185. [Google Scholar] [CrossRef]
- Zhou, R.; Crocker, M.J. Sound transmission loss of foam-filled honeycomb sandwich panels using statistical energy analysis and theoretical and measured dynamic properties. J. Sound Vib. 2010, 329, 673–686. [Google Scholar] [CrossRef]
- Wang, T.; Li, S.; Rajaram, S.; Nutt, S.R. Predicting the sound transmission loss of sandwich panels by statistical energy analysis approach. J. Vib. Acoust. 2010, 132, 011004. [Google Scholar] [CrossRef]
- Chavan, T.; Manik, D.N. Optimum design of vibro-acoustic systems using SEA. Int. J. Acoust. Vib. 2008, 13, 67–81. [Google Scholar]
- Nilsson, A.; Baro, S.; Piana, E.A. Vibro-acoustic properties of sandwich structures. Appl. Acoust. 2018, 139, 259–266. [Google Scholar] [CrossRef]
- Craik, R.J. Non-resonant sound transmission through double walls using statistical energy analysis. Appl. Acoust. 2003, 64, 325–341. [Google Scholar] [CrossRef]
- Parrinello, A.; Kesour, K.; Ghiringhelli, G.L.; Atalla, N. Diffuse field transmission through multilayered cylinders using a Transfer Matrix Method. Mech. Syst. Signal Process. 2020, 136, 106514. [Google Scholar] [CrossRef]
- Liu, Y.; He, C. Diffuse field sound transmission through sandwich composite cylindrical shells with poroelastic core and external mean flow. Compos. Struct. 2016, 135, 383–396. [Google Scholar] [CrossRef]
- Hua, X.; Jiang, C.; Herrin, D.W.; Wu, T.W. Determination of transmission and insertion loss for multi-inlet mufflers using impedance matrix and superposition approaches with comparisons. J. Sound Vib. 2014, 333, 5680–5692. [Google Scholar] [CrossRef]
- Ghinet, S.; Atalla, N. Modeling thick composite laminate and sandwich structures with linear viscoelastic damping. Comput. Struct. 2011, 89, 1547–1561. [Google Scholar] [CrossRef]
- Mejdi, A.; Atalla, N.; Ghinet, S. Wave spectral finite element model for the prediction of sound transmission loss and damping of sandwich panels. Comput. Struct. 2015, 158, 251–258. [Google Scholar] [CrossRef]
- Qu, Y.; Peng, Z.; Zhang, W.; Meng, G. Nonlinear vibro-acoustic behaviors of coupled sandwich cylindrical shell and spring-mass-damper systems. Mech. Syst. Signal Process. 2019, 124, 254–274. [Google Scholar] [CrossRef]
- Mace, B.R.; Manconi, E. Modelling wave propagation in two-dimensional structures using finite element analysis. J. Sound Vib. 2008, 318, 884–902. [Google Scholar] [CrossRef]
- Droz, C.; Zhou, C.; Ichchou, M.N.; Lainé, J.P. A hybrid wave-mode formulation for the vibro-acoustic analysis of 2D periodic structures. J. Sound Vib. 2016, 363, 285–302. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Ichchou, M.; Troclet, B.; Bareille, O. Computing the broadband vibroacoustic response of arbitrarily thick layered panels by a wave finite element approach. Appl. Acoust. 2014, 77, 89–98. [Google Scholar] [CrossRef]
- Yang, Y.; Mace, B.R.; Kingan, M.J. Prediction of sound transmission through, and radiation from, panels using a wave and finite element method. J. Acoust. Soc. Am. 2017, 141, 2452–2460. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Mace, B.R.; Kingan, M.J. Wave and finite element method for predicting sound transmission through finite multi-layered structures with fluid layers. Comput. Struct. 2018, 204, 20–30. [Google Scholar] [CrossRef]
- Zergoune, Z.; Ichchou, M.N.; Bareille, O.; Harras, B.; Benamar, R.; Troclet, B. Assessments of shear core effects on sound transmission loss through sandwich panels using a two-scale approach. Comput. Struct. 2017, 182, 227–237. [Google Scholar] [CrossRef]
- Legault, J.; Atalla, N. Numerical and experimental investigation of the effect of structural links on the sound transmission of a lightweight double panel structure. J. Sound Vib. 2009, 324, 712–732. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Bolton, J.S.; Shiau, N.M.; Kang, Y.J. Sound transmission through multi-panel structures lined with elastic porous materials. J. Sound Vib. 1996, 191, 317–347. [Google Scholar] [CrossRef]
- Daudin, C.; Liu, Y. Vibroacoustic Behaviour of Clamped Double-Wall Panels Lined with Poroelastic Materials. In Proceedings of the 23rd International Congress on Sound and Vibrations, Athenes, Greece, 10–14 July 2016. [Google Scholar]
- Talebitooti, R.; Choudari Khameneh, A.M.; Zarastvand, M.R.; Kornokar, M. Investigation of three-dimensional theory on sound transmission through compressed poroelastic sandwich cylindrical shell in various boundary configurations. J. Sandw. Struct. Mater. 2018, 21, 2313–2357. [Google Scholar] [CrossRef]
- Ramezani, H.; Saghafi, A. Optimization of a composite double-walled cylindrical shell lined with porous materials for higher sound transmission loss by using a genetic algorithm. Mech. Compos. Mater. 2014, 50, 71–82. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.; Kim, H.J. Simplified method to solve sound transmission through structures lined with elastic porous material. J. Acoust. Soc. Am. 2001, 110, 2282–2294. [Google Scholar] [CrossRef]
- Panneton, R.; Atalla, N. Numerical prediction of sound transmission through finite multilayer systems with poroelastic materials. J. Acoust. Soc. Am. 1996, 100, 346–354. [Google Scholar] [CrossRef]
- Decraene, C.; Dijckmans, A.; Reynders, E.P. Fast mean and variance computation of the diffuse sound transmission through finite-sized thick and layered wall and floor systems. J. Sound Vib. 2018, 422, 131–145. [Google Scholar] [CrossRef]
- Langley, R.S.; Cotoni, V. Response variance prediction for uncertain vibro-acoustic systems using a hybrid deterministic-statistical method. J. Acoust. Soc. Am. 2007, 122, 3445–3463. [Google Scholar] [CrossRef] [PubMed]
- Reynders, E.; Langley, R.S.; Dijckmans, A.; Vermeir, G. A hybrid finite element–statistical energy analysis approach to robust sound transmission modeling. J. Sound Vib. 2014, 333, 4621–4636. [Google Scholar] [CrossRef]
- Alimonti, L.; Atalla, N.; Berry, A.; Sgard, F. A hybrid finite element–transfer matrix model for vibroacoustic systems with flat and homogeneous acoustic treatments. J. Acoust. Soc. Am. 2015, 137, 976–988. [Google Scholar] [CrossRef]
- Alimonti, L.; Atalla, N.; Berry, A.; Sgard, F. Assessment of a hybrid finite element-transfer matrix model for flat structures with homogeneous acoustic treatments. J. Acoust. Soc. Am. 2014, 135, 2694–2705. [Google Scholar] [CrossRef]
- Guyader, J.L.; Cacciolati, C.; Chazot, D. Transmission Loss Prediction of Double Panels Filled with Porous Materials and Mechanical Stiffeners. In Proceedings of the ICA 2010, Sydney, Australia, 23–27 August 2010; Volume 7. [Google Scholar]
- Kesour, K.; Atalla, N. A hybrid patch Transfer-Green functions method to solve transmission loss problems of flat single and double walls with attached sound packages. J. Sound Vib. 2018, 429, 1–7. [Google Scholar] [CrossRef]
- Tang, Y.; Li, F.; Xin, F.; Lu, T.J. Heterogeneously perforated honeycomb-corrugation hybrid sandwich panel as sound absorber. Mater Des. 2017, 134, 502–512. [Google Scholar] [CrossRef]
- Ma, X.; Chen, K.; Xu, J. Active control of sound transmission through orthogonally rib stiffened double-panel structure: Mechanism analysis. Appl. Sci. 2019, 9, 3286. [Google Scholar] [CrossRef]
- Onbaşlı, M.C. Design and Modeling of High-Strength, High-Transmission Auto Glass with High Sound Transmission Loss. In Handbook of Materials Modeling; Andreoni, W., Yip, S., Eds.; Springer: Cham, Switzerland, 2019; pp. 1–18. [Google Scholar] [CrossRef]
- Gulia, P.; Gupta, A. Sound attenuation in triple panel using locally resonant sonic crystal and porous material. Appl. Acoust. 2019, 156, 113–119. [Google Scholar] [CrossRef]
- Howard, C.; Cazzolato, B. Acoustic Analyses Using MATLAB and ANSYS.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Shi, S.X.; Jin, G.Y.; Liu, Z.G. Vibro-acoustic behaviors of an elastically restrained double-panel structure with an acoustic cavity of arbitrary boundary impedance. Appl. Acoust. 2014, 76, 431–444. [Google Scholar] [CrossRef]
- Ghosh, S.; Bhattacharya, P. Energy transmission through a double-wall curved stiffened panel using Green’ s theorem. J. Sound Vib. 2015, 342, 218–240. [Google Scholar] [CrossRef]
- Mitra, N. A methodology for improving shear performance of marine grade sandwich composites: Sandwich composite panel with shear key. Compos. Struct. 2010, 92, 1065–1072. [Google Scholar] [CrossRef]
- Dimino, I.; Vigliotti, A.; Aliabadi, M.F. Vibro-acoustic design of an aircraft-type active window, Part 1, dynamic modelling and experimental validation. J. Theor. Appl. Mech. 2012, 50, 169–192. [Google Scholar]
- Aloufi, B.; Behdinan, K.; Zu, J. Theoretical vibro-acoustic modeling of acoustic noise transmission through aircraft windows. J. Sound Vib. 2016, 371, 344–369. [Google Scholar] [CrossRef]
- Legault, J.; Atalla, N. Sound transmission through a double panel structure periodically coupled with vibration insulators. J. Sound Vib. 2010, 329, 3082–3100. [Google Scholar] [CrossRef]
- Song, Y.; Feng, L.; Wen, J.; Yu, D.; Wen, X. Reduction of the sound transmission of a periodic sandwich plate using the stop band concept. Compos. Struct. 2015, 128, 428–436. [Google Scholar] [CrossRef]
- Oyelade, A.O. Analytical modelling of sound transmission through finite clamped double-wall panels with magnetic-linked stiffness. Acoust. Aust. 2019, 156, 1–11. [Google Scholar] [CrossRef]
- Kim, H.; Ryue, J.; Thompson, D.J.; Müller, A.D. Application of a wavenumber domain numerical method to the prediction of the radiation efficiency and sound transmission of complex extruded panels. J. Sound Vib. 2019, 449, 98–120. [Google Scholar] [CrossRef]
- de Melo Filho, N.G.; Van Belle, L.; Claeys, C.; Deckers, E.; Desmet, W. Dynamic mass based sound transmission loss prediction of vibro-acoustic metamaterial double panels applied to the mass-air-mass resonance. J. Sound Vib. 2019, 442, 28–44. [Google Scholar] [CrossRef]
- Gulia, P.; Gupta, A. Effect of sidewalls on sound transmission loss through sonic crystal. Acoust. Phys. 2018, 64, 665–672. [Google Scholar] [CrossRef]
- Magniez, J.; Chazot, J.D.; Hamdi, M.A.; Troclet, B. A mixed 3D-Shell analytical model for the prediction of sound transmission through sandwich cylinders. J. Sound Vib. 2014, 333, 4750–4770. [Google Scholar] [CrossRef]
- Liu, Y.; Sebastian, A. Effects of external and gap mean flows on sound transmission through a double-wall sandwich panel. J. Sound Vib. 2015, 344, 399–415. [Google Scholar] [CrossRef]
- Li, S.; Mao, D.; Huang, S.; Wang, X. Enhanced transmission loss in acoustic materials with micro-membranes. Appl. Acoust. 2018, 130, 92–98. [Google Scholar] [CrossRef]
- Golzari, M.; Jafari, A.A. Sound transmission through truncated conical shells. Appl. Acoust. 2019, 156, 186–207. [Google Scholar] [CrossRef]
- Van Belle, L.; Claeys, C.; Deckers, E.; Desmet, W. The impact of damping on the sound transmission loss of locally resonant metamaterial plates. J. Sound Vib. 2019, 461, 114909. [Google Scholar] [CrossRef]
- Xin, F.X.; Lu, T.J. Effects of core topology on sound insulation performance of lightweight all-metallic sandwich panels. Mater. Manuf. Process. 2011, 26, 1213–1221. [Google Scholar] [CrossRef]
- Malakooti, S.; Churu, H.G.; Lee, A.; Rostami, S.; May, S.J.; Ghidei, S.; Wang, F.; Lu, Q.; Luo, H.; Xiang, N.; et al. Sound transmission loss enhancement in an inorganic-organic laminated wall panel using multifunctional low-density nanoporous polyurea aerogels: Experiment and modeling. Adv. Eng. Mater. 2018, 20, 1700937. [Google Scholar] [CrossRef]
- Fu, T.; Chen, Z.; Yu, H.; Wang, Z.; Liu, X. An analytical study of sound transmission through stiffened double laminated composite sandwich plates. Aerosp. Sci. Technol. 2018, 82, 92–104. [Google Scholar] [CrossRef]
- Nouri, A.; Astaraki, S. Optimization of sound transmission loss through a thin functionally graded material cylindrical shell. Shock Vib. 2014. [Google Scholar] [CrossRef]
- Kanarachos, S.; Griffin, J.; Fitzpatrick, M.E. Efficient truss optimization using the contrast-based fruit fly optimization algorithm. Comput. Struct. 2017, 182, 137–148. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. Ray optimization for size and shape optimization of truss structures. Comput. Struct. 2013, 117, 82–94. [Google Scholar] [CrossRef]
- Shojaeifard, M.H.; Talebitooti, R.; Yadollahi, A. Optimization of sound transmission through laminated composite cylindrical shells by using a genetic algorithm. Mech. Compos. Mater. 2011, 47, 481–494. [Google Scholar] [CrossRef]
- Tanneau, O.; Casimir, J.B.; Lamary, P. Optimization of multilayered panels with poroelastic components for an acoustical transmission objective. J. Acoust. Soc. Am. 2006, 120, 1227–1238. [Google Scholar] [CrossRef]
- Zhou, J.; Bhaskar, A.; Zhang, X. Optimization for sound transmission through a double-wall panel. Appl. Acoust. 2013, 74, 1422–1428. [Google Scholar] [CrossRef]
- Denli, H.; Sun, J.Q. Structural–acoustic optimization of sandwich cylindrical shells for minimum interior sound transmission. J. Sound Vib. 2008, 316, 32–49. [Google Scholar] [CrossRef]
- Errico, F.; Ichchou, M.; De Rosa, S.; Franco, F.; Bareille, O. Investigations about periodic design for broadband increased sound transmission loss of sandwich panels using 3D-printed models. Mech. Syst. Signal Process. 2020, 136, 106432. [Google Scholar] [CrossRef]
- Tsai, Y.T.; Pawar, S.J.; Huang, J.H. Optimizing material properties of composite plates for sound transmission problem. J. Sound Vib. 2015, 335, 174–186. [Google Scholar] [CrossRef]
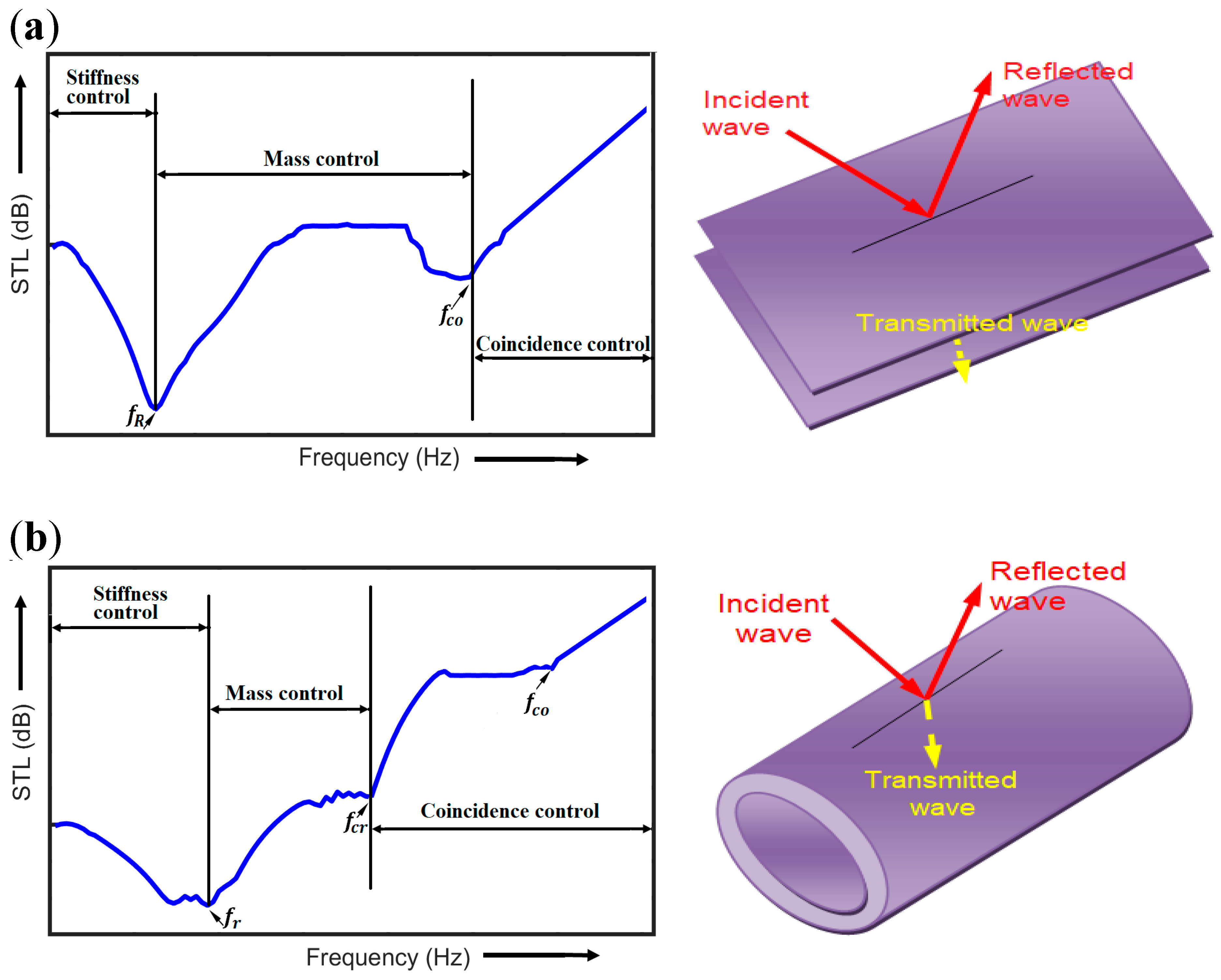
| Frequency | Symbol | Formula | Definition | Reference |
|---|---|---|---|---|
| Resonance | - Frequency at which the vibrating double panel structure (DPS) reaches its natural frequency. Typical to flat panels. | [12] | ||
| Mass–air–mass resonance | - Frequency at which the double panels vibrates on the stiffness of the separating air layer. | [31,32] | ||
| Ring | Transition frequency where a reduction in STL first occurs especially for curved panels. | [33,34] | ||
| Critical | Dip frequency where the circumferential wave number and mode per radius of shell become equal. | [34,35] | ||
| Coincidence | - Dip frequency at which the structural and acoustic wave number coincides. | [34,36] |
| Group | Parameter | Reference | Influence on STL | |||
|---|---|---|---|---|---|---|
| Frequency Region | Remark | |||||
| Low | Mid | High | ||||
| Geometrical | Core heights | [51,64,71] | - Increased STL. | |||
| Core radii | [64,69] | - Increased STL. | ||||
| Cylindrical Shell radii | [68,69,86] | - Decreased STL with higher radius. | ||||
| Plate/shell thicknesses | [51,69,144,145] | - Increased STL. | ||||
| Cylindrical shell lengths | [145] | - Decreased STL. | ||||
| Finite dimension of panels/shell | [51,146] | - Lower STL than infinite dimension. | ||||
| Infinite dimension of panels | [51,146] | - Higher STL than finite dimension. | ||||
| Different boundary conditions | [13,145] | - STL most significant at low frequency regime. | ||||
| Different core topologies | [70,147] | - Significant difference in STL. | ||||
| Material | Mach numbers | [11,64,69,100] | - Poor STL. | |||
| Damping loss factors | [64] | - STL decreased; however, it increased at dip frequencies only. | ||||
| Young’s modulus | [31,63,69] | - Improved STL. | ||||
| Shear modulus | [29,69] | - No significant difference in STL. | ||||
| Poisson ratios | [69] | - No significant difference in STL. | ||||
| Stiffness | [69] | - Improved STL. | ||||
| Structural | Cavity gas types | [46,86] | - STL largely influenced. | |||
| Core types | [31,70] | - STL largely influenced. | ||||
| Porous and fibrous material in the core | [118,148] | - Higher STL than cores without porous material. | ||||
| Different metallic plate/shell combination | [64,85,149] | - Magnitude of STL varies with different materials and combinations. | ||||
| Different Composite plate/shell types | [69,71] | - Magnitude of STL varies with different composite materials. | ||||
| Different FGM plate/shell types | [150] | - Magnitude of STL varies with different functionally graded materials (FGMs). | ||||
| Orientated | Incident/elevation angles | [60,69,145] | - Poor STL performance. | |||
| Azimuthal angles | [72,100] | - STL Increased slowly at mid-high frequency zones. | ||||
| Core inclination angle | [51] | - Poor STL performance. | ||||
| Temperatures | [72] | - Decreased STL. | ||||
| Stacking sequences | [49,68,69,71] | - STL improves with more zero plies. | ||||
| Cone angles | [145] | - STL poorly increase at mid frequency region. | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaac, C.W.; Pawelczyk, M.; Wrona, S. Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls. Appl. Sci. 2020, 10, 1543. https://doi.org/10.3390/app10041543
Isaac CW, Pawelczyk M, Wrona S. Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls. Applied Sciences. 2020; 10(4):1543. https://doi.org/10.3390/app10041543
Chicago/Turabian StyleIsaac, Chukwuemeke William, Marek Pawelczyk, and Stanislaw Wrona. 2020. "Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls" Applied Sciences 10, no. 4: 1543. https://doi.org/10.3390/app10041543
APA StyleIsaac, C. W., Pawelczyk, M., & Wrona, S. (2020). Comparative Study of Sound Transmission Losses of Sandwich Composite Double Panel Walls. Applied Sciences, 10(4), 1543. https://doi.org/10.3390/app10041543






