Frequency Characteristics of Multiscale Hybrid Nanocomposite Annular Plate Based on a Halpin–Tsai Homogenization Model with the Aid of GDQM
Abstract
1. Introduction
2. Theory and Formulation
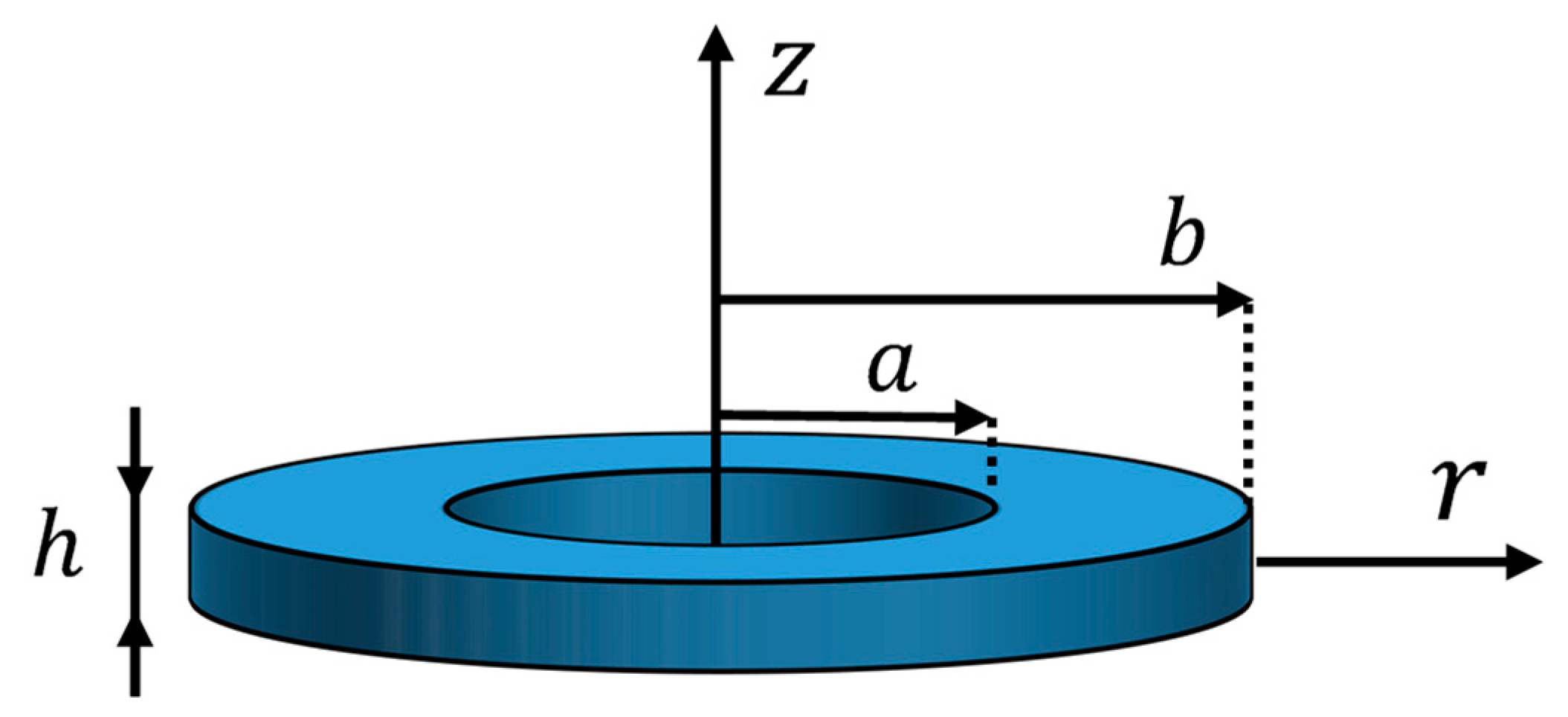
2.1. Problem Description
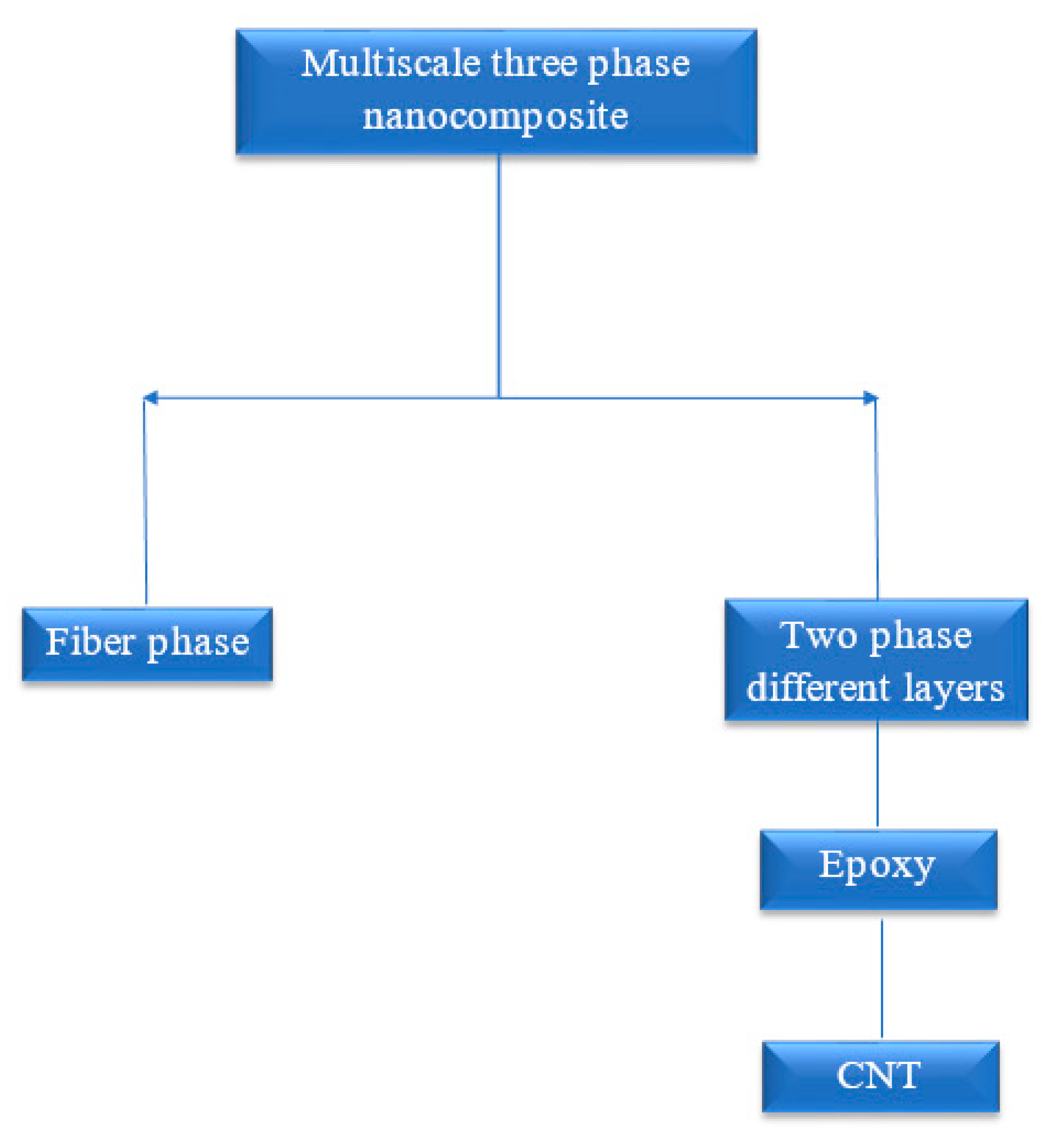
2.2. The Homogenization Process of MHC
2.3. Kinematic Relations
2.4. Hamilton’s Principle
2.5. Governing Equations
3. Solution Procedure
4. Numerical Results and Discussion
4.1. Verification
4.2. Vibration Study
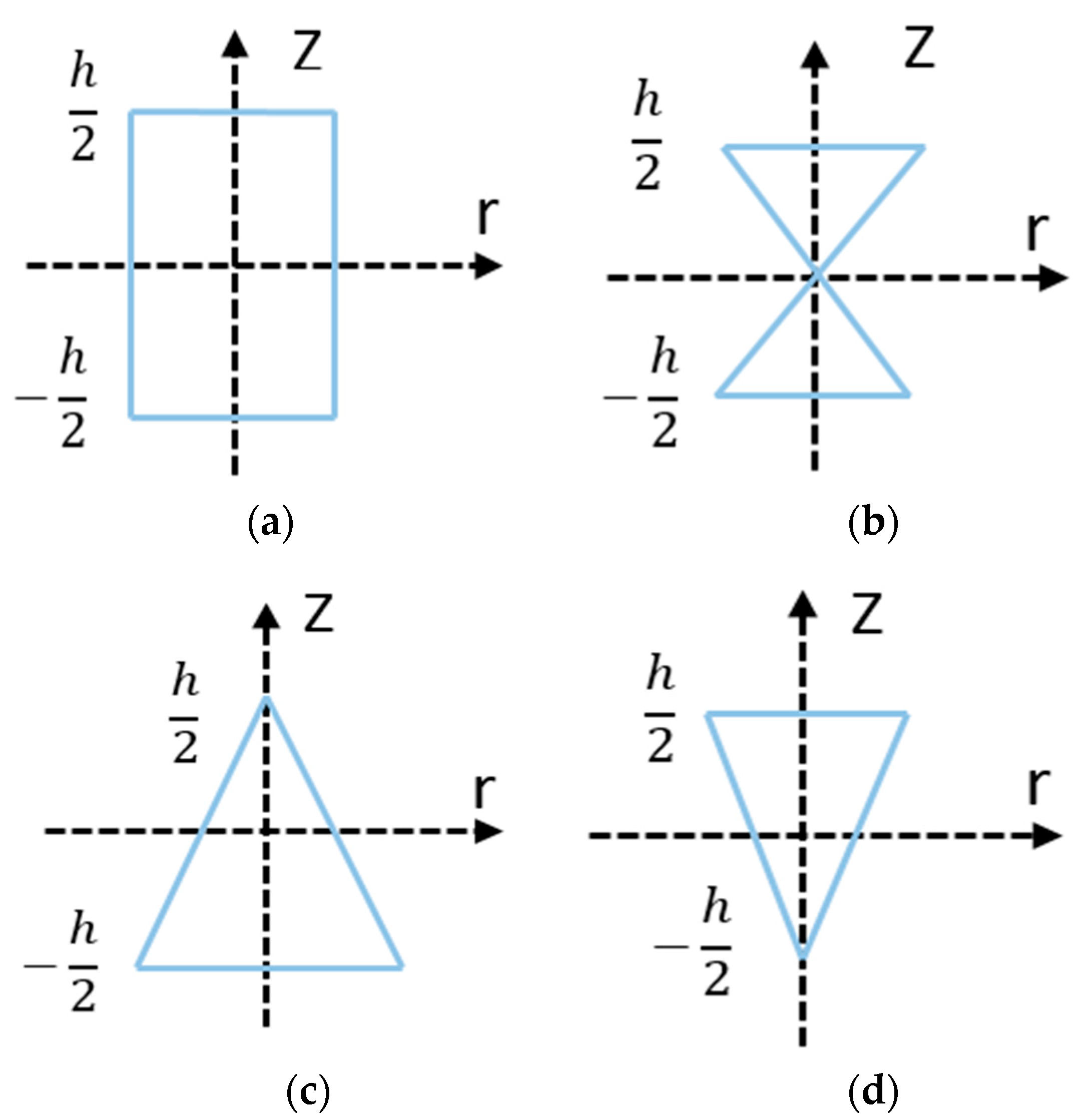
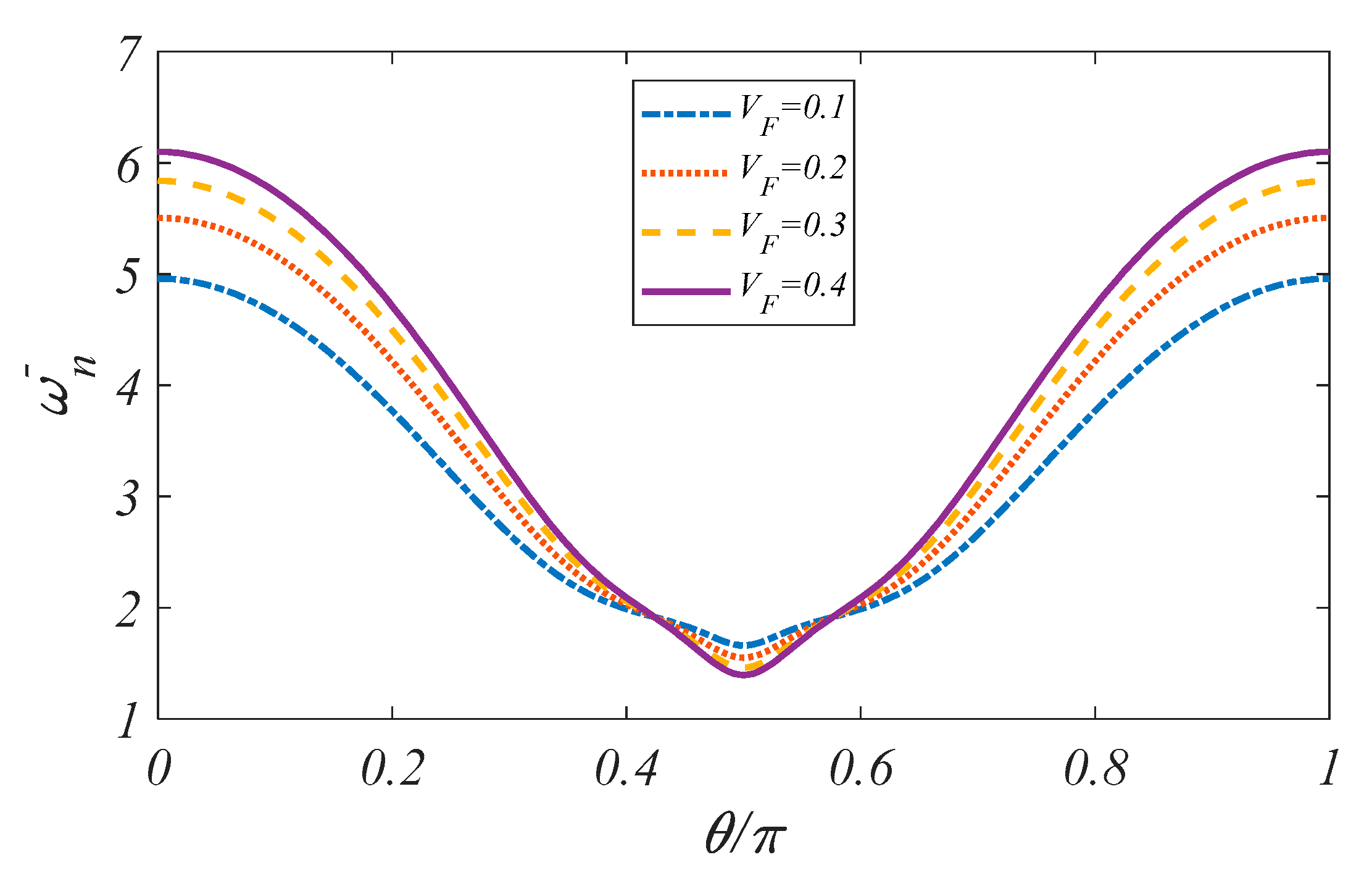
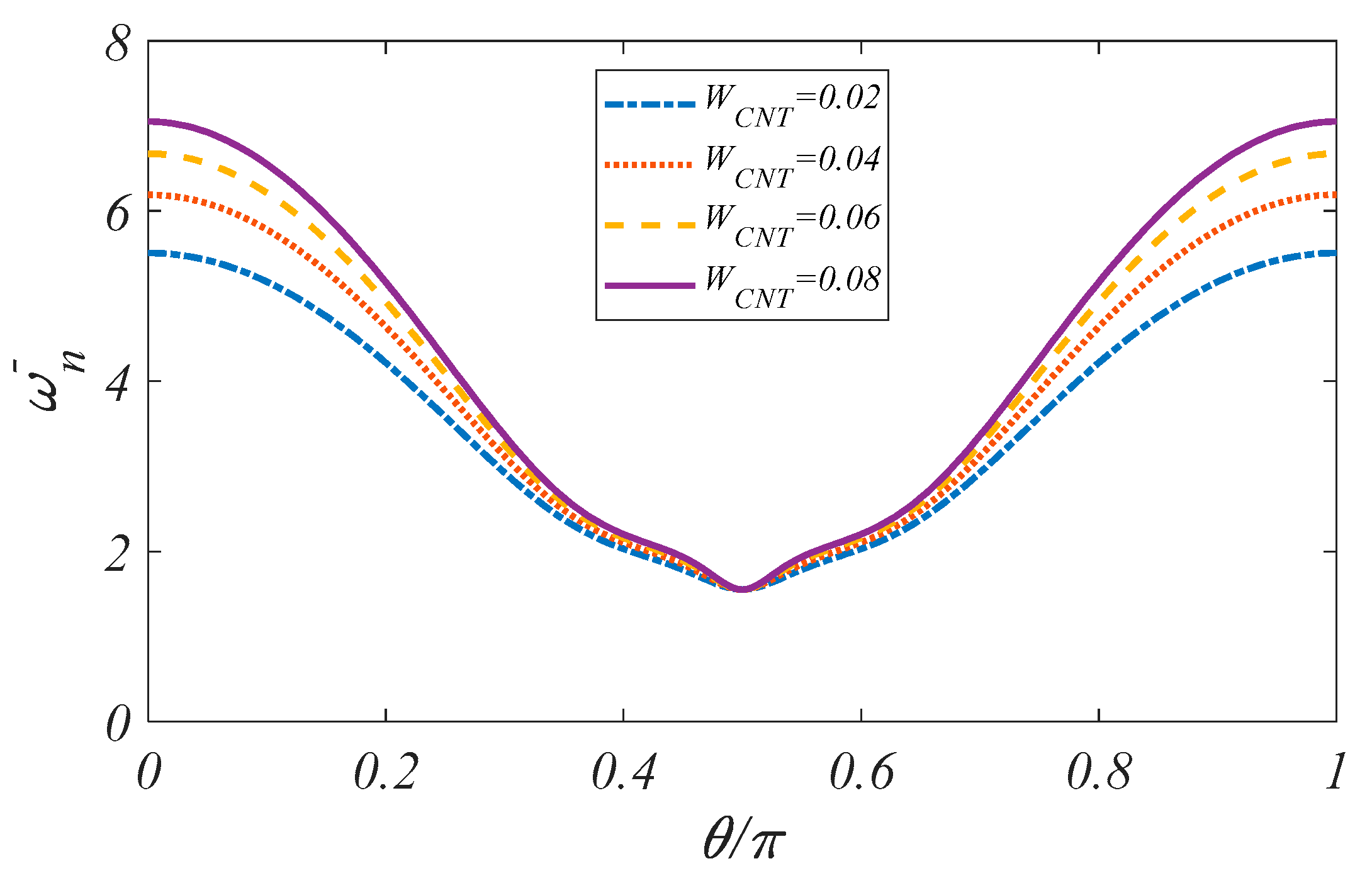
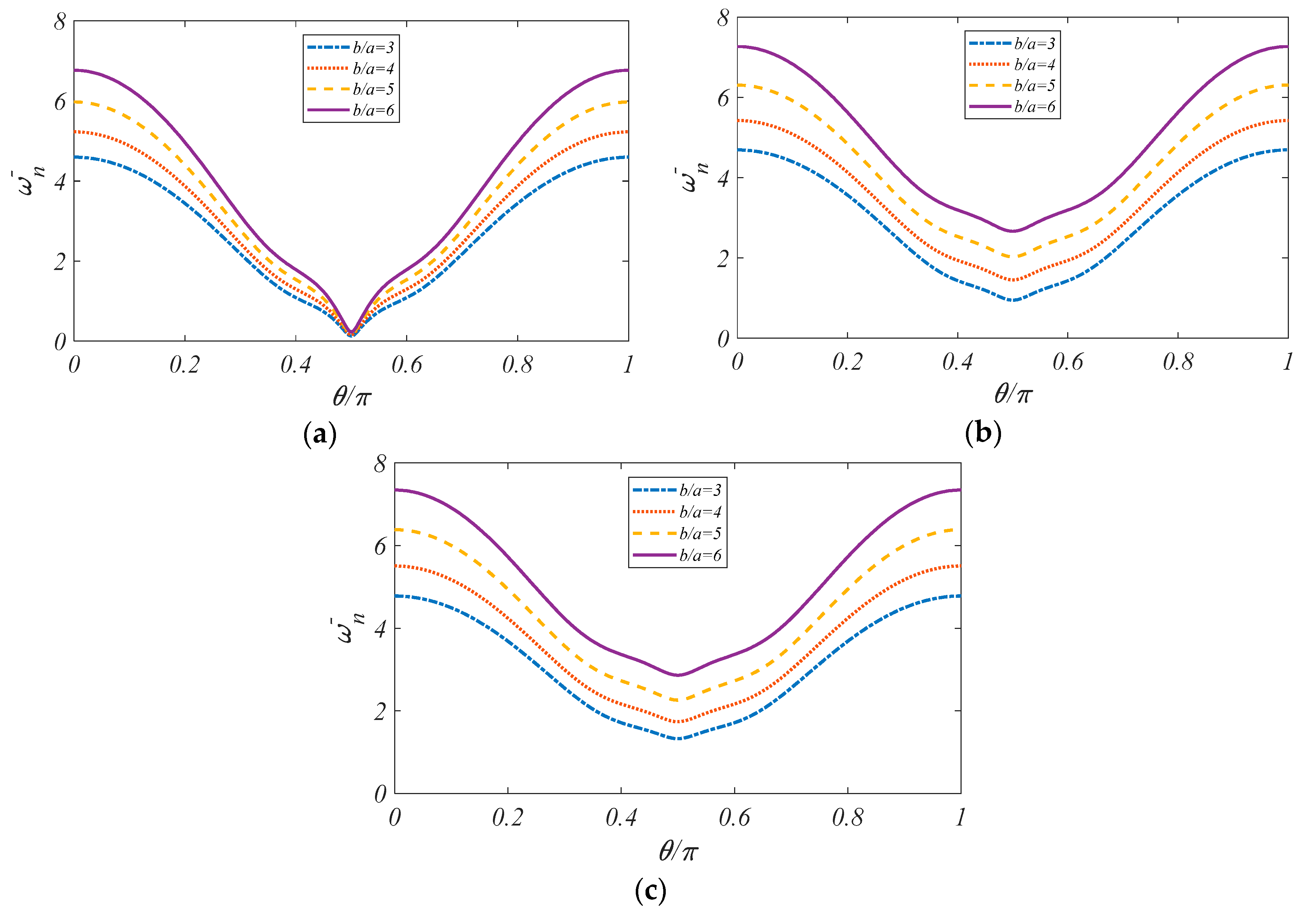
4.2.1. Parametric Vibration Study
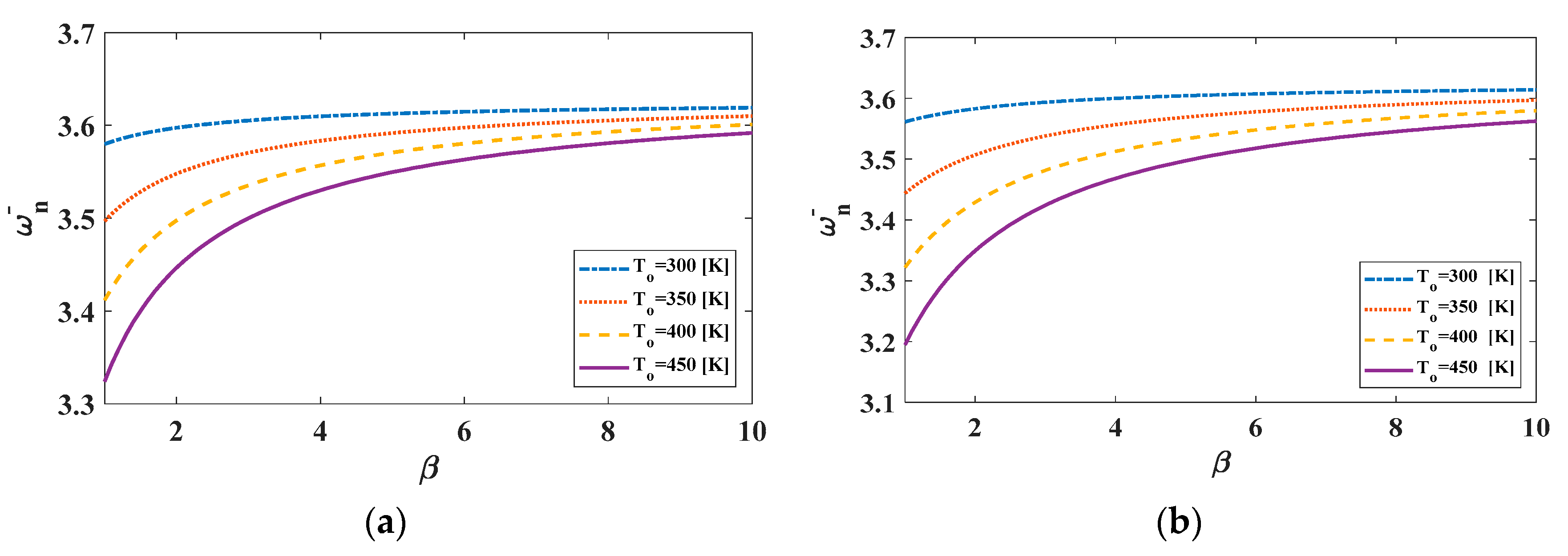
4.2.2. Sensitivity Analysis of Vibration
5. Conclusions
- Annular plates with lower thickness to outer radius ratio presented better vibration performance.
- Reinforcing MHCAP with FG-A as the distribution pattern of CNTs exhibited the best vibration response in comparison with any other patterns tested.
- In the case of Pasternak-type elastic substrate, the lowest natural frequency was associated with b/a = 2.3 as the outer radius to inner radius ratio of the MHCAP.
- The effect of the Winkler coefficient on the vibration performance of the plate was more significant when the outer radius to inner radius ratio was higher.
- Applying a sinusoidal temperature rise results to a highest natural compared with associated results of other patterns of temperature rise.
- When the outer radius to inner radius ratio of the MHCAP was larger, the minimum frequency occurred at higher, corresponding temperature of the top surface.
- Unlike compression load, applying higher load in extensional direction led to higher natural frequencies.
Author Contributions
Funding
Conflicts of Interest
References
- Chakrapani, S.K.; Barnard, D.J.; Dayal, V. Nonlinear forced vibration of carbon fiber/epoxy prepreg composite beams: Theory and experiment. Compos. Part B Eng. 2016, 91, 513–521. [Google Scholar] [CrossRef]
- Emam, S.; Eltaher, M.A. Buckling and postbuckling of composite beams in hygrothermal environments. Compos. Struct. 2016, 152, 665–675. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Compos. Part B Eng. 2016, 89, 187–218. [Google Scholar] [CrossRef]
- Banić, D.; Bacciocchi, M.; Tornabene, F.; Ferreira, A.J.M. Influence of Winkler-Pasternak Foundation on the Vibrational Behavior of Plates and Shells Reinforced by Agglomerated Carbon Nanotubes. Appl. Sci. 2017, 7, 1228. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hajilak, Z.E.; Habibi, M.; Safarpour, H. Buckling and vibration characteristics of a carbon nanotube-reinforced spinning cantilever cylindrical 3D shell conveying viscous fluid flow and carrying spring-mass systems under various temperature distributions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4590–4605. [Google Scholar] [CrossRef]
- Maghamikia, S.; Jam, J.E. Buckling analysis of circular and annular composite plates reinforced with carbon nanotubes using FEM. J. Mech. Sci. Technol. 2011, 25, 2805–2810. [Google Scholar] [CrossRef]
- Tahouneh, V.; Yas, M. Influence of equivalent continuum model based on the Eshelby-Mori-Tanaka scheme on the vibrational response of elastically supported thick continuously graded carbon nanotube-reinforced annular plates. Polym. Compos. 2014, 35, 1644–1661. [Google Scholar] [CrossRef]
- Tahouneh, V.; Jam, J.E. A Semi-analytical Solution for 3-D Dynamic Analysis of Thick Continuously Graded Carbon Nanotube-reinforced Annular Plates Resting on a Two-parameter Elastic Foundation. Mech. Adv. Compos. Struct. 2014, 1, 113–130. [Google Scholar] [CrossRef]
- Tornabene, F. Free vibration analysis of functionally graded conical, cylindrical shell and annular plate structures with a four-parameter power-law distribution. Comput. Methods Appl. Mech. Eng. 2009, 198, 2911–2935. [Google Scholar] [CrossRef]
- Safarpour, H.; Esmailpoor, H.Z.; Habibi, M. A size-dependent exact theory for thermal buckling, free and forced vibration analysis of temperature dependent FG multilayer GPLRC composite nanostructures restring on elastic foundation. Int. J. Mech. Mater Des. 2018. [Google Scholar] [CrossRef]
- Ebrahimi-Mamaghani, A.; Mirtalebi, S.H.; Ahmadian, M.-T. Magneto-mechanical stability of axially functionally graded supported nanotubes. Mater Res. Express 2020, 6, 1250. [Google Scholar] [CrossRef]
- Esfahani, S.; Khadem, S.E.; Mamaghani, A.E. Nonlinear vibration analysis of an electrostatic functionally graded nano-resonator with surface effects based on nonlocal strain gradient theory. Int. J. Mech. Sci. 2019, 151, 508–522. [Google Scholar] [CrossRef]
- Mirtalebi, S.H.; Ebrahimi-Mamaghani, A.; Ahmadian, M.T. Vibration Control and Manufacturing of Intelligibly Designed Axially Functionally Graded Cantilevered Macro/Micro-tubes. IFAC-PapersOnLine 2019, 52, 382–387. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Shojaei, M.F. Buckling and vibration analysis of embedded functionally graded carbon nanotube-reinforced composite annular sector plates under thermal loading. Compos. Part B Eng. 2017, 109, 197–213. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Asadi, H.; Wang, Q. Postbuckling analysis of smart FG-CNTRC annular sector plates with surface-bonded piezoelectric layers using generalized differential quadrature method. Comput. Methods Appl. Mech. Eng. 2017, 325, 689–710. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Asadi, H.; Aghdam, M.M. Geometrical nonlinear free vibration responses of FG-CNT reinforced composite annular sector plates integrated with piezoelectric layers. Compos. Struct. 2017, 171, 100–112. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Asadi, H.; Wang, Q. Large amplitude vibration of FG-CNT reinforced composite annular plates with integrated piezoelectric layers on elastic foundation. Thin-Walled Struct. 2017, 120, 203–214. [Google Scholar] [CrossRef]
- Torabi, J.; Ansari, R. Nonlinear free vibration analysis of thermally induced FG-CNTRC annular plates: Asymmetric versus axisymmetric study. Comput. Methods Appl. Mech. Eng. 2017, 324, 327–347. [Google Scholar] [CrossRef]
- Pang, F.; Li, H.; Du, Y.; Shan, Y.; Ji, F. Free Vibration of Functionally Graded Carbon Nanotube Reinforced Composite Annular Sector Plate With General Boundary Supports. Curved Layer. Struct. 2018, 5, 49–67. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Hassani, R. In-plane and shear buckling analysis of FG-CNTRC annular sector plates based on the third-order shear deformation theory using a numerical approach. Comput. Math. Appl. 2018, 75, 486–502. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Geometrically nonlinear resonance of higher-order shear deformable functionally graded carbon-nanotube-reinforced composite annular sector plates excited by harmonic transverse loading. Eur. Phys. J. Plus 2018, 133, 56. [Google Scholar] [CrossRef]
- Mercan, K.; Baltacıoglu, A.K.; Civalek, Ö. Free vibration of laminated and FGM/CNT composites annular thick plates with shear deformation by discrete singular convolution method. Compos. Struct. 2018, 186, 139–153. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Faghih Shojaei, M. Free vibration analysis of embedded functionally graded carbon nanotube-reinforced composite conical/cylindrical shells and annular plates using a numerical approach. J. Vib. Control 2018, 24, 1123–1144. [Google Scholar] [CrossRef]
- Ansari, R.; Torabi, J.; Hasrati, E. Axisymmetric nonlinear vibration analysis of sandwich annular plates with FG-CNTRC face sheets based on the higher-order shear deformation plate theory. Aerosp. Sci. Technol. 2018, 77, 306–319. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, Q.; Tang, J.; Shuai, C.; Qin, B. Vibration analysis of functionally graded carbon nanotube reinforced composites (FG-CNTRC) circular, annular and sector plates. Compos. Struct. 2018, 194, 49–67. [Google Scholar] [CrossRef]
- Civalek, Ö.; Baltacıoğlu, A.K. Vibration of carbon nanotube reinforced composite (CNTRC) annular sector plates by discrete singular convolution method. Compos. Struct. 2018, 203, 458–465. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.R.; Alibeigloo, A. Static and free vibration analysis of graphene platelets reinforced composite truncated conical shell, cylindrical shell, and annular plate using theory of elasticity and DQM. Mech. Based Des. Struct. Mach. 2019, 1–29. [Google Scholar] [CrossRef]
- Habibi, M.; Hashemabadi, D.; Safarpour, H. Vibration analysis of a high-speed rotating GPLRC nanostructure coupled with a piezoelectric actuator. Eur. Phys. J. Plus 2019, 134, 307. [Google Scholar] [CrossRef]
- Bisheh, H.; Alibeigloo, A.; Safarpour, M.; Rahimi, A. Three-Dimensional Static and Free Vibrational Analysis of Graphene Reinforced Composite Circular/Annular Plate using Differential Quadrature Method. Int. J. Appl. Mech. 2019, 11, 1950–1973. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hashemabadi, D.; Habibi, M.; Safarpour, H. Thermal buckling and forced vibration characteristics of a porous GNP reinforced nanocomposite cylindrical shell. Microsyst. Technol. 2019, 26, 461–473. [Google Scholar] [CrossRef]
- Safarpour, M.; Rahimi, A.; Alibeigloo, A.; Bisheh, H.; Forooghi, A. Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech. Based Des. Struct. Mach. 2019, 1–31. [Google Scholar] [CrossRef]
- Moayedi, H.; Habibi, M.; Safarpour, H.; Safarpour, M.; Foong, L.K. Buckling and Frequency Responses of A Graphen Nanoplatelet Reinforced Composite Microdisk. Int. J. Appl. Mech. 2020. [Google Scholar] [CrossRef]
- Esmailpoor Hajilak, Z.; Pourghader, J.; Hashemabadi, D.; Sharifi Bagh, F.; Habibi, M.; Safarpour, H. Multilayer GPLRC composite cylindrical nanoshell using modified strain gradient theory. Mech. Based Des. Struct. Mach. 2019, 47, 521–545. [Google Scholar] [CrossRef]
- Habibi, M.; Mohammadi, A.; Safarpour, H.; Ghadiri, M. Effect of porosity on buckling and vibrational characteristics of the imperfect GPLRC composite nanoshell. Mech. Based Des. Struct. Mach. 2019, 1–30. [Google Scholar] [CrossRef]
- Rahimi, A.; Alibeigloo, A.; Safarpour, M. Three-dimensional static and free vibration analysis of graphene platelet–reinforced porous composite cylindrical shell. J. Vib. Control 2020. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.-F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Setoodeh, A.R.; Shojaee, M. Vibration of FG-GPLs eccentric annular plates embedded in piezoelectric layers using a transformed differential quadrature method. Comput. Methods Appl. Mech. Eng. 2018, 340, 451–479. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Asymmetric nonlinear bending analysis of polymeric composite annular plates reinforced with graphene nanoplatelets. JMC 2019, 17, 156. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Li, W.Z.; Wang, D.Z.; Ren, Z.F.; Chou, T.W. Carbon nanotube/carbon fiber hybrid multiscale composites. J. Appl. Phys. 2002, 91, 6034–6037. [Google Scholar] [CrossRef]
- Song, Y.S. Multiscale fiber-reinforced composites prepared by vacuum-assisted resin transfer molding. Polym. Compos. 2007, 28, 458–461. [Google Scholar] [CrossRef]
- Bekyarova, E.; Thostenson, E.T.; Yu, A.; Kim, H.; Gao, J.; Tang, J.; Hahn, H.T.; Chou, T.-W.; Itkis, M.E.; Haddon, R.C. Multiscale Carbon Nanotube−Carbon Fiber Reinforcement for Advanced Epoxy Composites. Langmuir 2007, 23, 3970–3974. [Google Scholar] [CrossRef]
- Bekyarova, E.; Thostenson, E.T.; Yu, A.; Itkis, M.E.; Fakhrutdinov, D.; Chou, T.W.; Haddon, R.C. Functionalized Single-Walled Carbon Nanotubes for Carbon Fiber−Epoxy Composites. J. Phys. Chem. C 2007, 111, 17865–17871. [Google Scholar] [CrossRef]
- Jiang, S.; Li, Q.; Wang, J.; He, Z.; Zhao, Y.; Kang, M. Multiscale graphene oxide–carbon fiber reinforcements for advanced polyurethane composites. Compos. Part A Appl. Sci. Manuf. 2016, 87, 1–9. [Google Scholar] [CrossRef]
- Cougo, d.S.; Matheus, C.; Pezzin, S.H.; Pachekoski, W.M.; Amico, S.C. Multiscale hybrid composites with carbon-based nanofillers. In Nanocarbon and Its Composites; Woodhead Publishing: Cambridge, UK, 2019. [Google Scholar]
- Kim, M.; Park, Y.-B.; Okoli, O.I.; Zhang, C. Processing, characterization, and modeling of carbon nanotube-reinforced multiscale composites. Compos. Sci. Technol. 2009, 69, 335–342. [Google Scholar] [CrossRef]
- Inam, F.; Wong, D.W.Y.; Kuwata, M.; Peijs, T. Multiscale hybrid micro-nanocomposites based on carbon nanotubes and carbon fibers. J. Nanomater. 2010, 2010, 9. [Google Scholar] [CrossRef]
- Wang, B.-C.; Zhou, X.; Ma, K.-M. Fabrication and properties of CNTs/carbon fabric hybrid multiscale composites processed via resin transfer molding technique. Compos. Part B Eng. 2013, 46, 123–129. [Google Scholar] [CrossRef]
- Lee, S.-B.; Choi, O.; Lee, W.; Yi, J.-W.; Kim, B.-S.; Byun, J.-H.; Yoon, M.-K.; Fong, H.; Thostenson, E.T.; Chou, T.-W. Processing and characterization of multi-scale hybrid composites reinforced with nanoscale carbon reinforcements and carbon fibers. Compos. Part A Appl. Sci. Manuf. 2011, 42, 337–344. [Google Scholar] [CrossRef]
- Guo, J.; Lu, C.; An, F.; He, S. Preparation and characterization of carbon nanotubes/carbon fiber hybrid material by ultrasonically assisted electrophoretic deposition. Mater. Lett. 2012, 66, 382–384. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Gangloff, J.J.; Li, C.; Byun, J.-H. Electrical anisotropy in multiscale nanotube/fiber hybrid composites. Appl. Phys. Lett. 2009, 95, 073111. [Google Scholar] [CrossRef]
- Qin, F.X.; Brosseau, C.; Peng, H.X. Microwave properties of carbon nanotube/microwire/rubber multiscale hybrid composites. Chem. Phys. Lett. 2013, 579, 40–44. [Google Scholar] [CrossRef]
- Pal, G.; Kumar, S. Multiscale modeling of effective electrical conductivity of short carbon fiber-carbon nanotube-polymer matrix hybrid composites. Mater. Des. 2016, 89, 129–136. [Google Scholar] [CrossRef]
- Sung, D.H.; Kim, M.; Park, Y.-B. Prediction of thermal conductivities of carbon-containing fiber-reinforced and multiscale hybrid composites. Compos. Part B Eng. 2018, 133, 232–239. [Google Scholar] [CrossRef]
- Rodriguez, A.J.; Guzman, M.E.; Lim, C.-S.; Minaie, B. Mechanical properties of carbon nanofiber/fiber-reinforced hierarchical polymer composites manufactured with multiscale-reinforcement fabrics. Carbon 2011, 49, 937–948. [Google Scholar] [CrossRef]
- Rahmanian, S.; Suraya, A.R.; Shazed, M.A.; Zahari, R.; Zainudin, E.S. Mechanical characterization of epoxy composite with multiscale reinforcements: Carbon nanotubes and short carbon fibers. Mater. Des. 2014, 60, 34–40. [Google Scholar] [CrossRef]
- Radue, M.S.; Odegard, G.M. Multiscale modeling of carbon fiber/carbon nanotube/epoxy hybrid composites: Comparison of epoxy matrices. Compos. Sci. Technol. 2018, 166, 20–26. [Google Scholar] [CrossRef]
- Li, W.; Dichiara, A.; Zha, J.; Su, Z.; Bai, J. On improvement of mechanical and thermo-mechanical properties of glass fabric/epoxy composites by incorporating CNT–Al2O3 hybrids. Compos. Sci. Technol. 2014, 103, 36–43. [Google Scholar] [CrossRef]
- Hadden, C.M.; Klimek-McDonald, D.R.; Pineda, E.J.; King, J.A.; Reichanadter, A.M.; Miskioglu, I.; Gowtham, S.; Odegard, G.M. Mechanical properties of graphene nanoplatelet/carbon fiber/epoxy hybrid composites: Multiscale modeling and experiments. Carbon 2015, 95, 100–112. [Google Scholar] [CrossRef]
- Aluko, O.; Gowtham, S.; Odegard, G.M. Multiscale modeling and analysis of graphene nanoplatelet/carbon fiber/epoxy hybrid composite. Compos. Part B Eng. 2017, 131, 82–90. [Google Scholar] [CrossRef]
- Al Mahmud, H.; Radue, M.; Chinkanjanarot, S.; Pisani, W.; Gowtham, S.; Odegard, G. Predicting the Effective Mechanical Properties of Graphene Nanoplatelet-Carbon Fiber-Epoxy Hybrid Composites Using ReaxFF: A Multiscale Modeling. Earth Space 2018, 16, 556. [Google Scholar]
- Al Mahmud, H.; Radue, M.S.; Chinkanjanarot, S.; Pisani, W.A.; Gowtham, S.; Odegard, G.M. Multiscale modeling of carbon fiber- graphene nanoplatelet-epoxy hybrid composites using a reactive force field. Compos. Part B Eng. 2019, 172, 628–635. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, W.; Zhang, J.; Ge, X.; Liu, X.; Zhan, Y. Multiscale graphene/carbon fiber reinforced copper matrix hybrid composites: Microstructure and properties. Mater. Sci. Eng. A 2019, 743, 512–519. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Habibi, S. Thermal effects on nonlinear dynamic characteristics of polymer-CNT-fiber multiscale nanocomposite structures. Struct. Eng. Mech. 2018, 67, 403–415. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Habibi, S. Nonlinear eccentric low-velocity impact response of a polymer-carbon nanotube-fiber multiscale nanocomposite plate resting on elastic foundations in hygrothermal environments. Mech. Adv. Mater. Struct. 2018, 25, 425–438. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ansari, R.; Rouhi, H. Studying buckling of composite rods made of hybrid carbon fiber/carbon nanotube reinforced polyimide using multiscale FEM. Sci. Iran. 2018, 27, 252–261. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ansari, R.; Rouhi, H. Free and forced vibration analysis of rectangular/circular/annular plates made of carbon fiber-carbon nanotube-polymer hybrid composites. Sci. Eng. Compos. Mater. 2019, 26, 70–76. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. On thermo-mechanical vibration analysis of multi-scale hybrid composite beams. J. Vib. Control 2019, 25, 933–945. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Vinyas, M. Nonlinear vibration analysis of multiscale doubly curved piezoelectric composite shell in hygrothermal environment. J. Intell. Mater. Syst. Struct. 2019, 30, 1594–1609. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Mahesh, V. Nonlinear free and forced vibration analysis of multiscale composite doubly curved shell embedded in shape-memory alloy fiber under hygrothermal environment. J. Vib. Control 2019, 25, 1945–1957. [Google Scholar] [CrossRef]
- Karimiasl, M.; Ebrahimi, F.; Akgöz, B. Buckling and post-buckling responses of smart doubly curved composite shallow shells embedded in SMA fiber under hygro-thermal loading. Compos. Struct. 2019, 223, 110988. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Vibration analysis of multi-scale hybrid nanocomposite plates based on a Halpin-Tsai homogenization model. Compos. Part B Eng. 2019, 173, 106955. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. An analytical solution for static stability of multi-scale hybrid nanocomposite plates. Eng. Comput. 2019, 1–15. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym. Compos. 2019, 40, 102–126. [Google Scholar] [CrossRef]
- Na, K.-S.; Kim, J.-H. Three-dimensional thermal buckling analysis of functionally graded materials. Compos. Part B Eng. 2004, 35, 429–437. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Ubertini, F.; Viola, E. Strong Formulation Finite Element Method Based on Differential Quadrature: A Survey. Appl. Mech. Rev. 2015, 67, 20801. [Google Scholar] [CrossRef]
- Shahgholian-Ghahfarokhi, D.; Safarpour, M.; Rahimi, A. Torsional buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (GPLs). Mech. Based Des. Struct. Mach. 2019, 10, 1–22. [Google Scholar] [CrossRef]
- Guo, H.; Zhuang, X.; Rabczuk, T. A Deep Collocation Method for the Bending Analysis of Kirchhoff Plate. CMC-Comput. Mater. Contin. 2019, 59, 433–456. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Shu, C.; Richards, B.E. Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 1992, 15, 791–798. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, R.; Safarpour, M. Vibration analysis of FG-GPLRC annular plate in a thermal environment. Mech. Based Des. Struct. Mach. 2020, 1–19. [Google Scholar] [CrossRef]
- Han, J.-B.; Liew, K. Axisymmetric free vibration of thick annular plates. Int. J. Mech. Sci. 1999, 41, 1089–1109. [Google Scholar] [CrossRef]
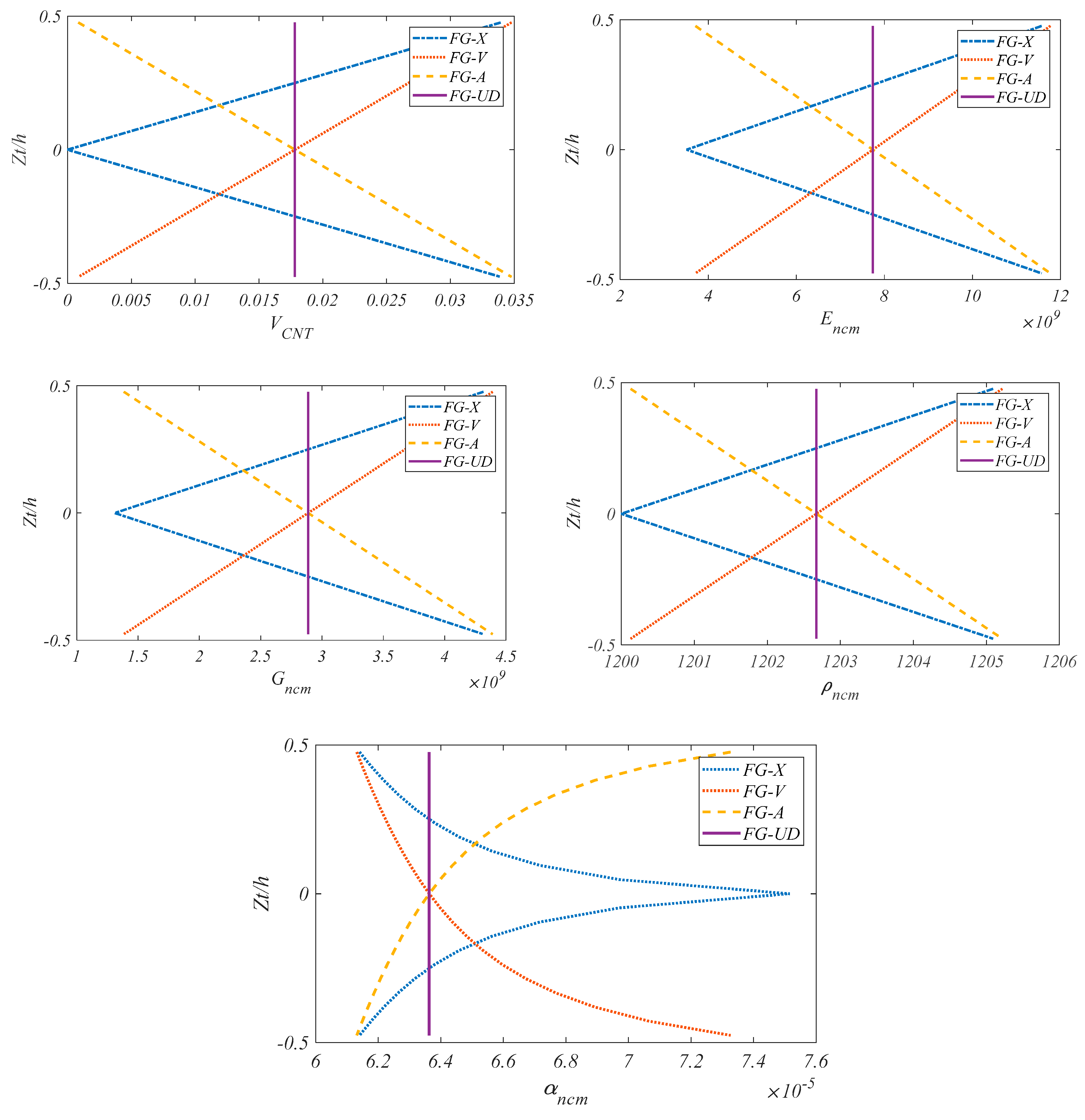




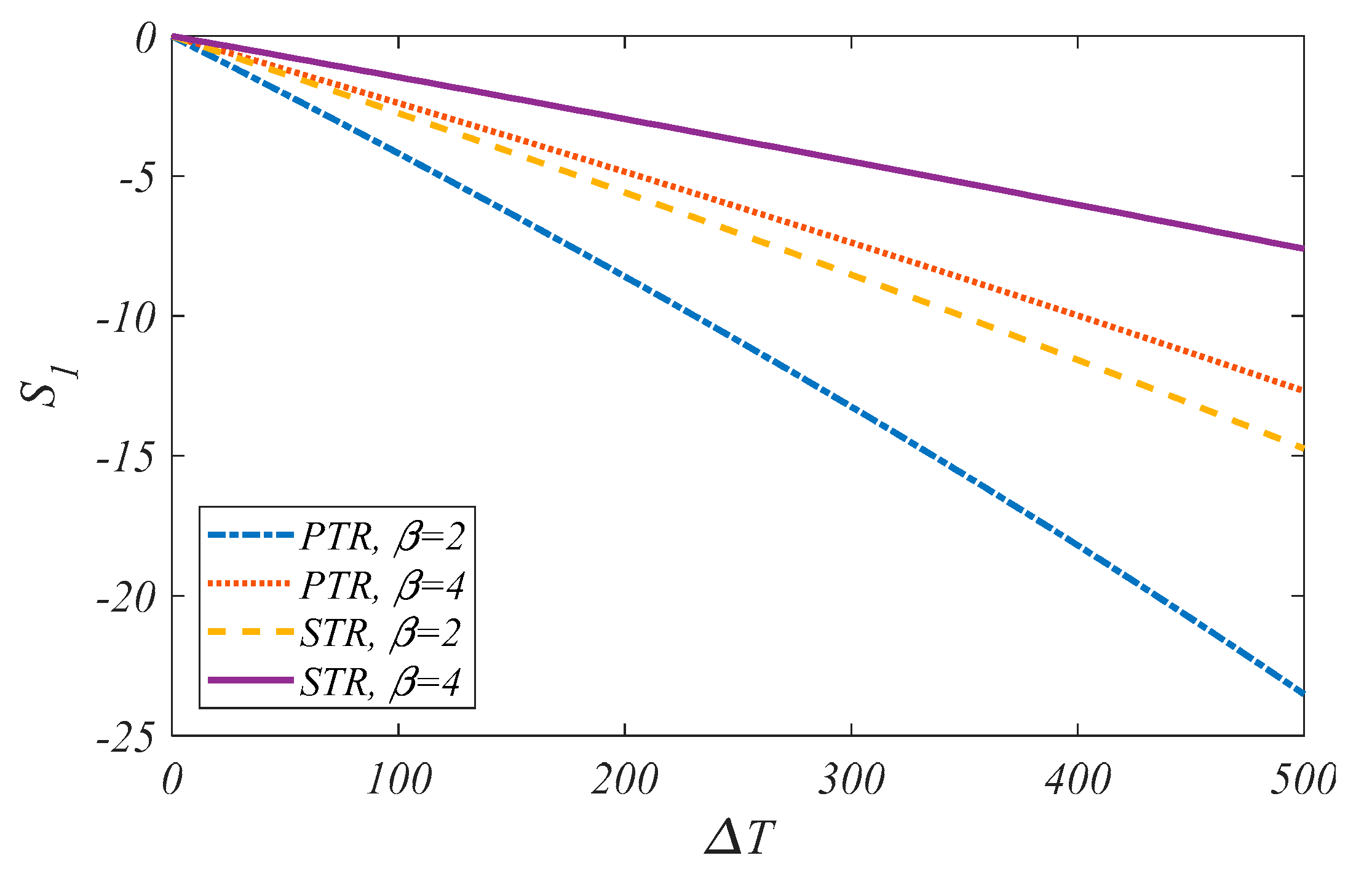
| Carbon fiber | |||||||||
| Epoxy Matrix | |||||||||
| Carbon nanotube | |||||||||
| Axisymmetric Vibration Mode Number | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 0.1 | Ref. [83] | 0.001 | 14.485 | 51.781 | 112.99 | 198.44 |
| Present | 0.001 | 13.624 | 50.302 | 111.86 | 198.61 | |
| Ref. [83] | 0.050 | 14.324 | 50.409 | 107.25 | 182.55 | |
| Present | 0.050 | 13.528 | 49.109 | 106.09 | 182.08 | |
| Ref. [83] | 0.100 | 13.874 | 46.947 | 94.670 | 151.91 | |
| Present | 0.100 | 13.254 | 46.061 | 93.794 | 151.36 | |
| Ref. [83] | 0.150 | 13.218 | 42.630 | 81.519 | 124.92 | |
| Present | 0.150 | 12.838 | 42.182 | 81.036 | 124.24 | |
| Ref. [83] | 0.200 | 12.450 | 38.337 | 70.224 | 104.20 | |
| Present | 0.200 | 12.326 | 38.243 | 70.075 | 104.04 | |
| 0.2 | Ref. [83] | 0.001 | 16.780 | 63.370 | 140.60 | 248.62 |
| Present | 0.001 | 16.652 | 63.003 | 140.90 | 250.68 | |
| Ref. [83] | 0.050 | 16.618 | 61.512 | 132.21 | 224.50 | |
| Present | 0.050 | 16.512 | 61.164 | 131.99 | 225.32 | |
| Ref. [83] | 0.100 | 16.164 | 56.912 | 114.70 | 182.50 | |
| Present | 0.100 | 16.118 | 56.621 | 114.14 | 181.93 | |
| Ref. [83] | 0.150 | 15.491 | 51.317 | 97.337 | 147.50 | |
| Present | 0.150 | 15.529 | 51.108 | 96.780 | 146.33 | |
| Ref. [83] | 0.200 | 14.688 | 45.866 | 82.963 | 121.66 | |
| Present | 0.200 | 14.819 | 45.751 | 82.567 | 121.21 | |
| Axisymmetric Vibration Mode Number | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 0.1 | Ref. [83] | 0.001 | 22.701 | 65.538 | 132.89 | 224.41 |
| Present | 0.001 | 20.852 | 63.734 | 131.50 | 223.86 | |
| Ref. [83] | 0.050 | 22.294 | 63.052 | 123.85 | 201.54 | |
| Present | 0.050 | 20.490 | 61.122 | 121.73 | 198.97 | |
| Ref. [83] | 0.100 | 21.200 | 56.912 | 105.46 | 161.99 | |
| Present | 0.100 | 19.512 | 54.993 | 102.79 | 158.00 | |
| Ref. [83] | 0.150 | 19.703 | 49.879 | 87.884 | 129.69 | |
| Present | 0.150 | 18.166 | 48.119 | 85.479 | 126.15 | |
| Ref. [83] | 0.200 | 18.073 | 43.431 | 73.899 | 106.37 | |
| Present | 0.200 | 16.695 | 41.972 | 72.128 | 104.17 | |
| 0.2 | Ref. [83] | 0.001 | 26.737 | 80.722 | 165.63 | 281.34 |
| Present | 0.001 | 25.772 | 79.931 | 165.66 | 282.52 | |
| Ref. [83] | 0.050 | 26.242 | 77.053 | 152.26 | 247.24 | |
| Present | 0.050 | 25.227 | 75.901 | 150.67 | 244.70 | |
| Ref. [83] | 0.100 | 24.916 | 68.635 | 126.72 | 193.10 | |
| Present | 0.100 | 23.785 | 66.912 | 123.76 | 188.24 | |
| Ref. [83] | 0.150 | 23.113 | 59.407 | 103.85 | 151.97 | |
| Present | 0.150 | 21.869 | 57.463 | 100.99 | 147.52 | |
| Ref. [83] | 0.200 | 21.162 | 51.247 | 86.427 | 123.40 | |
| Present | 0.200 | 19.853 | 49.456 | 84.276 | 120.89 | |
| Axisymmetric Vibration Mode Number | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 0.1 | Ref. [83] | 0.001 | 27.280 | 75.364 | 148.21 | 245.47 |
| Present | 0.001 | 28.514 | 77.363 | 151.05 | 249.05 | |
| Ref. [83] | 0.050 | 26.534 | 71.228 | 135.24 | 215.08 | |
| Present | 0.050 | 27.679 | 72.766 | 136.36 | 214.46 | |
| Ref. [83] | 0.100 | 24.629 | 62.140 | 111.12 | 167.16 | |
| Present | 0.100 | 25.558 | 62.834 | 110.39 | 163.41 | |
| Ref. [83] | 0.150 | 22.230 | 52.762 | 90.286 | 131.35 | |
| Present | 0.150 | 22.909 | 52.835 | 88.962 | 127.51 | |
| Ref. [83] | 0.200 | 19.843 | 44.913 | 74.860 | 106.81 | |
| Present | 0.200 | 20.294 | 44.683 | 73.628 | 103.75 | |
| 0.2 | Ref. [83] | 0.001 | 34.609 | 95.738 | 188.14 | 311.40 |
| Present | 0.001 | 35.712 | 97.395 | 190.61 | 314.62 | |
| Ref. [83] | 0.050 | 33.533 | 89.550 | 168.60 | 265.78 | |
| Present | 0.050 | 34.426 | 90.285 | 168.15 | 262.39 | |
| Ref. [83] | 0.100 | 30.841 | 76.560 | 134.71 | 200.02 | |
| Present | 0.100 | 31.274 | 75.895 | 131.87 | 193.37 | |
| Ref. [83] | 0.150 | 27.545 | 63.827 | 107.32 | 154.20 | |
| Present | 0.150 | 27.534 | 62.466 | 104.32 | 152.53 | |
| Ref. [83] | 0.200 | 24.348 | 53.574 | 87.870 | 123.93 | |
| Present | 0.200 | 24.022 | 52.122 | 85.531 | 121.89 | |
| VF | CNT Distribution | |||||
|---|---|---|---|---|---|---|
| 0.02 | 0.04 | 0.06 | 0.08 | 0.1 | ||
| 0.2 | FG-X | 2.7059 | 2.9976 | 3.2255 | 3.4195 | 3.5921 |
| FG-V | 2.7869 | 3.0596 | 3.2498 | 3.4018 | 3.5325 | |
| FG-A | 2.8217 | 3.1038 | 3.3006 | 3.4589 | 3.5958 | |
| FG-UD | 2.8089 | 3.0889 | 3.2854 | 3.4439 | 3.5812 | |
| 0.3 | FG-X | 2.9599 | 3.2604 | 3.4808 | 3.6596 | 3.8132 |
| FG-V | 3.0806 | 3.3817 | 3.5783 | 3.7265 | 3.8479 | |
| FG-A | 3.1203 | 3.4291 | 3.6294 | 3.7809 | 3.9058 | |
| FG-UD | 3.1070 | 3.4156 | 3.6170 | 3.7695 | 3.8950 | |
| 0.4 | FG-X | 3.1711 | 3.4722 | 3.6836 | 3.8486 | 3.9859 |
| FG-V | 3.3139 | 3.6278 | 3.8245 | 3.9670 | 4.0796 | |
| FG-A | 3.3563 | 3.6766 | 3.8753 | 4.0191 | 4.1332 | |
| FG-UD | 3.3437 | 3.6662 | 3.8675 | 4.0132 | 4.1283 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safarpour, M.; Rahimi, A.; Noormohammadi Arani, O.; Rabczuk, T. Frequency Characteristics of Multiscale Hybrid Nanocomposite Annular Plate Based on a Halpin–Tsai Homogenization Model with the Aid of GDQM. Appl. Sci. 2020, 10, 1412. https://doi.org/10.3390/app10041412
Safarpour M, Rahimi A, Noormohammadi Arani O, Rabczuk T. Frequency Characteristics of Multiscale Hybrid Nanocomposite Annular Plate Based on a Halpin–Tsai Homogenization Model with the Aid of GDQM. Applied Sciences. 2020; 10(4):1412. https://doi.org/10.3390/app10041412
Chicago/Turabian StyleSafarpour, Mehran, Alireza Rahimi, Omid Noormohammadi Arani, and Timon Rabczuk. 2020. "Frequency Characteristics of Multiscale Hybrid Nanocomposite Annular Plate Based on a Halpin–Tsai Homogenization Model with the Aid of GDQM" Applied Sciences 10, no. 4: 1412. https://doi.org/10.3390/app10041412
APA StyleSafarpour, M., Rahimi, A., Noormohammadi Arani, O., & Rabczuk, T. (2020). Frequency Characteristics of Multiscale Hybrid Nanocomposite Annular Plate Based on a Halpin–Tsai Homogenization Model with the Aid of GDQM. Applied Sciences, 10(4), 1412. https://doi.org/10.3390/app10041412






