Micromagnetic Modeling of All Optical Switching of Ferromagnetic Thin Films: The Role of Inverse Faraday Effect and Magnetic Circular Dichroism
Abstract
Featured Application
Abstract
1. Introduction
2. Micromagnetic Model
3. Results
3.1. Helicity-Dependent All Optical Switching (HD-AOS)
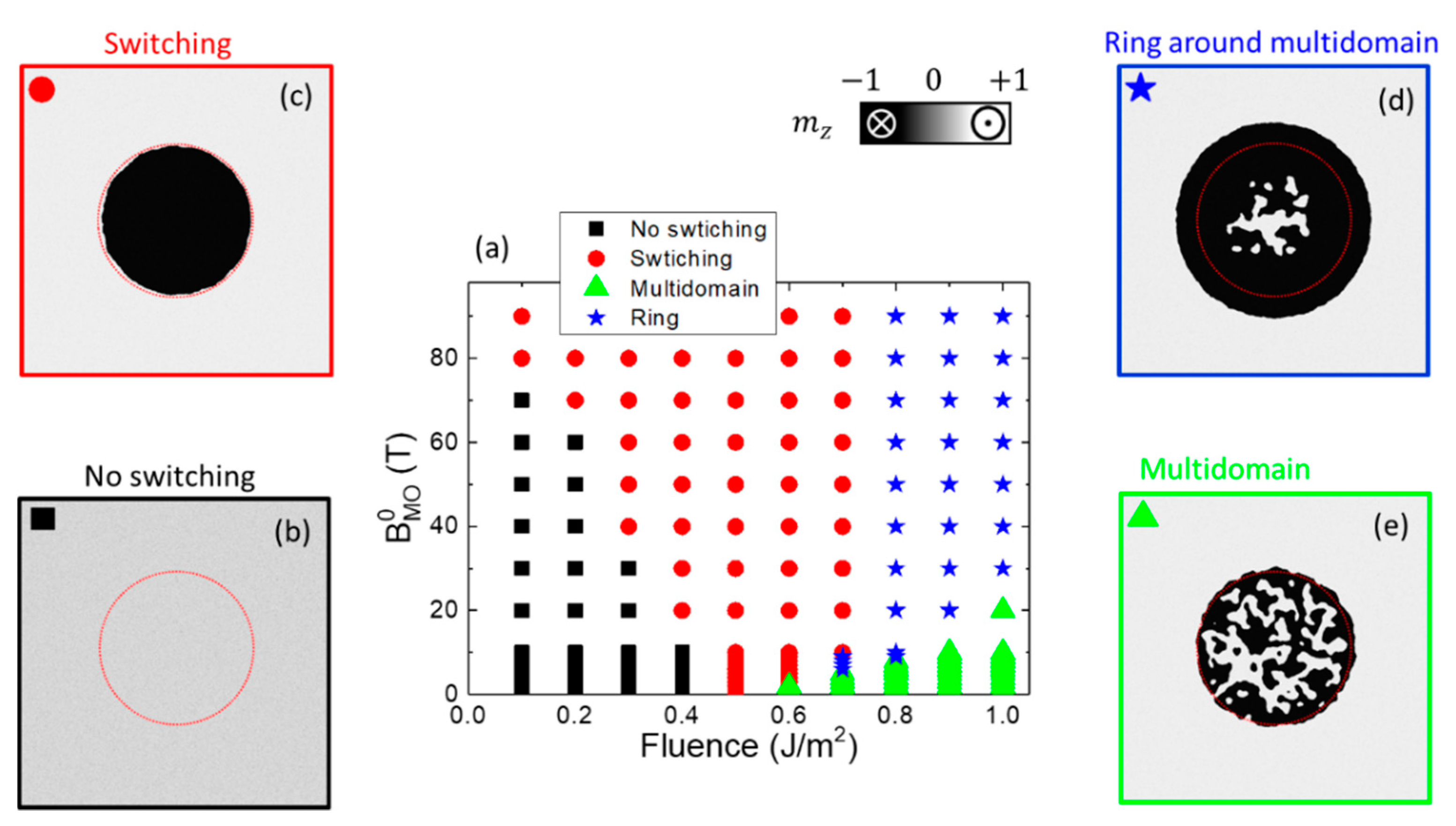
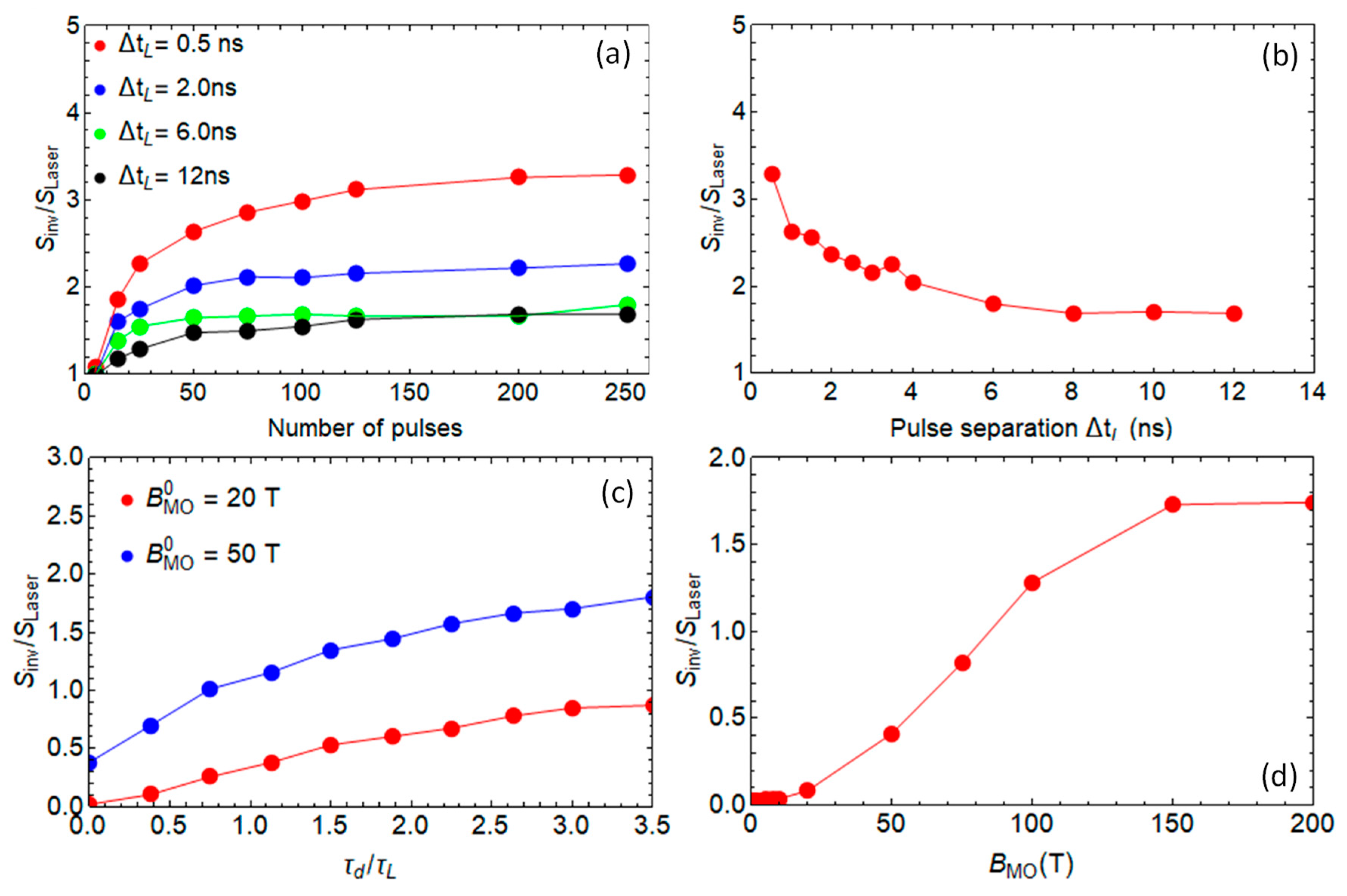
3.1.1. Helicity-Dependent All Optical Switching with Inverse Faraday Effect
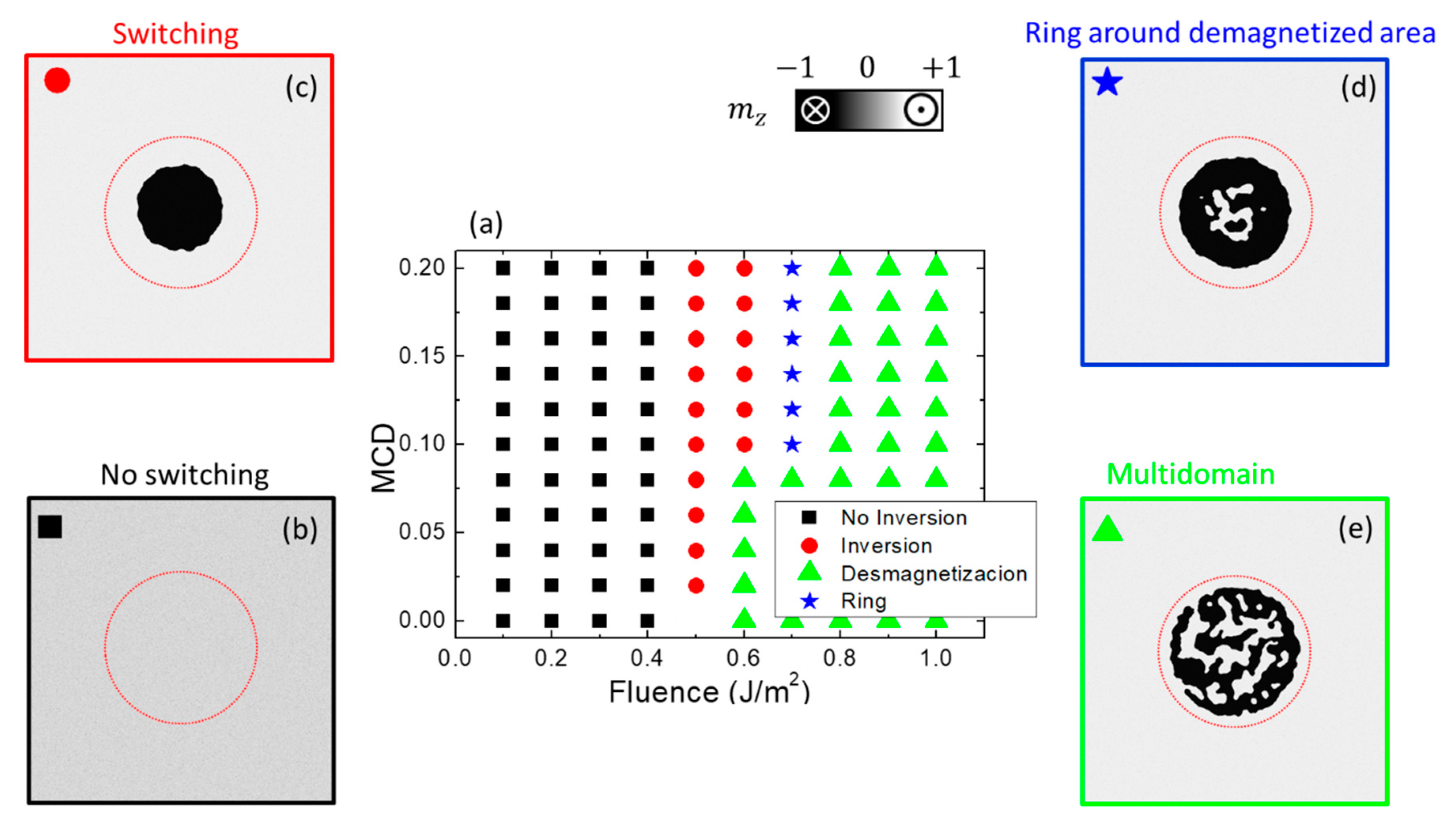
3.1.2. Helicity-Dependent All Optical Switching with Magnetic Circular Dichroism
3.2. Helicity-Dependent Domain Wall Motion (HD-DWM)
3.2.1. Helicity-Dependent Domain Wall Motion with Inverse Faraday Effect
3.2.2. Helicity-Dependent Domain Wall Motion with Magnetic Circular Dichroism
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 1996, 76, 4250–4253. [Google Scholar] [CrossRef] [PubMed]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef] [PubMed]
- Vahaplar, K.; Kalashnikova, A.M.; Kimel, A.V.; Gerlach, S.; Hinzke, D.; Nowak, U.; Chantrell, R.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; et al. All-optical magnetization reversal by circularly polarized laser pulses: Experiment and multiscale modeling. Phys. Rev. B 2012, 85, 104402. [Google Scholar] [CrossRef]
- Lalieu, M.L.M.; Peeters, M.J.G.; Haenen, S.R.R.; Lavrijsen, R.; Koopmans, B. Deterministic all-optical switching of synthetic ferrimagnets using single femtosecond laser pulses. Phys. Rev. B 2017, 96, 220411(R). [Google Scholar] [CrossRef]
- Liao, J.W.; Vallobra, P.; O’Brien, L.; Atxitia, U.; Raposo, V.; Petit, D.; Vemulkar, T.; Malinowski, G.; Hehn, M.; Martínez, E.; et al. Controlling All-Optical Helicity-Dependent Switching in Engineered Rare-Earth Free Synthetic Ferrimagnets. Adv. Sci. 2019, 1901876. [Google Scholar] [CrossRef] [PubMed]
- Hadri, M.S.; Pirro, P.; Lambert, C.-H.; Petit-Watelot, S.; Quessab, Y.; Hehn, M.; Montaigne, F.; Malinowski, G.; Mangin, S. Two types of all-optical magnetization switching mechanisms using femtosecond laser pulses. Phys. Rev. B 2016, 94, 064412. [Google Scholar] [CrossRef]
- Medapalli, R.; Afanasiev, D.; Kim, D.K.; Quessab, Y.; Manna, S.; Montoya, S.A.; Kirilyuk, A.; Rasing, T.; Kimel, A.V.; Fullerton, E.E. Mechanism of all-optical control of ferromagnetic multilayers with circularly polarized light. arXiv 2016, arXiv:1607.02505. [Google Scholar]
- Medapalli, R.; Afanasiev, D.; Kim, D.K.; Quessab, Y.; Manna, S.; Montoya, S.A.; Kirilyuk, A.; Rasing, T.; Kimel, A.V.; Fullerton, E.E. Multiscale dynamics of helicity-dependent all-optical magnetization reversal in ferromagnetic Co/Pt multilayers. Phys. Rev. B 2017, 96, 224421. [Google Scholar] [CrossRef]
- Tsema, Y.; Kichin, G.; Hellwig, O.; Mehta, V.; Kimel, A.V.; Kirilyuk, A.; Rasing, T. Helicity and field dependent magnetization dynamics of ferromagnetic Co/Pt multilayers. Appl. Phys. Lett. 2016, 109, 072405. [Google Scholar] [CrossRef]
- Lambert, C.H.; Mangin, S.; Varaprasad, B.S.D.C.S.; Takahashi, Y.K.; Hehn, M.; Cinchetti, M.; Malinowski, G.; Hono, K.; Fainman, Y.; Aeschlimann, M.; et al. All-optical control of ferromagnetic thin films and nanostructures. Science 2014, 345, 1337–1340. [Google Scholar] [CrossRef]
- Quessab, Y.; Medapalli, R.; El Hadri, M.S.; Hehn, M.; Malinowski, G.; Fullerton, E.E.; Mangin, S. Helicity-dependent all-optical domain wall motion in ferromagnetic thin films. Phys. Rev. B 2018, 97, 054419. [Google Scholar] [CrossRef]
- Mendil, J.; Nieves, P.; Chubykalo-Fesenko, O.; Walowski, J.; Santos, T.; Pisana, S.; Münzenberg, M. Resolving the role of femtosecond heated electrons in ultrafast spin dynamics. Sci. Rep. 2014, 4, 3980. [Google Scholar] [CrossRef] [PubMed]
- Koopmans, B.; Malinowski, G.; Dalla Longa, F.; Steiauf, D.; Fähnle, M.; Roth, T.; Cinchetti, M.; Aeschlimann, M. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 2010, 9, 259–265. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.; Davies, J.R.; Mendonca, J.T. Inverse faraday effect with linearly polarized laser pulses. Phys. Rev. Lett. 2010, 105, 035001. [Google Scholar] [CrossRef] [PubMed]
- Hertel, R. Theory of the inverse Faraday effect in metals. J. Magn. Magn. Mater. 2006, 303, L1–L4. [Google Scholar] [CrossRef]
- Taguchi, K.; Ohe, J.I.; Tatara, G. Ultrafast magnetic vortex core switching driven by the topological inverse Faraday effect. Phys. Rev. Lett. 2012, 109, 127204. [Google Scholar] [CrossRef]
- Khorsand, A.R.; Savoini, M.; Kirilyuk, A.; Kimel, A.V.; Tsukamoto, A.; Itoh, A.; Rasing, T. Role of magnetic circular dichroism in all-optical magnetic recording. Phys. Rev. Lett. 2012, 108, 127205. [Google Scholar] [CrossRef]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Laser-induced magnetization dynamics and reversal in ferrimagnetic alloys. Reports Prog. Phys. 2013, 76, 026501. [Google Scholar] [CrossRef]
- Rudolf, D.; La-O-Vorakiat, C.; Battiato, M.; Adam, R.; Shaw, J.M.; Turgut, E.; Maldonado, P.; Mathias, S.; Grychtol, P.; Nembach, H.T.; et al. Ultrafast magnetization enhancement in metallic multilayers driven by superdiffusive spin current. Nat. Commun. 2012, 3, 1036–1037. [Google Scholar] [CrossRef]
- Razdolski, I.; Alekhin, A.; Ilin, N.; Meyburg, J.P.; Roddatis, V.; DIesing, D.; Bovensiepen, U.; Melnikov, A. Nanoscale interface confinement of ultrafast spin transfer torque driving non-uniform spin dynamics. Nat. Commun. 2017, 108, 15007. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Naseri, N.; Bychenkov, V.Y.; Rozmus, W. Axial magnetic field generation by intense circularly polarized laser pulses in underdense plasmas. Phys. Plasmas 2010, 17, 083109. [Google Scholar] [CrossRef]
- Haines, M.G. Generation of an axial magnetic field from photon spin. Phys. Rev. Lett. 2001, 87, 135005. [Google Scholar] [CrossRef] [PubMed]
- Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; Atxitia, U.; Chubykalo-Fesenko, O.; El Moussaoui, S.; Le Guyader, L.; Mengotti, E.; Heyderman, L.J.; et al. Ultrafast heating as a sufficient stimulus for magnetization reversal in a ferrimagnet. Nat. Commun. 2012, 3, 666. [Google Scholar] [CrossRef]
- Cornelissen, T.D.; Córdoba, R.; Koopmans, B. Microscopic model for all optical switching in ferromagnets. Appl. Phys. Lett. 2016, 108, 142405. [Google Scholar] [CrossRef]
- Kimling, J.; Kimling, J.; Wilson, R.B.; Hebler, B.; Albrecht, M.; Cahill, D.G. Ultrafast demagnetization of FePt:Cu thin films and the role of magnetic heat capacity. Phys. Rev. B 2014, 90, 224408. [Google Scholar] [CrossRef]
- Evans, R.F.L.; Hinzke, D.; Atxitia, U.; Nowak, U.; Chantrell, R.W.; Chubykalo-Fesenko, O. Stochastic form of the Landau-Lifshitz-Bloch equation. Phys. Rev. B 2012, 85, 014433. [Google Scholar] [CrossRef]
- Anisimov, S.; Kapeliovich, B.; Perel’Man, T. Electron emission from metal surfaces exposed to ultrashort laser pulses. Sov. J. Exp. Theor. Phys. 1974, 39, 776–781. [Google Scholar]
- Moretti, S.; Raposo, V.; Martinez, E.; Moretti, S.; Raposo, V.; Martinez, E. Influence of Joule heating on current-induced domain wall depinning Influence of Joule heating on current-induced domain wall depinning. J. Appl. Phys. 2016, 119, 213902. [Google Scholar] [CrossRef]
- Lopez-Diaz, L.; Aurelio, D.; Torres, L.; Martinez, E.; Hernandez-Lopez, M.A.; Gomez, J.; Alejos, O.; Carpentieri, M.; Finocchio, G.; Consolo, G. Micromagnetic simulations using Graphics Processing Units. J. Phys. D 2012, 45, 323001. [Google Scholar] [CrossRef]
- Chubykalo-Fesenko, O.; Nowak, U.; Chantrell, R.W.; Garanin, D. Dynamic approach for micromagnetics close to the Curie temperature. Phys. Rev. B 2006, 74, 094436. [Google Scholar] [CrossRef]
- Moretti, S.; Raposo, V.; Martinez, E.; Lopez-Diaz, L. Domain wall motion by localized temperature gradients. Phys. Rev. B 2017, 95, 064419. [Google Scholar] [CrossRef]
- Hansteen, F.; Kimel, A.; Kirilyuk, A.; Rasing, T. Femtosecond photomagnetic switching of spins in ferrimagnetic garnet films. Phys. Rev. Lett. 2005, 95, 047402. [Google Scholar] [CrossRef] [PubMed]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731–2784. [Google Scholar] [CrossRef]
- Nieves, P.; Chubykalo-Fesenko, O. Modeling of Ultrafast Heat and Field-Assisted Magnetization Dynamics in FePt. Phys. Rev. Appl. 2016, 5, 014006. [Google Scholar] [CrossRef]
- Gorchon, J.; Yang, Y.; Bokor, J. Model for multishot all-thermal all-optical switching in ferromagnets. Phys. Rev. B 2016, 94, 020409. [Google Scholar] [CrossRef]
- Raposo, V.; Luis Martinez, R.F.; Martinez, E. Current-driven skyrmion motion along disordered magnetic tracks. AIP Adv. 2017, 7, 056017. [Google Scholar] [CrossRef]
- Raposo, V.; Moretti, S.; Hernandez, M.A.; Martinez, E. Domain wall dynamics along curved strips under current pulses: The influence of Joule heating. Appl. Phys. Lett. 2016, 108, 042405. [Google Scholar] [CrossRef]





| 1.1 | 1.25 | 15 | 2.25 | 91 | 930 | 3.7 | 550 | 0.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raposo, V.; Guedas, R.; García-Sánchez, F.; Hernández, M.A.; Zazo, M.; Martínez, E. Micromagnetic Modeling of All Optical Switching of Ferromagnetic Thin Films: The Role of Inverse Faraday Effect and Magnetic Circular Dichroism. Appl. Sci. 2020, 10, 1307. https://doi.org/10.3390/app10041307
Raposo V, Guedas R, García-Sánchez F, Hernández MA, Zazo M, Martínez E. Micromagnetic Modeling of All Optical Switching of Ferromagnetic Thin Films: The Role of Inverse Faraday Effect and Magnetic Circular Dichroism. Applied Sciences. 2020; 10(4):1307. https://doi.org/10.3390/app10041307
Chicago/Turabian StyleRaposo, Victor, Rodrigo Guedas, Felipe García-Sánchez, M. Auxiliadora Hernández, Marcelino Zazo, and Eduardo Martínez. 2020. "Micromagnetic Modeling of All Optical Switching of Ferromagnetic Thin Films: The Role of Inverse Faraday Effect and Magnetic Circular Dichroism" Applied Sciences 10, no. 4: 1307. https://doi.org/10.3390/app10041307
APA StyleRaposo, V., Guedas, R., García-Sánchez, F., Hernández, M. A., Zazo, M., & Martínez, E. (2020). Micromagnetic Modeling of All Optical Switching of Ferromagnetic Thin Films: The Role of Inverse Faraday Effect and Magnetic Circular Dichroism. Applied Sciences, 10(4), 1307. https://doi.org/10.3390/app10041307





