The Rational Spline Interpolation Based-LOD Method and Its Application to Rotating Machinery Fault Diagnosis
Abstract
1. Introduction
2. Local Oscillatory-Characteristic Decomposition and its Defects
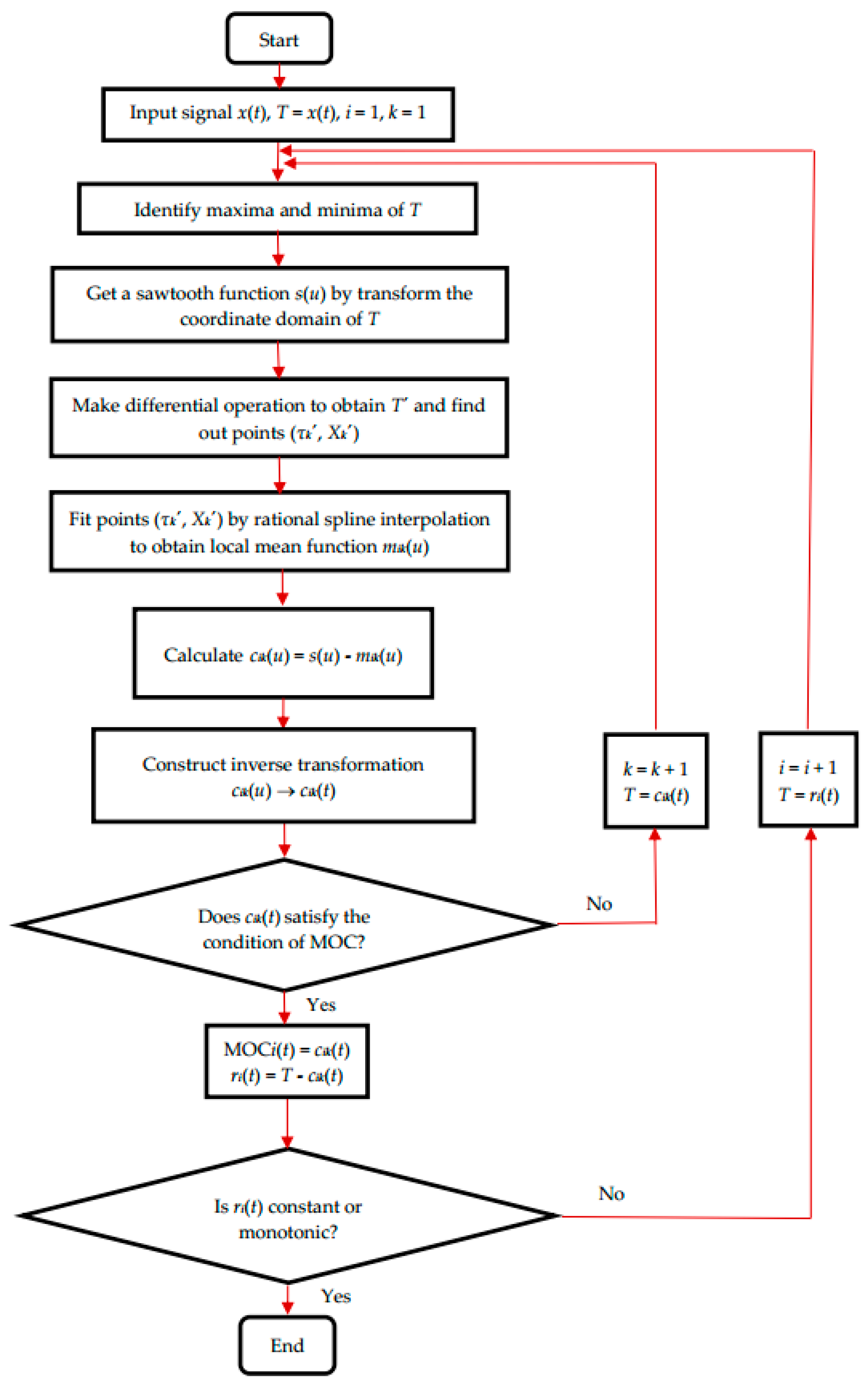
3. Design Implementation of the Rational Spline Based-LOD Method
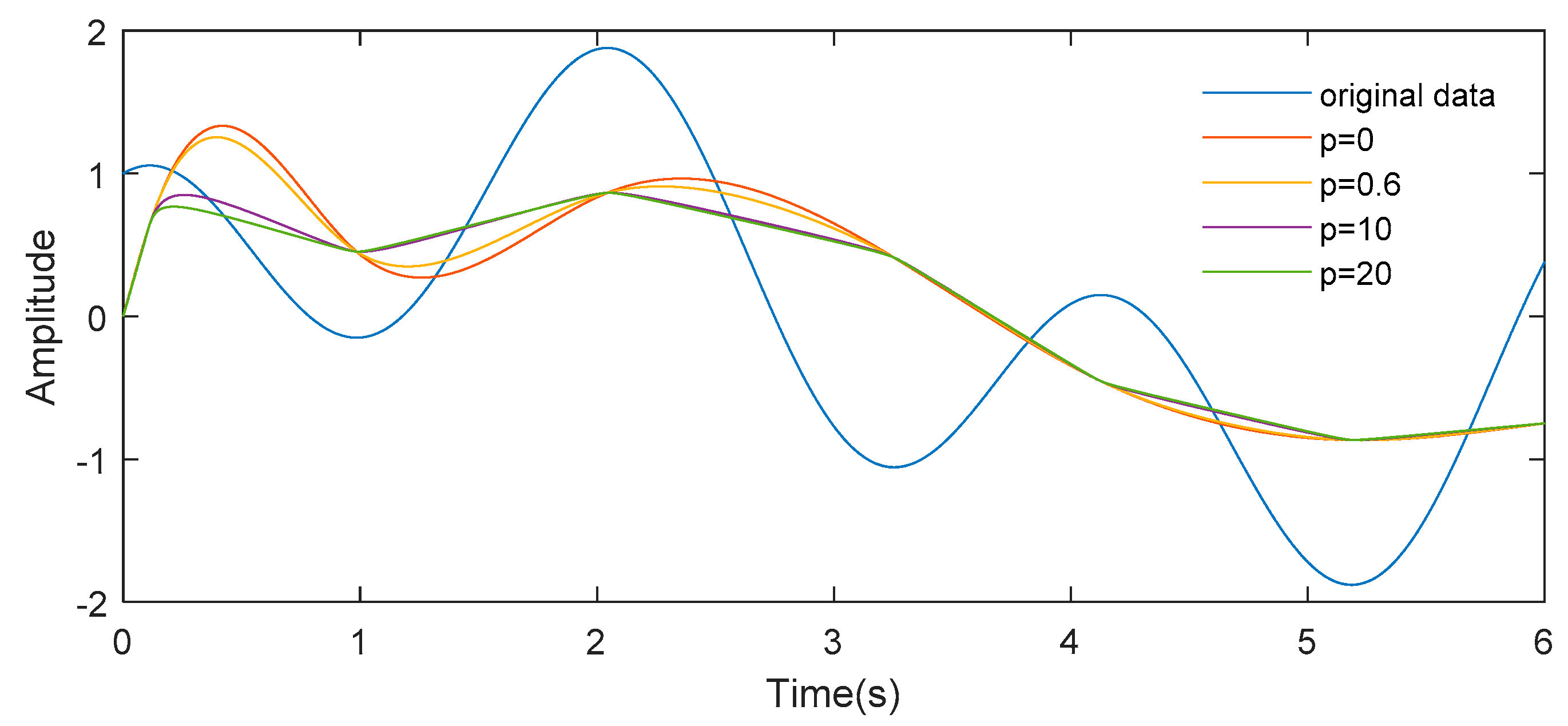
3.1. Rational Spline Interpolation
3.2. Rational Spline Based-LOD Method
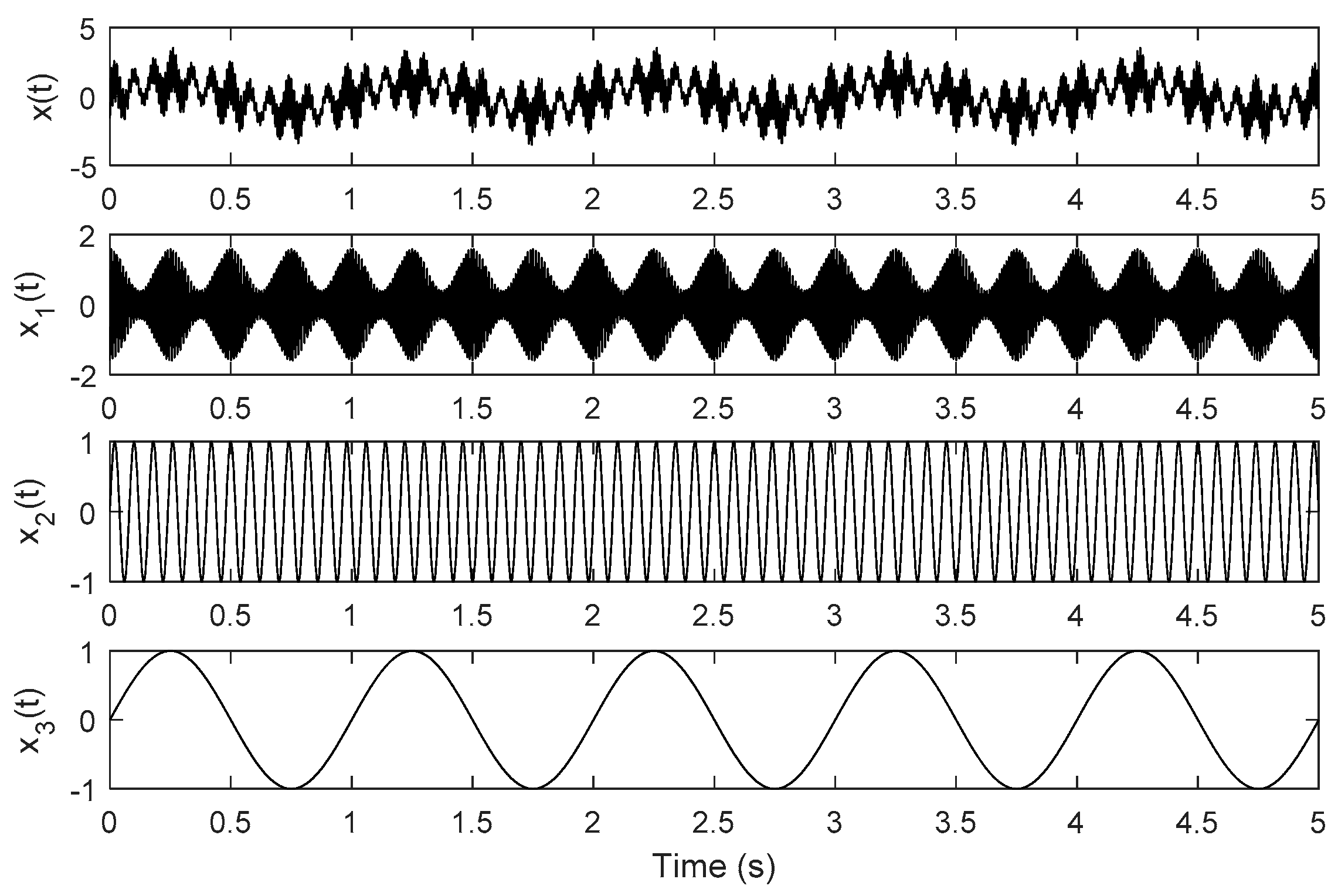
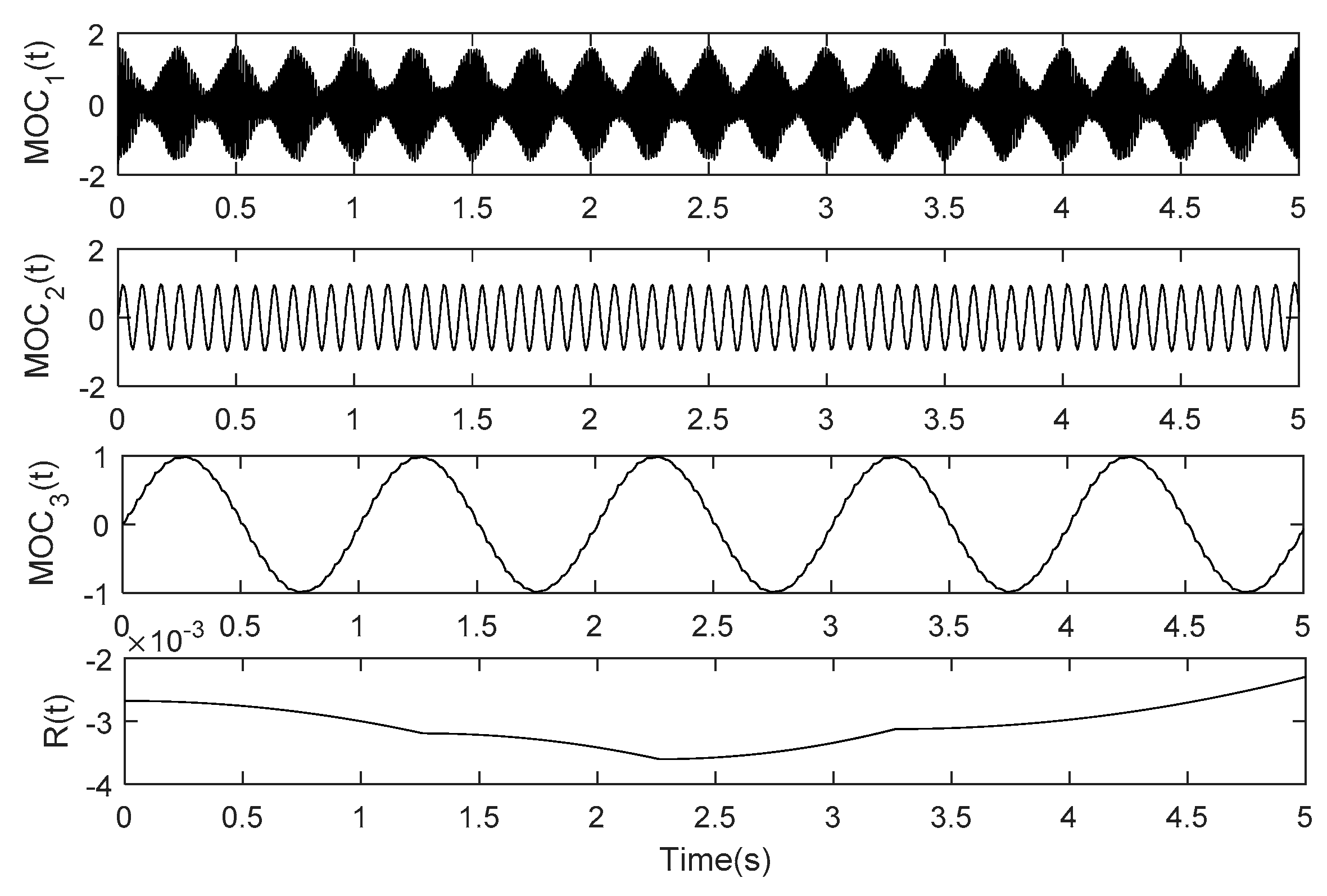
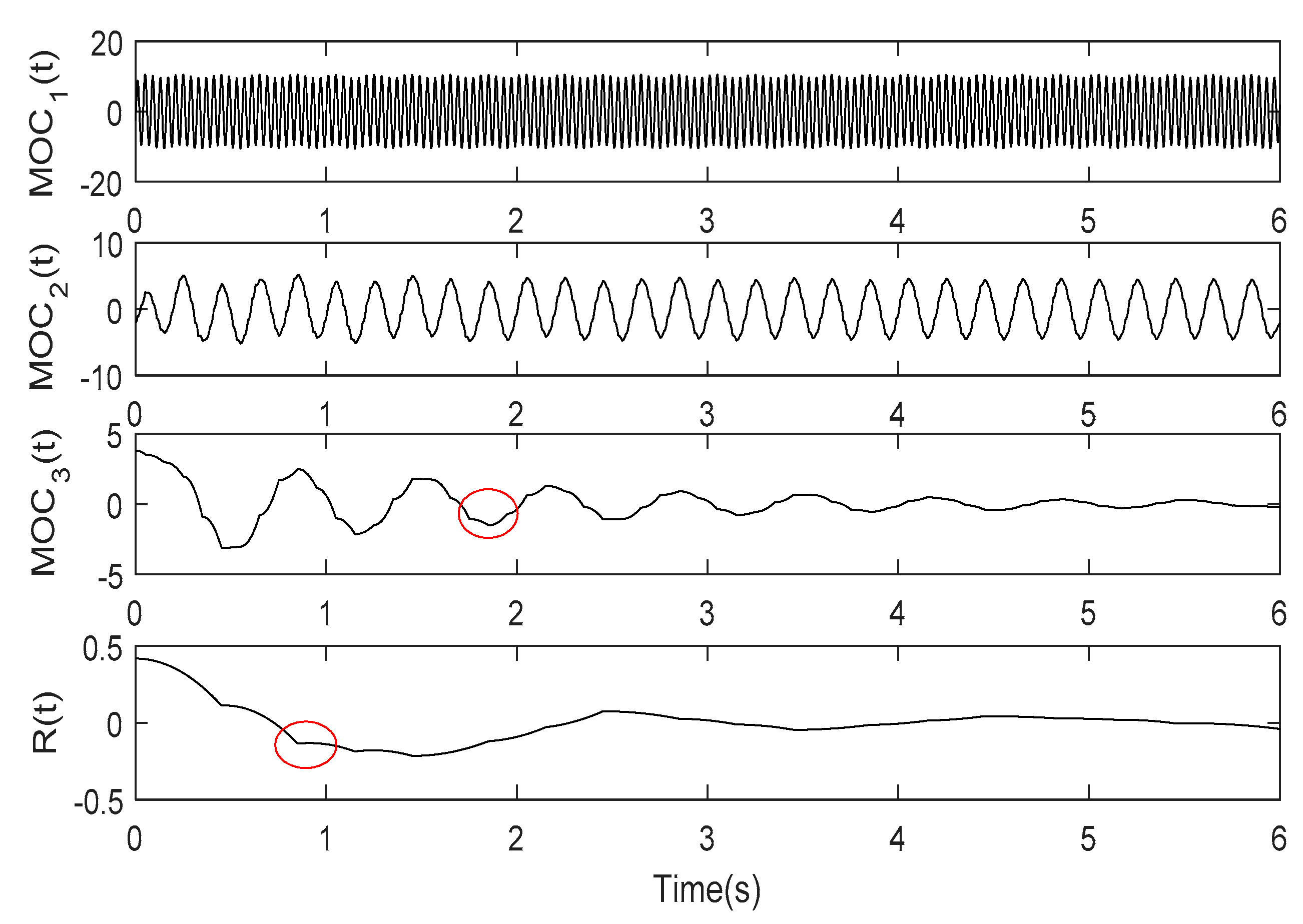
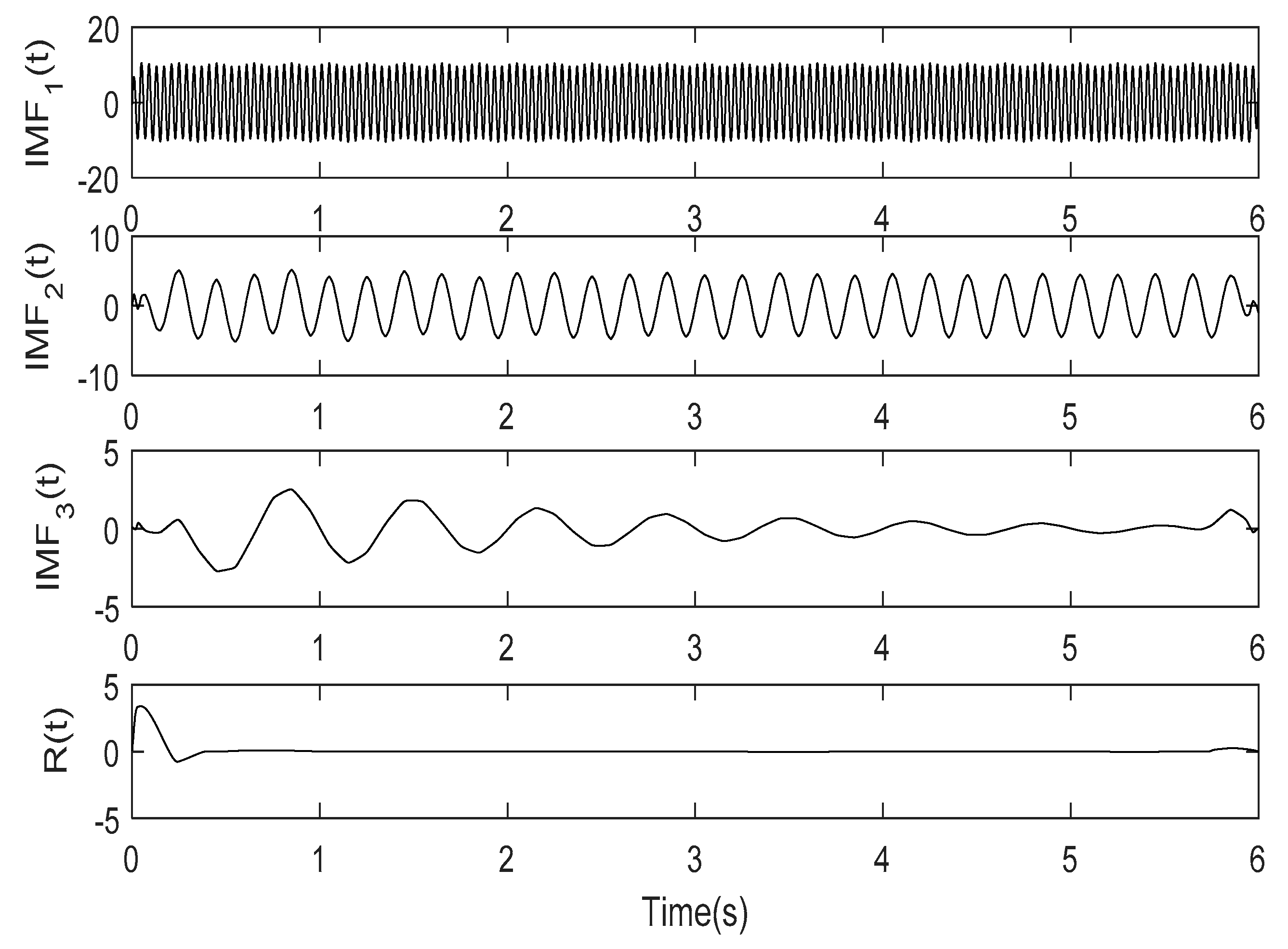
4. Application to Simulation Signal
5. Application to Rotating Machinery Fault Diagnosis
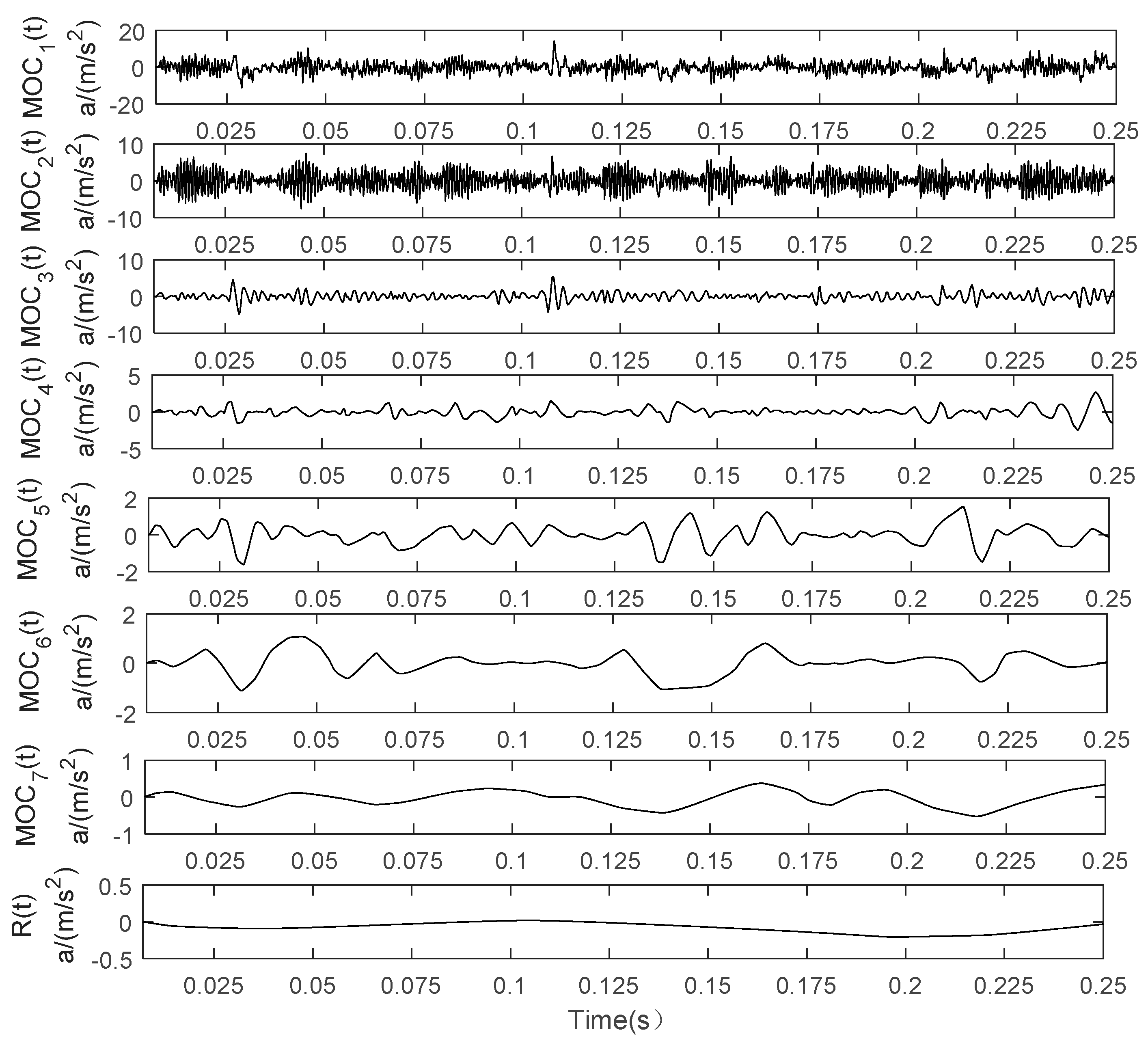
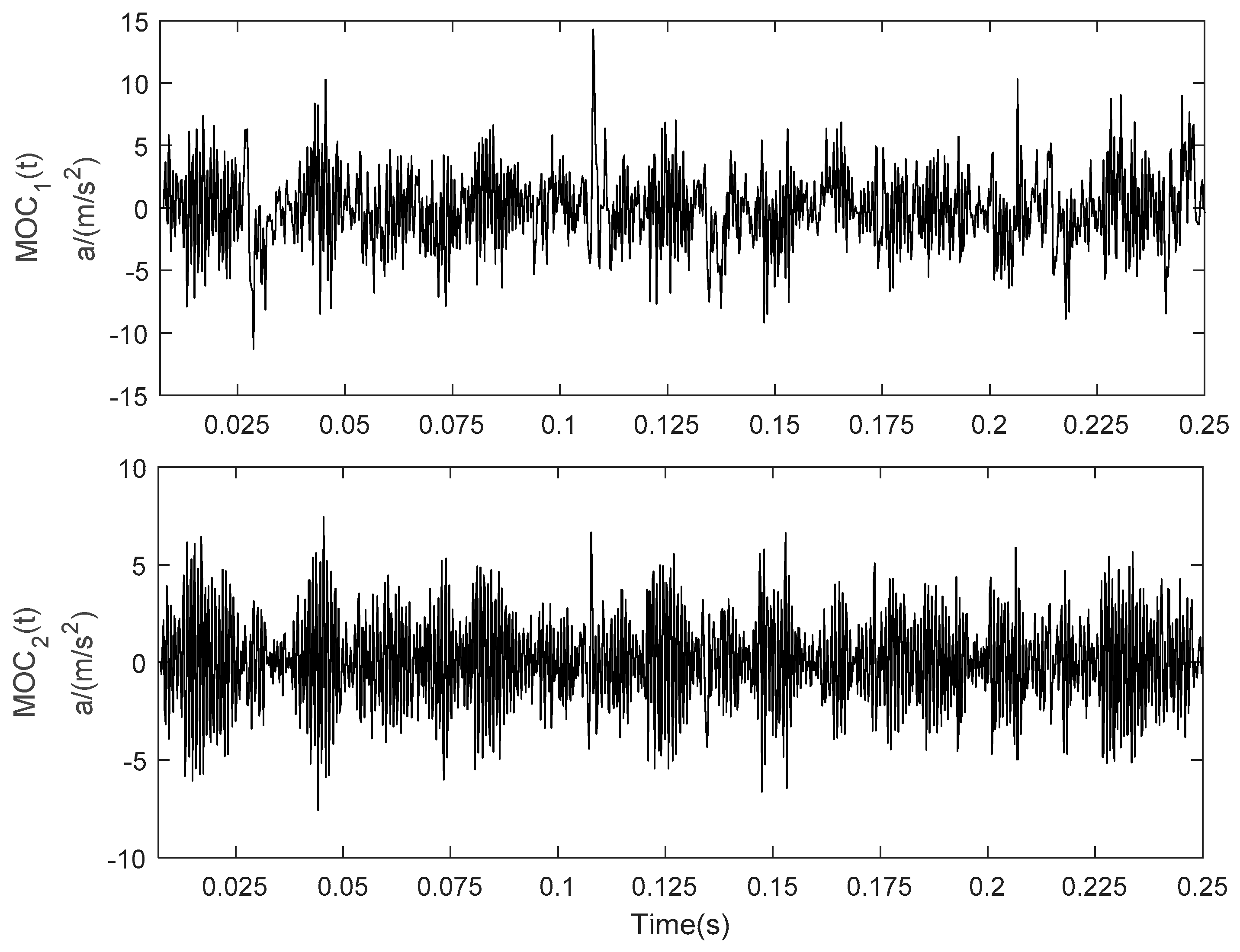
5.1. Application to Rolling Bearing Fault Diagnosis
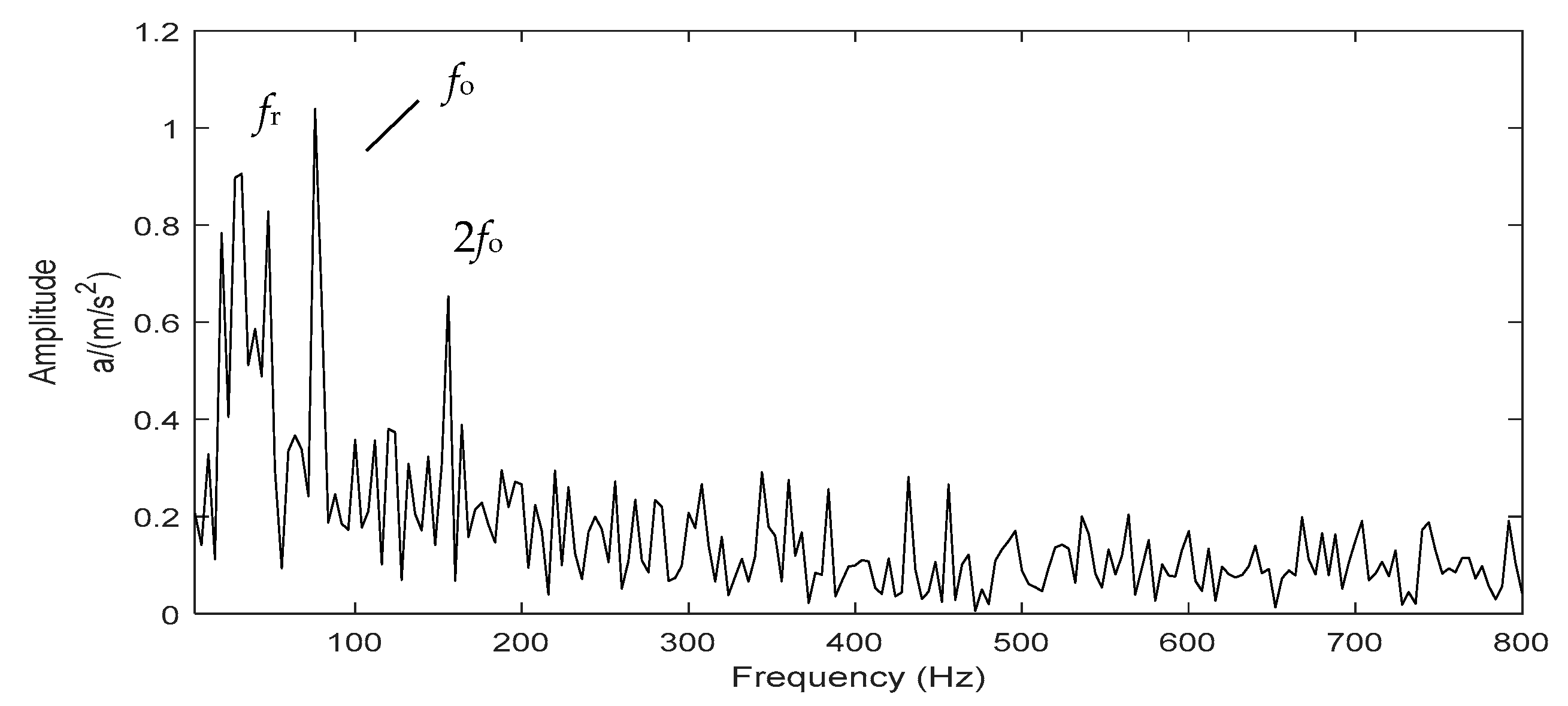
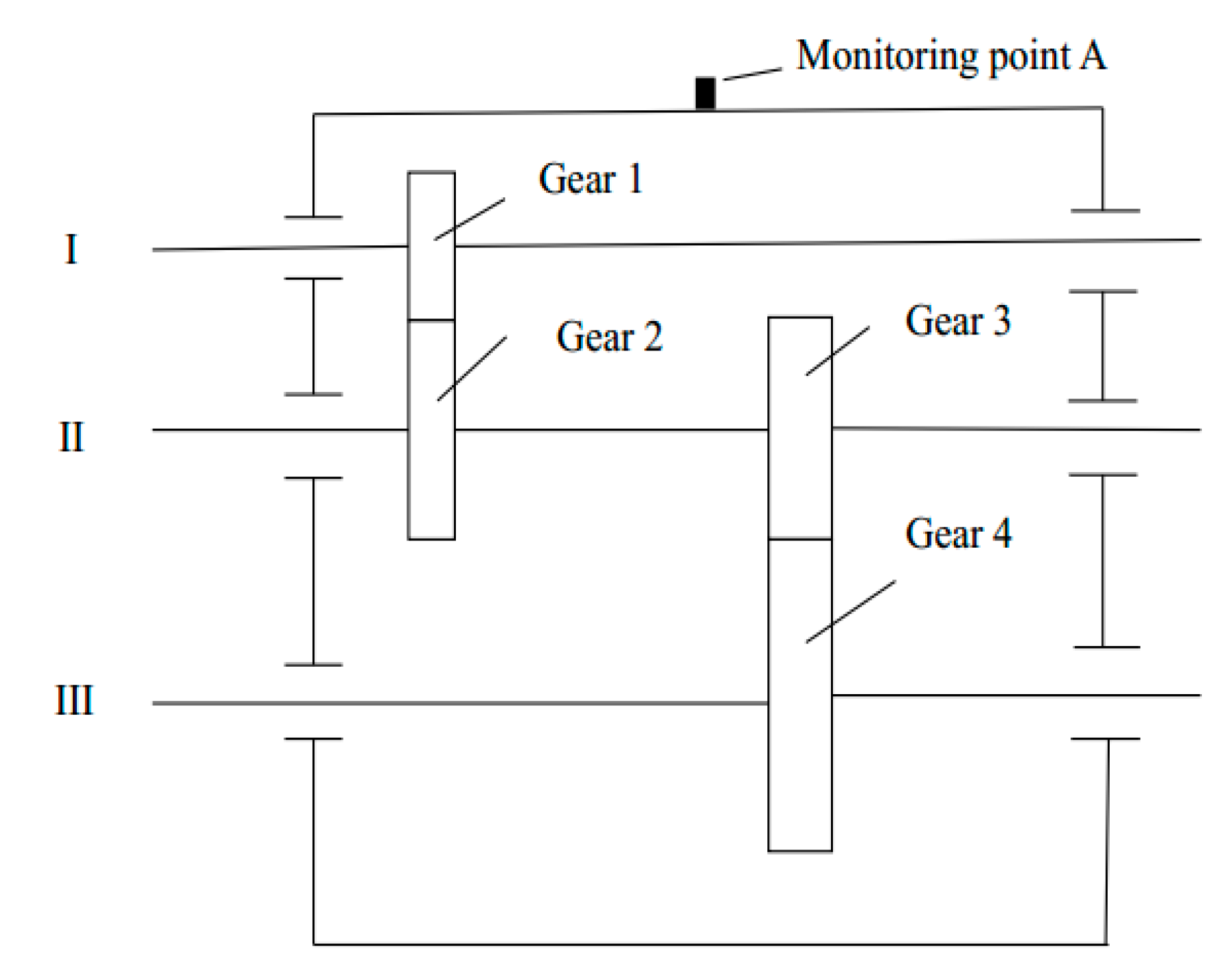
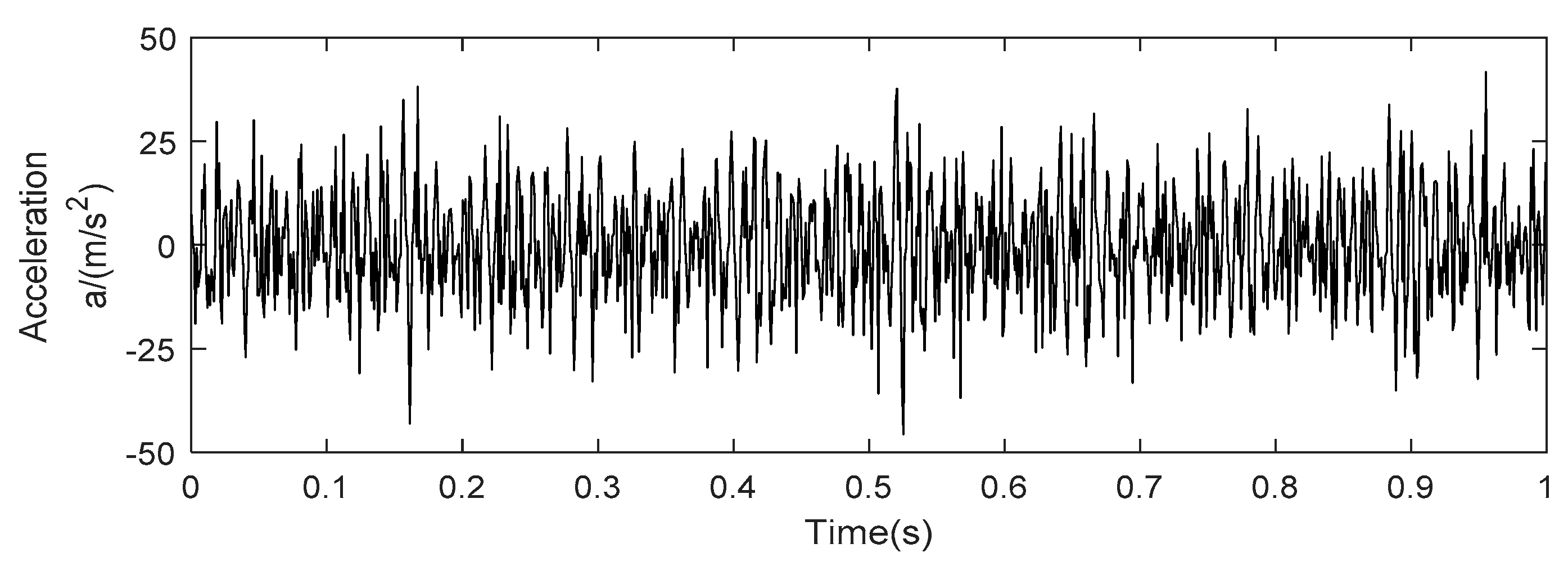
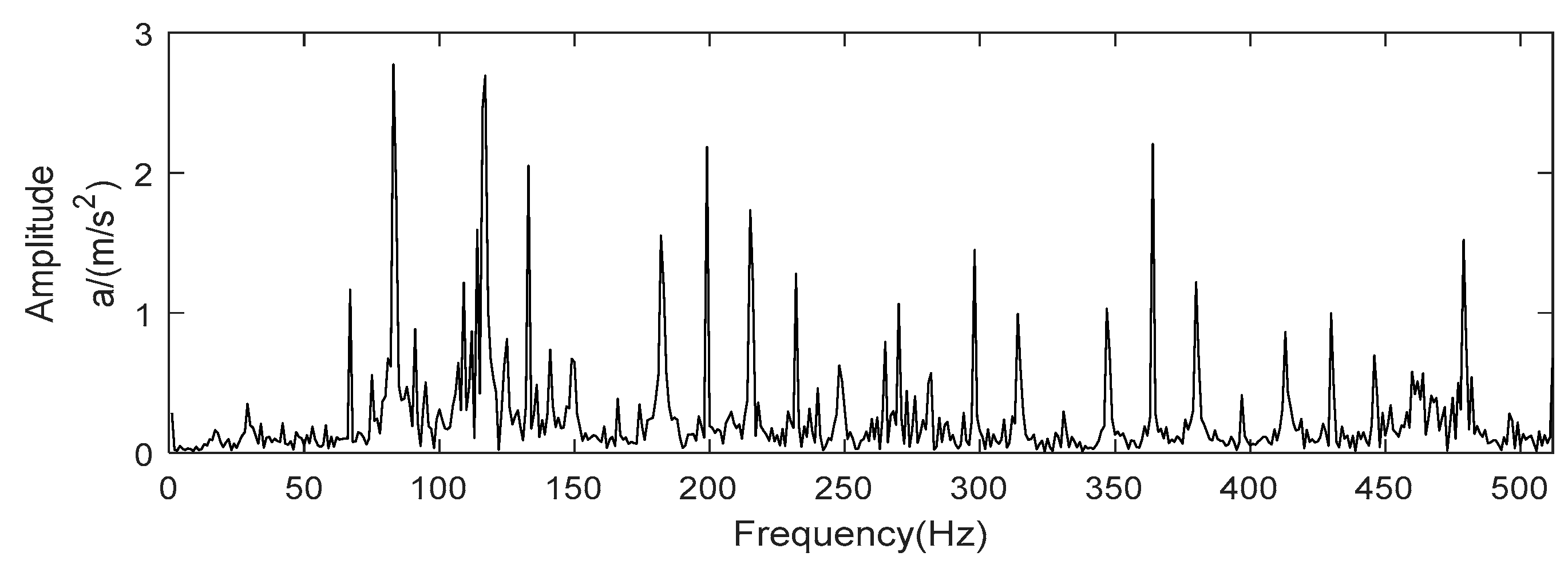
5.2. Application to Fan Gearbox Fault Diagnosis
6. Discussion
7. Conclusions
- The analysis of the simulation signal shows that although the consuming time of the RS-LOD method is a little longer than the original LOD method, it solves the problems of MOC component poor smoothness and distortion in the original LOD method, and overall analysis effects are also better than that of EMD and LOD method.
- The analyses of fault vibration signals of rolling bearing and fan gearbox show that the envelope spectrum based on RS-LOD can effectively extract the characteristic fault information of the corresponding vibration signal, which provides a new effective way to extract the vibration signal feature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Prudhom, A.; Antonino-Daviu, J.; Razik, H.; Vicente, C.-A. Time-frequency vibration analysis for the detection of motor damages caused by bearing currents. Mech. Syst. Signal Process. 2017, 84, 747–762. [Google Scholar] [CrossRef]
- Stanković, L.; Mandić, D.; Daković, M.; Brajovića, M. Time-frequency decomposition of multivariate multicomponent signals. Signal Process. 2018, 142, 468–479. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, K.; Ma, C.; Li, X.; Zhang, J. An improved empirical wavelet transform and its applications in rolling bearing fault diagnosis. Appl. Sci. 2018, 8, 2352. [Google Scholar] [CrossRef]
- Dhamande, L.S.; Chaudhari, M.B. Compound gear-bearing fault feature extraction using statistical features based on time-frequency method. Measurement 2018, 125, 63–77. [Google Scholar] [CrossRef]
- Mateo, C.; Talavera, J.A. Short-time Fourier transform with the window size fixed in the frequency domain. Digit. Signal Process. 2018, 77, 13–21. [Google Scholar] [CrossRef]
- Yoo, Y.; Baek, J.-G. A novel image feature for the remaining useful lifetime prediction of bearings based on continuous wavelet transform and convolutional neural network. Appl. Sci. 2018, 8, 1102. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 2, 443–454. [Google Scholar] [CrossRef]
- Dong, S.; Xu, X.; Luo, J. Mechanical fault diagnosis method based on LMD Shannon entropy and improved fuzzy C-mean clustering. Int. J. Acoust. Vib. 2017, 22, 211–217. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, X.; Zhang, X.; He, Z. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM. Measurement 2012, 45, 30–40. [Google Scholar] [CrossRef]
- Lu, L.; Yan, J.; Silva, C.W. Feature selection for ECG signal processing using improved genetic algorithm and empirical mode decomposition. Measurement 2016, 94, 372–381. [Google Scholar] [CrossRef]
- Sang, Y.F.; Wang, Z.; Liu, C. Period identification in hydrologic time series using empirical mode decomposition and maximum entropy spectral analysis. J. Hydrol. 2012, 424–425, 154–164. [Google Scholar] [CrossRef]
- Fauchereau, N.; Pegram, G.G.S.; Sinclair, S. 2-D Empirical Mode Decomposition on the sphere: Application to the spatial scales of surface temperature variations. Hydrol. Earth Syst. Sci. 2008, 12, 933–941. [Google Scholar] [CrossRef]
- Wolszczak, P.; Łygas, K.; Litak, G. Monitoring of cutting conditions with the empirical mode decomposition. Adv. Sci. Technol. Res. J. 2017, 11, 96–103. [Google Scholar] [CrossRef]
- He, Z.; Shen, Y.; Wang, Q. Boundary extension for Hilbert–Huang transform inspired by gray prediction model. Signal Process. 2012, 92, 685–697. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Zheng, J.; Cheng, J.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. A comparative study on the local mean decomposition and empirical mode decomposition and their application to rotating machinery health diagnosis. J. Vib. Acoust. 2010, 132, 1–10. [Google Scholar] [CrossRef]
- Hu, J.; Ren, D.; Yang, S. Spline-Based local mean decomposition method for vibration signal. J. Data Acquis. Process. 2009, 24, 82–86. [Google Scholar] [CrossRef]
- Chen, B.; He, Z.; Chen, X.; Cao, H.; Cai, G.; Zi, Y. A demodulating approach based on local mean decomposition and its applications in mechanical fault diagnosis. Meas. Sci. Technol. 2011, 22, 055704. [Google Scholar] [CrossRef]
- Zhang, K.; Shi, Y.; Tang, M.; Wu, J. Local oscillatory-characteristic decomposition and its application in roller bearing fault diagnosis. J. Vib. Shock 2016, 35, 89–95. [Google Scholar] [CrossRef]
- Wu, J.; Peng, X.; Yang, Y.; Zhang, K.; Cheng, J. Quantitative diagnosis method of gear cracks based on noise-assisted LOD. China Mech. Eng. 2016, 27, 3183–3189. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, X.; Liao, L.; Tang, M.; Wu, J. A new rotating machinery fault diagnosis method based on local oscillatory-characteristic decomposition. Digit. Signal Process. 2018, 78, 98–107. [Google Scholar] [CrossRef]
- Pegram, G.G.S.; Peel, M.C.; McMahon, T.A. Empirical mode decomposition using rational splines: An application to rainfall time series. Proc. R. Soc. A 2008, 464, 1483–1501. [Google Scholar] [CrossRef]
- Peel, M.C.; McMahon, T.A.; Pegram, G.G.S. Assessing the performance of rational spline-based empirical mode decomposition using a global annual precipitation dataset. Proc. R. Soc. A 2009, 465, 1919–1937. [Google Scholar] [CrossRef]
- Zhang, K.; Cheng, J.; Yang, Y. The local mean decomposition method based on rational spline and its application. J. Vib. Eng. 2011, 24, 96–103. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Lin, J.; Lu, F. Phenomenological models of vibration signals for condition monitoring and fault diagnosis of epicyclic gearboxes. J. Sound Vib. 2016, 369, 266–281. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Borboni, A.; Aggogeri, F.; Elamvazuthi, I.; Incerti, G.; Magnani, P.L. Effects of profile interpolation in cam mechanisms. Mech. Mach. Theory 2020, 144, 103652. [Google Scholar] [CrossRef]
- Aggogeri, F.; Borboni, A.; Strano, S.; Terzo, M. Effects of DAC interpolation on the dynamics of a high speed linear actuator. In Proceedings of the 14th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Oulu, Finland, 2–4 July 2018. [Google Scholar] [CrossRef]






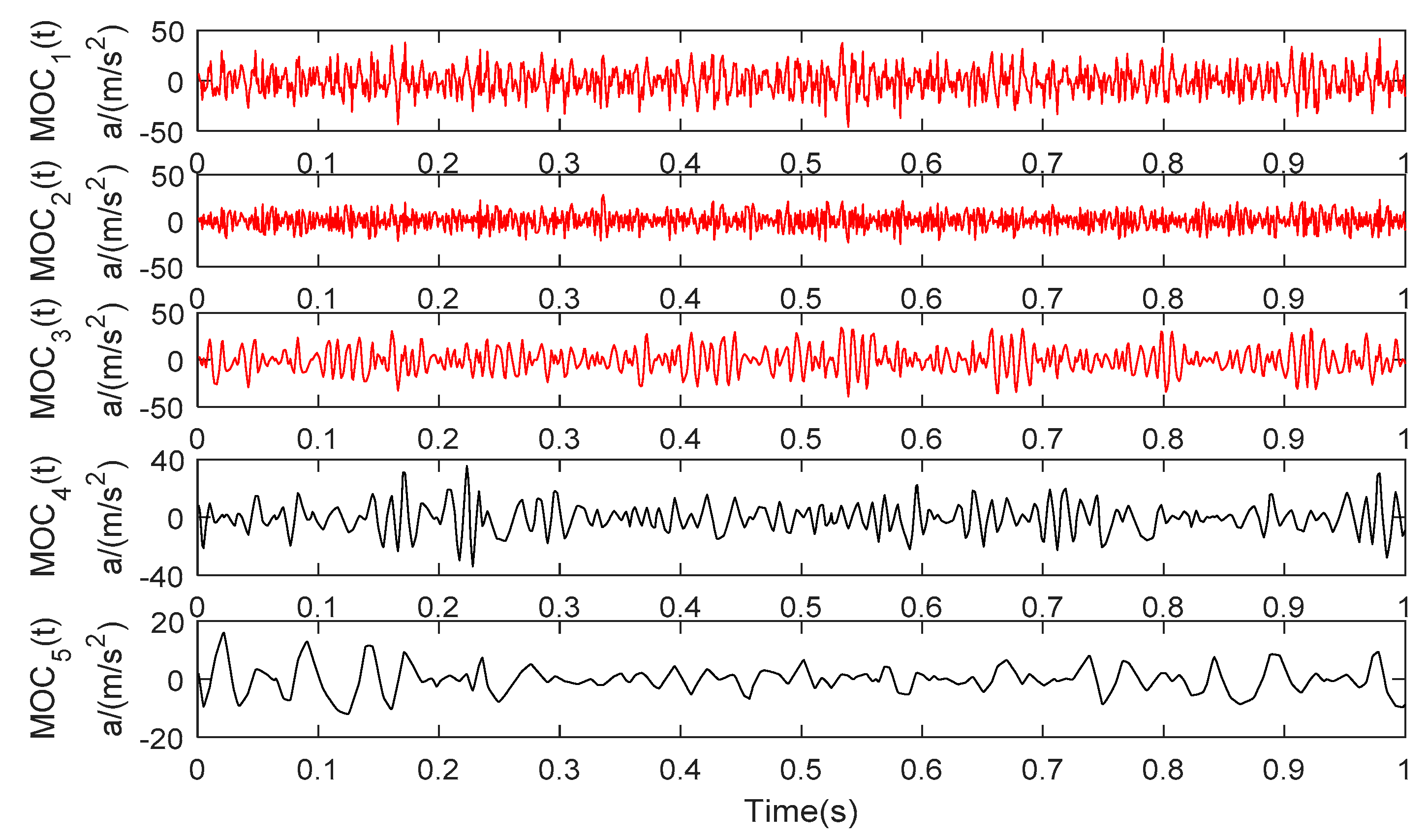
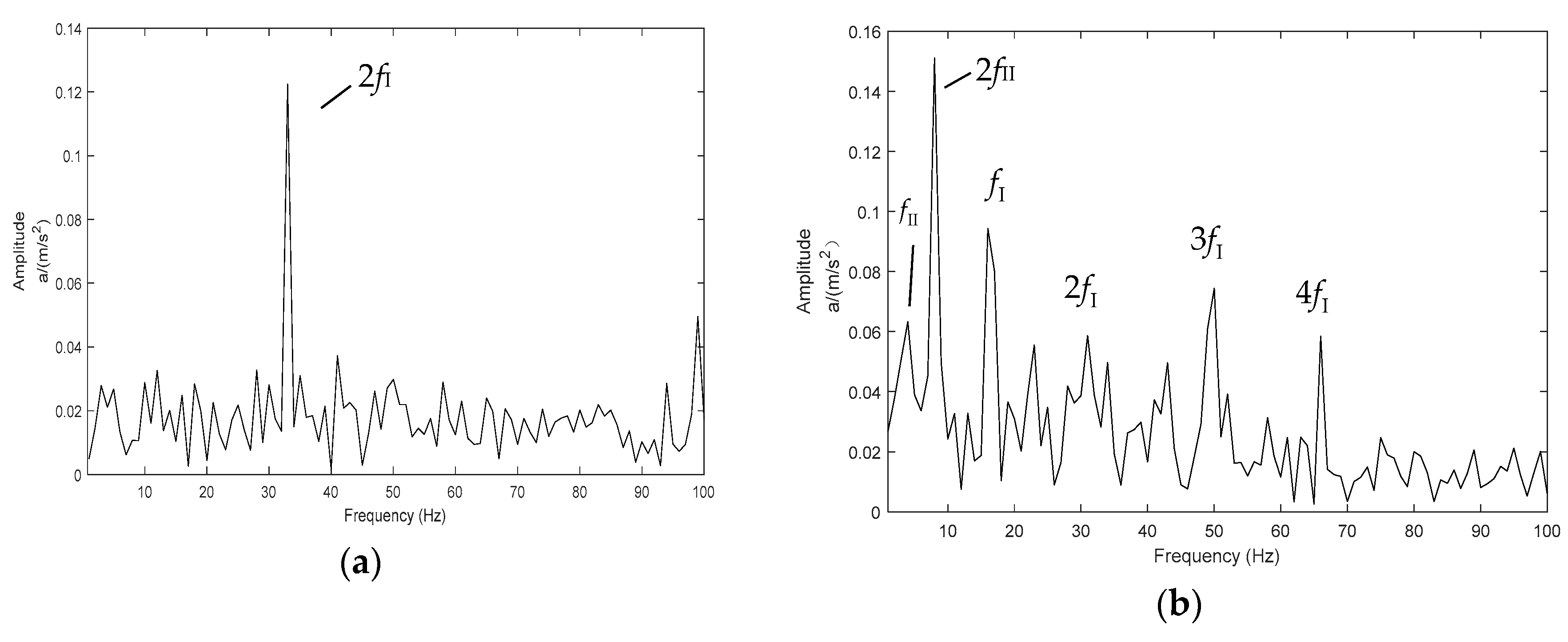
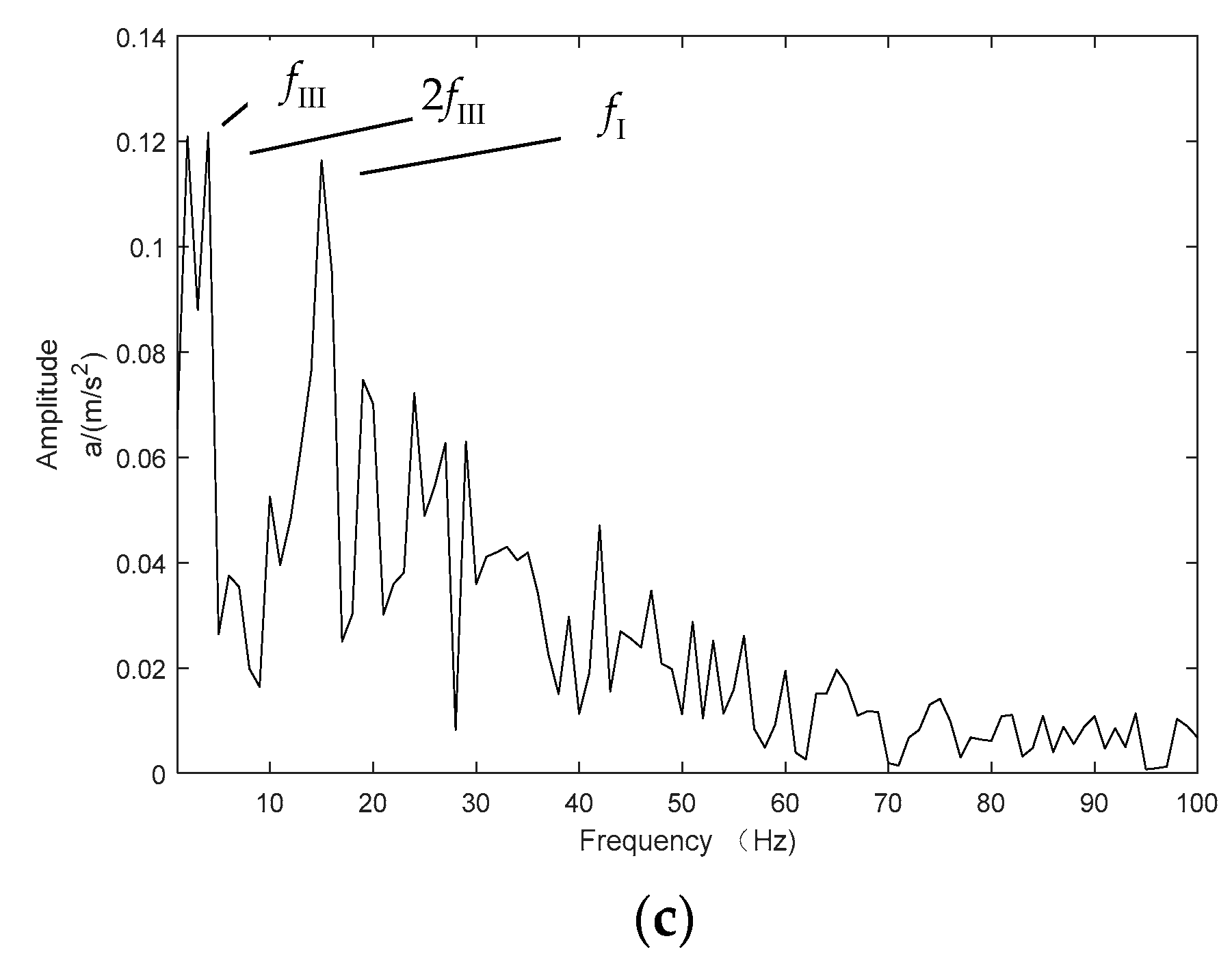
| Method | Number of Sifting Times | IO | Consuming Time(s) |
|---|---|---|---|
| EMD | 38 | 0.0834 | 4.0328 |
| LOD | 27 | 0.0574 | 0.0381 |
| RS-LOD | 30 | 0.0347 | 1.3226 |
| p | MOC1(t) | MOC2(t) | MOC3(t) | MOC4(t) | MOC5(t) | MOC6(t) | MOC7(t) | MOC8(t) | Total |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 7 | 6 | 7 | - | - | - | - | 25 |
| 0.5 | 5 | 6 | 6 | 8 | 8 | - | - | - | 33 |
| 1 | 5 | 7 | 6 | 7 | 8 | 8 | - | - | 41 |
| 2 | 5 | 7 | 6 | 6 | 8 | 7 | - | - | 39 |
| 5 | 5 | 7 | 6 | 6 | 8 | 7 | 8 | - | 47 |
| 10 | 5 | 7 | 7 | 6 | 7 | 7 | 7 | - | 46 |
| 20 | 5 | 7 | 8 | 8 | 8 | 8 | 7 | 8 | 59 |
| 50 | 5 | 7 | 8 | 7 | 7 | 8 | 8 | 8 | 58 |
| p | 0 | 0.5 | 1 | 2 | 5 | 10 | 20 | 50 |
|---|---|---|---|---|---|---|---|---|
| IO | 0.1990 | 0.1846 | 0.1725 | 0.1408 | 0.1192 | 0.0140 | 0.0135 | 0.0132 |
| Consuming time(s) | 0.4792 | 0.4501 | 0.4799 | 0.5264 | 0.6810 | 0.5438 | 0.7909 | 0.9873 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Zhang, K.; Wan, C.; Chen, X.; Liao, L.; Tian, Z. The Rational Spline Interpolation Based-LOD Method and Its Application to Rotating Machinery Fault Diagnosis. Appl. Sci. 2020, 10, 1259. https://doi.org/10.3390/app10041259
Niu X, Zhang K, Wan C, Chen X, Liao L, Tian Z. The Rational Spline Interpolation Based-LOD Method and Its Application to Rotating Machinery Fault Diagnosis. Applied Sciences. 2020; 10(4):1259. https://doi.org/10.3390/app10041259
Chicago/Turabian StyleNiu, Xiaorui, Kang Zhang, Chao Wan, Xiangmin Chen, Lida Liao, and Zeyu Tian. 2020. "The Rational Spline Interpolation Based-LOD Method and Its Application to Rotating Machinery Fault Diagnosis" Applied Sciences 10, no. 4: 1259. https://doi.org/10.3390/app10041259
APA StyleNiu, X., Zhang, K., Wan, C., Chen, X., Liao, L., & Tian, Z. (2020). The Rational Spline Interpolation Based-LOD Method and Its Application to Rotating Machinery Fault Diagnosis. Applied Sciences, 10(4), 1259. https://doi.org/10.3390/app10041259





