Experimental and Analytical Investigation on Flexural Retrofitting of RC T-Section Beams Using CFRP Sheets
Abstract
1. Introduction
2. Research Significance
3. Test Program
3.1. Materials Properties and Test Specimens
3.2. Test Setup and Procedures
4. Experimental Test Results
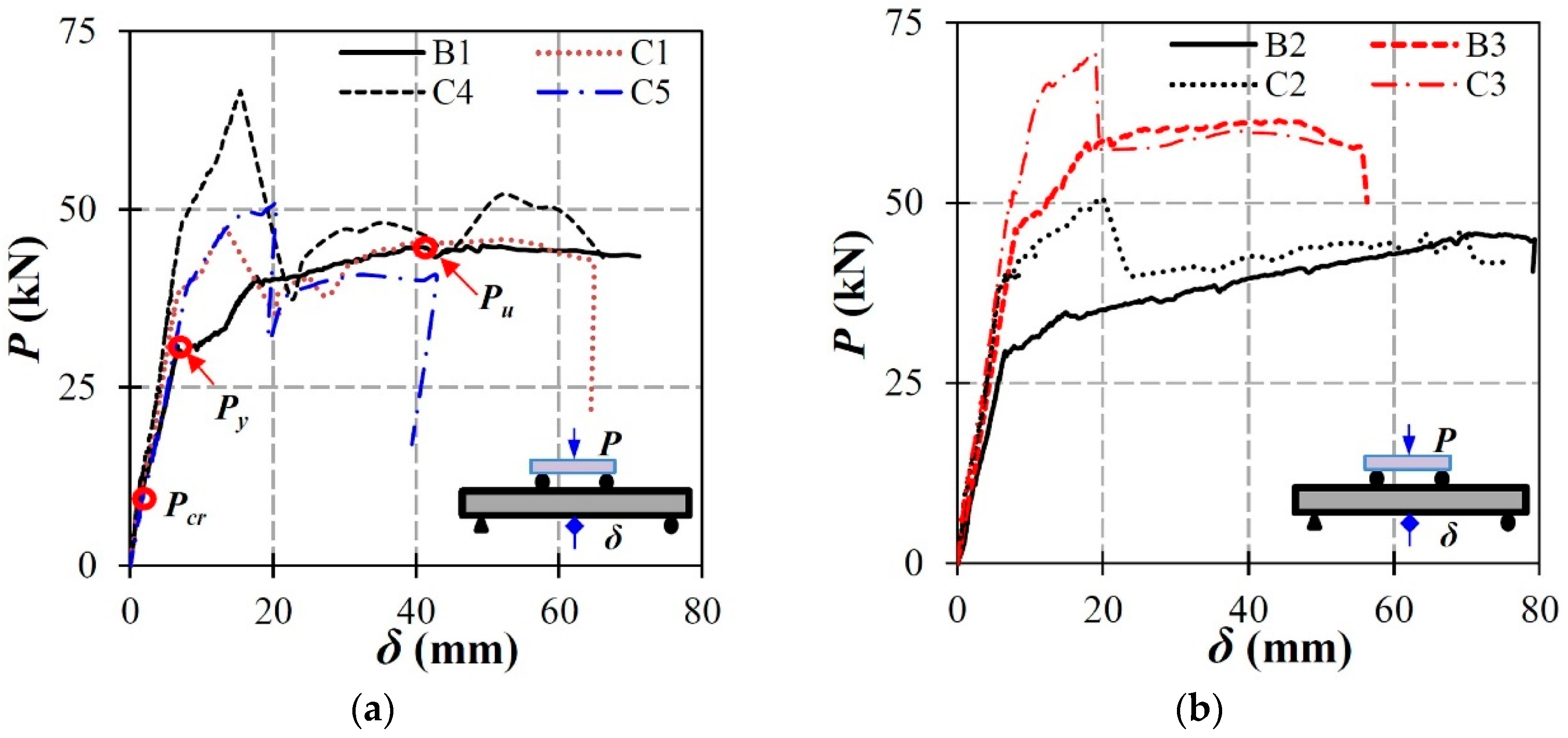
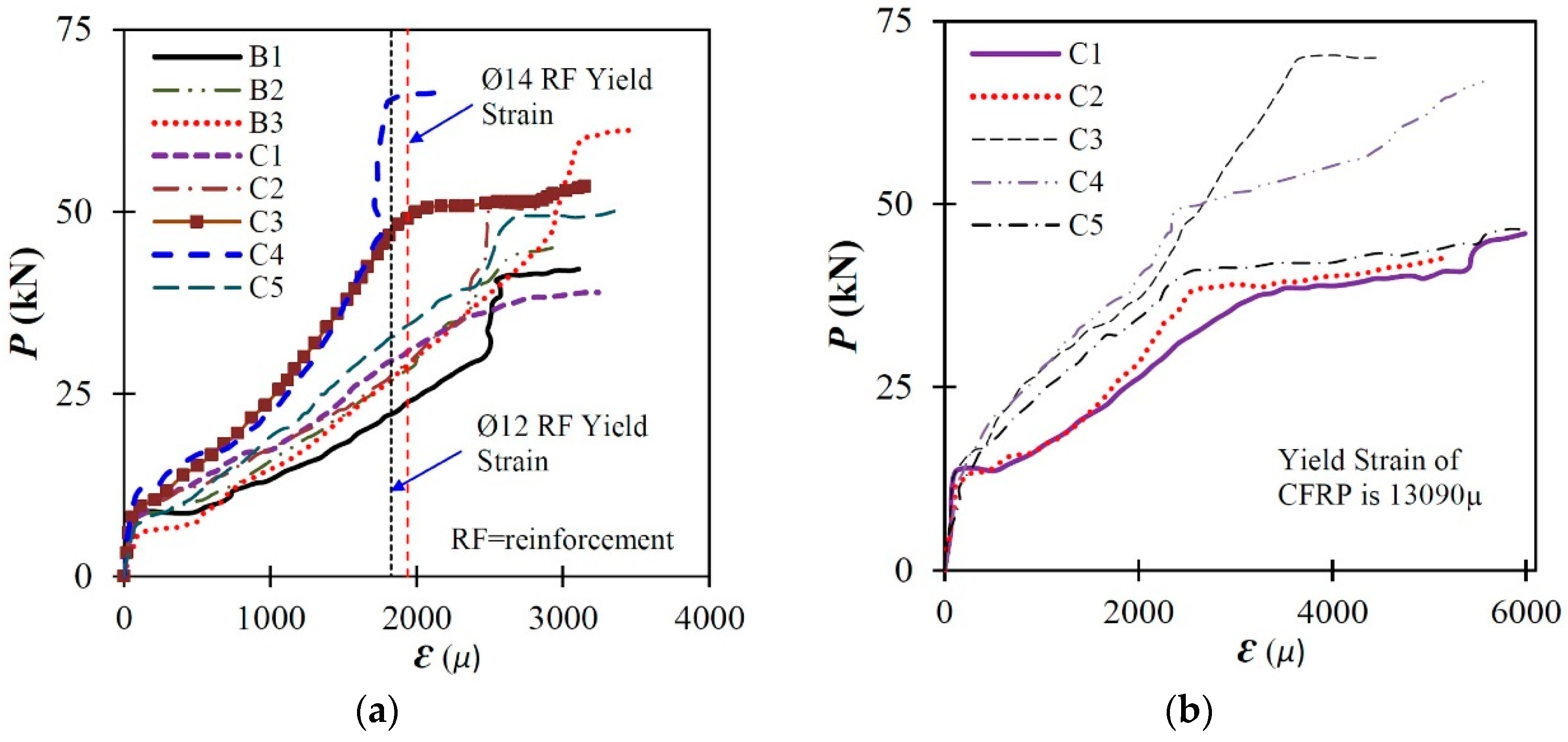
4.1. General Behavior
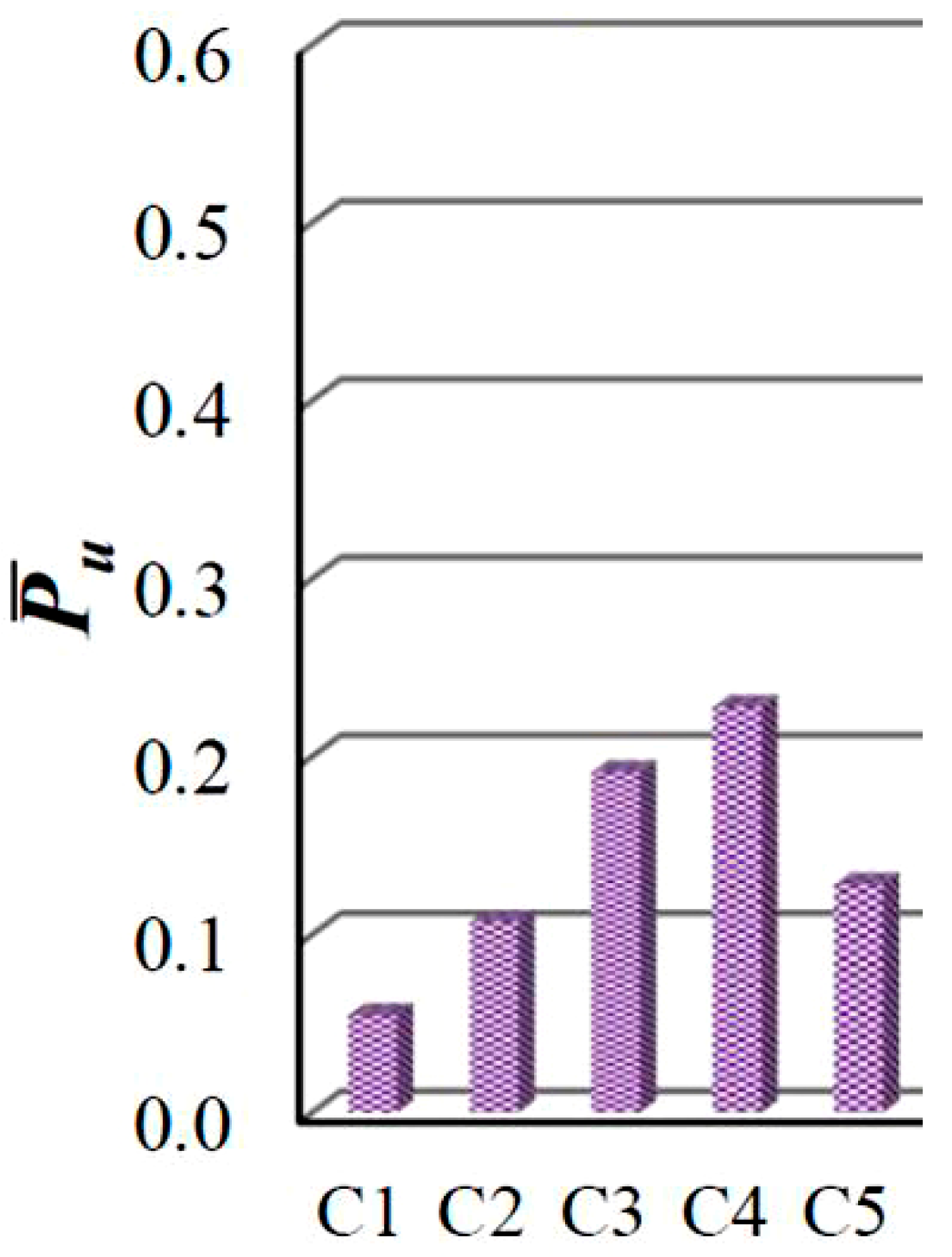
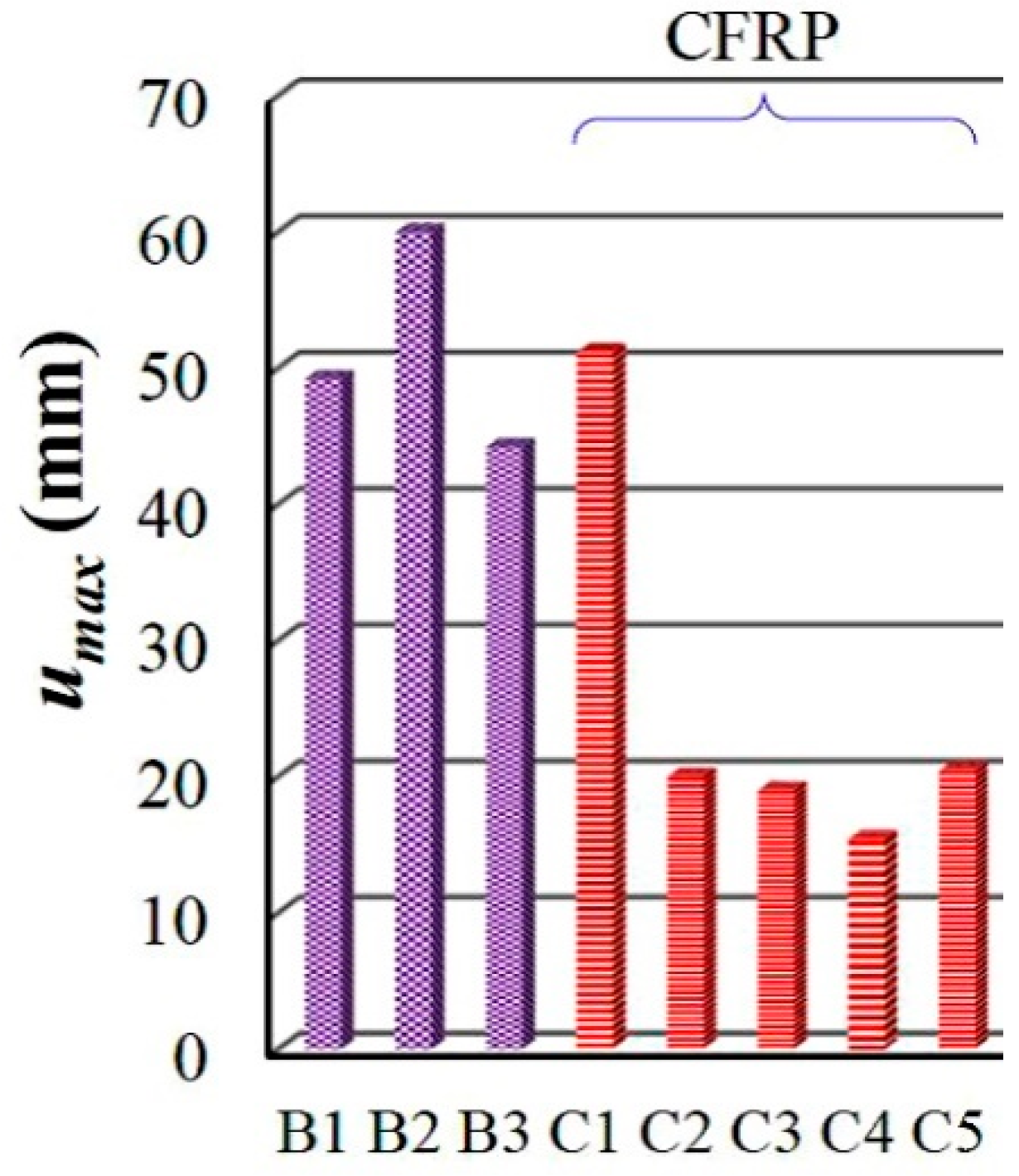
4.2. Load Resistance and Failure Modes
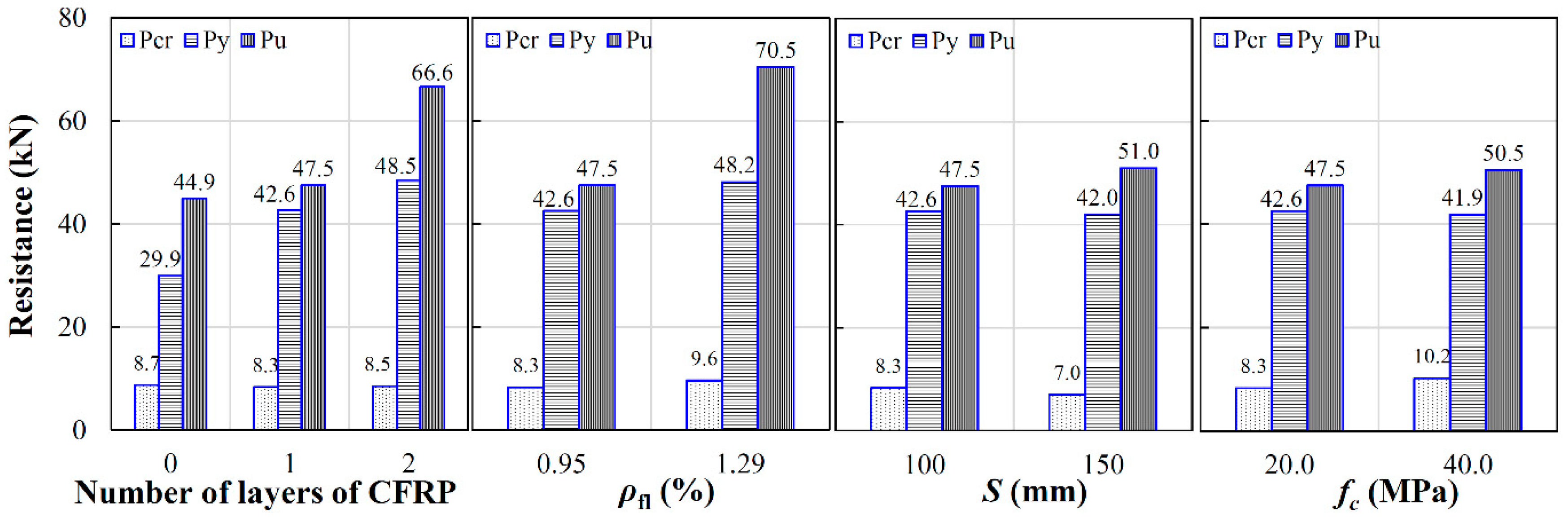
4.3. Effect of Different Parameters
5. Discussion
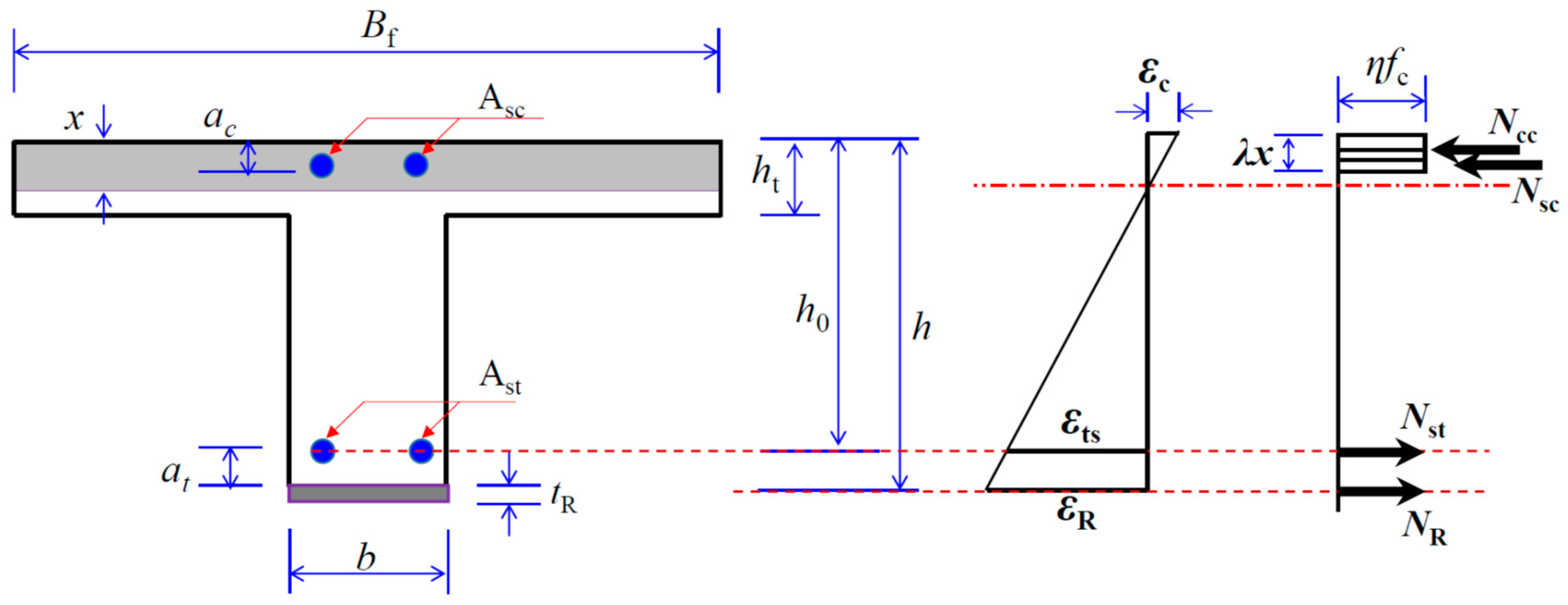
6. Ultimate Load Carrying Capacity of strengthened T-Section Beams
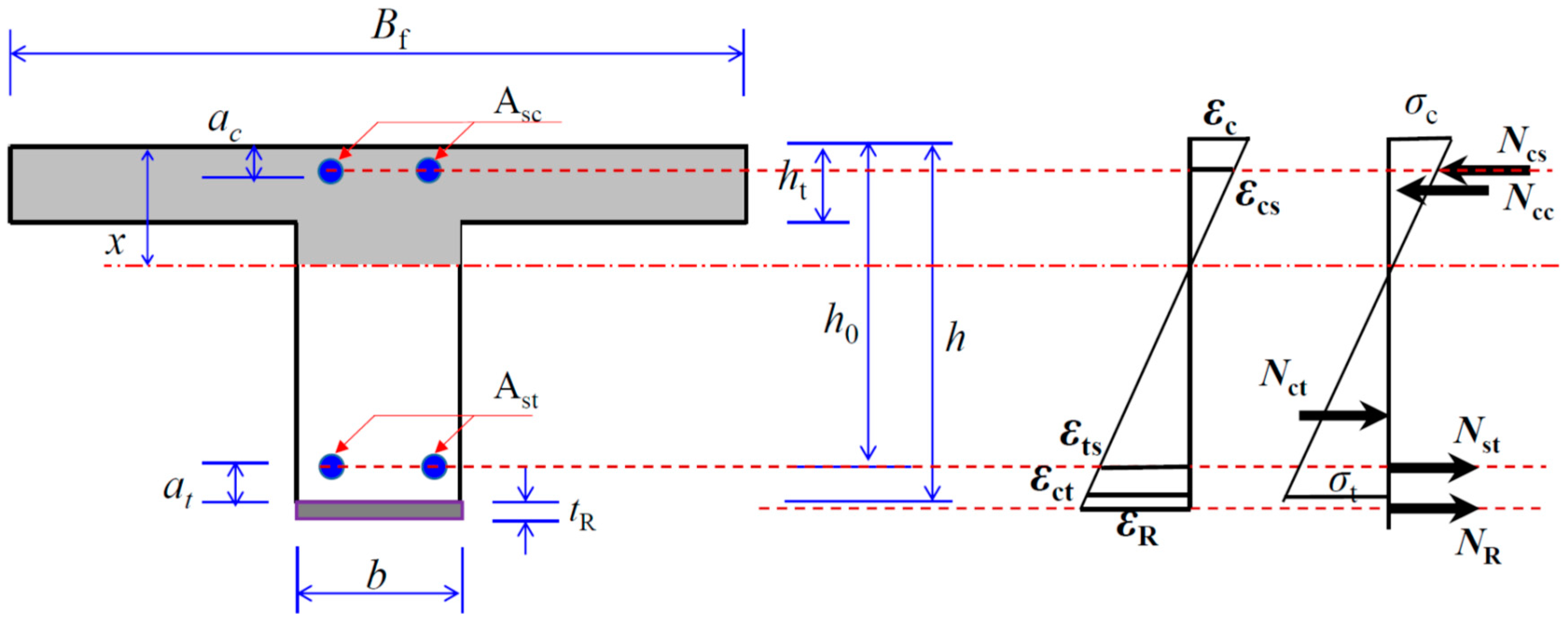
6.1. Resistance of T-Section Beams Corresponding to Crack Initiation Pcr
6.2. Yielding Resistance and Ultimate Resistance of Strengthened T-Section Beams
7. Conclusions
- (1)
- The RC T-section beam specimens strengthened with CFRP sheets failed in a flexural failure. Increasing the thickness of the strengthening CFRP did not enhance the cracking resistance of the beam, but significantly improved the yielding and ultimate resistance.
- (2)
- Increasing the flexural reinforcing ratio of the beam by 36% from 0.95% to 1.29% increased the Pcr, Py, and Pu by 17%, 13%, and 48%, respectively.
- (3)
- Increasing the CFRP U-wrap spacing had little effect on the resistance of the RC T-section beams. Moreover, increasing the compressive strength of concrete only had marginal influence on the yielding and ultimate resistance of the CFRP strengthened RC T-section beams.
- (4)
- The T-section beams strengthened by CFRP sheets exhibited lower ductility at the final failure stage due to brittle failure of the bond between the CFRP sheet and concrete.
- (5)
- The developed analytical models offered reasonable predictions of the cracking resistance, yielding and ultimate resistance of the RC T-section beams strengthened with CFRP sheets. The average test-to-prediction ratios (or COVs) for Pcr, Py, and Pu were 1.01 (0.12), 1.10 (0.12), and 1.08 (0.10), respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Yubing, L. The Field Investigation and Study of Concrete Bridge Structure; Shenyang Jianzhu University: Shenyang, China, 2016; pp. 3–5. [Google Scholar]
- Hui, P.; Jianren, Z.; Shouping, S. Experimental study of flexural fatigue performance of reinforced concrete beams strengthened with prestressed CFRP plates. Eng. Struct. 2016, 127, 62–72. [Google Scholar]
- Esfahani, M.R.; Kianoushb, M.R.; Tajaria, A.R. Flexural behaviour of reinforced concrete beams strengthened by CFRP sheets. Eng. Struct. 2007, 29, 2428–2444. [Google Scholar] [CrossRef]
- Arslan, G.; Sevuk, F.B.; Ekiz, I. Steel plate contribution to load-carrying capacity of strengthened RC beams. Constr. Build. Mater. 2008, 22, 143–153. [Google Scholar] [CrossRef]
- Hadjazi, K.; Sereir, Z.; Amziane, S. Creep response of intermediate flexural cracking behavior of reinforced concrete beam strengthene d with an externally bonde d FRP plate. Int. J. Solids Struct. 2016, 94, 196–205. [Google Scholar] [CrossRef]
- Hugo, C.; Biscaia, C.; Chastre, M.; Silva, A.G. A smeared crack analysis of reinforced concrete T-section beams strengthened with GFRP composites. Eng. Struct. 2013, 56, 1346–1361. [Google Scholar]
- Carvalho, T.; Chastre, C.; Biscaia, H.; Paula, R. Flexural behaviour of RC T-section beams strengthened with different FRP materials. In Third International Fib Congress; Fib: Lausanne, Switzerland; Washington, DC, USA, 2010. [Google Scholar]
- Ascione, L.; Feo, L. Modeling of composite/concrete interface of RC beams strengthened with composite laminates. Compos. Part B Eng. 2000, 31, 535–540. [Google Scholar] [CrossRef]
- Bonacci, J.F.; Maalej, M. Behavioral trends of RC beams strengthened withexternally bonded FRP. J. Compos. Constr. 2001, 5, 102–113. [Google Scholar] [CrossRef]
- Badawi, M.; Soudki, K. Flexural strengthening of RC beams with prestressed NSM CFRP rods: Experimental and analytical investigation. Constr. Build. Mater. 2009, 23, 3292–3300. [Google Scholar] [CrossRef]
- Al-Mahmoud, F.; Castel, A.; François, R.; Tourneur, C. Strengthening of RC members with near-surface mounted CFRP rods. Compos. Struct. 2009, 91, 138–147. [Google Scholar] [CrossRef]
- Yost, J.R.; Gross, S.P.; Dinehart, D.W.; Mildenberg, J.J. Flexural behavior of concrete beams strengthened with near-surface-mounted CFRP strips. Aci. Struct. J. 2007, 104, 430–437. [Google Scholar]
- Bilotta, A.; Ceroni, F.; Di Ludovico, M.; Nigro, E.; Pecce, M.; Manfredi, G. Bond efficiency of EBR and NSM FRP systems for strengthening concrete members. J. Compos. Constr. 2011, 15, 757–772. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Fortes, A.S. Flexural strengthening of concrete beams with CFRP laminates bonded into slits. Cem. Concr. Compos. 2005, 27, 471–480. [Google Scholar] [CrossRef]
- Nanni, A.; Ludovico, D.M.; Parretti, R. Shear strengthening of a PC bridge girder with NSM CFRP rectangular bars. Adv. Struct. Eng. 2004, 7, 297–309. [Google Scholar] [CrossRef]
- EN. B. 1-1. Eurocode 2. Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; Eur. Comm. Stand.: Dublin, Ireland, 2004; 277p. [Google Scholar]
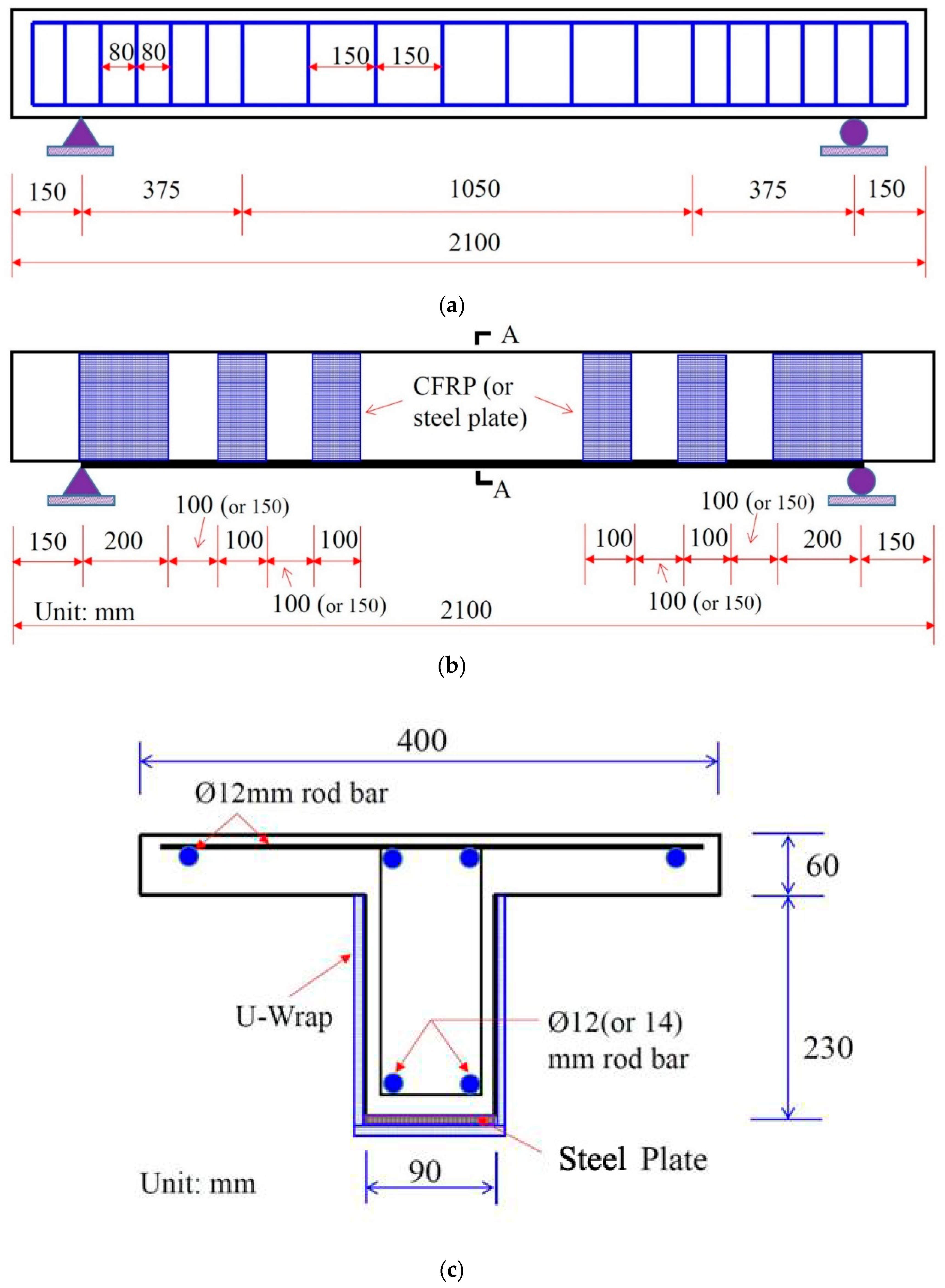
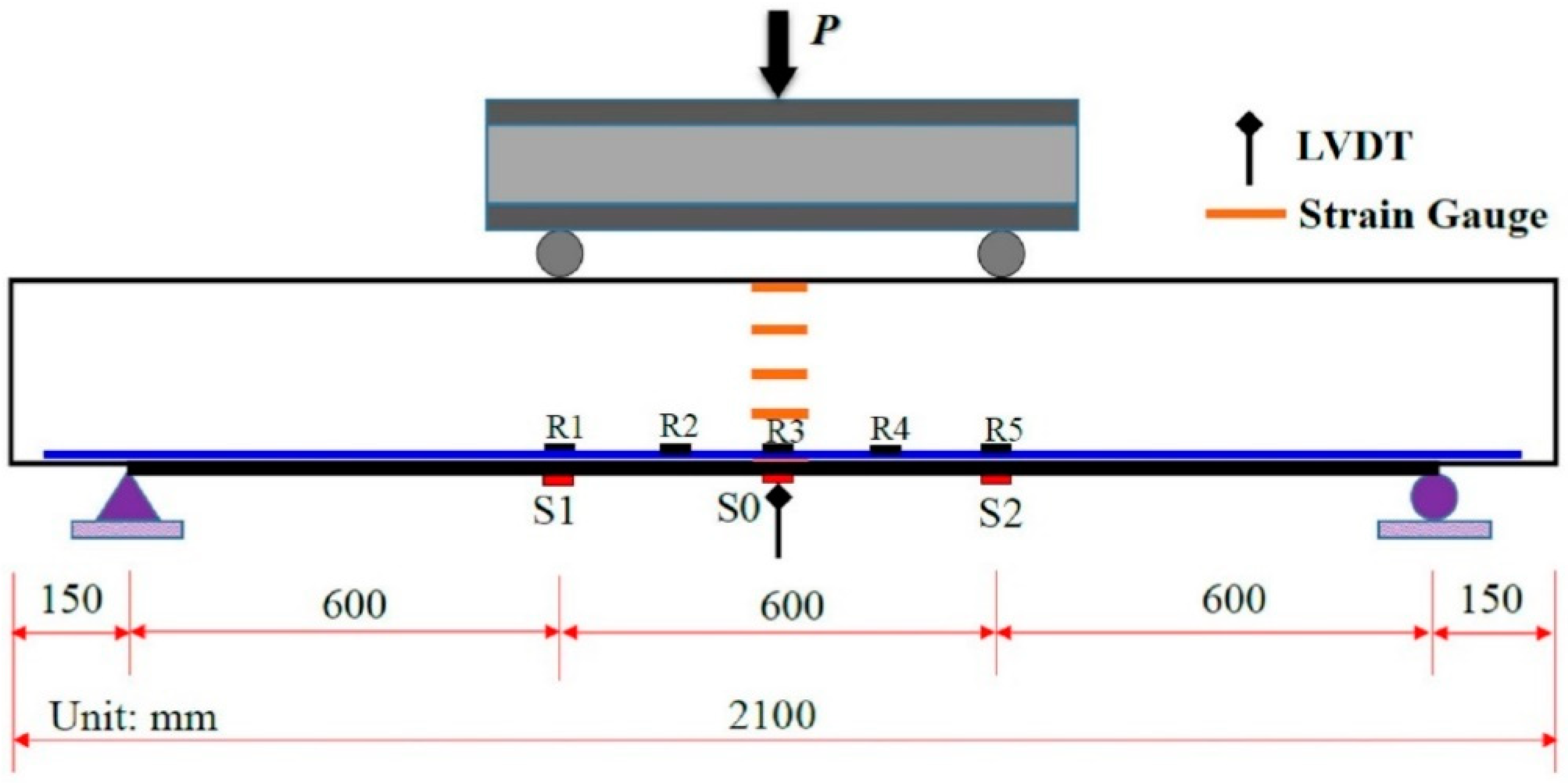

| Item | Conc Grade | ρfl (%) | Bonding Layers | S (mm) | uy (mm) | umax (mm) | Pcr,T (kN) | Py,T (kN) | Pu,T (kN) | Failure Mode | Pcr (kN) | Pcr,T/Pcr ratio | Py (kN) | Py,T/Py Ratio | Pu (kN) | Pu,T/Pu Ratio |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | C20 | 0.95 | - | - | 6.6 | 49.2 | 8.7 | 29.9 | 44.9 | FB | 7.7 | 1.13 | 24.7 | 1.21 | 37.7 | 1.19 |
| B2 | C40 | 0.95 | - | - | 7.1 | 60.0 | 9.3 | 29.5 | 45.4 | FB | 10.7 | 0.87 | 26.5 | 1.11 | 38.0 | 1.20 |
| B3 | C20 | 1.29 | - | - | 8.0 | 44.2 | 7.5 | 46.2 | 61.4 | FB | 7.9 | 0.95 | 34.6 | 1.33 | 52.7 | 1.17 |
| C1 | C20 | 0.95 | 1 | 100 | 6.6 | 51.2 | 9.2 | 42.6 | 47.5 | FB&DB | 7.8 | 1.07 | 38.7 | 1.10 | 50.1 | 0.95 |
| C2 | C40 | 0.95 | 1 | 100 | 7.3 | 20.0 | 9.0 | 41.9 | 50.5 | FB&DB | 10.8 | 0.94 | 39.2 | 1.07 | 51.1 | 0.99 |
| C3 | C20 | 1.29 | 1 | 100 | 7.8 | 19.0 | 8.2 | 48.2 | 70.5 | FB&DB | 8.0 | 1.20 | 46.9 | 1.03 | 62.2 | 1.13 |
| C4 | C20 | 0.95 | 2 | 100 | 7.3 | 15.5 | 11.4 | 48.5 | 66.6 | FB&DB | 7.8 | 1.09 | 54.4 | 0.89 | 67.6 | 0.99 |
| C5 | C20 | 0.95 | 1 | 150 | 6.5 | 20.5 | 9.7 | 42.0 | 51.0 | FB&DB | 7.8 | 0.90 | 38.7 | 1.08 | 50.1 | 1.02 |
| Mea | 1.01 | 1.10 | 1.08 | |||||||||||||
| Cov | 0.12 | 0.12 | 0.10 |
| Type | Es (GPa) | fy (MPa) | Fu (MPa) | δu (%) |
|---|---|---|---|---|
| Ø8 HPB235 | 200 | 308 | 538 | 30.5 |
| Ø12 HRB335 | 200 | 365 | 550 | 28.5 |
| Ø14 HRB335 | 200 | 388 | 605 | 27.5 |
| Type | fy (MPa) | EF (GPa) | δu (%) | τc (MPa) |
|---|---|---|---|---|
| CFRP | 3168 | 242 | 1.71 | 3.5 |
| JGJ-20 | 43 | 2.59 | - | 3.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Nehdi, M.L. Experimental and Analytical Investigation on Flexural Retrofitting of RC T-Section Beams Using CFRP Sheets. Appl. Sci. 2020, 10, 1233. https://doi.org/10.3390/app10041233
Zhang Y, Nehdi ML. Experimental and Analytical Investigation on Flexural Retrofitting of RC T-Section Beams Using CFRP Sheets. Applied Sciences. 2020; 10(4):1233. https://doi.org/10.3390/app10041233
Chicago/Turabian StyleZhang, Yannian, and Moncef L. Nehdi. 2020. "Experimental and Analytical Investigation on Flexural Retrofitting of RC T-Section Beams Using CFRP Sheets" Applied Sciences 10, no. 4: 1233. https://doi.org/10.3390/app10041233
APA StyleZhang, Y., & Nehdi, M. L. (2020). Experimental and Analytical Investigation on Flexural Retrofitting of RC T-Section Beams Using CFRP Sheets. Applied Sciences, 10(4), 1233. https://doi.org/10.3390/app10041233






