Cyclic Plasticity of the As-Built EOS Maraging Steel: Preliminary Experimental and Computational Results
Abstract
1. Introduction
2. Materials and Methods
3. Cyclic Plasticity Mathematical Modelling
4. Results and Discussion
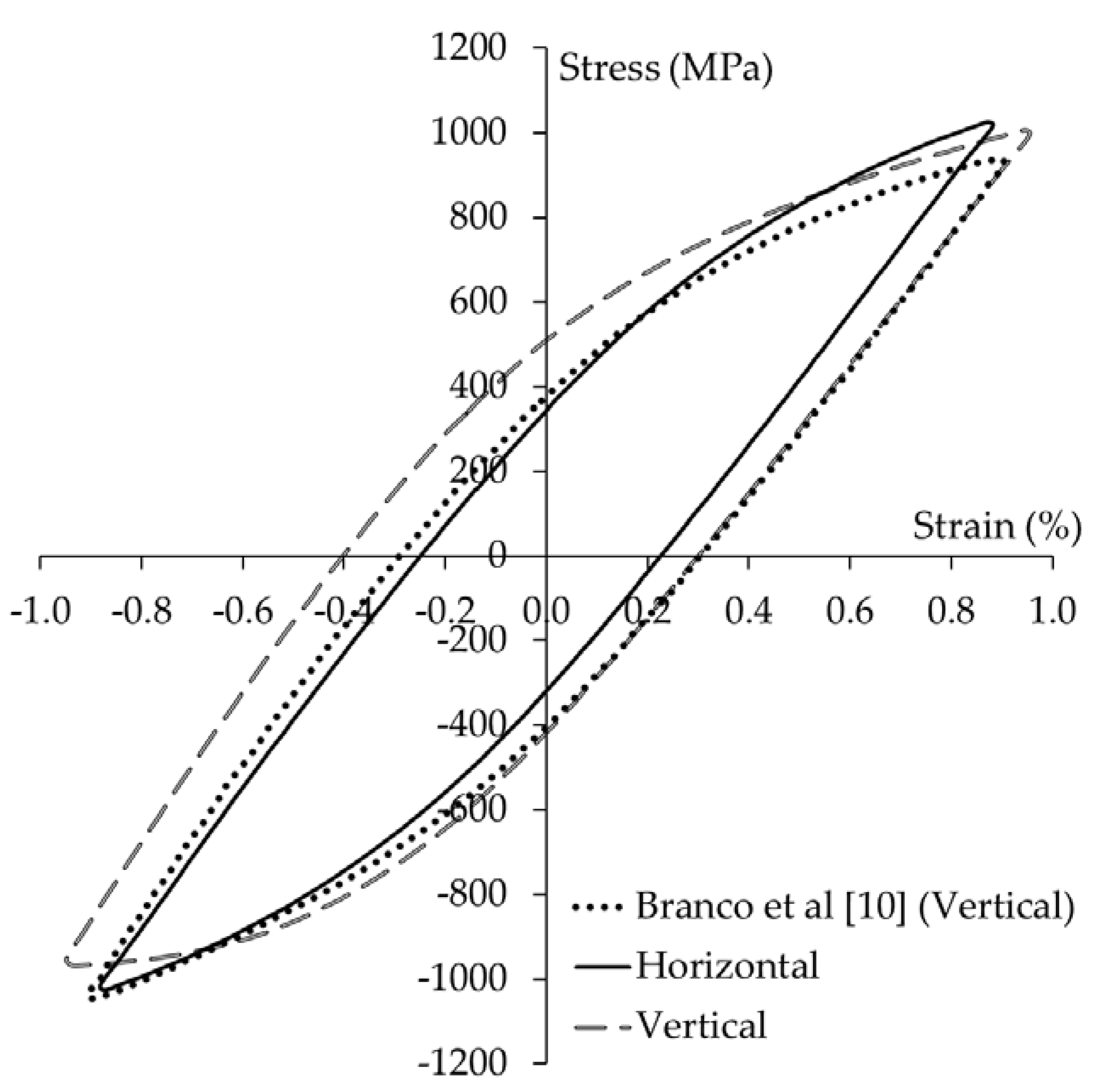
4.1. Cyclic Mechanical Testing
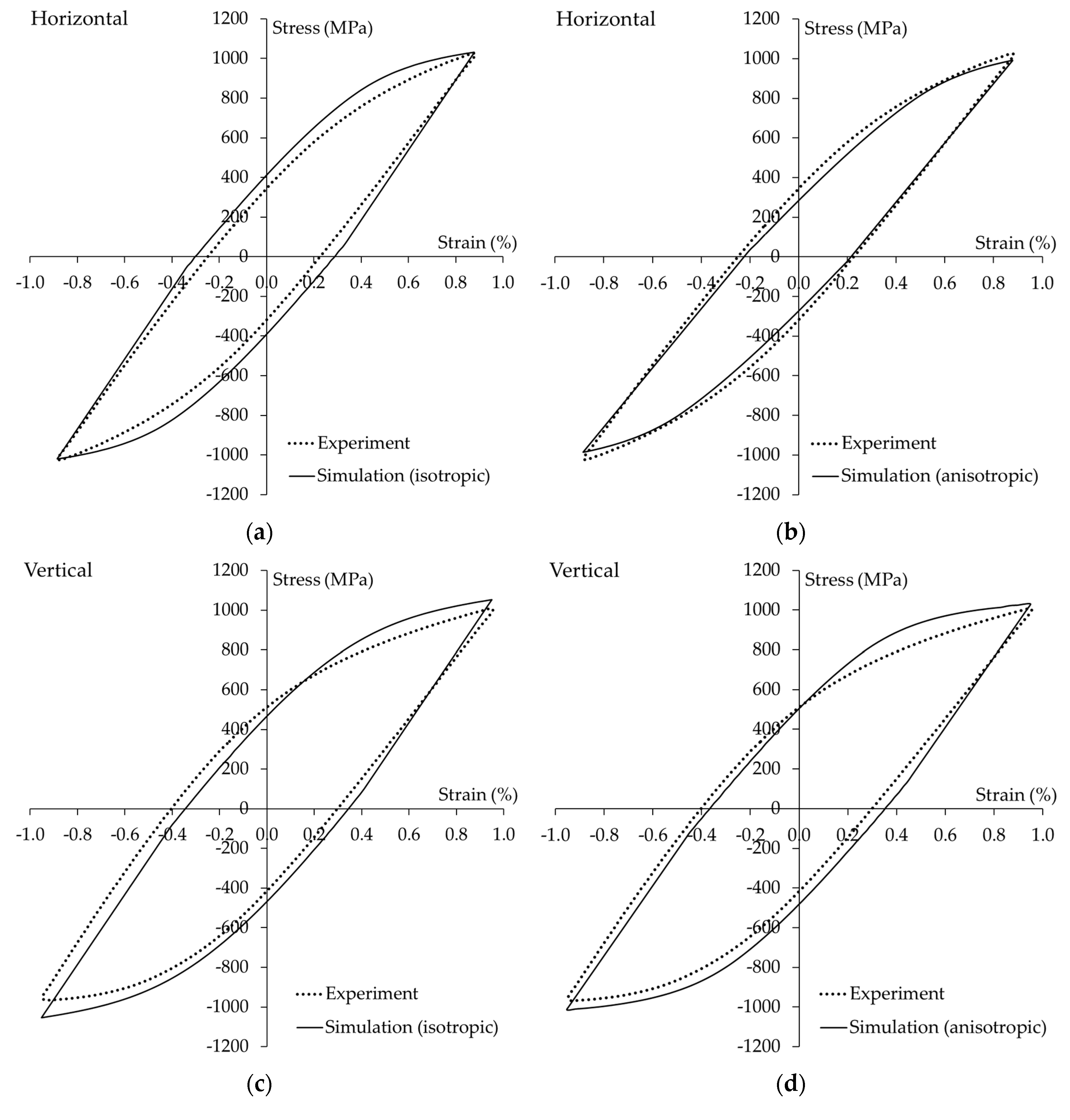
4.2. Cyclic Plasticity Simulation
5. Conclusions
- The stress–strain hysteresis loops produced from cyclic elastoplastic strain loading exhibited symmetrical characteristics, for both horizontal and vertical test coupons.
- Vertical test coupons appear to have a higher capacity for plastic strain energy dissipation than horizontal coupons, as indicated by their hysteresis loop area.
- The plasticity models used in this study were capable of simulating the hysteresis loops well.
- The anisotropic plasticity model offers a more representative description of the mechanical behaviour of this metal, resulting in higher accuracy simulations than the isotropic model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Casati, R.; Lemke, J.N.; Tuissi, A.; Vedani, M. Aging behaviour and mechanical performance of 18-Ni 300 steel processed by selective laser melting. Metals 2016, 6, 218. [Google Scholar] [CrossRef]
- Becker, T.H.; Dimitrov, D. The achievable mechanical properties of SLM produced Maraging Steel 300 components. Rapid Prototyp. J. 2016, 22, 487–494. [Google Scholar] [CrossRef]
- Tan, C.; Zhou, K.; Ma, W.; Zhang, P.; Liu, M.; Kuang, T. Microstructural evolution, nanoprecipitation behavior and mechanical properties of selective laser melted high-performance grade 300 maraging steel. Mater. Des. 2017, 134, 23–34. [Google Scholar] [CrossRef]
- Suryawanshi, J.; Prashanth, K.G.; Ramamurty, U. Tensile, fracture, and fatigue crack growth properties of a 3D printed maraging steel through selective laser melting. J. Alloys Compd. 2017, 725, 355–364. [Google Scholar] [CrossRef]
- Mooney, B.; Kourousis, K.I.; Raghavendra, R. Plastic anisotropy of additively manufactured maraging steel: Influence of the build orientation and heat treatments. Addit. Manuf. 2019, 25, 19–31. [Google Scholar] [CrossRef]
- Song, J.; Tang, Q.; Feng, Q.; Ma, S.; Setchi, R.; Liu, Y.; Han, Q.; Fan, X.; Zhang, M. Effect of heat treatment on microstructure and mechanical behaviours of 18Ni-300 maraging steel manufactured by selective laser melting. Opt. Laser Technol. 2019, 120, 105725. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G.; Robusto, F.; Kostic, S.C.; Vranic, A.; Bogojevic, N. Fatigue response of as-built DMLS maraging steel and effects of aging, machining, and peening treatments. Metals 2018, 8, 505. [Google Scholar] [CrossRef]
- Damon, J.; Hanemann, T.; Dietrich, S.; Graf, G.; Lang, K.-H.; Schulze, V. Orientation dependent fatigue performance and mechanisms of selective laser melted maraging steel X3NiCoMoTi18-9-5. Int. J. Fatigue 2019, 127, 395–402. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G.; Robusto, F.; Ciric-Kostic, S.; Moraca, S.; Bogojevic, N. Sensitivity of direct metal laser sintering Maraging steel fatigue strength to build orientation and allowance for machining. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 374–386. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.M.; Berto, F.; Razavi, S.M.J.; Ferreira, J.A.M.; Capela, C.; Santos, L.; Antunes, F. Low-cycle fatigue behaviour of AISI 18Ni300 maraging steel produced by selective laser melting. Metals 2018, 8, 32. [Google Scholar] [CrossRef]
- Mooney, B.; Kourousis, K.I.; Raghavendra, R.; Agius, D. Process phenomena influencing the tensile and anisotropic characteristics of additively manufactured maraging steel. Mater. Sci. Eng. A 2019, 745, 115–125. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect; G.E.G.B. Report RD/B/N 731; Berkeley, CA, USA, 1996. [Google Scholar]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc Lond. Ser. A Math. Phys. Sci. 1948, 193, 281–297. [Google Scholar]
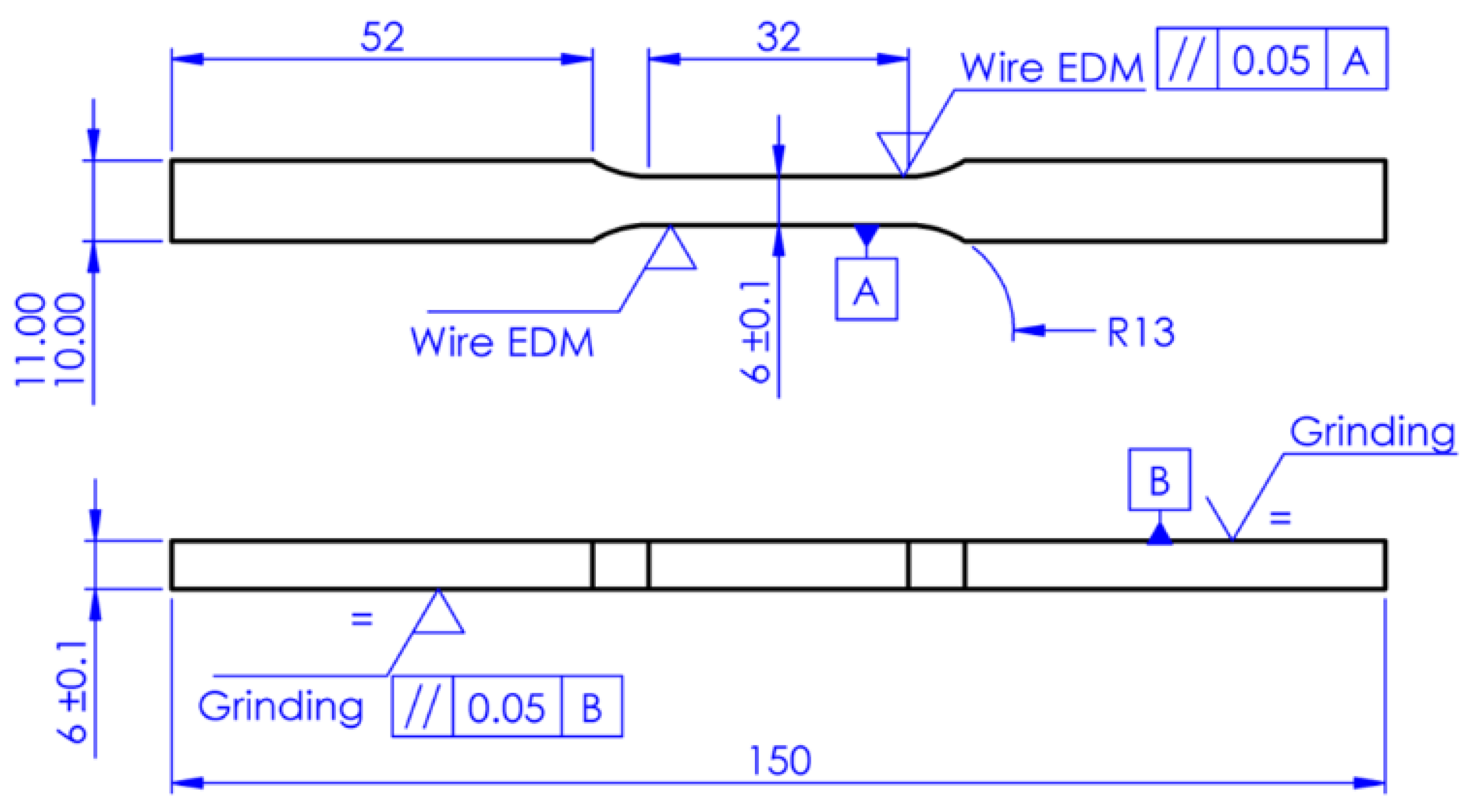
| Ni | Mo | Co | Ti | Al | Cr | Mn | C | Fe | |
|---|---|---|---|---|---|---|---|---|---|
| MS1 (MS300) | 18.14 | 5.67 | 8.94 | 0.87 | 0.05–0.15 | ≤0.5 | ≤0.01 | ≤0.03 | Balance |
| Kinematic Hardening | |||
|---|---|---|---|
| 241,800 MPa | 930 | ||
| 98,280 MPa | 945 | ||
| 14,112 MPa | 96 | ||
| Hill | Orthotropic Hooke | ||||
|---|---|---|---|---|---|
| F | 0.798 | E1 | 137 GPa | 0.43 | |
| G | 0.638 | E2 | 161 GPa | 0.93 | |
| H | 0.202 | E3 | 122 GPa | 0.26 | |
| L | 1.167 | G12 | 122 GPa | 0.01 | |
| M | 1.500 | G12 | 122 GPa | 0.24 | |
| N | 1.500 | G23 | 122 GPa | 0.35 | |
| Isotropic | Anisotropic | |
|---|---|---|
| Vertical | 43.5% | 36.3% |
| Horizontal | 58.6% | 21.1% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mooney, B.; Agius, D.; Kourousis, K.I. Cyclic Plasticity of the As-Built EOS Maraging Steel: Preliminary Experimental and Computational Results. Appl. Sci. 2020, 10, 1232. https://doi.org/10.3390/app10041232
Mooney B, Agius D, Kourousis KI. Cyclic Plasticity of the As-Built EOS Maraging Steel: Preliminary Experimental and Computational Results. Applied Sciences. 2020; 10(4):1232. https://doi.org/10.3390/app10041232
Chicago/Turabian StyleMooney, Barry, Dylan Agius, and Kyriakos I. Kourousis. 2020. "Cyclic Plasticity of the As-Built EOS Maraging Steel: Preliminary Experimental and Computational Results" Applied Sciences 10, no. 4: 1232. https://doi.org/10.3390/app10041232
APA StyleMooney, B., Agius, D., & Kourousis, K. I. (2020). Cyclic Plasticity of the As-Built EOS Maraging Steel: Preliminary Experimental and Computational Results. Applied Sciences, 10(4), 1232. https://doi.org/10.3390/app10041232





