Numerical Investigation of Vortex-Induced Vibrations of a Flexible Riser with Staggered Buoyancy Elements

Abstract

This paper presents a numerical algorithm used together with a Finite-Element based Vortex-Induced Vibration (VIV) prediction software VIVANA to obtain a hydrodynamic force coefficient database based on response measurements of flexible riser VIV model test of staggered buoyancy elements. The excitation coefficient database is parameterized; and the representative parameters are systematically varied in VIVANA simulations until the predicted responses in terms of mode number, response frequency, root-mean-square (RMS) response amplitude, and RMS curvature agree well with the experimental data under same flow and boundary conditions. An optimal set of force coefficient database for both the buoyancy element and the bare riser section is obtained and a significant improvement in VIV prediction by VIVANA is achieved. The obtained hydrodynamic force coefficient database can be also applied to other empirical VIV prediction programs. The sensitivity of using the same database to predict the VIV of different configurations has also been investigated.

1. Introduction

Vortex-Induced Vibrations (VIV) of long flexible structures with bluff cross-sections are encountered in a great variety of physical problems, ranging from Aeolian vibrations hanging in the air to the vibrations of slender marine structures in deepwaters, e.g., cables and risers placed in ocean currents. The interaction between fluid flow and slender bodies results in the periodic hydrodynamic forces that are induced due to VIV. If the vibration period is close to the natural period of the system, it can lead to the fast accumulation of fatigue damage to the risers and amplified drag loads on the riser systems.

In recent years, Steel Lazy Wave Riser (SLWR) has become an attractive deepwater riser system design due to its functionality in improved fatigue life. When subjected to external flow, both the buoyancy elements and the bare riser section may experience VIV. The vortex shedding frequency of the buoyancy element is lower than that of the bare riser section due to its larger diameter. Moreover, these two vortex-shedding processes will interact with each other and influence the VIV responses.

There have been extensive experimental studies on VIV responses, as reviewed by Sarpkaya [1], Williamson and Govardhan [2], and Wu et al. [3]. Model tests with rigid cylinders are normally carried out either on elastic supports or with forced motions [4,5,6]. Prototype Reynolds numbers can be achieved in some of the tests with a rigid cylinder section [7,8,9]. Test results demonstrated that VIV responses are affected by the Reynolds number and surface roughness, especially in the critical Reynolds number range. However, no complete hydrodynamic database at the prototype Reynolds number exists considering the large parameter space. High mode VIV tests with flexible pipes have been carried out by Trim et al. [10], Vandiver et al. [11] and Lie et al. [12], which further revealed the complexity of the response, such as dual resonance, multi-mode vibration, unsteady lock-in, higher harmonic fluid forces and traveling wave dominant response.

However, our understanding of the VIV responses of a riser with staggered buoyancy elements remains limited. Several model tests were carried out to investigate the interaction between VIV responses of the bare riser sections and the buoyancy elements [13,14,15]. It was observed that such interactions were influenced by many parameters, such as buoyancy element dimensions and their arrangement (i.e., spacing between two buoyancy elements) [16]. In these tests with flexible riser models, accelerations and bending strains along the length of the tested model were measured. However, the hydrodynamic forces along the riser models were not directly measured. Large differences were observed while predicting VIV responses of the riser with staggered buoyancy elements using the default hydrodynamic coefficients for both bare and the buoyancy elements [17]. A forced motion test of a rigid cylinder with staggered buoyancy elements was carried out to extract hydrodynamic coefficients on buoyancy elements and bare pipe sections by Wu et al. [18]. In their tests, hydrodynamic force coefficients subjected to pure CF motions were obtained. It was shown that the hydrodynamic coefficients of the buoyancy elements differed significantly from the bare section.

It is also known that the hydrodynamic coefficients of a cylinder oscillating in both in-line (IL) and CF directions will differ from those from pure CF motions ([19,20]). Hence, it is of interest to extract hydrodynamic coefficients directly from the VIV test with flexible pipe models. The inverse analysis is one such method which uses measured response data to calculate the external VIV loads by assuming that the mechanical properties (stiffness, mass, etc.) are known. The hydrodynamic coefficients are then calculated from the estimated forces [21]. The obtained hydrodynamic coefficients provide valuable insights for better understanding the behavior of a flexible cylinder. However, the coefficients obtained from the inverse method are often not in a complete amplitude ratio and non-dimensional frequency parameter space. Methods to derive the hydrodynamic coefficient database for the usage in the empirical tools are still needed. Mukundan et al. [22] applied an optimization scheme to obtain an optimal hydrodynamic coefficient database based on model tests with a bare cylinder.

Semi-empirical tools, such as VIVANA [23], SHEAR7 [24] and VIVA [25] are widely used in the offshore industry to predict VIV responses. These tools rely on empirical parameters, including hydrodynamic force coefficient database. The hydrodynamic force coefficient database was derived based on model test data.

In the present study, a numerical algorithm is developed to obtain hydrodynamic force coefficient database based on the response measurements of elastic pipe VIV tests. The method has been applied to Shell VIV model test ([14,16]) with staggered buoyancy elements and the optimal set of force coefficient databases for each buoyancy element and the bare riser section is obtained. Significant improvement in prediction is achieved by VIVANA with the optimal force coefficient databases. The obtained hydrodynamic force coefficient database can be applied to other empirical VIV prediction software as well. The sensitivity of using the same database to predict the VIV of different configurations has also been investigated.

2. Semi-Empirical VIV Prediction Programs

Semi-empirical VIV prediction programs are the most commonly used VIV prediction tools by the industry. VIVINA is selected as the prediction tool in the present study. In VIVANA, structures are modeled as beam elements using the finite element method. Structures with arbitrary geometry and material properties can also be modeled.

The main VIV coefficients are the excitation coefficients, added mass and damping coefficients. The default VIV coefficients included in VIVANA may be used or users may specify other coefficients. Hydrodynamic damping is applied outside the excitation zone. The default excitation coefficient database is generalized from rigid bare cylinder VIV model tests. It is assumed that the response will occur at one or more discrete response frequencies. These frequencies are eigen frequencies with the added mass effect in agreement with the non-dimensional frequency corresponding to the response frequency.

The equation of dynamic equilibrium may be written as

$$M\ddot{r}+M\dot{r}+Kr=R$$

(1)

where M, K, and C are the structural mass, structural stiffness, and structural damping matrices, respectively. Here R is the external load vector, and r is the response vector.

The external loads R will be harmonic with frequency ω, but loads at all degrees of freedom are not necessary in phase. It is convenient to describe this type of load pattern by a complex load vector X with harmonic time variation.

$$R=X{e}^{i\omega t}$$

(2)

The response vector r will also be given by a complex vector x and a harmonic time variation. Hence, it becomes,

$$r=x{e}^{i\omega t}$$

(3)

By introducing in the hydrodynamic mass $M_H$ and damping matrices $C_s$ dynamic equilibrium can now be expressed as:

$$-{\omega }^2(M_s+M_H)x+i\omega (C_s+C_H)x+Kx=x$$

(4)

where, $M_s$ and $C_s$ are the structural mass and structural damping, respectively.

The main VIV coefficients are the added mass ($C_a$) and excitation coefficients ($C_e$). Hydrodynamic damping is applied outside the excitation zone. The excitation force in CF direction at a given position on the structure is defined as the component of the hydrodynamic force that is in phase with the response velocity at the same location. The excitation force on an element with length ∆L is given by:

$$F_e=\frac{1}{2}\rho C_{e}D{U}_N^2∆L$$

(5)

where U_N is the local flow speed normal to the riser, $D$ is the local hydrodynamic diameter and $C_e$ is the excitation coefficient.

The response is solved in the frequency domain. A more detailed description of VIVANA may be found in Passano et al. [23]. Other empirical VIV prediction programs, such as SHEAR7 and VIVA, also rely on empirical hydrodynamic force coefficient models. However, different methods are applied for the calculation of the dynamic responses.

3. Methodology

An efficient numerical algorithm is developed to obtain the hydrodynamic force coefficient database based on response measurements of VIV tests with elastic pipes by (1) the hydrodynamic force coefficient database is parameterized; (2) these parameters are systematically scaled to create a sufficient amount of different excitation coefficient databases; (3) numerical simulations with generated databases are carried out and then the optimal parameter set is selected when the predicted responses are in good agreement with the test data.

3.1. Parameterize Excitation Coefficient Database

The CF excitation coefficient is a function of the non-dimensional amplitude (A/D) and the normalized oscillation frequency ($f_{osc}$) of the cylinder (${\widehat{f}}_{CF}=\frac{f_{osc}D}{U}$). The excitation coefficient database in empirical programs is often represented by a set of parameters.

The default set of excitation parameters in VIVANA are defined as a function of response amplitude ratio and excitation coefficient for a given non-dimensional frequency as shown in Figure 1. Four values are used to define one excitation coefficient curve at each non-dimensional frequency.

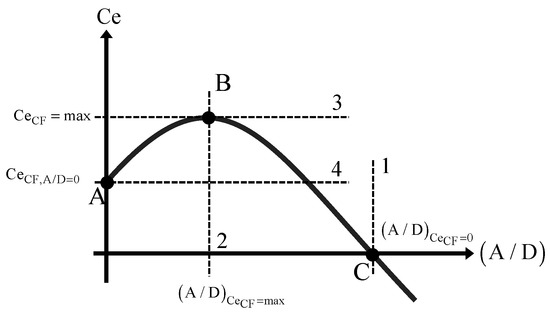
Figure 1. Three-point excitation coefficient curve for CF response.

The curve in Figure 1 is explained as follows:

• Point A presents the CF excitation coefficient value where the amplitude ratio (A/D) is zero, i.e., $C{e}_{CF,\left(A/D\right)=0}$. Here D is the corresponding cylinder diameter.
• Point B outlines the maximum CF excitation coefficient $C{e}_{CF}=max$ to the corresponding amplitude ratio ${(A/D)}_{C{e}_{CF}=max}$.
• Point C states the A/D values where $C{e}_{CF}$ is zero.

The default excitation database in VIVANA contains curves for 26 different non-dimensional frequencies as shown in Figure 2. These 26 curves are simplified to 3 representative non-dimensional frequencies (${\widehat{f}}_{CF}$) (vertical lines) as shown in Figure 2 and the corresponding values are presented in Table 1. This curve is represented by 4 excitation parameters. This curve is systematically changed by using 2 modification factors of amplitude ratio and excitation coefficient. The lower and upper ranges of non-dimensional frequency ranges are the same as the default set of parameters and they remain constant. The values between specified points will be linearly interpolated.

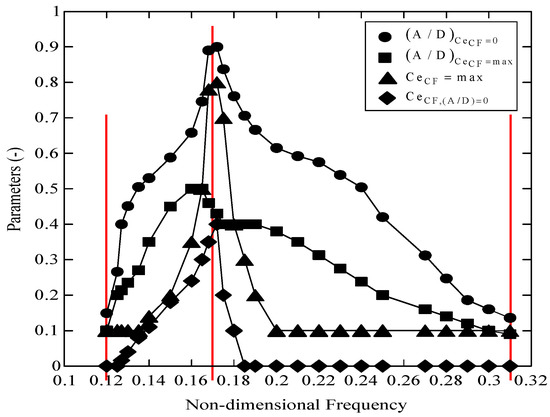
Figure 2. Parameterization of the excitation coefficient curves.

Table 1. Default set of parameters at three non-dimensional frequencies.

${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$
0.120	0.149	0.100	0.100	0.000
0.172	0.900	0.430	0.800	0.400
0.310	0.160	0.100	0.100	0.000

There may exist several frequencies that can be potentially excited along the length $L_{e,i}$ of the structure. The length of the occupied excitation zones of each frequency is defined by the corresponding non-dimensional frequency range (${\widehat{f}}_{CF}$ = 0.12 – 0.31 is used as the default range). In order to define the priority among all possibly acting frequencies, an excitation parameter based on energy considerations has been defined:

$$E_i={\int }_{L_{e,i}}{U}_N^3\left(s\right)D_{}^2\left(s\right){(A/D)}_{Ce=0}ds$$

(6)

The integrals for the excitation parameters are computed over the excitation zone for each frequency. The parameter ${(A/D)}_{Ce=0}$ is the non-dimensional amplitude where the excitation coefficient $Ce$ changes from a positive to a negative value. For a riser with a constant diameter subjected to the uniform flow, the dominating response frequency is around non-dimensional frequency 0.172, where ${(A/D)}_{Ce=0}$ has the highest value.

3.2. Scaling of Excitation Coefficient Database

As can be seen in Figure 3, the excitation coefficient curve at a given non-dimensional frequency consists of two parabolic curves. It is defined by at least four parameters, i.e., ${(A/D)}_{C{e}_{CF}=0}$, ${(A/D)}_{C{e}_{CF}=max}$, $C{e}_{CF=max}$, and $C{e}_{CF,\left(A/D\right)=0}$, refer to Table 1. It is difficult and not efficient to derive a reasonable new excitation coefficient curve by randomly varying these parameters. Instead, two scaling parameters (${\gamma }_{A/D}$, ${\gamma }_{Ce}$) are introduced, which scales the amplitude parameters ${(A/D)}_{C{e}_{CF}=0}$, ${(A/D)}_{C{e}_{CF}=max}$, and excitation coefficient parameters, $C{e}_{CF=max}$ and $C{e}_{CF,\left(A/D\right)=0}$, respectively. Representative excitation coefficient curves can be generated by systematically varying these two scaling parameters.

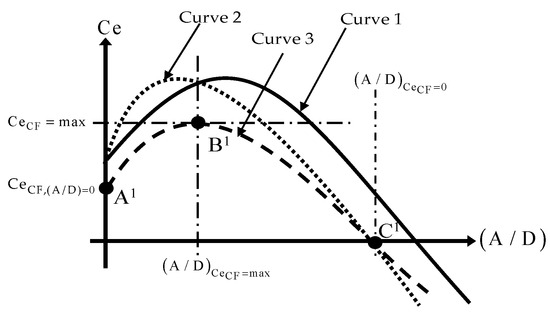
Figure 3. Illustration of the parameter scaling procedure by three curves: Curve 1: default CF excitation coefficient curve at a particular non-dimensional frequency in VIVANA, Curve 2: after amplitude modification, Curve 3: after the excitation coefficient modification.

The scaling is carried out in two steps as explained in the following:

Step 1: Amplitude modification process: The A/D modification factor is termed as

$${\gamma }_{A/D}=\frac{{(A/D)}_{C{e}_{CF}=0}}{{\left({(A/D)}_{C{e}_{CF}=0}\right)}_{def}}$$

(7)

where ${(A/D)}_{C{e}_{CF}=0}$ and ${\left({(A/D)}_{C{e}_{CF}=0}\right)}_{def}$ are defined as the modified maximum response amplitude ratio and default maximum response amplitude ratio, respectively. ${\gamma }_{A/D}$ is the amplitude modification factor.

From VIVANA, ${\left({(A/D)}_{C{e}_{CF}=0}\right)}_{def}$ is 0.9 at ${\widehat{f}}_{CF}$ of 0.172; and in the present analysis, the amplitude ratio modification factor is ranged between 0.5–1.3. For example, when ${\gamma }_{A/D}=0.8$,

$${(A/D)}_{C{e}_{CF}=0}={\left({(A/D)}_{C{e}_{CF}=0}\right)}_{def}\times {\gamma }_{A/D}=0.9\times 0.8=0.72$$

(8)

Figure 3 presents the modification process of hydrodynamic coefficients. The curve 2 in Figure 3 shows the modified excitation coefficient curve after applying a modification factor less than 1. It is obvious that A/D values at points B and C become smaller than the original curve, but the Ce values at points A and B remain the same.

Step 2: Excitation Coefficient Modification: The Ce modification factor is defined as:

$${\gamma }_{Ce}=\frac{{C{e}_{A/D}}_{=max}}{{\left(C{e}_{A/D=max}\right)}_{def}}$$

(9)

where ${C{e}_{A/D}}_{=max}$ and ${\left(C{e}_{A/D=max}\right)}_{def}$ are defined as the modified excitation coefficient and default excitation coefficient, respectively. ${\gamma }_{Ce}$ is the excitation coefficient modification factor.

The default peak value from VIVANA for ${\left(C{e}_{A/D=max}\right)}_{def}$ is 0.8 at ${\widehat{f}}_{CF}=0.172$. In the present analysis, the excitation coefficient modification factor (${\gamma }_{Ce}$) ranges between 0.5–2.25. For example, if ${\gamma }_{Ce}=0.8$ then

$${C{e}_{A/D}}_{=max}={\left(C{e}_{A/D=max}\right)}_{def}\times {\gamma }_{Ce}=0.8\times 0.8=0.64$$

(10)

As shown in Figure 3, by applying the amplitude ratio modification factor (step 1) at each non-dimensional frequency, the curve 2 coefficient curve is obtained. Based on step 1, the final excitation coefficient curve (curve 3) is obtained after applying the excitation coefficient modification factor (step 2).

These two scaling parameters are systematically varied to create sufficient amount of different excitation coefficient databases.

3.3. Derive the Optimal Parameters

Numerical model of the experiment setup is constructed in VIVANA. Simulations are carried out with derived databases. The predicted responses, e.g., the frequency, mode number, RMS (Root-Mean-Square) amplitude ratio, and RMS curvature, are compared with the measurements. The optimal parameter is selected based on the pre-defined criteria.

4. Validation of the Numerical Algorithm for Simulated Bare Riser VIV Response

In this section, a validation of the proposed algorithm using the VIVANA program is explained. A numerical case study for a bare riser at a flow speed of 1.0 m/s is conducted. The analysis results with default excitation coefficient parameters from VIVANA are compared with the newly generated excitation coefficient parameters until the predicted response frequency, the mode number and the maximum fatigue damage matches with the default test data provided by VIVANA. The obtained excitation coefficients are compared with the default values to examine the validity of the algorithm.

In this validation study, new sets of excitation coefficient parameters are generated after applying the modification factors. The non-dimensional frequency for this section ranges between 0.130–0.190 with a step of 0.002, whereas the modification factors for A/D and Ce ranges between 0.5–1.2 with a step of 0.1, and 0.9–1.6 with a step of 0.05, respectively. Table 2 shows the newly generated data sets with ${\gamma }_{A/D}$ ranging from 0.5–1.2 and ${\gamma }_{Ce}=0.8$. In the present analysis, the flow of current is perpendicular to the riser model.

Table 2. New datasets of excitation coefficient parameters for different modification factors.

Set No.	${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$	${\mathit{\gamma }}_{\mathit{A}/\mathit{D}}$	${\mathit{\gamma }}_{{\mathit{C}}_{\mathit{e}}}$
2193	0.166	0.45	0.215	0.64	0.32	0.5	0.8
2194	0.166	0.54	0.258	0.64	0.32	0.6	0.8
2195	0.166	0.63	0.301	0.64	0.32	0.7	0.8
2196	0.166	0.72	0.344	0.64	0.32	0.8	0.8
2197	0.166	0.81	0.387	0.64	0.32	0.9	0.8
2198	0.166	0.90	0.430	0.64	0.32	1	0.8
2199	0.166	0.99	0.473	0.64	0.32	1.1	0.8
2200	0.166	1.08	0.516	0.64	0.32	1.2	0.8

Based on the non-dimensional frequency range and the modification factors, 3720 different sets of excitation parameters are generated. Thus, 3720 simulations with these input parameters are carried out. Examples of new parameter sets are presented in Table 2. The set of parameters which presents good approximation with default parameters is selected based on specified criteria as presented in Table 3.

Table 3. Specified criteria for selecting the optimal set of parameters.

Specified Criteria	Deviation of Predicted Response from Test Case
Mode number	0
Response Frequency	±10%
Fatigue damage	±10%

The optimal parameter set presented in Table 4. The corresponding fatigue damage comparison is shown in Figure 4. The comparison of the predicted mode number, response frequency is presented in Table 5. The prediction with set no. 2660, the mode number and response frequency are identical to the default test case with 4 and response frequency 2.78 Hz, respectively. The maximum accumulated fatigue damage for set no. 2660 is 6.5% less than the default test case which is acceptable based on the specified criteria as shown in Table 4.

Table 4. Identified optimal parameter set.

Set No.	${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$	${\mathit{\gamma }}_{\mathit{A}/\mathit{D}}$	${\mathit{\gamma }}_{{\mathit{C}}_{\mathit{e}}}$
2660	0.12	0.149	0.100	0.10	0.000	-	-
	0.170	0.900	0.430	0.80	0.400	1.0	1.0
	0.300	0.160	0.100	0.100	0.000	-	-

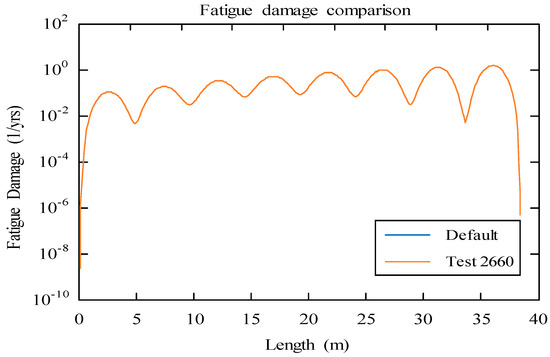
Figure 4. Comparison of the predicted fatigue damage between parameter set no. 2660 and default parameters. The results using the default parameters overlap with the results using parameter set no. 2660.

Table 5. Predicted responses for the default set of parameters and parameter with set no. 2660.

Set No.	Max. Fatigue Damage (/yr.)	Response
		Mode No.	Frequency
Default parameters	1.57	8	5.67
2660	1.57	8	5.67

The identified excitation coefficient parameter corresponds to a lower non-dimensional frequency (yellow line in Figure 5b) compared to the default values (middle red line in Figure 5a). The comparison of the identified parameters and the default parameters are presented in Table 6. The comparison shows that this algorithm can identify the simplified excitation coefficient database with good accuracy.

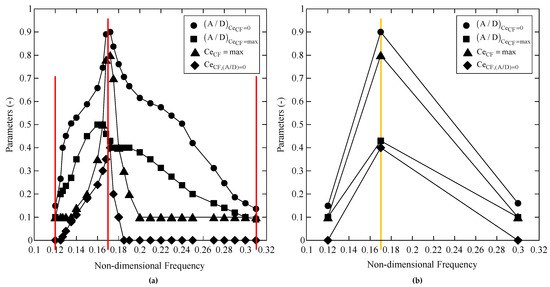
Figure 5. Comparison between the contour curves of (a) default parameters; (b) identified optimal parameter set no. 2660.

Table 6. Comparison between the identified parameters by the algorithm and the default parameters.

	${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$
Default	0.172	0.900	0.430	0.800	0.400
Identified	0.170	0.900	0.430	0.800	0.400

5. Analysis of the VIV Model Test Data of Flexible Riser with Staggered Buoyancy Elements

The main data source for this study is from the Shell experiment conducted in Ocean Laboratory at SINTEF Ocean ([14,16]). Figure 6 shows the schematic diagram of a flexible riser attached with buoyancy elements. In these tests, L_B represents the length of the buoyancy module and L_C represents the length of the bare riser section between two adjacent buoyant modules, respectively. Five different buoyancy element configurations were tested as shown in Figure 7. Here L_c is the length of the bare riser section and L_B is the length of the buoyancy element. The material properties of the bare riser section and the buoyancy element are listed in Table 7. The shedding frequency of the bare riser section is higher than the buoyancy element due to its smaller diameter (D_B/D_c = 8/3). Here D_B is the diameter of the buoyancy element and D_c is the diameter of the bare riser section.

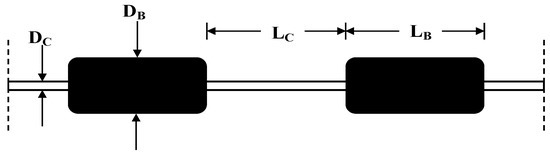
Figure 6. Definitions of LC, LB, DC, and DB.

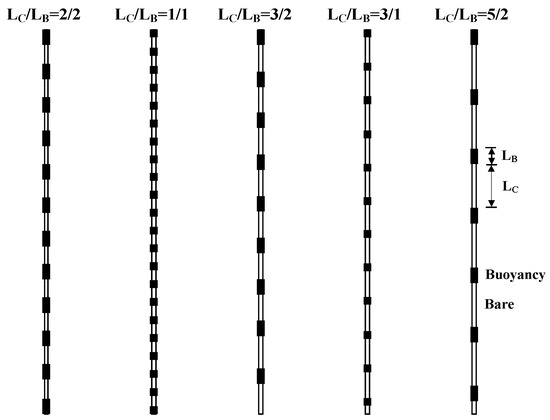
Figure 7. Staggered buoyancy configurations over the riser.

Table 7. The material properties of the bare riser section and the buoyancy element.

Parameters	Bare Riser	Buoyancy Element
Total length between pinned ends (m)	38.00	38.00
Outer diameter (mm)	30.00	80.00
Outer/inner diameter of fiberglass rod/pipe (mm)	27/21	27/21
The length of one buoyancy element (m)	--	0.4086
Bending stiffness, EI (N.m2)	572.3	572.3
Young’s modulus, E (N/m2)	3.46 × 1010	3.46 × 1010
Mass in the air (kg/m)	1.088	5.708
Weight in water (kg/m)	0.579	0.937
Mass ratio (-)	1.54	1.14
Reynolds number (-)	1.32 × 105 - 3.16 × 105	3.51 × 105 - 8.42 × 105

5.1. Prediction with Default Parameters

The numerical model to predict the response of the flexible riser with staggered buoyancy elements is constructed in VIVANA. The structural damping is set to be 1% of the critical damping.

The default excitation coefficient parameters from VIVANA are used to predict the VIV response. The predicted response frequencies from the default set of excitation coefficients and the measured responses are presented as a function of towing speed in Figure 8. The non-dimensional frequency ($\widehat{f}=\frac{f_{osc}D}{U}$) corresponding to the bare riser’s excitation frequency typically ranges 0.125–0.155 for different configurations in the model test [16]. The non-dimensional frequency for the buoyancy element was generally lower than that for the bare riser section. Significantly lower non-dimensional frequency (${\widehat{f}}_{CF}$ ≈ 0.1) could be found in model tests for shorter buoyancy element (L_B/D_B = 1) configuration [18]. When comparing with the measured responses, the response frequencies are, in general, over-predicted by the VIVANA model with the default set of excitation coefficients. This suggests the over-prediction of the excited modes, hence, higher stress and fatigue damage.

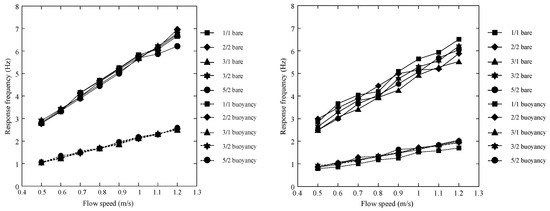
Figure 8. Excited response frequencies for five configurations at flow speeds between 0.5–1.2 m/s. (Left): prediction using the default set of excitation coefficients from VIVANA; (Right): measured response frequencies from Shell Test.

Figure 9 shows the curvature RMS values for the default set of parameters for different configurations. It is observed from the test data that 1/1 configuration has the lowest curvature, whereas L_C/L_B = 3/1 configuration has the highest curvature. It can also be noted that the configuration L_C/L_B = 2/2 has higher curvature even the percentage of buoyancy element coverage is the same as the 1/1 configuration. The maximum RMS curvature using the default set of parameters is in general over-predicted than the measurements.

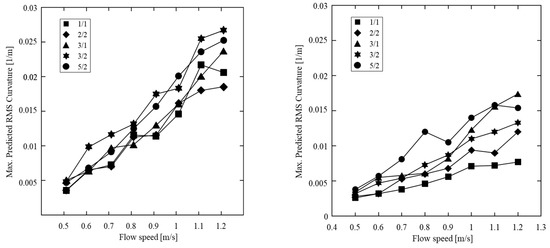
Figure 9. Curvature RMS values for five configurations at flow speeds between 0.5–1.2 m/s. (Left): prediction using the default set of excitation coefficients from VIVANA; (Right): measured curvature from Shell Test.

The predicted A/D for 2/2 configuration at U = 1.0 m/s are presented in Figure 10. It shows that the riser is excited at two response frequencies and modes due to excitations from the bare sections and the buoyancy sections of the riser. The predicted vortex shedding frequency of the buoyancy section is 2.1 Hz and the 5th mode of the riser system is excited. The vortex shedding frequency of the bare riser section is 5.8 Hz, which corresponds to the 14th mode.

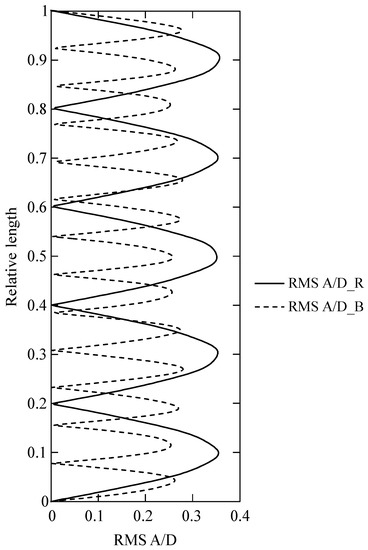
Figure 10. Predicted response amplitude components with default dataset from VIVANA for 2/2 configuration at 1.0 m/s flow speed.

5.2. Identification of an Optimal Dataset of Excitation Coefficient Parameters for the Flexible Riser with Staggered Buoyancy Elements

5.2.1. Criteria for the Selection of the Optimal Parameter Set

In order to obtain an optimal set of parameters, different datasets of excitation coefficient parameters are generated using modification factors for A/D and Ce and these datasets are used to run the numerical simulations. The predicted responses are compared with the test results in terms of mode number, response frequency, displacement amplitude and RMS curvature. The best approximation is selected as the optimal set of parameters which meet the specified criteria as shown in Table 8. The predicted mode number is required to be the same as that from the measurement. The predicted response frequency and the RMS curvature values need to be within ±10% of the measured values. The deviation in RMS A/D should be within ±5% of the test results.

Table 8. Specified criteria for selecting an optimal set of parameters for bare section and buoyancy element.

Specified Criteria	Deviation of Predicted Responses from Test Results
Mode	0
Response Frequency	±10%
Response A/D	±5%
RMS Curvature	±10%

5.2.2. Generating New Set of Excitation Parameters

The A/D and Ce modification factors (${\gamma }_{A/D}$ and ${\gamma }_{Ce}$) are used to generate the new datasets of excitation coefficient parameters to obtain an optimal dataset of parameters by comparing the predicted and measured responses in terms of mode number, response frequency, RMS A/D and RMS curvature.

For generating new sets of excitation parameters, the upper and lower range of ${\widehat{f}}_{CF}$ remains constant and the middle row ${\widehat{f}}_{CF}=0.72$ will be changing within the defined range from the VIVANA theory manual presented in Table 1. Modification factors are used to multiply these excitation parameters to generate new sets of excitation parameters.

The range of ${\gamma }_{A/D}$ is taken as 0.5–1.3 with a step of 0.10. This range is selected based on criteria that A/D is normally smaller than 1.2 based on the rigid cylinder tests, e.g., [5,6]. The range for ${\gamma }_{Ce}$ is 0.5–2.25 with a step of 0.05. Different new datasets of excitation coefficient parameters are generated by considering the ranges for non-dimensional frequency, A/D and Ce.

5.3. Optimal Excitation Parameters

A flexible riser with 2/2 configuration of bare and buoyancy elements at 1.0 m/s flow speed is used to derive the optimal dataset of excitation parameters. In the present analysis, simulations are carried out using two different datasets of excitation parameters i.e., one for the bare parts and one for the buoyancy sections of the riser, to obtain an optimal set of excitation parameters. The predicted responses from VIVANA are compared with the measured results.

By considering the ranges of ${\widehat{f}}_{CF}$, ${\gamma }_{A/D}$ and ${\gamma }_{Ce}$, 18650 simulations have been performed. The current direction is perpendicular to the riser model; the added mass coefficient is taken as 1.0; and the effect of the Reynolds number effect is not considered in the present analysis.

The optimized excitation coefficient parameter sets corresponding to the bare and the buoyancy sections are presented in Table 9 and Table 10, respectively. The corresponding contour curves are presented in Figure 11. The predicted RMS A/D, with an optimized set of parameters is presented in Figure 12.

Table 9. Optimal excitation coefficient parameters with modification factors for bare part of the riser.

Set No.	${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$	${\mathit{\gamma }}_{\mathit{A}/\mathit{D}}$	${\mathit{\gamma }}_{{\mathit{C}}_{\mathit{e}}}$
5522	0.120	0.1490	0.100	0.100	0.000	-	-
	0.156	0.900	0.430	0.450	0.225	1.0	0.5625
	0.300	0.1600	0.100	0.100	0.000	-	-

Table 10. Optimal excitation coefficient parameters with modification factors for buoyancy part.

Set No.	${\widehat{\mathit{f}}}_{\mathit{C}\mathit{F}}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=0}$	${\left(\mathit{A}/\mathit{D}\right)}_{\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F}}=\mathit{m}\mathit{a}\mathit{x}$	$\mathit{C}{\mathit{e}}_{\mathit{C}\mathit{F},\left(\mathit{A}/\mathit{D}\right)=0}$	${\mathit{\gamma }}_{\mathit{A}/\mathit{D}}$	${\mathit{\gamma }}_{{\mathit{C}}_{\mathit{e}}}$
5522	0.120	0.149	0.100	0.100	0.000	-	-
	0.142	1.080	0.516	0.560	0.280	1.20	0.70
	0.300	0.160	0.100	0.100	0.000	-	-

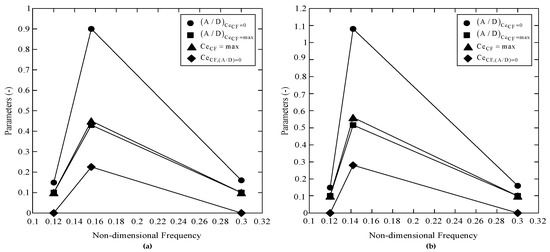
Figure 11. The optimal excitation parameter set for 2/2 configuration at 1.0 m/s flow speed for (a) bare part of the riser; (b) buoyancy section of the riser.

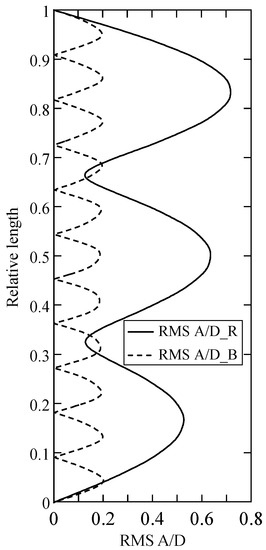
Figure 12. Predicted CF RMS A/D with the obtained optimal parameter set for the 2/2 configuration at U = 1.0 m/s.

5.4. Improved Prediction for the Selected Test Case (U = 1.0 m/s) of the 2/2 Configuration

The measured dominant response mode/frequency, amplitude ratio and curvature are compared with predicted values for the 2/2 configuration at flow speed of 1.0 m/s in Table 11. It can be seen that the responses (i.e., mode/frequency, A/D and curvature) prediction for both the bare riser section and the buoyancy element have been improved with the optimal parameters. The prediction error compared to the measurement is within the specified criteria in Table 8. The predicted displacement is presented in Figure 12.

Table 11. Comparison of the prediction and measurements for the 2/2 configuration at U = 1.0 m/s.

Comparison	Mode and fR (Hz)	Mode and fB (Hz)	Max. RMS (A/D)R	Max. RMS (A/D)B	Max. RMS Curvature(1/m)
Measurement	~11 and 5.15	3 and 1.82	0.200	0.71	0.0095
Default parameters	14 and 5.800	5 and 2.100	0.250	0.35	0.016
Optimal parameters	11 and 5.15	3 and 2.00	0.201	0.72	0.0086

F_R and F_B are Response frequencies for bare and buoyancy parts, respectively. Max. RMS A/D_R and Max. RMS A/D_B are Maximum Root Mean Square Amplitude ratios for bare riser buoyancy.

5.5. Improved Prediction for other Cases of the 2/2 Configuration

The optimized parameters are used to predict the responses of the 2/2 configuration for U = 0.5–1.2 m/s. Figure 13 presents the comparison of the prediction with the optimal parameters and the measured response frequencies. It can be seen that the predicted response frequency is in good agreement with the measured values.

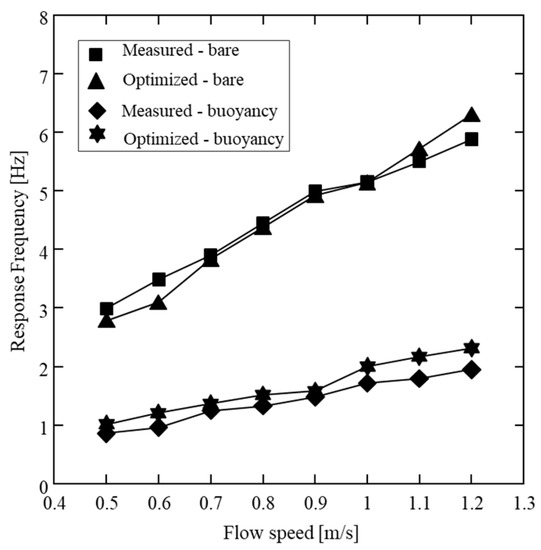
Figure 13. Comparison between the measured and predicted response frequencies for the 2/2 configuration for flow speed between 0.5–1.2 m/s.

Table 12 presents the measured responses from the experiment by Rao et al. [16] and the predicted responses from an optimal dataset of excitation coefficient parameters. The results show that the mode has been correctly predicted and the error in the frequency prediction is within 10% for the chosen case (U = 1.0 m/s). The error in the frequency prediction for the other cases of the same configuration L_C/L_B = 2/2 is within 10% and 20% for the bare riser section and the buoyancy element, respectively.

Table 12. Comparison between measured results and predicted response frequencies with an optimal dataset of excitation coefficient parameters for 2/2 configuration for flow speed between 0.5–1.2 m/s.

Flow Speed [m/s]	Bare Part				Buoyancy Part
	Measured Response		Predicted Response		Measured Response		Predicted Response
	M*	F*	M*	F*	M*	F*	M*	F*
0.5	-	2.99	7	2.78	-	0.86	2	1.01
0.6	-	3.48	8	3.09	-	0.96	2	1.20
0.7	-	3.90	10	3.83	-	1.25	2	1.36
0.8	-	4.45	11	4.37	-	1.33	2	1.51
0.9	-	4.99	12	4.91	-	1.48	2	1.58
1.0	11	5.15	11	5.14	3	1.82	3	2.0
1.1	-	5.50	13	5.72	-	1.86	3	2.16
1.2	-	5.88	14	6.3	-	1.95	3	2.31

M* = mode number, F* = Response Frequency.

Figure 14 presents the comparison of the predicted RMS curvatures with the default parameters and the optimized parameters as well as the RMS curvatures obtained from the measured responses as a function of flow speed (U = 0.5–1.2 m/s). The prediction with optimized parameters shows a good agreement with the measured rms curvature when compared with the prediction with the default excitation parameters.

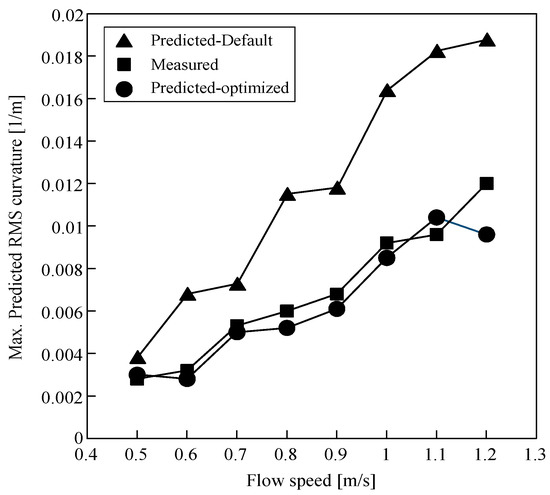
Figure 14. The predicted RMS curvature as a function of flow speed for the 2/2 configuration. (The measured values are adapted from Rao et al. [16]).

5.6. Sensitivity in the Prediction for Different Buoyancy Element Configurations

It is also of interest to see how robust the prediction can be when the same set of parameters is used to predict VIV responses for other buoyancy configurations. The optimal excitation parameter set presented in Table 9 and Table 10 are applied to predict the responses of all five configurations.

Figure 15 presents the predicted response frequencies for with five different configurations using the derived optimal set of excitation parameters based on the 2/2 configuration and the measured frequencies. The prediction is reasonable in general. However, it can also be observed that the predicted response frequencies of the five configurations are almost the same at the same flow speed; while, model test results indicate the frequencies will be different dependent on the specific configuration.

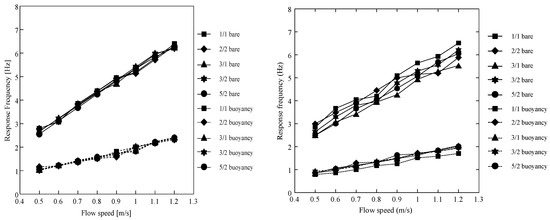
Figure 15. Excited response frequencies for five configurations at flow speeds between 0.5 m/s–1.2 m/s. (Left): prediction using the derived excitation coefficients from VIVANA; (Right): measured response frequencies from Shell Test.

The ratio of the predicted and measured maximum curvature for five buoyancy element configurations is presented in Figure 16. The predictions for the 2/2 and 3/2 configurations show a good agreement with the measured data, e.g., the difference in curvature is less than 20%. The curvature of the 1/1 configuration is in general over-predicted up to 50%. The increasing in spacing between two buoyancy elements (L_C/L_B) >3/2 seems to lead to under-prediction. The curvature of the 3/1 and 5/2 configurations are, in general, under-predicted by up to 50%.

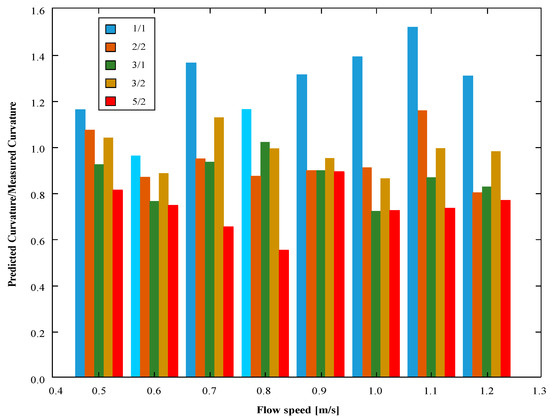
Figure 16. The ratio of the predicted over measured maximum RMS curvature values at different flow speeds for five configurations.

This comparison indicates the sensitivity of VIV response related to the geometry difference. One set of excitation parameters may not be valid for a different buoyancy element configuration. It will be of interest to derive the optimal parameter sets for the other configurations once more detailed test results become available.

6. Conclusions

A numerical algorithm has been developed to obtain parameterized excitation coefficient data based on VIV model test data of a flexible riser with buoyancy elements. Two sets of excitation coefficient parameters are used to represent the bare riser parts and the buoyancy elements, respectively. The parameters are systematically varied by multiplying with modification factors and the optimal set of excitation parameters is selected when the predicted response agrees well with the model test results. The optimal datasets of excitation coefficient parameters are significantly different from the default data based on bare riser tests. A significant improvement in prediction is achieved in terms of mode, response frequency, response amplitude and RMS curvature.

The hydrodynamic parameters are derived based on one case from one of the five staggered buoyancy element configurations. The prediction results are consistent for the other cases of the same configuration. The prediction accuracy has been significantly improved compared to the use of the default parameters. However, the prediction shows larger deviation compared to the measurements when applied to a different configuration. This is what can be expected as the interaction between the bare riser section and the buoyancy element is complicated. The hydrodynamic parameters will not be the same as the configuration or the dimension of the buoyancy element changes, as also seen in other such tests. Therefore, it can be difficult to generalize the result. However, the present approach offers one way to estimate these key hydrodynamic parameters directly from model test with elastic pipes. It can be applied to available tests to estimate and map the parameters, so that the physical basis in the hydrodynamic load modelling can be further improved. This approach can also be applied to other VIV tests.