Anomalous Humidity Dependence in Photoacoustic Spectroscopy of CO Explained by Kinetic Cooling
Abstract
Featured Application
Abstract
1. Introduction
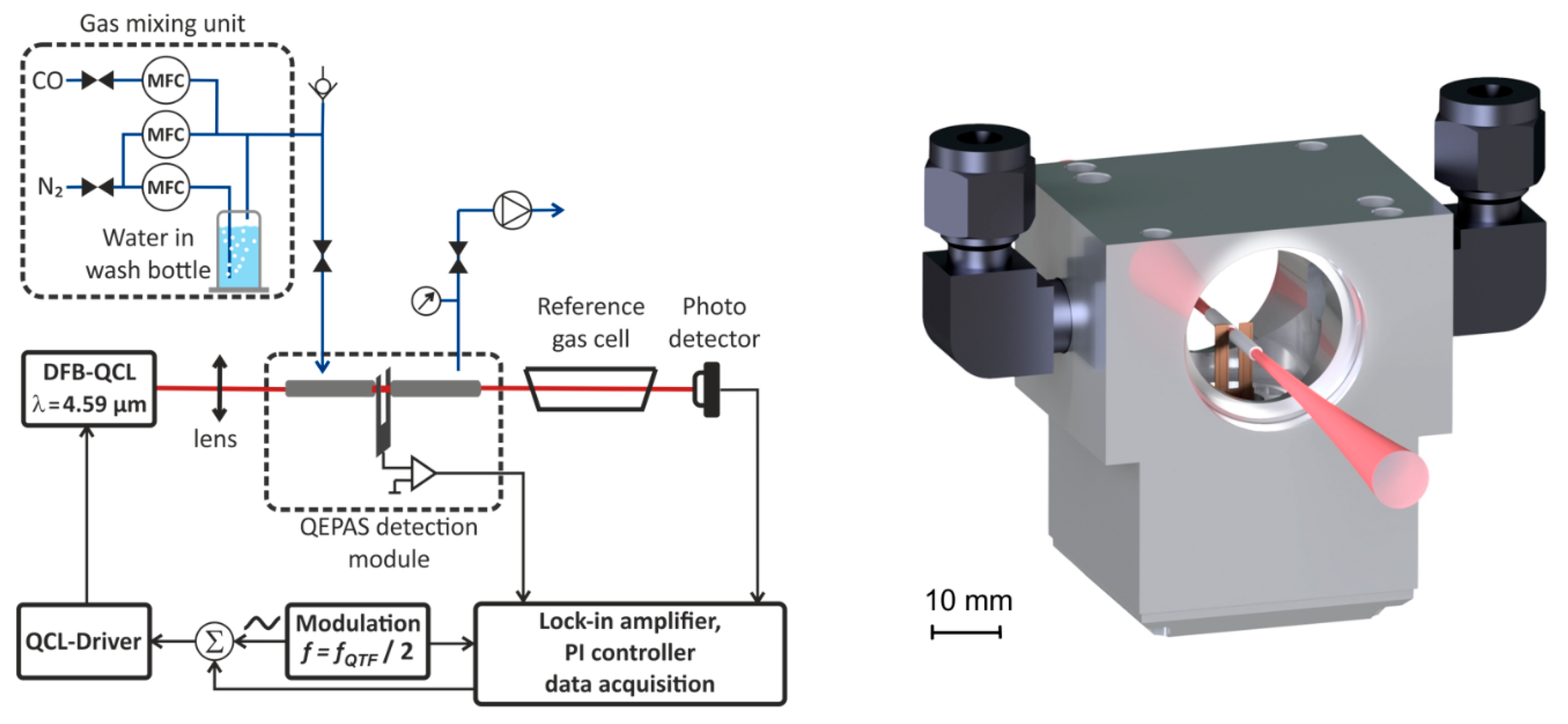
2. Materials and Methods
2.1. Measurement of Humidity Dependent 2f-WM-QEPAS Signals of CO
2.2. Collisional Energy Transfer and Relaxation
3. Results
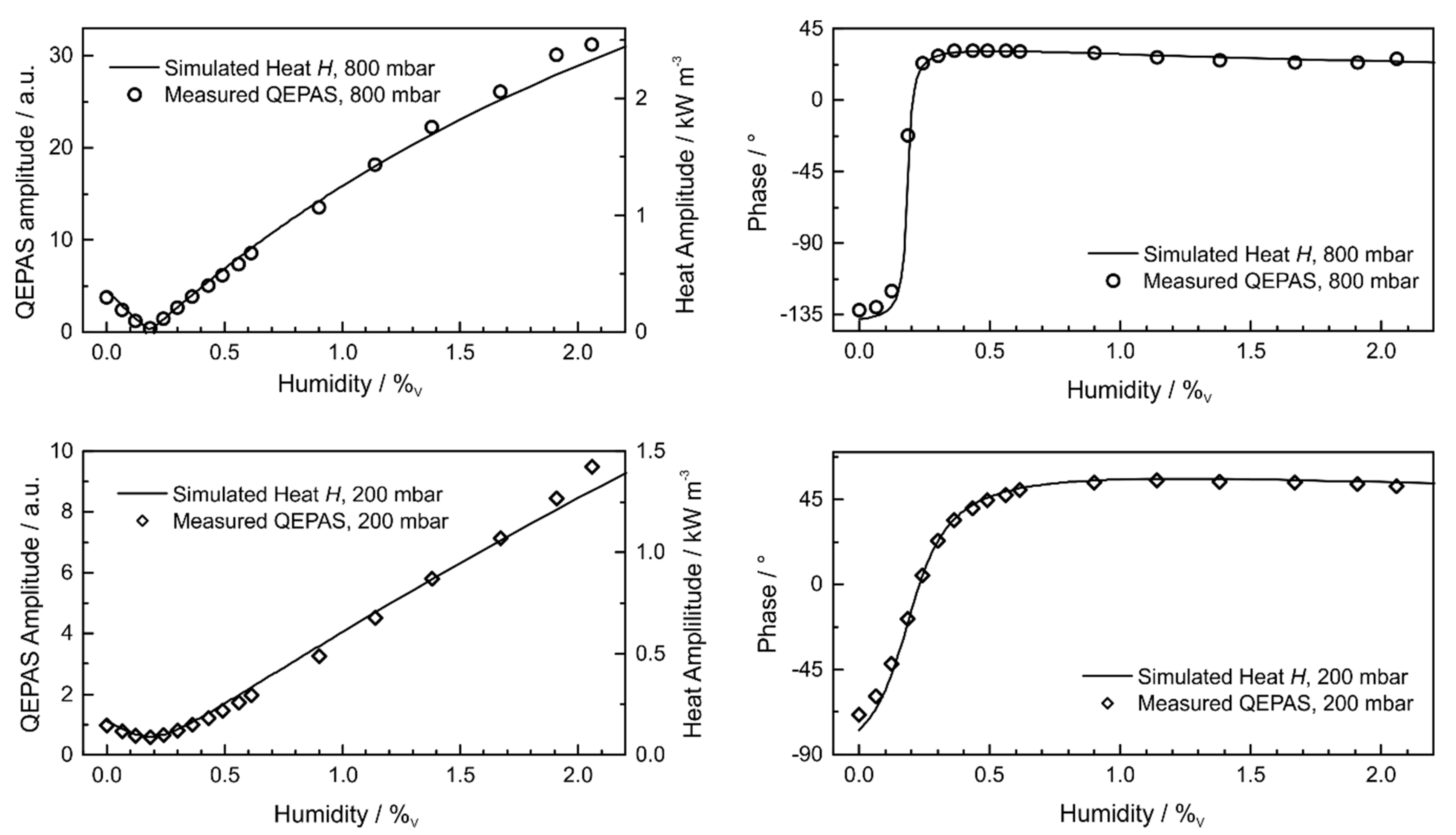
3.1. Humidity Dependence in the Experiment
3.2. Collisional Relaxation in the CO, N2, and H2O System
3.3. Rate Equations and Quantitative Model
3.4. Simulation Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kosterev, A.A.; Mosely, T.S.; Tittel, F.K. Impact of humidity on quartz-enhanced photoacoustic spectroscopy based detection of HCN. Appl. Phys. B 2006, 85, 295–300. [Google Scholar] [CrossRef]
- Lambert, J.D. Vibrational and Rotational Relaxation in Gases; The International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1977; ISBN 0-19-855605-5. [Google Scholar]
- Ma, Y.; Lewicki, R.; Razeghi, M.; Tittel, F.K. QEPAS based ppb-level detection of CO and N2O using a high power CW DFB-QCL. Opt. Express 2013, 21, 1008–1019. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Lewicki, R.; Liu, K.; Buerki, P.R.; Weida, M.J.; Tittel, F.K. Ultra-sensitive carbon monoxide detection by using EC-QCL based quartz-enhanced photoacoustic spectroscopy. Appl. Phys. B 2012, 107, 275–283. [Google Scholar] [CrossRef]
- Wood, A.D.; Camac, M.; Gerry, E.T. Effects of 10.6-μ laser induced air chemistry on the atmospheric refractive index. Appl. Opt. 1971, 10, 1877–1884. [Google Scholar] [CrossRef] [PubMed]
- Hammerich, M.; Ólafsson, A.; Henningsen, J. Photoacoustic study of kinetic cooling. Chem. Phys. 1992, 163, 173–178. [Google Scholar] [CrossRef]
- Santosa, I.E.; Oetama, E.J.; Harren, F.J.M. Phasor representation for the nonlinear photoacoustic signal. Eur. J. Phys. 2017, 38, 065803. [Google Scholar] [CrossRef]
- Siebert, D.R.; Grabiner, F.R.; Flynn, G.W. Time—resolved thermal lensing studies of laser—induced translational energy fluctuations in CD4, SO2, and OCS. J. Chem. Phys. 1974, 60, 1564–1574. [Google Scholar] [CrossRef]
- Wysocki, G.; Kosterev, A.A.; Tittel, F.K. Influence of molecular relaxation dynamics on quartz-enhanced photoacoustic detection of CO2 at λ = 2 μm. Appl. Phys. B 2006, 85, 301–306. [Google Scholar] [CrossRef]
- Rooth, R.A.; Verhage, A.J.L.; Wouters, L.W. Photoacoustic measurement of ammonia in the atmosphere: Influence of water vapor and carbon dioxide. Appl. Opt. 1990, 29, 3643–3653. [Google Scholar] [CrossRef]
- Truong, N.; Buüscher, S.; Kuühnemann, F.; Harith, M.A. Detecting Carbon Monoxide (CO) With Photoacoustic Spectroscopy: The Role of Molecular Collision Dynamics. In Proceedings of the AIP Conference Proceedings, University Park, MD, USA, 8 October 2009; pp. 3–8. [Google Scholar]
- Patimisco, P.; Sampaolo, A.; Giglio, M.; dello Russo, S.; Mackowiak, V.; Rossmadl, H.; Cable, A.; Tittel, F.K.; Spagnolo, V. Tuning forks with optimized geometries for quartz-enhanced photoacoustic spectroscopy. Opt. Express 2019, 27, 1401–1415. [Google Scholar] [CrossRef]
- Giglio, M.; Elefante, A.; Patimisco, P.; Sampaolo, A.; Sgobba, F.; Rossmadl, H.; Mackowiak, V.; Wu, H.; Tittel, F.K.; Dong, L.; et al. Quartz-enhanced photoacoustic sensor for ethylene detection implementing optimized custom tuning fork-based spectrophone. Opt. Express 2019, 27, 4271–4280. [Google Scholar] [CrossRef] [PubMed]
- Moser, H. Development and Implementation of An Industrial Process Gas Monitoring System for H2S Based on Mid-Infrared Quantum Cascade Laser Spectroscopy; Technische Univerisät Wien: Vienna, Austria, 2016. [Google Scholar]
- Baumgartner, B.; Hayden, J.; Loizillon, J.; Steinbacher, S.; Grosso, D.; Lendl, B. Pore size-dependent structure of confined water in mesoporous silica films from water adsorption-desorption using ATR-FTIR spectroscopy. Langmuir 2019, 35, 11986–11994. [Google Scholar] [CrossRef] [PubMed]
- Johnson, T.J.; Sams, R.L.; Sharpe, S.W. The PNNL Quantitative Infrared Database for Gas-Phase Sensing: A Spectral Library for Environmental, Hazmat, and Public Safety Standoff Detection; Sedlacek, A.J., III, Colton, R., Vo-Dinh, T., Eds.; International Society for Optical and Engineering: Washington, DC, USA, 2004; Volume 5269, p. 159. [Google Scholar] [CrossRef]
- Rosencwaig, A. Photoacoustics and Photoacoustic Spectroscopy; Wiley: Bacon, NJ, USA, 1980; ISBN 0471044954. [Google Scholar]
- Wojcik, M.D.; Phillips, M.C.; Cannon, B.D.; Taubman, M.S. Gas-phase photoacoustic sensor at 8.41 μm using quartz tuning forks and amplitude-modulated quantum cascade lasers. Appl. Phys. B 2006, 85, 307–313. [Google Scholar] [CrossRef]
- Matteuci, S.; Yampolskii, Y.; Freeman, B.D.; Pinnau, I. Transport of Gases and Vapors. In Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley & Sons, Ltd.: Bacon, NJ, USA, 2015; pp. 1–47. ISBN 978-0-470-85345-0. [Google Scholar]
- Zittel, P.F.; Masturzo, D.E. Vibrational relaxation of H2O from 295 to 1020 K. J. Chem. Phys. 1989, 90, 977–989. [Google Scholar] [CrossRef]
- Kung, R.T.V.; Center, R.E. High temperature vibrational relaxation of H2O by H2O, He, Ar, and N2. J. Chem. Phys. 1975, 62, 2187–2194. [Google Scholar] [CrossRef]
- Whitson, M.E.; McNeal, R.J. Temperature dependence of the quenching of vibrationally excited N2 by NO and H2O. J. Chem. Phys. 1977, 66, 2696–2700. [Google Scholar] [CrossRef]
- Frey, R.; Lukasik, J.; Ducuing, J. Tunable raman excitation and vibrational relaxation in diatomic molecules. Chem. Phys. Lett. 1972, 14, 514–517. [Google Scholar] [CrossRef]
- Hilborn, R.C. Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 1982, 50, 982–986. [Google Scholar] [CrossRef]
- Šimečková, M.; Jacquemart, D.; Rothman, L.S.; Gamache, R.R.; Goldman, A. Einstein A-coefficients and statistical weights for molecular absorption transitions in the HITRAN database. J. Quant. Spectrosc. Radiat. Transf. 2006, 98, 130–155. [Google Scholar] [CrossRef]
- Fischer, J.; Gamache, R.R.; Goldman, A.; Rothman, L.S.; Perrin, A. Total internal partition sums for molecular species in the 2000 edition of the HITRAN database. J. Quant. Spectrosc. Radiat. Transf. 2003, 82, 401–412. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Szakáll, M.; Huszár, H.; Bozóki, Z.; Szabó, G. On the pressure dependent sensitivity of a photoacoustic water vapor detector using active laser modulation control. Infrared Phys. Technol. 2006, 48, 192–201. [Google Scholar] [CrossRef]
- Waclawek, J.P.; Bauer, V.C.; Moser, H.; Lendl, B. 2f-wavelength modulation Fabry-Perot photothermal interferometry. Opt. Express 2016, 24, 28958–28967. [Google Scholar] [CrossRef] [PubMed]
- Hayden, J.; Baumgartner, B.; Waclawek, J.P.; Lendl, B. Mid-infrared sensing of CO at saturated absorption conditions using intracavity quartz-enhanced photoacoustic spectroscopy. Appl. Phys. B 2019, 125, 159. [Google Scholar] [CrossRef]
- Hayden, J. Novel Techniques of Cavity Enhanced Spectroscopy for Trace Gas Sensing; TU Wien: Vienna, Austria, 2019. [Google Scholar]
- Giusfredi, G.; Galli, I.; Mazzotti, D.; Cancio, P.; De Natale, P. Theory of saturated-absorption cavity ring-down: Radiocarbon dioxide detection, a case study. J. Opt. Soc. Am. B 2015, 32, 2223–2237. [Google Scholar] [CrossRef]



| Process | ZA-B [109 s−1atm−1] | ZA-B/Ẑ [s−1atm−1] | ||
|---|---|---|---|---|
| R-T, CO (N2) | 7.0 | 3 | 2.3 × 109 | 37 |
| V-V, CO → N2 | 7.0 | 4.9 × 104 | 1.4 × 105 | −188 |
| V-V, N2 → CO | 7.0 | 2.0 × 104 | 3.5 × 105 | 188 |
| V-V, CO → H2O | 6.0 | 1.1 × 103 | 5.5 × 106 | 548 |
| V-V, N2 → H2O | 5.7 | 2.6 × 104 | 2.2 × 105 | 736 |
| V-T, N2 (N2) | 6.8 | 4 × 109 | 1.7 | 2331 |
| V-T, H2O (N2) | 5.7 | 4.7 × 102 | 1.2 × 107 | 1595 |
| V-T, H2O (H2O) | 4.5 | 4 | 1.1 × 109 | 1595 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayden, J.; Baumgartner, B.; Lendl, B. Anomalous Humidity Dependence in Photoacoustic Spectroscopy of CO Explained by Kinetic Cooling. Appl. Sci. 2020, 10, 843. https://doi.org/10.3390/app10030843
Hayden J, Baumgartner B, Lendl B. Anomalous Humidity Dependence in Photoacoustic Spectroscopy of CO Explained by Kinetic Cooling. Applied Sciences. 2020; 10(3):843. https://doi.org/10.3390/app10030843
Chicago/Turabian StyleHayden, Jakob, Bettina Baumgartner, and Bernhard Lendl. 2020. "Anomalous Humidity Dependence in Photoacoustic Spectroscopy of CO Explained by Kinetic Cooling" Applied Sciences 10, no. 3: 843. https://doi.org/10.3390/app10030843
APA StyleHayden, J., Baumgartner, B., & Lendl, B. (2020). Anomalous Humidity Dependence in Photoacoustic Spectroscopy of CO Explained by Kinetic Cooling. Applied Sciences, 10(3), 843. https://doi.org/10.3390/app10030843





