Estimating Daily Global Solar Radiation with No Meteorological Data in Poland
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region and Data Collection
2.2. Calibration of Model Coefficients
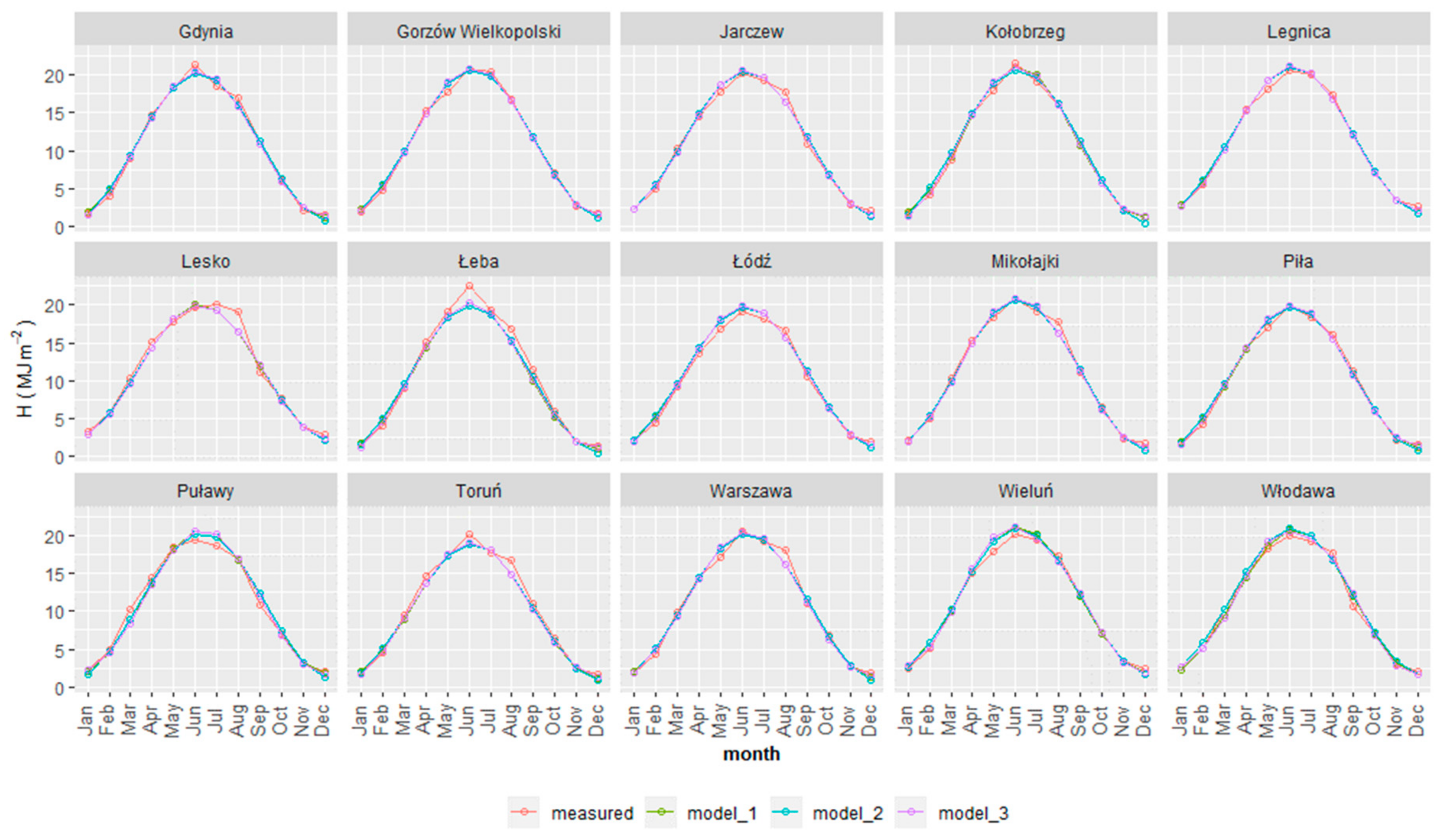
2.3. Model validation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bryś, K. Dynamics of Net radiation Balance of Grass Surface and Bare Soil; Monograph; Wrocław University of Environmental and Life Science: Wrocław, Poland, 2013. (In Polish) [Google Scholar]
- Matuszko, D. Long–term variability in solar radiation in Krakow based on measurements of sunshine duration. Int. J. Climatol. 2014, 23, 228–234. [Google Scholar] [CrossRef]
- Podstawczyńska, A. UV and global solar radiation in Łódź, Central Poland. Int. J. Climatol. 2010, 30, 1–10. [Google Scholar] [CrossRef]
- Kleniewska, M.; Chojnicki, B.H.; Acosta, M. Long–term total solar radiation variability at the Polish Baltic coast in Kołobrzeg within the period 1964–2013. Meteor. Hydr. Water Manag. 2016, 4, 35–40. [Google Scholar] [CrossRef]
- Uscka–Kowalkowska, J. An atmospheric extinction of direct solar radiation on Mt. Kasprowy Wierch, Poland. Atmos. Res. 2013, 134, 175–185. [Google Scholar] [CrossRef]
- Bogdańska, B.; Podogrocki, J. The Variability of total Solar Radiation in Poland within the Period 1961–1995; Institute of Meteorology and Water Management: Wrocław, Poland, 2000; p. 30. (In Polish) [Google Scholar]
- Kuczmarska, L. The Relations between Total Solar Radiation and Sunshine Duration in Poland. Wiad. Służ. Hydrol. Met. 1970, 6, 82. (In Polish) [Google Scholar]
- Podogrocki, J. Spatial distribution of global solar radiation in Poland. Publ. Ins. Geophys. Pol. Acad. Sci. 1976, D–5–120, 17–30. [Google Scholar]
- Bogawski, P.; Bednorz, E. Comparison and Validation of Selected Evapotranspiration Models for Conditions in Poland (Central Europe). Water Resour. Manag. 2014, 28. [Google Scholar] [CrossRef]
- Kimball, H.H. Variations in the total and luminous solar radiation with geographical position in the United States. Mon. Weather Rev. 1919, 47, 769–793. [Google Scholar] [CrossRef]
- Angström, A. Solar and terrestrial radiation. Q. J. R. Meteor. Soc. 1924, 50, 121–126. [Google Scholar]
- Prescott, J.A. Evaporation from a water surface in relation to solar radiation. Trans. R. Soc. South Aust. 1940, 64, 114–118. [Google Scholar]
- Almorox, J.; Hontoria, C. Global solar radiation estimation using sunshine duration in Spain. Energy Convers. Manag. 2004, 45, 1529–1535. [Google Scholar] [CrossRef]
- Suehrcke, H.; Bowden, R.S.; Hollands, K.G.T. Relationship between sunshine duration and solar radiation. Sol. Energy 2013, 92, 160–171. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain Div. 1982, 108, 225–230. [Google Scholar]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar–radiation and daily maximum and minimum temperature. Agric. For. Meteor. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Stanek, P.; Kuchar, L.; Otop, I. Estimation of diurnal total radiation based on meteorological variables in the period of plant vegetation in Poland. ITM Web Conf. 2018, 23, 00032. [Google Scholar] [CrossRef][Green Version]
- Black, J.N. The distribution of solar radiation over the Earth’s surface. Arch. Met. Geophy. Biokl. B 1956, 7, 165–189. [Google Scholar] [CrossRef]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]
- Lindauer, M.; Schmid, H.P.; Grote, R.; Steinbrecher, R.; Mauder, M.; Wolpert, B. A Simple New Model for Incoming Solar Radiation Dependent Only on Screen–Level Relative Humidity. J. Appl. Meteor. Climatol. 2017, 56, 1817–1825. [Google Scholar] [CrossRef]
- Bindi, M.; Miglietta, F. Estimating daily global radiation from air temperature and rainfall meaasurements. Clim. Res. 1991, 1, 117–124. [Google Scholar] [CrossRef]
- Bulut, H.; Buykukalaca, O. Simple model for the generation of daily global solar radiation data in Turkey. Appl. Energy 2007, 84, 477–491. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kaplani, E. A model to predict expected mean and stochastic hourly global solar radiation I (h,nj) values. Renew. Energy 2007, 32, 1414–1425. [Google Scholar] [CrossRef]
- Li, H.; Ma, W.; Lian, Y.; Wang, X. Estimating daily global solar radiation by day of year in China. Appl. Energy 2010, 87, 3011–3017. [Google Scholar] [CrossRef]
- El Mghouchi, Y.; Ajzoul, T.; El Bouardi, A. Prediction of daily solar radiation intensity by day of the year in twenty–four cities of Morocco. Renew. Sustain. Energy Rev. 2016, 53, 823–831. [Google Scholar] [CrossRef]
- Gasser, E.; Hassan, M.; Elsayed, Y.; Mohamed, A.; Ali, Z.E.; Mohamed, A.I. Performance assessment of different day of the year based models for estimation global solar radiation—Case study: Egypt. J. Atmos. Sol. 2016, 149, 69–80. [Google Scholar] [CrossRef]
- Aoun, N.; Bouchouicha, K. Estimating Global Solar Radiation by day of the year in Algeria. Eur. Phys. J. Plus 2017, 132, 216. [Google Scholar] [CrossRef]
- Khorasanizadeh, H.; Mohammadi, K.; Jalilvand, M. A statistical comparative study to demonstrate the merit of day of the year–based models for estimation of horizontal global solar radiation. Energy Conver. Manag. 2014, 87, 37–47. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.I.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Lorenc, H. (Ed.) Climate Atlas of Poland (Atlas Klimatu Polski); IMGW–PIB: Warszawa, Poland, 2005. (In Polish) [Google Scholar]
- Institute of Meteorology and Water Management-National Research Institute. Available online: www.imgw.pl (accessed on 17 June 2019).
- World Radiation Data Centre. Available online: http://wrdc.mgo.rssi.ru (accessed on 17 June 2019).
- Chwieduk, D.; Bogdańska, B. Some recommendations for inclinations and orientations of building elements under solar radiation in Polish conditions. Renew. Energy 2004, 29, 1569–1581. [Google Scholar] [CrossRef]
- Olejnik, J.; Leśny, J.; Eulenstein, F. The application of Fourier expansion in estimating the annual variation to the vertical gradient of some meteorological parameters. Geogr. Pol. 2000, 73, 141–152. [Google Scholar]
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckmann, W.A. Solar Engineering of Thermal Processes; John Wiley&Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
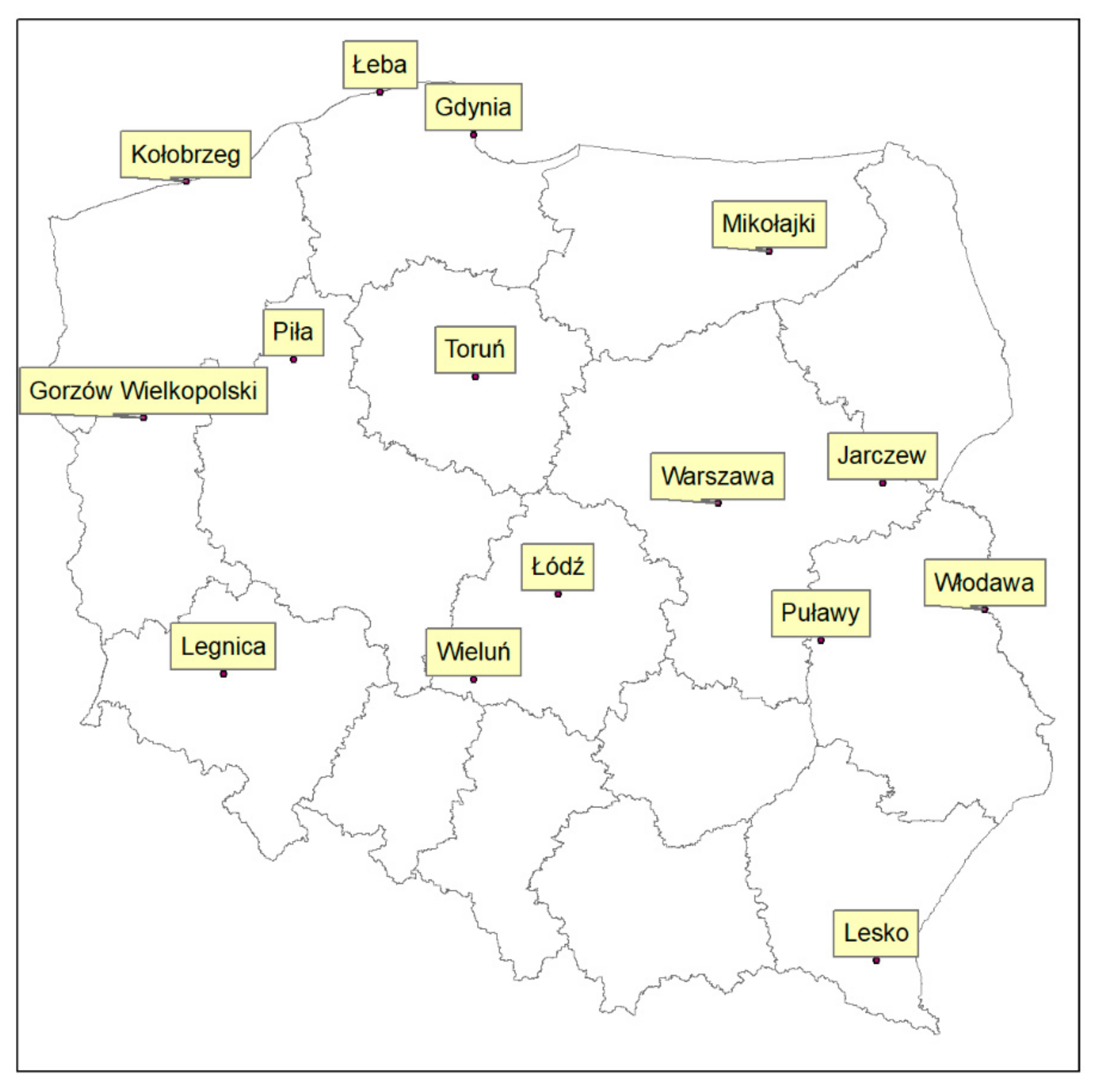
| Station | λ (E) | φ (N) | h (m) | Gaps |
|---|---|---|---|---|
| Gdynia | 18°33′34″ | 54°31′08″ | 2 | I,II,III 2001; XII 2003; I,IV 2004 |
| Gorzów Wielkopolski | 15°16’38" | 52°44’28" | 71 | 2000–2002 |
| Jarczew | 21°58′24″ | 51°48′53″ | 180 | V,VI 2003; VII 2004; XI 2005; IX,X,XI 2015 |
| Kołobrzeg | 15°34′47″ | 54°10′57″ | 3 | |
| Legnica | 16°12′28″ | 51°11′33″ | 122 | X, XI 2014 |
| Łeba | 17°32′05″ | 54°45′13″ | 2 | VIII, IX 2012 |
| Łódź | 19°23′14″ | 51°43′06″ | 175 | IV 2015 |
| Lesko | 22°20′30″ | 49°27′59″ | 420 | III 2003 |
| Mikołajki | 21°35′23″ | 53°47′21″ | 127 | |
| Piła | 16°44′50″ | 53°07′50″ | 72 | XI, XII 2014; I,II,III,IV 2015 |
| Puławy | 21°57′58″ | 51°24′46″ | 142 | XI 2001; II,III,IV 2005;V 2004, 2015 |
| Toruń | 18°35′44″ | 53°02′31″ | 69 | |
| Warszawa | 20°57′48″ | 52°16′53″ | 98 | |
| Wieluń | 18°33′24″ | 51°12′37″ | 199 | X,XI,XII 2014 |
| Włodawa | 23°31′46″ | 51°33′12″ | 177 |
| Station | Model | a | b | c | d | e | f | g | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Gdynia | 1 | 1.06 | 19.53 | 10.71 | 2.25 | 0.96 | |||
| 2 | 10.39 | −9.87 | 10.57 | 0.96 | |||||
| 3 | 10.79 | −9.11 | 1.05 | −4.08 | −5.54 | 1.03 | 5.20 | 0.96 | |
| Gorzów | 1 | 1.34 | 19.69 | 10.39 | 2.15 | 0.96 | |||
| 2 | 10.91 | −9.91 | 10.35 | 0.96 | |||||
| 3 | 11.23 | −10.05 | 1.04 | −4.25 | −3.87 | 1.03 | 4.94 | 0.96 | |
| Jarczew | 1 | 1.44 | 19.25 | 10.45 | 2.11 | 0.96 | |||
| 2 | 10.86 | −9.68 | 10.45 | 0.96 | |||||
| 3 | 11.13 | −9.81 | 1.03 | −4.21 | −3.95 | 1.03 | 4.94 | 0.96 | |
| Kołobrzeg | 1 | 1.09 | 20.10 | 11.75 | 2.34 | 0.97 | |||
| 2 | 10.54 | −10.19 | 11.55 | 0.96 | |||||
| 3 | 11.05 | −8.41 | 1.06 | −3.98 | −6.59 | 1.05 | 5.36 | 0.97 | |
| Legnica | 1 | 1.97 | 19.36 | 10.83 | 2.17 | 0.96 | |||
| 2 | 11.34 | −9.76 | 10.77 | 0.96 | |||||
| 3 | 11.65 | −6.82 | 1.04 | −3.76 | −7.43 | 1.03 | 5.60 | 0.96 | |
| Lesko | 1 | 2.3 | 17.91 | 8.51 | 2.14 | 0.94 | |||
| 2 | 11.03 | −9.02 | 8.50 | 0.94 | |||||
| 3 | 11.29 | −6.29 | 1.03 | −3.69 | −7.42 | 1.03 | 5.57 | 0.94 | |
| Łeba | 1 | 1.03 | 19.38 | 13.51 | 2.35 | 0.96 | |||
| 2 | 10.12 | −9.83 | 13.19 | 0.96 | |||||
| 3 | 10.54 | −7.10 | 1.06 | −3.79 | −7.51 | 1.04 | 5.59 | 0.96 | |
| Łódź | 1 | 1.46 | 18.59 | 10.74 | 2.17 | 0.96 | |||
| 2 | 10.46 | −9.37 | 10.68 | 0.96 | |||||
| 3 | 10.74 | −5.22 | 1.04 | −3.54 | −8.33 | 1.03 | 5.79 | 0.96 | |
| Mikołajki | 1 | 1.11 | 19.89 | 11.75 | 2.15 | 0.96 | |||
| 2 | 10.78 | −10.02 | 11.72 | 0.96 | |||||
| 3 | 11.10 | −4.72 | 1.04 | −3.50 | −8.92 | 1.03 | 5.89 | 0.96 | |
| Piła | 1 | 1.11 | 18.97 | 11.66 | 2.17 | 0.96 | |||
| 2 | 10.30 | −9.56 | 11.57 | 0.96 | |||||
| 3 | 10.56 | −3.21 | 1.06 | −3.31 | −9.40 | 1.03 | 6.06 | 0.96 | |
| Puławy | 1 | 1.68 | 19.25 | 5.97 | 2.36 | 0.96 | |||
| 2 | 10.69 | −9.76 | 6.03 | 0.96 | |||||
| 3 | 11.37 | −0.93 | 0.98 | −3.17 | −9.36 | 1.08 | 6.04 | 0.96 | |
| Toruń | 1 | 1.07 | 18.03 | 11.7 | 2.12 | 0.96 | |||
| 2 | 9.88 | −9.07 | 11.63 | 0.96 | |||||
| 3 | 10.06 | −1.89 | 1.08 | −2.93 | −9.64 | 1.02 | 6.22 | 0.96 | |
| Warszawa | 1 | 1.27 | 19.3 | 10.05 | 2.2 | 0.96 | |||
| 2 | 10.57 | −9.74 | 10.00 | 0.96 | |||||
| 3 | 10.95 | −0.85 | 1.07 | −2.84 | −9.91 | 1.04 | 6.25 | 0.96 | |
| Wieluń | 1 | 1.86 | 19.36 | 10.7 | 2.14 | 0.96 | |||
| 2 | 11.28 | −9.75 | 10.64 | 0.96 | |||||
| 3 | 11.79 | −0.57 | 2.54 | −6.99 | −9.44 | 1.05 | 6.32 | 0.97 | |
| Włodawa | 1 | 1.48 | 19.41 | 8.75 | 2.14 | 0.96 | |||
| 2 | 10.93 | −9.78 | 8.77 | 0.96 | |||||
| 3 | 11.07 | −0.49 | 3.09 | −8.48 | −9.74 | 1.02 | 6.39 | 0.96 | |
| Poland | 1 | 1.41 | 19.19 | 10.50 | 2.19 | 0.96 |
| Station | RMSE eq1/eq1_Pl | RMSE eq2 | RMSE eq3 | MABE eq1/eq1_Pl | MABE eq2 | MABE eq3 | MAPE eq1/eq1_Pl | MAPE eq2 | MAPE eq3 |
|---|---|---|---|---|---|---|---|---|---|
| units | [MJ·m−2] | [MJ·m−2] | [MJ·m−2] | [MJ·m−2] | [MJ·m−2] | [MJ·m−2] | [%] | [%] | [%] |
| Gdynia | 0.56/0.64 | 0.63 | 0.54 | 0.45/0.53 | 0.51 | 0.4 | 6.61/9.8 | 10.4 | 6.78 |
| Gorzów | 0.48/0.54 | 0.49 | 0.47 | 0.34/0.48 | 0.38 | 0.31 | 5.35/5.9 | 6.41 | 4.02 |
| Jarczew | 0.63/0.64 | 0.64 | 0.61 | 0.49/0.46 | 0.50 | 0.48 | 6.72/6.1 | 7.43 | 6.37 |
| Kołobrzeg | 0.52/0.62 | 0.63 | 0.51 | 0.39/0.54 | 0.51 | 0.37 | 4.97/11.1 | 10.90 | 5.05 |
| Legnica | 0.46/0.73 | 0.47 | 0.45 | 0.34/0.66 | 0.35 | 0.33 | 4.16/10.9 | 5.68 | 4.31 |
| Lesko | 0.95/1.29 | 0.99 | 0.94 | 0.64/1.04 | 0.66 | 0.65 | 5.96/14.7 | 6.80 | 6.17 |
| Łódź | 0.64/0.85 | 0.66 | 0.64 | 0.54/0.68 | 0.59 | 0.52 | 7.16/8.0 | 8.60 | 6.22 |
| Łeba | 1.02/0.84 | 1.10 | 1.01 | 0.76/0.66 | 0.87 | 0.76 | 8.71/11.4 | 14.2 | 9.15 |
| Mikołajki | 0.63/0.69 | 0.62 | 0.62 | 0.48/0.51 | 0.50 | 0.48 | 7.19/6.6 | 8.49 | 7.05 |
| Piła | 0.53/0.68 | 0.53 | 0.52 | 0.42/0.49 | 0.42 | 0.42 | 7.43/8.3 | 8.53 | 7.00 |
| Puławy | 0.91/0.61 | 0.80 | 0.92 | 0.69/0.48 | 0.68 | 0.69 | 7.48/6.2 | 10.60 | 7.40 |
| Toruń | 0.78/0.72 | 0.77 | 0.77 | 0.59/0.49 | 0.56 | 0.58 | 7.46/7.0 | 8.10 | 7.38 |
| Warszawa | 0.62/0.63 | 0.61 | 0.61 | 0.55/0.52 | 0.49 | 0.46 | 7.54/7.6 | 8.20 | 6.01 |
| Wieluń | 0.59/0.67 | 0.57 | 0.70 | 0.43/0.59 | 0.42 | 0.53 | 5.78/9.0 | 5.78 | 6.85 |
| Włodawa | 0.60/0.61 | 0.730 | 0.72 | 0.48/0.47 | 0.64 | 0.54 | 5.75/6.2 | 8.92 | 7.71 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleniewska, M.; Mitrowska, D.; Wasilewicz, M. Estimating Daily Global Solar Radiation with No Meteorological Data in Poland. Appl. Sci. 2020, 10, 778. https://doi.org/10.3390/app10030778
Kleniewska M, Mitrowska D, Wasilewicz M. Estimating Daily Global Solar Radiation with No Meteorological Data in Poland. Applied Sciences. 2020; 10(3):778. https://doi.org/10.3390/app10030778
Chicago/Turabian StyleKleniewska, Małgorzata, Dorota Mitrowska, and Michał Wasilewicz. 2020. "Estimating Daily Global Solar Radiation with No Meteorological Data in Poland" Applied Sciences 10, no. 3: 778. https://doi.org/10.3390/app10030778
APA StyleKleniewska, M., Mitrowska, D., & Wasilewicz, M. (2020). Estimating Daily Global Solar Radiation with No Meteorological Data in Poland. Applied Sciences, 10(3), 778. https://doi.org/10.3390/app10030778





