A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation
Abstract
1. Introduction
- (1).
- The proposed controller can ensure better stable levitation of maglev system tackling the problems of disturbance and time delay simultaneously
- (2).
- The designed method does not require the magnitude of external disturbances, and it can attenuate chattering in control inputs effectively.
- (3).
- As verified by the experimental results, the proposed method shows increased control performance in a time-delay environment.
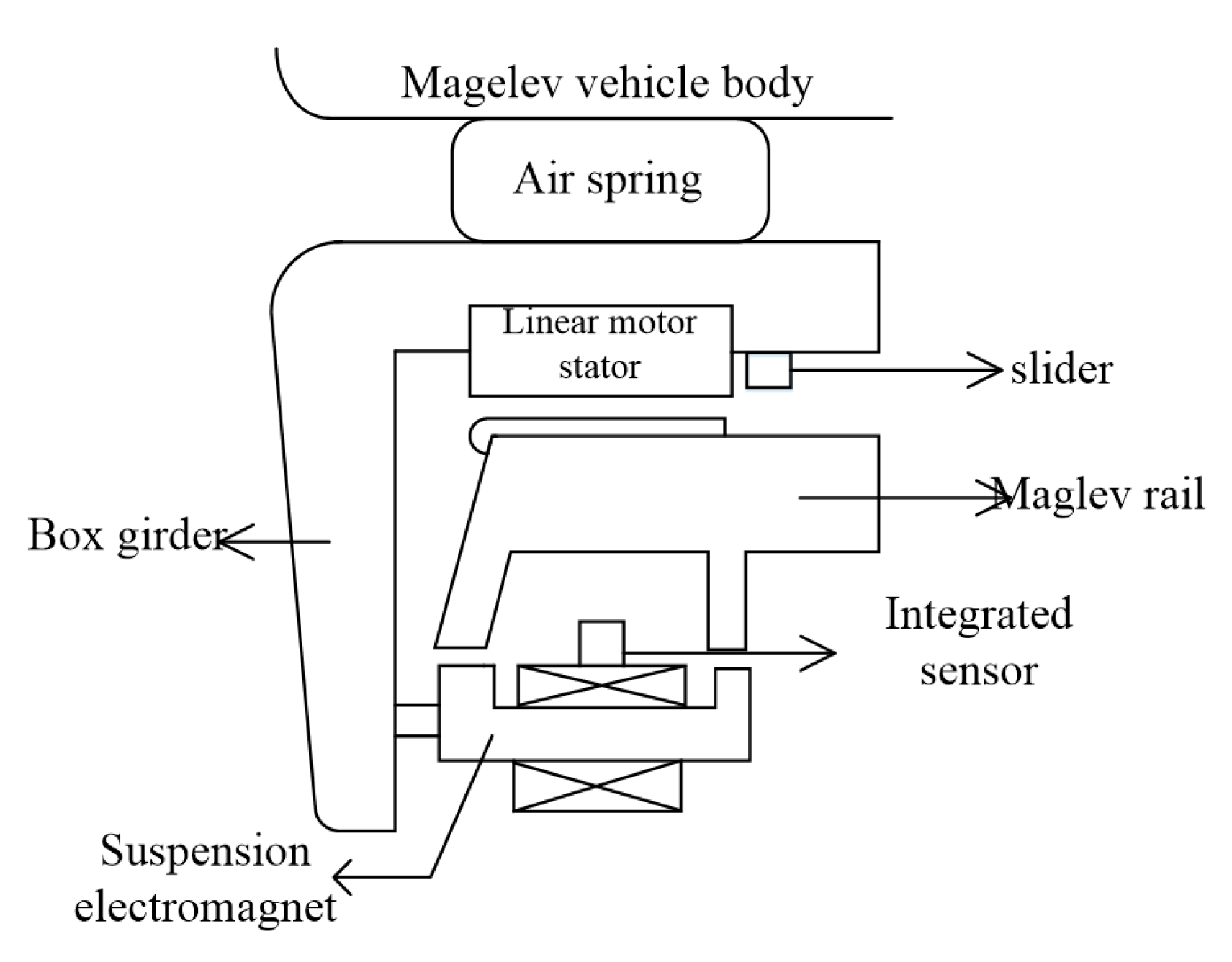
2. Problem Statement
2.1. System Dynamics
2.2. Control Object
3. Controller Design
4. Closed-Loop Stability Analysis
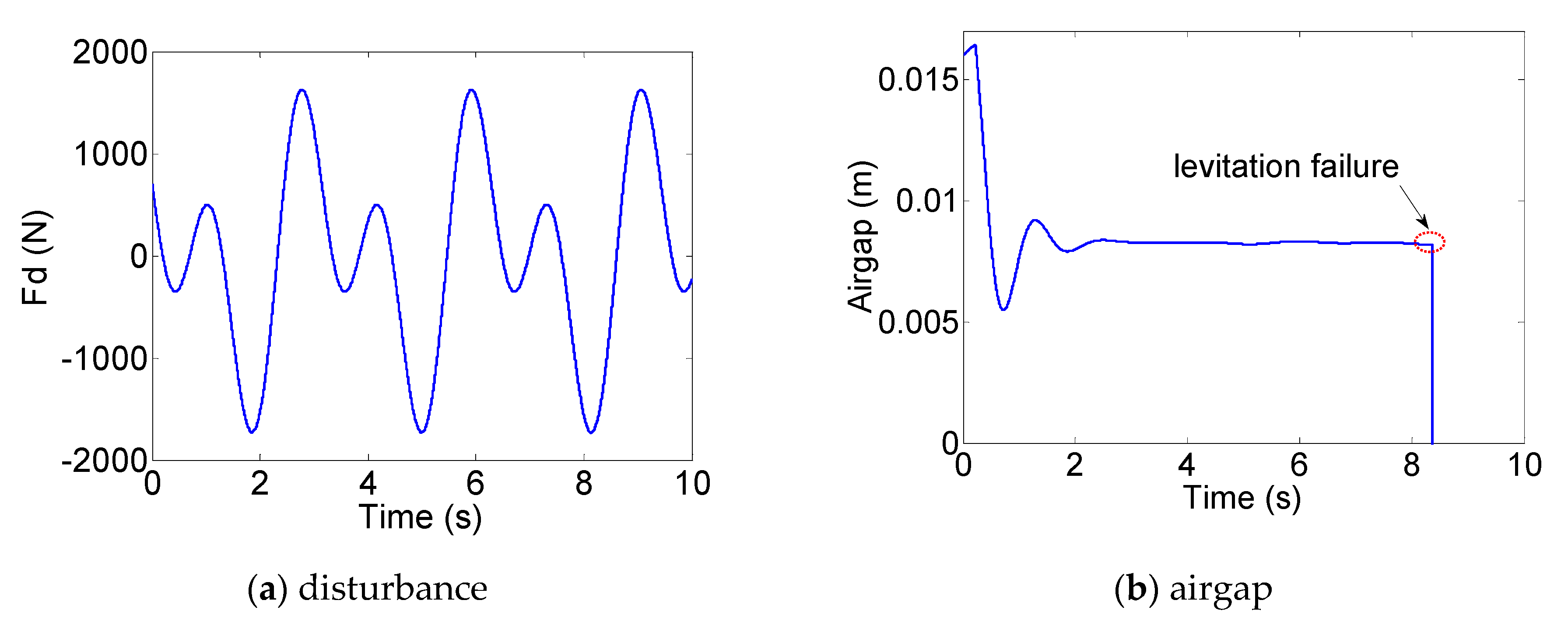
5. Simulation Results
6. Hardware Experiments
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thornton, R.D. Efficient and Affordable Maglev Opportunities in the United States. Proc. IEEE 2009, 97, 1901–1921. [Google Scholar] [CrossRef]
- Murai, M. Maglev Train HSST is Now on Commercial Operation as LINIMO. J. Jpn. Soc. Mech. Eng. 2008, 111, 472–473. [Google Scholar]
- Ohtani, S.; Hosokawa, O.; Siraki, A. Design of the Linimo Maglev Train. IATSS Rev. 2007, 32, 14–20. [Google Scholar]
- Luguang, Y. The maglev development and commercial application in China. In Proceedings of the 2007 International Conference on Electrical Machines and Systems, Seoul, Korea, 8–11 October 2007; pp. 1942–1949. [Google Scholar]
- Luguang, Y. Progress of the maglev transportation in China. IEEE Trans. Appl. Supercond. ASC 2006, 16, 1138. [Google Scholar] [CrossRef]
- Yau, J. Vibration control of maglev vehicles traveling over a flexible guideway. J. Sound Vib. 2009, 321, 184–200. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Qiang, H.; Lin, G. Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental verification. IEEE Trans. Ind. Electron. 2019, 66, 8589–8599. [Google Scholar] [CrossRef]
- He, G.; Li, J.; Cui, P. Nonlinear control scheme for the levitation module of maglev train. J. Dyn. Syst. Meas. Control Trans. ASME 2016, 138, 1–8. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhou, D.; Cui, P.; Wang, L.; Yu, P. The active control of maglev stationary self-excited vibration with a virtual energy harvester. IEEE Trans. Ind. Electron. 2015, 62, 2942–2951. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, P.; Wang, L.; Li, J. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vib. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- MacLeod, C.; Goodall, R.M. Frequency shaping LQ control of maglev suspension systems for optimal performance with deterministic and stochastic inputs. IEE Proc. Control. Theory Appl. 1996, 143, 25–30. [Google Scholar] [CrossRef]
- Xu, J.; Du, Y.; Chen, Y.H.; Guo, H. Adaptive robust constrained state control for non-linear maglev vehicle with guaranteed bounded airgap. IET Control Theory Appl. 2018, 12, 1573–1583. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, X.; Shen, G. Analysis and experimental study on the MAGLEV vehicle-guideway interaction based on the full-state feedback theory. J. Vib. Control 2015, 21, 408–416. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, J.; Huang, L.; Zhang, Z. Stability and bifurcation analysis in a maglev system with multiple delays. Int. J. Bifurc. Chaos 2015, 25, 1550074. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, L.; Zhang, Z. Stability and Hopf bifurcation of the maglev system with delayed position and speed feedback control. Nonlinear Dynam. 2009, 57, 197–207. [Google Scholar] [CrossRef]
- Hong-Po, W.; Jie, L.I.; Zhang, K. Stability and Hopf bifurcation of the maglev system with delayed speed feedback control. Acta Autom. Sin. 2007, 33, 829–834. [Google Scholar]
- Zhang, L.; Campbell, S.A.; Huang, L. Nonlinear analysis of a maglev system with time-delayed feedback control. Physica D 2011, 240, 1761–1770. [Google Scholar] [CrossRef]
- Xu, J.; Chen, C.; Gao, D.; Luo, S.; Qian, Q. Nonlinear dynamic analysis on maglev train system with flexible guideway and double time-delay feedback control. J. Vibroeng. 2017, 19, 6346–6362. [Google Scholar]
- Sun, N.; Liang, D.; Wu, M.; Chen, Y.; Qin, Y.; Fang, Y. Adaptive control for pneumatic artificial muscle systems with parametric uncertainties and unidirectional input constraints. IEEE Trans. Ind. Electron. 2019. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, Y.; Xie, X. Stochastic Barbalat’s lemma and its applications. IEEE Trans. Autom. Control. 2011, 57, 1537–1543. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Chen, H.; Fang, Y. Neural network-based adaptive antiswing control of an underactuated ship-mounted crane with roll motions and input dead zones. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef]
- Sun, Y.; Li, W.; Lin, G.; Xu, J. Dynamic Modeling and Nonlinear Control Research on Magnetic Suspension Systems of Low-speed Maglev Train. Tongji Daxue Xuebao J. Tongji Univ. 2017, 45, 741–749. [Google Scholar]
- Zhang, M.; Zhang, Y.; Ouyang, H.; Ma, C.; Cheng, X. Adaptive integral sliding mode control with payload sway reduction for 4-DOF tower crane systems. Nonlinear Dyn. 2020, in press. [Google Scholar] [CrossRef]
- Shengquan, L.; Juan, L.; Yongwei, T.; Yanqiu, S.; Wei, C. Model-based model predictive control for a direct-driven permanent magnet synchronous generator with internal and external disturbances. Trans. Inst. Meas. Control 2020, 42, 586–597. [Google Scholar] [CrossRef]
- Chen, H.; Sun, N. Nonlinear control of underactuated systems subject to both actuated and unactuated state constraints with experimental verification. IEEE Trans. Ind. Electron. 2019, in press. [Google Scholar] [CrossRef]
- Sun, N.; Fu, Y.; Yang, T.; Zhang, J.; Fang, Y.; Xin, X. Nonlinear motion control of complicated dual rotary crane systems without velocity feedback: Design, analysis, and hardware experiments. IEEE Trans. Autom. Sci. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Chen, H.; Xuan, B.; Yang, P.; Chen, H. A new overhead crane emergency braking method with theoretical analysis and experimental verification. Nonlinear Dyn. 2019, 98, 2211–2225. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Ji, B.; Ma, C.; Cheng, X. Modeling and energy-based sway reduction control for tower crane systems with double-pendulum and spherical-pendulum effects. Meas. Control 2019, in press. [Google Scholar] [CrossRef]














| Physical Quantity | Value |
|---|---|
| Levitation mass () | 100 |
| Coil resistance () | 0.420 |
| Coil inductance () | 177.8 |
| Number of coil turns | 340 |
| Magnetic-pole width () | 28 |
| Magnetic-pole length () | 700 |
| Air permeability | |
| Target levitation air gap () | 8.5 |
| Experiment (Time Delay) | PID | SMC | Proposed Method | |
|---|---|---|---|---|
| Case 1: normal | Time | 2.10 s | 1.05 s | 0.82 s |
| Error | 0.248 mm | 0.07 mm | <0.01 mm | |
| overshoot | 29.4% | 0 | 0 | |
| Chattering | None | yes | None | |
| Case 2: disturbance | Time | 2.18 s | 1.12 s | 0.91 s |
| Max Error | Unstable | 0.3 mm | <0.1 mm | |
| Air-gap fluctuation | Unstable | >3.5% | <1% | |
| Chattering | / | yes | none | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.-g.; Xie, S.; Xu, J.-q.; Lin, G.-b. A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation. Appl. Sci. 2020, 10, 1179. https://doi.org/10.3390/app10031179
Sun Y-g, Xie S, Xu J-q, Lin G-b. A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation. Applied Sciences. 2020; 10(3):1179. https://doi.org/10.3390/app10031179
Chicago/Turabian StyleSun, You-gang, Si Xie, Jun-qi Xu, and Guo-bin Lin. 2020. "A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation" Applied Sciences 10, no. 3: 1179. https://doi.org/10.3390/app10031179
APA StyleSun, Y.-g., Xie, S., Xu, J.-q., & Lin, G.-b. (2020). A Robust Levitation Control of Maglev Vehicles Subject to Time Delay and Disturbances: Design and Hardware Experimentation. Applied Sciences, 10(3), 1179. https://doi.org/10.3390/app10031179







