Abstract
To simplify the design and optimization of new-generation nanomaterials and related electronic and optoelectronic quantum devices, energy dissipation versus decoherence phenomena are often simulated via local models based on the Wigner-function formalism. Such a local description is, however, intrinsically incompatible with the fully quantum-mechanical (i.e., non-local) nature of the dissipation-free carrier dynamics. While the limitations of such hybrid treatments have already been pointed out in the past in diverse contexts, the spirit of the present work is to provide a more cohesive and critical review. To this aim, we focus on the fundamental link between the Wigner-function picture and the density-matrix formalism. In particular, we show that, starting from well-established density-matrix-based models, the resulting Wigner-function dissipation and/or thermalization dynamics is necessarily non-local. This leads to the conclusion that the use of local Wigner function models borrowed from the semiclassical Boltzmann theory is formally not justified and may produce unreliable results, and that such simplified local treatments should be replaced by fully non-local quantum models derived, e.g., via the density-matrix formalism.
1. Introduction
Despite its intrinsically quantum-mechanical nature, the steady-state electro-optical response of a conduction electron within a bulk crystal may be safely described via semiclassical models based on the Boltzmann transport theory [1]. This fact has allowed the development of a wide variety of semiclassical simulation strategies [2], and, during the last decades, the latter have provided a strong impetus to the development of semiconductor physics and technology [3].
The continuous progress in nanoelectronics and nanooptics, however, pushes device dimensions toward space- and time-scales where the semiclassical picture is questionable, and should at least be compared with authentic quantum approaches [4,5,6,7,8,9,10,11,12,13,14,15]. The latter can be qualitatively grouped into two main classes: double-time approaches based on the nonequilibrium Green’s function technique [16,17,18] and single-time approaches based on the density-matrix theory [19,20], including phase-space treatments within the Wigner-function formalism [21].
The replacement of semiclassical simulation schemes with genuine quantum-mechanical treatments implies, in general, a considerable increase in computational effort and resources; indeed, a microscopic treatment of various scattering mechanisms via proper Monte Carlo simulations [2] is often computationally too demanding already within the conventional Boltzmann theory; for quantum-transport simulations, the situation is even worse.
The design and optimization of new-generation nanomaterials as well as of related electronic and optoelectronic quantum devices is therefore frequently performed via partially phenomenological transport models based on the Wigner-function formalism [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]; within such simplified quantum-simulation schemes, energy dissipation versus decoherence phenomena are still described via local models borrowed from the semiclassical Boltzmann theory, namely relaxation-time treatments or Boltzmann-type scattering approaches. Such a local description is, however, intrinsically incompatible with the fully quantum-mechanical (i.e., non-local) nature of the dissipation-free carrier dynamics within the device active region. Indeed, during the last decades the intrinsic limitations of such hybrid treatments have been repeatedly pointed out, both for the case of thermalization models based on the conventional inflow-boundary-condition scheme [34,37,45,46,47,67] and for the case of dissipation versus decoherence treatments based on the relaxation-time approximation as well as on Boltzmann-like scattering models [61,64].
The aim of the present paper is twofold: on the one hand, we review and discuss selected simulated experiments pointing out these intrinsic limitations in different contexts, providing in addition a cohesive theoretical treatment able to clearly identify the origin of such diverse anomalies within the Wigner-function picture; and, on the other hand, starting from the density-matrix formalism, we discuss how to derive genuine quantum-mechanical dissipation models, able to overcome the intrinsic limitations just recalled. The main conclusion is that within the Wigner-function picture a correct treatment of both dissipation versus decoherence phenomena within the device active region and of the device-reservoir thermalization process requires the use of intrinsically non-local scattering models.
The paper is organized as follows. In Section 2, we briefly recall the fundamentals of the semiclassical transport theory applied to the simulation of semiconductor devices, while, in Section 3, the latter is generalized to the quantum-mechanical case, replacing the semiclassical distribution function with the Wigner function but still employing the very same energy dissipation as well as thermalization models used in the semiclassical case, In contrast, starting from well-established quantum models based on the density-matrix formalism, in Section 4, we derive fully non-local dissipation and thermalization superoperators acting on the Wigner function. Finally, in Section 5, we summarize and draw a few conclusions.
2. Fundamentals of Semiclassical Device Modeling
The key ingredient of the semiclassical transport theory is the carrier distribution function. More specifically, adopting a simplified model based on a single conduction band, the semiclassical distribution function describes the probability distribution of the conduction electrons over the single-particle phase-space , and is thus always positive-definite.
The primary goal of any semiclassical device simulation is the investigation of the carrier distribution function within the device volume , often referred to as the device active region. This is the result of a highly non-trivial interplay between the deterministic (i.e., scattering-free) carrier dynamics and the stochastic one induced on the carrier system by dissipation phenomena within the device active region as well as by thermalization processes due to the coupling of the device with external carrier reservoirs (see Figure 1). Regardless of the specific dissipation and thermalization models considered, the time evolution of the carrier distribution function can always be written as the sum of a deterministic (det) and of a stochastic (stoc) contribution,
where the latter, in turn is the sum of a dissipation (diss) and of a thermalization (th) term,
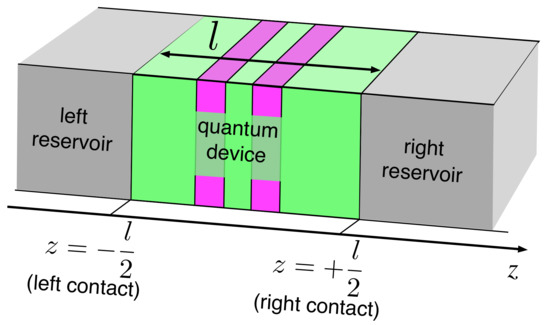
Figure 1.
(Color online) Schematic representation of a typical semiconductor-based quantum device as an open system connected to two external charge reservoirs. Here, the distance between the interfaces is l and z is the longitudinal transport direction. Reprinted from [67].
In the presence of slowly-varying electromagnetic forces and relatively large device sizes (compared to the typical electron de Broglie wavelength) the deterministic carrier dynamics can be safely described in classical terms via the conventional drift-diffusion model of the Boltzmann transport theory [2,18,20]. More specifically, adopting the customary parabolic-band approximation (with effective mass ) and in the presence of a static electric field only (i.e., no magnetic fields) described by a force , the deterministic contribution in Equation (1) is given by:
where denotes the carrier group velocity.
As anticipated, in a conventional semiconductor device, the deterministic carrier dynamics in Equation (3) is significantly modified by a variety of stochastic processes described by Equation (2); the latter, in turn, take place both within the device active region due to different scattering mechanisms (carrier–impurity, carrier–phonon, carrier–carrier, etc.) and close to the device spatial boundaries due to carrier exchange between the device and one or more external charge reservoirs. The explicit form of the corresponding dissipation and thermalization contributions in Equation (2) strongly depends on the nature of the transport model adopted. As we now discuss, in any semiclassical simulation scheme, dissipation as well as thermalization processes are always described via spatially local models, and the same applies to the Wigner-function modeling as well (see Section 3). Such local treatments can, however, be subdivided into two different classes: phenomenological models based on relaxation-time schemes where the total electronic charge within the device is not necessarily conserved (open-system paradigm) and kinetic models based on Boltzmann-type schemes where the total number of simulated carriers is always conserved (closed-system paradigm).
2.1. Phenomenological Dissipation and Thermalization Models
As far as energy-dissipation within the device active region is concerned, the simplest choice is the adoption of a phenomenological model based on the relaxation-time approximation (RTA) [18,20], i.e.,
where the relaxation of the carrier distribution in toward its equilibrium value is described in terms of a space- and momentum-dependent relaxation rate encoding all relevant scattering mechanisms characterizing the operational conditions of the device under investigation; the space and momentum/energy dependence of may be extracted from fully microscopic Monte Carlo simulations [2] or modeled via simplified Fermi’s Golden rule treatments.
As far as the device-reservoir thermalization is concerned, within the semiclassical picture, the latter may be easily described via a net spatial separation between the device active region and the external charge reservoirs (given by one or more electrical contacts/device terminals). Within this spirit, the simplest and physically more intuitive thermalization model is the so-called inflow-boundary-condition (IBC) scheme [2], where the carrier distribution function entering the device at its spatial boundary region coincides with the quasiequilibrium distribution in the external charge reservoirs. More specifically, denoting with the generic point of the device boundary surface and with the carrier distribution function entering the device at the surface point , such a boundary condition can be easily fulfilled/implemented via the following thermalization operator [20]
where
is the incoming component of the carrier group velocity at the boundary point ( being the unit vector normal to the boundary surface ). Indeed, according to its definition in Equation (6), is different from zero for incoming carriers only; moreover, in view of the Dirac delta function, the action of the thermalization operator in Equation (5) is limited to the device boundary surface . As a result, the above thermalization scheme is able, as requested, to fix the incoming carrier distribution to that of the external reservoirs, i.e., , and has no influence on the outgoing carrier flux.
The simplest physically relevant implementation of the IBC scheme in Equation (5) is that of a one-dimensional system/device () of length l in thermal contact with a left and a right charge reservoir. As schematically shown in Figure 2, in this case, the boundary surface of the three-dimensional case reduces to two points: . This amounts to fixing the value of the incoming distribution function at these two points, i.e., and .
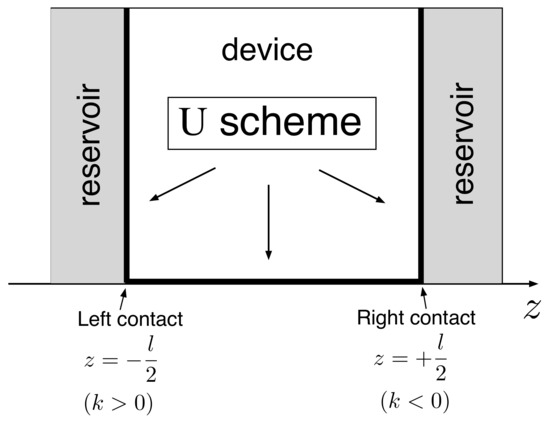
Figure 2.
The conventional inflow or U boundary condition scheme adopted in semiclassical device modeling [20] for a one-dimensional problem. The value of the distribution function is specified at the boundaries of the active region, i.e., and are fixed by the incoming/inflowing carrier distribution function. Reprinted from [67].
From a physical point of view, the action and role played by the IBC thermalization scheme in Equation (5) are significantly different from those of the dissipation term in Equation (4): while the latter modifies the carrier distribution in any point inside the device volume , the former simply fixes the value of the incoming distribution on the boundary surface and has no effect inside the device. Despite these profound differences, the two models share a common formal structure, i.e., they are both RTA-type operators of the form:
where, for the dissipation model in Equation (4), we have
while, for the IBC thermalization model in Equation (5), we have
It is worth stressing that, while for the dissipation model in Equation (8) the relaxation rate acts as a simple algebraic multiplication, for the IBC thermalization model in Equation (9) the latter is an integral operator acting on our phase-space coordinates .
As we discuss in Section 4, such formal similarity may help in understanding the common origin of diverse anomalous results obtained applying the local dissipation and thermalization models introduced thus far to quantum-transport simulations based on the Wigner-function formalism.
2.2. Kinetic Dissipation and Thermalization Models
To overcome the well-known limitations of the phenomenological dissipation model in Equation (4), the key step is to replace the RTA scheme with a Boltzmann collision term of the form [2,18,20]
where
denotes the low-density scattering rate in for the generic transition , weighted by the usual Pauli-blocking factor, and simply reduces to in the low-density limit (). The Boltzmann-type collision operator in Equation (10) provides a kinetic description of energy dissipation in terms of stochastic carrier transitions dictated by the low-density scattering rates . Opposite to the phenomenological nature of the relaxation rate in Equation (4), such scattering rates can be microscopically derived in quantum-mechanical terms via the well-known Fermi’s golden rule including all relevant interaction mechanisms. Moreover, such a stochastic dynamics may be efficiently and intuitively simulated via a wide variety of Monte Carlo approaches [2].
As anticipated, the Boltzmann-type kinetic treatment in Equation (10) is intrinsically charge conserving, which implies that in this case the possible time variation of the total carrier number inside the device active region is due to device-reservoir thermalization processes only, customarily described via the phenomenological IBC scheme in Equation (5). As a result, most of the semiclassical device modeling is currently based on a kinetic treatment of dissipation phenomena inside the device properly combined with a phenomenological treatment of environment-induced carrier thermalization processes. This is typically accomplished via generalized (i.e., particle non-conserving) Monte Carlo simulations able to account for the presence of external reservoirs by means of corresponding injection versus loss terms [15].
As already stressed, the IBC thermalization model in Equation (5) is grounded on an artificial spatial separation between device and external contacts/reservoirs (see Figure 1 and Figure 2); such an abrupt jump is, in general, not well justified, and one may expect that for some device operating conditions the distribution of incoming carriers may display nonequilibrium features as well. To properly describe the (continuous) device-reservoir transition, the key step is to include in the simulated region a significant portion of the electrical contacts as well; to this aim, in addition to the Boltzmann collision operator in Equation (10) (describing energy-dissipation phenomena inside the device), carrier thermalization due to the presence of the electrical contacts can be described again via a corresponding Boltzmann-type operator, whose thermalization rates are different from zero within the contact regions only. As a result, one deals with a kinetic treatment of both dissipation and thermalization phenomena, and the latter may be conveniently simulated via standard (i.e., particle conserving) Monte Carlo simulations [2]. Compared to the phenomenological IBC scheme, such kinetic treatments of the device-reservoir coupling are by far computationally more demanding. To overcome this limitation, an alternative Monte Carlo scheme, especially suited for the modeling of one-dimensional devices, has been also proposed [68,69]; the latter provides a solution of a Boltzmann-like equation defined over the single-particle electronic states of the device, and is thus more efficient compared to conventional phase-space () simulations.
3. Partially Quantum-Mechanical Device Modeling Based on the Wigner-Function Formalism
The Wigner function is introduced as the Weyl–Wigner transform of the single-particle density matrix. Even though the latter is defined over the very same phase-space of the semiclassical distribution, and that very often the notation is used for the Wigner function as well, this new quantum distribution, while still being a real quantity, is no longer positive-definite. Its time evolution is described by the so-called Wigner transport equation. The latter can still be written analogously to Equation (1); due to this similarity, Monte Carlo simulation techniques for its solution (so-called Wigner Monte Carlo schemes [32,35]) have been developed. However, despite this formal resemblance, the explicit form of the deterministic as well as of the stochastic Wigner-function terms are expected to differ from their semiclassical counterparts.
The deterministic contribution is the quantum-mechanical generalization of the diffusion-plus-drift term in Equation (3) and can be conveniently formulated in terms of Moyal brackets [70]. Indeed, denoting with the scalar potential corresponding to the electric force , one has
where
is the nonlocal Weyl–Wigner superoperator corresponding to the scalar-potential profile [20]. Comparing Equation (12) with its semiclassical counterpart in Equation (3), we notice that the diffusion term remains unchanged while the quantum-mechanical version of the drift term is still local in but non-local in .
The stochastic contribution can still be cast in terms of dissipation as well as thermalization phenomena, as in Equation (2). It is then a common practice to treat these processes within the same local models previously described, namely the RTA model in Equation (7) and the Boltzmann collision operator in Equation (10). However, within the Wigner-function picture, this local approach suffers of intrinsic limitations. The latter is highlighted in the remainder of this section, where selected examples focusing on the analysis of energy dissipation versus decoherence phenomena [61] (Section 3.1) and on the device-reservoir carrier thermalization dynamics [67] (Section 3.2) are briefly reviewed.
3.1. Failure of Local Dissipation Models
The incompatibility between the local dissipation models of the semiclassical theory and the (non-local) deterministic Wigner-function dynamics in Equation (12) is already evident in modeling a basic prototypical quantum-well (QW) device such as the one sketched in Figure 3. The effects of device spatial boundaries as well as the role of device-reservoir thermalization phenomena may be neglected assuming semi-infinite barriers and limiting our investigation to QW bound states only.
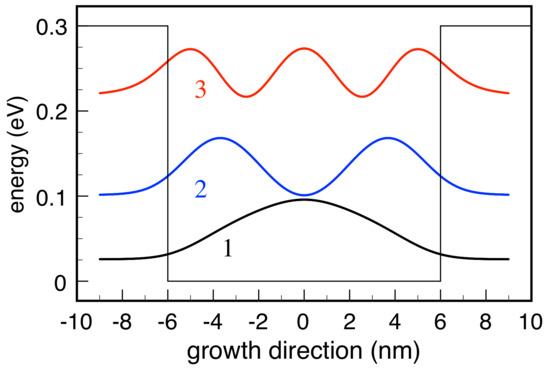
Figure 3.
Conduction band profile along the growth direction for the prototypical GaAs/AlGaAs QW nanostructure considered in our simulated experiments. Energy levels of the three 1D bound states are shown, together with the corresponding squared envelope functions. Readapted from [61].
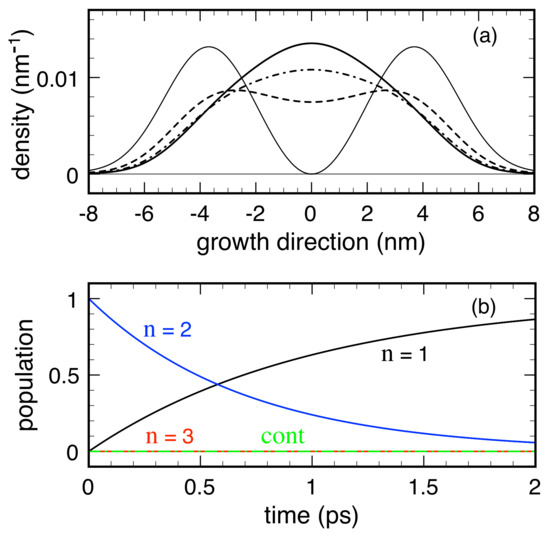
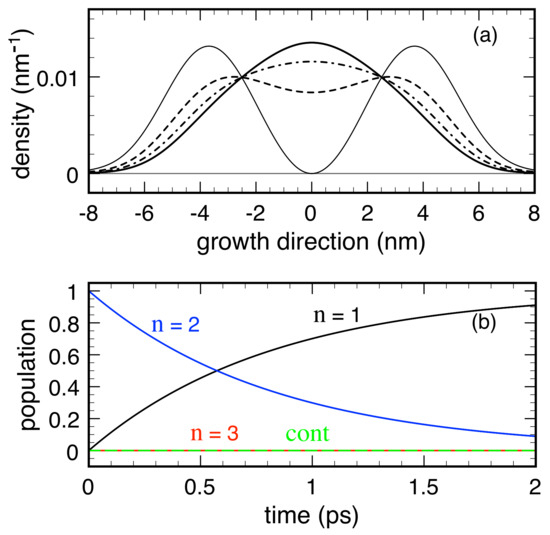
Due to confinement along the growth (z) direction, the system three-dimensional (3D) electronic states exhibit the usual subband structure. However, within the prescription of the RTA dissipation model in Equation (4), we neglect the in-plane phase-space coordinates and adopt an effective one-dimensional (1D) description: The set of single-particle quantum numbers then reduces to the discrete index () of the confined 1D state only and . Figure 3 shows the three bound energy levels and squared envelope functions for the model case of a GaAs/(Al,Ga)As 12 nm-thick QW, with a conduction band offset of 0.3 eV. In the following, we resume the results of simulated experiments performed on this nanosystem in the low-temperature regime, thus assuming that the QW lowest energy level () corresponds to the thermal-equilibrium condition. In particular, we analyze the spatial carrier-density profile, along the growth direction, corresponding to the 1D Wigner function , namely
and investigate its time evolution, when the system is initially prepared in the first excited level (), by solving the 1D version of the Wigner transport equation (Equation (1)) with the quantum-mechanical deterministic term in Equation (12) and the conventional RTA scheme in Equation (4).
In Figure 4, the dissipation dynamics induced on our prototypical QW system by three different versions of the RTA approach are compared. Within the model labeled M1, we assume a space- and energy-independent rate ; this is often called phenomenological or macroscopic RTA approach. Within the model M2, we employ a space-dependent but energy-independent rate , assumed to vanish within a given region , and equal to outside; this may partially mimic the case of material-dependent semiclassical scattering rates, such as in the case of complex multi-layer quantum heterostructures. Finally, within the model M3, we consider a space-independent but momentum/energy-dependent rate , vanishing for and equal to otherwise; this may describe the typical energy-threshold scenario of electron-optical phonon scattering in a variety of nanomaterials and nanodevices, e.g., new-generation quantum-cascade lasers [15].
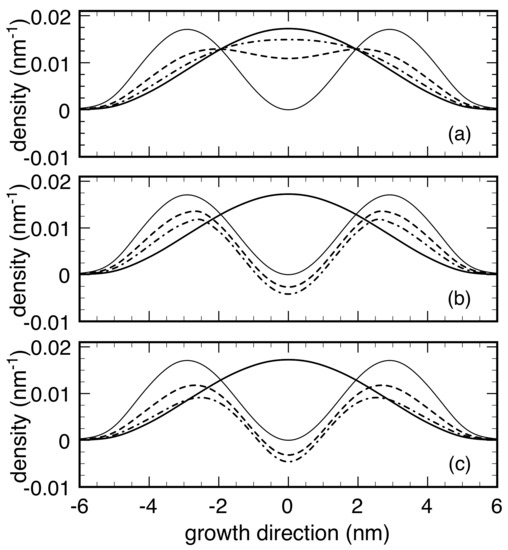
Figure 4.
Low-temperature dissipation dynamics in the 12 nm thick GaAs/AlGaAs QW of Figure 3. The carrier density in Equation (14) is plotted as a function of position at different times (0 ps: thin solid curve; ps: dashed curve; and ps: dash-dotted curve) for models: M1 (a); M2 (b); and M3 (c). Here, the following parameters are employed: ps for M1, ps and nm for M2, and ps and meV for M3. The equilibrium carrier density is also shown for comparison (solid curve). Reprinted from [61].
The dissipation dynamics resulting from M1 [Figure 4a] agrees with the physically valid scenario in which the charge distribution in the QW ground state increases, at the expenses of the one of the initial state (thin solid curve); after ps (dash-dotted curve) the electronic system is already pretty close to its equilibrium distribution (solid curve). In the case of M2 [Figure 4b] and M3 [Figure 4c], the scenario is substantially different: besides a significant slowdown of the excited-level decay process, negative carrier distributions arise; this crucial difference with respect to M1 is an unambiguous fingerprint of unphysical electronic states.
A closer inspection of the dissipation dynamics may be provided by looking at the carrier populations of the QW states. The latter are given by the diagonal terms of the single-particle density matrix, which can be obtained from the 1D Wigner function via the inverse of the 1D Weyl–Wigner transform. In Section 4, the link between the density matrix and the Wigner function is more extensively addressed. Here, we just anticipate that the populations can be obtained applying to the 1D Wigner function the inverse of the 1D Weyl–Wigner transform , i.e.,
Figure 5 shows the time evolution of the populations of the three QW bound states (, , and ) as well as of the continuum, the latter being defined as , with denoting the total number of carriers. As expected, model M1 [Figure 5a] shows a simple exponential depopulation of the initial level into the ground state , while level and the continuum are not affected by the dissipation dynamics.
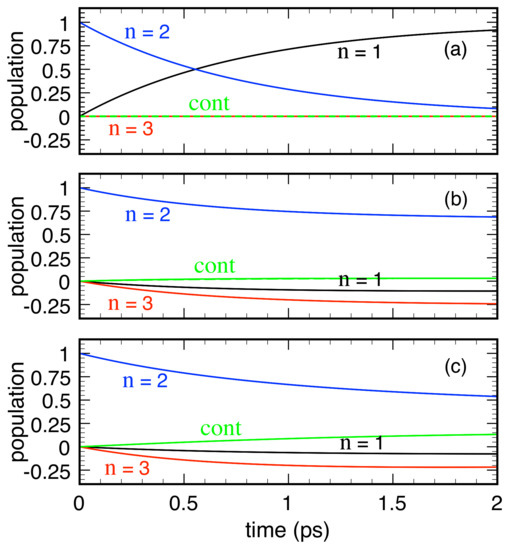
Figure 5.
Bound-state populations [see Equation (15)] as well as the continuum (cont) contribution as a function of time for model:s M1 (a); M2 (b); and M3 (c). Reprinted from [61].
Such a plausible scenario is, however, lost in models M2 [Figure 5b] and M3 [Figure 5c], where we do observe: (i) a slowdown of the state depopulation; (ii) negative population values for states and ; and (iii) particularly for M3, a marked charge transfer into the continuum in spite of our zero-temperature analysis. The unavoidable conclusion is that the conventional RTA dissipation model in Equation (4) does not preserve the positivity of the carrier populations , and induces a fictitious interlevel coupling; the latter, in turn, may also artificially generate interlevel phase coherence.
The unphysical results of M2 and M3 are not related to the charge non-conserving nature of the RTA model and/or to the effective 1D modeling of our nanodevice. In the following, we attest that analogous problems also arise when: (i) a fully 3D treatment of the prototypical QW nanostructure is adopted; and (ii) the RTA dissipation scheme in Equation (4) is replaced by the (charge-conserving) Boltzmann collision term in Equation (10).
Concerning the latter, it has the well-established in- minus out-scattering structure and may also be written as
with
and
Both superoperators, and , are local in ; is local in as well.
The rates entering the Boltzmann collision term in Equation (10) are evaluated via the conventional Fermi’s golden rule using as noninteracting states standard 3D plane waves, instead of the nanostructure single-particle wavefunctions, and assuming as main dissipation mechanism the carrier interaction with a bulk GaAs LO-phonon system [2]. The quantities are therefore space-independent. Within such 3D description, the Weyl–Wigner phase-space of the QW device is given by and . The effective 1D carrier-density profile along the growth direction (z) in Equation (14) is then now replaced by
and the effective 1D level population in Equation (15) by the following subband population
Here, is the population of the generic carrier state in subband with in-plane wavevector , obtained via the 3D version () of the Weyl–Wigner transform in Equation (15).
Figure 6 shows the low-temperature and low-density energy-dissipation dynamics for the GaAs/(Al,Ga)As prototypical QW nanostructure of Figure 3, resulting from the fully 3D Boltzmann bulk model just described. The spatial carrier density profile [Figure 3a] is now only marginally affected by negative-value regions, if compared to the unphysical results obtained via the RTA dissipation model (Figure 4 and Figure 5). However, analogously to the RTA case, a marked slowdown of the excited-level decay is evident: after ps (dash-dotted curve), the charge distribution is still far from equilibrium (solid curve). Such anomalous scenario is confirmed by an insight into the various subband populations (Figure 3b), showing: (i) a marked slowdown out of the initial subband ; (ii) negative values in subband ; and (iii) despite our zero-temperature analysis, considerable values in the continuum.
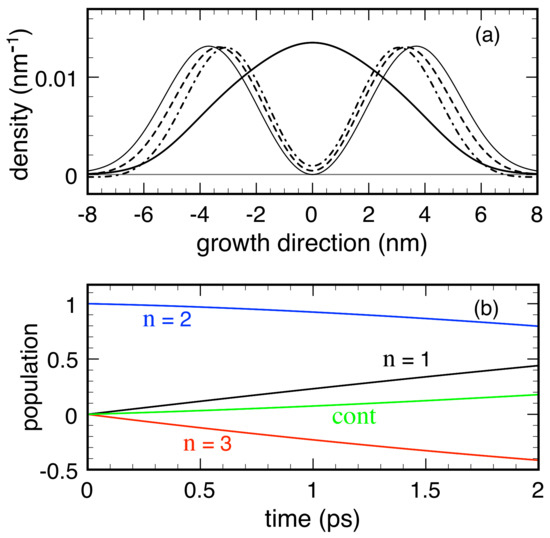
Figure 6.
Low-temperature and low-density dissipation dynamics in the 12 nm thick GaAs/AlGaAs QW of Figure 3 resulting from the fully 3D local Boltzmann model in Equation (10) in the low-density limit. (a) Carrier density in Equation (19) as a function of position at different times: 0 ps (thin solid curve), ps (dashed curve), and ps (dash-dotted curve); the equilibrium carrier density is also shown for comparison (solid curve). (b) Bound-state subband populations [see Equation (20)] as well as continuum (cont) contribution as a function of time. Reprinted from [61].
A further close-up in the analysis may be achieved repeating the simulated experiment reported in Figure 6 with a different initial condition, e.g., the QW low-temperature thermal-equilibrium state . In this case, a correct scattering superoperator would leave the electronic system unmodified. However, the results, reported in Figure 7, show that the Boltzmann collision term in Equation (10) drives the electronic system out of equilibrium, populates the continuum, and induces negative populations of the excited QW subbands. These outcomes confirm the intrinsic limitations of local treatments, which are known to be intrinsically incompatible with any quantum-mechanical framework.
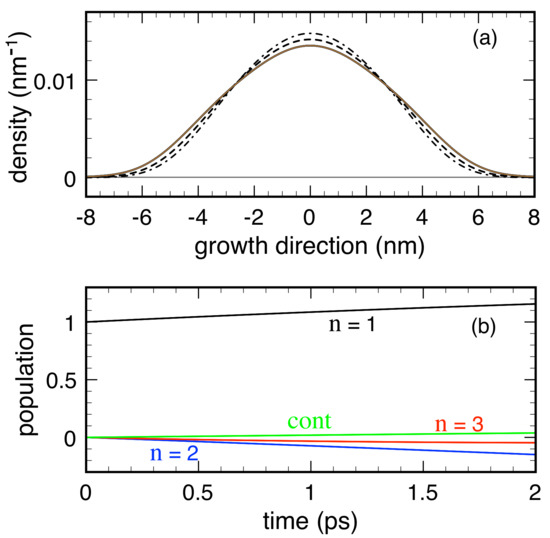
Figure 7.
(a,b) The same as in Figure 6 but considering as initial state the thermal-equilibrium state . Reprinted from [61].
Indeed, both the RTA results in Figure 4 and Figure 5 and the Boltzmann-type ones in Figure 6 and Figure 7 are based on bulk-like scattering models, where the relaxation rate in Equation (4) and the semiclassical scattering probability in Equation (10) do not account for the QW electronic subband structure. The two terms in the Wigner transport equation (Equation (1)) are then intrinsically conflicting: the deterministic one accounts for the QW subband structure via its confinement potential , while the scattering one does not. This contradiction, recently pointed out also within the density-matrix formalism [71], is responsible for the dissipation slowdown as well as for the wrong thermalization dynamics. Indeed, the steady-state solution of the bulk-like Boltzmann collision term in Equation (10) is just the Fermi–Dirac distribution. The latter is space-independent and has nothing to do with the thermal-equilibrium Wigner function of the quantum device, which is space-dependent and significantly different from zero within the QW region only.
As a final remark, we notice that the unphysical features of the low-density Boltzmann-type simulations just reviewed come out to be further amplified in the presence of high carrier concentrations. As discussed in detail in [64], in high-density conditions, the Wigner function may still be negative, but also greater than unity. This implies that, for high carrier concentrations, the role played by the Pauli factor () in Equation (11) may deviate significantly with respect to the conventional semiclassical scenario (where it is always bounded between 0 and 1), leading to highly counter-intuitive effects such as a sort of “negative dissipation”.
3.2. Failure of Local Thermalization Models
In the presence of a significant device-reservoir thermal coupling, the primary goal of any quantum simulation scheme is the solution of the steady-state Wigner transport equation
in particular, two crucial issues need to be assessed: (i) Is the solution of Equation (21) always unique? (ii) When this is the case, is it always physically acceptable?
As we now discuss, the answers to these questions depend crucially on the choice of the thermalization model as well as on the presence/absence of dissipation phenomena within the device active region. In particular, we now briefly review the detailed analysis originally presented in [67]. The latter has shown intrinsic limitations of Wigner-function simulations based on the conventional IBC thermalization scheme in Equation (5), providing the following answers: (i) in the coherent limit, the solution of the steady-state Wigner equation (compatible with given spatial boundary conditions) is definitely not unique; and (ii) when dissipation phenomena are taken into account, the solution, although unique, may be physically unacceptable.
It is useful to start with a simplified 1D model, having the notable advantage to allow for an exact analytical treatment; in particular: (i) the deterministic dynamics is described via a delta-like potential profile; (ii) the dissipation dynamics is neglected (so-called coherent limit); and (iii) the device-reservoir thermalization is described via the semiclassical IBC scheme in Equation (5), whose 1D version is schematically depicted in Figure 2. Within such a simplified scheme, it is possible to demonstrate [67] that the solution is not unique. This is a consequence of the double degeneracy of the 1D electronic scattering states corresponding to our potential profile, which in turn is due to the time-reversal symmetry of the dissipation-free dynamics.
In the presence of energy dissipation phenomena, in contrast, the time-reversal symmetry is lost, and the solution of the steady-state Wigner equation is found to always be unique. However, such mathematical solution does not necessarily correspond to a physically acceptable Wigner function, namely to the Weyl–Wigner transform of a genuine single-particle density matrix (see Section 4).
To better focus on this intrinsic limitation, let us consider a realistic GaAs-based nanostructure characterized by a rectangular potential barrier and assume a monoenergetic carrier injection from the left spatial boundary only. Moreover, we describe energy dissipation via the RTA scheme in Equation (4), with a space- and energy-independent relaxation rate .
The resulting spatial carrier-density profiles corresponding to the coherent limit (solid curve) as well as to two different values of the relaxation time [ ps (dashed curve) and fs (dash-dotted curve)] are reported in Figure 8. In the coherent limit, a strongly anomalous feature shows up: the density profile comes out to be rigorously symmetric, despite the assumed left-injection into a significantly high potential barrier. The presence of energy dissipation mechanisms (dashed and dash-dotted curve) induces some (apparently more physical) spatial asymmetry. However, for the parameters considered here, the barrier transmission coefficient is so small (of the order of ) that no charge should be present in the right portion of the device (see also Figure 10 in Section 4.1). Moreover, in addition to this, all three density profiles display negative-value regions. This outcome is qualitatively similar to the one reported in [37] for the case of a cosine-like potential, thus confirming the physical limitations of conventional Wigner-function simulations based on the semiclassical IBC scheme.
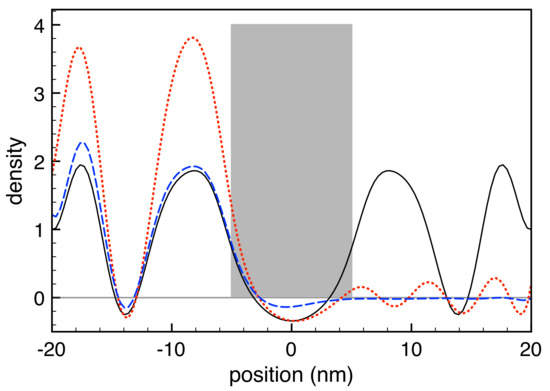
Figure 8.
Room-temperature spatial carrier density (in units of its barrier-free value) corresponding to a GaAs-based rectangular-barrier profile (device length nm, barrier width nm, and barrier height meV) in the presence of a monoenergetic injection from the left ( meV). Here, the coherent-limit () density profile (solid curve) is compared to the results corresponding to two different values of the relaxation time: ps (dashed curve) and fs (dash-dotted curve). Readapted from [67].
Again, similar to the case of the local dissipation models previously discussed, the physical origin of these anomalies is that the deterministic and the thermalization term entering the steady-state Wigner equation (Equation (21)) are intrinsically incompatible. While the former accounts for the QW subband structure via the nanostructure potential [see Equation (12)], the same does not apply to the semiclassical IBC scheme [see Equation (5)], where the carriers injected into the device active region are implicitly treated as free particles (i.e., plane waves), regardless of the presence of the confinement potential.
4. Fully Quantum-Mechanical Device Modeling Based on the Density-Matrix Formalism
In view of the intrinsic limitations of local dissipation as well as thermalization models discussed thus far, it is imperative to replace such semiclassical treatments with fully quantum-mechanical schemes. Despite of the level of accuracy/approximation of the latter, intimately related to the nanosystem as well as to the specific phenomenon under investigation, two basic requirements are, however, always mandatory: (i) the positive-definite character of the quantum-mechanical state has to be preserved at any time; and (ii) in the absence of external electro-optical excitations as well as of nonequilibrium carrier injection, the solution of the steady-state Wigner equation (Equation (21)) should coincide with the thermal-equilibrium state.
It is in general a highly non-trivial task to check the conformity to the above requirements; to this aim, it is crucial to exploit the close relation between the Wigner function and the corresponding single-particle density matrix [11,15]. More specifically, adopting the very same notation employed in [67], and by compactly labeling with the set of relevant quantum numbers for the single-particle electronic states of our semiconductor nanostructure, the density matrix (whose diagonal terms of the density matrix describe the population of the generic single-particle state , while the off-diagonal terms describe the quantum-mechanical phase coherence (or polarization) between states and ) can be written in terms of the Wigner function as
where
denotes the well-known Weyl–Wigner transform [70], and the real-space wavefunction of the electronic state .
Applying the inverse Weyl–Wigner transform equation (Equation (22)) to the original Wigner transport equations (Equations (1) and (2)), in the absence of external electromagnetic excitations, the latter can be easily translated into the density-matrix equation
with
where is the energy of state , and
As far as the deterministic dynamics is concerned, the density-matrix term in Equation (25) is by far simpler compared to its Wigner-function version in Equation (12): the diagonal terms () do not change in time, while the non-diagonal terms () simply rotate with frequency . As far as the dissipation and thermalization terms in Equation (26) are concerned, the latter may be conveniently described via well-established density-matrix models able to fulfill the two basic requirements mentioned above [72].
Based on the density-matrix picture just recalled, in the remainder of this section, we discuss in a more formal way the intrinsic limitations of the semiclassical treatments, and, starting from physically reliable and robust density-matrix models, we derive their Wigner-function versions given by fully non-local scattering superoperators.
4.1. Non-Local Relaxation-Time Models
As discussed in Section 2, both dissipation and thermalization processes are routinely described via the generic RTA scheme in Equation (7). To better clarify the intrinsic limitations of such local model within a Wigner-function simulation, it is useful to analyze its density-matrix version. To this aim, applying to Equation (7) the inverse Weyl–Wigner transform equation (Equation (22)), one gets [61]
with
where denotes the inverse Weyl–Wigner transform of the equilibrium or quasiequilibrium distribution function in Equation (7).
It is now worth comparing Equation (27) (obtained by applying a semiclassical RTA model to the Wigner function) to the equation obtained applying the RTA scheme straightforwardly to the density-matrix evolution, i.e.,
where denotes the (diagonal) equilibrium or quasiequilibrium density matrix (with respect to our single-particle basis ). Here, can be regarded as a sort of state-dependent effective inverse life-time, involving all relevant dissipation/thermalization mechanisms acting on the carrier in state ; indeed, in the semiclassical limit (), the density-matrix RTA model in Equation (29) reduces to the well-known injection-loss scheme [15] of conventional device modeling.
In addition to the population dynamics in (30), the density-matrix RTA model in (29) describes the dissipation/thermalization-induced decay of the interlevel polarization, known as decoherence process.
As one can see, while the superoperator in Equation (29) is diagonal in the single-particle basis , the superoperator in Equation (27) is, in general, non-diagonal in such basis. Moreover, while it is possible to show [72] that the density-matrix RTA model in Equation (29) is always positivity preserving, the same does not apply, in general, to the non-diagonal RTA model in Equation (27) [and therefore to its Wigner-function version in Equation (7)], as confirmed by the negative carrier populations in Figure 4 and Figure 5). The only exception is the case of a space- and energy-independent relaxation rate, , as well as a state-independent rate, , for which the two RTA models in Equations (27) and (29) coincide. This is indeed confirmed by the convincing results in Figure 4a.
The density-matrix analysis presented so far suggests to replace the highly problematic semiclassical-like RTA scheme in Equation (7) with a fully quantum-mechanical Wigner-function model. To this aim, our strategy, originally proposed in [61], is to start from the physically sound density-matrix RTA scheme in Equation (29) and apply to it the following Weyl–Wigner transform:
The resulting Wigner-function model is given by
where
is a fully nonlocal RTA superoperator expressed in terms of the relaxation rates of the density-matrix theory, and is the Weyl–Wigner transform of the equilibrium or quasiequilibrium density matrix .
In striking contrast to the standard RTA model in Equation (7), the generalized version in Equation (32) intrinsically ensures the positivity of the spatial charge density as well as of the single-particle state populations; indeed: (i) the density-matrix RTA model in Equation (29) is known to preserve the positive-definite character of the density matrix ; and (ii) the action of the Weyl–Wigner transform in Equation (31) does not alter such property.
At this point, it is crucial to recall (see Section 2) that the original local RTA model in Equation (7) may be employed to describe both dissipation and thermalization phenomena, and the same applies to the density-matrix based RTA model in Equation (29) as well. Indeed, as discussed in more detail in [72], the generic relaxation rate may describe energy dissipation inside the device toward an equilibrium-state population (, ), or device-reservoir thermalization toward the quasiequilibrium state population induced by one or more external charge reservoirs (, ). It follows that also the new RTA model in Equation (32) may be employed for the description of dissipation as well as thermalization phenomena, and that in both cases the action of the new RTA superoperator is always non-local.
To illustrate the quality and physical soundness of the proposed non-local RTA scheme in Equation (32), we focus first on the study of energy dissipation phenomena. To this end, the new non-local RTA model has been applied once again to the prototypical QW nanosystem in Figure 3 adopting again the very same effective 1D model introduced in Section 3.1. In this case, the in-plane carrier dynamics is neglected and the confined states of our QW system as well as the corresponding dissipation rates are labeled by the integer number only, i.e., . In particular, Figure 9 shows the results obtained by setting ps and ps. A comparison with Figure 4 and Figure 5 shows that, here, opposite to the pathological behaviors obtained via the RTA models M2 and M3, both the spatial carrier distributions (Figure 9a) and the corresponding level populations (Figure 9b) are always positive-definite. Moreover, as for the case of model M1, we deal again with a correct relaxation dynamics toward the equilibrium state (solid curve in Figure 9a) without unphysical interlevel relaxation couplings and continuum population.
Let us finally apply the proposed non-local RTA scheme in Equation (32) to the investigation of device-reservoir thermalization. To this end, let us consider again the 1D problem of Figure 8, namely the steady-state quantum transport across a rectangular barrier due to a monoenergetic carrier injection from left. In this case, the single-particle states corresponding to the 1D rectangular potential profile are conventional scattering states labeled by their 1D carrier wavevector k, and the device-reservoir relaxation rates depend on k as well, i.e., . To mimic the monoenergetic-injection scenario of Figure 8, let us assume a monoenergetic carrier distribution in the left reservoir, i.e., , denoting the wavevector corresponding to the injection energy . As a result, in this case, the device-reservoir coupling is described via a single relaxation rate . The latter can be regarded as the inverse of the so-called device transit time of the semiclassical theory [15], i.e., the ratio between the device length l and the injection carrier group velocity , which for our simulation parameters is of the order of 100 fs.
The results obtained via the new non-local RTA model in Equation (32) are reported in Figure 10, where we have assumed again a monoenergetic thermalization with meV, and we have employed a device-reservoir relaxation time fs. Opposite to the highly non-physical results of the local IBC scheme in Figure 8, here, the charge distributions are always non-negative, thus confirming the positive-definite character of the proposed non-local RTA model in Equation (32). Moreover, regardless of the dissipation level, the amount of charge in the right portion of the device is now definitely negligible, in total agreement with the fact that for our simulation parameters the transmission coefficient across the rectangular barrier is extremely small (of the order of ). In addition, while in the coherent limit (solid curve) as well as in the weak dissipation regime (dashed curve) one deals with the typical interference scenario between incoming and reflected wavefunctions, in the strong-dissipation regime (dash-dotted curve), such interference process is partially suppressed due to dissipation induced decoherence [20].
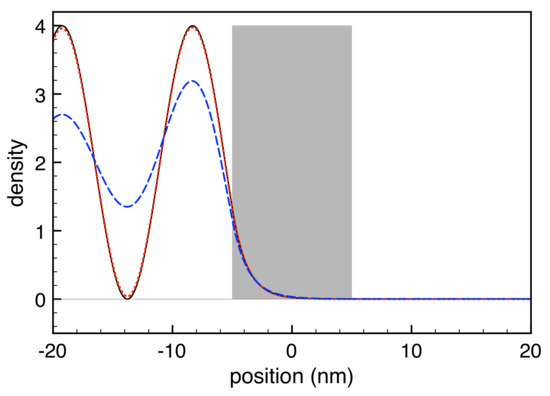
Figure 10.
The same as in Figure 8 but replacing the semiclassical IBC scheme based on the local RTA model in Equation (7) with the fully non-local model in Equation (32). To this end, the monoenergetic left injection of the IBC scheme employed in Figure 8 is replaced by a thermal coupling of the device with a corresponding monoenergetic distribution in the left reservoir via a relaxation time fs. The coherent-limit result (solid curve) and the weak-dissipation one (dashed curve) are basically coincident; the dash-dotted curve refers to the strong-dissipation regime.
Comparing once again the present convincing results with the highly problematic ones in Section 3.2, we also notice that, while there, in Figure 8, the curves corresponding to the coherent-limit result (solid line) and the weak-dissipation one (dashed line) differ significantly, here, in Figure 10, they basically coincide (the two profiles are hardly distinguishable). Recalling that the so-called coherent limit () is concretely fulfilled when the dissipation time is much larger than any other characteristic time, and that for our system the only other time-scale is the thermalization time (of the order of 100 fs), it is clear that in the weak-dissipation regime ( ps) the dissipation time is about fifty times larger than the thermalization one; this tells us that the weak-dissipation result (dashed curve) should closely resemble the coherent-limit one (solid curve). Such a physically sound scenario is fully confirmed by the results shown in Figure 10. This is instead not the case for Figure 8, where, as discussed in more detail in [67], the anomalous difference between the weak-dissipation result (dashed curve) and the coherent-limit solution (solid curve) is due to the fact that the latter is not unique. The coherent-limit result shown in Figure 8 (solid curve) should be therefore totally disregarded, and the dissipation-free scenario is well reproduced by the weak-dissipation result (dashed curve).
To confirm the quality and physical soundness of the non-local RTA model in Equation (32), we have repeated the simulated experiments of Figure 10 for a thinner ( nm) and lower ( meV) barrier. Opposite to the original (almost transmission-free) barrier profile in Figure 10, in this case, the transmission coefficient is about 25 %, leading to a significant tunneling dynamics across the barrier. This scenario is fully confirmed by the new results reported in Figure 11: while in the left portion of the device the role played by dissipation phenomena is similar to the one reported in Figure 10, here, in addition, we deal with a relevant tunneling across the barrier, leading to a significant charge distribution in the right portion of the device as well. In particular, while the coherent-limit result (solid curve) coincides again with the weak-dissipation one (dashed curve), in the strong-dissipation regime (dash-dotted curve), we deal again with a suppression of the left-side interference pattern, and to a decoherence-induced suppression of the tunneling dynamics.
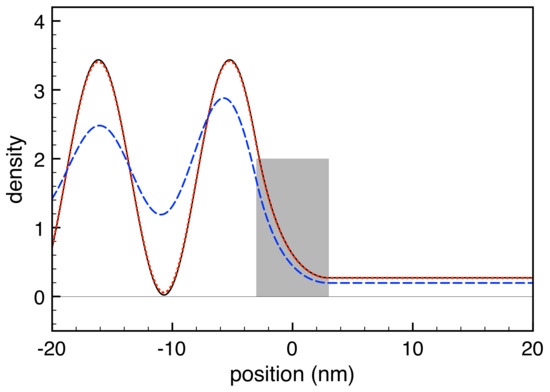
Figure 11.
The same as in Figure 10 but for a thinner ( nm) and lower ( meV) barrier (see text).
It is finally important to stress once again that the physically sound results in Figure 9, Figure 10 and Figure 11 obtained employing the new RTA model in Equation (32) are primarily due to its non-local character. To better elucidate the link between the non-local RTA model in Equation (32) and its local version in Equation (7), it is useful to realize that the former reduces to the latter in the presence of a fully local relaxation function, namely:
Recalling that, for the thermalization IBC scheme in Equation (5), we have , the explicit form of the local relaxation function in Equation (34) is given by:
This clearly shows that the local action of the conventional IBC scheme takes place on the device boundary region only, in clear contrast to the action of the non-local relaxation function in Equation (33). Indeed, regarding again any RTA model as an injection/source minus a loss/drain term [see Equation (30)], while in the conventional IBC scheme carrier injection versus loss takes place on the device spatial boundaries only, in the non-local model, the action of both injection and loss phenomena due to the presence of external charge reservoirs is present inside the device as well.
4.2. Non-Local Boltzmann-Type Models
The very same generalization procedure employed to derive the nonlocal RTA model in Equation (32) can also be adopted to overcome the limitations of the Boltzmann-like treatment pointed out in Section 3.1 (see Figure 6 and Figure 7). Instead of defining the scattering superoperator directly within the Weyl–Wigner phase-space (), one can start from a reliable dissipation model for the density matrix, and then translate it into the Wigner-function picture.
To this aim, we refer to the nonlinear density-matrix approach proposed in [73], which: (i) applies to any generic nanostructure; (ii) accounts for high-density effects; (iii) provides the correct thermal-equilibrium state; and (iv) preserves the positive-definite character of the single-particle density matrix. More specifically, for both carrier–phonon and carrier–carrier interaction mechanisms, energy dissipation and decoherence is described by the following nonlinear scattering superoperator
where are generalized scattering rates, whose explicit form is given in [73]. The nonlinearity factors can be regarded as the quantum-mechanical generalization of the Pauli factors of the conventional Boltzmann theory [see Equation (10)].
The key step is then to apply to the density-matrix scattering superoperator in Equation (36) the Weyl–Wigner transform in Equation (31). The resulting Wigner-function scattering superoperator still has the in-minus-out structure of Equation (16), with the local terms of the semiclassical theory in Equations (17) and (18) replaced with the following nonlocal generalizations.
with
and
It is worth stressing that, despite the strong formal similarity with the conventional Boltzmann transport theory, the generalized Wigner-function scattering rates in Equation (37) are not necessarily positive-definite.
The proposed quantum-mechanical generalization of the standard Boltzmann collision term in Equation (10) is thus intrinsically nonlocal. In particular, comparing Equation (37) with its semiclassical counterpart in Equation (11), it is evident that the action of the Pauli exclusion principle within the Wigner phase-space is itself nonlocal: the generalized in and out scattering rates for a given transition depend on the value of the Wigner function in any other phase-space point via the Pauli factor . A detailed investigation of such Pauli-blocking nonlocality is outside the scope of the present work and can be found in [64].
To test the suitability of the proposed nonlocal Boltzmann superoperator, we have applied the latter to the case of the simulated experiment of Figure 6; the resulting energy-dissipation dynamics is presented in Figure 12. Here, opposite to the unphysical behaviors obtained via the semiclassical Boltzmann model (see Figure 6 and Figure 7), both the spatial carrier distributions (Figure 12a) and the corresponding subband populations (Figure 12b) are always positive-definite. Moreover, analogously to the physically sound results of the RTA model M1 [see Figure 4a and Figure 5a], the system now correctly relaxes toward the equilibrium state (solid curve in panel a) without unphysical interlevel couplings and continuum populations. Here, due to the trace-preserving character of the original density-matrix model in Equation (36), the proposed nonlocal Boltzmann-type superoperator in Equation (37) is intrinsically charge-conserving.
As pointed out in Section 2.2, a possible strategy to improve the quality of semiclassical device modeling is to replace the standard IBC thermalization scheme with a global simulation of the device-plus-reservoir system. To this aim, an efficient approach is to describe reservoir-induced carrier thermalization via an effective Boltzmann-type collision term, as originally proposed in [68,69]. It is worth stressing that the very same strategy can be adopted for quantum-simulation schemes as well; indeed, instead of accounting for thermalization phenomena via the non-local RTA scheme in Equation (32), it is possible, in principle, to describe reservoir-induced carrier thermalization via the non-local Boltzmann-type superoperator in Equation (16) equipped with corresponding device-reservoir thermalization rates formally identical to the non-local dissipation rates in Equation (37).
5. Summary and Conclusions
The simulation of novel nanomaterials and of related electronic quantum devices is often grounded on partially phenomenological transport models based on the Wigner-function formalism. Within these simplified modeling strategies, energy dissipation versus decoherence phenomena are still described via local models borrowed from the semiclassical Boltzmann theory, namely relaxation-time treatments or Boltzmann-type scattering approaches. Such a semiclassical treatment is intrinsically incompatible with the fully quantum-mechanical coherent (i.e., dissipation-free) carrier dynamics within the device active region. Indeed, during the last decades, the intrinsic limitations of such hybrid treatments emerged in different contexts, both for semiclassical thermalization models based on the conventional boundary-condition scheme and for dissipation versus decoherence treatments based on the relaxation-time approximation, as well as on Boltzmann-like scattering models.
In this paper, our primary goal is twofold: (i) We review selected simulated experiments, showing the above-mentioned limitations in different contexts, and providing a cohesive theoretical treatment able to clearly identify the origin of such diverse anomalies faced within the Wigner-function picture. (ii) Starting from the density-matrix formalism, we show how to derive genuine quantum mechanical dissipation models, able to overcome the intrinsic limitations just reviewed.
The main conclusion of our analysis is as follows: within the Wigner-function picture, a correct treatment of both dissipation versus decoherence phenomena inside the device and of the device-reservoir thermalization process requires the use of intrinsically non-local scattering models. In addition, our investigation shows that the most natural theoretical framework for a fully quantum-mechanical simulation of electronic and optoelectronic nanodevices is the density-matrix picture, which comes out to also be computationally less expensive. Indeed, in the presence of non-local dissipation and/or thermalization models, a direct numerical solution of the corresponding transport equation via finite-difference schemes over the Wigner phase-space is by far computationally more demanding (compared to the local case), and a direct numerical solution of the density-matrix equation comes out to be, in general, less expensive. No matter which is the adopted computational strategy (Wigner-function versus density-matrix solution), at any time, one can simply switch between the two pictures via the corresponding Weyl–Wigner transform.
Author Contributions
Investigation, R.C.I.; supervision, F.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashcroft, N.; Mermin, N. Solid State Physics; Cengage Learning India Private Limited: New Delhi, India, 2011. [Google Scholar]
- Jacoboni, C.; Lugli, P. The Monte Carlo Method for Semiconductor Device Simulation; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Yu, P.; Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties; Number v. 3 in Advanced Texts in Physics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Bastard, G. Wave Mechanics Applied to Semiconductor Heterostructures; Monographies de Physique, Les Éditions de Physique; EDP Sciences: Les Ulis, France, 1988. [Google Scholar]
- Frensley, W.R. Boundary-conditions for open quantum-systems driven far from equilibrium. Rev. Mod. Phys. 1990, 62, 745–791. [Google Scholar] [CrossRef]
- Lent, C.S.; Tougaw, P.D.; Porod, W.; Bernstein, G.H. Quantum cellular automata. Nanotechnology 1993, 4, 49. [Google Scholar] [CrossRef]
- Di Carlo, A.; Vogl, P.; Pötz, W. Theory of Zener tunneling and Wannier-Stark states in semiconductors. Phys. Rev. B 1994, 50, 8358–8377. [Google Scholar] [CrossRef] [PubMed]
- Savasta, S.; Girlanda, R. Quantum Optical Effects and Nonlinear Dynamics in Interacting Electron Systems. Phys. Rev. Lett. 1996, 77, 4736–4739. [Google Scholar] [CrossRef]
- Fischetti, M.V. Master-equation approach to the study of electronic transport in small semiconductor devices. Phys. Rev. B 1999, 59, 4901–4917. [Google Scholar] [CrossRef]
- Datta, S. Nanoscale device modeling: The Green’s function method. Superlattice Microst. 2000, 28, 253–278. [Google Scholar] [CrossRef]
- Rossi, F.; Kuhn, T. Theory of ultrafast phenomena in photoexcited semiconductors. Rev. Mod. Phys. 2002, 74, 895–950. [Google Scholar] [CrossRef]
- Axt, V.M.; Kuhn, T. Femtosecond spectroscopy in semiconductors: A key to coherences, correlations and quantum kinetics. Rep. Prog. Phys. 2004, 67, 433–512. [Google Scholar] [CrossRef]
- Jacoboni, C.; Bordone, P. The Wigner-function approach to non-equilibrium electron transport. Rep. Prog. Phys. 2004, 67, 1033. [Google Scholar] [CrossRef]
- Pecchia, A.; Di Carlo, A. Atomistic theory of transport in organic and inorganic nanostructures. Rep. Prog. Phys. 2004, 67, 1497–1561. [Google Scholar] [CrossRef]
- Iotti, R.C.; Rossi, F. Microscopic theory of semiconductor-based optoelectronic devices. Rep. Prog. Phys. 2005, 68, 2533–2571. [Google Scholar] [CrossRef]
- Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Haug, H.; Jauho, A. Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Jacoboni, C. Theory of Electron Transport in Semiconductors: A Pathway from Elementary Physics to Nonequilibrium Green Functions; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Haug, H.; Koch, S. Quantum Theory of the Optical and Electronic Properties of Semiconductors; World Scientific: Singapore, 2004. [Google Scholar]
- Rossi, F. Theory of Semiconductor Quantum Devices: Microscopic Modeling and Simulation Strategies; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Buot, F. Nonequilibrium Quantum Transport Physics in Nanosystems: Foundation of Computational Nonequilibrium Physics in Nanoscience and Nanotechnology; World Scientific: Singapore, 2009. [Google Scholar]
- Frensley, W.R. Transient Response of a Tunneling Device Obtained from the Wigner Function. Phys. Rev. Lett. 1986, 57, 2853–2856. [Google Scholar] [CrossRef] [PubMed]
- Kluksdahl, N.C.; Kriman, A.M.; Ferry, D.K.; Ringhofer, C. Self-consistent study of the resonant-tunneling diode. Phys. Rev. B 1989, 39, 7720–7735. [Google Scholar] [CrossRef]
- Buot, F.A.; Jensen, K.L. Lattice Weyl-Wigner formulation of exact many-body quantum-transport theory and applications to novel solid-state quantum-based devices. Phys. Rev. B 1990, 42, 9429–9457. [Google Scholar] [CrossRef]
- Jensen, K.; Buot, F. The effects of scattering on current-voltage characteristics, transient response, and particle trajectories in the numerical simulation of resonant tunneling diodes. J. Appl. Phys. 1990, 67, 7602–7607. [Google Scholar] [CrossRef]
- Miller, D.R.; Neikirk, D.P. Simulation of intervalley mixing in double-barrier diodes using the lattice Wigner function. Appl. Phys. Lett. 1991, 58, 2803–2805. [Google Scholar] [CrossRef]
- McLennan, M.J.; Lee, Y.; Datta, S. Voltage drop in mesoscopic systems: A numerical study using a quantum kinetic equation. Phys. Rev. B 1991, 43, 13846–13884. [Google Scholar] [CrossRef] [PubMed]
- Tso, H.C.; Horing, N.J.M. Wigner-function formulation of nonlinear electron-hole transport in a quantum well and analysis of the linear transient and steady state. Phys. Rev. B 1991, 44, 11358–11380. [Google Scholar] [CrossRef]
- Gullapalli, K.K.; Miller, D.R.; Neikirk, D.P. Simulation of quantum transport in memory-switching double-barrier quantum-well diodes. Phys. Rev. B 1994, 49, 2622–2628. [Google Scholar] [CrossRef]
- Fernando, C.L.; Frensley, W.R. Intrinsic high-frequency characteristics of tunneling heterostructure devices. Phys. Rev. B 1995, 52, 5092–5104. [Google Scholar] [CrossRef]
- El Sayed, K.; Kenrow, J.A.; Stanton, C.J. Femtosecond relaxation kinetics of highly excited electronic wave packets in semiconductors. Phys. Rev. B 1998, 57, 12369–12377. [Google Scholar] [CrossRef]
- Pascoli, M.; Bordone, P.; Brunetti, R.; Jacoboni, C. Wigner paths for electrons interacting with phonons. Phys. Rev. B 1998, 58, 3503–3506. [Google Scholar] [CrossRef]
- Kim, K.Y.; Lee, B. Wigner-function formulation in anisotropic semiconductor quantum wells. Phys. Rev. B 2001, 64, 115304. [Google Scholar] [CrossRef]
- Proietti Zaccaria, R.; Rossi, F. On the problem of generalizing the semiconductor Bloch equation from a closed to an open system. Phys. Rev. B 2003, 67, 113311. [Google Scholar] [CrossRef]
- Nedjalkov, M.; Kosina, H.; Selberherr, S.; Ringhofer, C.; Ferry, D.K. Unified particle approach to Wigner-Boltzmann transport in small semiconductor devices. Phys. Rev. B 2004, 70, 115319. [Google Scholar] [CrossRef]
- Nedjalkov, M.; Vasileska, D.; Ferry, D.K.; Jacoboni, C.; Ringhofer, C.; Dimov, I.; Palankovski, V. Wigner transport models of the electron-phonon kinetics in quantum wires. Phys. Rev. B 2006, 74, 035311. [Google Scholar] [CrossRef]
- Taj, D.; Genovese, L.; Rossi, F. Quantum-transport simulations with the Wigner-function formalism: Failure of conventional boundary-condition schemes. Europhys. Lett. 2006, 74, 1060–1066. [Google Scholar] [CrossRef]
- Weetman, P.; Wartak, M.S. Self-consistent model of a nanoscale semiconductor laser using Green and Wigner functions in two bases. Phys. Rev. B 2007, 76, 035332. [Google Scholar] [CrossRef]
- Querlioz, D.; Saint-Martin, J.; Bournel, A.; Dollfus, P. Wigner Monte Carlo simulation of phonon-induced electron decoherence in semiconductor nanodevices. Phys. Rev. B 2008, 78, 165306. [Google Scholar] [CrossRef]
- Morandi, O. Multiband Wigner-function formalism applied to the Zener band transition in a semiconductor. Phys. Rev. B 2009, 80, 024301. [Google Scholar] [CrossRef]
- Wójcik, P.; Spisak, B.; Wołoszyn, M.; Adamowski, J. Self-consistent Wigner distribution function study of gate-voltage controlled triple-barrier resonant tunnelling diode. Semicond. Sci. Tech. 2009, 24, 095012. [Google Scholar] [CrossRef]
- Barraud, S. Phase-coherent quantum transport in silicon nanowires based on Wigner transport equation: Comparison with the nonequilibrium-Green-function formalism. J. Appl. Phys. 2009, 106, 063714. [Google Scholar] [CrossRef]
- Yoder, P.D.; Grupen, M.; Smith, R. Demonstration of Intrinsic Tristability in Double-Barrier Resonant Tunneling Diodes With the Wigner Transport Equation. IEEE Trans. Electron Devices 2010, 57, 3265–3274. [Google Scholar] [CrossRef]
- Álvaro, M.; Bonilla, L.L. Two miniband model for self-sustained oscillations of the current through resonant-tunneling semiconductor superlattices. Phys. Rev. B 2010, 82, 035305. [Google Scholar] [CrossRef]
- Jiang, H.; Cai, W. Effect of boundary treatments on quantum transport current in the Green’s function and Wigner distribution methods for a nano-scale DG-MOSFET. J. Comput. Phys. 2010, 229, 4461–4475. [Google Scholar] [CrossRef]
- Jiang, H.; Cai, W.; Tsu, R. Accuracy of the Frensley inflow boundary condition for Wigner equations in simulating resonant tunneling diodes. J. Comput. Phys. 2011, 230, 2031–2044. [Google Scholar] [CrossRef]
- Savio, A.; Poncet, A. Study of the Wigner function at the device boundaries in one-dimensional single- and double-barrier structures. J. Appl. Phys. 2011, 109, 033713. [Google Scholar] [CrossRef]
- Trovato, M.; Reggiani, L. Quantum maximum-entropy principle for closed quantum hydrodynamic transport within a Wigner function formalism. Phys. Rev. E 2011, 84, 061147. [Google Scholar] [CrossRef]
- Nedjalkov, M.; Schwaha, P.; Selberherr, S.; Sellier, J.; Vasileska, D. Wigner quasi-particle attributes—An asymptotic perspective. Appl. Phys. Lett. 2013, 102, 163113. [Google Scholar] [CrossRef]
- Sellier, J.; Amoroso, S.; Nedjalkov, M.; Selberherr, S.; Asenov, A.; Dimov, I. Electron dynamics in nanoscale transistors by means of Wigner and Boltzmann approaches. Physica A 2014, 398, 194–198. [Google Scholar] [CrossRef]
- Sellier, J.; Dimov, I. A Wigner approach to the study of wave packets in ordered and disordered arrays of dopants. Physica A 2014, 406, 185–190. [Google Scholar] [CrossRef]
- Jacoboni, C.; Bordone, P. Wigner transport equation with finite coherence length. J. Comput. Electron. 2014, 13, 257–263. [Google Scholar] [CrossRef]
- Jonasson, O.; Knezevic, I. Dissipative transport in superlattices within the Wigner function formalism. J. Comput. Electron. 2015, 14, 879–887. [Google Scholar] [CrossRef]
- Hamerly, R.; Mabuchi, H. Quantum noise of free-carrier dispersion in semiconductor optical cavities. Phys. Rev. A 2015, 92, 023819. [Google Scholar] [CrossRef]
- Cabrera, R.; Bondar, D.I.; Jacobs, K.; Rabitz, H.A. Efficient method to generate time evolution of the Wigner function for open quantum systems. Phys. Rev. A 2015, 92, 042122. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kim, S. Effect of uncertainty principle on the Wigner function-based simulation of quantum transport. Solid State Electron. 2015, 111, 22–26. [Google Scholar] [CrossRef]
- Dorda, A.; Schürrer, F. A WENO-solver combined with adaptive momentum discretization for the Wigner transport equation and its application to resonant tunneling diodes. J. Comput. Phys. 2015, 284, 95–116. [Google Scholar] [CrossRef]
- Schulz, L.; Schulz, D. Application of a slowly varying envelope function onto the analysis of the wigner transport equation. IEEE Trans. Nanotechnol. 2016, 15, 801–809. [Google Scholar] [CrossRef]
- Woloszyn, M.; Spisak, B. Dissipative transport of thermalized electrons through a nanodevice. Phys. Rev. B 2017, 96, 075440. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, M. Quantum transport simulation of nanowire resonant tunneling diodes based on a Wigner function model with spatially dependent effective masses. IEEE Trans. Nanotechnol. 2017, 16, 1028–1036. [Google Scholar] [CrossRef]
- Iotti, R.C.; Dolcini, F.; Rossi, F. Wigner-function formalism applied to semiconductor quantum devices: Need for nonlocal scattering models. Phys. Rev. B 2017, 96, 115420. [Google Scholar] [CrossRef]
- Weinbub, J.; Ferry, D. Recent advances in Wigner function approaches. Appl. Phys. Rev. 2018, 5, 055304. [Google Scholar] [CrossRef]
- Ferry, D.; Welland, I. Relativistic Wigner functions in transition metal dichalcogenides. J. Comput. Electron. 2018, 17, 110–117. [Google Scholar] [CrossRef]
- Iotti, R.; Rossi, F. Microscopic Theory of Energy Dissipation and Decoherence in Solid-State Quantum Devices: Need for Nonlocal Scattering Models. Entropy 2018, 20, 726. [Google Scholar] [CrossRef]
- Lee, J.H.; Shin, M.; Seo, J. Performance limitations of nanowire resonant-tunneling transistors with steep switching analyzed by Wigner transport simulation. J. Appl. Phys. 2019, 125, 174502. [Google Scholar] [CrossRef]
- Ballicchia, M.; Ferry, D.K.; Nedjalkov, M.; Weinbub, J. Investigating Quantum Coherence by Negative Excursions of the Wigner Quasi-Distribution. Appl. Sci. 2019, 9, 1344. [Google Scholar] [CrossRef]
- Rosati, R.; Dolcini, F.; Iotti, R.C.; Rossi, F. Wigner-function formalism applied to semiconductor quantum devices: Failure of the conventional boundary condition scheme. Phys. Rev. B 2013, 88, 035401. [Google Scholar] [CrossRef]
- Proietti Zaccaria, R.; Ciancio, E.; Iotti, R.C.; Rossi, F. Modeling of open quantum devices within the closed-system paradigm. Phys. Rev. B 2004, 70, 195311. [Google Scholar] [CrossRef]
- Proietti Zaccaria, R.; Iotti, R.C.; Rossi, F. Monte Carlo simulation of hot-carrier phenomena in open quantum devices: A kinetic approach. Appl. Phys. Lett. 2004, 84, 139–141. [Google Scholar] [CrossRef]
- Moyal, J.E. Quantum mechanics as a statistical theory. Math. Proc. Camb. Phil. Soc. 1949, 45, 99–124. [Google Scholar] [CrossRef]
- Zhan, Z.; Colomés, E.; Oriols, X. Unphysical features in the application of the Boltzmann collision operator in the time-dependent modeling of quantum transport. J. Comput. Electron. 2016, 15, 1206–1218. [Google Scholar] [CrossRef]
- Dolcini, F.; Iotti, R.C.; Rossi, F. Interplay between energy dissipation and reservoir-induced thermalization in nonequilibrium quantum nanodevices. Phys. Rev. B 2013, 88, 115421. [Google Scholar] [CrossRef]
- Rosati, R.; Iotti, R.C.; Dolcini, F.; Rossi, F. Derivation of nonlinear single-particle equations via many-body Lindblad superoperators: A density-matrix approach. Phys. Rev. B 2014, 90, 125140. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).