Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions
2. The Proposed Method
2.1. Notations on 3D Line Representation and Triangulation in Plücker Coordinates
2.1.1. Two-View Line Triangulation
2.1.2. Multi-View Line Reconstruction in Plücker Coordinates
2.2. A New Minimal Spatial Line Representation Tailored for Uncertainty Analysis
2.3. Conversion between the Proposed Line Representation and the Plücker Line
2.3.1. From Plücker Line to the Proposed Representation
2.3.2. From the Proposed Representation to Plücker Line
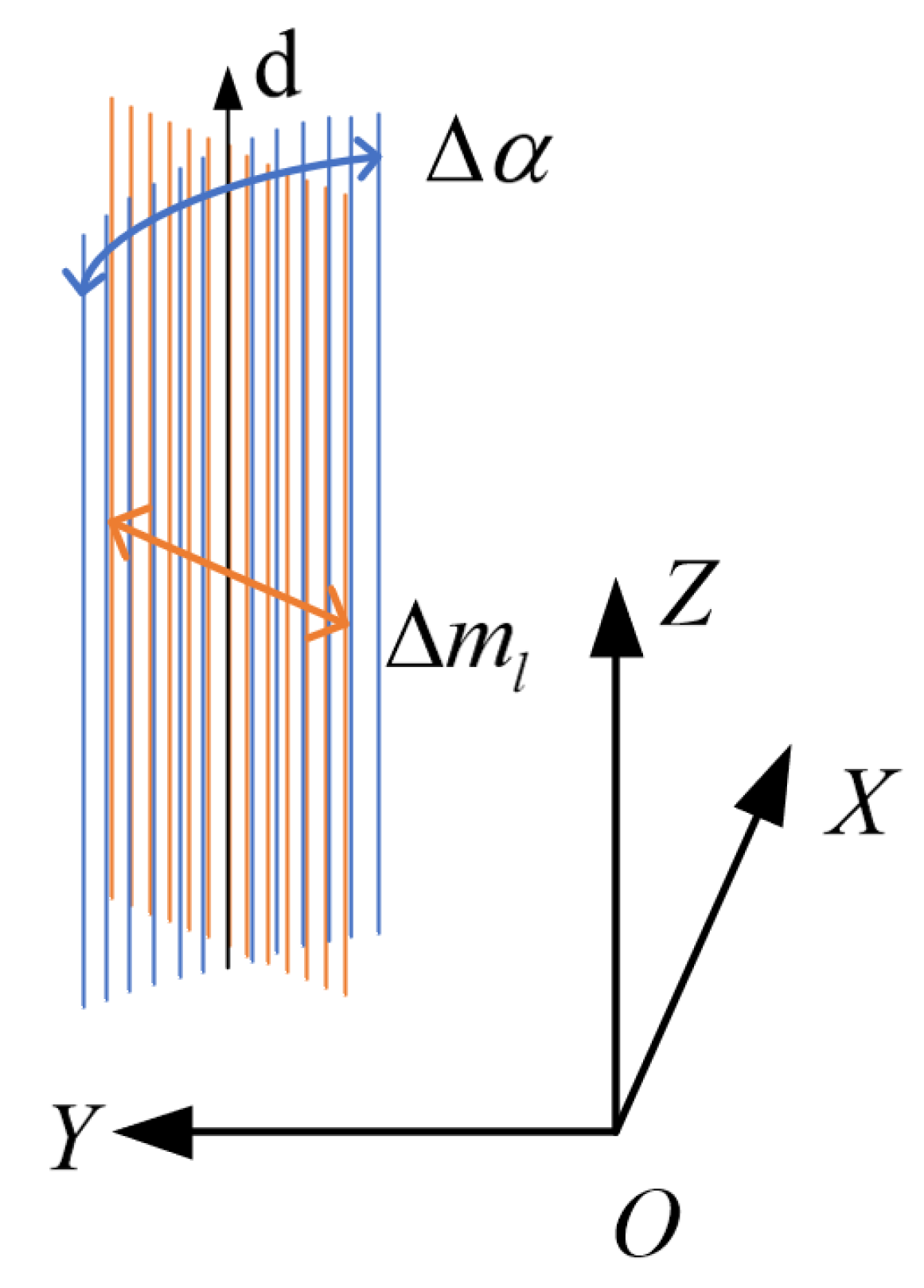
2.4. Uncertainty Estimation and Visualization for Two-View Line Triangulation
2.4.1. Uncertainty Estimation
2.4.2. Uncertainty Visualization
2.4.3. Uncertainty Analysis
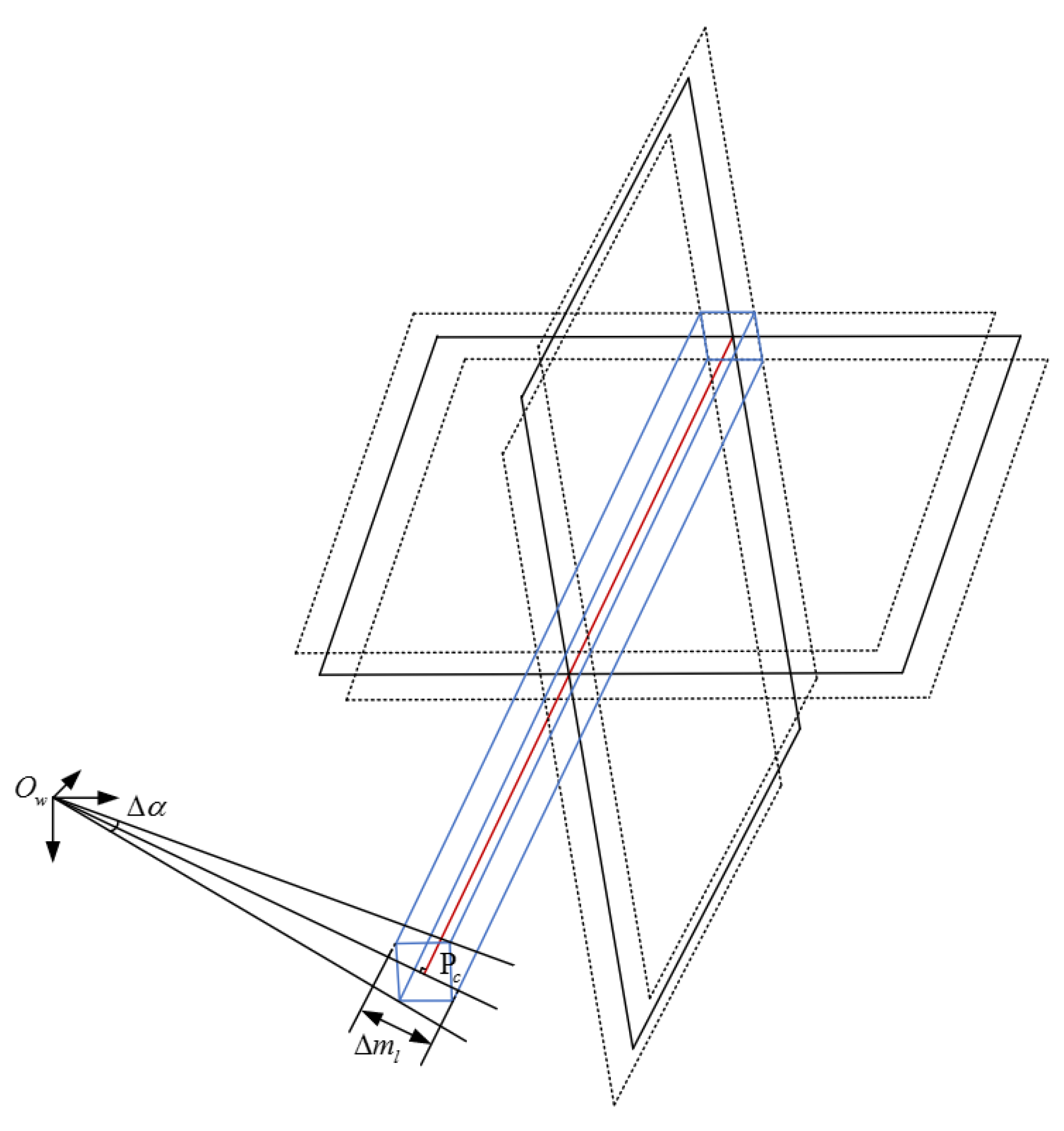
2.5. Uncertainty Update by Multiple Triangulations
3. Results
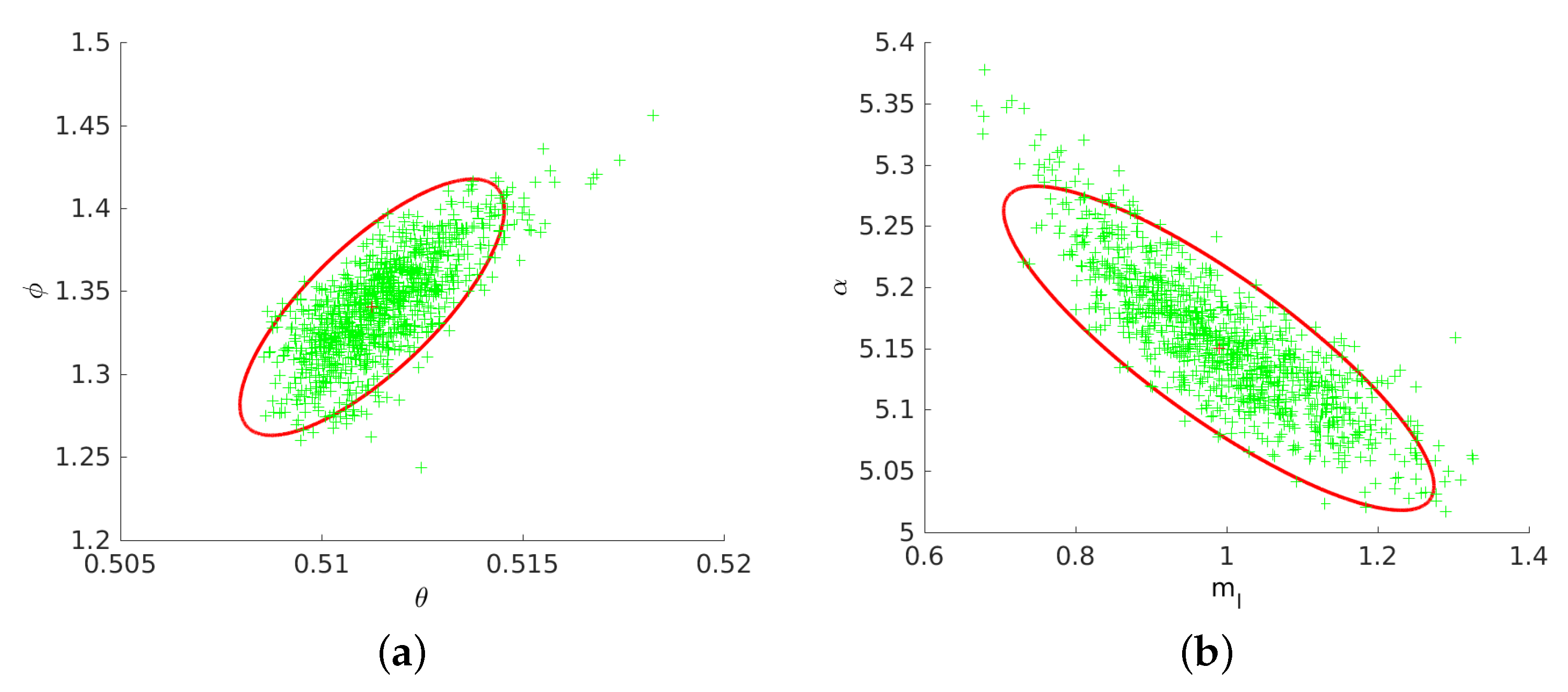
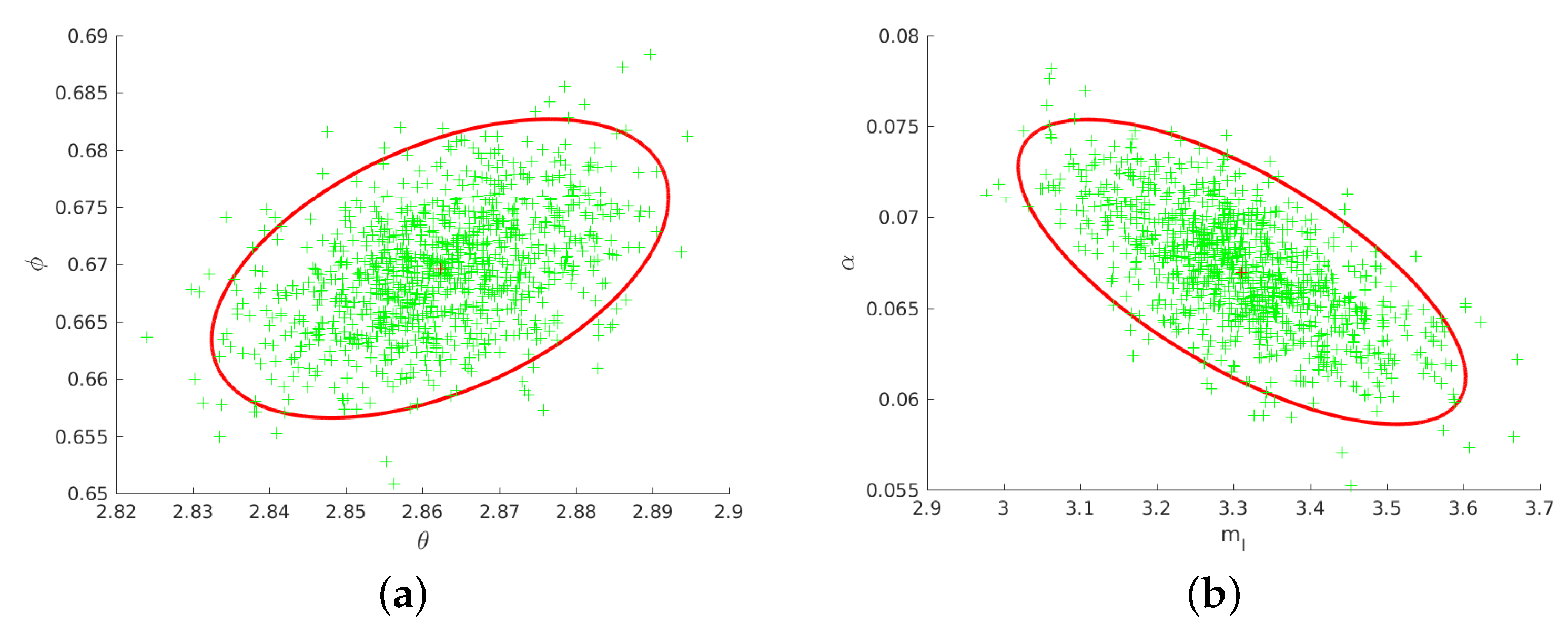
3.1. Experiments on Simulation Data
3.1.1. Experiment on Simulation Data to Validate and Visualize Uncertainty of Two-View Line Triangulation
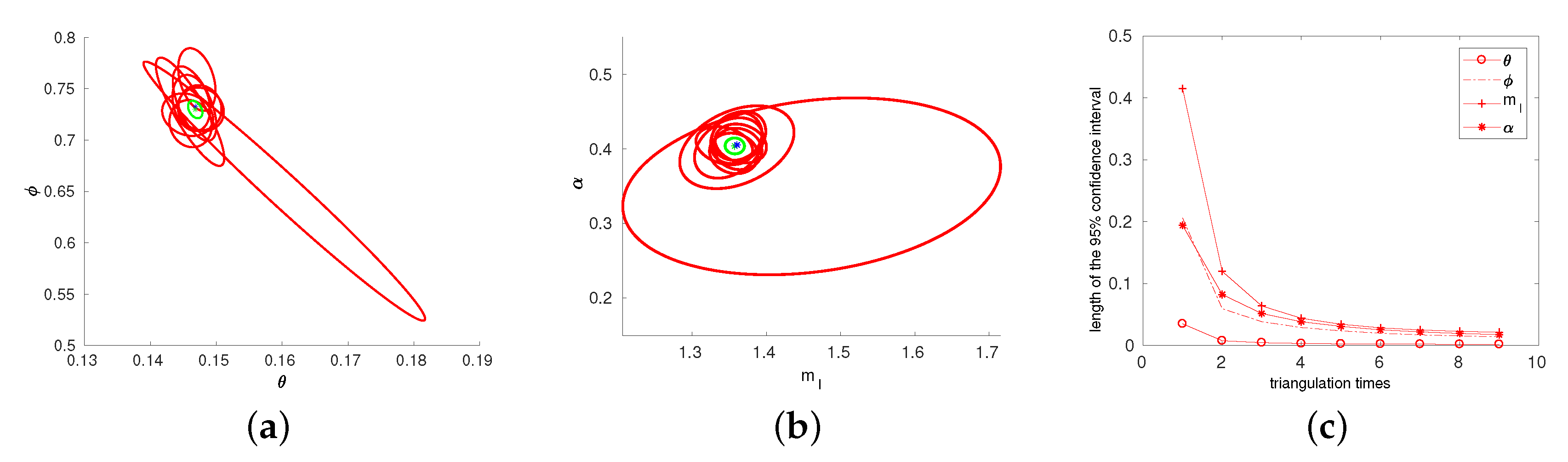
3.1.2. Experiment on Simulation Data to Validate and Visualize Uncertainty of Multi-View Line Reconstruction
3.1.3. Experiment on Simulation Data to Validate Uncertainty Decrease by Multiple Observations
3.2. Experiment on Synthetic Image Sequence
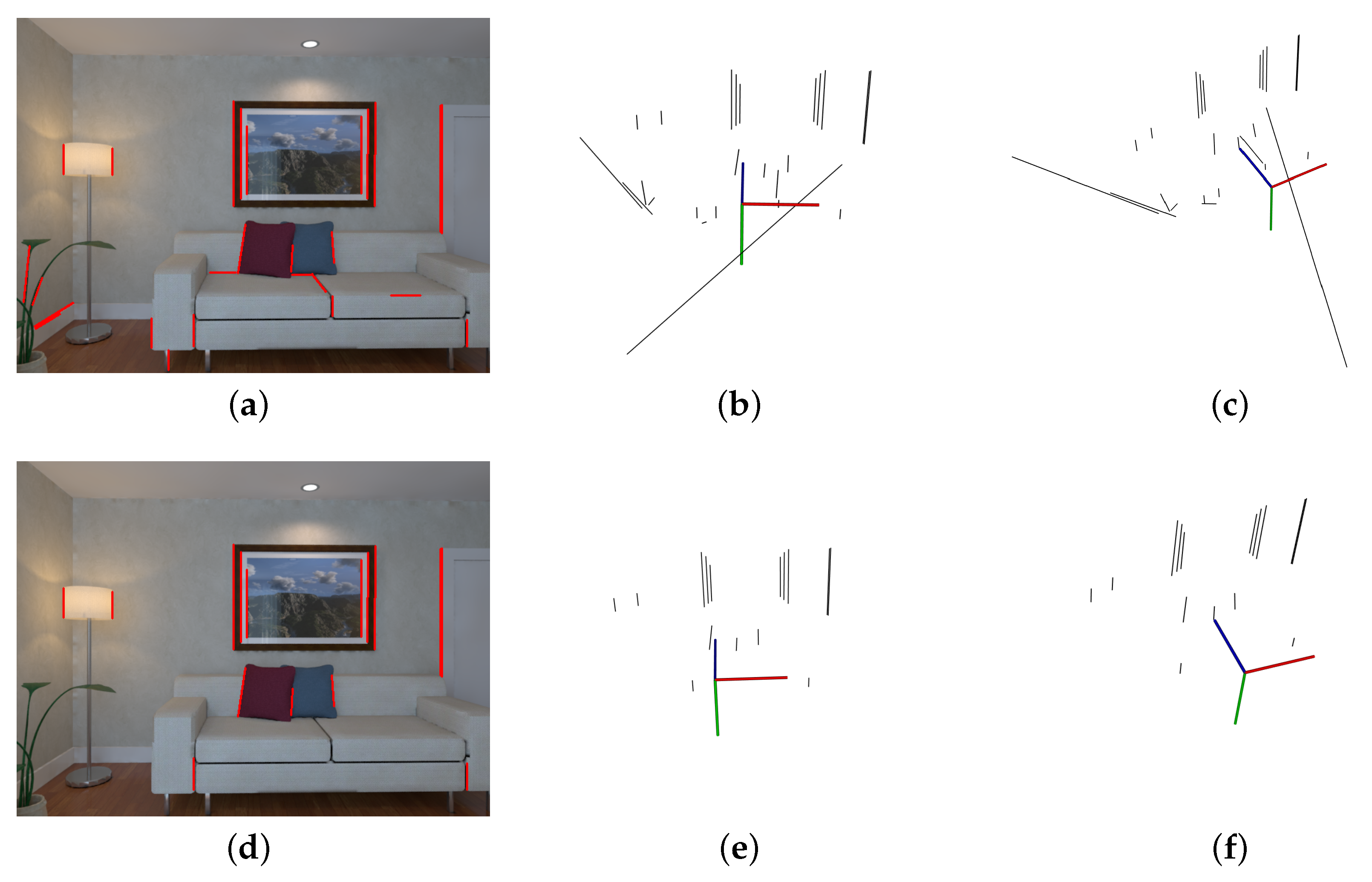
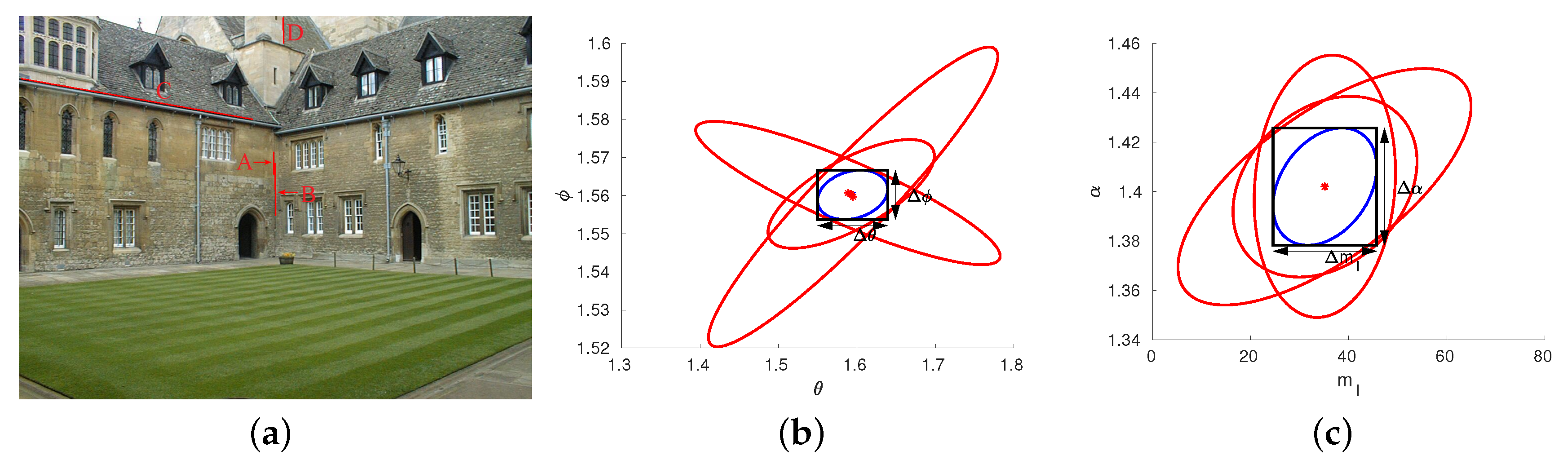
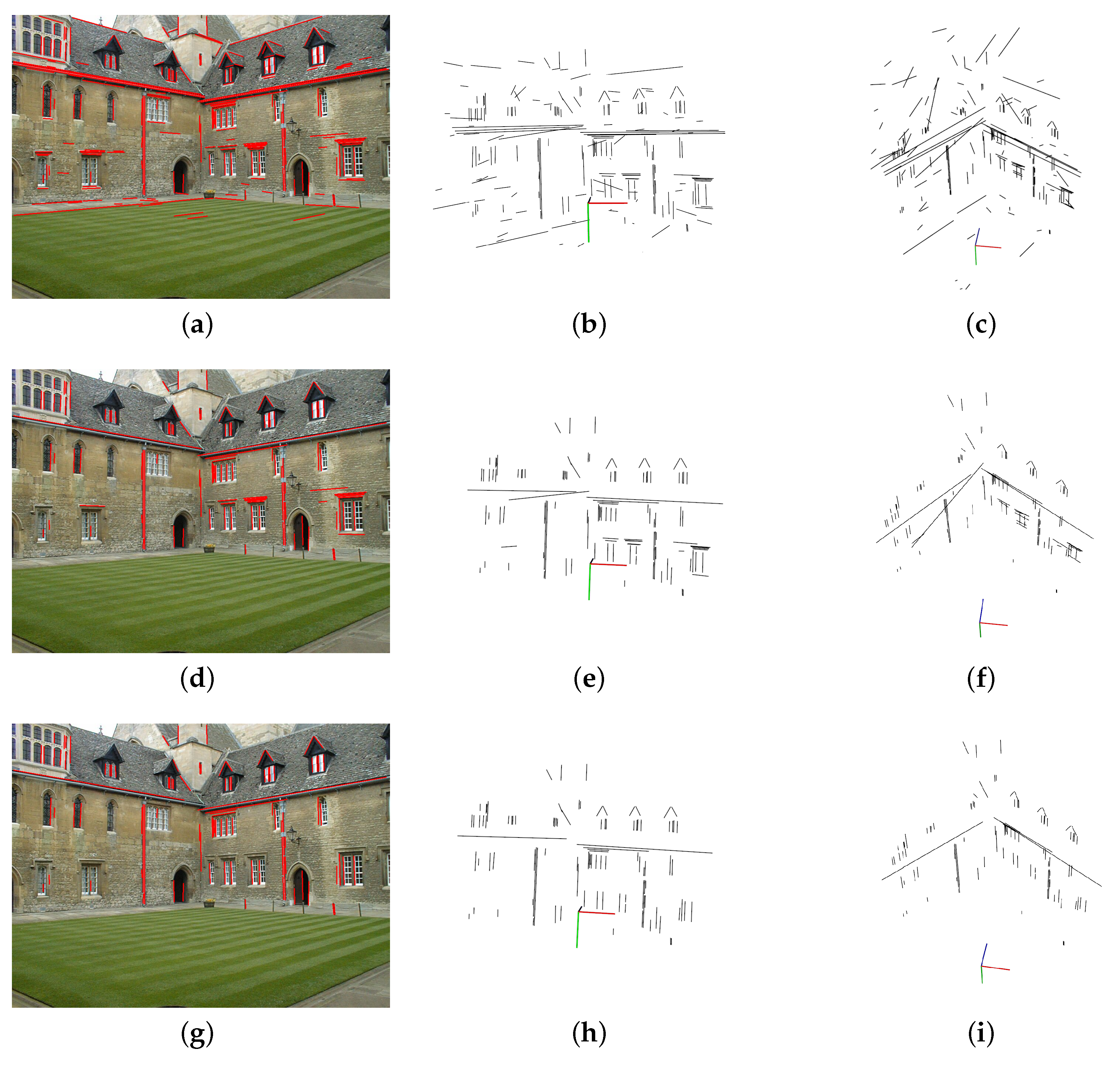
3.3. Experiment on rEal-World Image Sequence
3.3.1. Implementation Details
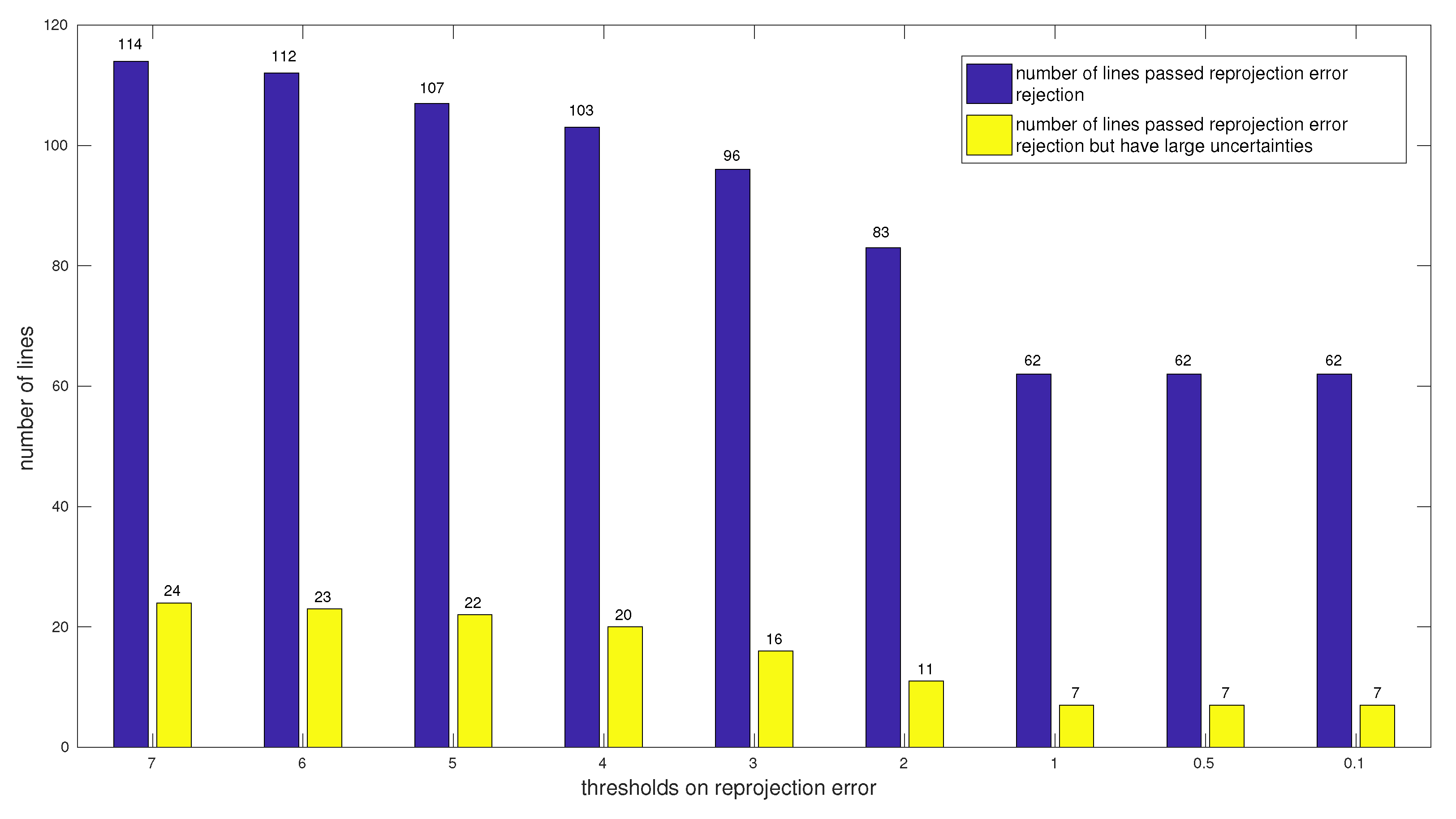
3.3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Jacobian of Conversion from a Plücker Line to the Proposed Representation
References
- Bartoli, A.; Sturm, P.F. Structure-from-motion using lines: Representation, triangulation, and bundle adjustment. Comput. Vis. Image Underst. 2005, 100, 416–441. [Google Scholar] [CrossRef]
- Zhang, L.; Koch, R. Structure and motion from line correspondences: Representation, projection, initialization and sparse bundle adjustment. J. Vis. Commun. Image Represent. 2014, 25, 904–915. [Google Scholar] [CrossRef]
- Taylor, C.J.; Kriegman, D.J. Structure and motion from line segments in multiple images. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 1021–1032. [Google Scholar] [CrossRef]
- Hofer, M.; Wendel, A.; Bischof, H. Incremental Line-based 3D Reconstruction using Geometric Constraints. In Proceedings of the British Machine Vision Conference (BMVC), Bristol, UK, 9–13 September 2013. [Google Scholar]
- Gomez-Ojeda, R.; Zuñiga-Noël, D.; Moreno, F.A.; Scaramuzza, D.; Gonzalez-Jimenez, J. PL-SLAM: A Stereo SLAM System through the Combination of Points and Line Segments. arXiv 2017, arXiv:1705.09479. [Google Scholar] [CrossRef]
- Pumarola, A.; Vakhitov, A.; Agudo, A.; Sanfeliu, A.; Moreno-Noguer, F. PL-SLAM: Real-time monocular visual SLAM with points and lines. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4503–4508. [Google Scholar]
- Gee, A.P.; Mayol-Cuevas, W. Real-time model-based SLAM using line segments. In Proceedings of the International Symposium on Visual Computing, Lake Tahoe, NV, USA, 6–8 November 2006; Springer: Berlin, Germany, 2006; pp. 354–363. [Google Scholar]
- Smith, P.; Reid, I.D.; Davison, A.J. Real-Time Monocular SLAM with Straight Lines. In Proceedings of the British Machine Vision Conference, Edinburgh, UK, 4–7 September 2006; pp. 17–25. [Google Scholar]
- Marzorati, D.; Matteucci, M.; Migliore, D.; Sorrenti, D.G. Integration of 3D Lines and Points in 6DoF Visual SLAM by Uncertain Projective Geometry. In Proceedings of the 2007 European Conference on Mobile Robots, Freiburg, Germany, 19–21 September 2007; pp. 96–101. [Google Scholar]
- Zuo, X.; Xie, X.; Liu, Y.; Huang, G. Robust visual SLAM with point and line features. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1775–1782. [Google Scholar]
- Gomez-Ojeda, R.; Briales, J.; Gonzalez-Jimenez, J. PL-SVO: Semi-direct Monocular Visual Odometry by combining points and line segments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4211–4216. [Google Scholar]
- He, Y.; Zhao, J.; Guo, Y.; He, W.; Yuan, K. PL-VIO: Tightly-Coupled Monocular Visual–Inertial Odometry Using Point and Line Features. Sensors 2018, 18, 1159. [Google Scholar] [CrossRef] [PubMed]
- Ok, A.Ö.; Wegner, J.D.; Heipke, C.; Rottensteiner, F.; Sörgel, U.; Toprak, V. Accurate Reconstruction of Near-Epipolar Line Segments from Stereo Aerial Images. Photogramm. Fernerkund. Geoinf. 2012, 2012, 341–354. [Google Scholar] [CrossRef]
- Hofer, M.; Maurer, M.; Bischof, H. Improving Sparse 3D Models for Man-Made Environments Using Line-Based 3D Reconstruction. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 535–542. [Google Scholar]
- Jain, A.; Kurz, C.; Thormählen, T.; Seidel, H.P. Exploiting Global Connectivity Constraints for Reconstruction of 3D Line Segments from Images. In Proceedings of the Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1586–1593. [Google Scholar]
- Hofer, M.; Maurer, M.; Bischof, H. Efficient 3D scene abstraction using line segments. Comput. Vis. Image Underst. 2017, 157, 167–178. [Google Scholar] [CrossRef]
- Sugiura, T.; Torii, A.; Okutomi, M. 3D surface reconstruction from point-and-line cloud. In Proceedings of the 2015 International Conference on 3D Vision (3DV), Lyon, France, 19–22 October 2015; pp. 264–272. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple view geometry in computer vision. Kybernetes 2004, 30, 1865–1872. [Google Scholar]
- Schmude, N.v. Visual Localization with Lines. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2017. [Google Scholar]
- Zhou, H.; Zhou, D.; Peng, K.; Fan, W.; Liu, Y. SLAM-based 3D Line Reconstruction. In Proceedings of the 2018 13th World Congress on Intelligent Control and Automation (WCICA), Changsha, China, 4–8 July 2018; pp. 1148–1153. [Google Scholar] [CrossRef]
- Zhou, H.; Fan, H.; Peng, K.; Fan, W.; Zhou, D.; Liu, Y. Monocular Visual Odometry Initialization With Points and Line Segments. IEEE Access 2019, 7, 73120–73130. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Huttenlocher, D.P. Efficient Graph-Based Image Segmentation. Int. J. Comput. Vis. 2004, 59, 167–181. [Google Scholar] [CrossRef]
- Donoser, M. Replicator Graph Clustering. In Proceedings of the British Machine Vision Conference (BMVC), Bristol, UK, 9–13 September 2013; pp. 38.1–38.11. [Google Scholar]
- Förstner, W.P.; Wrobel, B. Photogrammetric Computer Vision; Springer International Publishing: Cham, Switzerland, 2016; Volume 11. [Google Scholar] [CrossRef]
- Blostein, S.D.; Huang, T.S. Error analysis in stereo determination of 3-d point positions. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 9, 765. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Rios, A.H.; Shih, F.L.; Marefat, M. Stereo Camera Pose Determination with Error Reduction and Tolerance Satisfaction for Dimensional Measurements. In Proceedings of the IEEE International Conference on Robotics & Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Morris, D.D. Gauge Freedoms and Uncertainty Modeling for Three-dimensional Computer Vision. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2001. [Google Scholar]
- Park, S.Y.; Subbarao, M. A multiview 3D modeling system based on stereo vision techniques. Mach. Vis. Appl. 2005, 16, 148–156. [Google Scholar] [CrossRef]
- Grossmann, E.; Santos-Victor, J. Uncertainty analysis of 3D reconstruction from uncalibrated views. Image Vis. Comput. 2000, 18, 685–696. [Google Scholar] [CrossRef]
- Polic, M.; Förstner, W.; Pajdla, T. Fast and Accurate Camera Covariance Computation for Large 3D Reconstruction. In Computer Vision—ECCV 2018; Springer International Publishing: Berlin, Germany, 2018; pp. 697–712. [Google Scholar]
- Wolff, L.B. Accurate measurement of orientation from stereo using line correspondence. In Proceedings of the CVPR ’89: IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 4–8 June 1989; pp. 410–415. [Google Scholar] [CrossRef]
- Balasubramanian, R.; Swaminathan, S.D.K. Error analysis in reconstruction of a line in 3-D from two arbitrary perspective views. Int. J. Comput. Math. 2001, 78, 191–212. [Google Scholar] [CrossRef]
- Lu, Y. Visual Navigation for Robots in Urban and Indoor Environments. Ph.D. Thesis, Chang’an University, Xi’an, China, 2015. [Google Scholar]
- Heuel, S.; Forstner, W. Matching, reconstructing and grouping 3D lines from multiple views using uncertain projective geometry. In Proceedings of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Weng, J.; Huang, T.S.; Ahuja, N. Motion and structure from line correspondences; closed-form solution, uniqueness, and optimization. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 318–336. [Google Scholar] [CrossRef]
- Seo, Y.; Hong, K.S. Sequential reconstruction of lines in projective space. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 1, pp. 503–507. [Google Scholar]
- Pottmann, H.; Hofer, M.; Odehnal, B.; Wallner, J. Line geometry for 3D shape understanding and reconstruction. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; Springer: Berlin, Germany, 2004; pp. 297–309. [Google Scholar]
- Ronda, J.I.; Gallego, G.; Valdés, A. Camera autocalibration using plucker coordinates. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 3, pp. III–800. [Google Scholar]
- Ohwovoriole, M.S. An Externsion of Screw Theory and Its Application to the Automation of Industrial Assemblies. Ph.D. Thesis, Mechanical Engineering. Standford University, Stanford, CA, USA, 1980. [Google Scholar]
- Krantz, S.G. Handbook of Complex Variables; Birkhäuser: Boston, MA, USA, 1999. [Google Scholar]
- Roberts, K.S. A new representation for a line. In Proceedings of the CVPR ’88: The Computer Society Conference on Computer Vision and Pattern Recognition, Ann Arbor, MI, USA, 5–9 June 1988; pp. 635–640. [Google Scholar] [CrossRef]
- Heuel, S. Uncertain Projective Geometry: Statistical Reasoning For Polyhedral Object Reconstruction (Lecture Notes in Computer Science); Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gioi, R.G.V.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Koch, R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency. J. Vis. Commun. Image Represent. 2013, 24, 794–805. [Google Scholar] [CrossRef]
- Schönberger, J.L.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 1–26 June 2016. [Google Scholar]




| Outlier Rejection Method | Mean Directional Error (deg) | Mean Distance Error (m) | Good Line Ratio |
|---|---|---|---|
| Reprojection error | 21.73 | 9.05 | 57.69% |
| Reprojection error + Uncertainty | 0.76 | 0.01 | 93.33% |
| Line Segment | (rad) | (rad) | (rad) | |
|---|---|---|---|---|
| A | 0.089 | 0.012 | 21.11 | 0.047 |
| B | 0.084 | 0.010 | 21.06 | 0.047 |
| C | 0.526 | 0.158 | 159.21 | 0.674 |
| D | 0.123 | 0.013 | 25.17 | 0.045 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Peng, K.; Zhou, D.; Fan, W.; Liu, Y. Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation. Appl. Sci. 2020, 10, 1096. https://doi.org/10.3390/app10031096
Zhou H, Peng K, Zhou D, Fan W, Liu Y. Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation. Applied Sciences. 2020; 10(3):1096. https://doi.org/10.3390/app10031096
Chicago/Turabian StyleZhou, Hang, Keju Peng, Dongxiang Zhou, Weihong Fan, and Yunhui Liu. 2020. "Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation" Applied Sciences 10, no. 3: 1096. https://doi.org/10.3390/app10031096
APA StyleZhou, H., Peng, K., Zhou, D., Fan, W., & Liu, Y. (2020). Uncertainty Analysis of 3D Line Reconstruction in a New Minimal Spatial Line Representation. Applied Sciences, 10(3), 1096. https://doi.org/10.3390/app10031096





