Denoising Directional Room Impulse Responses with Spatially Anisotropic Late Reverberation Tails

Abstract

Directional room impulse responses (DRIR) measured with spherical microphone arrays (SMA) enable the reproduction of room reverberation effects on three-dimensional surround-sound systems (e.g., Higher-Order Ambisonics) through multichannel convolution. However, such measurements inevitably contain a nondecaying noise floor that may produce an audible “infinite reverberation effect” upon convolution. If the late reverberation tail can be considered a diffuse field before reaching the noise floor, the latter may be removed and replaced with an extension of the exponentially-decaying tail synthesized as a zero-mean Gaussian noise. This has previously been shown to preserve the diffuse-field properties of the late reverberation tail when performed in the spherical harmonic domain (SHD). In this paper, we show that in the case of highly anisotropic yet incoherent late fields, the spatial symmetry of the spherical harmonics is not conducive to preserving the energy distribution of the reverberation tail. To remedy this, we propose denoising in an optimized spatial domain obtained by plane-wave decomposition (PWD), and demonstrate that this method equally preserves the incoherence of the late reverberation field.

1. Introduction

Room impulse response (RIR) convolution has become a widespread method for reproducing room reverberation effects in digital audio processing applications. In the particular case of three-dimensional surround-sound systems, such as those using Higher-Order Ambisonics (HOA), directional room impulse responses (DRIR) measured with spherical microphone arrays (SMA) can reproduce spatialized room reverberation effects through multichannel convolution. However, such measured DRIRs inevitably contain a nondecaying noise floor that may produce an audible “infinite reverberation effect” upon convolution with an input sound source. In order for a measured DRIR to be usable in a spatialized convolution reverberation processor, this nondecaying noise floor must therefore be compensated.

Room reverberation has long been modeled as an exponentially decaying stochastic process [1], and this has been shown to be valid assuming sufficiently high echo density and modal overlap is achieved [2]. These conditions lead to a lower time limit for echo density, known as the “mixing time”, and a lower frequency limit for modal overlap, known as the “Schroeder frequency”. Beyond these limits, the late reverberation field is considered to be fully “diffuse”, i.e., a spatially isotropic distribution of a statistically significant number of stochastically independent [3] and therefore incoherent [4] plane waves. In such a case, the nondecaying background noise present in a measured RIR can be replaced with a zero-mean Gaussian noise filtered by a prolongation of the reverberation tail’s exponentially-decaying time-frequency envelope, parameterized by decay rates and initial spectra extracted from the RIR’s energy decay relief (EDR) [5]. This idea can be extended to spatialized DRIRs measured with an SMA by performing such tail resynthesis directly in the spherical harmonic domain (SHD) [6], where the orthogonality and spatial symmetry of the SHD components guarantee that the diffuseness properties of the late reverberation will be preserved [7]. It should be noted that other noise compensation techniques have been presented in the literature [8], but these have rarely dealt with reproduction of reverberation effects through convolution (a notable exception being Cabrera et al. [9]) and even less with the spatialized DRIR case.

In certain cases, however, the late reverberation field of a DRIR may become spatially incoherent without being energetically isotropic [10]; in other words, the stochastic process describing the plane waves incident on the SMA will have a certain spatial power distribution (or an amplitude density distribution, strictly speaking). This may be due to the particular geometric and/or absorptive characteristics of the measured space (e.g., coupled volumes, semi-open spaces, highly heterogeneous absorptive surfaces, etc.), in combination with the directivity and orientation of the sound source (which in general may not be perfectly omnidirectional), and can be investigated using directional energy decay curves (DEDC) [11] or energy decay deviations (EDD) [12] calculated on a spatial representation of the DRIR. As we show below, such anisotropic spatial distributions of the late reverberation tail cannot be arbitrarily recreated through analysis and synthesis in the SHD, and a different spatial representation must therefore be used for denoising.

2. Stochastic Model for Anisotropic Late Reverberation

We assume that at any given time in the stochastic late reverberation domain (i.e., above the Schroeder frequency and after the mixing time), the anisotropic sound field can be seen from the surface of an SMA ($\Omega \equiv (\theta ,\varphi )\in S^2$) as an infinite number of independent plane waves subject to an arbitrary amplitude density distribution (which we will write homogeneous to a power) over the incident directions $\Omega$:

$$x(f,\Omega ,t)=\sqrt{P(f,\Omega ,t)}\Phi (f,\Omega ,t),$$

(1)

where $P(f,\Omega ,t)$ is the power envelope and $\Phi (f,\Omega ,t)=e^{i\phi (f,\Omega ,t)}$ is the plane wave phase function such that $|\Phi (f,\Omega ,t\left)\right|=1\forall f,\Omega ,t$ and $\mathrm{E}\left\{\Phi (f,\Omega ,t){\Phi }^{*}(f,{\Omega }^{\prime },t)\right\}={\delta }_{\Omega ,{\Omega }^{\prime }}$, where $\mathrm{E}\left\{.\right\}$ denotes mathematical expectation and ${\delta }_{\Omega ,{\Omega }^{\prime }}$ is the Kronecker delta.

The HOA format [13] is based on the spherical harmonic (SH) decomposition of the sound field measured by an SMA. For the continuous function $x(f,\Omega ,t)$ defined on $S^2$, the ideal SH transform is written as follows [14]:

$$X_{l,m}(f,t)={\int }_{\Omega \in S^2}x(f,\Omega ,t)Y_{l,m}(\Omega )d\Omega ,$$

(2)

where $Y_{l,m}(\Omega )$ are the real spherical harmonics of order $l\in {\mathbb{N}}_0$ and degree $m\in [-l,l]$. Using an SMA, this transform is approximated by sampling over the Q transducer positions using a weighted finite sum, with the specific weights chosen such that the sum approaches the continuous integral of Equation (2) (e.g., by least-squares minimization [15]).

As a result of this discretization, the maximum encoding order L is limited such that the ${(L+1)}^2\times Q$ encoding matrix must have $K={(L+1)}^2\le Q$ nonvanishing singular values [16]. Truncating the SHD to a finite maximum order has the added consequence of introducing a spatial aliasing limit $ka\simeq L$, where $k=2\pi f/c$ is the wavenumber (with c the speed of sound and a the SMA radius) [17]. Finally, to obtain a representation of the measured sound field that is independent of the measurement array, a correction for the mode strengths (or holographic functions) of the SMA must be applied. In HOA, the theory describing optimal correction filters is provided by Daniel and Moreau [13].

In the SHD, a spatially incoherent sound field can be defined per component as [7]

$${\widehat{X}}_{l,m}(f,t)=\sqrt{{\widehat{P}}_{l,m}(f,t)}{\widehat{\Phi }}_{l,m}(f,t),$$

(3)

with ${\widehat{\Phi }}_{l,m}(f,t)$ stochastically independent such that

$$\mathrm{E}\left\{{\widehat{\Phi }}_{l,m}(f,t){\widehat{\Phi }}_{l^{\prime },m^{\prime }}^{*}(f,t)\right\}={\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}.$$

(4)

Since classic reverberation theory and its accompanying algorithms are based on energy decay or power envelopes, we take the power of the (ideal, infinite-order) inverse SH transform of Equation (3),

$$\begin{array}{cc}\hfill \widehat{P}(f,\Omega ,t)& =\mathrm{E}\left\{\widehat{x}(f,\Omega ,t){\widehat{x}}^{*}(f,\Omega ,t)\right\}\hfill \\ \hfill & =\sum _{l=0}^{\infty }\sum _{m=-l}^l\sum _{l^{\prime }=0}^{\infty }\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}\mathrm{E}\left\{{\widehat{X}}_{l,m}(f,t)Y_{l,m}(\Omega ){\widehat{X}}_{l^{\prime },m^{\prime }}^{*}(f,t)Y_{l^{\prime },m^{\prime }}^{*}(\Omega )\right\}\hfill \\ \hfill & =\sum _{l=0}^{\infty }\sum _{m=-l}^l\sum _{l^{\prime }=0}^{\infty }\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}\sqrt{{\widehat{P}}_{l,m}(f,t){\widehat{P}}_{l^{\prime },m^{\prime }}(f,t)}\mathrm{E}\left\{{\widehat{\Phi }}_{l,m}(f,t){\widehat{\Phi }}_{l^{\prime }{m}^{\prime }}^{*}(f,t)\right\}{Y}_{l,m}(\Omega )Y_{l^{\prime },m^{\prime }}^{*}(\Omega )\hfill \\ \hfill & =\sum _{l=0}^{\infty }\sum _{m=-l}^l{\widehat{P}}_{l,m}(f,t){\left|Y_{l,m}(\Omega )\right|}^2\hfill \end{array}$$

(5)

and observe that since both ${\widehat{P}}_{l,m}(f,t)$ and $|Y_{l,m}{(\Omega )|}^2$ are real and non-negative, $\widehat{P}(f,\Omega ,t)$ cannot be constructed to be arbitrarily anisotropic by acting on ${\widehat{P}}_{l,m}(f,t)$ alone. Such is the case, for example, in anisotropic late reverberation tails presenting a single energetically privileged direction. A different approach must therefore be taken in order to resynthesize late reverberation tails with spatially anisotropic decay envelopes in the aim of replacing the nondecaying noise floors of such measured DRIRs.

2.1. Spatial Incoherence under an Arbitrary Power Distribution

The spatial coherence function between two incident directions $\Omega$ and ${\Omega }^{\prime }$ is defined as

$$\gamma {(f,t)}_{\Omega ,{\Omega }^{\prime }}=\frac{\Psi {(f,t)}_{\Omega ,{\Omega }^{\prime }}}{\sqrt{\Psi {(f,t)}_{\Omega ,\Omega }\Psi {(f,t)}_{{\Omega }^{\prime },{\Omega }^{\prime }}}},$$

(6)

where $\Psi {(f,t)}_{\Omega ,\Omega }$ and $\Psi {(f,t)}_{\Omega ,{\Omega }^{\prime }}$ are, respectively, the auto- and cross-power spectral densities (PSD):

$$\Psi {(f,t)}_{\Omega ,{\Omega }^{\prime }}=\mathrm{E}\left\{x(f,\Omega ,t)x^{*}(f,{\Omega }^{\prime },t)\right\}.$$

(7)

For the signal model in Equation (1), this gives a cross-PSD of

$$\Psi {(f,t)}_{\Omega ,{\Omega }^{\prime }}=P(f,\Omega ,t){\delta }_{\Omega ,{\Omega }^{\prime }},$$

(8)

leading to a spatial coherence of

$$\gamma {(f,t)}_{\Omega ,{\Omega }^{\prime }}={\delta }_{\Omega ,{\Omega }^{\prime }},$$

(9)

a value independent of whether the uncorrelated plane wave field has a direction-dependent power distribution or not. In the SHD, however, the result only holds for a spatially isotropic field [18], which gives a coherence of $\tilde{\gamma }{(f,t)}_{n,n^{\prime }}={\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}$ between SH components (with component index $n=l^2+l+m$). In general, an anisotropic distribution will deviate from this result with nonzero cross-component coherence, even though the original plane wave field may be incoherent (see Section 3.1 below). The fact that this characteristic coherence result can only be derived in the SHD for an isotropic field implies that SHD-based measures of spatial coherence (such as those proposed by Jarrett et al. [18], for example) are unadapted to the analysis of anisotropic cases.

3. Plane Wave Decomposition and Spatial Analysis

The result of Equation (9) is valid for incident directions distributed around a single reference point, which is precisely the representation enabled by the SHD (assuming the proper corrections for the mode strengths of the SMA have been applied). From this modal representation, a direction-dependent view can be constructed by plane-wave decomposition (PWD) for a given set of “steering” or “look” directions around the unit sphere. The practical implementation of the PWD for finite-order SHD signals can be seen from a beamforming perspective as the “natural” or maximum directivity index (max-DI) beamformer, with coefficients ${\alpha }_l=1\forall l\in [0,L]$, and a main lobe peak-to-null half-width ${\Theta }_{\mathrm{PN}}\approx \pi /L$ [19]. The finite-order PWD can thus be written simply in matrix form:

$${\mathbf{x}}_{\mathrm{PWD}}(f,t)=\mathbf{Y}{\mathbf{x}}_{\mathrm{SHD}}(f,t),$$

(10)

where ${\mathbf{x}}_{\mathrm{PWD}}$ is the signal column vector corresponding to the D look directions ${\Omega }_d$, $\mathbf{Y}$ is the $D\times {(L+1)}^2$ decomposition matrix of elements $y_{d,n}={\alpha }_l{Y}_{l,m}\left({\Omega }_d\right)$ (with indices $n=l^2+l+m$ and $d\in [1,D]$), and ${\mathbf{x}}_{\mathrm{SHD}}$ is the length ${(L+1)}^2$ signal column vector in the SHD.

The beamforming view of the PWD highlights the problem of lobe overlap when analyzing several look directions; in any finite-order implementation, the resulting spatial-domain signals will inevitably include contributions from directions other than their target look direction ${\Omega }_d$, which may compromise their independence and hence the coherence analysis described above. The first crucial constraint is that the decomposition matrix $\mathbf{Y}$ must not introduce any linear dependence itself; since any look direction ${\Omega }_d$ can be written as a linear combination of any number of others, the number of linearly independent signals is restricted by the number of spherical harmonics, i.e., $D\le {(L+1)}^2$ (which follows from the fact that the spherical harmonics are linearly independent basis functions). However, if the PWD is to be useful as a spatial representation for denoising anisotropic DRIRs, the resulting (denoised) signals must also be transformed back into the SHD for posterior use in HOA-based spatialization systems. Since the rank of the SHD re-encoding matrix $\mathbf{Z}$ will be limited by $D\le {(L+1)}^2$ from the PWD step, complete linear independence throughout the full process can only be ensured if $D={(L+1)}^2$. As such, the re-encoding step can be written

$$\begin{array}{cc}\hfill \mathbf{Z}{\mathbf{x}}_{\mathrm{PWD}}& =\mathbf{Z}\mathbf{Y}{\mathbf{x}}_{\mathrm{SHD}}\hfill \\ \hfill & ={\mathbf{x}}_{\mathrm{SHD}}\mathrm{if}\mathbf{Z}\mathbf{Y}={\mathbf{I}}_{{(L+1)}^2}.\hfill \end{array}$$

(11)

The signal overlap due to the beamforming directivity lobes can be further quantified by analyzing the interactions between the directivity functions of each look direction $w_d(\Omega )$, obtained by evaluating the PWD with respect to ${\Omega }_d$:

$$w_d(\Omega )={\mathbf{y}}^{\mathrm{T}}(\Omega )\mathbf{y}\left({\Omega }_d\right),$$

(12)

where $\mathbf{y}(\Omega )$ is the length ${(L+1)}^2$ column vector of elements $y_n(\Omega )={\alpha }_l{Y}_{l,m}(\Omega )$ and ${.}^{\mathrm{T}}$ represents the simple transpose. As the beamforming patterns $w_d(\Omega )$ are axisymmetric, the dimensionality of the interaction between two look directions ${\Omega }_d$ and ${\Omega }_{d^{\prime }}$ can be reduced to a single relative angle $\Theta$ along the great circle joining the two. Figure 1 shows the interaction between the directivity functions of two adjacent look directions at different relative distances (central angles) $\Delta \Omega$ apart.

Figure 1b in particular highlights a critical value of the relative angle $\Theta$, the main lobe peak-to-null half-width ${\Theta }_{\mathrm{PN}}$. This separation describes the resolution limit of the beamformer; any adjacent look directions ${\Omega }_d$ and ${\Omega }_{d^{\prime }}$ closer than this will result in a combined directivity whose peaks are no longer centered on the original targets (see Figure 1c).

In the context of a PWD performed over D look directions, each resulting signal will overlap with every one of the other $D-1$ directions, leading to a total combined directivity of [20]

$$W(\Omega )=\sum _{d=1}^D{w}_d^2(\Omega ).$$

(13)

If any look directions are less than ${\Theta }_{\mathrm{PN}}$ apart, we therefore risk the loss of their individual directivity peaks, thereby compromising the independence between the corresponding signals.

Although the optimal arrangement of points on the surface of a sphere is a vast research topic that is beyond the scope of this article, the considerations detailed above will allow us to choose, with respect to the problem at hand, the most appropriate among various known solutions (e.g., Sloan-Womersley hyperinterpolation grids [21], Fliege t-designs [22]). For a given grid solution of $D={(L+1)}^2$ look directions, the central angles between all nearest neighbors can be calculated and compared to ${\Theta }_{\mathrm{PN}}$ to assess the risk of “fusing” directivity peaks, as in Figure 1c, and the variance (or standard deviation) in the total coverage $W(\Omega )$ can be calculated to ensure that the spatial analysis is as “flat” as possible. Indeed, since we have assumed our anisotropic late reverberation field to be made up of an infinity of incident plane waves under an arbitrary spatial power distribution, this “flatness” in $W(\Omega )$ is necessary in order to avoid any subspaces of the sphere being privileged over others.

Note that the “flat coverage” condition can be fulfilled exactly using t-designs with $D>{(L+1)}^2$ [20], but these would break the linear independence conditions described above.

3.1. Covariance Analysis in the Spatial Domain

The decomposition matrix rank, angular separation, and flat coverage criteria described above provide a good starting point for selecting a set of D look directions for the PWD, but the spatial coherence properties of the resulting sound field will directly determine the ability of a given set to decompose an incoherent SHD field into independent directional signals. The sound field’s spatial coherence can be examined using the covariance matrix of the PWD signals; following the results of Section 2.1, this should approach the identity matrix for any incoherent field of independent plane waves if the covariance calculation is made independent of the signal magnitudes by dividing out their expected values:

$$C_{d,d^{\prime }}=\frac{\mathrm{E}\left\{s({\Omega }_d,t)s({\Omega }_{d^{\prime }},t)\right\}}{\sqrt{\mathrm{E}\left\{s^2({\Omega }_d,t)\right\}\mathrm{E}\left\{s^2({\Omega }_{d^{\prime }},t)\right\}}},$$

(14)

where $s({\Omega }_d,t)$ is the time-domain signal obtained by PWD for the look direction ${\Omega }_d$. If we assume that the chosen set of D look directions leads to signals that sufficiently represent $s({\Omega }_d,t)=\mathrm{Re}\left\{{\mathcal{F}}^{-1}\left[x(f,{\Omega }_d,t)\right]\right\}$ (where ${\mathcal{F}}^{-1}\left[.\right]$ is the inverse Fourier transform and $\mathrm{Re}\left\{.\right\}$ is the real part of a complex number), Equation (14) should indeed approach a spatially discretized version of Equation (9).

As a result, a global sound field incoherence measure, analogous to the COMEDIE diffuseness measure proposed by Epain and Jin [23] in the SHD, can be defined over the set of D look directions. Denoted $\Gamma$ in this paper, this measure is calculated using an eigendecomposition of the covariance matrix [23]:

$$\Gamma =\frac{{\sum }_{i=1}^D|e_i-\overline{e}|}{2(D-1)\overline{e}},$$

(15)

where $e_i$ are the eigenvalues of the covariance matrix and $\overline{e}$ is their mean.

To investigate the incoherence preservation of various sets of look directions, a plane-wave field is synthesized as 8192-sample Gaussian noise signals over 625 independent incident directions, distributed using a Sloan-Womersley hyperinterpolation grid [21] (in order to sample the space of incident directions as evenly as possible). Both a fully isotropic and a highly anisotropic version are created, the latter by applying a cardioid directivity pattern with a dynamic range of 60 dB to the synthesized signals. The signals are encoded to the 4th-order truncated SHD and subsequently decomposed onto 5 different arrangements of 25 look directions by PWD. The mean and minimum angular separation between nearest neighbors, the flatness of the combined directivity $W(\Omega )$, and the global resulting incoherence $\Gamma$ are reported for each in

Table 1. Evaluation of 5 different arrangements of 25 look directions over the sphere. The mean and minimum separations refer to the angular distance between nearest-neighbor look directions. ${\sigma }_W$ is the standard deviation in the total combined directivity $W(\Omega )$ (Equation (13)), and $\Gamma$ is calculated using Equation (15).

Arrangement	Mean Separation	Min. Separation	${\mathit{\sigma }}_{\mathit{W}}$ (dB)	${\mathbf{\Gamma }}_{\mathbf{iso}}$	${\mathbf{\Gamma }}_{\mathbf{aniso}}$
Hyperinterpolation	40.5°	39.5°	0.477	0.884	0.751
Fliege	40.9°	39.6°	0.400	0.896	0.743
Spherical Covering [24]	38.7°	36.8°	0.456	0.890	0.743
Spherical Maximal Volume [24]	40.1°	38.6°	0.437	0.893	0.743
Spherical Packing [24]	41.6°	41.6°	0.552	0.871	0.741

. The incoherence measures in the anisotropic case being highly similar among the 5 sets, the 25-point Fliege t-design [22] is finally chosen due to its flatness, its relatively high angular separation, and its high isotropic incoherence.

Figure 2 then shows the covariance matrices for the Fliege arrangement for the two types of synthesized signals (isotropic, Figure 2a,c; anisotropic, Figure 2b,d), in both the SHD (Figure 2a,b) and PWD look direction domain (Figure 2c,d). The incoherence measures $\Gamma$ are included in each case to confirm that the PWD domain maintains its incoherence under highly anisotropic conditions.

As can be expected analytically, the SHD covariance matrix only tends to the identity matrix for a spatially isotropic field (see Figure 2, also shown by Epain and Jin [23]), confirming the necessity of analyzing incoherence in the PWD domain for highly anisotropic cases. Despite the additional “background” coherence inevitably generated by the finite-order PWD’s overlapping directivity lobes (see Figure 1 and Figure 2c,d), these investigations show that the use of a set of look directions chosen according to the “maximum independent coverage” criteria detailed in the above sections enables a spatial representation with a high degree of independence between signals, even in such an extremely anisotropic example.

3.2. Frequency Dependence of the PWD

It should be noted that in the case of a sound field captured by an SMA and encoded to HOA, the SH order-dependent SMA mode strength correcting filters introduce a frequency dependence into the PWD’s directivity. Indeed, the theory presented by Daniel and Moreau [13] (and more recently refined by Politis and Gamper [25] and Zotter [26], among others) makes use of an increasingly lower cutoff frequency by order so as to avoid the known “infinite bass boost” problem upon inversion of the SMA’s so-called mode strength or holographic function [27]; as a result, lower frequencies are rendered almost entirely omnidirectional, and directivity increases with frequency until all orders are equally present, before decreasing again with the emergence of strong sidelobes beyond the order-dependent spatial aliasing limit [17].

4. Denoising by Tail Resynthesis

With a maximum independent coverage spatial domain determined, the main EDR analysis and tail resynthesis procedure presented in [7] can be applied to each look direction individually. However, certain aspects of the process originally relying on the assumption of an isotropic field must be adjusted. In this section, we will review the main steps of the denoising procedure and highlight the particularities of the anisotropic case.

4.1. EDR Analysis

The EDR is a time-frequency extension of Schroeder’s reverse-integrated broadband Energy Decay Curve (EDC), from which frequency-dependent characteristics of the RIR can be extracted by analyzing each frequency bin individually [5]. In particular, we are interested in the decay envelope parameters, the decay rate $\delta \left(f\right)$ (more commonly represented as the 60-dB reverberation time $T_{60}=3ln\left(10\right)/\delta$), and the initial power spectrum $P_0\left(f\right)$, as well as the noise floor time limit $t_{\lim }\left(f\right)$ from which point onward the nondecaying noise floor is to be replaced with a synthesized prolongation of the late reverberation tail.

As presented in [7], the analysis method consists of three main steps applied in turn to each frequency bin of the dB-scale EDR: first, the noise floor is determined by fitting the theoretical profile of a reverse-integrated constant power noise; then, the exponential decay region of the curve is determined by allowing for a certain headroom above this noise floor and avoiding nonexponentially-decaying early reflection regimes; and finally, the decay parameters are determined by fitting an exponential decay model to the determined region.

4.2. Mixing Time Estimation by Incoherence

In order to replace the nondecaying noise floor with a prolongation of the reverberation tail resynthesized as independent zero-mean Gaussian noise signals, it must be verified that the DRIR has reached maximum incoherence before falling below the noise floor. Verifying this condition requires two quantities: the moment maximum incoherence is reached, which can be seen as an analogue of the mixing time; and a global, broadband value of the moment the reverberation tail falls below the noise floor.

The first may be determined by analyzing the evolution of the incoherence measure $\Gamma$ over the length of the DRIR, as was done with measures of the sound field’s diffuseness in the SHD in [7] (and similarly by Götz et al. [28]). The mixing time will be marked by the incoherence measure reaching a maximum value after an initial period of instability due to the arrival of coherent early reflections, and can be estimated algorithmically using $\Gamma \left(t\right)$ (see Section 5.2 below).

In the context of spatial PWD analysis, an overall estimation of the noise floor time limit requires taking into account the possibility that the noise floor may not be reached at the same time in all directions, due to the assumed anisotropic nature of the late reverberation tail and the possibly anisotropic or localized nature of the noise source(s). Furthermore, since the mixing time estimated using the incoherence measure $\Gamma \left(t\right)$ is a broadband value, the frequency-dependent $t_{\lim }^{\left(d\right)}\left(f\right)$ values returned by the EDR analysis must be reduced to a single value for each look direction in an appropriate manner.

As proposed in [7], the frequency dimension can be reduced in a perceptually-informed manner by performing an average over Bark-scale frequency bands weighted by the ITU-R 468 standard noise filter. If this is done for each look direction, the condition described above can be verified by making sure that the minimum of the averaged ${\overline{t}}_{\lim }^{\left(d\right)}$ values is greater than the estimated mixing time.

Note that since the EDR analysis is done in a direction-dependent manner, the proposed method also has an additional advantage over the SHD-based denoising procedure originally proposed in [7] in the case of localized noise sources; indeed, these would contribute to the nondecaying noise floor of multiple SH components, whereas they risk affecting only a limited number of PWD look directions.

4.3. Summary of Proposed Denoising Process

The full proposed process of denoising DRIRs measured with an SMA and presenting a spatially anisotropic late reverberation field can therefore be summarized in the following way:

• Exponential sweep method (ESM) [29] measurement by SMA, nonstationary artifact reduction [7], and DRIR deconvolution.
• HOA encoding (SH transform and SMA mode strength correction).
• PWD on a set of $D\le {(L+1)}^2$ look directions satisfying the maximum independent coverage criteria.
• Incoherence analysis by covariance matrix eigendecomposition [23] in the PWD domain and subsequent mixing time estimation.
• EDR analysis in the PWD domain (per look direction) and verification of incoherent field condition $t_{\mathrm{mix}}<min\left({\overline{t}}_{\lim }^{\left(d\right)}\right)$.
• Replacement of nondecaying noise floor by reverberation tail resynthesis in the PWD domain: zero-mean Gaussian noise signals synthesized per PWD look direction and subjected to frequency-dependent decay envelope from EDR analysis are used to replace and prolong (noisy) PWD domain DRIR signals from $t_{\lim }^{\left(d\right)}$ onwards.
• Re-encode back to HOA with full-rank matrix $\mathbf{Z}={\mathbf{Y}}^{-1}$, which imposes $D={(L+1)}^2$.

5. Results

We now present two sets of results obtained using the proposed denoising procedure: first, by applying it to a simulated reverberation tail with temporally increasing anisotropy (i.e., using anisotropic spatial distributions of both the initial spectrum $P_0$ and the reverberation time $T_{60}$); and then, to a DRIR measured at the Dominicans of Haute-Alsace cultural center using an mh acoustics Eigenmike^® SMA.

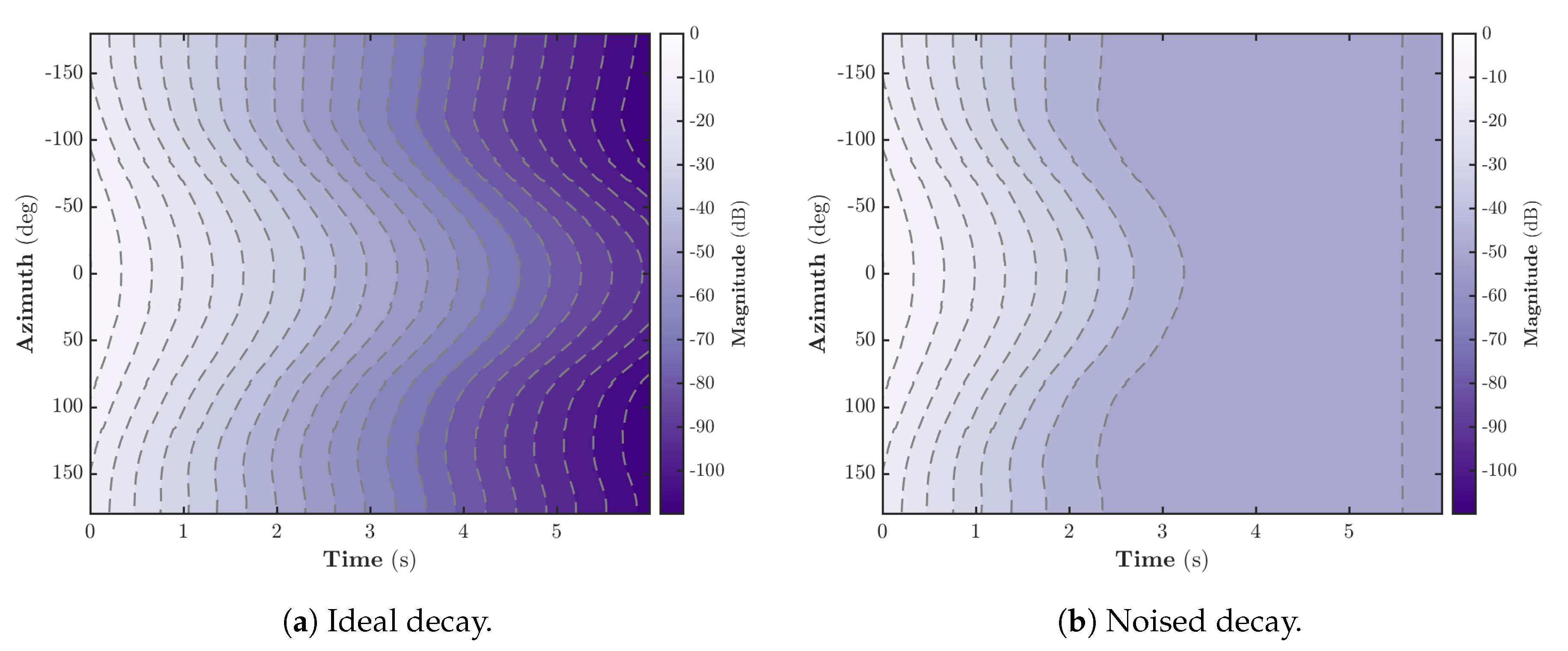
5.1. Simulated Reverberation Tail

A fully incoherent reverberation tail is simulated once again using 625 zero-mean Gaussian noise signals, each associated to an incident direction on a corresponding Sloan-Womersley hyperinterpolation grid. To create highly anisotropic conditions, a broadband (frequency-independent) exponential decay envelope is applied to the synthesized signals using cardioid distributions for both the initial power $P_0(\Omega )$ (over a 15-dB dynamic range) and the reverberation time $T_{60}(\Omega )$ (from 4 s at the maximum of the power distribution to 2 s at its minimum), both centered on $\Omega =(0°,0°)$. Finally, a −60-dB constant-power noise floor is synthesized over the 625-signal grid and added to the decaying signals. As before, this simulation is encoded to the 4th-order truncated SHD and then decomposed onto a 25-point Fliege set of look directions by PWD. The spatial energy decay of the resulting PWD-domain signals is shown in Figure 3; the EDCs are calculated individually for each look direction and then projected onto the azimuthal plane by cubic Hermite spherical interpolation [30] in dB scale.

The proposed denoising process is then applied in turn to each PWD look direction signal, as described above (Section 4). Note that only steps 5 and 6 of the complete procedure outlined in Section 4.3 are performed here, since, by construction, the simulation is known to be incoherent (furthermore, the SMA measurement is not simulated; the synthesized spatial signals are directly transformed to the SHD).

Due to the large difference in dynamic range between the noisy simulated reverberation tail and the result of the denoising procedure (whose arbitrary dynamic range is fixed to match the quantization noise floor for a given bit depth), it is more appropriate to use a spatial energy decay deviation (EDD) [12] to compare the two. The EDD is determined by

$$\mathrm{EDD}({\Omega }_d,t)={\mathrm{EDC}}_{\mathrm{dB}}({\Omega }_d,t)-{\overline{\mathrm{EDC}}}_{\mathrm{dB}}\left(t\right),$$

(16)

where ${\overline{\mathrm{EDC}}}_{\mathrm{dB}}\left(t\right)$ is the spatial mean over the dB-scale EDCs of the D look directions at each time step. Figure 4 shows the EDD (projected once more onto the azimuthal plane by cubic Hermite spherical interpolation) for the simulated late reverberation tail, before (Figure 4a, corresponding to Figure 3b) and after applying the proposed denoising process (Figure 4b).

Figure 4a clearly shows the isotropic noise floor reached around 3 s (in broadband terms), concurring with Figure 3b. As expected due to the anisotropic conditions created upon synthesis (cardioid distributions for both $P_0(\Omega )$ and $T_{60}(\Omega )$), the dynamic range of the denoised EDD (Figure 4b) increases as the reverberation tail decays. This provides the first clear evidence that the proposed procedure preserves and correctly extends the spatial features of anisotropic late reverberation.

To examine how well these features correspond to that of the originally simulated reverberation tail, Figure 5 compares the results of the PWD-domain EDR analysis (which parameterize the tail resynthesis in the denoising process) with the target cardioid distributions used in the simulation.

Figure 5 thus reveals the impact of the inevitable spatial overlap due to the finite-order PWD on the spatial features of the anisotropic reverberation tail. More specifically, it appears that spatial anisotropy in the reverberation time $T_{60}$ is less well retained than in the initial spectrum $P_0$; the analyzed $T_{60}$ range is only 40.1% of its target range (49% for a 7th-order analysis), while this goes up to 67.1% for $P_0$ (78.7% for 7th-order). However, the mean relative errors (17.2% for $T_{60}$ and 15.9% for $P_0$ at 4th-order; 13.6% and $8.45\%$, respectively, at 7th-order, averaged over the 25 analyzed look directions) are comparable, although the $P_0$ analysis sees greater improvement with increased order. Furthermore, comparisons between the $P_0$ in dB and the $T_{60}$ in seconds are not necessarily straightforward.

Indeed, any evaluation of the reconstruction of spatial variations in these parameters must take into account the secondary lobe behavior of the finite-order PWD’s directivity, especially with respect to the cardioid configuration used in this simulation. The most important secondary lobe in $w_d(\Omega )$ is the “back” lobe, centered $180°$ opposite the look direction ${\Omega }_d$ (see Figure 1; the back lobe peaks at around $-14$ dB). For a look direction pointing near the “back” of the cardioid distribution used for $P_0$ and $T_{60}$, i.e., ${\Omega }_d=(\pm 180°,0°)$, where both $P_0(\Omega )$ and $T_{60}(\Omega )$ are at their respective minima, the signal contribution from the back lobe located near $\Omega =(0°,0°)$, where $P_0(\Omega )$ and $T_{60}(\Omega )$ at their respective maxima will become increasingly important, and very quickly even more so than that from the main lobe (since the latter will be decaying faster and from a lower starting power).

If such is the case, the use of a beamformer optimized to reduce contributions from the back lobes instead of the “natural” PWD weighting used so far (${\alpha }_l=1\forall l\in [0,L]$) should help remedy this problem. The maximum front-to-back ratio (MFB) beamformer [31] is designed precisely through such an optimization, at the cost of an increased main lobe width. Figure 6 shows the analysis results obtained using a 4th-order MFB beamformer, compared to the 4th-order natural PWD and the synthesized cardioid distributions. The relative errors for $P_0$ and $T_{60}$ fall to $15.3\%$ and $13.3\%$, respectively, and it is qualitatively clear that the distributions’ shapes are more closely matched.

Unfortunately, the MFB beamformer cannot be used directly as-is for denoising anisotropic DRIRs, as the increased overlap between adjacent main lobes heavily affects the independence of the beamformed signals and therefore the overall spatial incoherence (${\Gamma }_{\mathrm{iso}}=0.469$ and ${\Gamma }_{\mathrm{aniso}}=0.442$). However, the results of Figure 6 suggest that a specific beamformer optimization constrained with respect to both the maximum independent coverage criteria elaborated in Section 3 as well as the front-to-back ratio may be able to increase the spatial accuracy of the EDR analysis while maintaining high incoherence between signals. Simultaneous optimization of the D look directions’ arrangement over the sphere may also be possible.

5.2. Application to a Measured DRIR

We now examine the results obtained on a DRIR measured in the neo-Gothic chapel at the Dominicans of Haute-Alsace cultural center, a 14th-century convent now dedicated to music and digital arts. The measurement was performed with a 32-capsule mh acoustics Eigenmike^® SMA, enabling 4th-order HOA encoding. Pretreatment and HOA encoding is performed as outlined in Section 4.3 (steps 1 and 2).

To further optimize the PWD, the direction of arrival (DOA) of the DRIR’s direct sound component is estimated (e.g., by pseudo-intensity vector analysis [32]) and the set of look directions is subsequently rotated such that one of the points is aligned with the direct sound. This ensures that the limitations of the finite-order PWD (see Section 3) have as little impact on the direct sound signal as possible. Additionally, it provides a common analysis frame across measured DRIRs, regardless of their direct sound’s DOA.

5.2.1. Incoherence Analysis and Mixing Time Estimation

Once the PWD has been performed, the temporal evolution of the incoherence measure $\Gamma \left(t\right)$ can be analyzed in order to estimate the mixing time, as proposed in Section 4.2. Figure 7 shows the result of this analysis; $t_{\mathrm{mix}}$ is estimated algorithmically by identifying the moment $\Gamma \left(t\right)$ levels out at a near-maximal value after the initial period of instability due to the arrival of coherent early reflections [7].

Two notable features in the evolution of $\Gamma \left(t\right)$ are its relatively high starting value (despite the fact that $t=0$ should correspond to the arrival of the direct sound only) and its gradual increase throughout the reverberation tail (the maximum time displayed in Figure 7 is based on a preliminary broadband estimation of the noise floor time limit). The first can be explained in part by the presence of incoherent background noise for directions other than the direct sound DOA, as well as the time averaging necessary for the coherence calculation, which may introduce the influence of later time frames with higher overall incoherence. The second feature is due to the increasing overall presence of the highly incoherent noise floor, especially at higher frequencies where the reverberation time is usually very short.

5.2.2. EDR Analysis and Tail Resynthesis

Next, the EDR analysis is performed for each look direction individually, as described above. Figure 8 presents the results of this analysis for the initial spectrum ($P_0(f,{\Omega }_d)$, Figure 8a) and reverberation time ($T_{60}(f,{\Omega }_d)$, Figure 8b), once more projected onto the azimuthal plane by cubic Hermite spherical interpolation. Since real room reverberation has a strong frequency dependence, these results are shown averaged over four octave bands in the SMA’s optimal frequency range (the spatial aliasing limit of the mh acoustics Eigenmike^® is $f_a\simeq 5200$ Hz with a radius of $4.2$ cm, and the directivity of the 4th-order PWD is essentially omnidirectional under 325 Hz).

Figure 8 suggests that the anisotropy of this particular DRIR stems from its initial spectrum $P_0(f,{\Omega }_d)$. However, it must be noted that any acoustical interpretation of such anisotropic analysis results will necessitate developments in stochastic reverberation modeling beyond the scope of this discussion. In the anisotropic case, contrary to classical diffuse reverberation theory, the quantities $P_0\left(f\right)$ and $T_{60}\left(f\right)$ cannot be considered independent either of each other or of the source and receiver positions in the room. As such, it is currently unclear which acoustical factors affect the anisotropy of these parameters, although the simulation results from Section 5.1 above show that their analysis through a PWD is affected by the lobe overlap of the beamformed signals.

With such reservations considered, it will be nonetheless interesting to note that while the dynamic range in $P_0$ increases with frequency, from $9.57$ dB in the $[325,650]$ Hz band to $15.1$ dB in the $[2600,5200]$ Hz band, the percent difference in $T_{60}$ (with respect to its maximum value) decreases from $11.3\%$ in the $[325,650]$ Hz band to only $3.38\%$ in the $[2600,5200]$ Hz band.

The spatial structure of this DRIR is shown in Figure 9, before (Figure 9a) and after (Figure 9b) application of the proposed denoising process, through the projection of the EDD onto the azimuthal plane by cubic Hermite spherical interpolation. Figure 9a reveals a slight amount of anisotropy in the nondecaying noise floor, showing that localized noise sources can be detected and removed by this method, as mentioned in Section 4.2. Figure 9b in turn confirms that the proposed procedure preserves the spatial distribution of the anisotropic reverberation tail as it is prolonged and resynthesized to replace the noise floor.

6. Conclusions

This paper has addressed the problem of removing the nondecaying noise floor from DRIRs measured with an SMA and presented spatially anisotropic yet incoherent late reverberation tails. Building on previous work done in the highly diffuse or spatially isotropic case, it has been shown that the noise floor can be replaced by a resynthesized prolongation of the late reverberation tail following a PWD of the HOA-encoded DRIR into a spatial domain carefully chosen to maximize independent coverage of the sphere. The spatial incoherence of the DRIR can be accurately analyzed in this domain, and its temporal evolution can be used to estimate the mixing time, a crucial step in verifying that the late reverberation tail has become maximally incoherent before reaching the noise floor and can therefore be synthesized as independent zero-mean Gaussian noise signals per look direction, subjected to the exponentially decaying envelope extracted from the DRIR by EDR analysis.

The proposed method is shown to correctly reconstruct the spatial characteristics of anisotropic late reverberation within the limitations inherent to a finite-order PWD. Further research will attempt to overcome these limitations by optimizing the beamforming characteristics of the PWD with respect to the maximum independent coverage criteria—the front-to-back ratio, which seems to enable more accurate spatial analysis of reverberation properties; and the arrangement of the look directions on the sphere. Any beamforming optimization will additionally have to work within the constraint of having $D={(L+1)}^2$ look directions in order for the spatial domain signals to be transformed back into the SHD for posterior applications in HOA spatialization systems, e.g., recreating spatialized reverberation effects by multichannel convolution.

Finally, the spatial EDR analysis results obtained from measured anisotropic DRIRs highlight the need for further developments in stochastic reverberation modeling. A theoretical basis for the analysis of anisotropic energy decay in enclosed spaces would provide the grounds for a true acoustical interpretation of such results. To this end, a preliminary exploration of the acoustic properties of anisotropic spaces could, for example, make use of the procedures presented in this paper to perform a comprehensive study of multiple source-receiver pairs in a single anisotropic space.