A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces
Abstract
1. Introduction
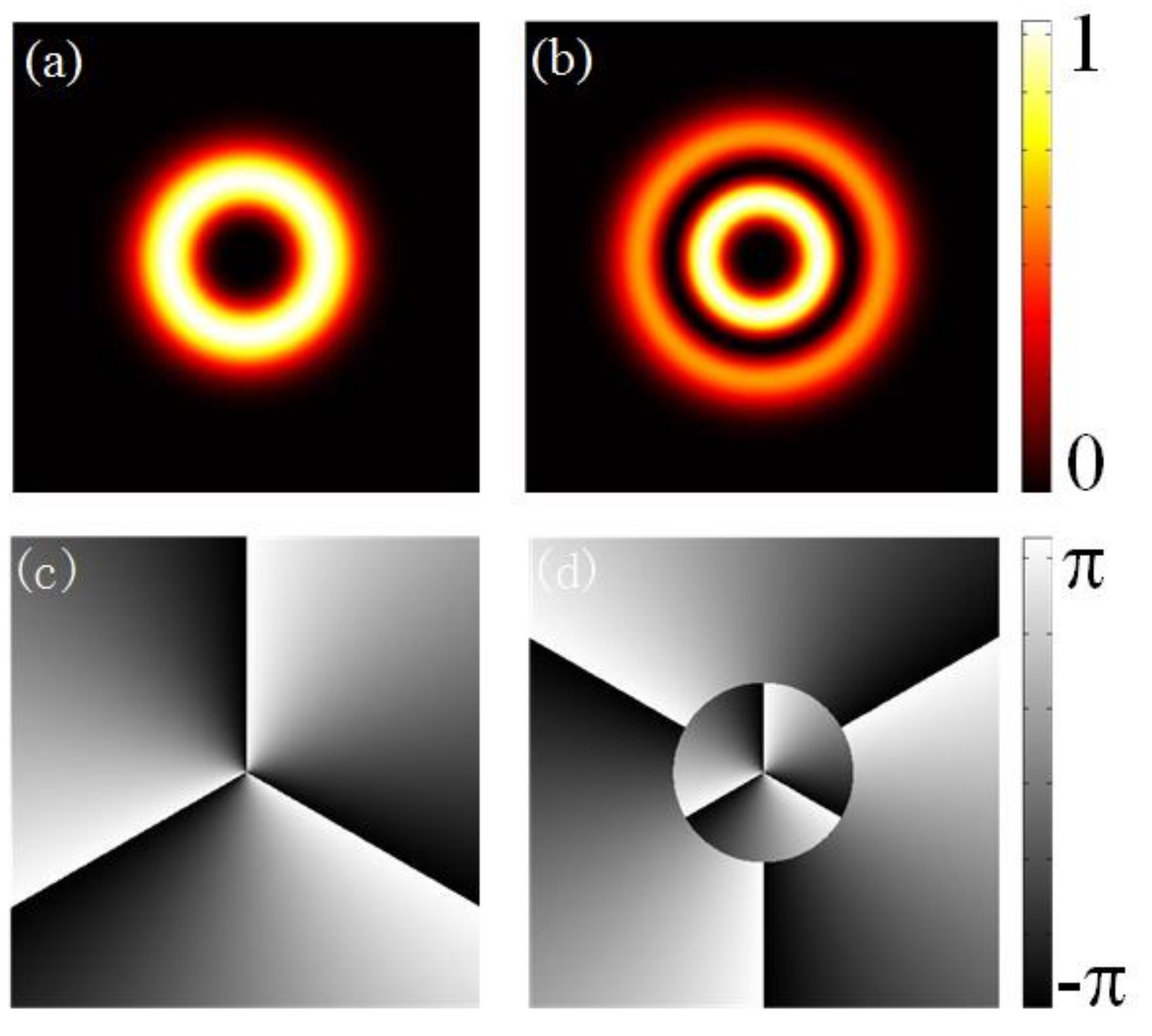
2. Laguerre–Gaussian Beams Carrying OAM
3. Classical Methods for Generating OAM Waves in RF Domain
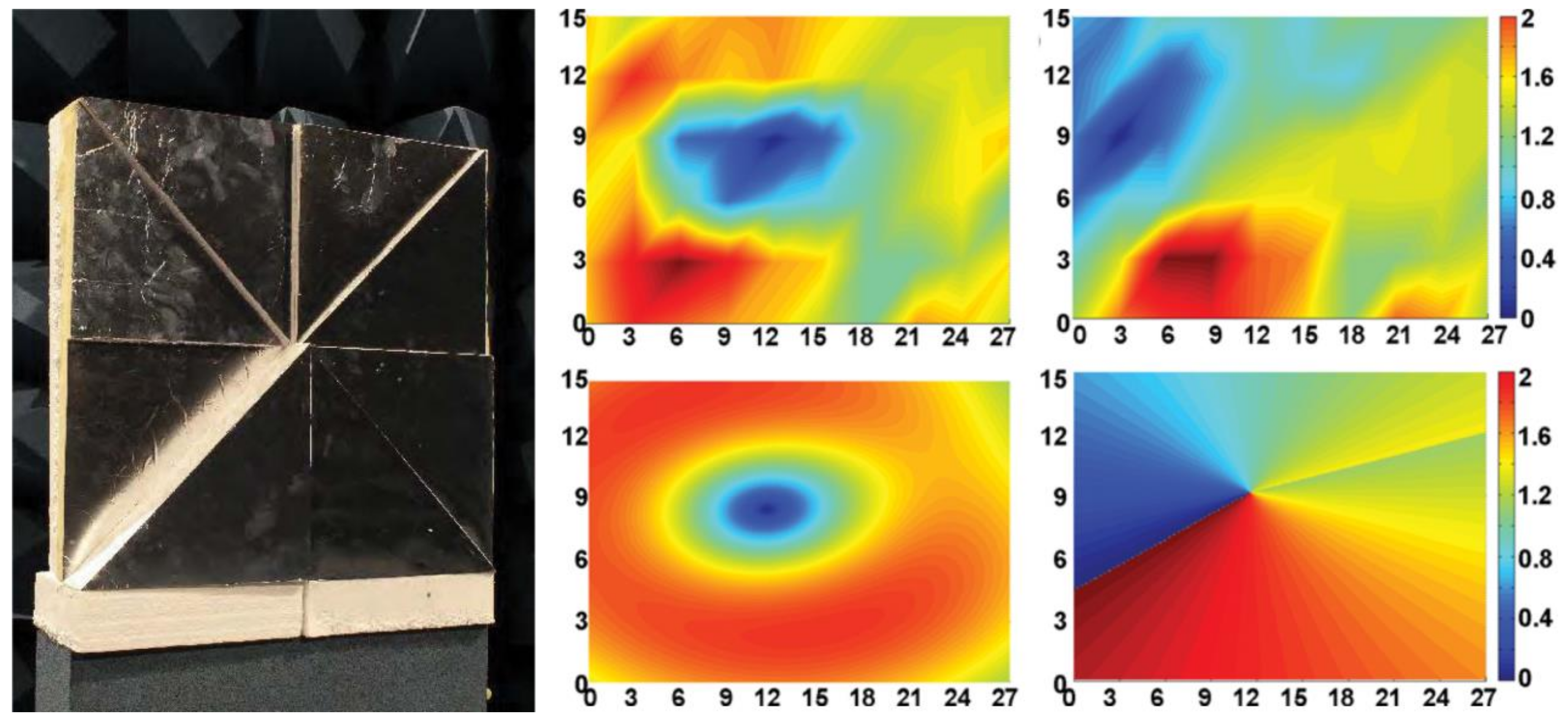
3.1. Spiral Phase Plate (SPP)
3.2. Flat Drilled Phase Plate
3.3. Diffraction Grating
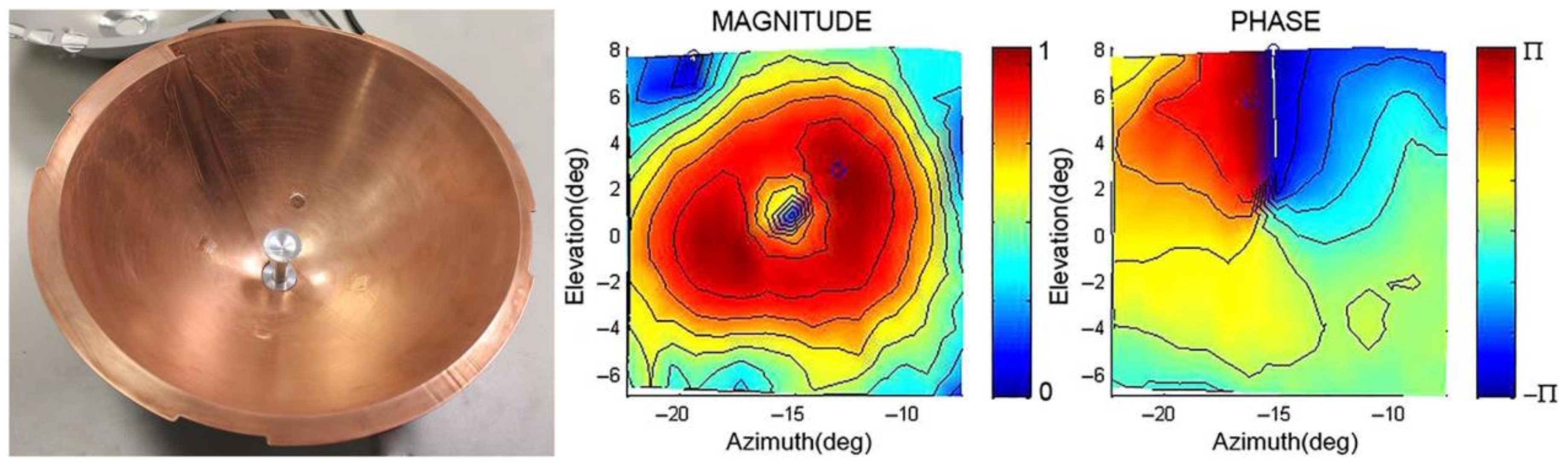
3.4. Spiral and Twisted Reflectors
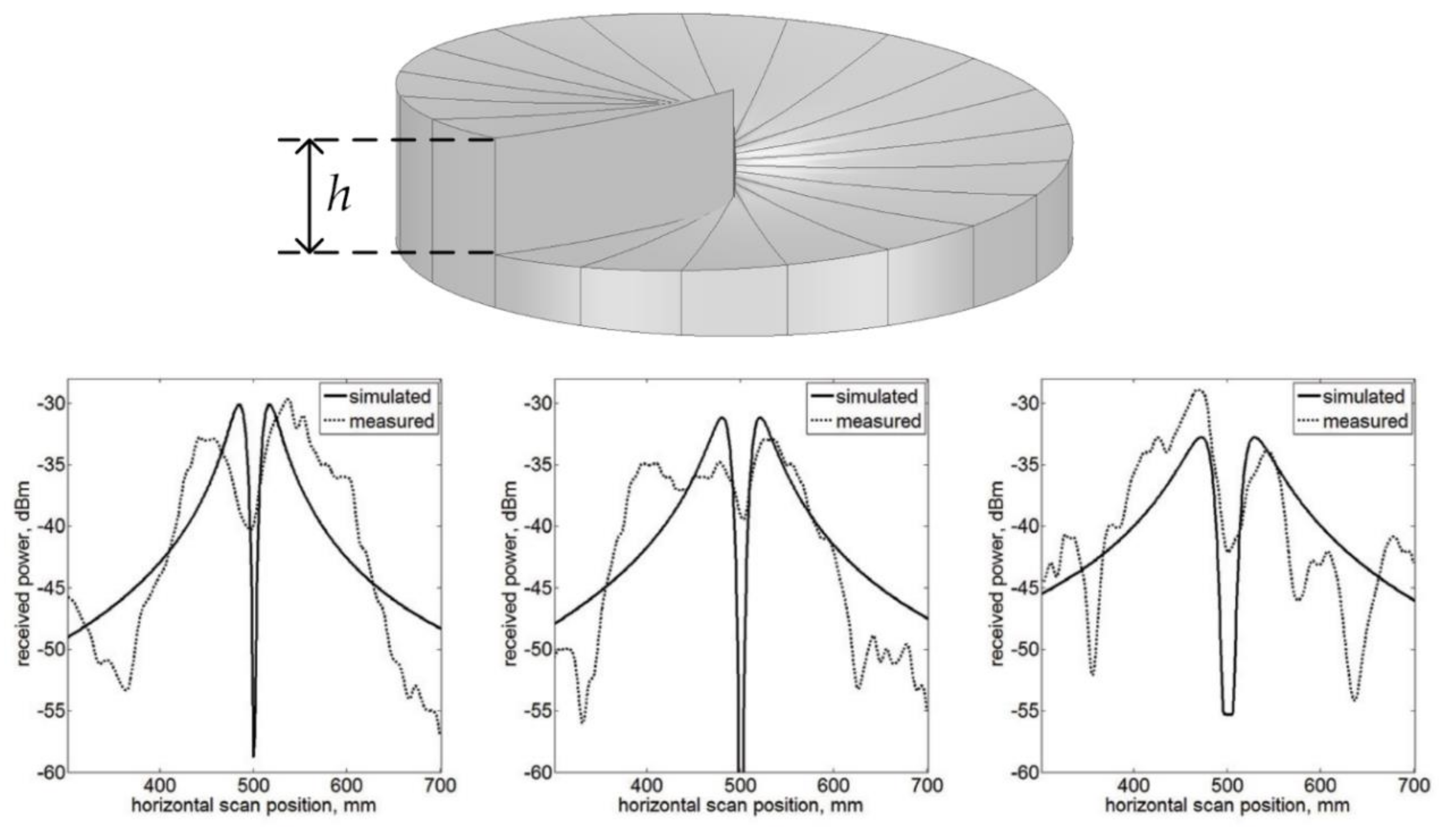
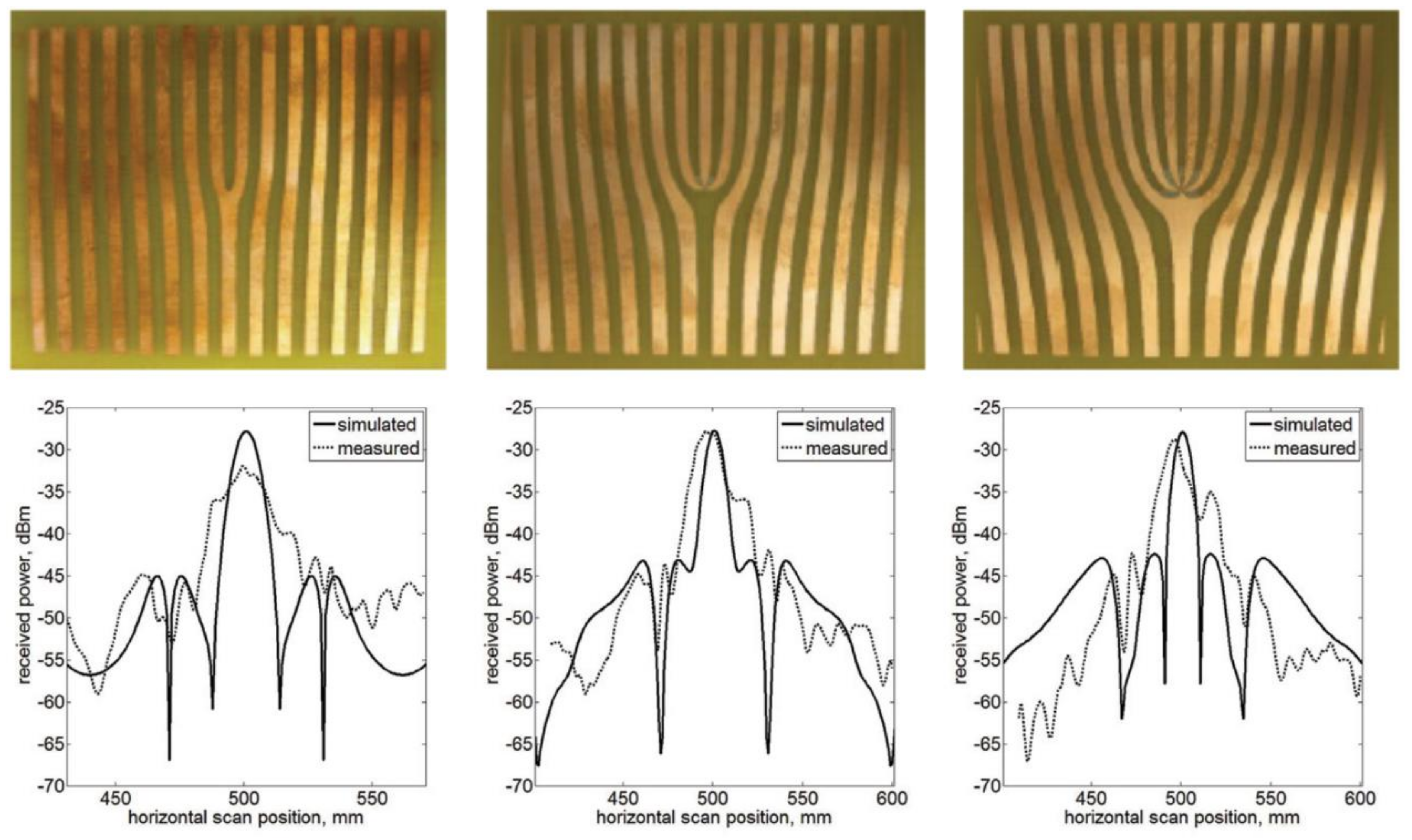
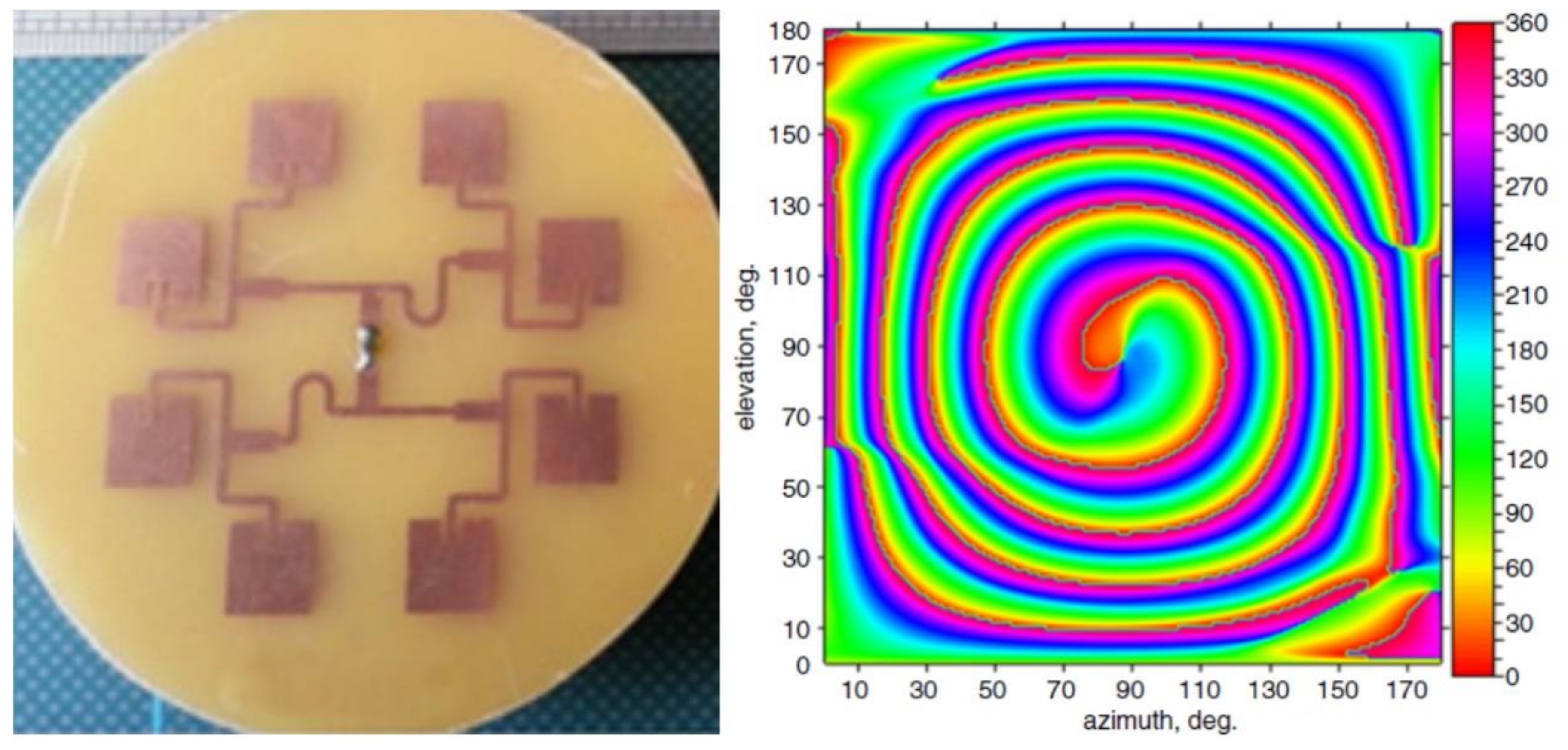
3.5. Circular Phased Arrays
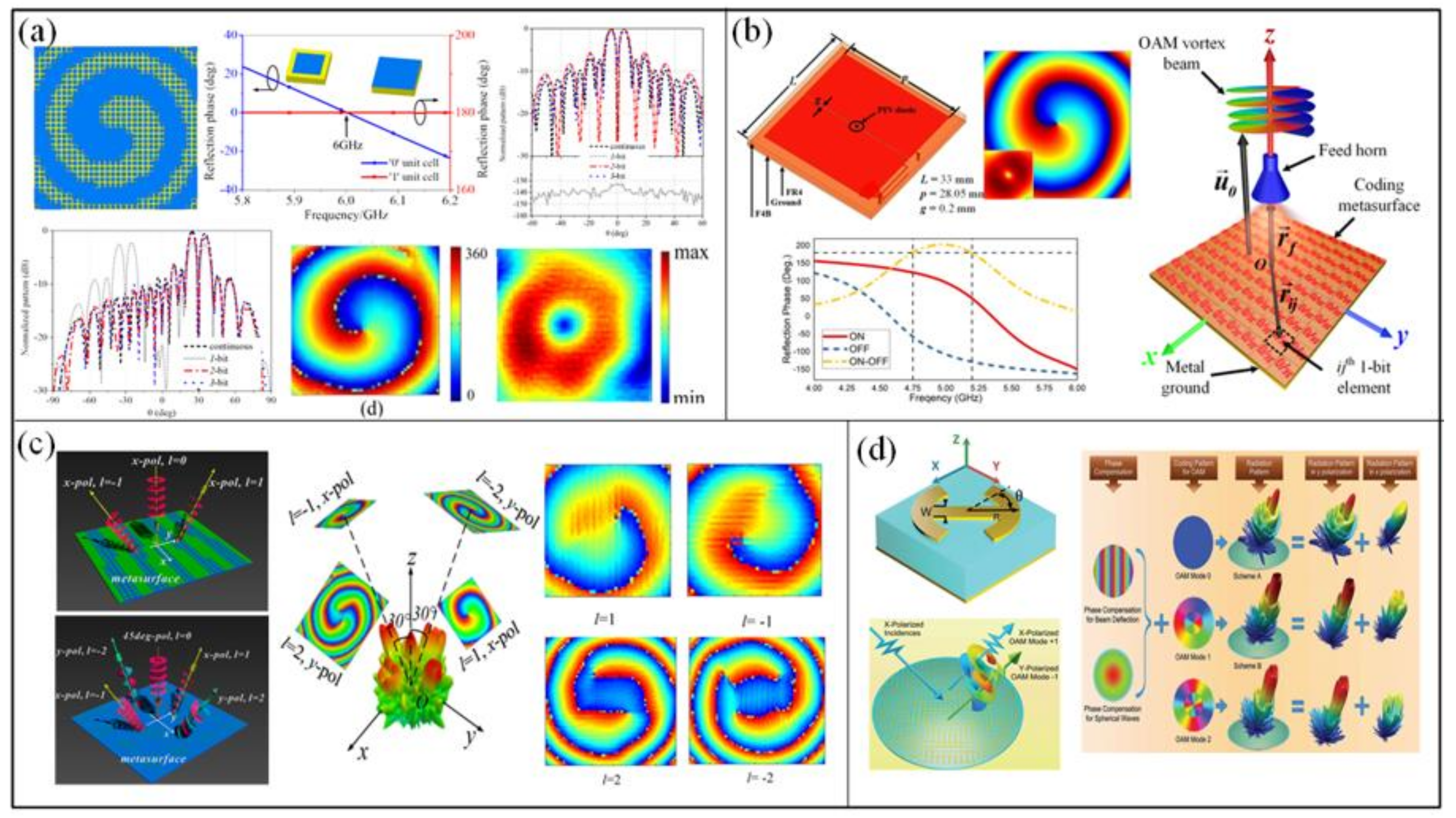
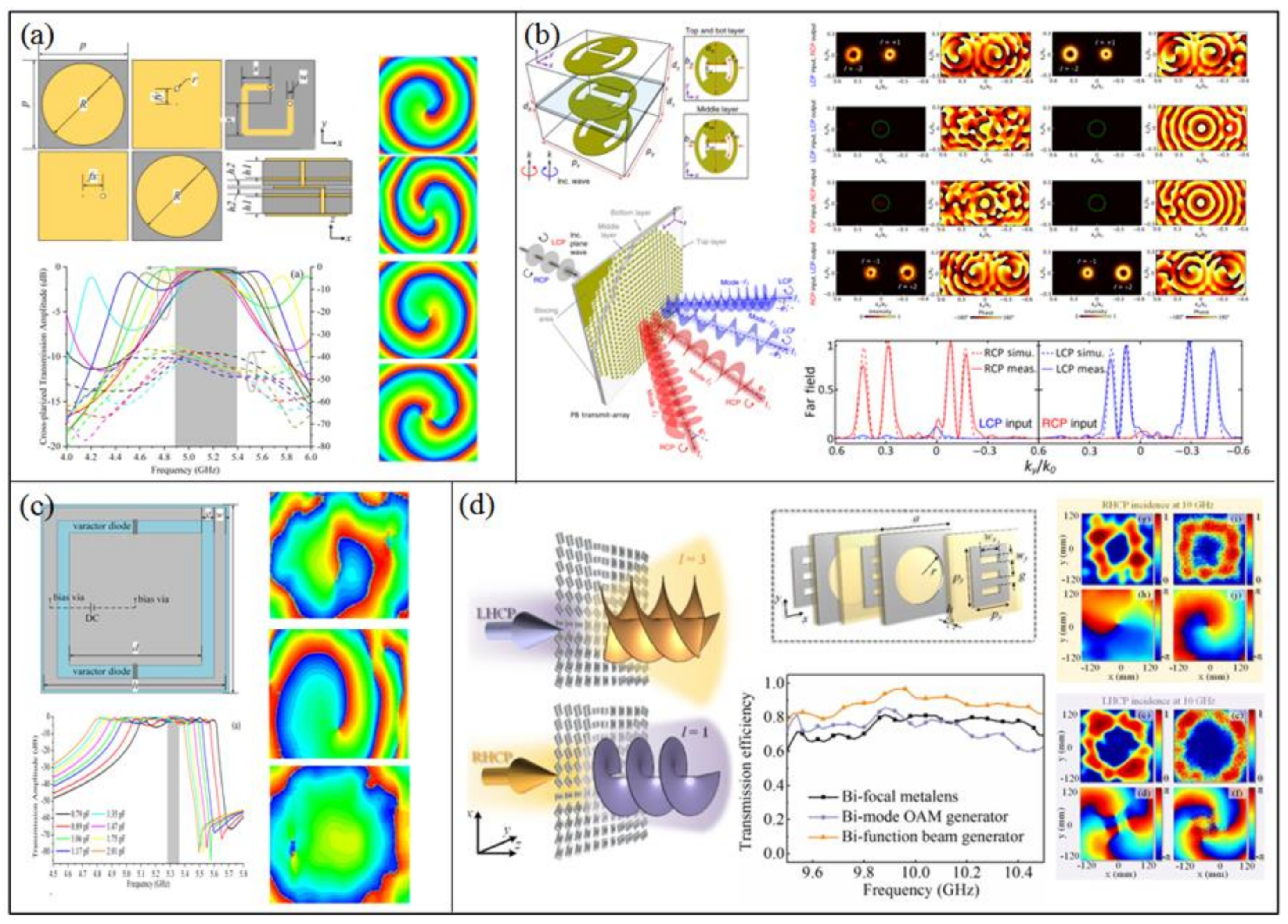
4. Metasurfaces for OAM Beam Generation
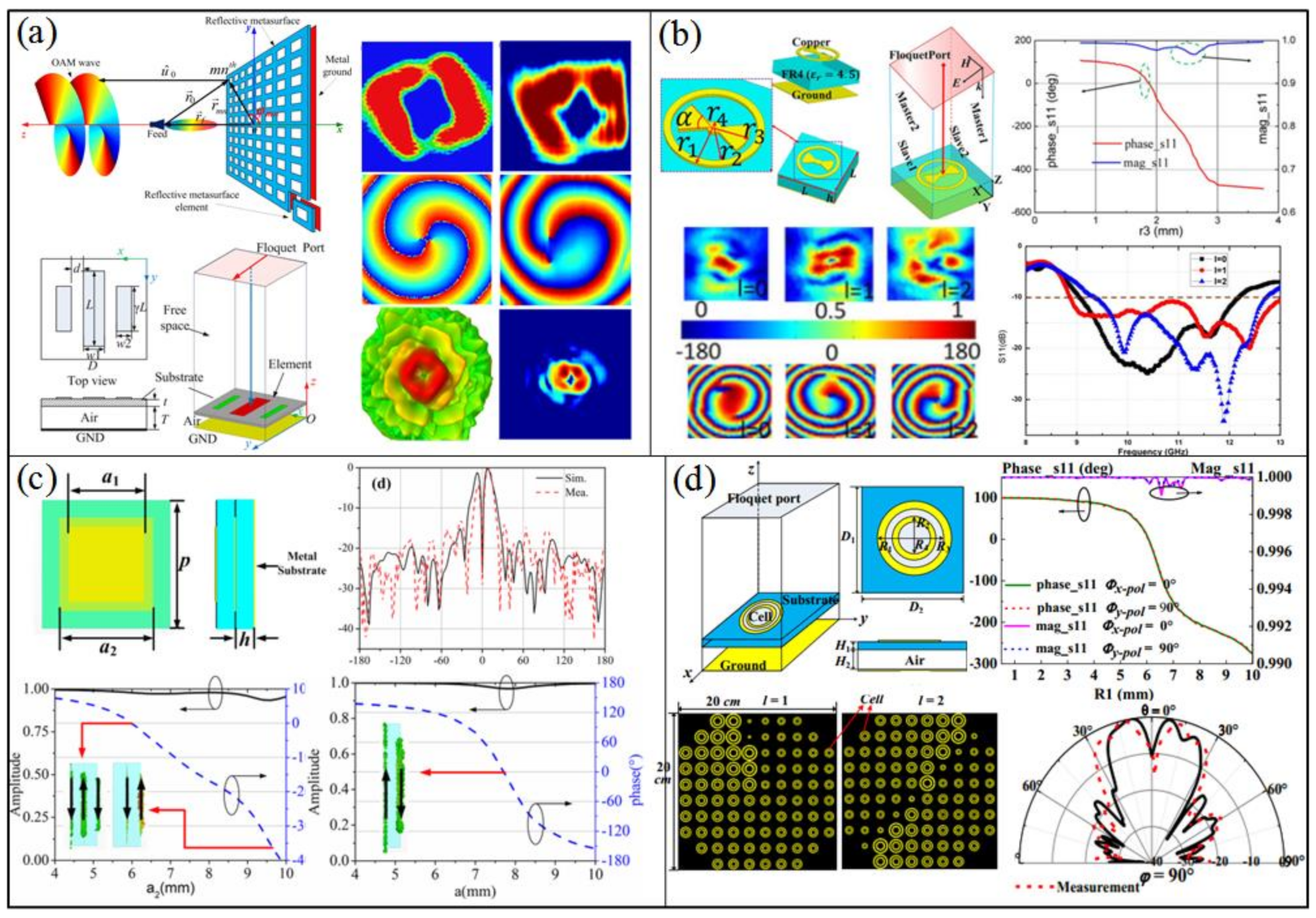
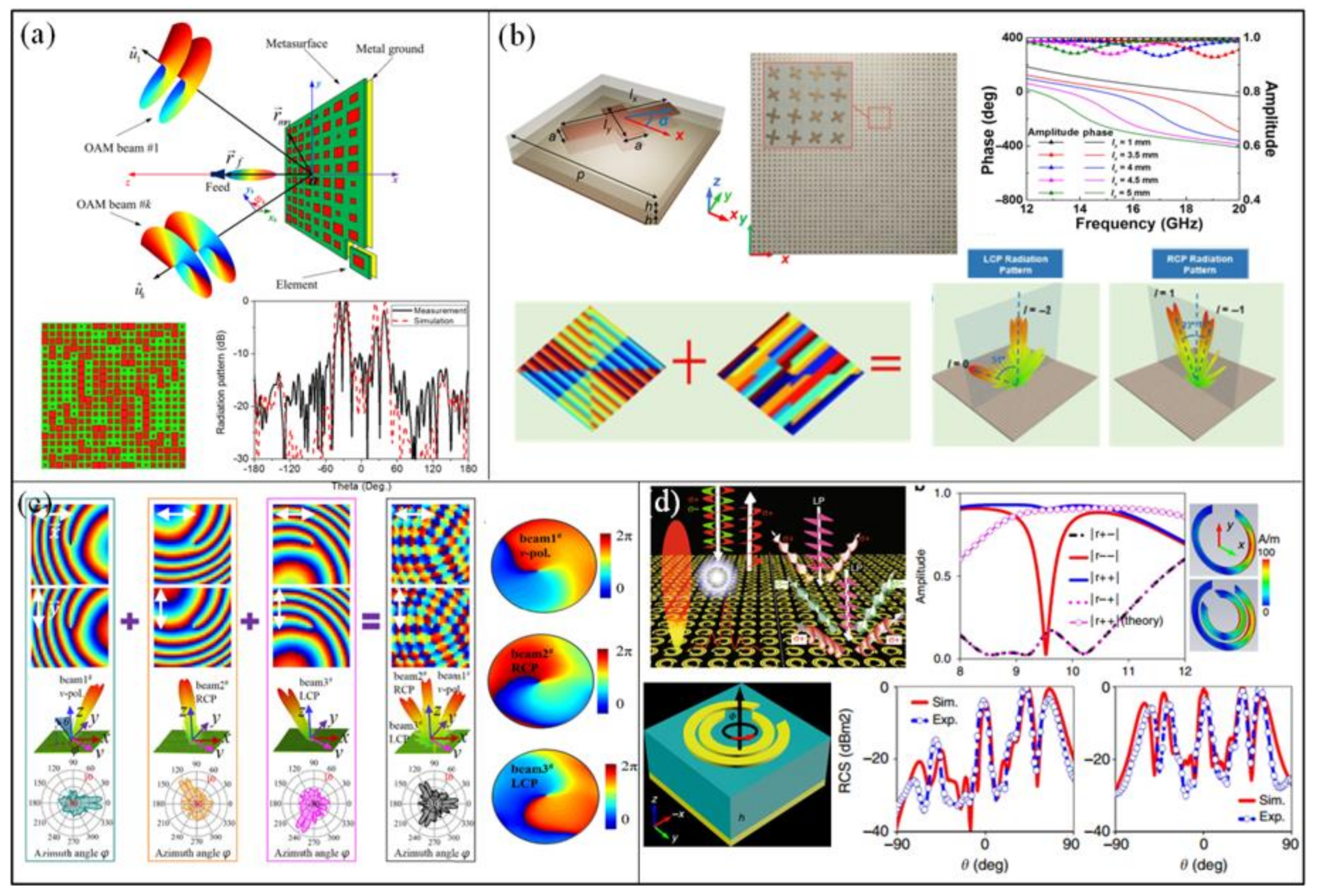
4.1. Reflective Metasurfaces
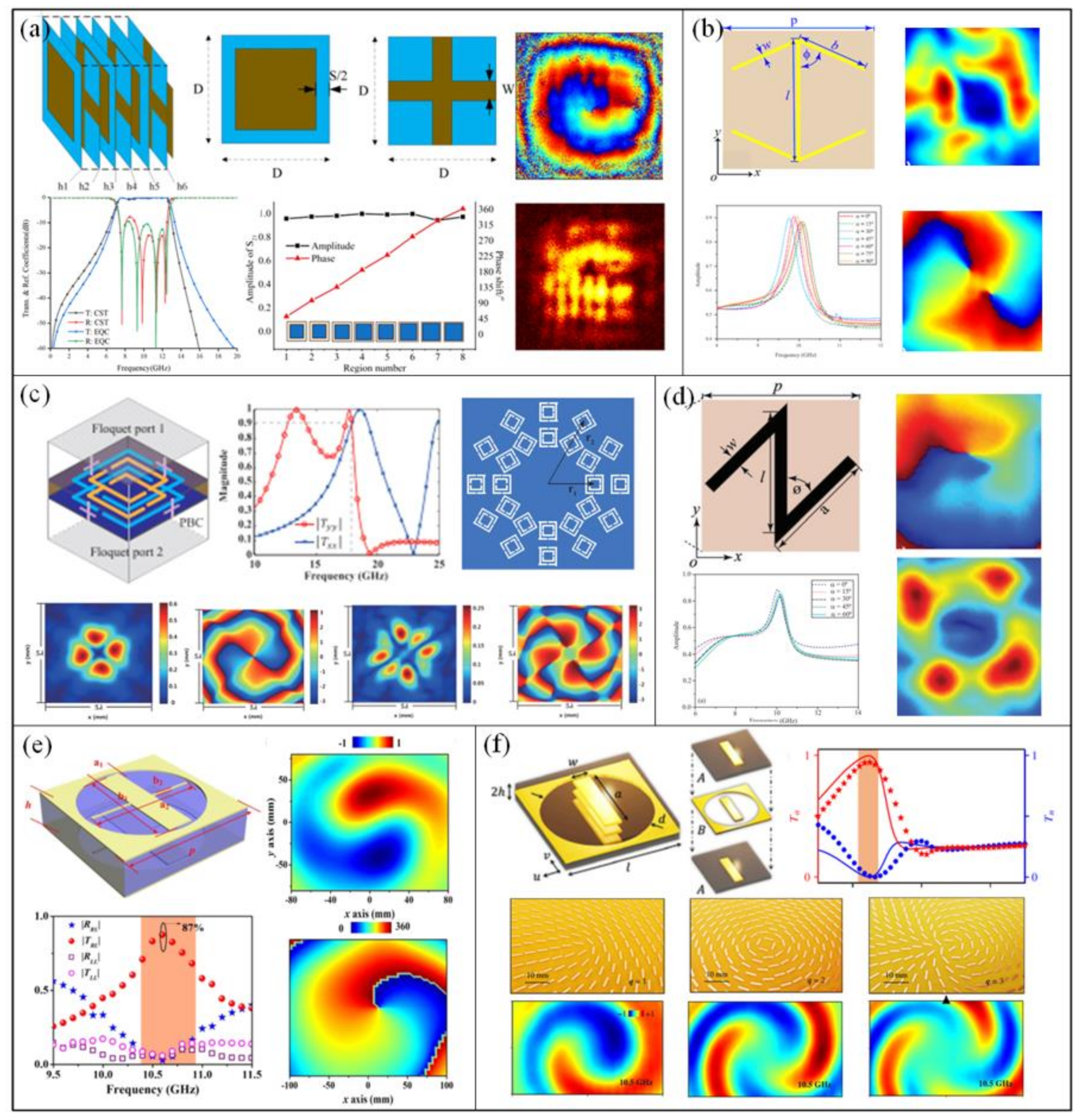
4.2. Transmissive Metasurfaces
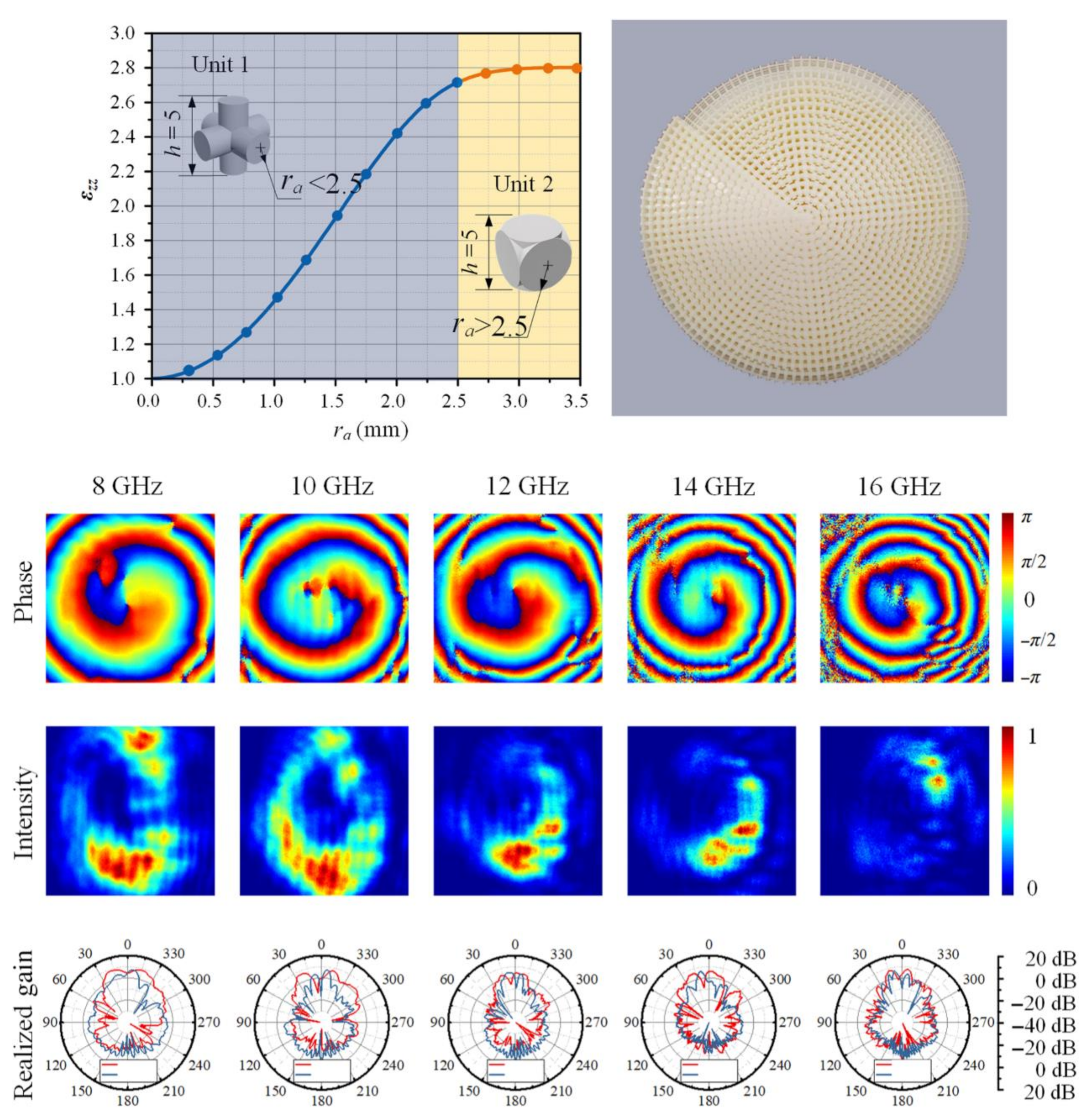
4.3. Divergence Reduction of OAM Vortex Beams
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Barnett, S.M.; Allen, L. Orbital angular momentum and nonparaxial light beams. Opt. Commun. 1994, 110, 670–678. [Google Scholar] [CrossRef]
- Curtis, J.E.; Grier, D.G. Structure of optical vortices. Phys. Rev. Lett. 2003, 90, 133901. [Google Scholar] [CrossRef] [PubMed]
- Gecevičius, M.; Drevinskas, R.; Beresna, M.; Kazansky, P.G. Single beam optical vortex tweezers with tunable orbital angular momentum. Appl. Phys. Lett. 2014, 104, 231110. [Google Scholar] [CrossRef]
- Knöner, G.; Parkin, S.; Nieminen, T.A.; Loke, V.L.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Integrated optomechanical microelements. Opt. Express 2007, 15, 5521–5530. [Google Scholar] [CrossRef] [PubMed]
- Kuga, T.; Torii, Y.; Shiokawa, N.; Hirano, T.; Shimizu, Y.; Sasada, H. Novel optical trap of atoms with a doughnut beam. Phys. Rev. Lett. 1997, 78, 4713. [Google Scholar] [CrossRef]
- Marzo, A.; Caleap, M.; Drinkwater, B.W. Acoustic virtual vortices with tunable orbital angular momentum for trapping of mie particles. Phys. Rev. Lett. 2018, 120, 044301. [Google Scholar] [CrossRef]
- Yan, L.; Gregg, P.; Karimi, E.; Rubano, A.; Marrucci, L.; Boyd, R.; Ramachandran, S. Q-plate enabled spectrally diverse orbital-angular-momentum conversion for stimulated emission depletion microscopy. Optica 2015, 2, 900–903. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef]
- Mohammadi, S.M.; Daldorff, L.K.S.; Bergman, J.E.S.; Karlsson, R.L.; Thide, B.; Forozesh, K.; Carozzi, T.D.; Isham, B. Orbital angular momentum in radio—A system study. IEEE Trans. Antennas Propag. 2010, 58, 565–572. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thide, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. N. J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.X.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Yan, Y.; Xie, G.D.; Lavery, M.P.J.; Huang, H.; Ahmed, N.; Bao, C.J.; Ren, Y.X.; Cao, Y.W.; Li, L.; Zhao, Z.; et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 4876. [Google Scholar] [CrossRef] [PubMed]
- Hui, X.N.; Zheng, S.L.; Chen, Y.L.; Hu, Y.P.; Jin, X.F.; Chi, H.; Zhang, X.M. Multiplexed millimeter wave communication with dual orbital angular momentum (OAM) mode antennas. Sci. Rep. 2015, 5, 10148. [Google Scholar] [CrossRef]
- Uribe-Patarroyo, N.; Fraine, A.; Simon, D.S.; Minaeva, O.; Sergienko, A.V. Object identification using correlated orbital angular momentum states. Phys. Rev. Lett. 2013, 110, 043601. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; Wang, H.; Qin, Y.; Li, X. Orbital-angular-momentum-based electromagnetic vortex imaging. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 711–714. [Google Scholar] [CrossRef]
- Lin, M.T.; Gao, Y.; Liu, P.G.; Liu, J.B. Improved OAM-based radar targets detection using uniform concentric circular arrays. Int. J. Antennas Propag. 2016, 2016, 1852659. [Google Scholar] [CrossRef]
- Lin, M.T.; Gao, Y.; Liu, P.G.; Liu, J.B. Super-resolution orbital angular momentum based radar targets detection. Electron. Lett. 2016, 52, 1168. [Google Scholar] [CrossRef]
- Bu, X.X.; Zhang, Z.; Chen, L.Y.; Liang, X.D.; Tang, H.B.; Wang, X.M. Implementation of vortex electromagnetic waves high-resolution synthetic aperture radar imaging. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 764–767. [Google Scholar] [CrossRef]
- Bu, X.X.; Zhang, Z.; Liang, X.D.; Chen, L.Y.; Tang, H.B.; Zeng, Z.; Wang, J. A novel scheme for MIMO-SAR systems using rotational orbital angular momentum. Sensors 2018, 18, 3511. [Google Scholar] [CrossRef]
- Cai, X.L.; Wang, J.W.; Strain, M.J.; Johnson-Morris, B.; Zhu, J.B.; Sorel, M.; O’Brien, J.L.; Thompson, M.G.; Yu, S.T. Integrated compact optical vortex beam emitters. Science 2012, 338, 363–366. [Google Scholar] [CrossRef]
- Coomber, S.; Cameron, C.; Hughes, J.; Sheerin, D.; Slinger, C.; Smith, M.A.G.; Stanley, M. Optically addressed spatial light modulators for replaying computer generated holograms. Spat. Light Modul. Technol. Appl. 2001, 4457, 9–19. [Google Scholar]
- Genevet, P.; Lin, J.; Kats, M.A.; Capasso, F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nat. Commun. 2012, 3, 1278. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.P.; Xiong, X.; Ren, X.F.; Cai, Y.J.; Rui, G.H.; Zhan, Q.W.; Guo, G.C.; Guo, G.P. Detecting orbital angular momentum through division-of-amplitude interference with a circular plasmonic lens. Sci. Rep. 2013, 3, 2402. [Google Scholar] [CrossRef] [PubMed]
- Rui, G.H.; Abeysinghe, D.C.; Nelson, R.L.; Zhan, W.Q. Demonstration of beam steering via dipole-coupled plasmonic spiral antenna. Sci. Rep. 2013, 3, 2237. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, T.; Yokota, M.; Fukumitsu, O. Propagation of light beams beyond the paraxial approximation. J. Opt. Soc. Am. A 1985, 2, 826–829. [Google Scholar] [CrossRef]
- Thide, B.; Then, H.; Sjoholm, J.; Palmer, K.; Bergman, J.; Carozzi, T.D.; Istomin, Y.N.; Ibragimov, N.H.; Khamitova, R. Utilization of photon orbital angular momentum in the low-frequency radio domain. Phys. Rev. Lett. 2007, 99, 087701. [Google Scholar] [CrossRef]
- Turnbull, G.; Robertson, D.; Smith, G.; Allen, L.; Padgett, M.J. The generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phaseplate. Opt. Commun. 1996, 127, 183–188. [Google Scholar] [CrossRef]
- Mahmouli, F.E.; Walker, S.D. 4-Gbps uncompressed video transmission over a 60-GHz orbital angular momentum wireless channel. IEEE Wirel. Commun. Lett. 2013, 2, 223–226. [Google Scholar] [CrossRef]
- Bennis, A.; Niemiec, R.; Brousseau, C.; Mahdjoubi, K.; Emile, O. Flat plate for OAM generation in the millimeter band. In Proceedings of the 2013 7th European Conference on Antennas and Propagation (Eucap), Gothenburg, Sweden, 8–12 April 2013; pp. 3203–3207. [Google Scholar]
- Niemiec, R.; Brousseau, C.; Mahdjoubi, K.; Emile, O.; Menard, A. Characterization of an OAM antenna using a flat phase plate in the millimeter frequency band. In Proceedings of the 2014 8th European Conference on Antennas and Propagation (EuCAP), The Hague, The Netherlands, 6–11 April 2014; pp. 3006–3010. [Google Scholar]
- Tamburini, F.; Mari, E.; Thide, B.; Barbieri, C.; Romanato, F. Experimental verification of photon angular momentum and vorticity with radio techniques. Appl. Phys. Lett. 2011, 99, 204102. [Google Scholar] [CrossRef]
- Mari, E.; Spinello, F.; Oldoni, M.; Ravanelli, R.A.; Romanato, F.; Parisi, G. Near-field experimental verification of separation of OAM channels. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 556–558. [Google Scholar] [CrossRef]
- Tennant, A.; Allen, B. Generation of OAM radio waves using circular time-switched array antenna. Electron. Lett. 2012, 48, 1365–1366. [Google Scholar] [CrossRef]
- Bai, Q.; Tennant, A.; Allen, B.; Rehman, M.U. Generation of orbital angular momentum (OAM) radio beams with phased patch array. In Proceedings of the 2013 Loughborough Antennas and Propagation Conference (LAPC), Loughborough, UK, 11–12 November 2013; pp. 410–413. [Google Scholar]
- Bai, Q.; Tennant, A.; Allen, B. Experimental circular phased array for generating OAM radio beams. Electron. Lett. 2014, 50, 1414. [Google Scholar] [CrossRef]
- Wei, W.L.; Mahdjoubi, K.; Brousseau, C.; Emile, O. Generation of OAM waves with circular phase shifter and array of patch antennas. Electron. Lett. 2015, 51, 442–443. [Google Scholar] [CrossRef]
- Bai, X.D.; Liang, X.L.; Jin, R.H.; Geng, J.P. Generation of OAM radio waves with three polarizations using circular horn antenna array. In Proceedings of the 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 13–17 April 2015. [Google Scholar]
- Li, L.; Zhou, X.X. Mechanically reconfigurable single-arm spiral antenna array for generation of broadband circularly polarized orbital angular momentum vortex waves. Sci. Rep. 2018, 8, 5128. [Google Scholar] [CrossRef] [PubMed]
- Gabor, D. A New Microscopic Principle; Nature Publishing Group: Berlin, Germany, 1948. [Google Scholar]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Feng, R.; Yi, J.; Burokur, S.N.; Kang, L.; Zhang, H.; Werner, D.H. Orbital angular momentum generation method based on transformation electromagnetics. Opt. Express 2018, 26, 11708–11717. [Google Scholar] [CrossRef]
- Yi, J.; Cao, X.; Feng, R.; Ratni, B.; Jiang, Z.; Zhu, D.; Zhu, L.; de Lustrac, A.; Werner, D.H.; Burokur, S.N. All-dielectric transformed material for microwave broadband orbital angular momentum vortex beam. Phys. Rev. Appl. 2019, 12, 024064. [Google Scholar] [CrossRef]
- Wei, W.L.; Mahdjoubi, K.; Brousseau, C.; Emile, O.; Sharaiha, A. Enhancement of directivity of an OAM antenna by using Fabry-Perot cavity. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016. [Google Scholar]
- Xi, R.; Liu, H.X.; Li, L. Generation and analysis of high-gain orbital angular momentum vortex wave using circular array and parasitic EBG with oblique incidence. Sci. Rep. 2017, 7, 17363. [Google Scholar] [CrossRef]
- Meng, Y.; Yi, J.; Burokur, S.N.; Kang, L.; Zhang, H.; Werner, D.H. Phase-modulation based transmitarray convergence lens for vortex wave carrying orbital angular momentum. Opt. Express 2018, 26, 22019–22029. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Li, D.; Feng, R.; Ratni, B.; Jiang, Z.; de Lustrac, A.; Werner, D.H.; Burokur, S.N. Design and validation of a metasurface lens for converging vortex beams. Appl. Phys. Express 2019, 12, 084501. [Google Scholar] [CrossRef]
- Li, T.; Feng, R.; Yi, J.; Burokur, S.N.; Mao, C.; Zhang, H.; Werner, D.H. All-dielectric transformation medium mimicking a broadband converging lens. Opt. Express 2018, 26, 20331–20341. [Google Scholar] [CrossRef]
- Yi, J.; Guo, M.; Feng, R.; Ratni, B.; Zhu, L.; Werner, D.H.; Burokur, S.N. Design and validation of an all-dielectric metamaterial medium for collimating orbital-angular-momentum vortex waves at microwave frequencies. Phys. Rev. Appl. 2019, 12, 034060. [Google Scholar] [CrossRef]
- Yu, S.X.; Li, L.; Shi, G.M.; Zhu, C.; Zhou, X.X.; Shi, Y. Design, fabrication, and measurement of reflective metasurface for orbital angular momentum vortex wave in radio frequency domain. Appl. Phys. Lett. 2016, 108, 121903. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Lyu, Y.; Wang, H.G.; Zhang, X.M.; Jin, X.F. Transforming surface wave to propagating OAM vortex wave via flat dispersive metasurface in radio frequency. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 172–175. [Google Scholar] [CrossRef]
- Ran, Y.Z.; Liang, J.G.; Cai, T.; Ji, W.Y.; Wang, G.M. High-performance broadband vortex beam generator based on double-layered reflective metasurface. AIP Adv. 2018, 8, 095201. [Google Scholar] [CrossRef]
- Huang, H.F.; Li, S.N. High-efficiency planar reflectarray with small-size for OAM generation at microwave range. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 432–436. [Google Scholar] [CrossRef]
- Ran, Y.; Liang, J.; Cai, T.; Li, H. High-performance broadband vortex beam generator using reflective Pancharatnam–Berry metasurface. Opt. Commun. 2018, 427, 101–106. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.F.; Han, Y.J.; Fan, Y.; Sui, S.; Chen, H.Y.; Wang, J.F.; Cheng, Q.; Cui, T.J.; Qu, S.B. Vortex beam generated by circular-polarized metasurface reflector antenna. J. Phys. D Appl. Phys. 2019, 52, 255306. [Google Scholar] [CrossRef]
- Xu, H.-X.; Liu, H.; Ling, X.; Sun, Y.; Yuan, F. Broadband vortex beam generation using multimode Pancharatnam–Berry metasurface. IEEE Trans. Antennas Propag. 2017, 65, 7378–7382. [Google Scholar] [CrossRef]
- Zhang, F.H.; Song, Q.; Yang, G.M.; Jin, Y.Q. Generation of wideband vortex beam with different OAM modes using third-order meta-frequency selective surface. Opt. Express 2019, 27, 34864–34875. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, K.; Yuan, Y.; Ding, X.; Ratni, B.; Burokur, S.N.; Wu, Q. Planar vortex beam generator for circularly polarized incidence based on FSS. IEEE Trans. Antennas Propag. 2019. [Google Scholar] [CrossRef]
- Chen, M.L.N.; Jiang, L.J.; Sha, W.E.I. Artificial perfect electric conductor-perfect magnetic conductor anisotropic metasurface for generating orbital angular momentum of microwave with nearly perfect conversion efficiency. J. Appl. Phys. 2016, 119, 064506. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, X.Y.; Yang, H.H.; Gao, J. Radiation performance synthesis for OAM vortex wave generated by reflective metasurface. IEEE Access 2018, 6, 28691–28701. [Google Scholar] [CrossRef]
- Han, J.Q.; Li, L.; Yi, H.; Shi, Y. 1-bit digital orbital angular momentum vortex beam generator based on a coding reflective metasurface. Opt. Mater. Express 2018, 8, 3470–3478. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, X.Y.; Yang, H.H.; Gao, J.; Zhu, X.W. Multiple OAM vortex beams generation using 1-bit metasurface. Opt. Express 2018, 26, 24804–24815. [Google Scholar] [CrossRef]
- Ma, Q.; Shi, C.B.; Bai, G.D.; Chen, T.Y.; Noor, A.; Cui, T.J. Beam-editing coding metasurfaces based on polarization bit and orbital-angular-momentum-mode bit. Adv. Opt. Mater. 2017, 5, 1700548. [Google Scholar] [CrossRef]
- Yu, S.X.; Li, L.; Shi, G.M.; Zhu, C.; Shi, Y. Generating multiple orbital angular momentum vortex beams using a metasurface in radio frequency domain. Appl. Phys. Lett. 2016, 108, 241901. [Google Scholar] [CrossRef]
- Ding, G.W.; Chen, K.; Luo, X.Y.; Zhao, J.M.; Jiang, T.; Feng, Y.J. Dual-helicity decoupled coding metasurface for independent spin-to-orbital angular momentum conversion. Phys. Rev. Appl. 2019, 11, 044043. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, C.; Ma, H.F.; Yuan, W.; Yang, L.X.; Ke, J.C.; Chen, M.Z.; Mahmoud, A.; Cheng, Q.; Cui, T.J. Tailoring polarization states of multiple beams that carry different topological charges of orbital angular momentums. Opt. Express 2018, 26, 31664–31674. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.X.; Hu, G.W.; Li, Y.; Han, L.; Zhao, J.L.; Sun, Y.M.; Yuan, F.; Wang, G.M.; Jiang, Z.H.; Ling, X.H.; et al. Interference-assisted kaleidoscopic meta-plexer for arbitrary spin-wavefront manipulation. Light Sci. Appl. 2019, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Monticone, F.; Zhang, K.; Zhang, L.; Gao, D.; Burokur, S.N.; de Lustrac, A.; Wu, Q.; Qiu, C.W.; Alù, A. Ultrathin Pancharatnam-Berry metasurface with maximal cross-polarization efficiency. Adv. Mater. 2015, 27, 1195–1200. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.J.; Sun, S.L.; Xu, H.X.; He, Q.; Zhou, L. Transmissive ultrathin Pancharatnam-Berry metasurfaces with nearly 100% efficiency. Phys. Rev. Appl. 2017, 7, 044033. [Google Scholar] [CrossRef]
- Liu, Y.H.; Liu, C.C.; Song, K.; Li, M.Z.; Zhao, X.P. A broadband high-transmission gradient phase discontinuity metasurface. J. Phys. D Appl. Phys. 2018, 51, 095103. [Google Scholar] [CrossRef]
- Wang, Y.X.; Zhang, K.; Yuan, Y.Y.; Ding, X.M.; Yang, G.H.; Fu, J.H.; Wu, Q. Generation of high-efficiency vortex beam carrying OAM mode based on miniaturized element frequency selective surfaces. IEEE Trans. Magn. 2019, 55, 7501104. [Google Scholar] [CrossRef]
- Akram, M.R.; Bai, X.D.; Jin, R.H.; Vandenbosch, G.A.E.; Premaratne, M.; Zhu, W.R. Photon spin Hall effect-based ultra-thin transmissive metasurface for efficient generation of OAM waves. IEEE Trans. Antennas Propag. 2019, 67, 4650–4658. [Google Scholar] [CrossRef]
- Chen, M.L.N.; Jiang, L.J.; Sha, W.E.I. Ultrathin complementary metasurface for orbital angular momentum generation at microwave frequencies. IEEE Trans. Antennas Propag. 2017, 65, 396–400. [Google Scholar] [CrossRef]
- Akram, M.R.; Mehmood, M.Q.; Bai, X.D.; Jin, R.H.; Premaratne, M.; Zhu, W.R. High efficiency ultrathin transmissive metasurfaces. Adv. Opt. Mater. 2019, 7, 1801628. [Google Scholar] [CrossRef]
- Tang, S.; Cai, T.; Liang, J.-G.; Xiao, Y.; Zhang, C.-W.; Zhang, Q.; Hu, Z.; Jiang, T. High-efficiency transparent vortex beam generator based on ultrathin Pancharatnam–Berry metasurfaces. Opt. Express 2019, 27, 1816–1824. [Google Scholar] [CrossRef]
- Shi, H.Y.; Wang, L.Y.; Zhao, M.R.; Chen, J.; Zhang, A.X.; Xu, Z. Transparent metasurface for generating microwave vortex beams with cross-polarization conversion. Materials 2018, 11, 2448. [Google Scholar] [CrossRef]
- Shi, H.Y.; Wang, L.Y.; Peng, G.T.; Chen, X.M.; Li, J.X.; Zhu, S.T.; Zhang, A.X.; Xu, Z. Generation of multiple modes microwave vortex beams using active metasurface. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 59–63. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Kang, L.; Hong, W.; Werner, D.H. Highly efficient broadband multiplexed millimeter-wave vortices from metasurface-enabled transmit-arrays of subwavelength thickness. Phys. Rev. Appl. 2018, 9, 064009. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, Y.; Ding, X.; Ratni, B.; Burokur, S.N.; Wu, Q. High-efficiency metalenses with switchable functionalities in microwave region. ACS Appl. Mater. Interfaces 2019, 11, 28423–28430. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.Z.; Yang, J.W.; Meng, H.F.; Dou, W.B.; Hu, S.M. Generating millimeter-wave Bessel beam with orbital angular momentum using reflective-type metasurface inherently integrated with source. Appl. Phys. Lett. 2018, 112, 141901. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, Y.; Zhang, D.; Ding, X.; Ratni, B.; Burokur, S.N.; Lu, M.; Tang, K.; Wu, Q. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 2018, 26, 1351–1360. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Wang, Y.; Yuan, Y.; Burokur, S.N. A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces. Appl. Sci. 2020, 10, 1015. https://doi.org/10.3390/app10031015
Zhang K, Wang Y, Yuan Y, Burokur SN. A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces. Applied Sciences. 2020; 10(3):1015. https://doi.org/10.3390/app10031015
Chicago/Turabian StyleZhang, Kuang, Yuxiang Wang, Yueyi Yuan, and Shah Nawaz Burokur. 2020. "A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces" Applied Sciences 10, no. 3: 1015. https://doi.org/10.3390/app10031015
APA StyleZhang, K., Wang, Y., Yuan, Y., & Burokur, S. N. (2020). A Review of Orbital Angular Momentum Vortex Beams Generation: From Traditional Methods to Metasurfaces. Applied Sciences, 10(3), 1015. https://doi.org/10.3390/app10031015





