Abstract
This paper deals with the numerical analysis of the particle inertia and volume fraction effects on colliding particle-pair velocity correlation immersed in an unsteady isotropic homogeneous turbulent flow. Such correlation function is required to build reliable statistical models for inter-particle collisions, in the frame of the Euler–Lagrange approach, to be used in a broad range of two-phase flow applications. Computations of the turbulent flow have been carried out by means of Direct Numerical Simulation (DNS) by the Lattice Boltzmann Method (LBM). Moreover, the dependence of statistical properties of collisions on particle inertia and volumetric fraction is evaluated and quantified. It has been found that collision locations of particles of intermediate inertia, , occurs in regions where the fluid strain rate and dissipation are higher than the corresponding averaged values at particle positions. Connected with this fact, the average kinetic energy of colliding particles of intermediate inertia (i.e., Stokes number around 1) is lower than the value averaged over all particles. From the study of the particle-pair velocity correlation, it has been demonstrated that the colliding particle-pair velocity correlation function cannot be approximated by the Eulerian particle-pair correlation, obtained by theoretical approaches, as particle separation tends to zero, a fact related with the larger values of the relative radial velocity between colliding particles.
1. Introduction
Inter-particle collision of small particles immersed in a turbulent flow is a common micro-process found in both industrial and natural environments. Examples of physical phenomena where the effects of inter-particle interactions are revealed as relevant are: models of planet formation from dust particle collisions and coalescence in turbulent protoplanetary nebulae [1,2], rain drops’ formation in warm clouds [3,4], chemical reaction rates enhancement due to active suspended particles in fluidised beds [5,6,7], particle transport and reduction of wall erosion in pneumatic conveying [8,9,10,11] and turbomachinery [12], or sand storm evolution and dune transport in deserts [13,14].
Fundamental ingredients of inter-particle collisions are the role of particles’ inertia and their interaction with the carrier turbulent flow structures, which lead to a non-linear increase of collision rates [15,16,17,18]. As a result of the efforts to understand and quantify the enhancement of collision rates induced by inertia, two main mechanisms have been identified: on the one hand, preferential concentration, i.e., particle clustering, increases the probability for two particles to be at a colliding distance, and, on the other hand, detachment from fluid trajectories may enhance the relative velocity between two approaching particles. Two limiting cases can be devised: in the case of vanishingly small inertia, particles behave almost as tracers so that their relative velocity is given by the fluid velocity shear; therefore, the deviation of a uniform concentration distribution is responsible for an enhancement of collisions. In the other limit, of very large inertia, particle motion is essentially ballistic, and they distribute uniformly but they may reach the same position with very different velocities.
Moreover, following Février et al. [19], interactions between the dispersed and continuous phases not only structure the particle number density, but also lead to correlation of the velocities of neighbouring particles, which is an alternative point of view of the description of enhancement of collision rates by inertia. For small-inertia particles, neighbouring velocities will be spatially correlated through the interactions with the same local fluid flow as basically both particles experience similar fluid velocities during long enough times. In contrast, for large-inertia particles with response times that are long compared to the fluid turbulence macroscales, neighbouring particle velocities are uncorrelated since these particles maintain a stronger connection (memory) to their interactions, with very distant, and independent, turbulent eddies. In the large inertia limit, statistics of the particle velocity distribution will satisfy the assumption of molecular chaos and can be described using kinetic theory (e.g., see Reference [20]). An important consequence is that in the large-inertia limit, the particle velocity distribution cannot be assumed to correspond to a spatially continuous velocity field. The random nature of the particle motion will lead to a crossing of individual trajectories, inducing a collision in physical systems.
The above small- and large-inertia limit cases illustrate that substantially different spatial features in the particle velocity are possible with these differences depending on particle inertia. In the tracer limit, the spatial correlation function between any two particle velocities should be accurately modelled by a decaying exponential, analogous to the correlation describing the fluid turbulence. On the other hand, in the limit of very inertial particles, motion becomes stochastically equivalent to a Brownian motion with independent random velocities, even for those particles passing close to each other, also called random uncorrelated motion [19]. For intermediate values of the particle response time, the particle velocity distribution should be expected to exhibit spatial features with characteristics representative of these two limiting regimes.
Particles of intermediate inertia (of similar relaxation time scales to those relevant flow time scales) experience two phenomena which lead to an enhancement of the collision rates. The first is the so-called preferential concentration effect, whereby particles of non-negligible inertia tend to concentrate at specific locations on the flow field characterised by lower than mean values of fluid vorticity and higher than mean values of strain rate. The second is known as the sling effect, by which particles experience interactions with strong intermittent turbulent events, causing modification of their movement [3]. The consequence is that particle trajectories cross thereafter in certain regions of the flow, called pockets by Bewley et al. [21], where the chance of collisions is remarkably augmented. Quite a number of studies (see Reference [22] and references therein) have been focused on these topics to determine an adequate collision frequency formulation in case of intermediate inertia particles. Williams and Crane [23] and later Kruis and Kusters [24] developed a generalised model for inter-particle collision frequency taking into account particle inertia which is formulated in dependence of the relative velocity of particle pairs. Moreover, several early numerical and theoretical studies looked at the effects of particle diameter, relaxation time and number density on collision frequency [15,18]. Particularly studied have been the particle–turbulent fluid interaction phenomena that lead to the formation of clusters in zones of low vorticity and high strain rate [25], favouring the occurrence of inter-particle collisions. Such effect, described by the radial distribution function, and the relative velocity between particle pairs at contact point are the usual two elements employed for writing the collision kernel, defined usually as the collision frequency over the particle number density.
The various mechanisms for enhancing inter-particle collision frequency at the intermediate inertia range were syncretised in a common framework by Bec et al. [26]. Starting from the phase space of particles (composed by their position and velocities), the particle clustering process can be thought of as the confluence of trajectories towards an attractor in the phase space which experiences a dynamical evolution. The features of the resulting fractal set as well as its statistical characteristics depend on the nature of particle–fluid turbulence interaction and the particle Stokes number, (defined here as the quotient between the average particle response time and the Kolmogorov time scale of the flow). In this picture, the increase of relative velocity among neighbouring particles arises from the attractor folding in the velocity subspace, where the folded region boundaries are denominated caustics [27]. As a consequence, the particle velocity field becomes multivalued in the coordinate space, a fact that has two implications for collisions: on the one hand, particles with very different velocities are able to cross their trajectories and, on the other hand, particle number density can grow without bound at the limits of caustics. This phenomenon, distinct from that of preferential concentration, may be responsible for the observed fast increase on collision frequency happening at ~0.5. In fact, it has been shown [28] that the caustics mechanism for inter-particle collisions prevails when > 0.75.
On the other hand, when practical two-phase flow computations for industrial or environmental applications are pursued, a direct detection of inter-particle collisions along the two-phase flow domain is no longer affordable. Statistical-like inter-particle collision models based on a Lagrangian frame offer an attractive alternative in such case. In this context, the two-particle probability density function (pdf) has proven suitable for predicting two-particle statistics and particle-pair dispersion in homogeneous isotropic turbulence [18]. Besides fundamental theoretical meaning, the two-particle pdf also has sound implications in developing models for predicting two-phase practical flows. For instance, modelling of inter-particle collisions in the frame of the Euler–Lagrange method for the numerical calculation of two-phase flows has so far been based mainly on two approaches: a direct simulation (deterministic model) and a stochastic model based on concepts of the kinetic theory of gases.
The most straightforward approach to account for inter-particle collisions is the direct detection approach, as it is usually performed in Direct Numerical Simulation (DNS), including the present study. This requires that all the particles have to be tracked simultaneously through the flow field. Thereby, the occurrence of collisions between any pair of particles can be judged based on their positions and relative motion during one time-step. This process is however very time consuming and its computational cost is, at least, proportional to (total number of tracked particles) at each Lagrangian time step. For instance, a recent study by van Wachem et al. [29] mentions that the computational time needed for the direct detection approach is two orders of magnitude higher than that for a stochastic approach. Once a collision occurs, the change in translational and angular particle velocities is determined by solving the equations for the conservation of linear and angular momentum in connection with Coulomb’s law of friction. When the duration of the collision process is negligibly small compared to the time of collisionless motion (i.e., hard sphere collision), the size of the colliding particles is not too different, and the ratio of solid particle density to the fluid density is much larger than unity, fluid dynamic effects during the collision process can be neglected and the collision efficiency may be assumed as 100% [30].
Stochastic inter-particle collision models [29,31,32], on the other hand, rely on the generation of fictitious collision partners and the calculation of the collision probability according to kinetic theory. The advantage of such models is that they do not require information on the location of the surrounding particles and hence they are also applicable if a sequential tracking of the particles is adopted, as it is usually done when applying the Euler–Lagrange approach to stationary flows. However, unsteady flows employing simultaneous tracking may also be conducted using the stochastic collision model [33]. During each time step of the trajectory calculation of the considered particle, a fictitious second particle is generated. The properties of this fictitious particle are randomly sampled from local distribution functions. The generation of the fictitious particle fluctuating velocities requires taking into account the correlation with the velocity of the considered particle due to turbulence. The degree to which the particle fluctuating velocities are correlated depends on their response to the turbulent fluctuations. Sommerfeld [31] compared his model computations with the Large Eddy Simulations (LES) published in Reference [34] and proposed an exponentially decreasing correlation, function of particle Stokes number, based on a trial-and-error basis. Such correlation has been employed successfully for predicting the effect of inter-particle collisions in pneumatic conveying and particle separation processes [9,10,11,35]. Lain et al. [36] developed a more rigorous way to determine the Eulerian particle-pair velocity correlation function between colliding particles in homogeneous isotropic turbulence, employing the model proposed in Zaichik and Alipchenkov [37] (or its refined version, Zaichik et al. [18]), showing good agreement with previous data [19]. Precisely, the adequacy of such correlation is evaluated and discussed in the present contribution in light of the new DNS results obtained in this work.
This paper deals with the numerical analysis of the collision statistics of point particles immersed in an unsteady isotropic homogeneous turbulent flow depending on particle inertia and volume fraction. The main goal is to determine the two-particle velocity correlation function of colliding particles, information that is appropriated to be used in inter-particle collision stochastic models for use in general-purpose two-phase flow Euler–Lagrange codes. Moreover, the effect of particle volume fraction on collisions’ statistics is illustrated, especially on the relative motion of colliding particles. The present article is organised as follows: Section 2 presents a context and a brief summary of the performed Direct Numerical Simulations based on the lattice Boltzmann method combined with the point-particle Lagrangian tracking. The main collision statistics as functions of particle inertia and void fraction are presented and discussed in Section 3. Section 4 is devoted to the study of the two-particle velocity correlation function of colliding particles, which is connected with the relative velocity statistics. The obtained dependence of it with volume fraction as a parameter is used to build a model for velocity correlation of colliding particles appropriate for inter-particle collision stochastic models. Finally, the main conclusions and perspectives are presented in Section 5.
2. Context and Summary of Numerical Simulations
The simplest and most extensively studied type of turbulence is statistically homogeneous isotropic turbulence of an incompressible fluid. In such configuration, it is well known that small-scale fields of velocity can be thought of as being more or less homogeneous and isotropic. Small-scale vortex structures are responsible for dissipation of turbulent energy and play a key role in the accumulation (clustering) of particles in a turbulent flow. Study of isotropic turbulence is thus of fundamental importance for both single-phase and two-phase flows and, therefore, it has been the configuration adopted in the present work.
In this work, the simulation of the turbulent behaviour of the flow has been performed by the Lattice Boltzmann Method with the in-house code described in Reference [38] and also employed in Reference [38] to study the effect of inter-particle collisions on several clustering measures of inertial particles in turbulent flows. For the details of the implementation of the Lattice Boltzmann Method (LBM) forcing scheme for generating the homogeneous isotropic turbulence and collision detection algorithm, the reader is referred to Reference [38]. Therefore, only an abridged summary of the main flow characteristics is mentioned here.
We focus on the dynamics of colliding particles in an isotropic homogeneous flow in a triple-periodic box of size . The fluid domain is uniformly discretised by grid points. Forcing parameters have been adjusted to guarantee a good resolution of all flow scales, providing a grid space slightly smaller than the Kolmogorov length scale . Additionally, particle size is much smaller than so they are treated as point particles; moreover, the simulated particle volume fractions are sufficiently small to keep the two-phase flow dilute, so the back-reaction force of the particles on the flow is neglected. For the same reason, only binary elastic collisions are considered in the framework of the hard sphere approach. A brief summary of the employed collision model and detection algorithm is presented in Appendix A. Particle trajectories are computed by the simplified particle equation of motion, retaining only the contribution of drag term, in combination with the Schiller and Naumann correlation [39,40]. Domain discretisation and particle volume fraction values have been chosen to keep the computational effort limited as the direct detection of particle collisions is very costly. The main parameters employed in the fluid simulation are presented in Table 1.

Table 1.
Turbulence characteristics of the Lattice Boltzmann Method (LBM)-based Direct Numerical Simulation (DNS).
As an illustration, Figure 1 shows the non-dimensional three-dimensional (3D) energy spectrum obtained in the present DNS. For comparison, the experimental results of Comte-Bellot and Corrsin [41] and the Kolmogorov spectrum are also presented.
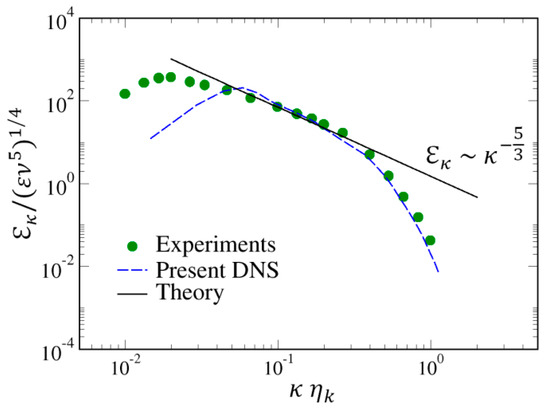
Figure 1.
Non-dimensional three-dimensional (3D) energy spectrum of the turbulent flow field of the present DNS. Experimental points correspond to Comte-Bellot and Corrsin [41] and the black solid line indicates the −5/3 scaling.
The considered particles have a fixed diameter, , which is more than five times smaller than the Kolmogorov length scale ; therefore, particle size is well in the dissipative range. Three different average particle volume fractions, 0.01%, 0.05% and 0.1%, have been simulated. Particle volume fraction is varied by changing the number of tracked particles: for 0.01% there are 50,066 particles, for 0.05% there are 250,329 particles and for 0.1%, there are 500,658 particles. Particle properties are summarised in Table 2.

Table 2.
Properties of the particles considered in this study.
Inertial particles’ dynamics depend on Stokes number, which characterises particle inertia and is equal to the ratio between the average response time of particles, , and the Kolmogorov time microscale, , The response time scale of the particle is defined as:
where is the Stokesian particle relaxation time, μ is the carrier fluid dynamic viscosity, is the particle drag coefficient which depends on the particle Reynolds number, , whose expression extended for Reynolds number higher than 0.5 is given in Reference [40] as:
whereas the Kolmogorov time microscale is expressed as:
In this study, variation of particle Stokes number is achieved by modifying its density according to the values shown in Table 2.
For quantifying the importance of inter-particle collisions on disperse phase transport, a collision Stokes number can be defined as , where is the mean inter-particle collision time, i.e., the average time between two consecutive collisions. As mentioned in Reference [42], allows drawing a boundary between dilute and dense flow conditions: if is larger than , the flow is ditute (i.e, ), and dense otherwise. In the case of dilute flows, the main particle transport mechanism is driven by its interaction with the turbulence, but in case of dense systems, collisions play a role in particle motion.
Although previous works have considered the effect of particle number density on inter-particle collision frequency (e.g., Reference [15]), it was in the article of Ernst and Sommerfeld [38] where a systematic study of the effect of particle volume fraction on collision statistics was performed. The employed DNS resolution of that work was low, only 643, and therefore the grid size was a factor two larger than the Kolmogorov length scale. Nevertheless, some interesting results were found: as expected, inter-particle collision frequency augmented with increasing volume fraction and Stokes number, the Lagrangian integral time scale of particles decreased with volume fraction but increased with due to the decorrelation of particle motion induced by the increase in the number of collisions, also, the particle pair relative velocity at collision rose with growing but it decreased for higher values of , with this last effect being more pronounced for large inertia particles. Such findings are revised in the next section with the results obtained in the present, more refined, DNS.
Finally, our previous work (Ernst et al. [39]) studied the effect of particle volume fraction and collisions on particle segregation and clustering in homogeneous isotropic turbulence in the same configuration and numerical set up as those employed in the present study. It was found that for particle volume fractions lower than 0.1%, the effect of increasing collision frequency with was marginal as all evaluated clustering measures (segregation parameter, correlation dimension, radial distribution, Voronoï diagrams and Minkowski functionals) were only slightly modified; however, for higher volume fractions, of about 1%, such measures were noticeably altered due to the re-dispersing effect of inter-particle collisions.
3. Statistical Properties of Inter-Particle Collisions
As an illustration, Figure 2 shows typical snapshots of a two-dimensional slice of particle distribution in the turbulent flow field depending on their inertia. Following Reference [39], particles tend to form distinct patterns in the flow, which depend on its inertia. For instance, for the case of , Figure 2a presents the case of , where well-differentiated narrow particle ropes can be observed in the background coloured by fluid strain rate (average strain rate in this configuration is 61 s−1). As it is clearly noticed, particles tend to preferentially sample zones with a higher than mean fluid strain rate (green to red colours), and also, although not shown, lower than mean fluid vorticity—a view that agrees with the previous literature. Figure 2b shows, on the other hand, the distribution of particles with ; here, no distinct clusters can be appreciated, and particles tend to be spread much more evenly than in Figure 2a, although some voids are noticed. As commented before, the reason for such distribution patterns lies in the particle–turbulence interaction: for intermediate particle inertia, , the centrifuging effect of particles towards the rim of vortical structures as well as the sling effect impulse them to show preferential concentration; on the other side, large inertia particles are only marginally affected by its interaction with turbulent vortices and tend to describe straight trajectories (the so-called inertia filtering effect), which are only modified by collisions, resulting in a much more uniform distribution along the fluid field.
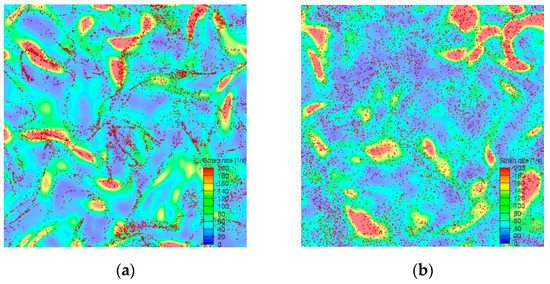
Figure 2.
Snapshot of a two-dimensional (2D) slice of the fluid turbulent field laden with particles, where background is coloured by fluid strain rate. Particle segregation illustration for particles with intermediate ( = 1) and large ( = 10) inertia, (a) and (b), respectively. Particle volume fraction = 0.1%. Edge lengths l and thickness s of the image sections: and , respectively. The diameter of the spheres is enlarged by a factor or 3 for the sake of better visibility.
Figure 3 illustrates the clustering behaviour of inertial particles as a function of their Stokes number by means of the so-called particle segregation parameter [39]. It compares the standard deviation of the actual particle number density distribution with that of a purely random distribution (which is described by a Poisson process). The value = 0 corresponds to a random particle distribution, < 0 corresponds to a uniform particle distribution, while > 0 indicates particle clustering.
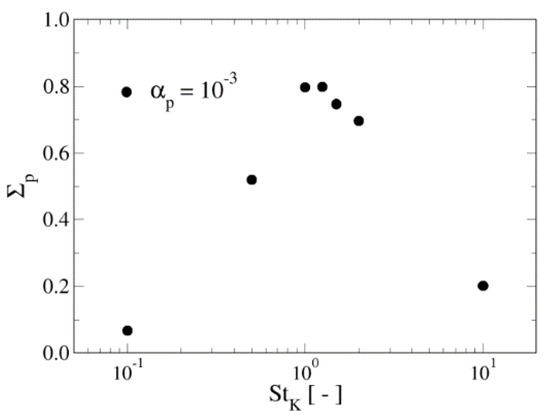
Figure 3.
Particle segregation parameter, , variation versus particle Stokes number. presents a peak for the maximum attained clustering, reached for . Data are for volume fraction = 0.1%.
As it is clearly seen from Figure 3, is positive for all Stokes numbers, showing a peak for around one and values closer to zero for Stokes numbers of 0.1 and 10, where particles tend to be distributed randomly along the fluid domain.
In the following, we present the effects of increasing particle volume fraction on the statistical collision properties of the particles in dependence on the Stokes number, which implies taking a second look at the results of Reference [38] in light of the present, more refined, DNS. It should be mentioned that the averaging period for computing the presented collision statistics was larger than 25 eddy turnover times (defined as ).
3.1. Analysis of Time Scales Related with Collisions
The inter-particle collision time, is defined as the average of elapsed time between two consecutive collisions and it is computed as the inverse of inter-particle collision frequency (which indicates the number of collisions per unit time). Figure 4 presents such quantity for the three considered volume fractions, , and it has been made non-dimensional with the Kolmogorov time scale, .
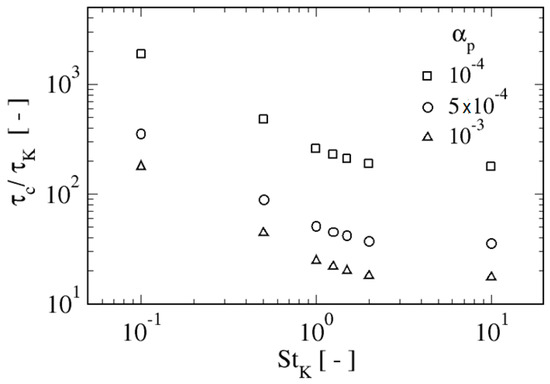
Figure 4.
Non-dimensional inter-particle collision time, as function of particle Stokes number, , for the three evaluated average volume fractions, .
As shown in Figure 4, inter-particle collision time is a decreasing function of the Stokes number, although for the largest Stokes numbers considered, it seems to reach an asymptotic value. This trend is similar to those presented in References [22] and [38]. Moreover, for a fixed value of , decreases almost linearly with increasing volume fraction, which is verified for all the considered Stokes number range. In the case of the smallest = 0.1, there are many repeated collisions among the same particle pair with very small radial relative velocity and nearly parallel velocities. In order to exclude possible false collision detections due to numerical errors in such small , only collision intervals larger than the Kolmogorov time scale are counted in the statistics [22].
Another point to be mentioned is that for the smallest values of not all the particles are involved in collisions. In fact, for the Stokes number of 0.1, at , only 17% of all tracked particles are experiencing at least one collision; in this case, particles tend to be nearly homogeneously distributed along the flow field and inter-particle collisions happen between particle pairs that have shared the same flow structures during long periods. As a result, the velocities of both particles are correlated, and the collision mechanism is that of fluid velocity shear. For , where particle accumulation is already noticeable, the number of particles involved in collisions increases up to 65%, whereas for the rest of the higher , such value is over 94%. Therefore, essentially all particles are participating in collisions for the cases with intermediate and large inertia.
In the next figure, the collision Stokes number, , is plotted as a function of the particle Stokes number for the three volume fractions (Figure 5).
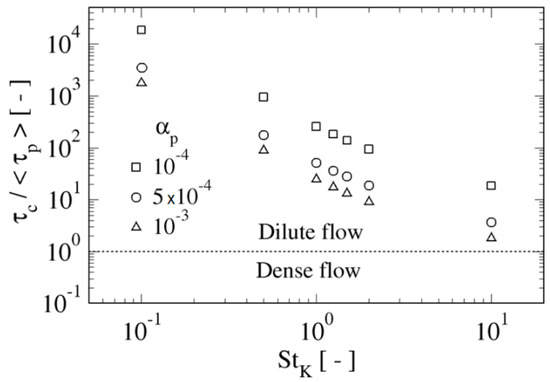
Figure 5.
Collision Stokes number, , as a function of particle Stokes number, , for the three evaluated average volume fractions.
It can be seen that, for all particle volume fractions and for all inertias, the flow can be considered dilute, as the collision Stokes number is always above unity. A pronounced decreasing of is observed for the three considered volume fractions and the curves run pretty much parallel, suggesting a linear dependence of with for a fixed particle Stokes number. The collision Stokes number decreases continuously with , following a nearly straight line in the double logarithmic diagram for the three values of particle volume fraction considered. Only for the most inertial particles did the values of become near the dilute-dense flow conditions boundary; however, in such case, the increment of the number of collisions is mainly ascribed to the increase of the caustics contribution (or random uncorrelated motion) to inter-particle collision rate [28].
According to Figure 5, all the considered cases are in the dilute regime, where ; therefore, the main mechanism affecting the particles’ motion is the aerodynamic transport, and particles have time to adapt to its local fluid environment between inter-particle collisions. Increasing has the effect of reducing inter-particle distance, so collisions are more frequent. However, such collisions are not dominant, they must be viewed instead as a modulating mechanism. This fact was demonstrated in Reference [39], where the cases with and without inter-particle collisions were compared: the differences between both cases in the considered clustering measures were marginal for . As a consequence, the increase in collision frequency with is expected to have only a moderate effect on the statistical quantities computed for colliding particle events, such as relative velocity, two-particle velocity correlation function or strain rate at collision locations, among others.
The importance of collisional effects on the turbulence-induced particle transport can be illustrated by plotting the behaviour of the particle Lagrangian integral time scale, , versus particle inertia. is computed as the integral of the particle Lagrangian autocorrelation function and it measures the time scale in which particle velocities are correlated in time along their trajectories [38]. Figure 6a shows the curves of the quotient depending on particle Stokes number, for the three considered values of . A decreasing trend with increasing is observed, which is due to the growing of the time scale with particle inertia, reflecting the fact that more inertial particles are less affected by turbulent fluctuations and that the particle motion becomes more correlated. As a consequence, large inertia particles tend to experience a ballistic motion between consecutive collisions. Regarding the effect of particle volume fraction on , it is found that the increase in the number of collisions has only a marginal effect on the particle Lagrangian autocorrelation timescale, where, nevertheless, a small decrease of this quantity can be observed with increasing (i.e., increase in ), as expected. This means that the particle motion becomes slightly more decorrelated as a consequence of the increasing collision rate and the resulting faster change of particle velocity.
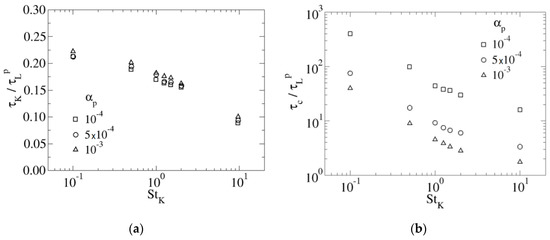
Figure 6.
Kolmogorov time scale over particle Lagrangian time scale (a) and inter-particle collision time over particle Lagrangian time scale (b) as a function of particle Stokes number for the three evaluated average volume fractions.
Figure 6b presents the behaviour of versus particle inertia. The same as in Figure 6a, a decreasing tendency is found for this variable, which is related to the fact that increases and decreases with growing . For all the computed cases, the quotient is above unity, meaning that inter-particle collision time is larger than the particle Lagrangian time scale. Similar to what happened with , the curves for the different particle volume fractions decrease pretty fast with increasing inertia and run quasi parallel. Moreover, the values of are always much larger than those of , which means that the main mechanism of particle velocity change is the interaction between particle inertia and underlying turbulence. Inter-particle collisions have a marginal effect modulating such primary mechanism.
3.2. Analysis of Kinematic Properties of Colliding Particles
Figure 7 illustrates the variation of the mean free path, with particle inertia and with particle volume fraction. The free path is computed as the distance travelled by a particle among two consecutive collisions. Particles with Stokes numbers well below one mainly interact with their closest neighbours, with whom they have shared the same fluid environment during long periods. This fact is reflected in a low relative velocity and collision angles between them (see Figure 8 below). Besides, as such particles do not experience remarkable clustering: interactions between the same pair of particles are common and only a small percentage of them undergo collisions (for and , only 17% of particles are involved in collisions with a partner and the percentage is even lower for smaller values of , 9% for and 2% for ). This means that the majority of particles present a free path equal to the length of the trajectory described during the total measured time, which in this case was 25 eddy turnover times. As a result, small particles present high values of mean free paths. As increases, the percentage of particles involved in collisions augments (65% for and ) at the same time that the number of repeated collisions among the same pair of particles is reduced; as a consequence, the mean free path reduces. For around unity and larger, nearly all the particles are involved in collisions, a fact favoured by clustering processes and the formation of caustics [22]. Both phenomena increase collision frequency and also reduce the value of the mean free path. Finally, for large enough particles become nearly irresponsive to fluid fluctuations and do not undergo appreciable clustering, so the main mechanism for inter-particle collisions is the so-called Random Uncorrelated Motion [19]. In this case, the number of collisions increases slightly, and the mean free path seems to reach an asymptotic value. Obviously, the effect of decreasing is reflected in a reduction of the inter-particle collision frequency, hence an increase of the mean free path, as shown in Figure 7.
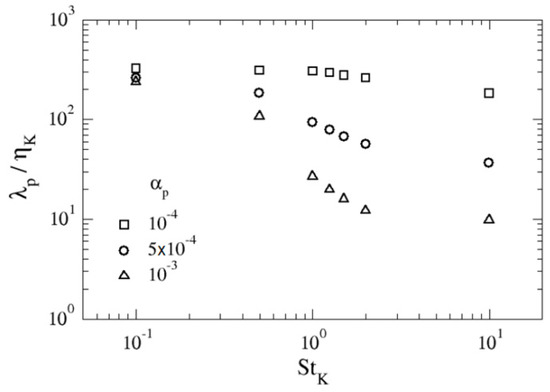
Figure 7.
Mean free path over Kolmogorov length scale as a function of particle Stokes number for the three evaluated average volume fractions.
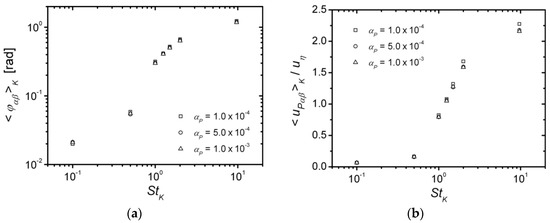
Figure 8.
Average velocity collision angles (a) and relative velocities (b) for colliding particles as a function of particle Stokes number for the three evaluated average volume fractions.
Figure 8a shows that average velocity collision angles, defined as the angle that particle velocities form at collision, increase continuously with . The same behaviour is seen for the relative velocity at collision (Figure 8b), which is a fact related with the increased uncorrelated motion of colliding particles with growing inertia. Therefore, particles can collide coming from rather different directions, a phenomenon that is enhanced by trajectory deflection after previous collisions. As mentioned before, particles with small inertia respond very fast to the fluid velocity fluctuations and colliding pairs are usually moving with pretty similar velocities in nearly parallel trajectories [22] because they are transported by the same eddy during long time periods, as a result, their velocities are very correlated, which is reflected in both small values of relative velocity and nearly zero-velocity angle of collision. In this context, there is no preferential concentration and the increased collision frequency, i.e., by augmenting , has no effect in the particle transport and collision mechanisms which are driven by the turbulent velocity fluctuations.
With increasing particle inertia, preferential concentration and the sling effects come into play, with the result of increasing the collision frequency, relative velocity at contact as well as velocity angle of collision. In this regime, the effect of increasing the particle volume fraction is hardly seen as the inter-particle collision time is still much higher than the particle Lagrangian time scale (see Figure 6b). Interestingly, for the mean velocity collision angle obtained in the present work, around 0.3 radians or 17°, is very close to that obtained in Choi et al. [22]. For larger inertia, the relative velocity of colliding pairs overcomes the Kolmogorov velocity and reaches a maximum in the present computations for , the same as the velocity collision angle (around 1.17 radians or 67°), which again is very similar to that reported in Reference [22]. When inertia is further increased, the relative velocity of colliding pairs decreases because particles become less responsive to fluid fluctuations [37] and the velocity collision angle tends asymptotically to 90°. For these large inertias, a marginal effect of starts to be appreciated as both relative velocity and collision angle are slightly reduced for increasing collision frequency. This fact was already noticed in Reference [38] and its explanation was ascribed to collective effects in clusters. Actually, the argument is that in situations where clustering is notable, particles spend most of the time in areas of high strain ratio and low vorticity so, besides some collisional effects, they have time to adapt its motion to that of the fluid, resulting finally in a reduced average relative particle velocity and collision angle. However, such explanation would not be appropriate for large inertia particles because in those conditions, particles are distributed fairly uniformly without appreciable clustering. This finding should be further investigated by using configurations with larger volume fractions and turbulent Reynolds numbers.
An interesting issue to be discussed is the distribution of the location of inter-particle collisions. As already mentioned, and illustrated in Figure 2a, particles with Stokes number around 1, experiencing appreciable clustering, tend to sample fluid locations with higher strain rate than particles with small and large Stokes numbers, where clustering is not observed. Figure 9a presents the ratio between the fluid strain rate at particle collision locations, averaged for all collisional events, , and the fluid strain rate at particle positions, averaged for all particles, . Interestingly, inter-particle collisions at clearly happen in fluid regions with noticeably higher strain rates than those averaged through all the particles. The maximum occurs for , whereas for the ratios are very close to 1, as in such cases no significant preferential concentration is observed. At this point, it is necessary to mention that Choi et al. [22] found that collision events in the case of particles with occurred in locations where the fluid dissipation was higher than the corresponding mean value experienced by all the tracked particles. Both observations are related, as in the configuration of homogeneous isotropic turbulence, both quantities, fluid strain rate and dissipation, are strongly correlated (correlation coefficient of 0.97 in present simulations).
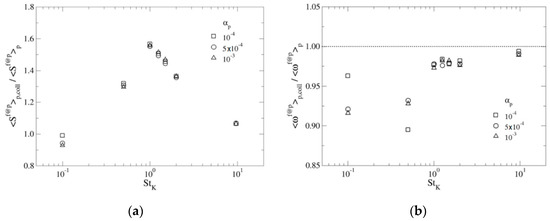
Figure 9.
(a) Average of sampled fluid strain rate by colliding pairs over mean sampled fluid strain rate by all the particles. (b) Average of sampled fluid vorticity of colliding particles over mean sampled fluid vorticity. Both variables are presented as a function of particle Stokes number for the three evaluated average volume fractions.
Figure 9b presents the ratio between the fluid vorticity at particle collision locations, averaged for all collisional events, , and the fluid vorticity at particle positions, averaged for all particles, . As it was said previously, particles tend to sample fluid locations with lower than mean vorticity. In our simulations, this behaviour also happens for the smallest inertia particles, , which otherwise approach the tracers’ behaviour. They are located in areas with lower than mean fluid vorticity, as already noted in Reference [22]. Looking at the locations where inter-particle collisions happen, , it is found that such locations are characterised by smaller values than (see Figure 9b). This observation is valid for all the Stokes numbers, although for particles with , the two values are very close. This fact is parallel to the tendency of particle collisions to occur in areas with fluid strain rate higher than the mean value computed at particle positions, , and, therefore, could be somehow expected. However, this last observation is contrary to that presented in Reference [22], where the fluid enstrophy sampled at collision locations was higher than the average value sampled at particle positions. At the moment, the reason for such discrepancy is not clear.
Finally, Figure 10 shows the ratio of the average particle turbulent energy of colliding particles, and the average particle turbulent energy of all the tracked particles, , . In this case, colliding particles with have smaller kinetic energy than the average, attaining a minimum of around 0.9 for and for all considered particle volume fractions. For particles with , the ratio is closer to 1, although the value for is higher than for the other two volume fractions. The fact that colliding particles with intermediate inertia, , possess on average less fluctuating energy than the mean value computed over all tracked particles could be understood as follows: as it has been shown before, inter-particle collisions tend to happen in locations with high values of fluid strain rate and, equivalently, high dissipation rate; in isotropic homogeneous turbulence, the decay of turbulent kinetic energy is larger at locations of higher dissipation, therefore, such regions possess, on average, lower values of turbulent energy. Consequently, it is expected that intermediate inertia particle collisions occur at fluid locations with lower than mean values of fluid kinetic energy, a fact that is found in the present simulations. Moreover, as it has been seen for particles of low and intermediate inertia, that values are much larger than 1, so those particles have time to accommodate to the local fluid conditions between collisions, meaning that their kinetic energy will also be lower than the mean kinetic energy computed for all tracked particles.
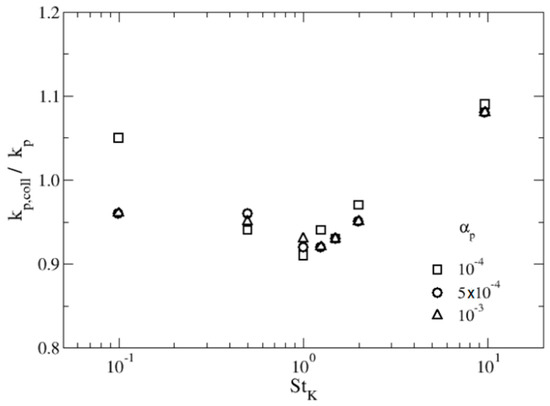
Figure 10.
Average of particle kinetic energy of colliding particles over mean particle kinetic energy over all particle locations, , as a function of particle Stokes number for the three evaluated average volume fractions.
In the case of large inertia particles, the situation is different as they are not preferentially sampling regions of high dissipation, and also, the collision Stokes number is only somewhat higher than 1. As a result, in the case of , the ratio is clearly above 1 for all volume fractions, indicating in this case that colliding particle pairs possess higher fluctuating velocity than the mean. According to the random uncorrelated motion interpretation, such result is expected, as inter-particle collisions are favoured by a higher particle fluctuating velocity.
3.3. Collision Frequency
A way of characterising inter-particle collision probability is the collision kernel, which is equal to two times the collision frequency over the particle number density (particles per unit volume) [43]. In the literature, there are two limiting cases for the behaviour of such collision kernel with particle Stokes number.
Saffman and Turner [44] provided an approximation for the collision kernel of drops in atmospheric turbulence. In their analysis, the particles are small compared to the smallest length scales of the fluid flow. Hence, particles follow the turbulent structures completely. The resulting collision kernel for mono-disperse particles is given by:
Another limiting case was studied by Abrahamson [45], in which the motion of heavy particles suspended in high-intensity turbulence neglecting external forces is analysed. According to the kinetic theory, the particle motion is completely uncorrelated concerning the underlying fluid motion. Under the assumption that all components of the particle fluctuating velocity are isotropic, the resulting collision kernel reads:
where represents the average particle turbulent energy of all tracked particles.
In practice, particles have finite inertia and, therefore, their collision kernel is expected to lie between both limiting values. Figure 11 presents the non-dimensional collision kernel obtained in this work as a function of the particle Stokes number for the three considered particle volume fractions. In addition, the collision kernels of Saffman and Turner, , as well as Abrahamson, , are also shown in Figure 11 for comparison.
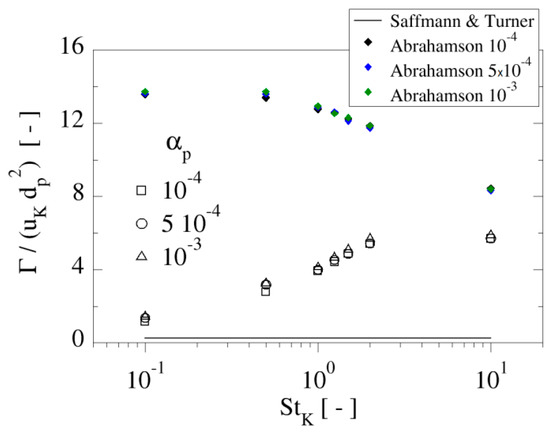
Figure 11.
Collision kernel, normalised by the Kolmogorov velocity, and the square of particle diameter, obtained by the present simulations as a function of the particle Stokes number and for the three average particle volume fractions. The Saffman and Turner [44] and Abrahamson [45] kernels for colliding particles are also shown for comparison.
Let us observe that the non-dimensional Saffman and Turner kernel is actually constant but that of Abrahamson depends on particle fluctuating velocity, which varies with particle volume fraction. However, for the simulated cases, is similar for the three values of .
As it can be readily seen in Figure 11, the computed collision kernel is between the Saffman and Turner (lower limit) and the Abrahamson kernels (upper limit), as it had to be expected. In the case of zero particle inertia, represented by the Saffman and Turner limit, particle collisions are only controlled by the smallest fluid scales. This regime is approached in the present simulations of the lowest inertia particles, where the inter-particle collision time is determined by the Kolmogorov time scale. On the other limit, the collision kernel is governed by the particle kinetic energy, which is approached in the present simulations for the highest considered Stokes number. Eventually, for larger inertia particles, the collision kernel will decrease because they tend to be less responsive to fluid turbulence. The trend of the computed kernel in present simulations agrees qualitatively with the results of Vosskuhle [46], showing a fast increase around Stokes numbers close to one and then growing much more moderately for higher Stokes numbers (here up to 10).
Regarding the dependence of the simulated non-dimensional collision kernel with particle volume fraction, Figure 11 shows that it does not have an appreciable effect: only a marginal increase of is observed with growing .
4. Two-Particle Velocity Correlation Function
As it was previously mentioned, it is necessary to account for the correlation of the motion of neighbouring particles and their preferential concentration when dealing with the description of inter-particle interactions in practical two-phase flow computations. As commented in the introduction section, in this context, Lagrangian-based stochastic collision models offer an alternative to the costly, and often impracticable, deterministic collision algorithms. In such stochastic models, along the trajectory of each particle, a fictitious collision partner is generated at each time step. The properties of the fictitious particle such as diameter or velocities are sampled randomly from previously constructed local distributions, and the probability of collision is computed according to kinetic theory. However, in this process, the fluctuating velocity correlation of both particles has to be taken into account [29,32] and such correlation depends on the particle response to the turbulent environment. In the original paper of Sommerfeld [31], it was modelled by the following decaying exponential:
where is the Stokes number based on the fluid Lagrangian integral time scale. Coefficients appearing in Equation (6) were obtained after comparison with LES computations of Reference [34] by trial and error. Such correlation has been employed successfully for predicting the effect of inter-particle collisions in pneumatic conveying and particle separation processes [9,10,11,35], and it is shown in Figure 12. A more rigorous way to determine the particle-pair velocity correlation function between colliding particles, , was developed in Lain et al. [36]. In such study, the model proposed in Zaichik and Alipchenkov [37] (or its refined version, [18]) developed for homogeneous isotropic turbulence was solved to build the Eulerian particle-pair velocity correlation function between colliding particles, . The conclusions obtained in Reference [36] are revised in this section in light of the new DNS results obtained.
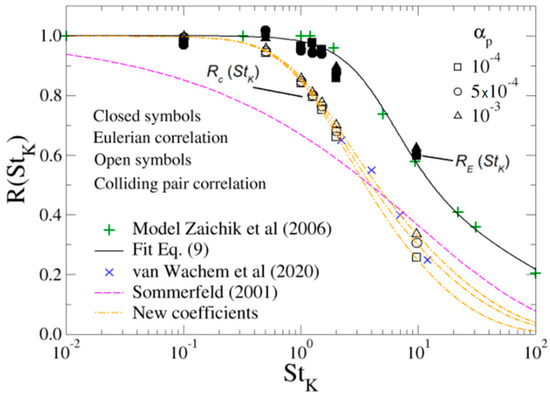
Figure 12.
Two-particle velocity correlation function . Plus (+) symbols represent the results obtained by solving the Zaichik and Alipchenkov model [18]. Cross (×) symbols show the results of Reference [28]. Correlation of Reference [30], Equation (6), corresponds to the purple dashed line. The rest of the symbols refer to the LBM-based DNS results obtained in this work for different average volume fractions. Closed symbols represent the Eulerian correlation evaluated at a distance , Equation (9), and open symbols represent the obtained colliding pair velocity correlation, Equation (10) (see text for details). The dot-dashed lines fit the colliding two-particle velocity correlation functions, , of the different volume fraction cases studied in this work.
The information relevant to the estimation of the correlation function of particle-pair fluctuating velocities can be extracted from the solution of the Zaichik and Alipchenkov model. To this end, they define the Eulerian two-particle velocity correlation as:
where is the kinetic energy of particles, is the particle structure function of the relative velocity between two particles and is the distance between the two particles [37]. Expression (7) is obtained assuming that there is a balance of net radial inward and outward fluxes implying a zero mean radial relative velocity. The longitudinal two-particle velocity correlation function is defined as in terms of the longitudinal space correlation, , which depends on the separation distance and Stokes number. As pointed out by Zaichik and Alipchenkov [37] and discussed in depth in Février et al. [19], in contrast to the well-known result for fluid turbulence, this correlation for inertial particles is not tending towards unity in the limit of . This specific feature of the spatial correlation indicates that as a consequence of the inertial bias in their trajectories, the velocities of particles are not completely correlated, even at . In the case of colliding particles, the distance between them tends to zero (obviously it cannot be less than the sum of the radii of both particles), so the colliding particle-pair velocity correlation could be expected to be approximated by the behaviour near the origin of the longitudinal space correlation, , which clearly depends on particle inertia. Based on the results obtained by solving the Zaichik and Alipchenkov model, Lain et al. [36] proposed the following functional form for the particle velocity correlation of colliding particles:
Equation (8) uses three parameters instead of the two originally proposed by Sommerfeld [30], Equation (6). The parameters take the values: α = 0.019, β = 1.725 and γ = 0.044.
Correlation (8) is shown in Figure 12 as a solid line together with our own results obtained solving the Zaichik and Alipchenkov model, represented by plus symbols. As it can be seen, tends to one in the limit of very small Stokes numbers according to the Saffman and Turner limit, where velocities of neighbouring particles are spatially correlated due to the interaction with the same local fluid flow. As increases, particle velocity correlation decreases smoothly, and in the limit of very high Stokes numbers, it tends to zero, where statistics of heavy particles satisfy the assumption of molecular chaos according to Abrahamson [45].
Results for the particle pair correlation function obtained in the present work within the frame of LBM-based DNS are also presented in Figure 12. The closed symbols correspond to the Eulerian two-particle velocity correlation function evaluated at the fixed distance , i.e.,
This corresponds to a situation where the longitudinal velocity correlation between neighbouring particles is evaluated at 1.5 times the particle diameter (i.e., around ) at a fixed time. Correlation has been computed at different times after the initial transient has been completed, showing stable values in all the range of Stokes numbers studied.
On the other hand, open symbols represent the two-particle velocity correlation for particle pairs that have actually collided, i.e.,
This corresponds to a situation where the longitudinal velocity correlation between neighbouring particles is computed for particle pairs that have experienced a collision along the development of the simulation. Statistics are computed based on 106 collision events.
From Figure 12, it can be clearly seen that the values obtained from LBM-based DNS agree reasonably well with the correlation Equation (8). Therefore, the theoretical model of Zaichik and Alipchenkov is adequate for describing the Eulerian velocity correlation between neighbouring particles, as it could be expected. Moreover, the DNS results for different solid volume fractions show nearly no scattering of values for all the range of studied Stokes numbers.
As already commented in the introduction, the decreasing of particle velocity correlation of neighbouring particles, i.e., , with increasing particle inertia is usually explained [19] in terms of an increase of the relative velocity between them, consistent with the existence of caustics and a component of random uncorrelated motion of particle velocity field. In fact, the connection between the decreasing of particle velocity correlation and the increase of the modulus of relative velocity (or vice versa) can be easily cast in mathematical terms. The average of the modulus of relative velocity between two particles is computed as:
Now, because the mean particle velocity in isotropic homogeneous turbulence is zero, , where is the fluctuating kinetic energy of the particles. Finally, solving for the two-particle velocity correlation, it is obtained:
where and are the velocities of particles 1 and 2 respectively, is their relative velocity and denotes the averaging operator.
As Equation (11) is a general relation, a reduction in the two-particle velocity correlation is accompanied by an increase in the modulus of relative velocity, and an increase of this quantity implies a decrease of the correlation. To support this affirmation, Figure 13 shows the modulus of radial relative velocity (RRV), defined as , between colliding particles, divided by the Kolmogorov velocity, , as a function of the particle Stokes number. It is clear that it increases with particle inertia, experiencing a rapid growth for Stokes numbers roughly between 0.5 and 2. The strong increase of the radial relative velocity for is connected with the strong enhancement of the inter-particle collision rate due to sling caustics occurrence. For larger Stokes numbers, of more than 10, a decrease of the RRV is expected because the particles become slower and less responsive to the fluid turbulence. Such results are in close agreement with those of Figure 2 in Reference [18].
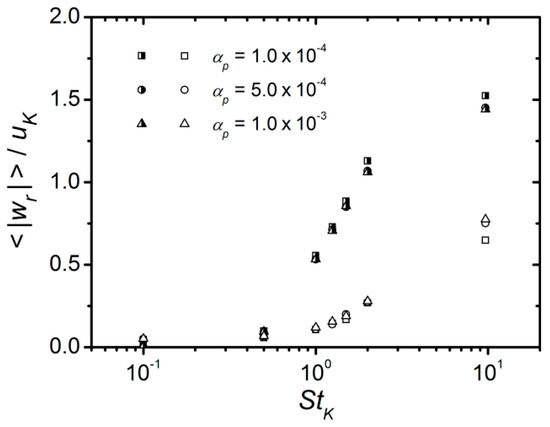
Figure 13.
Modulus of mean radial relative velocity (RRV) between particle pairs, , as a function of the particle Stokes number normalised by the Kolmogorov velocity, . Half-closed symbols represent colliding particles while open symbols denote the average of close particle pairs at a distance lower than based on Eulerian evaluations of the radial distribution.
The behaviour of the colliding particles velocity correlation function, in Figure 12 deserves attention. At small values of particle inertia, here = 0.1, there is no difference with the Eulerian correlation as the collision events are governed by the fluid turbulent shear. As soon as inertia increases, adopts significantly lower values than ; for instance, in Figure 12, at = 0.5, the difference between the two correlations is already appreciable. Such differences are increasing with augmenting particle Stokes number. The reason for the smaller values of , regarding , is that in three-dimensions, not all particle pairs that are close enough to interact do really collide, it is necessary that they approximate each other with the right radial relative velocity to have the interaction. In fact, the curves cannot be obtained as because the RRV’s are different, as already remarked in Reference [16]. The reason is that in the Eulerian case, the average of the RRV is zero, as it was implied in the derivation of Equation (7), while in the colliding particle case, this RRV is effectively negative. As a result, the modulus of the particle relative velocity is higher in the colliding case than in the Eulerian case which, due to Equation (10), has the consequence that the values of are smaller than those of . As the modulus of the RRV increases with Stokes number (Figure 13), the distance between both curves augments with particle inertia. Moreover, the results of the recent study of van Wachem et al. [29] for are also depicted in Figure 12 as crosses, showing a good agreement with those obtained in the present simulations. However, in Reference [29], the volume fraction values were different for the four particle types analysed and ranged from 0.3% to 2%.
Another interesting fact that can be observed in the correlation functions in Figure 12 is that, for a fixed particle Stokes number, their values increase with increasing solid volume fraction. The counterpart, seen in Figure 13, is that the radial relative velocity between colliding particles decreases with increasing volume fraction. This fact was already shown by the authors of Reference [38], who also observed that the mean angle formed by the velocities of colliding particles was increasing with particle inertia. These authors ascribed such behaviour to a kind of collective motion of particles in clusters. Such phenomenon has also been found in the present work and it was illustrated in Figure 8a. However, in the present study, such trend is not as evident as in that research because they employed higher values of than in this work.
In summary, it has been found that the colliding particle pair velocity correlation is smaller than that computed by the Eulerian particle pair velocity correlation as particle separation tends to zero. The practical consequence for the stochastic collision models in the Euler–Lagrange frame is that the velocity correlation between the real and fictitious particles cannot be drawn out from the Eulerian two-particle velocity correlation given by the model of Zaichik and Alipchenkov, but instead should be built from the colliding particle-pair correlation function, which depends on both particle inertia and volume fraction. As an example (which does not pretend to be universally valid), functional forms for such correlation can be devised from the presented DNS results and Table 3 shows the fitted coefficients for the curves to Equation (8) for the volume fraction cases studied in this work. The corresponding curves of such fits are also plotted in Figure 12 for comparison, which could be used for building the fluctuating component of fictitious collision partners in stochastic models of inter-particle collisions, e.g., Equation (23) in Reference [31]. Nevertheless, it would be necessary to study the dependence of such correlations on turbulent Reynolds number and in a larger range of particle volume fractions.

Table 3.
Coefficients of the fit Equation (8) to the curves.
5. Conclusions
In this paper, the effect of particle inertia and void fraction, and therefore inter-particle collisions, on the colliding particle-pair velocity correlation in homogeneous isotropic turbulence has been addressed by using direct numerical simulations based on the Lattice Boltzmann Method. Three particle volume fractions have been considered, , in the dilute regime.
In the range of void fractions studied, collisions have a marginal impact on particle transport, with the aerodynamic interaction with fluid turbulence being the main mechanism that drives it. This is reflected in the fact that collision Stokes number has been always larger than one, keeping the dilute flow conditions. A main result of the performed study is that collision locations of particles of intermediate inertia, , happens in areas where the fluid strain rate and dissipation are higher than the corresponding averaged values at particle positions. Connected with this fact, the average kinetic energy of colliding particles of is lower than the value averaged over all particles. This finding was explained by the fact that the fluid kinetic energy at collision positions is lower than the mean value and, because , particles have enough time to accommodate to the fluid environment between consecutive collisions. In case of the highest inertia, , particles do not experience noticeable clustering in areas of high strain rate and in that case, inter-particle collisions are favoured by high kinetic energy; as a result, the colliding particle kinetic energy is higher than the corresponding averaged value over all particles.
Later, the Eulerian and colliding two-particle velocity correlation functions were computed in the same homogeneous isotropic turbulence configuration. As a result, the Eulerian function was well reproduced by the Zaichik and Alipchenkov [37] model, but the colliding particles correlation showed remarkably smaller values due to the role played by the mean radial relative velocity. In particular, it was demonstrated that the colliding pair correlation cannot be obtained as a limiting value of the Eulerian correlation. Moreover, it has been confirmed that the colliding particles velocity correlation increases with particle volume fraction, a fact related with the decreasing of the average relative velocity between the colliding particles and attributed to the particle dynamics inside clusters. However, the decreasing of radial relative velocity with increasing was also found for large particle inertia, where no appreciable clustering was observed. Therefore, further studies are needed to confirm if the same phenomenon happens for a wider set of conditions than those presented here, such as larger volume fractions and turbulent Reynolds numbers.
The obtained results in the present study can be used to support inter-particle collision stochastic models (e.g., Reference [31]) for use in general-purpose two-phase flow Euler–Lagrange codes. However, it is necessary to study the dependence of such correlations on turbulent Reynolds number and in a larger range of particle volume fractions.
Author Contributions
Conceptualisation, S.L., M.E. and M.S.; methodology, S.L.; software, M.E.; validation, M.E. and S.L.; formal analysis, S.L.; investigation, M.E. and S.L.; resources, M.S.; data curation, S.L. and M.E.; writing—original draft preparation, S.L. and M.E.; writing—review and editing, S.L.; visualisation, M.E.; supervision, S.L. and M.S.; project administration, M.S.; funding acquisition, M.S. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Council (DFG), grant number SO 204-33/1-3 (Priority program 1273 “Colloidal Process Engineering”).
Acknowledgments
The financial support by the German Research Council (DFG) through Grants SO 204-33/1-3 (Priority program 1273 “Colloidal Process Engineering”) is gratefully acknowledged. Santiago Lain acknowledges Universidad Autónoma de Occidente for the support and funding through several research projects.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In the present study, the modelling and detection of particle–particle collisions was computed using a deterministic collision model proposed in Reference [47]. This model assumes that the collisions are binary and quasi-instantaneous. Furthermore, the elastic contact between two hard spheres occurs in a single point. In order to determine whether a collision occurs, the time-sequenced collision detection algorithm described in detail in Reference [38] was applied. Such algorithm is briefly summarised here.
Firstly, all particles are tracked to the end of the present Lagrangian particle time step, . Inter-particle collisions have occurred if particles overlap after the actual time interval. In the case of a collision, the distance between their centers is equal to or less than the half sum of the two particle diameters. The determination of all existing collision pairs is realised under application of the cell-index method [47]. The potential collision partners of a given particle are found among the other particles in the cell plus the particles in all 26 neighbouring cells. The list of particles in each cell is set up and updated using linked lists. Assuming that the particles move at constant velocities during the particle time step, the collision time for each overlapping pair, is calculated by solving the following quadratic equation:
Here, and are the relative position and velocity of particles and which have diameters and , respectively. Equation (A1) suffers from the limitation that it will not detect a particle–particle collision if complete interpenetration occurs during the given particle time step. Subsequently, the determined collision times (i.e., the time between the beginning of the actual time step and the time of particle collisions) are sorted in descending order. In the time-sequenced implementation, the first overlapping pair is moved backward in time to the position of collision. The determination of the post-collision velocities of the collision couple is based on the laws of impact for hard spheres provided in Reference [48]. A detailed derivation of the used collision operators can be found in Reference [38].
After the collision is computed, both particles are again moved forward in time to complete the actual particle tracking time step. New overlaps may be added to the list of colliding particles, i.e., in the case of multiple particle collisions within one tracking time step, while processed or non-existent ones are deleted. These collision computations are carried out until no overlaps are left.
The computational cost of the searching collision partners can be estimated as follows. In the employed Cell Index Method, the simulation box is divided in a regular array of cells; on average, there are particles ( is the total number of particles) within each cell, where 27 neighbouring cells have to be searched per particle. Therefore, avoiding double counting, the search algorithm requires operations [47].
References
- Safronov, V.S. Evolution of the protoplanetary cloud and formation of the Earth and the planets. Nauka NASA Tech. Transl. 1969, 677, 1–206. [Google Scholar]
- Zsom, A.; Ormel, C.W.; Guettler, C.; Blum, J.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? II. Introducing the bouncing barrier. Astron. Astrophys. 2010, 513, A57. [Google Scholar] [CrossRef]
- Falkovich, G.; Fouxon, A.; Stepanov, M.G. Acceleration of rain initiation by cloud turbulence. Nature 2002, 419, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Shaw, R.A. Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 2003, 35, 183–227. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.C.; Grebogi, C. Reactive dynamics of inertial particles in nonhyperbolic chaotic flows. Phys. Rev. E 2003, 68, 056307. [Google Scholar] [CrossRef] [PubMed]
- Varas, A.E.C.; Peters, E.A.J.F.; Kuipers, J.A.M. CFD-DEM simulations and experimental validation of clustering phenomena and riser hydrodynamics. Chem. Eng. Sci. 2017, 169, 246–258. [Google Scholar] [CrossRef]
- Cahyadi, A.; Anantharaman, A.; Yang, S.; Reddy Karri, S.B.; Findlay, J.G.; Cocco, R.A.; Chew, J.W. Review of cluster characteristics in circulating fluidized bed (CFB) risers. Chem. Eng. Sci. 2017, 158, 70–95. [Google Scholar] [CrossRef]
- Laín, S.; Sommerfeld, M. Euler/Lagrange computations of pneumatic conveying in a horizontal channel with different wall roughness. Powder Technol. 2008, 184, 76–88. [Google Scholar] [CrossRef]
- Laín, S.; Sommerfeld, M. Numerical calculation of pneumatic conveying in horizontal channels and pipes: Detailed analysis of conveying behavior. Int. J. Multiph. Flow 2012, 39, 105–120. [Google Scholar] [CrossRef]
- Laín, S.; Sommerfeld, M. Characterization of pneumatic conveying systems using the Euler/Lagrange approach. Powder Technol. 2013, 235, 764–782. [Google Scholar] [CrossRef]
- Laín, S.; Sommerfeld, M. Numerical prediction of particle erosion of pipe bends. Adv. Powder Technol. 2019, 30, 366–383. [Google Scholar] [CrossRef]
- Laín, S.; García, M.; Quintero, B.; Orrego, S. CFD Numerical simulations of Francis turbines. Rev. Fac. Ing. Univ. Antioq. 2010, 51, 24–33. [Google Scholar]
- Westphal, D.L.; Toon, O.B.; Carlson, T.N. A two-dimensional numerical investigation of the dynamics and microphysics of Saharan dust storms. J. Geophys. Res. 1987, 92, 3027–3049. [Google Scholar] [CrossRef]
- Kroy, K.; Sauermann, G.; Herrmann, H.J. Minimal model for aeolian sand dunes. Phys. Rev. E 2002, 66, 031302. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, S.; Collins, L.R. Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 1997, 335, 75–109. [Google Scholar] [CrossRef]
- Wang, L.P.; Wexler, A.S.; Zhou, Y. Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 2000, 415, 117–153. [Google Scholar] [CrossRef]
- Reade, W.C.; Collins, L.R. Effect of preferential concentration on turbulent collision rates. Phys. Fluids 2000, 12, 2530–2540. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M.; Avetissian, A.R. Modelling turbulent collisions rates of inertial particles. Int. J. Heat Fluid Flow 2006, 27, 937–944. [Google Scholar] [CrossRef]
- Février, P.; Simonin, O.; Squires, K.D. Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: Theoretical formalism and numerical study. J. Fluid Mech. 2005, 533, 1–46. [Google Scholar] [CrossRef]
- Reeks, M.W. On the dispersion of small particles suspended in an isotropic turbulent field. J. Fluid Mech. 1977, 83, 529–546. [Google Scholar] [CrossRef]
- Bewley, G.P.; Saw, E.W.; Bodenschatz, E. Observation of the sling effect. New J. Phys. 2013, 15, 083051. [Google Scholar] [CrossRef]
- Choi, J.; Park, Y.; Kwon, O.; Lee, C. Interparticle collision mechanism in turbulence. Phys. Rev. E 2016, 93, 013112. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.J.E.; Crane, R.I. Particle collision rate in turbulent flow. Int. J. Multiph. Flow 1983, 9, 421–435. [Google Scholar] [CrossRef]
- Kruis, F.E.; Kusters, K.A. The collision rate of particles in turbulent media. J. Aerosol Sci. 1996, 27, 263–264. [Google Scholar] [CrossRef]
- Ireland, P.J.; Bragg, A.D.; Collins, L.R. The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 2016, 796, 617–658. [Google Scholar] [CrossRef]
- Bec, J.; Celani, A.; Cencini, M.; Musacchio, S. Clustering and collisions of heavy particle in random smooth flows. Phys. Fluids 2005, 17, 073301. [Google Scholar] [CrossRef]
- Wilkinson, M.; Mehlig, B. Caustics in turbulent aerosols. Europhys. Lett. 2005, 71, 186–192. [Google Scholar] [CrossRef]
- Vosskuhle, M.; Pumir, A.; Lévêque, E.; Wilkinson, M. Prevalence of the sling effect for enhancing collision rates in turbulent suspensions. J. Fluid Mech. 2014, 749, 841–852. [Google Scholar] [CrossRef]
- Van Wachem, B.; Curran, T.; Evrard, F. Fully Correlated Stochastic Inter-Particle Collision Model for Euler–Lagrange Gas–Solid Flows. Flow Turb. Comb. 2020. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Laín, S. From elementary processes to the numerical prediction of industrial particle-laden flows. Multiph. Sci. Technol. 2009, 21, 123–140. [Google Scholar] [CrossRef]
- Sommerfeld, M. Validation of a stochastic Lagrangian modeling approach for inter-particle collisions in homogeneous isotropic turbulence. Int. J. Multiph. Flow 2001, 27, 1829–1858. [Google Scholar] [CrossRef]
- Berlemont, A.; Achim, P.; Chang, Z. Lagrangian approaches for particle collisions: The colliding particle velocity correlation in the multiple particles tracking method and in the stochastic approach. Phys. Fluids 2001, 13, 2946–2956. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Lipowsky, J.; Laín, S. (Keynote lecture). Transient Euler/Lagrange modelling for predicting unsteady rope behaviour in gas-particle flows. In Proceedings of the FEDSM2010 ASME Joint U.S.–European Fluids Engineering Summer Meeting, Montreal, QB, Canada, 1–5 August 2010. Paper No. FEDSM-ICNMM2010-31335. [Google Scholar]
- Laviéville, J.; Deutsch, E.; Simonin, O. Large eddy simulation of interactions between colliding particles and a homogeneous isotropic turbulence field. Gas-Solid-Flows 1995, 228, 347–357. [Google Scholar]
- Lipowsky, J.; Sommerfeld, M. Time dependent simulation of a swirling two-phase flow using an anisotropic turbulent dispersion model. In Proceedings of the ASME Fluids Engineering Summer Conference, Houston, TX, USA, 19–23 June 2005. Paper No. FEDSM2005-77210. [Google Scholar]
- Laín, S.; Ernst, M.; Sommerfeld, M. Colliding particle-pair velocity correlation function in turbulent flows. In Proceedings of the 7th International Conference on Multiphase Flow, ICMF 2010, Tampa, FL, USA, 30 May–4 June 2010. [Google Scholar]
- Zaichik, L.I.; Alipchenkov, V.M. Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 2003, 15, 1776–1787. [Google Scholar] [CrossRef]
- Ernst, M.; Sommerfeld, M. On the volume fraction effects of inertial colliding particles in homogeneous isotropic turbulence. ASME J. Fluids Eng. 2012, 134, 031302. [Google Scholar] [CrossRef]
- Ernst, M.; Sommerfeld, M.; Laín, S. Quantification of preferential concentration of colliding particles in a homogeneous isotropic turbulent flow. Int. J. Multiph. Flow 2019, 117, 163–181. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. Über die grundlegenden Berechnungen bei der Schwerkraftaufbe-reitung. Z. Ver. Deut. Ing. 1933, 77, 318–320. [Google Scholar]
- Comte-Bellot, G.; Corrsin, S. Simple Eulerian time correlation of full and narrow-band velocity signals in grid-generated, ‘isotropic’ turbulence. J. Fluid Mech. 1971, 48, 273–337. [Google Scholar] [CrossRef]
- Crowe, C.T. On the relative importance of particle-particle collisions in gas-particle flows. In Proceedings of the Conference on Gas Borne Particles, Oxford, UK, June 1981; pp. 135–137. Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCAL82X0129704 (accessed on 5 October 2020).
- Ten Cate, A.; Derksen, J.J.; Portela, L.M.; van den Akker, H.E.A. Fully resolved simulations of colliding monodisperse spheres in forced isotropic turbulence. J. Fluid Mech. 2004, 519, 233–271. [Google Scholar] [CrossRef]
- Saffman, P.G.; Turner, J.S. On the collisions of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Abrahamson, J. Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Vosskuhle, M. Particle Collisions in Turbulent Flows. Ph.D. Thesis, University of Lyon, Lyon, France, 2013. [Google Scholar]
- Sundaram, S.; Collins, L.R. Numerical Considerations in Simulating a Turbulent Suspension of Finite-Volume Particles. J. Comp. Phys. 1996, 124, 337–350. [Google Scholar] [CrossRef]
- Tanaka, T.; Tsuji, Y. Numerical simulation of gas-solid two-phase flow in a vertical pipe: On the effect of inter-particle collisions. ASME Gas-Solid-Flows 1991, 121, 123–128. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).