Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms
Abstract
1. Introduction
- The development and testing of a new functionality for the dual arm aerial manipulator: estimating the position of the robot relative to the grabbing point with one of the arms while the other is intended to conduct the operation on flight.
- The evaluation of the positioning accuracy in the estimation provided by the grabbing arm compared to the ground truth given by an Opti-Track system.
- The combination of passive (mechanical) and active (control) compliance methods in the grabbing arm to facilitate the accommodation of the aerial robot to sustained grabbing forces.
- The experimental evaluation and qualitative analysis of the effects of the grabbing arm and the injected disturbances over the stability of the multirotor controller.
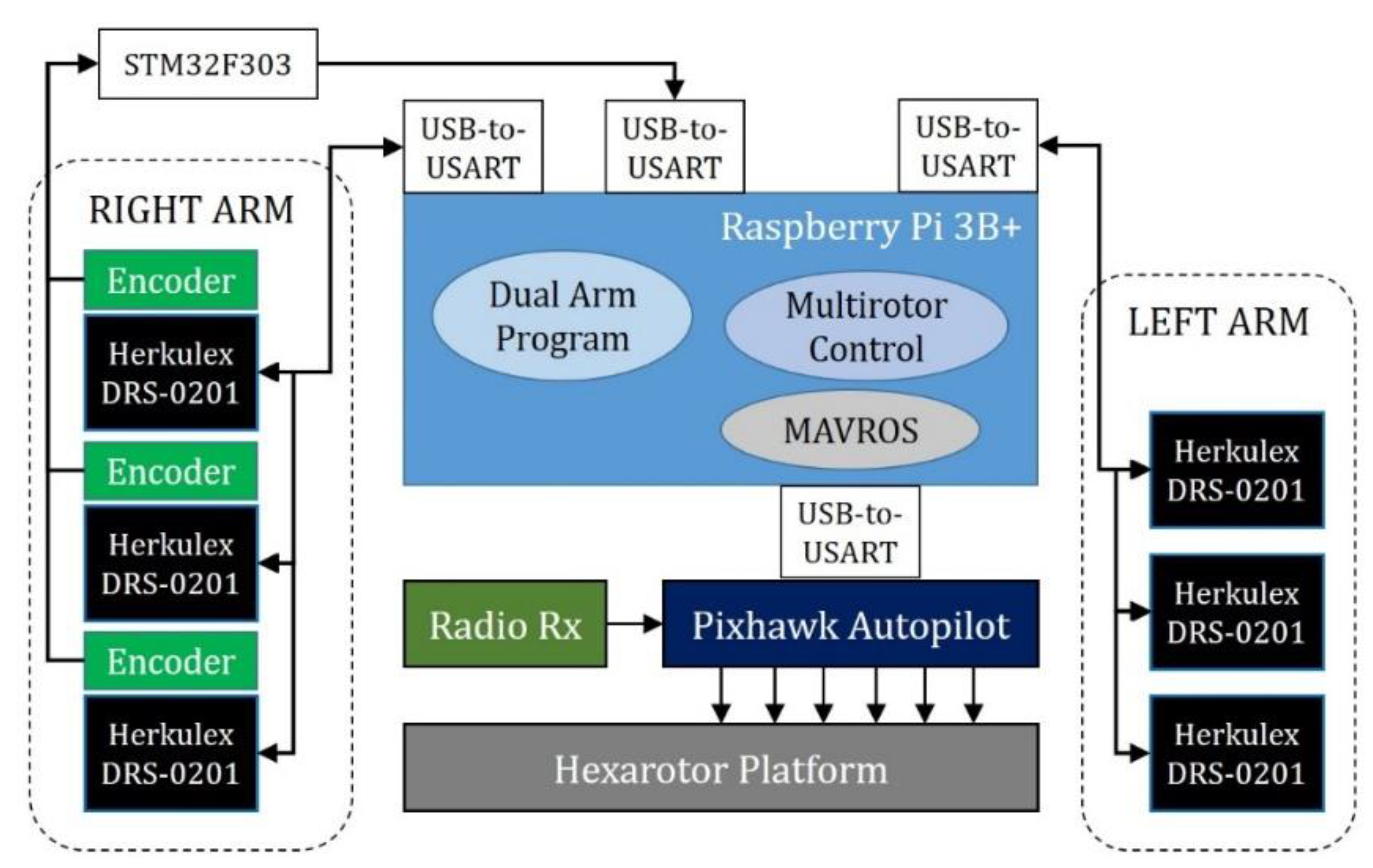
2. System Description
2.1. Compliant Dual Arm
2.2. Aerial Manipulation Robot
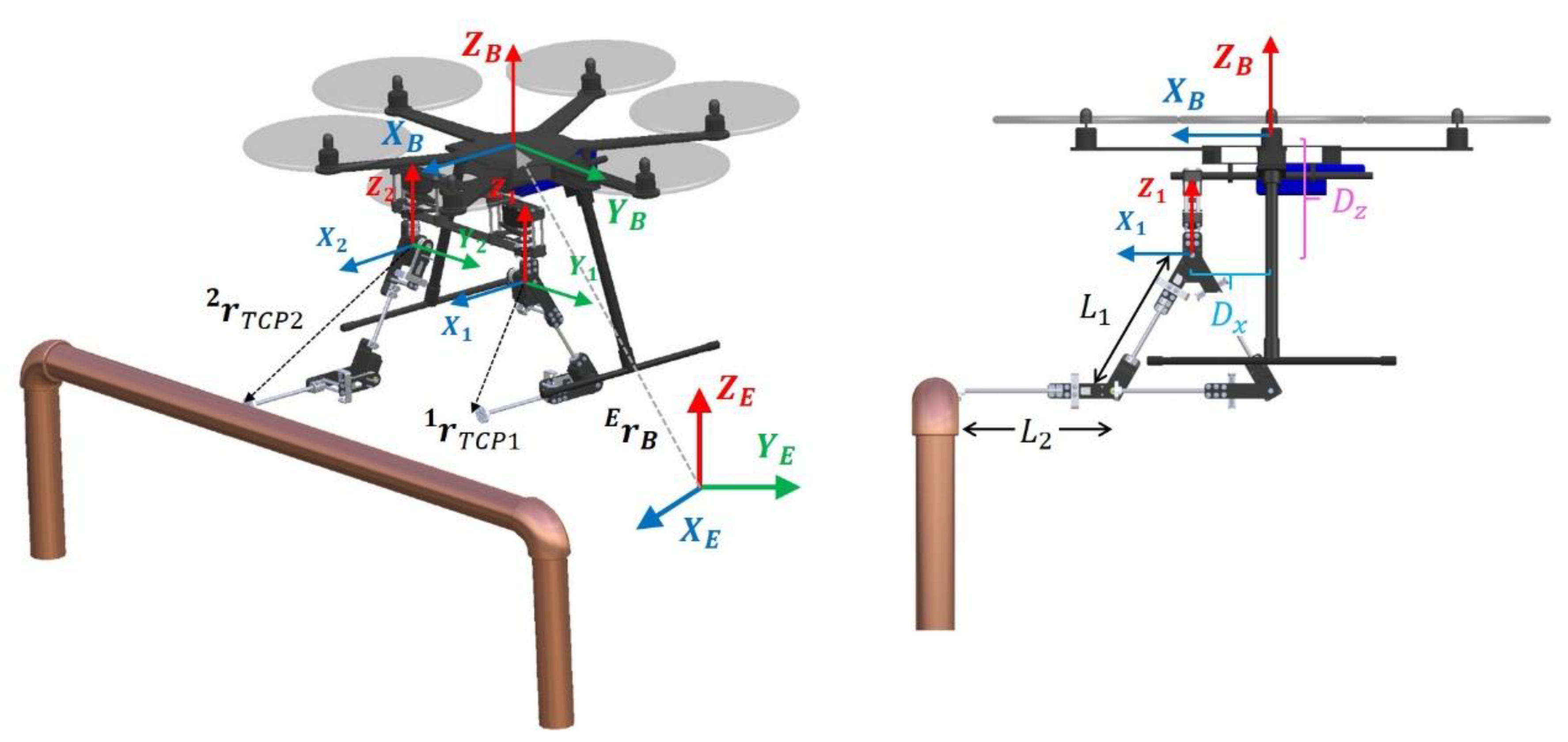
3. Modelling
3.1. Kinematics
3.2. Relative Position Estimation
3.3. Dynamics
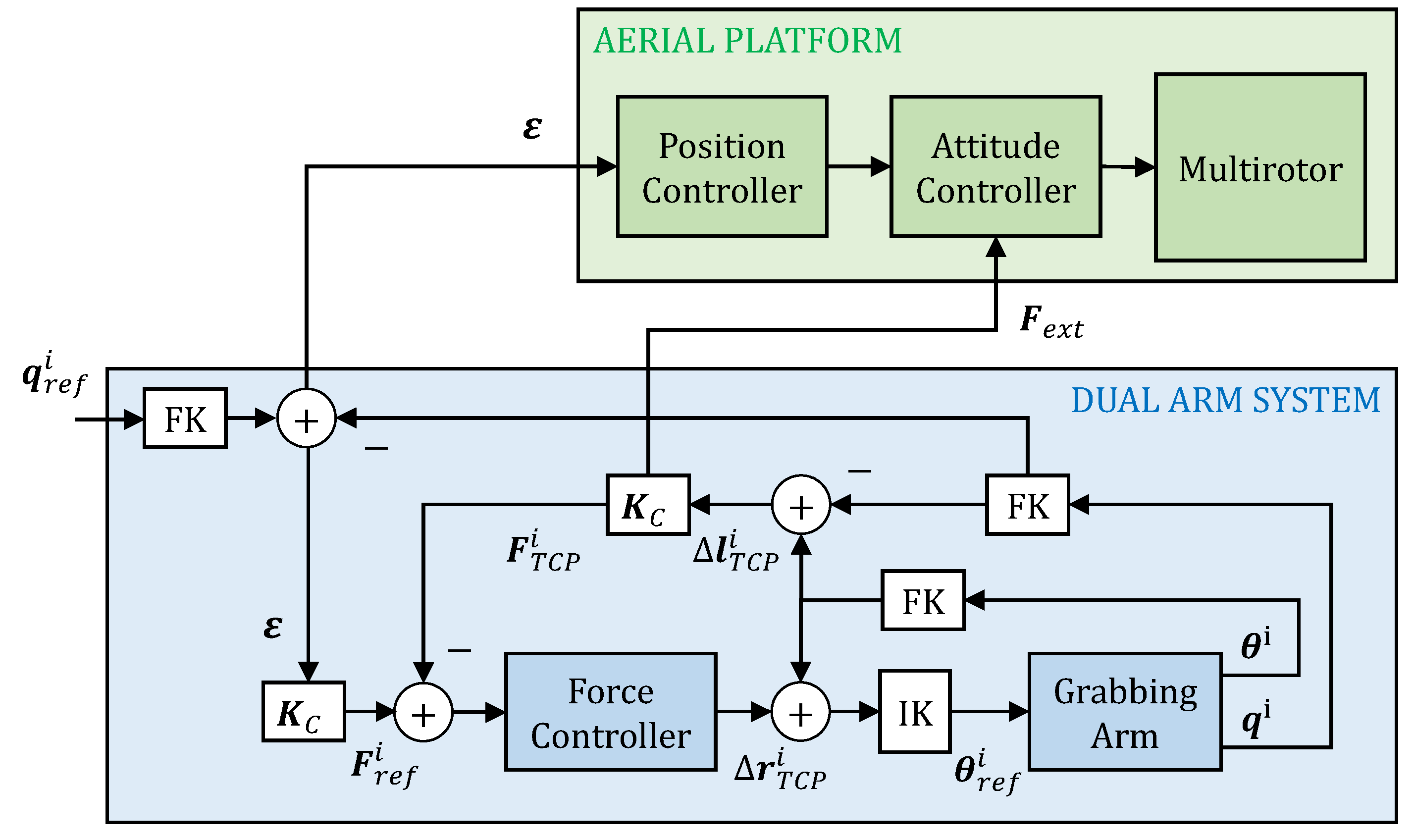
4. Control
4.1. Definition of the Control Task
- As relative position sensor, with zero torque control, so the reaction wrenches induced over the multirotor are relatively small.
- As an active impedance link, exerting a controlled force over the aerial platform to compensate external forces and guide the multirotor towards the reference position.
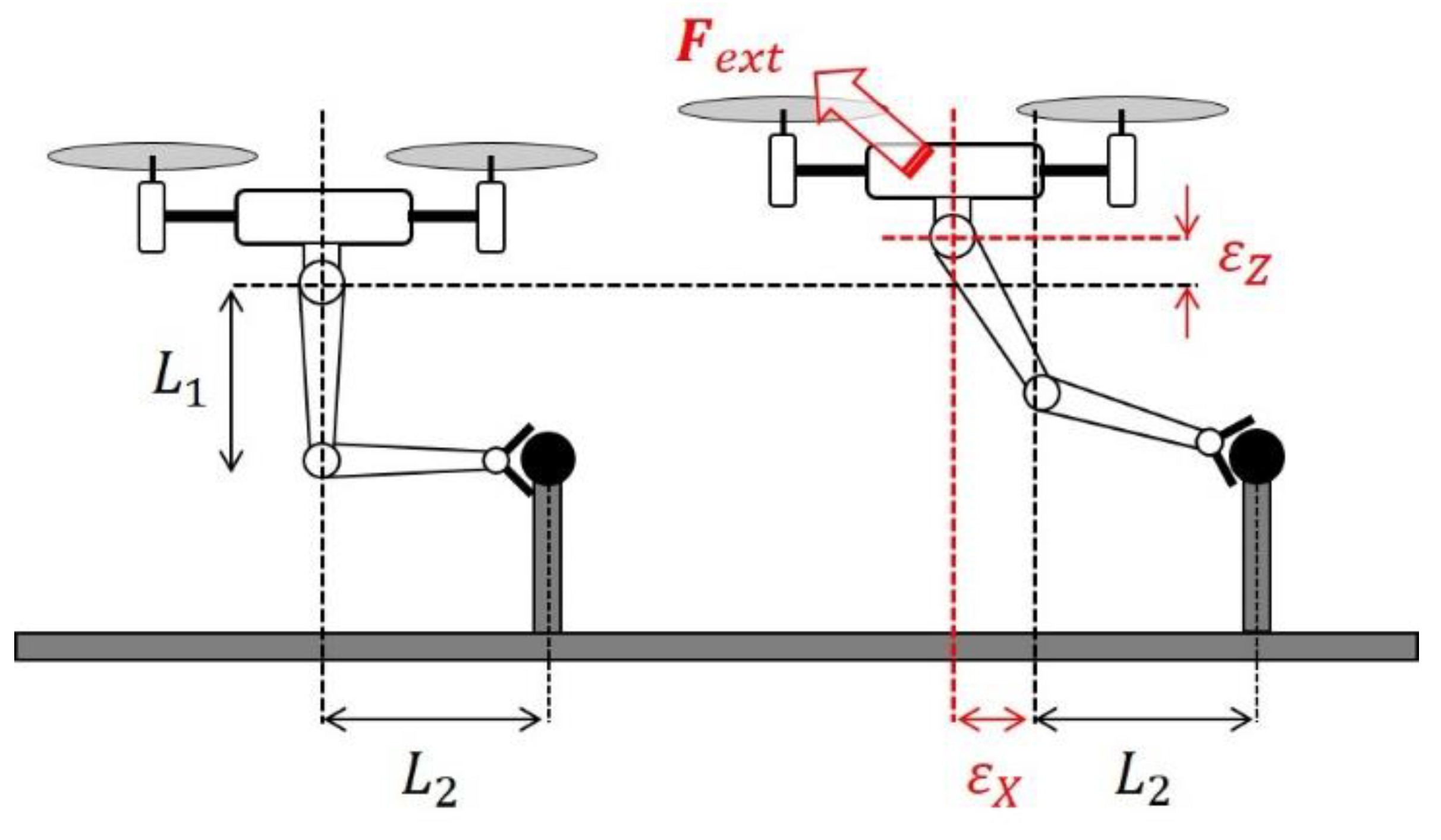
4.2. Impedance Control in Grabbing Conditions
4.3. Force Control Based on Cartesian Deflection
5. Experimental Results
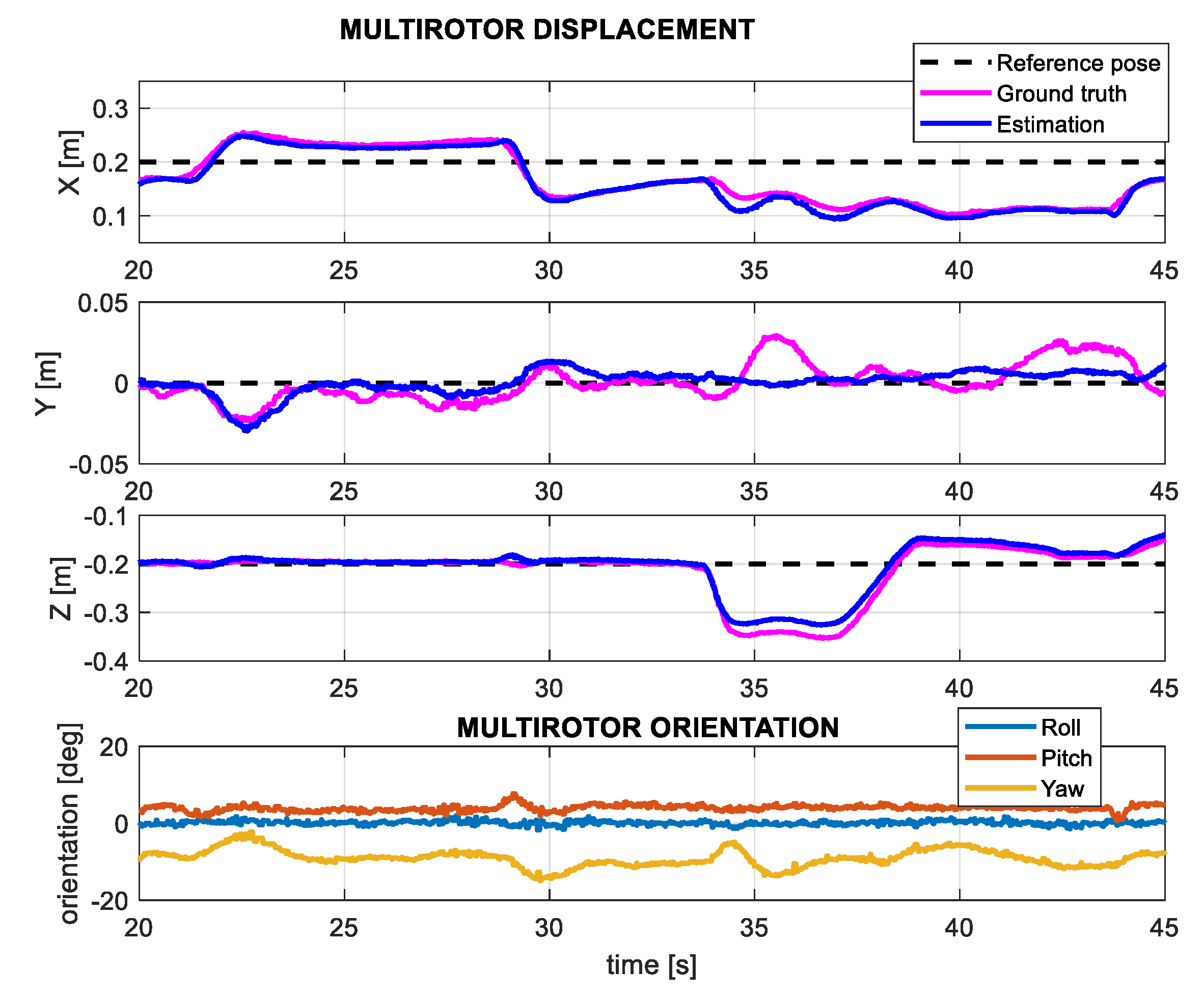
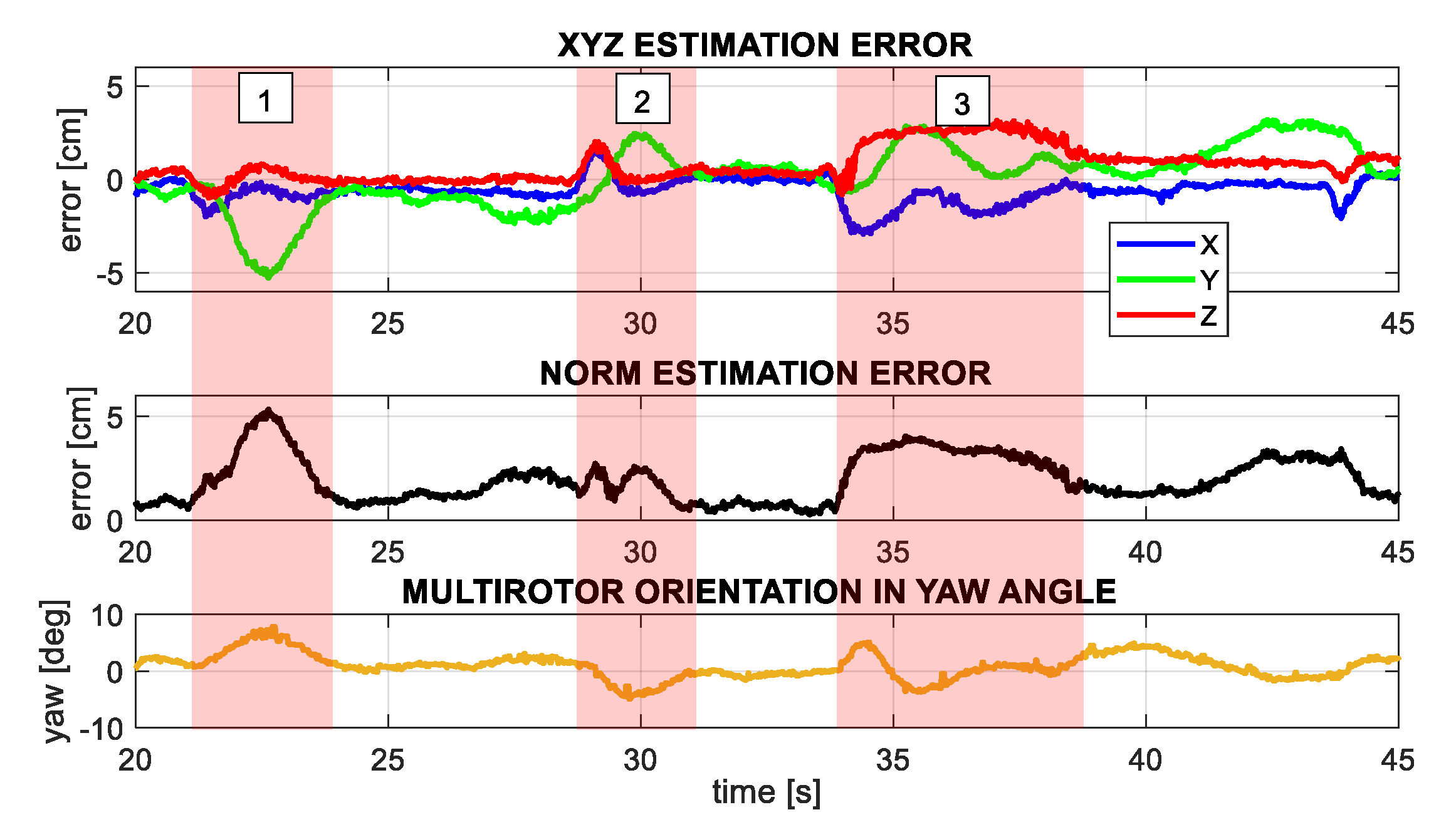
5.1. Position Estimation with Zero Deflection/Torque Control
- (1)
- The multirotor takes off.
- (2)
- The arms adopt the nominal operation pose given by Equation .
- (3)
- The aerial robot approaches the contact point using the Opti Track system for navigating.
- (4)
- Once the arm grabs the support structure, the zero-torque controller and the estimator are enabled while the multirotor is controlled in position with the Opti Track system.
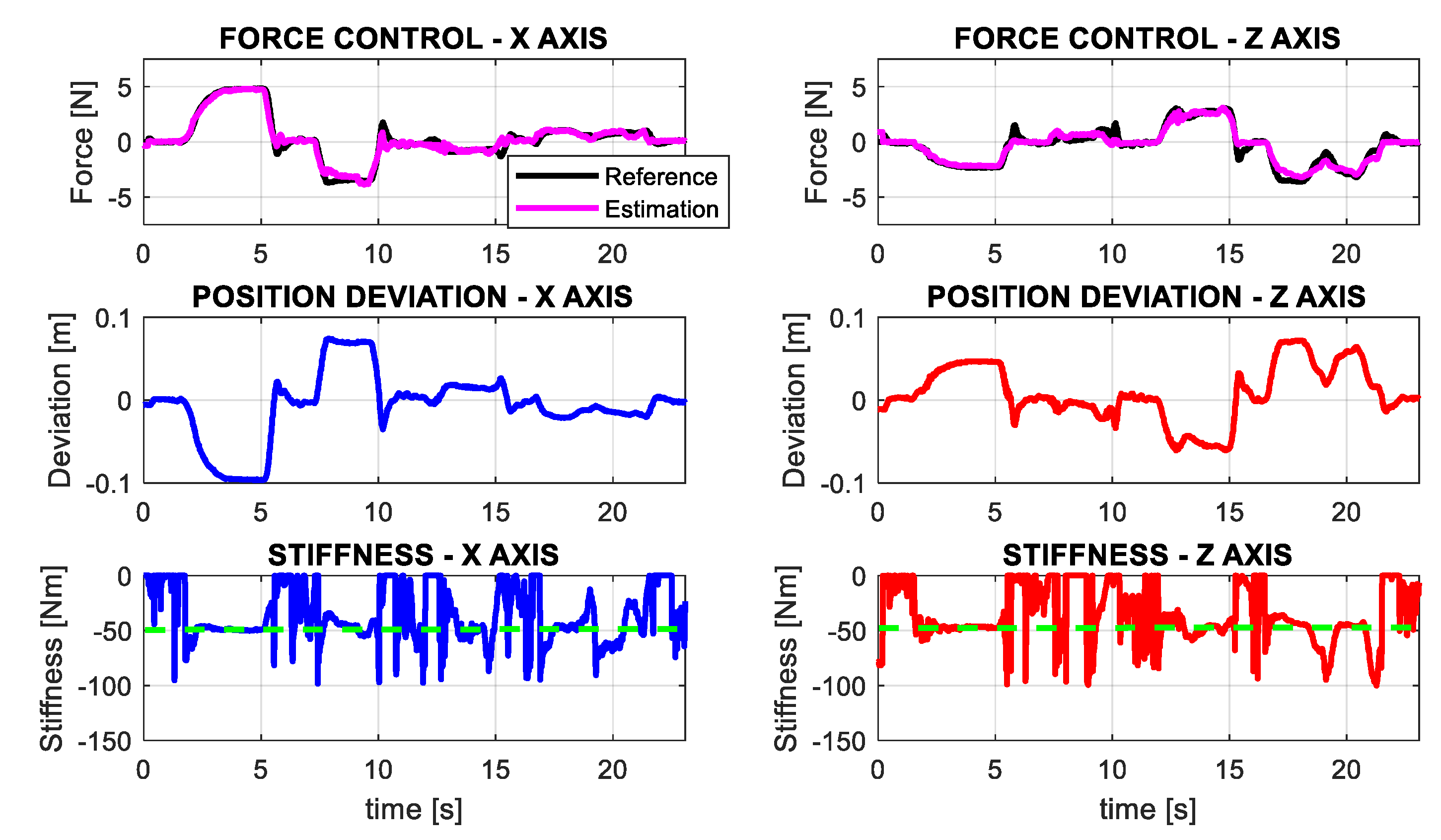
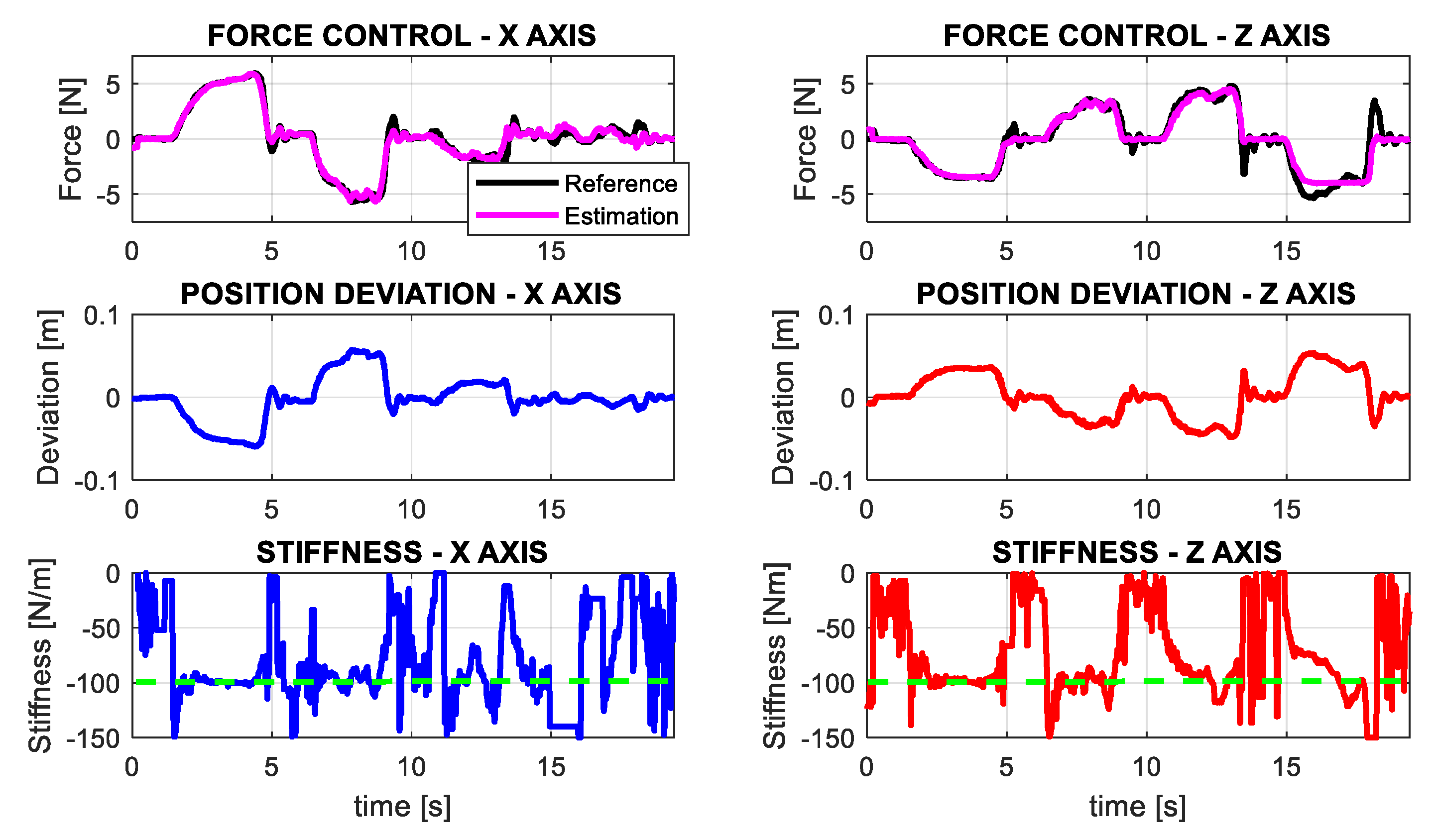
5.2. Impedance Control in Test-Bench
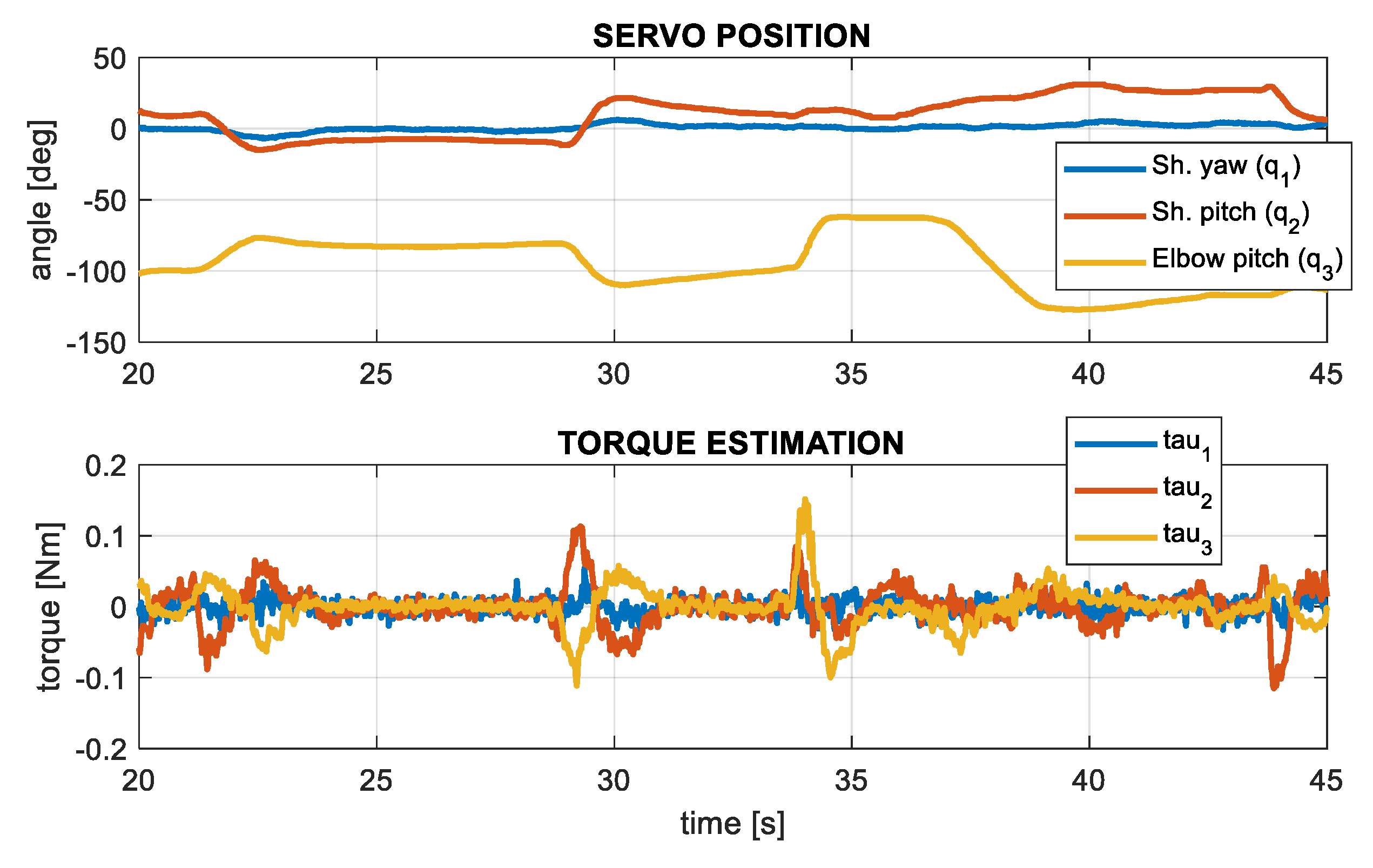
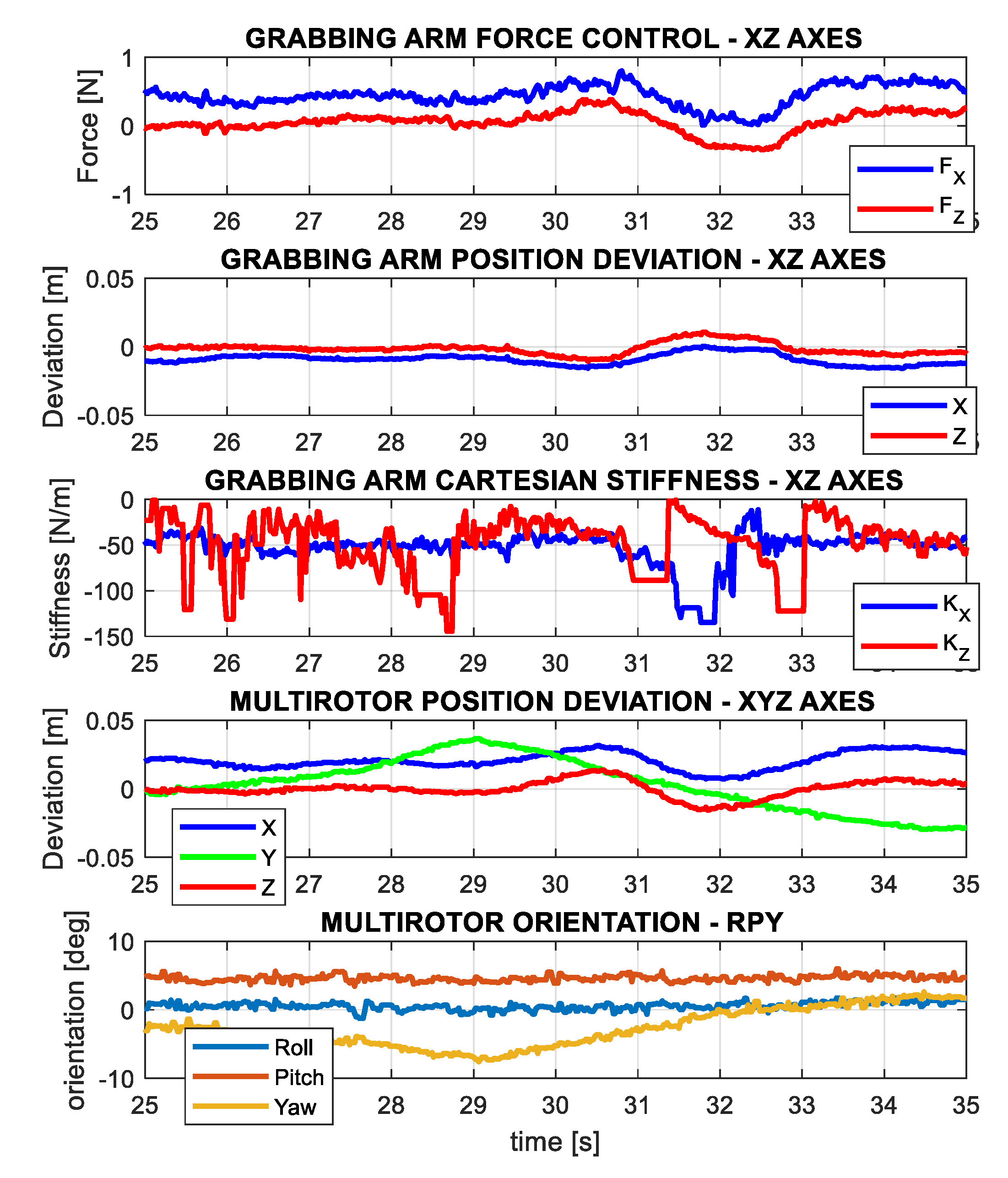
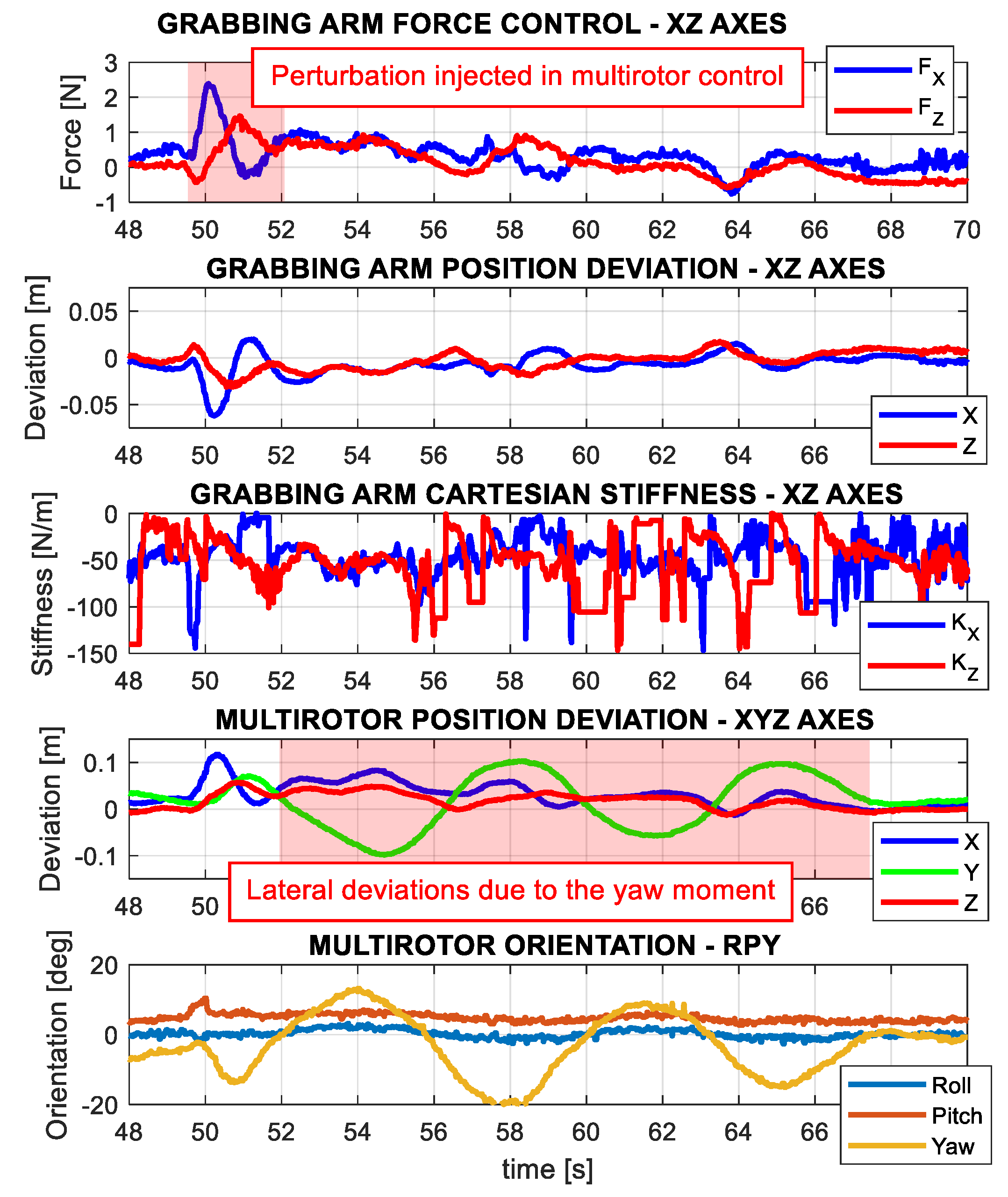
5.3. Grabbing Interaction on Flight with Impedance Control
- The aerial manipulator takes off with the arms resting in landing configuration.
- The grabbing arm adopts the nominal pose (L-shaped) while the operation arm is retracted.
- The impedance controller is enabled, imposing a zero reference for the first joint ().
- The aerial manipulator approaches to the linear structure until the magnetic gripper grabs it.
- The aerial manipulator hovers while the impedance controller of the grabbing arm is active.
- A position disturbance is injected through the radio controller to observe the response of the aerial manipulator and the reaction of the grabbing arm.
- The torque control of the servos is disabled to release the grabbing arm.
- The arms adopt the landing pose, and the platform goes back and lands.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Suarez, A.; Vega, V.M.; Fernandez, M.; Heredia, G.; Ollero, A. Benchmarks for Aerial Manipulation. IEEE Robot. Autom. Lett. 2020, 5, 2650–2657. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.; Kim, H.J. Aerial manipulation using a quadrotor with a two DOF robotic arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4990–4995. [Google Scholar]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Dexterous aerial robots—Mobile manipulation using unmanned aerial systems. IEEE Trans. Robot. 2017, 33, 1453–1466. [Google Scholar] [CrossRef]
- Cataldi, E.; Muscio, G.; Trujillo, M.A.; Rodriguez, Y.; Pierri, F.; Antonelli, G.; Caccavale, F.; Viguria, A.; Chiaverini, S.; Ollero, A. Impedance control of an aerial-manipulator: Preliminary results. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 3848–3853. [Google Scholar]
- Santamaria-Navarro, A.; Grosch, P.; Lippiello, V.; Solà, J.; Andrade-Cetto, J. Uncalibrated visual servo for unmanned aerial manipulation. Trans. Mechatron. 2017, 22, 1610–1621. [Google Scholar] [CrossRef]
- Tognon, M.; Chavez, H.A.T.; Gasparin, E.; Sable, Q.; Bicego, D.; Mallet, A.; Lany, M.; Santi, G.; Revaz, B.; Cortess, J.; et al. A truly-redundant aerial manipulator system with application to push-and-slide inspection in industrial plants. IEEE Robot. Autom. Lett. 2019, 4, 1846–1851. [Google Scholar] [CrossRef]
- Jimenez-Cano, A.E.; Sanchez-Cuevas, P.J.; Grau, P.; Ollero, A.; Heredia, G. Contact-based bridge inspection multirotors: Design, modeling, and control considering the ceiling effect. IEEE Robot. Autom. Lett. 2019, 4, 3561–3568. [Google Scholar] [CrossRef]
- Rhudy, M.B.; Chao, H.; Gu, Y. Wide-field optical flow aided inertial navigation for unmanned aerial vehicles. In Proceedings of the IEEE/RSJ Int. Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 674–679. [Google Scholar]
- Schmid, K.; Tomic, T.; Ruess, F.; Hirschmüller, H.; Suppa, M. Stereo vision based indoor/outdoor navigation for flying robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3955–3962. [Google Scholar]
- Faessler, M.; Fontana, F.; Forster, C.; Mueggler, E.; Pizzoli, M.; Scaramuzza, D. Autonomous, vision-based flight and live dense 3D mapping with a quadrotor micro aerial vehicle. J. Field Robot. 2016, 33, 431–450. [Google Scholar] [CrossRef]
- Huh, S.; Shim, D.H.; Kim, J. Integrated navigation system using camera and gimbaled laser scanner for indoor and outdoor autonomous flight of UAVs. In Proceedings of the IEEE/ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 3158–3163. [Google Scholar]
- Ramon Soria, P.; Arrue, B.C.; Ollero, A. A 3D-printable docking system for aerial robots: Controlling aerial robotic manipulators in outdoor industrial applications. IEEE Robot. Autom. Mag. 2019, 26, 44–53. [Google Scholar] [CrossRef]
- Ruggiero, F.; Trujillo, M.A.; Cano, R.; Ascorbe, H.; Viguria, A.; Perez, C.; Lippiello, V.; Ollero, A.; Siciliano, B. A multilayer control for multirotor UAVs equipped with a servo robot arm. In Proceedings of the IEEE Int. Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4014–4020. [Google Scholar]
- Suarez, A.; Jimenez-Cano, A.E.; Vega, V.M.; Heredia, G.; Rodriguez-Castaño, A.; Ollero, A. Design of a lightweight dual arm system for aerial manipulation. Mechatronics 2018, 50, 30–44. [Google Scholar] [CrossRef]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Forte, F.; Keemink, A.Q.L.; Stramigioli, S.; Carloni, R.; Marconi, L. Developing an aerial manipulator prototype: Physical interaction with the environment. IEEE Robot. Autom. Mag. 2014, 21, 41–50. [Google Scholar] [CrossRef]
- Hamaza, S.; Georgilas, I.; Fernandez, M.; Sanchez, P.; Richardson, T.; Heredia, G.; Ollero, A. Sensor installation and retrieval operations using an unmanned aerial manipulator. IEEE Robot. Autom. Lett. 2019, 4, 2793–2800. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Physical-virtual impedance control in ultralightweight and compliant dual-arm aerial manipulators. IEEE Robot. Autom. Lett. 2018, 3, 2553–2560. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfändler, P.; Angst, U.; Siegwart, R.; Nieto, J. An omnidirectional aerial manipulation platform for contact-based inspection. In Proceedings of Robotics: Science and Systems. arXiv 2019, arXiv:1905.03502. [Google Scholar]
- Ruggiero, F.; Cacace, J.; Sadeghian, H.; Lippiello, V. Impedance control of VToL UAVs with a momentum-based external generalized forces estimator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2093–2099. [Google Scholar]
- Tomić, T.; Haddadin, S. A unified framework for external wrench estimation, interaction control and collision reflexes for flying robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4197–4204. [Google Scholar]
- Suarez, A.; Real, F.; Vega, V.M.; Heredia, G.; Rodriguez-Castaño, A.; Ollero, A. Compliant bimanual aerial manipulation: Standard and long reach configurations. IEEE Access 2020, 8, 88844–88865. [Google Scholar] [CrossRef]
- Suarez, A.; Heredia, G.; Ollero, A. Lightweight compliant arm with compliant finger for aerial manipulation and inspection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4449–4454. [Google Scholar]
- AERIAL-CORE Project Home Page. Available online: https://aerial-core.eu/ (accessed on 12 October 2020).
- Real, F.; Torres-González, A.; Ramon-Soria, P.; Capitan, J.; Ollero, A. UAL: An abstraction layer for unmanned aerial vehicles. In Proceedings of the 2nd International Symposium on Aerial Robotics, Philadelphia, PA, USA, 11–12 June 2018. [Google Scholar]
- Perez-Jimenez, M.; Montes-Grova, M.A.; Ramon-Soria, P.; Arrue, B.C.; Ollero, A. POSITRON: Lightweight active positioning compliant joints robotic arm in power lines inspection. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 729–736. [Google Scholar]
- Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Characterization of the aerodynamic ground effect and its influence in multirotor control. Int. J. Aerosp. Eng. 2017, 2017, 1823056. [Google Scholar] [CrossRef]
- Liu, T.; Lei, Y.; Han, L.; Xu, W.; Zou, H. Coordinated resolved motion control of dual-arm manipulators with closed chain. Int. J. Adv. Robot. Syst. 2016, 13, 80. [Google Scholar] [CrossRef]
- Lee, J.; Chang, P.H.; Jamisola, R.S. Relative impedance control of dual-arm robots performing asymmetric bimanual tasks. Trans. Ind. Electron. 2014, 61, 3786–3796. [Google Scholar] [CrossRef]
- Stolfi, A.; Gasbarri, P.; Sabatini, M. A combined impedance-PD approach for controlling a dual-arm space manipulator in the capture of a non-cooperative target. Acta Astronaut. 2017, 139, 243–253. [Google Scholar] [CrossRef]


| Total Weight | 1.0 (kg) |
|---|---|
| Maximum lift load (1 s playtime) | At elbow: 0.3 (kg) |
| At shoulder: 0.12 (kg) | |
| Joint stiffness | 5 (Nm/rad)—all joints |
| Maximum joint speed | 300 (°/s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suarez, A.; Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms. Appl. Sci. 2020, 10, 8927. https://doi.org/10.3390/app10248927
Suarez A, Sanchez-Cuevas PJ, Heredia G, Ollero A. Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms. Applied Sciences. 2020; 10(24):8927. https://doi.org/10.3390/app10248927
Chicago/Turabian StyleSuarez, Alejandro, Pedro J. Sanchez-Cuevas, Guillermo Heredia, and Anibal Ollero. 2020. "Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms" Applied Sciences 10, no. 24: 8927. https://doi.org/10.3390/app10248927
APA StyleSuarez, A., Sanchez-Cuevas, P. J., Heredia, G., & Ollero, A. (2020). Aerial Physical Interaction in Grabbing Conditions with Lightweight and Compliant Dual Arms. Applied Sciences, 10(24), 8927. https://doi.org/10.3390/app10248927






