1. Introduction
The marine world is rapidly changing as humans perform a number of activities, such as fish stocking, shipping, aquaculture, pollution and habitat modification, which result in ecological and economic damage. Species distribution models (SDMs) provide a measure of species occupancy in response to the local/regional oceanographic and environmental conditions and habitat [
1]. Such models combine occurrence locations of known species with a series of environmental layers, by developing a statistical inference system which unveils the impact of environmental parameters on specific species distribution patterns and by expanding the species distribution layer towards unknown areas. Distribution models for marine organisms and habitat mapping are essential tools in understanding the links between the ecology of marine fishes and the factors that affect species presence/absence patterns [
2].
The ecosystem approach to fisheries has been gaining attention, with spatial fishing restrictions and marine protected areas being considered as vital tools against overfishing [
3]. Reliable distribution models with high resolution and extensive coverage are required to improve and replace existing ones (i.e., AquaMaps
www.aquamaps.org from FishBase
www.fishbase.de).
Furthermore, the improvement of fish distribution models is of great importance within the context of climate change [
4], especially in the case of the Mediterranean Sea, where the number of marine species migrating through the Suez Canal—as a result of sea warming (among other factors)—has been increasing rapidly during the last 20 years [
5]. Sea warming also affects the native marine fauna of the Mediterranean Sea, by changing their geographical distribution, depending on thermal preferences of each species [
6]. Species with preference for warmer waters expand northwards and increase their abundance, whereas species with preference for colder waters decline in abundance and restrict their range [
7].
Small and medium pelagic fishes are highly affected by oceanographic, environmental, and climatic changes, as well as by human impact. They correspond to about one quarter of the globally exploited marine fisheries catch, while clupeoid species account to more than 40% of the total catches in the Mediterranean Sea [
8]. European sardine (
Sardina pilchardus) and European anchovy (
Engraulis encrasicolus) make up the vast majority of landings across the western, central, and eastern Mediterranean [
9]. In the Mediterranean Sea, small pelagic fishes are mainly being exploited by the purse-seine fleet, which also collects, albeit at lower quantities, medium pelagic fishes such as Atlantic mackerel (
Scomber scombrus), Atlantic chub mackerel (
Scomber colias), and horse mackerels (
Trachurus spp.). Limited quantities of small and medium pelagic fishes are also caught by bottom-trawlers and boat-seiners depending on the area and the season.
The landings of most small pelagic species in most areas of the Mediterranean Sea appear to be declining partly due to their overexploitation and partly due to climate and environmental forcing. Because of their fast life history strategy (rapid growth, early maturity, short lifespan), small pelagic fishes and especially their recruitment [
10] are dependent on climate and environmental factors [
9,
11,
12,
13].
Although the environmental effects on fish species distribution and population dynamics in terms of presence/absence or probability of occurrence have been described well enough at various parts of the Mediterranean [
14,
15,
16], a comprehensive approach to the relative impact of each environmental component on fish species distribution for the whole Sea is still missing. SDMs, or else ‘environmental niche models’, may provide quantified relationships between fish species occurrence and environmental predictors, while assuming other ecological processes as unimportant.
Several researchers have developed models for various species using different training samples, predictors, study areas, machine learning algorithms, and models [
17,
18,
19,
20,
21,
22,
23,
24,
25]. Almost all models follow the presence/absence approach with observation records obtained from online data collections like OBIS, GBIF, Catalog of Life, ICES, Reef Life Survey (RLS) [
17,
19,
20,
22], museums and literature [
20,
23,
25], environmental projects [
22], and own sampling [
21,
26]. Some studies also create pseudo-absence records in their attempt to device a reliable model [
17,
27].
A potential drawback of the above mentioned data-driven models would be the generally limited records in the databases used (ranging from 30 to 8000, with 250 on average). The spatial resolution of the variables varies depending on spatial coverage—mostly
arc-minutes for large-scale studies, with the exceptions of low resolutions of 1 to 2 arc-minutes [
23] and high resolutions of
arc-minutes for local studies [
28]. The most frequently studied seas are the Atlantic [
20,
23] and the North Sea [
22], while there are a few models for the Mediterranean, mostly for regional seas [
18,
28], and rarely for the whole basin [
17].
The machine learning algorithms that have been used in these fishery SDMs are Logistic Regression [
17], other Generalized Linear Models (GLM) [
19,
22,
25], Support Vector Machines (SVM) [
17,
22], Gradient Boosting Models (GBM) [
22,
25], Decision Trees [
18], Genetic Algorithms for Rule Set Production (GARP) [
22,
23], Random Forests [
19,
22,
25], Multivariate Adaptive Regression Splines (MARS) [
22,
25], Maximum Entropy (MaxEnt) [
19,
22,
25,
29] and Artificial Neural Network (ANN) [
17,
18]. Some studies use ensembles [
17], while others test existing environmental models [
17,
19,
22] and Favourability Functions [
30].
Regarding the number of predictors, to our knowledge, all studies except one [
29] used about 5 to 20 features. Very few took advantage of feature selection and variable importance pre-processing, and the ones that did used correlation [
19,
28], some filter methods [
18], permutation importance [
25], and embedded MaxEnt variable importance [
29]. Finally, there are various SDM approaches [
24], that model the distribution of multiple species and their interrelations simultaneously. These approaches are out of scope of the current work.
As it can be concluded from the previous works and according to Leidenberger et al. [
20] and Elith et al. [
31], there are some limitations to SDMs and most of them can be improved in a number of ways. Typically, there are insufficient observations and a limited number of environmental variables available to train effective machine learning models, presence-absence data are unbalanced, absence data are often not available or artificially created, resolution is poor, and there is collinearity in the data. Therefore, the principal aim of the present work is to overcome these challenges.
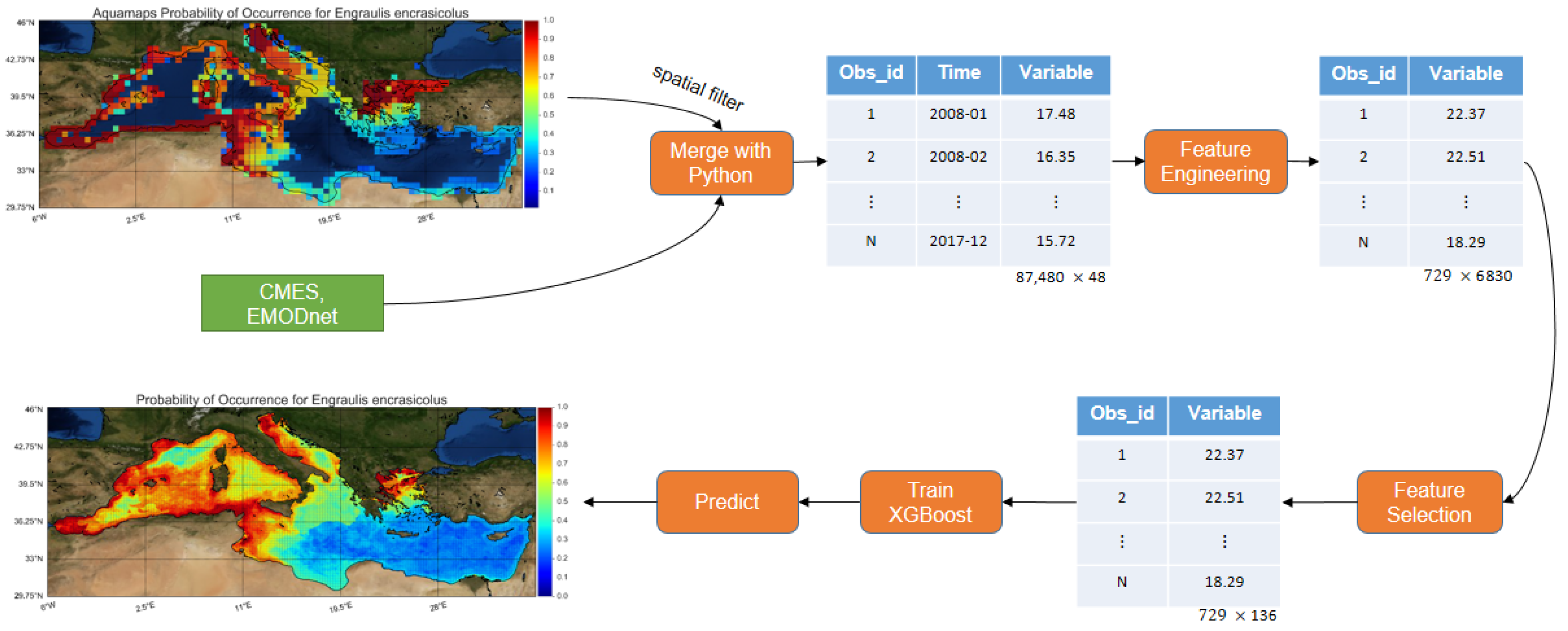
More specifically, the herein developed model was trained with roughly
times more observations than the average related work (improvement over observations). With the use of feature engineering, 6830 features were extracted and subsequently, feature selection was performed, leading to the selection of the most important ones (improvement over features and collinearity). Finally, a machine learning algorithm that has never been applied in previous SDM literature, namely, XGBoost [
32] was used. XGBoost offers regularization preventing the model from overfitting, it can handle missing values and it provides the optimum number of boosting iterations in a single run, minimizing the time needed for its performance. Instead of using presence-absence data for binary classification, like most studies do, the problem was transformed to a regression one (improving the unbalance of presence-absence datasets) and predict the probability of occurrence based on data provided by the AquaMaps database. Furthermore, fish species distributions were interrelated to oceanographic and environmental conditions, utilizing the high resolution Copernicus Marine Environmental Service (CMEMS) products [
33] and the European Marine Observation and Data Network (EMODnet) [
34] databases for the whole Mediterranean Sea. The best feature categories and environmental predictors for each species and overall were analyzed. Finally, with the use of the trained SDM, AquaMaps spatial resolution was improved (
higher) and high resolution maps (0.0625 arc-minutes) without any spatial gaps were constructed, covering the whole Mediterranean Sea, for the eight commercial pelagic fish species.
4. Discussion
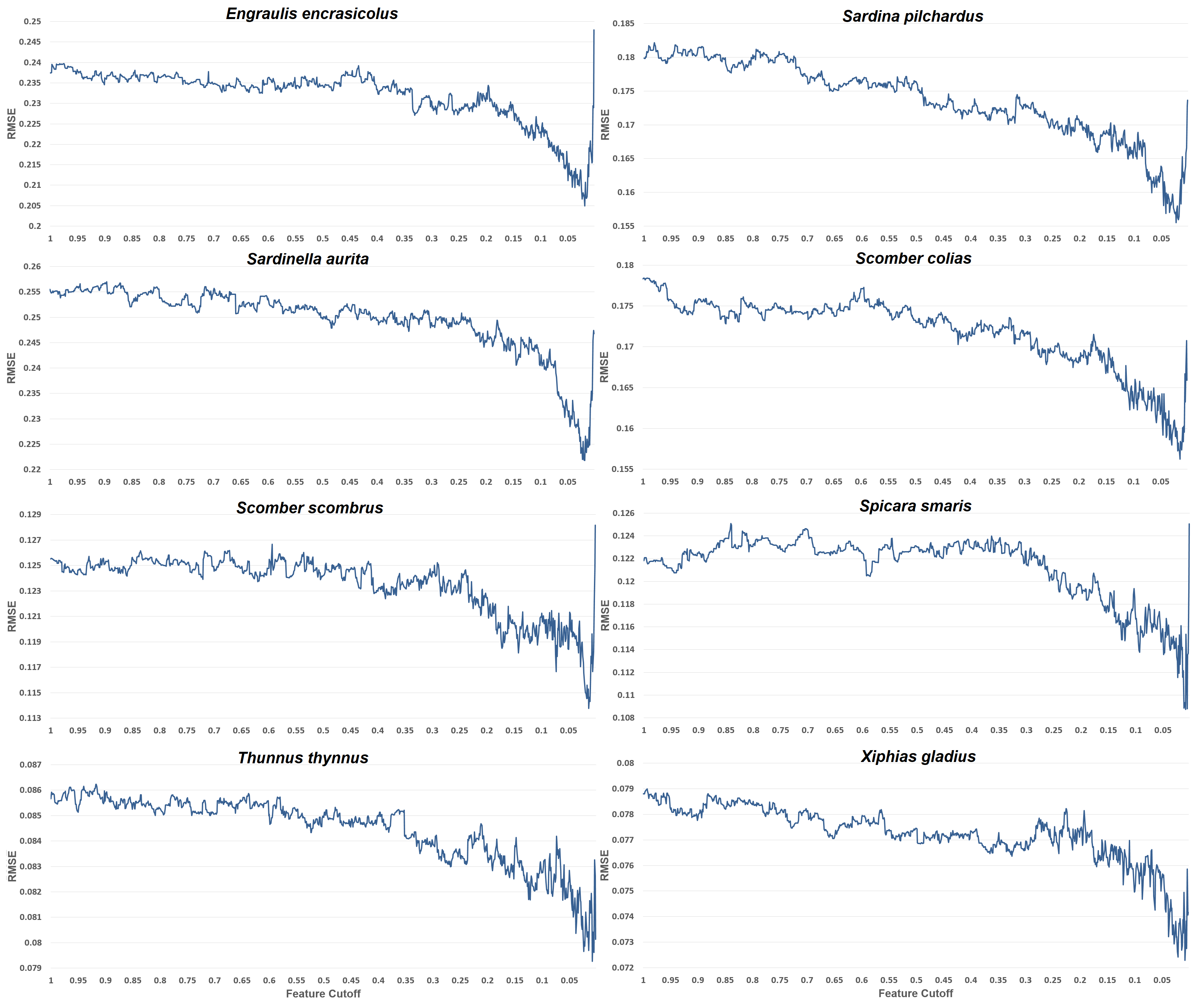
Understanding the environmental processes influencing fish species abundance is important in order to manage the fishing grounds and offer advice on the exploitation of this important resource. It is evident that out of the 6830 features that our feature engineering process generated, about 136 (or 2%) of these are the most important and are advised to be used to reach the lowest possible prediction error. Most of the other species distribution studies, use about 5 to 20 features for their models, which are an order fewer than the 136 used in the present model. This happens because (a) very few studies (if any of them) use time series features, (b) they do not generate such a huge number of features to choose from, (c) they empirically pick the features depending on their domain knowledge and data availability. The present approach is different from the existing studies in this respect. It is not limited to basic features like maximum sea surface temperature or mean salinity, but it expands upon very detailed time series features. It suggests that about 2% of such features are appropriate for all our datasets, and if less predictors are used, then performance worsens. For overfitting and generalization purposes the exact number of features that minimizes their RMSE for each species is not used, but rather a better bias-variance trade-off feature cutoff is preferred.
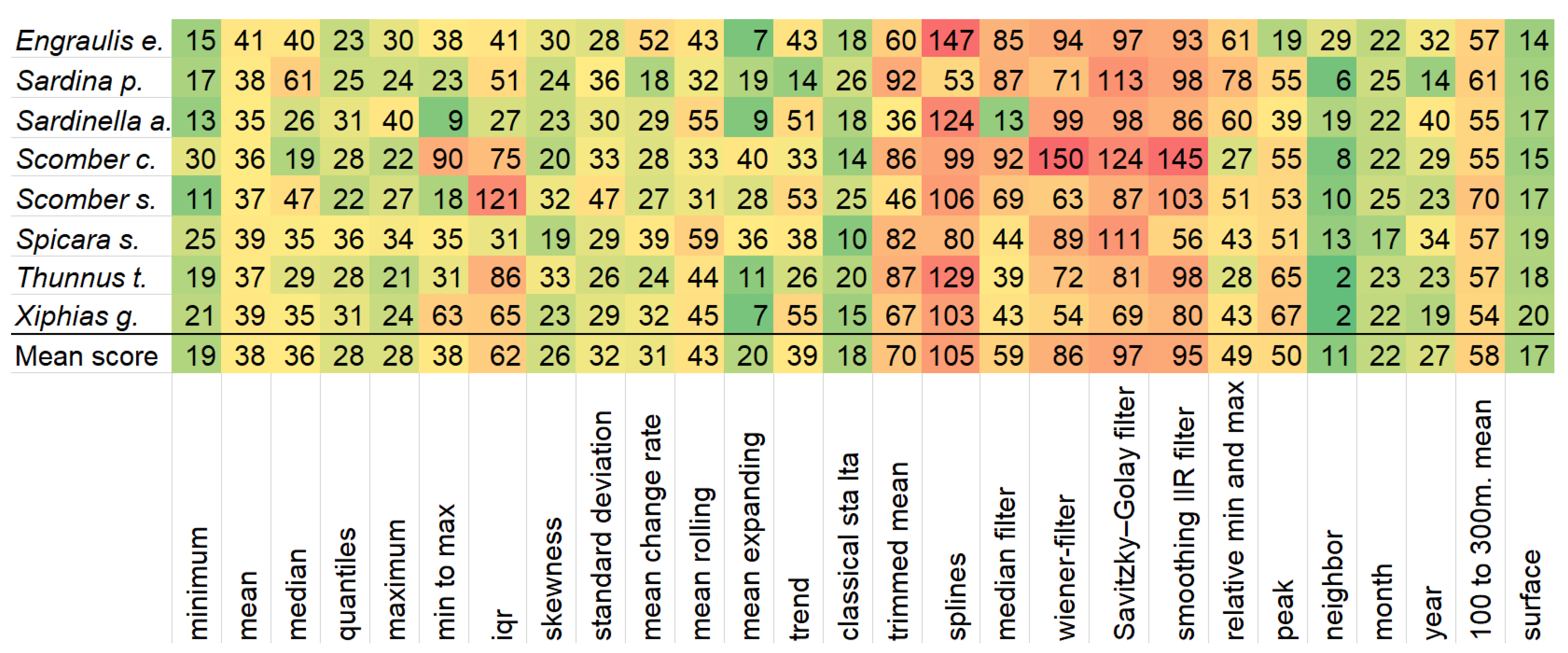
Having very few features, the model’s reliability diminishes, since these features are very specialized, and case only the very top-ranked ones are kept, whole predictors like chlorophyll or nitrate cease to exist in the model. Thus, having only variations of temperature is not enough. The whole feature selection process not only boosts execution time and performance, but also gives valuable insights into which variables are most important for each species. These insights are depicted in
Figure 4, where the importance of feature categories generated by the feature engineering process is visible.
The figure clearly shows which feature categories are worth investing time in feature engineering and which are not. The neighbor-based features seem to be the strongest ones. This is the only hand-crafted feature and it computes the minimum, mean, maximum and standard deviation of the eight cells that surround the given one on all predictors. For example, the feature ‘temperatureSurface_neighbor_mean’ calculates for every observation the mean surface temperature of its eight neighboring observations. Surrounding cells have been mentioned before [
28] that might influence the distribution of species. It is evident that the probability of species presence is greatly affected by the conditions of the neighboring environmental parameters. This means that the species live in large areas next to each other and not in small isolated ones with different conditions. The importance of neighboring features comes in agreement with the fact that longitude and latitude predictors are also vital as it will be demonstrated later on. In the same manner, features with extreme values depict strong importance. Minima, maxima and quantiles are much stronger in terms of importance than means and medians. These results are in line with the bibliography, as the authors of Reference [
57] state that quantiles near the maximum create good features when other variables are not limiting, and Reference [
58] claims that low quantiles are relevant to estimate the lowest recruitment level for a species. Another feature of descriptive statistics, which is of major importance is skewness.
It is very common for researchers to use mean-monthly data [
16,
59] and only rarely mean-annual data. In this study, it was demonstrated that both feature categories are strong, with the monthly features being slightly better. This happens because some stages in fish life, such as breeding and migration, occur in certain months. By comparing the surface values to the mean of 100 to 300 m, it becomes clear that the latter falls behind. Conditions found below the surface are rarely accurately known [
60], thus it is advised to use surface values. All feature categories from the signal processing area related to filters are the worst performing ones. The mean expanding (exponential window) and classical sta-lta (Short Time Average over Long Time Average), which is used in seismic events, obtained very high importance. One would expect that relative minima and maxima and peaks would be good feature categories, like the minimums and maximums of the descriptive statistics. This is not true, as all the temporal environmental variables have high seasonality and the peaks are insignificant.
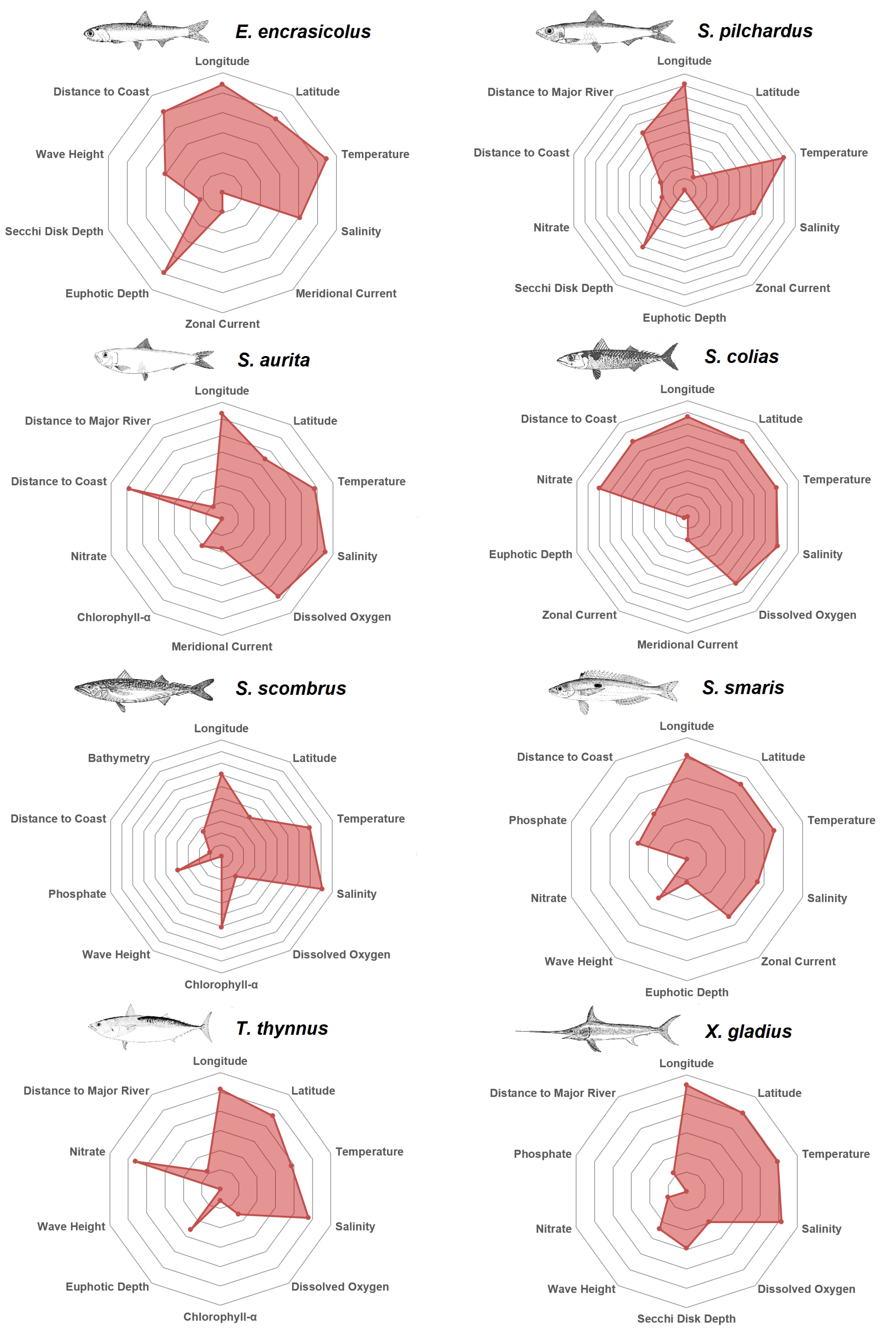
After having investigated the features and their respective predictors that were considered as most valuable by the Reciprocal Ranking technique, in
Figure 5 the top 10 predictors for each species are depicted in alphabetical order. The plots are qualitative and normalized so that the 10th predictor would be at the center of the plot. Every decagon represents one unit in terms of Reciprocal Ranking importance. For example, anchovy zonal current is five times less important than distance from the coast. Longitude is among the top predictors for every species, in agreement with the western-to-eastern gradient in the trophic conditions of the Mediterranean Sea. This longitudinal gradient represents changes in water temperature, chlorophyll concentration and mixed layer depth over the epipelagic layer [
61]. The Anchovy is mostly affected by the distance from the coast, the temperature and the euphotic depth; pilchard by water temperature, salinity, secchi disk depth and distance from the major rivers; round sardinella by salinity, temperature, distance from the coast and dissolved oxygen; atlantic chub mackerel by salinity, temperature, latitude, nitrate and distance to from the coast; atlantic mackerel by salinity, temperature and chlorophyll-
; picarel by temperature, zonal current, salinity and latitude; bluefin tuna by salinity, nitrate and latitude, and swordfish by salinity, temperature and latitude.
Because of their fast life history strategy (rapid growth, early maturation, short lifespan), small pelagic fishes and especially their recruitment success [
10], hence their distribution, abundance and fishery catches, are vulnerable to climate and environmental forcing [
12,
13,
42]. However, the decline in landings of most small and medium pelagic species is only partially attributed to climate and environmental factors because, especially in the Mediterranean Sea, over-exploitation still remains the main driving force of their populations [
9,
62]. Indeed, overfishing has been reported to modify the abundance, composition, and distribution of pelagic species, but also to induce drastic changes of state [
63].
Following the above-described west-to-east gradient, the probability of occurrence of small pelagic fishes was higher in the western Mediterranean Sea and declined eastwards (
Figure 6) with the exception of picarel, which was abundant throughout the basin. For medium and large-sized pelagic fishes, the probability of occurrence was higher in certain areas of the western and northern Mediterranean, while they were completely absent from the southeastern part of the basin, as a results of the raised temperature and salinity and the low chlorophyll levels at the surface layer (
Figure 6). Small and medium pelagic species are generally concentrated in areas of high productivity because most of them are mainly plankton feeders [
64]. These areas are associated with cooler and fresher nutrient rich water masses that could be either upwelling areas (e.g., west African coast: [
63]), coastal areas affected by riverine input (e.g. NW Mediterranean: [
65]) or areas affected by both riverine input and other water masses (e.g. Black Sea Water influx in the northern Aegean Sea: [
66]). These conditions are typical for the northern Mediterranean coastline and create a northwestern-to-southeastern gradient in productivity. Indeed, biological productivity in the Mediterranean basin has been reported to decrease from north to south and from west to east and it is inversely related to the increase in temperature and salinity [
67] indicating that the Mediterranean Sea is highly heterogeneous between its basins [
68]. This gradient makes longitude appear vital in the distribution of pelagic species and even latitude seems significant, despite the narrow latitudinal axis of the Mediterranean due to riverine input that mostly affects the northern coastline. Changes in primary productivity, the composition of plankton community and the abundance of key plankton species, that may be climate-driven [
69], directly affect the distribution of small pelagic fishes, which preferentially feed on zooplankton, such us anchovy and sardine [
70], but they could also indirectly affect their somatic condition [
10]. Enhanced primary and secondary productivity benefits these planktivorous species by increasing the availability of their prey (bottom-up control), but at the same time improves their somatic condition [
71]. Although NW Mediterranean is richer in pelagic fishes, sharp regional gradients and gaps in the probability of occurrence exist, mostly in anchovy and round sardinella distribution (
Figure 6a,c). Strong currents and meso-scale eddies in Alboran Sea, the Tyrrhenian Current and the Liguro-Provençal Current favor the presence of these species. In the Gulf of Lions the freshwater impact of Rhone River and the up- and downwelling events explain the sharp differences in fish species occurrence.
According to the findings of the present work (
Figure 5,
Table 7), temperature and salinity are the main drivers of the distribution of most small and medium pelagic fishes in the Mediterranean. The spatial distribution and the abundance of small and medium pelagic species may be directly affected by sea surface temperature (SST) [
72], but the effect of SST can be also indirect through changes in the planktonic components of the food webs [
13] that constitute the main prey for small pelagic fishes [
64]. The effect of SST, however, is not uniform across species and it depends on their thermal preferences [
7], which may vary among the pelagic fishes [
9]. Sardine, for example shows preference for colder waters compared to round sardinella and anchovy, and appears to confine its distribution and shrink its spawning grounds to colder waters when SST increases [
46], a condition that affects its fisheries. This negative relationship between sardine landings and SST, indicates that the long-term temperature changes in the Mediterranean could have a negative impact on sardine abundance [
72]. In contrast, there is a positive relationship between sardine landings and chlorophyll concentration in the Alboran Sea [
72] which has also been related to other areas of the Mediterranean Sea [
73].
The distribution of large pelagic fishes may also be associated with various environmental conditions, despite their highly migratory activity. Several populations of swordfish have shifted latitudinally, whereas the Mediterranean population has shifted longitudinally towards the west, as a result of climate change [
74]. Local conditions, such as clusters of higher density occurring near converging fronts and strong thermoclines may also affect swordfish distribution at a more local scale [
75]. The regional distribution and abundance of Atlantic bluefin tuna has also been recently reported to be affected by climatic oscillation and water temperature [
76]. Again, overfishing plays a crucial role in distribution and abundance patterns of large pelagic species, since the stocks of these two species are among the most valued and commercially exploited globally [
76].
Salinity may also play a role in the distribution of small and medium pelagic fishes, yet along the northern Mediterranean coastline, where the pelagic fishes are mostly abundant, salinity is greatly influenced by precipitation and riverine input, as well as by the inflow of Black Sea water in the Aegean Sea [
66]. Thus, other processes including precipitation and runoff are also involved affecting salinity and in turn the distribution of small pelagic species [
72]. Anchovy larvae have been reported to preferentially occupy coastal areas, which are areas that are often influenced by river plumes [
77]. The effect of precipitation is stronger for pelagic fishes that are distributed along the coast (such as sardine and anchovy [
78,
79]) and may also affect their catches [
14]. Species with a more oceanic distribution such as the scombrids and swordfish are less impacted.
In the NW Mediterranean, sardine and anchovy have been fluctuating in synchrony for over 30 years [
70,
80] rather than alternating in high abundances, as globally observed for anchovy-sardine coexisting populations [
81,
82]. Local environmental conditions, including river runoff, wind mixing, sea surface temperature and chlorophyll concentrations, influenced by climatic oscillations [
80,
83] have been reported to control the fluctuations in abundance of these species in this area [
14,
65,
84] and probably explain the high probability of occurrence for both species in the western Mediterranean. A regional index, the Western Mediterranean Oscillation index, which has been developed to explain the precipitation variability of the Iberian Peninsula [
85], seems to represent well the suitable environmental conditions for sardine and anchovy in the west Mediterranean [
80].
Furthermore, in the case of small pelagic fishes, the spawning areas and larval distributions are also highly related to environment and recruitment success, and they may determine adult abundance and affect spatial distribution. At the same time, inter-specific competition for resources may provide advantage for the species that has spawned earlier or is more abundant [
86]. For example, when outnumbered, round sardinella larvae are concentrated in areas where competition is minimized because the food availability would be higher [
87,
88]. This behaviour is a characteristic of opportunistic and easy to adapt species [
89], such as round sardinella. Similar results have been reported for the NW Mediterranean coast [
87], with the less abundant round sardinella larvae occupying the less favourable for survival areas, in order to avoid potential competition with anchovy. Round sardinella larvae may be disadvantageous compared to anchovy, because their bathymetric distribution is limited to the upper 50m of the water column. Thus, they cannot feed on the deep chlorophyll maximum layer probably due to their inability to tolerate lower temperatures [
90].
Finally, it is interesting to see what percentage of the Mediterranean Sea is covered by high probability occurrence for each species. Considering 80% and greater as high occurrence probability, following
Figure 6, it was computed that anchovy covers 14.7% of the Mediterranean, sardine 17.8%, round sardinella 30.7%, Atlantic chub mackerel 2%, Atlantic mackerel 0.7%, picarel 82.3%, bluefin tuna 4% and swordfish 1.8%. Locations with constant species presence are the Adriatic Sea, the North Aegean Sea, the Alboran Sean, and the sea surrounding the coasts from South France to East Tunisia.