An Efficient Estimation of the Number of Optimal Iterations for GS Pre-coding in Downlink Massive MIMO Systems
Abstract
1. Introduction
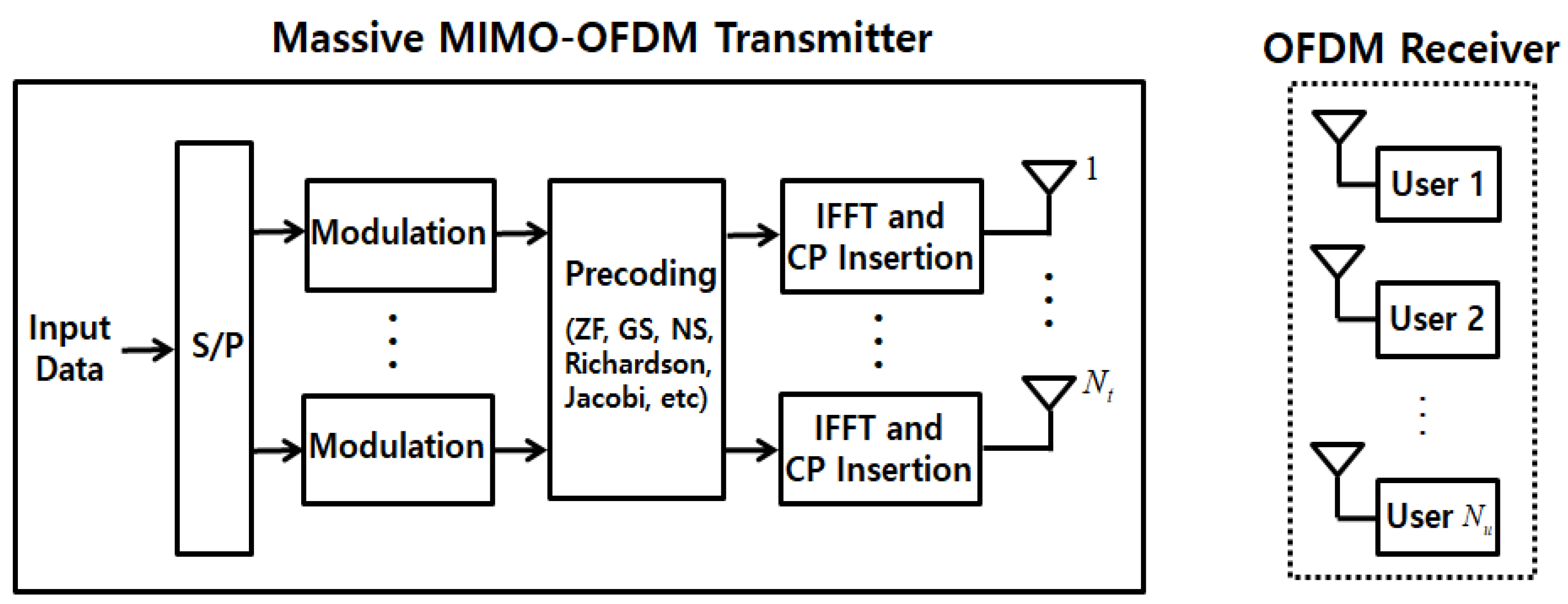
2. Downlink Massive MIMO-OFDM System Model
3. Conventional GS Pre-coding
4. Proposed Estimation Scheme
4.1. Methodology
4.2. Detailed Expression for Proposed Scheme
| Algorithm 1. An algorithm for GS pre-coding using proposed estimation scheme |
| Input and Initialization: Output: s in (6) |
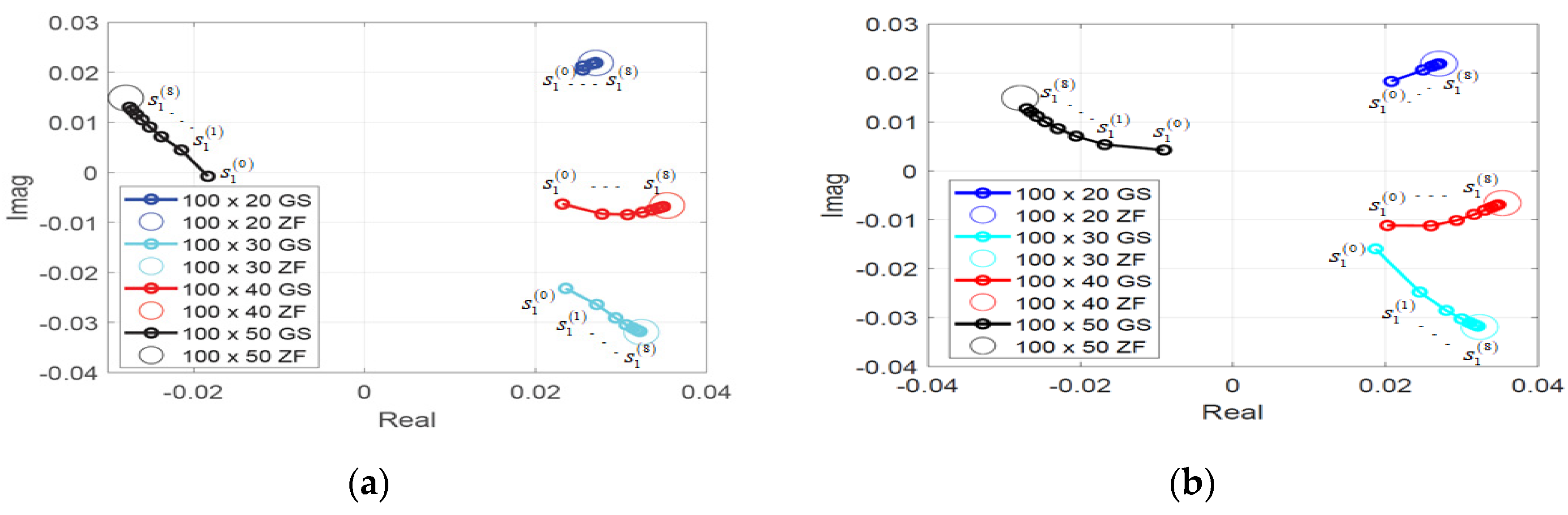
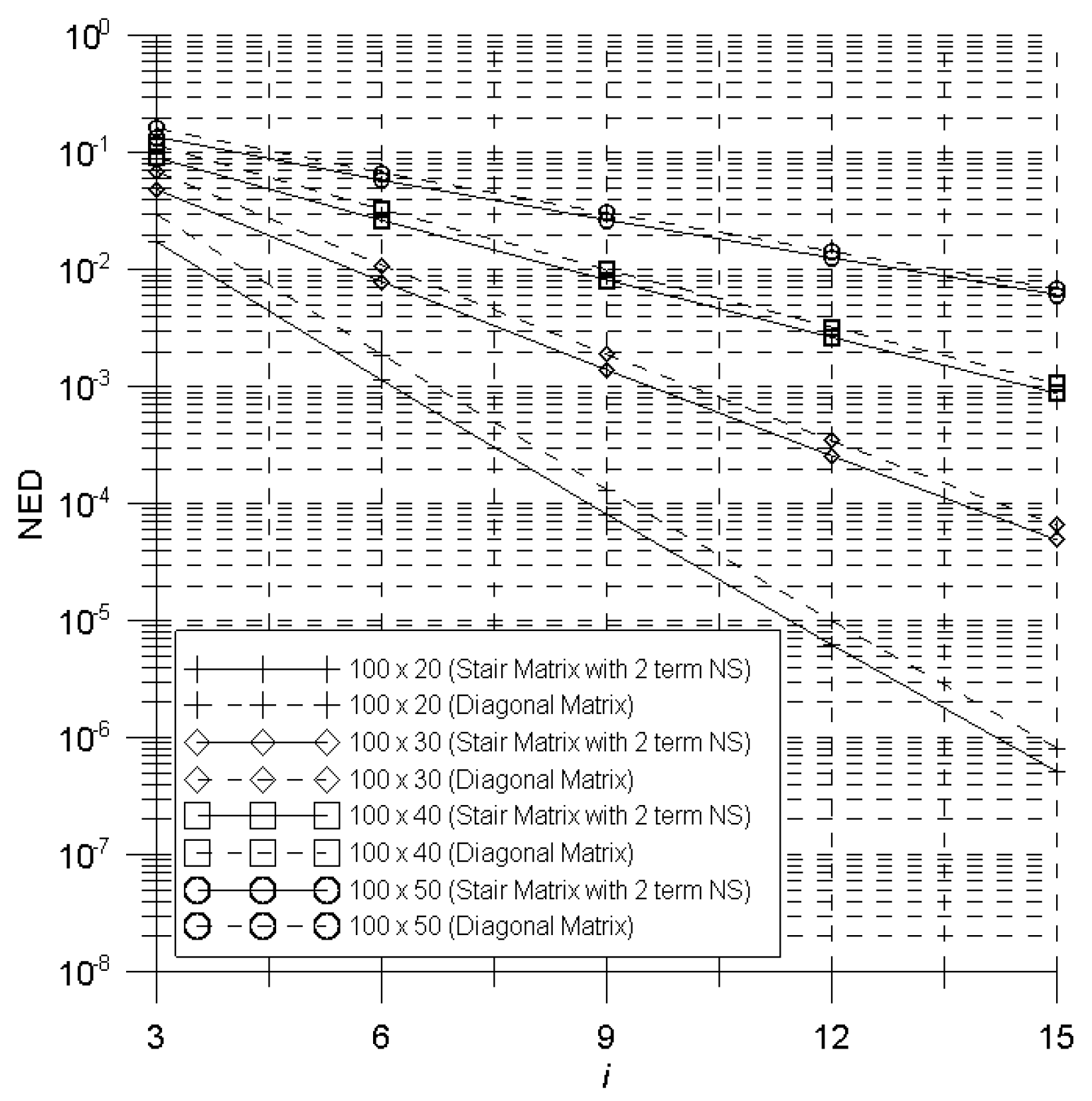
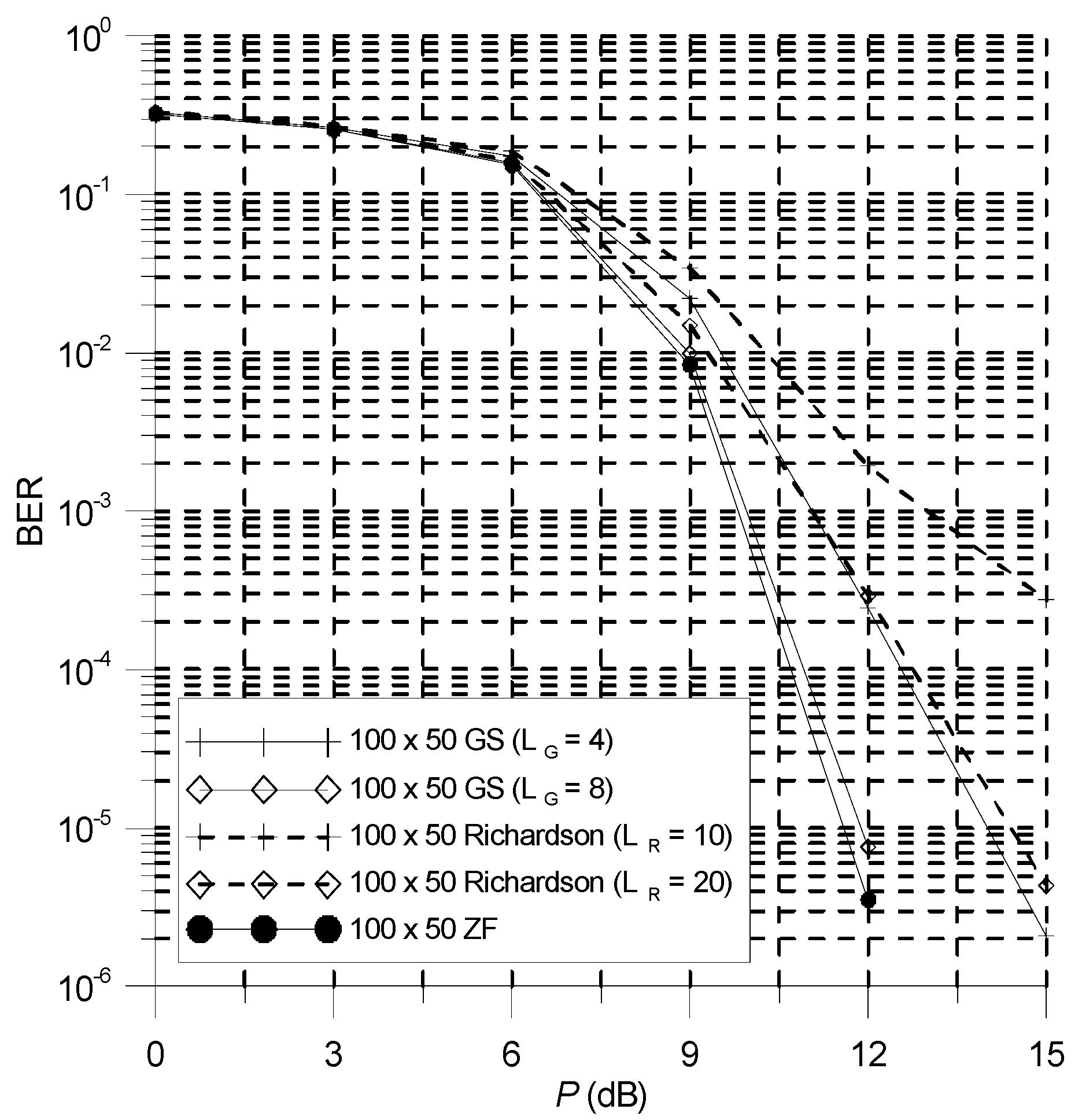
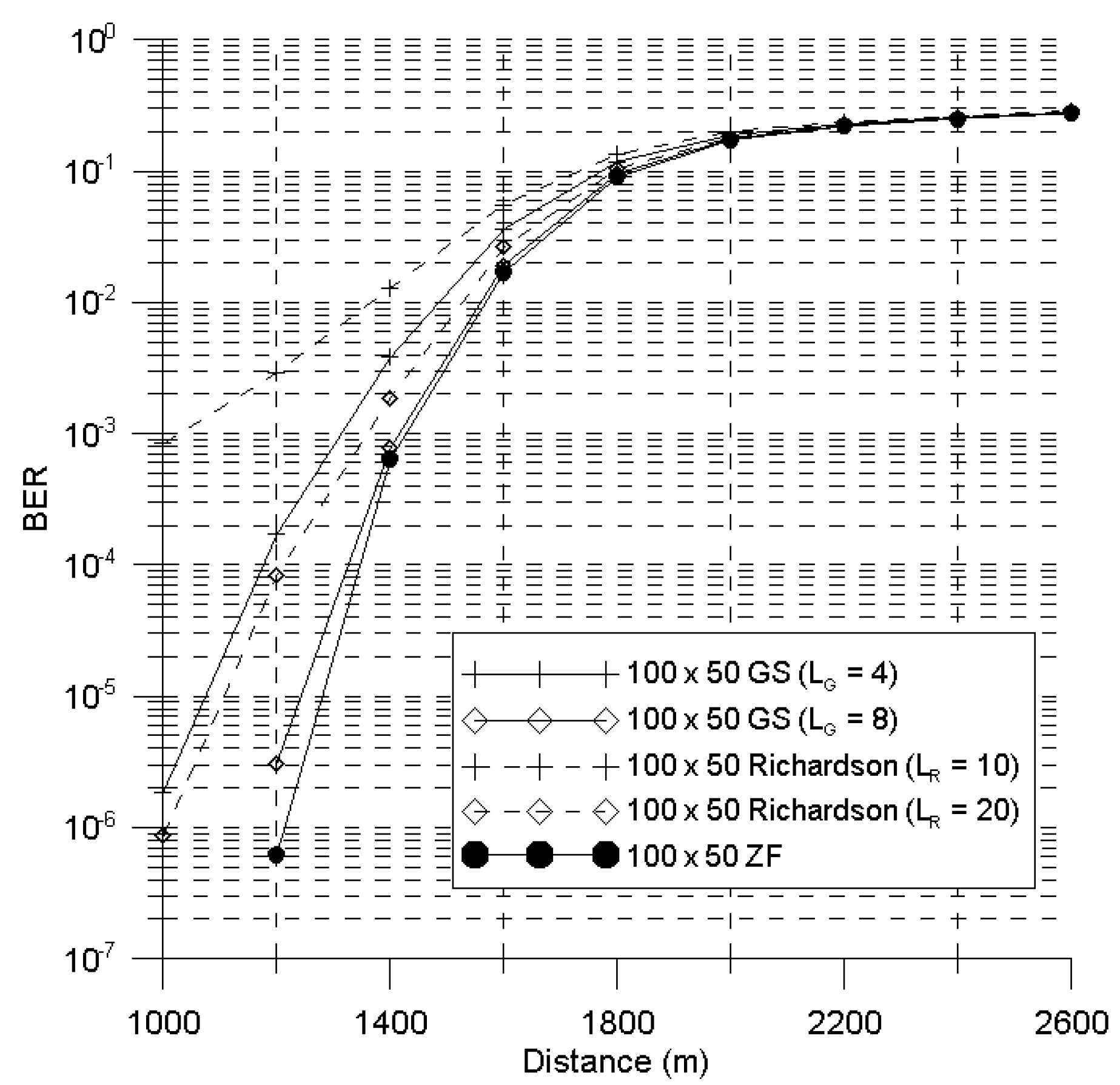
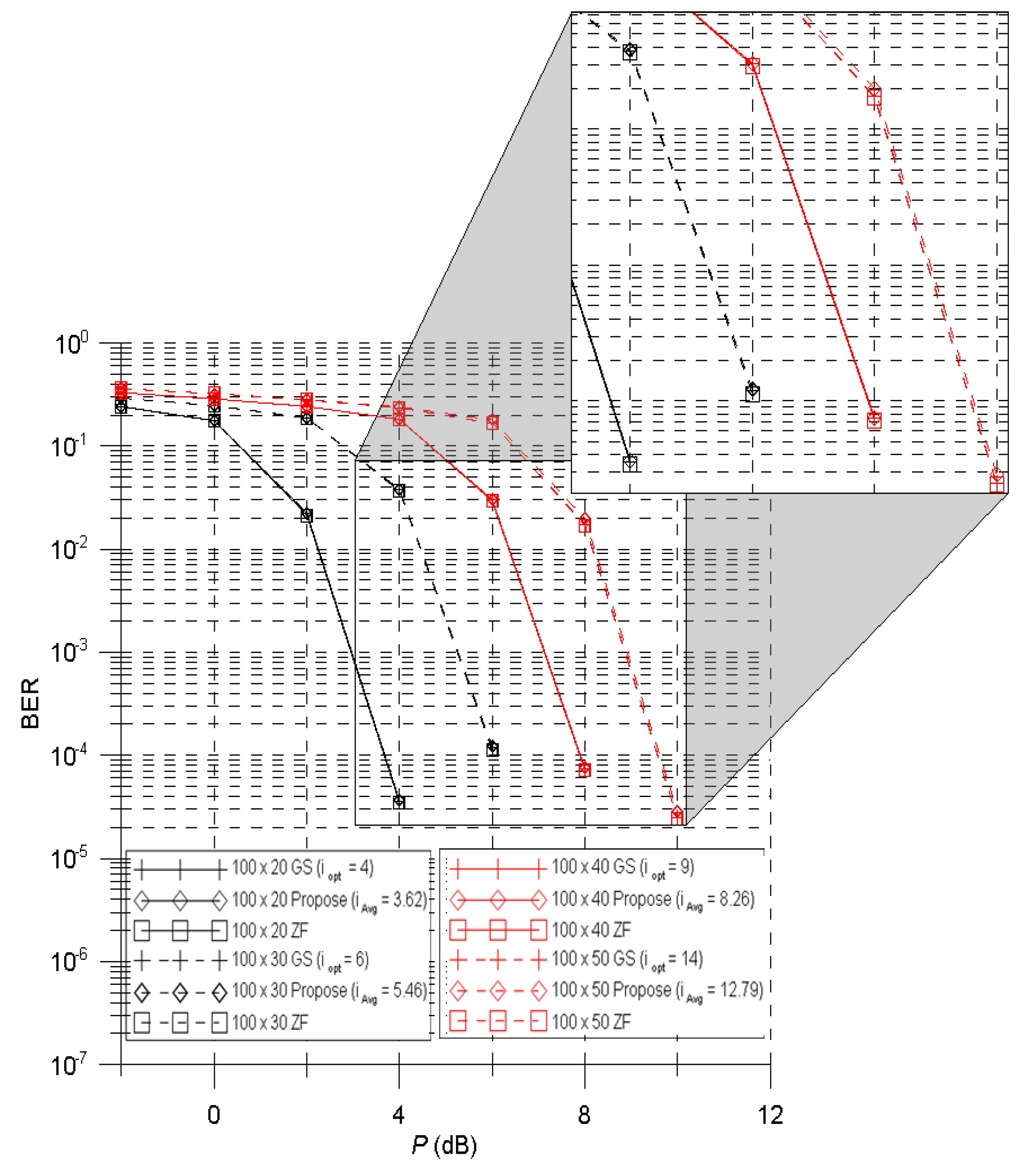
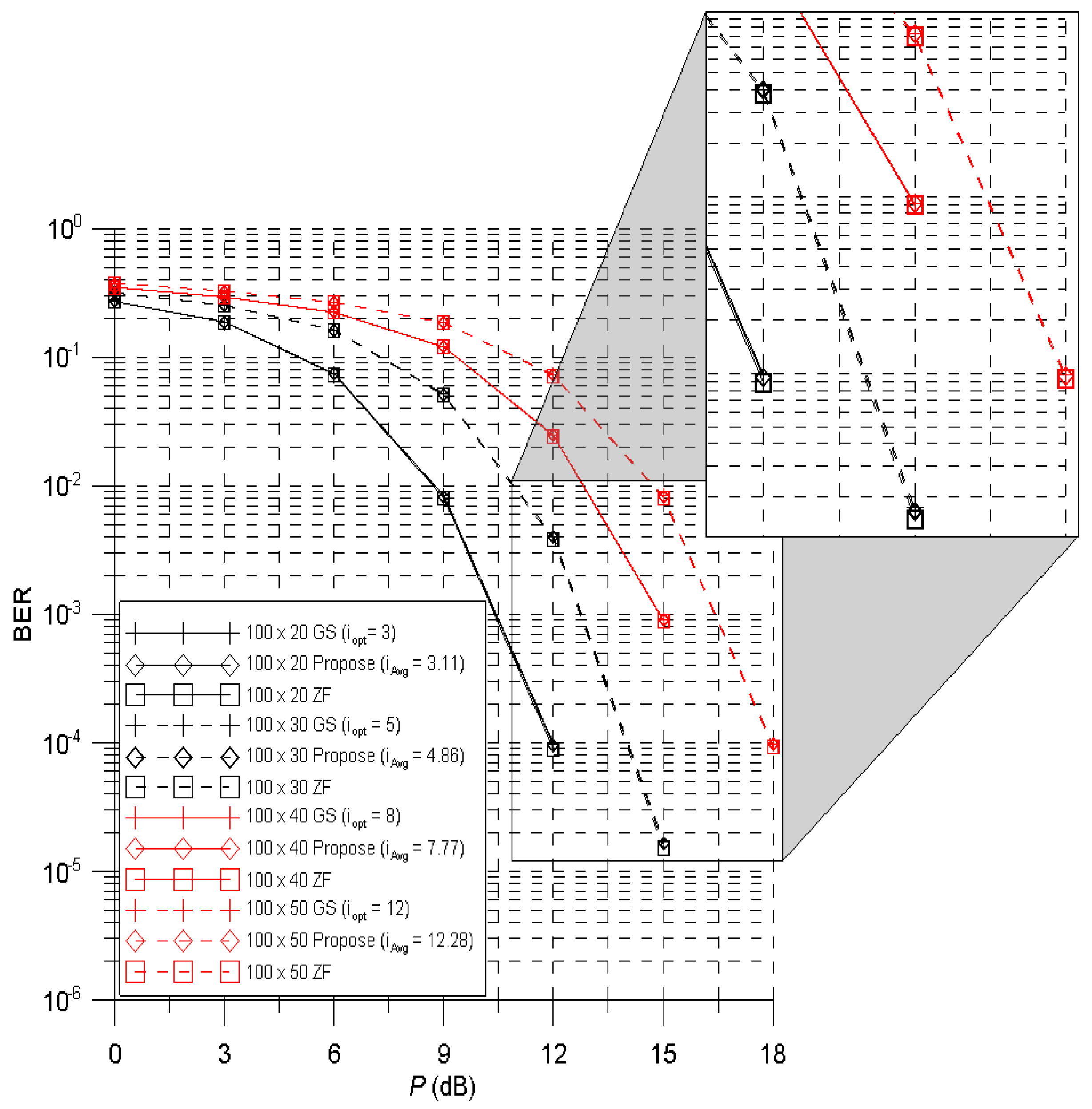
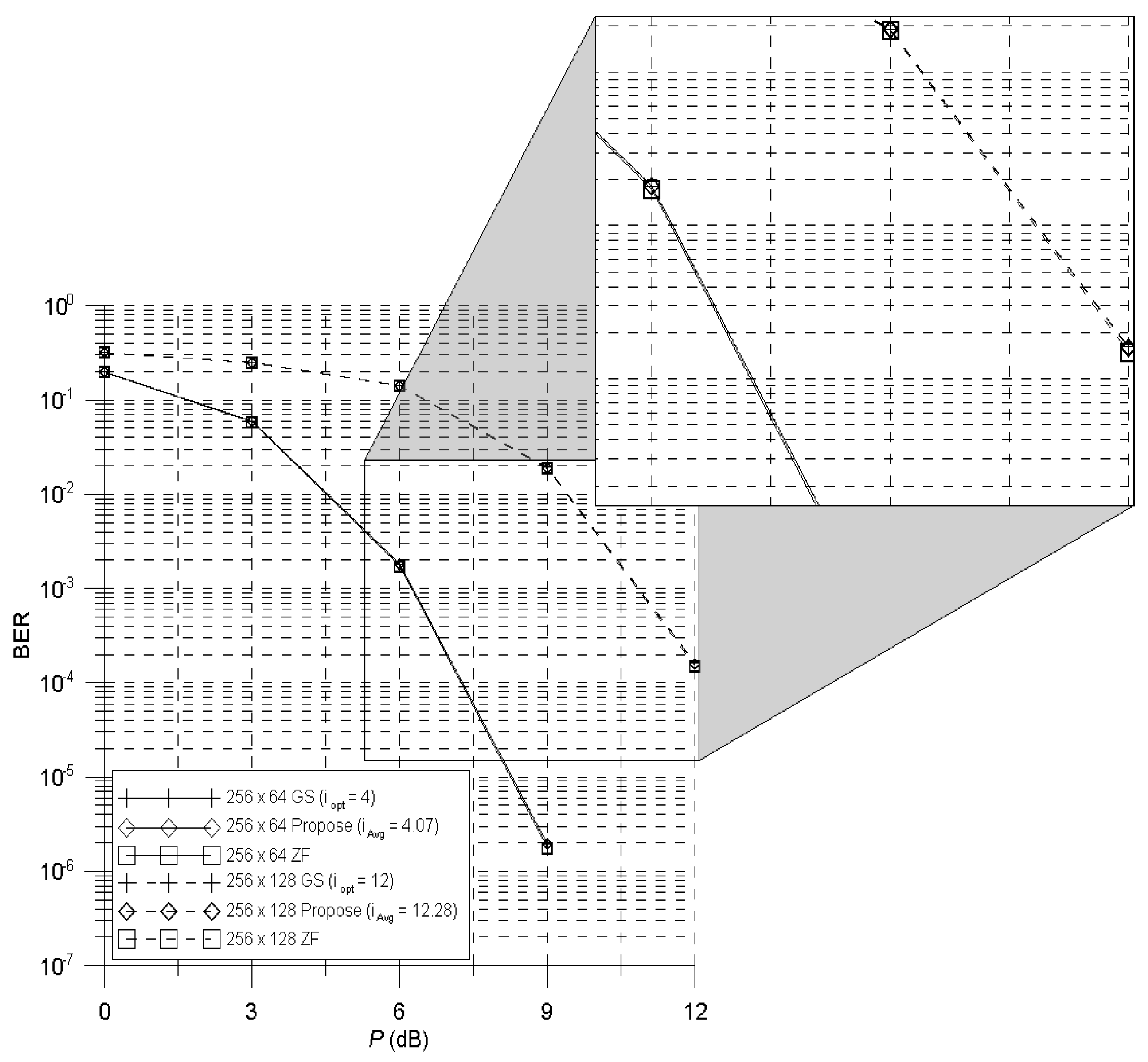
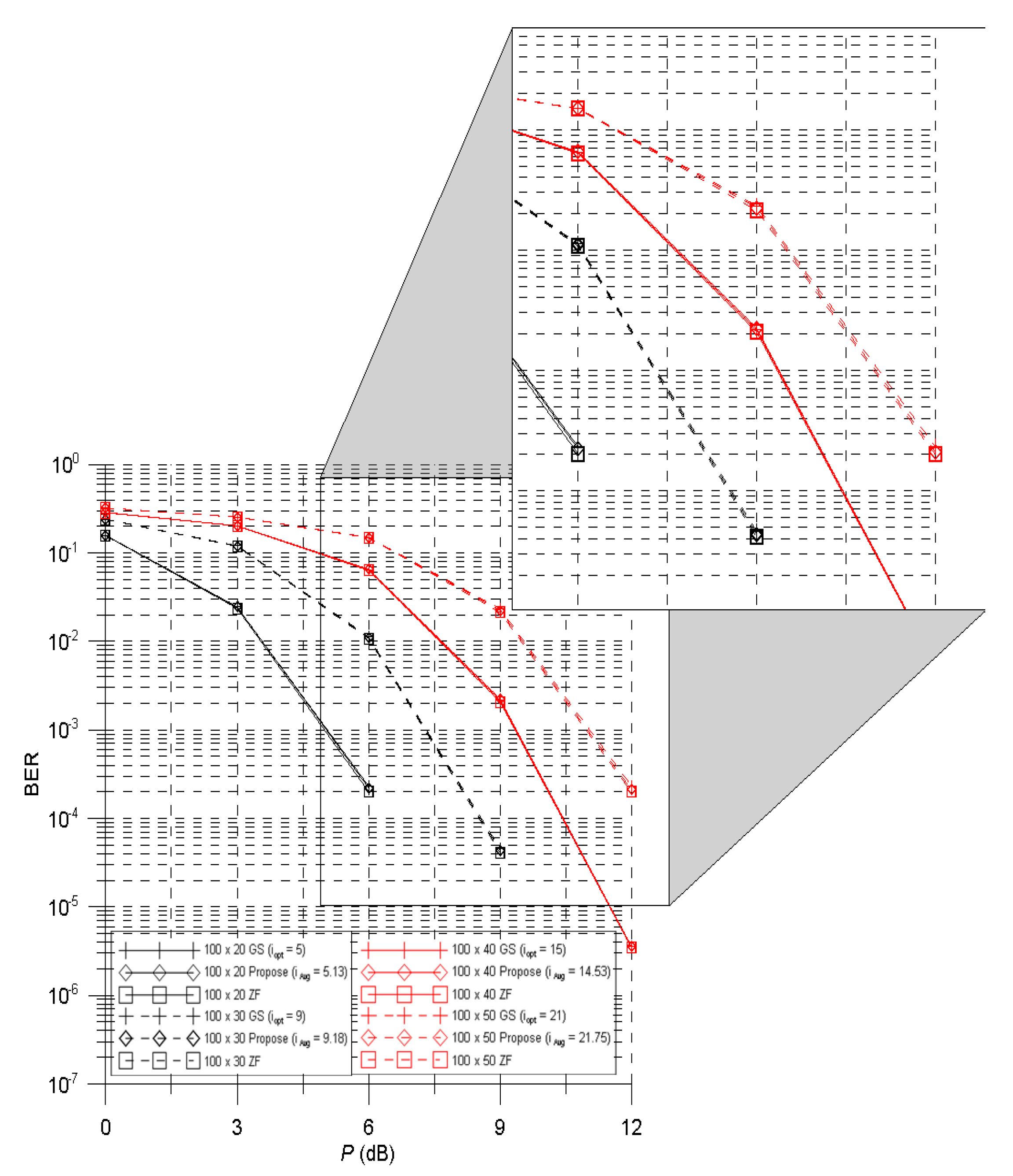
5. Performance Evaluations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Marzetta, T.L. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency. Found. Trends Signal Process. 2017, 11. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal. Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Cao, J.; Yu, S.; Yang, J.; Zhang, Y.; Zhao, S. Massive MIMO two-hop relay systems over Rician fading channels. KSII Trans. Internet Inf. Syst. 2019, 13, 5410–5426. [Google Scholar]
- Hong, J.K. Performance analysis of MRT-based dual-polarized massive MIMO system with space-polarization division multiple access. KSII Trans. Internet Inf. Syst. 2018, 12, 4006–4020. [Google Scholar]
- Tebe, P.I.; Wen, G.; Li, J.; Huang, Y.; Ampoma, A.E.; Gyasi, K.O. Massive MIMO with transceiver hardware impairments: Performance analysis and phase noise error minimization. KSII Trans. Internet Inf. Syst. 2019, 13, 2357–2380. [Google Scholar]
- Li, P.; Gao, Y.; Li, Z.; Yang, D. Pilot sequence assignment for spatially correlated massive MIMO circumstances. KSII Trans. Internet Inf. Syst. 2019, 13, 237–253. [Google Scholar]
- Kim, K.; Lee, J. Deep CNN based pilot allocation scheme in massive MIMO systems. KSII Trans. Internet Inf. Syst. 2020, 14, 4214–4230. [Google Scholar]
- Fatema, N.; Hua, G.; Xiang, Y.; Peng, D.; Natgunanathan, I. Massive MIMO linear precoding: A survey. IEEE Syst. J. 2018, 12, 3920–3931. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO detection techniques: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Albreem, M.A.; El-Saleh, A.A.; Juntti, M. On approximate matrix inversion methods for massive MIMO detectors. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019. [Google Scholar]
- Zhang, Z.; Wu, J.; Ma, X.; Dong, Y.; Wang, Y.; Chen, S.; Dai, X. Reviews of recent progress on low-complexity linear detection via iterative algorithms for massive MIMO systems. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Chengdu, China, 27–19 July 2016; pp. 1–6. [Google Scholar]
- Gao, X.; Dai, L.; Zhang, J.; Han, S.C.I. Capacity-approaching linear precoding with low-complexity for large-scale MIMO systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1577–1582. [Google Scholar]
- Lee, Y.; Sou, S. On improving Gauss-Seidel iteration for signal detection in uplink multiuser massive MIMO systems. In Proceedings of the 2018 3rd International Conference on Computer and Communication Systems (ICCCS), Nagoya, Japan, 27–30 April 2018; pp. 268–272. [Google Scholar]
- Minango, J.; de Almeida, C. Low-complexity MMSE detector based on refinement Gauss-Seidel method for massive MIMO systems. In Proceedings of the 2017 IEEE 9th Latin-American Conference on Communications (LATINCOM), Guatemala City, Guatemala, 8–10 November 2017; pp. 1–5. [Google Scholar]
- Jiang, F.; Li, C.; Gong, Z.; Su, R. Stair matrix and its applications to massive MIMO uplink data detection. IEEE Trans. Commun. 2018, 66, 2437–2455. [Google Scholar] [CrossRef]
- Albreem, M.; Juntti, M.; Shahabuddin, S. Efficient initialization of iterative linear massive MIMO detectors using a stair matrix. Electron. Lett. 2020, 56, 50–52. [Google Scholar] [CrossRef]
- Albreem, M.A.; Alsharif, M.H.; Kim, S. Impact of stair and diagonal matrices in iterative linear massive MIMO uplink detectors for 5G wireless networks. Symmetry 2020, 12, 71. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, C.; Xue, Y.; Xu, S.; You, X. Efficient architecture for soft-output massive MIMO detection with Gauss-Seidel method. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1886–1889. [Google Scholar]
- Zhang, C.; Wu, Z.; Studer, C.; Zhang, Z.; You, X. Efficient soft-output Gauss-Seidel data detector for massive MIMO systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 1–12. [Google Scholar] [CrossRef]
- Dai, L.; Gao, X.; Su, X.; Han, S.I.C.; Wang, Z. Low-complexity soft-output signal detection based on Gauss–Seidel method for uplink multiuser large-scale MIMO systems. IEEE Trans. Veh. Technol. 2015, 64, 4839–4845. [Google Scholar] [CrossRef]
- Gao, X.; Lu, Z.; Han, Y.; Ning, J. Near-optimal signal detection with low complexity based on Gauss-Seidel method for uplink large-scale MIMO systems. In Proceedings of the 2014 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Beijing, China, 25–27 June 2014; pp. 1–4. [Google Scholar]
- Zeng, J.; Lin, J.; Wang, Z. An improved Gauss-Seidel algorithm and its efficient architecture for massive MIMO systems. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1194–1198. [Google Scholar] [CrossRef]
- Wu, Z.; Xue, Y.; You, X.; Zhang, C. Hardware efficient detection for massive MIMO uplink with parallel Gauss-Seidel method. In Proceedings of the 2017 22nd International Conference on Digital Signal. Processing (DSP), London, UK, 23–25 August 2017; pp. 1–5. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Zhu, D.; Li, B.; Liang, P. On the matrix inversion approximation based on Neumann series in massive MIMO systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1763–1769. [Google Scholar]
- Prabhu, H.; Rodrigues, J.; Edfors, O.; Rusek, F. Approximative matrix inverse computations for very-large MIMO and applications to linear pre-coding systems. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2710–2715. [Google Scholar]
- Ro, J.; Lee, W.; Ha, J.; Song, H. An efficient precoding method for improved downlink massive MIMO system. IEEE Access 2019, 7, 112318–112326. [Google Scholar] [CrossRef]
- Tulino, A.M.; Verdu, S. Random Matrix Theory and Wireless Communications; Now Publishers Inc.: Delft, The Netherlands, 2004. [Google Scholar]


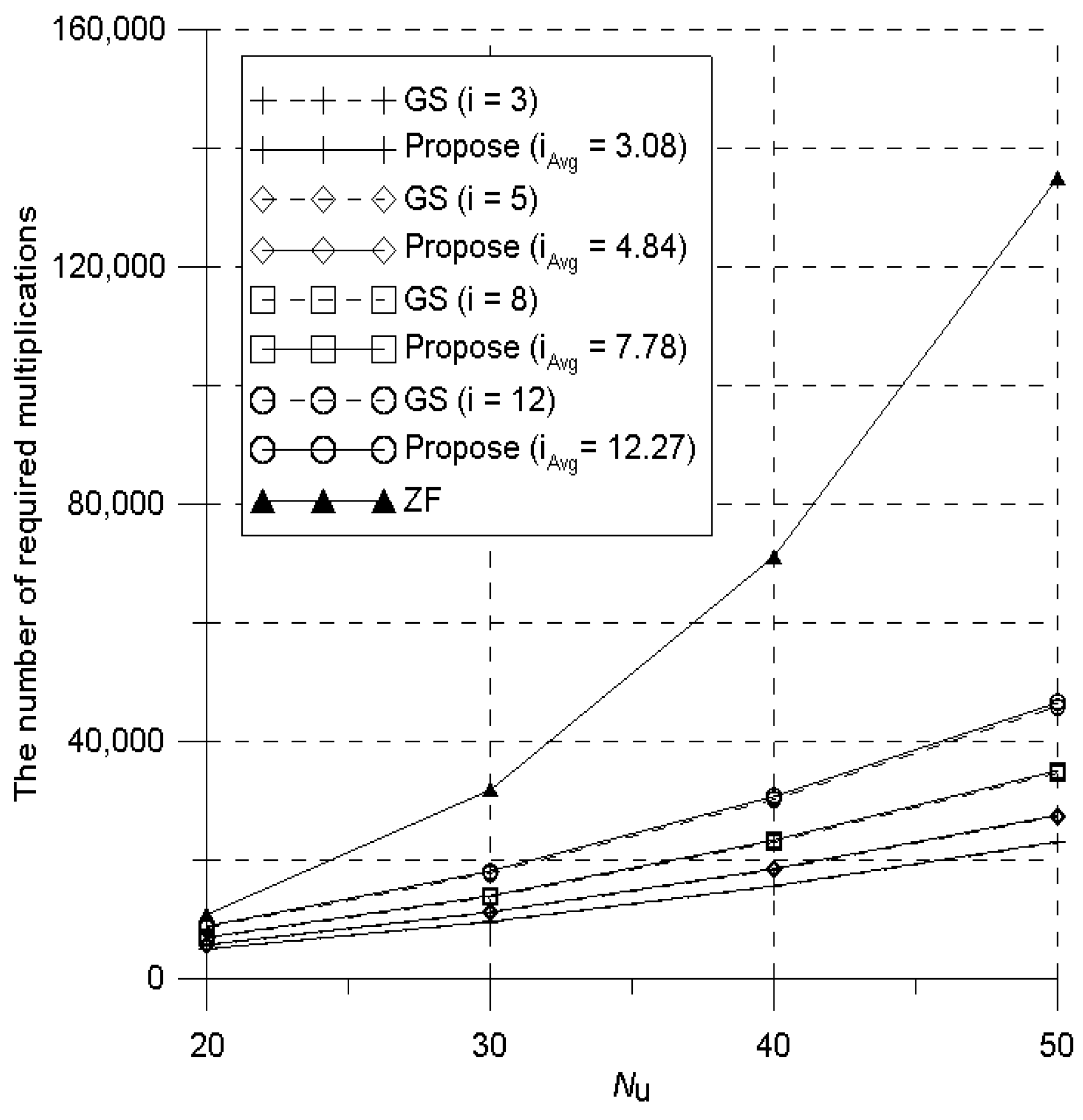
| Scheme | The Number of Multiplications |
|---|---|
| GS pre-coding without estimation | |
| [12] | |
| GS pre-coding based on proposed estimation scheme | |
| ZF pre-coding | |
| [28,29] |
| 20 | 30 | 40 | 50 | |
| 16 | 26 | 36 | 46 |
| Parameter | Value or Scheme |
|---|---|
| Digital modulation | 16-quadrature amplitude modulation (QAM), 64-QAM |
| Channel coding | 1/2 rate low density parity check (LDPC) |
| 100, 256 | |
| 20, 30, 40, 50, 64, 128 | |
| The number of cells | Single cell |
| Channel model | 8 multi-path Rayleigh fading |
| AWGN (Gaussian noise) | Zero mean and unit power (Base station (BS) controls transmit power ) |
| Duplexing mode | Time division duplexing (TDD) |
| Channel estimation | Least square (LS) based on uplink pilot |
| Parameter | Value |
|---|---|
| 37 dBm (6 dBm less than maximum total radiated power in 5G new radio (NR) standards) | |
| 3.5 GHz | |
| 3 | |
| 17 dB | |
| (: Bandwidth which is set as 100 MHz) |
| 20 | 30 | 40 | 50 | |
|---|---|---|---|---|
| for | 3 | 5 | 8 | 12 |
| for | 4 | 6 | 9 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ro, J.-H.; Lee, W.-S.; Hwang, H.-S.; Hwang, D.; You, Y.-H.; Song, H.-K. An Efficient Estimation of the Number of Optimal Iterations for GS Pre-coding in Downlink Massive MIMO Systems. Appl. Sci. 2020, 10, 8735. https://doi.org/10.3390/app10238735
Ro J-H, Lee W-S, Hwang H-S, Hwang D, You Y-H, Song H-K. An Efficient Estimation of the Number of Optimal Iterations for GS Pre-coding in Downlink Massive MIMO Systems. Applied Sciences. 2020; 10(23):8735. https://doi.org/10.3390/app10238735
Chicago/Turabian StyleRo, Jae-Hyun, Woon-Sang Lee, Hyun-Sun Hwang, Duckdong Hwang, Young-Hwan You, and Hyoung-Kyu Song. 2020. "An Efficient Estimation of the Number of Optimal Iterations for GS Pre-coding in Downlink Massive MIMO Systems" Applied Sciences 10, no. 23: 8735. https://doi.org/10.3390/app10238735
APA StyleRo, J.-H., Lee, W.-S., Hwang, H.-S., Hwang, D., You, Y.-H., & Song, H.-K. (2020). An Efficient Estimation of the Number of Optimal Iterations for GS Pre-coding in Downlink Massive MIMO Systems. Applied Sciences, 10(23), 8735. https://doi.org/10.3390/app10238735





