Uncertainty Assessment for Determining the Discharge Coefficient C for a Multi-Opening Orifice
Abstract
:1. Introduction
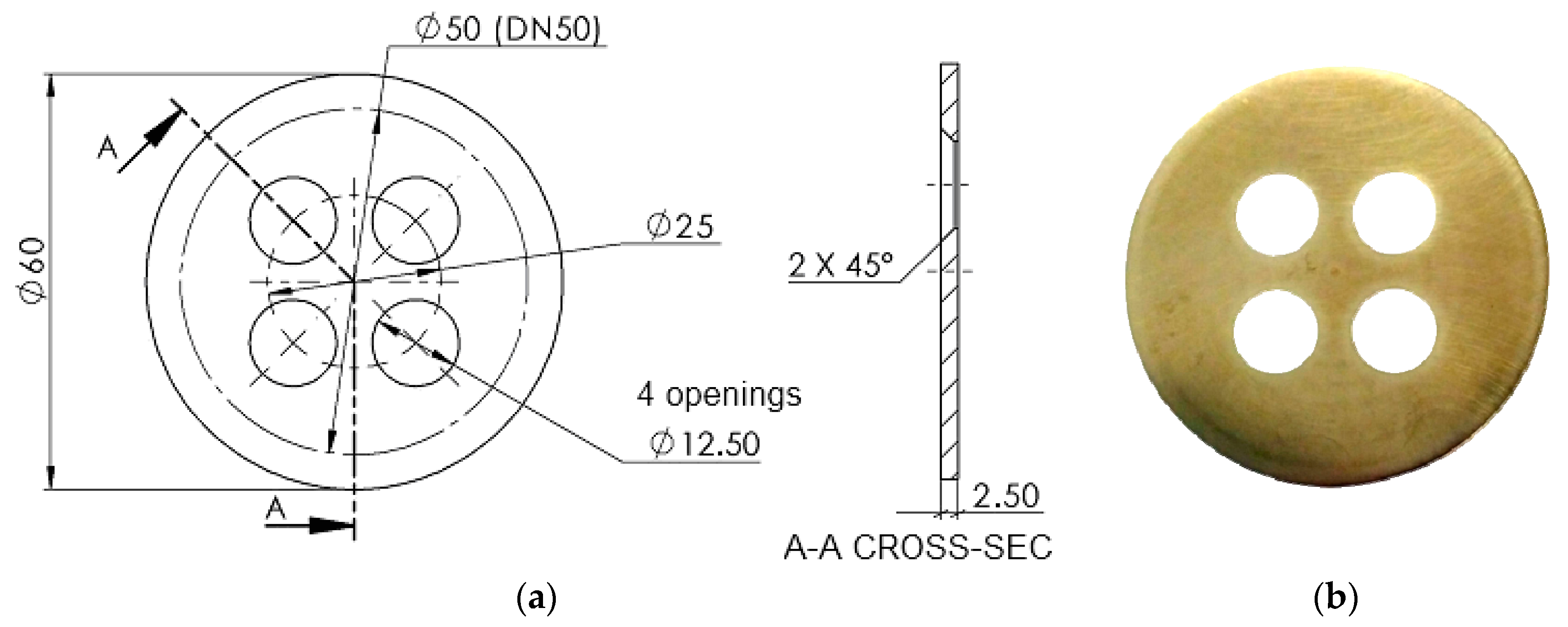
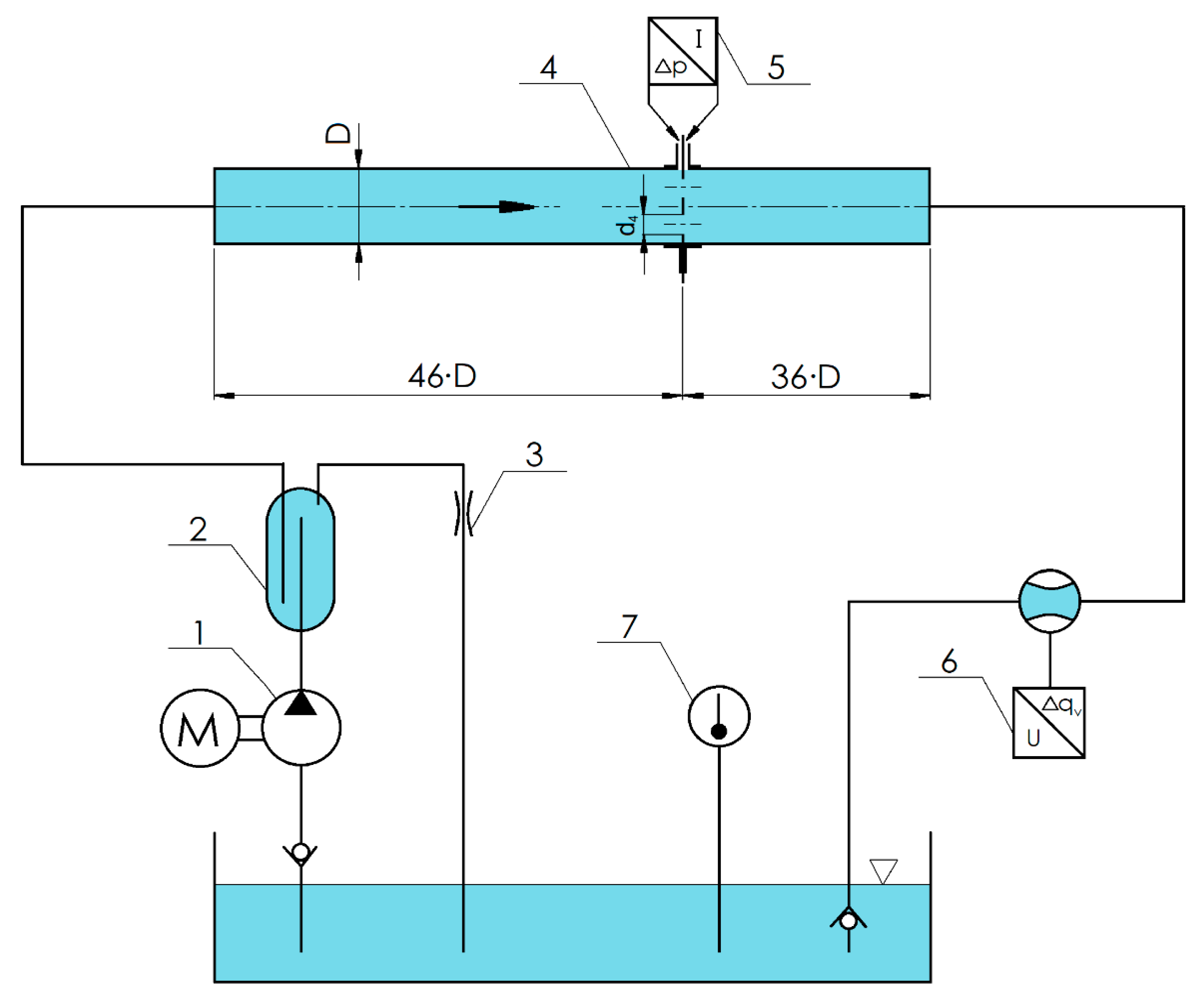
2. The Subject of Study and Measurement Result
3. Determining the Uncertainty of the Discharge Coefficient
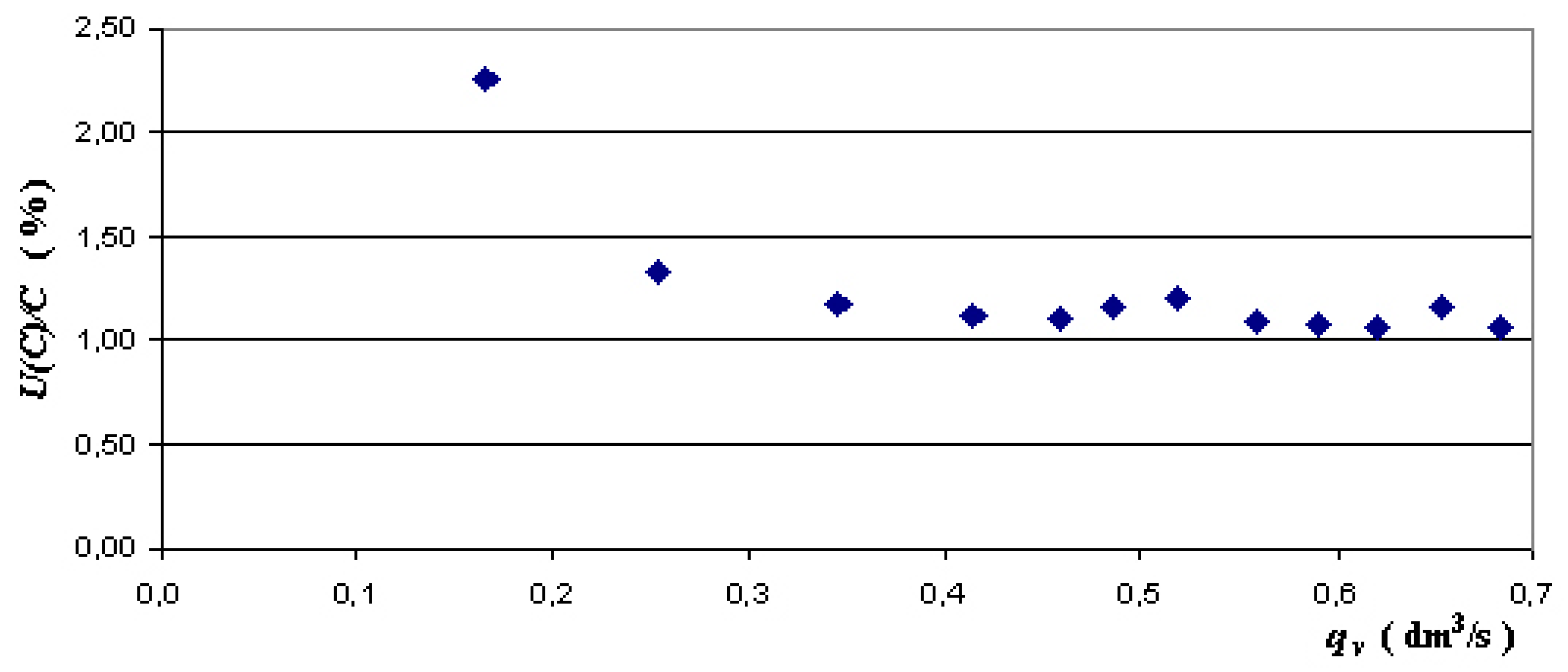
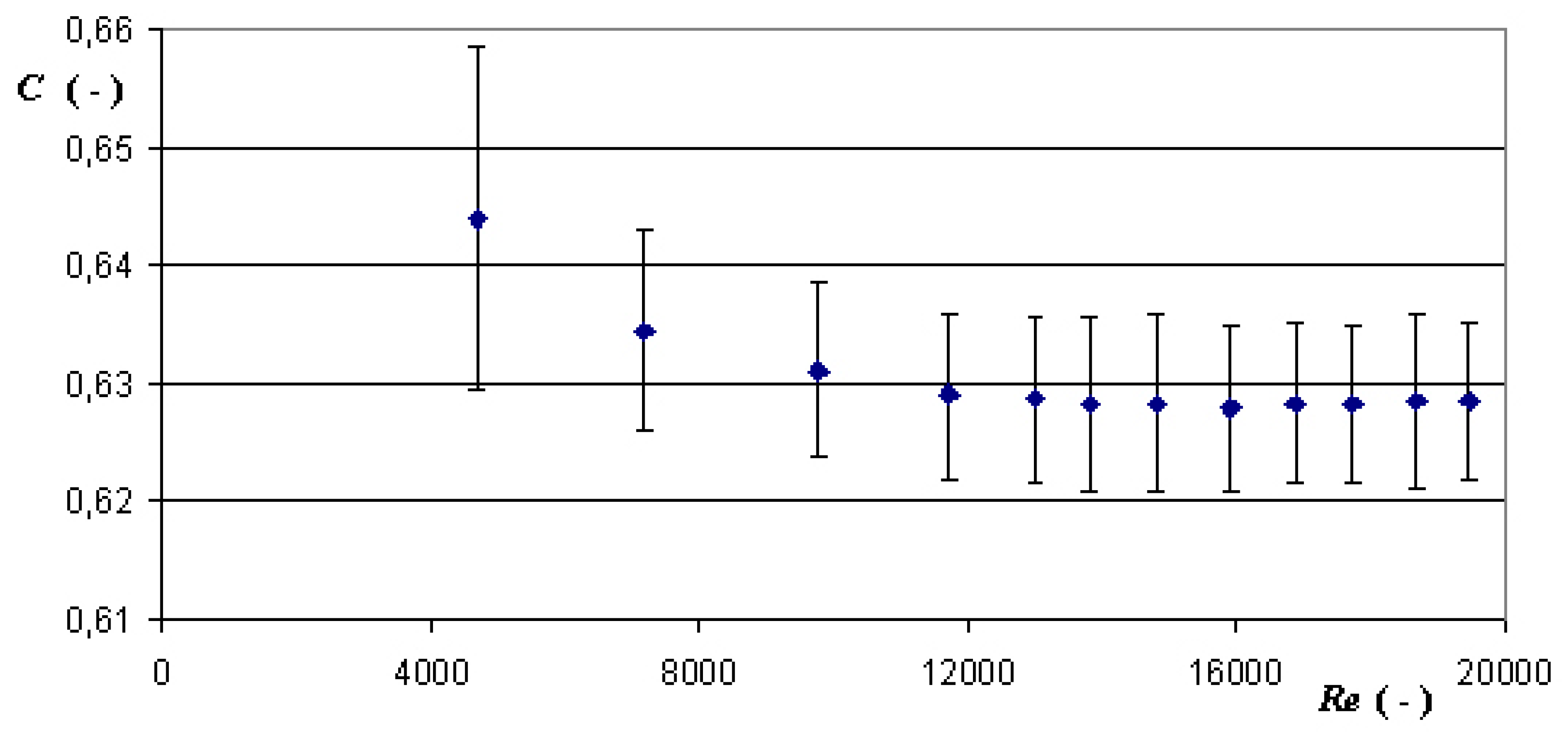
4. Results and Discussion
5. Conclusions
- There is the constancy of discharge coefficient (its average value C = 0.6286) which is higher than the discharge coefficient for a centrical orifice by ca. 2.0% with the same constriction;
- Relative expanded uncertainty of determining discharge coefficient U(C)/C does not exceed 1.25% and is close in value to standardized orifices.
Funding
Conflicts of Interest
Abbreviations
| C | discharge coefficient |
| D | measurement pipeline diameter (m) |
| d4 | orifice openings diameter (m) |
| F04 | orifice constriction area (m2) |
| kn | Student’s distributoon critical factor |
| kp | coverage factor |
| m | orifice module |
| qv | volume stream (m3/s) |
| Re | Reynolds number |
| S | standard deviation of the measured values |
| T | fluid (water) temperature (°C) |
| u(C) | standard uncertainty of the measured estimation, C |
| U(C)/C | relative expanded uncertainty of discharge coefficient |
| u(D) | standard uncertainty of the measured estimation, D |
| u(d4) | standard uncertainty of the measured estimation, d4 |
| u(qv) | standard uncertainty of the measured estimation, qv |
| u(Äp) | standard uncertainty of the measured estimation, Äp |
| u(ń) | standard uncertainty of the measured estimation, ń |
| â | substitute constriction factor |
| â4 | constriction of one of the four orifice openings (â4 = d4/D) |
| Ä | maximum limiting errors of measuring instruments used |
| Äp | pressure difference before and behind the orifice (Pa) |
| ĺ | expansion factor |
| ń | fluid density (kg/m3) |
References
- Zhang, R.; Hang, Y. An Experimental Study of Pulsatile Flow in a Compliant Aortic Root Model dunder Varied Cardiac Outputs. Fluids 2018, 3, 71. [Google Scholar] [CrossRef] [Green Version]
- Gondek, A. Przepływomierze Spiętrzające Przepływ (Flow Meters that Bank up the Flow); Politechnika Krakowska: Kraków, Poland, 2009. (In Polish) [Google Scholar]
- Kremlowski, P.P. Raschodimiery i Scetciki Kolicestva, Vescestv; Izd. Politechnika: Saint Petersburg, Russia, 2002. [Google Scholar]
- Turkowski, M. Metrologia Przepływów (Flow Metrology); Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2018. (In Polish) [Google Scholar]
- International Organization for Standardization. EN ISO 5167-1: 2003 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 1: General Principles and Requirements; ISO: Geneva, Switzerland, 2003. [Google Scholar]
- International Organization for Standardization. EN ISO 5167-2: 2003 Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 2: Orifice Plates; ISO: Geneva, Switzerland, 2003. [Google Scholar]
- Golijanek-Jędrzejczyk, A.; Mrowiec, A.; Hanus, R.; Zych, M.; Świsulski, D. Uncertainty of mass flow measurement using centric and eccentric orifice for Reynolds number in the range 10,000 ≤ Re ≤ 20,000. Measurement 2020, 160, 107851. [Google Scholar] [CrossRef]
- Tomaszewska-Wach, B.; Rząsa, M.R.; Majer, M. Measurement of two-phase gas-liquid flow using standard and slotted orifice. Inf. Autom. Pomiary Gospod. Ochr. Śr. 2019, 9, 30–33. [Google Scholar] [CrossRef]
- Dhumal, D.S.; More, Y.R.; Gawai, U.S. Design, Fabrication & Analysis of Multi-Hole Orifice Plate. Int. J. Eng. Technol. 2017, 6, 353–357. [Google Scholar]
- Huang, S.; Ma, T.; Wang, D.; Lin, Z. Study on discharge coefficient of perforated orifices as a new kind of flowmeter. Exp. Therm. Fluid Sci. 2013, 46, 74–83. [Google Scholar] [CrossRef]
- Romanik, G.; Rogula, J. The novel solution of ball valve witch replaceable orifice. Numericl and field tests. Open Eng. 2019, 9, 253–259. [Google Scholar] [CrossRef]
- Mahendra Babu, K.J.; Gangadhara Gowda, C.J.; Ranjith, K. Numerical Study on Performance Characteristics of Multihole Oriface Plate. IOP Conf. Ser. Mater. Sci. Eng. 2018, 376. [Google Scholar] [CrossRef]
- Durdewic, M.; Bukurov, M.; Tasin, S.; Bikic, S. Experimental research of single-hole and multi-hole orifice gas flow meters. Flow Meas. Instrum. 2019, 70, 101615. [Google Scholar] [CrossRef]
- Bagade, V.S.; Suryawanshi, P.M.; Nalavade, S.M. A review of multi-hole orifice plate. Int. J. Res. Appl. Sci. Eng. Technol. 2019, 7, 3197–3208. [Google Scholar] [CrossRef]
- Hao, C.Z.; Song, X.M.; Jia, Z.N. Influence of the hole chamfer on the characteristics of a multi-hole orifice flowmeter. Fluid Dyn. Mater. Process. 2019, 15, 391–401. [Google Scholar] [CrossRef]
- Singh, V.K.; Tharakan, T.J. Numerical simulations for multi-hole orifice flow meter. Flow Meas. Instrum. 2015, 45, 375–383. [Google Scholar] [CrossRef]
- Drikakis, D.; Asproulis, N. Quantification of Computational Uncertainty in Science and Engineering. ASME Appl. Mech. Rev. 2011, 64. [Google Scholar] [CrossRef]
- Barmparousis, C.; Drikakis, D. Multidimensional quantification of uncertainty and application to a turbulent mixing model. Int. J. Numer. Meth. Fluids 2017, 85, 385–403. [Google Scholar] [CrossRef] [Green Version]
- Guide to the Expression of Uncertainty in Measurement, Joint Committee for Guides in Metrology (JCGM) 100:2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 16 October 2020).
- Diaz, R.P.; Dalfre Filho, J.G.; de Lucca, Y.F.L. Water flow meter measurement uncertainties. Water Resour. Manag. 2013, 171. [Google Scholar] [CrossRef]
- Wiora, J.; Wiora, A. Measurement Uncertainty Calculations for pH Value Obtained by an Ion-Selective Electrode. Sensors 2018, 18, 1915. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| D | d | T | qv | Δp | Re | C |
|---|---|---|---|---|---|---|
| (mm) | (mm) | (°C) | (dm3/s) | (Pa) | (-) | (-) |
| 50.20 | 12.54 | 25.30 | 0.6825 | 2289.4 | 19,479 | 0.6283 |
| 50.26 | 12.53 | 25.40 | 0.6536 | 2098.9 | 18,696 | 0.6284 |
| 50.37 | 12.53 | 25.40 | 0.6202 | 1891.1 | 17,740 | 0.6282 |
| 50.28 | 12.52 | 25.35 | 0.5907 | 1715.4 | 16,879 | 0.6283 |
| 50.31 | 12.52 | 25.25 | 0.5580 | 1533.0 | 15,909 | 0.6278 |
| 50.36 | 12.51 | 25.20 | 0.5196 | 1327.5 | 14,798 | 0.6283 |
| 50.26 | 12.51 | 25.10 | 0.4858 | 1160.2 | 13,802 | 0.6283 |
| 50.25 | 12.52 | 25.00 | 0.4590 | 1035.0 | 13,012 | 0.6285 |
| 50.40 | 12.51 | 24.95 | 0.4145 | 843.1 | 11,739 | 0.6289 |
| 50.22 | 12.53 | 24.90 | 0.3456 | 581.9 | 9774 | 0.6310 |
| 50.35 | 12.52 | 24.85 | 0.2537 | 310.4 | 7168 | 0.6344 |
| 50.24 | 12.52 | 24.75 | 0.1666 | 130.0 | 4697 | 0.6439 |
| Partial Derivatives | Equation (6) Components | |
|---|---|---|
| (7) | ||
| (8) | ||
| (9) | ||
| (10) | ||
| (11) |
| (13) | |
| (14) | |
| (15) | |
| (16) | |
| (17) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mrowiec, A. Uncertainty Assessment for Determining the Discharge Coefficient C for a Multi-Opening Orifice. Appl. Sci. 2020, 10, 8503. https://doi.org/10.3390/app10238503
Mrowiec A. Uncertainty Assessment for Determining the Discharge Coefficient C for a Multi-Opening Orifice. Applied Sciences. 2020; 10(23):8503. https://doi.org/10.3390/app10238503
Chicago/Turabian StyleMrowiec, Andrzej. 2020. "Uncertainty Assessment for Determining the Discharge Coefficient C for a Multi-Opening Orifice" Applied Sciences 10, no. 23: 8503. https://doi.org/10.3390/app10238503
APA StyleMrowiec, A. (2020). Uncertainty Assessment for Determining the Discharge Coefficient C for a Multi-Opening Orifice. Applied Sciences, 10(23), 8503. https://doi.org/10.3390/app10238503




