Analyzing Major Track Quality Indices and Introducing a Universally Applicable TQI
Abstract
1. Introduction
2. Literature Study
2.1. Calculation Parameters
2.1.1. Computation Type
2.1.2. Influence Length
2.2. Existing Track Quality Indices
2.2.1. Isolated Defects
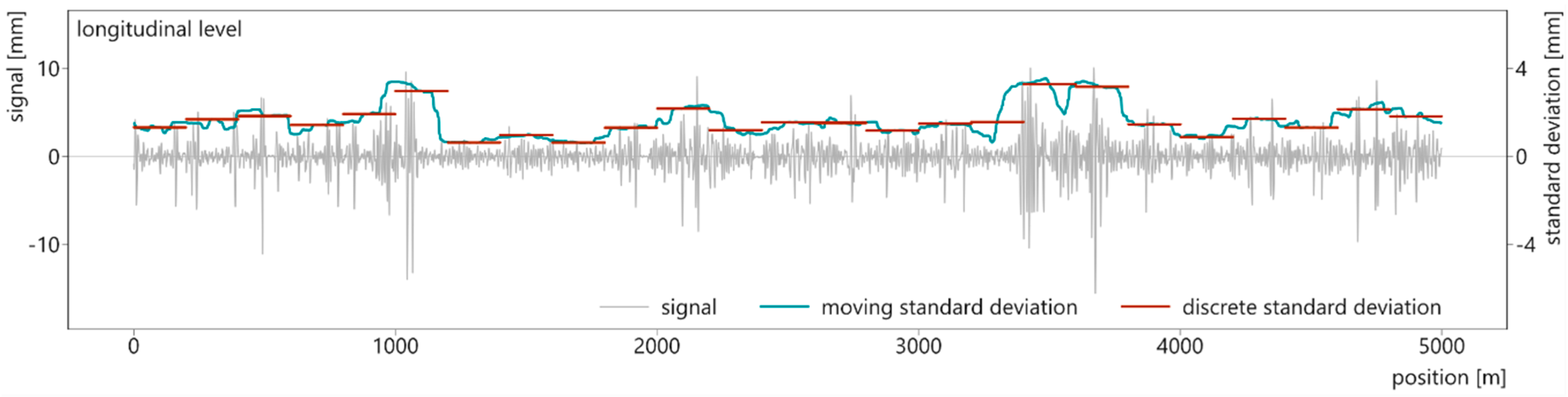
2.2.2. Combined Standard Deviation
2.2.3. MDZ-A Number
2.2.4. The Chinese Track Quality Index
2.2.5. The CN Track Quality Index
2.2.6. J Coefficient
2.2.7. Q-Value
2.2.8. K-Value
2.2.9. Netherlands Q Index
2.2.10. Track Geometry Index
2.2.11. Overall Track Geometry Index
2.2.12. Five-Parameter Track Defectiveness
2.2.13. Track Roughness Index
2.2.14. FRA Track Quality Index
2.3. Analysis of the Evaluated Track Quality Indices
3. Methodology
- The index must describe the overall geometrical quality of the track, which includes both peak values and scattering of the individual signals.
- The index must rely on physical and objective principles while avoiding subjective weighting factors.
- The index must enable the combination of all main track geometry parameters (Table 1).
- The index must be universally applicable for different types of track, varying line speeds, and different nominal track gauges.
- The index must not be negatively affected by gauge widening in curves and intended twist in transition elements.
- The index must be easy to understand and should be simple to implement.
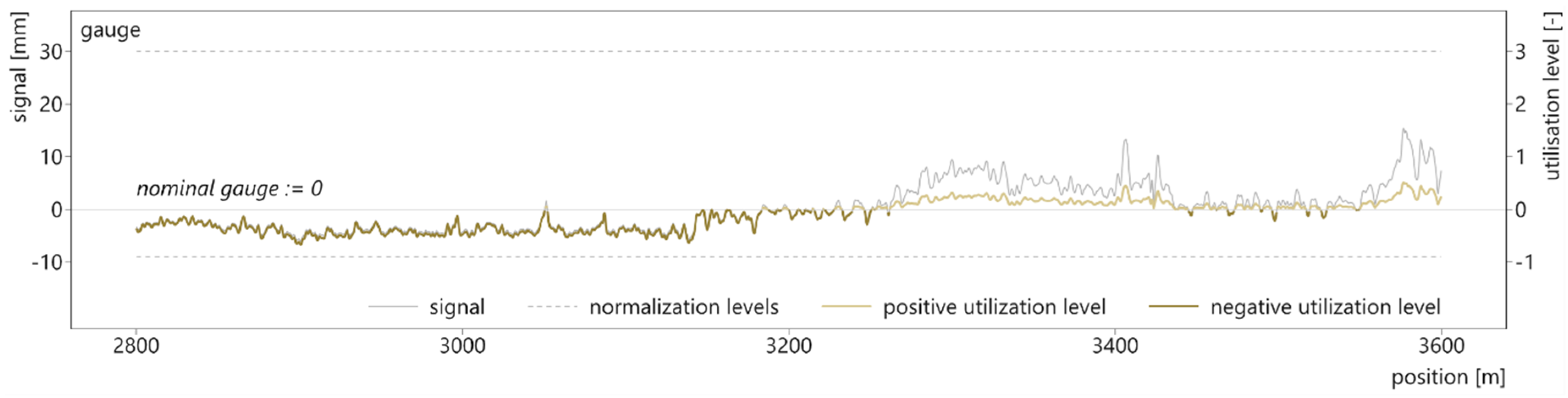
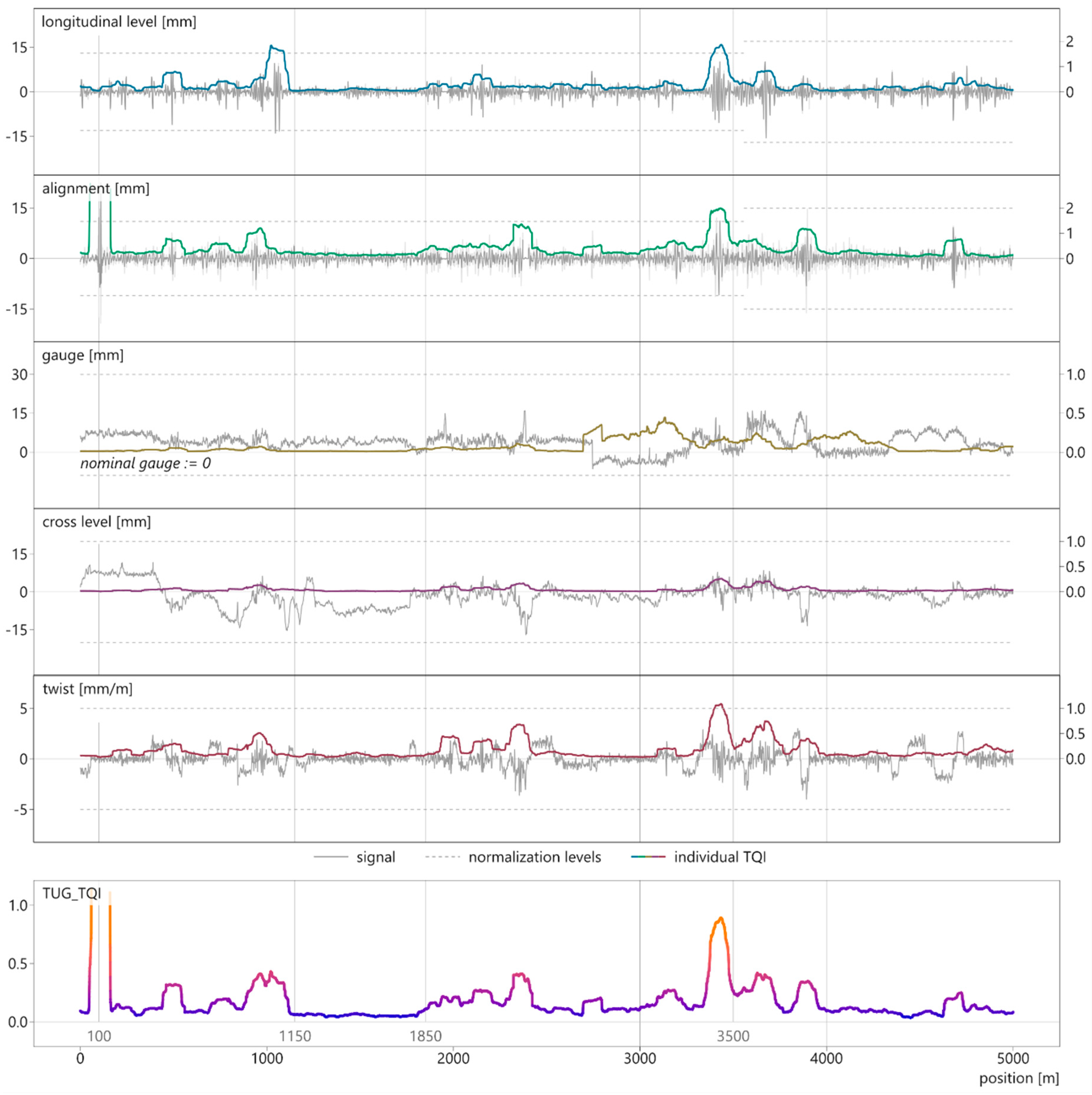
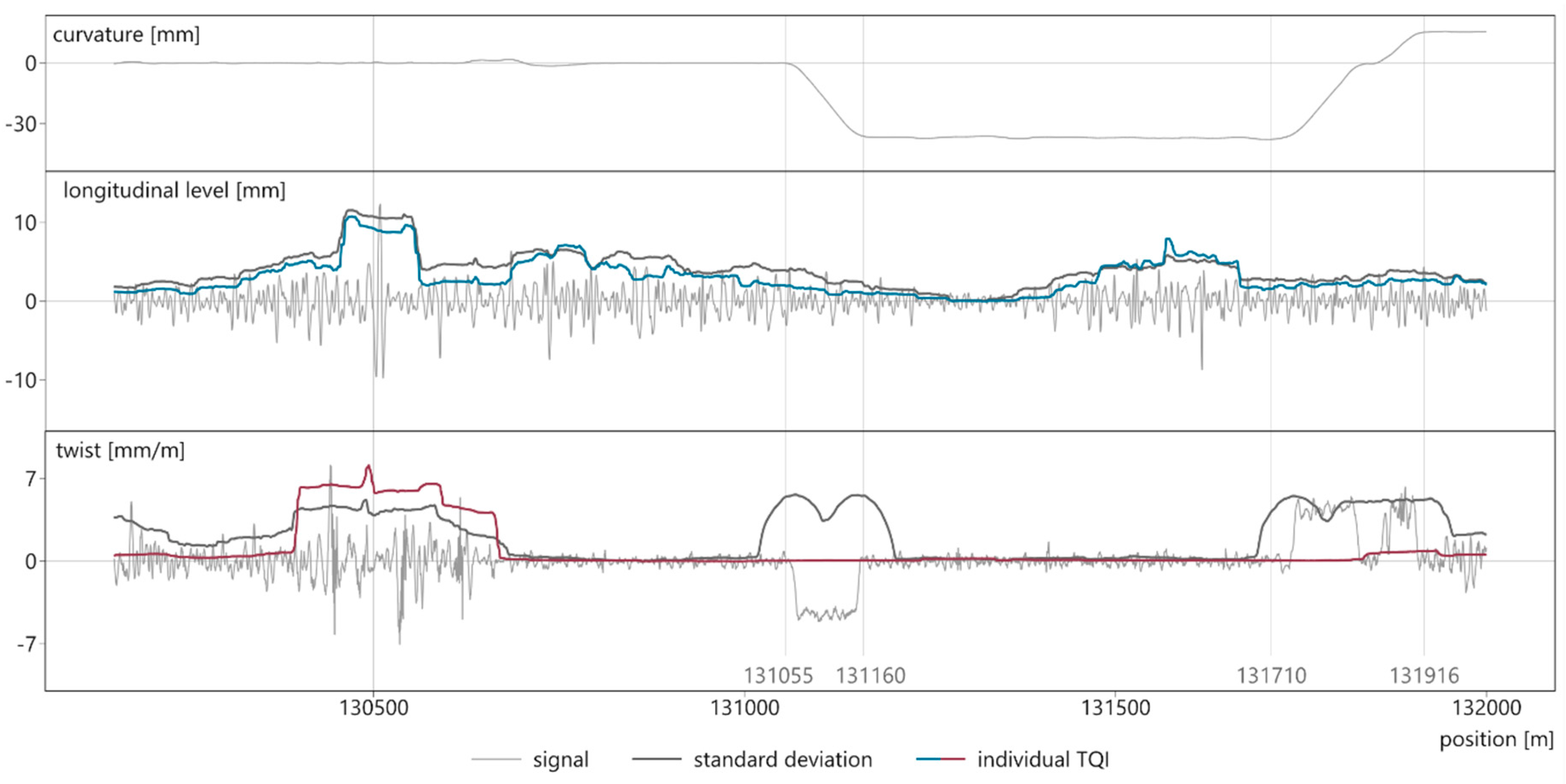
4. Results and Discussion
5. Summary
- The mathematical model is applicable for every measurement signal and nominal track gauge and thus for any railway network.
- The TUG_TQI can incorporate any measurement signal for which a reliable threshold level is defined.
- The underlying methodology reacts to scattering and peak values of the signals.
- Intended gauge widening in curves and twists in transition elements do not distort the respective indices.
- The gauge signal is split into a positive and a negative part because of differing threshold levels.
- By normalizing the signals, the line speed is implicitly considered.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fourie, C.J.; Zhuwaki, N.T. A modelling framework for railway infrastructure reliability analysis. S. Afr. J. Ind. Eng. 2017, 28, 150–160. [Google Scholar] [CrossRef][Green Version]
- Yuan, F.Q. Overall reliability index development for railway infrastructure and rolling stock with case study. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; pp. 1264–1268. [Google Scholar]
- Hidirov, S.; Guler, H. Reliability, availability and maintainability analyses for railway infrastructure management. Struct. Infrastruct. Eng. 2019, 15, 1221–1233. [Google Scholar] [CrossRef]
- Lidén, T. Railway Infrastructure Maintenance - A Survey of Planning Problems and Conducted Research. Transp. Res. Procedia 2015, 10, 574–583. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Wang, J.; Wang, Y.; Xu, G. An Incentive Factor-Based Dynamic Comprehensive Evaluation on a High-Speed Railway Track. Appl. Sci. 2020, 10, 5546. [Google Scholar] [CrossRef]
- Cannon, D.F.; Edel, K.; Grassie, S.L.; Sawley, K. Rail defects: An overview. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 865–886. [Google Scholar] [CrossRef]
- Abadi, T.; Le Pen, L.; Zervos, A.; Powrie, W. Effect of Sleeper Interventions on Railway Track Performance. J. Geotech. Geoenviron. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Sadeghi, J.; Zakeri, J.A.; Najar, M.E.M. Developing Track Ballast Characteristic Guideline in Order to Evaluate Its Performance. Int. J. Railw. 2016, 9, 27–35. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, P.; Dai, F. Advances in design theories of high-speed railway ballastless tracks. J. Mod. Transp. 2011, 19, 154–162. [Google Scholar] [CrossRef]
- Austrian Standards Institute. EN 13848-6: Railway Applications–Track–Track Geometry Quality–Part6: Characterisation of Track Geometry Quality; Austrian Standards Institute: Vienna, Austria, 2014; Available online: https://standards.iteh.ai/catalog/standards/cen/741d0eac-5fda-472d-842c-0f78e01a1d47/en-13848-6-2014 (accessed on 26 March 2014).
- Ižvolta, L.; Šmalo, M. Assessment of the Track Geometry Quality from the Aspect of Safe and Reliable Operation of the Railway Track. Procedia Eng. 2015, 111, 344–350. [Google Scholar] [CrossRef]
- Berawi, A.R.B.; Delgado, R.; Calçada, R.; Vale, C. Evaluating track geometrical quality through different methodologies. Int. J. Technol. 2010, 1, 38–47. [Google Scholar]
- Soleimanmeigouni, I.; Ahmadi, A.; Nissen, A.; Xiao, X. Prediction of railway track geometry defects: A case study. Struct. Infrastruct. Eng. 2019, 16, 987–1001. [Google Scholar] [CrossRef]
- Soleimanmeigouni, I.; Ahmadi, A.; Kumar, U. Track geometry degradation and maintenance modelling: A review. Proc. Inst. Mech. Eng. Part. F J. Rail Rapid Transit. 2016, 232, 73–102. [Google Scholar] [CrossRef]
- Khajehei, H.; Ahmadi, A.; Soleimanmeigouni, I. Forecasting Railway Track Geometry Condition Using Neural Network Approach. 2017. Available online: https://www.researchgate.net/publication/320170135_Forecasting_Railway_Track_Geometry_Condition_Using_Neural_Network_Approach (accessed on 13 September 2018).
- Fellinger, M.; Neuhold, J.; Marschnig, S. Ballast Condition Monitoring for Turnouts Using Power Spectral Density. J. Transp. Eng. Part. A Syst. 2020, 146, 04020099. [Google Scholar] [CrossRef]
- Landgraf, M.; Hansmann, F. Fractal analysis as an innovative approach for evaluating the condition of railway tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2018, 233, 596–605. [Google Scholar] [CrossRef]
- Sadeghi, J. Development of Railway Track Geometry Indexes Based on Statistical Distribution of Geometry Data. J. Transp. Eng. 2010, 136, 693–700. [Google Scholar] [CrossRef]
- Liu, R.-K.; Xu, P.; Sun, Z.-Z.; Zou, C.; Sun, Q.-X. Establishment of Track Quality Index Standard Recommendations for Beijing Metro. Discret. Dyn. Nat. Soc. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Andrews, J.; Prescott, D.; De Rozières, F. A stochastic model for railway track asset management. Reliab. Eng. Syst. Saf. 2014, 130, 76–84. [Google Scholar] [CrossRef]
- Vidovic, I.; Marschnig, S. Optical Fibres for Condition Monitoring of Railway Infrastructure—Encouraging Data Source or Errant Effort? Appl. Sci. 2020, 10, 6016. [Google Scholar] [CrossRef]
- Soleimanmeigouni, I.; Ahmadi, A.; Khajehei, H.; Nissen, A. Investigation of the effect of the inspection intervals on the track geometry condition. Struct. Infrastruct. Eng. 2019, 16, 1138–1146. [Google Scholar] [CrossRef]
- Austrian Standards Institute. EN 13848-1: Railway Applications-Track-Track Geometry Quality-Part 1: Characterization of Track Geometry; Austrian Standards Institute: Vienna, Austria, 2019. [Google Scholar]
- Neuhold, J.; Vidovic, I.; Marschnig, S. Preparing Track Geometry Data for Automated Maintenance Planning. J. Transp. Eng. Part. A Syst. 2020, 146, 04020032. [Google Scholar] [CrossRef]
- El-Sibaie, M.; Zhang, Y.-J. Objective Track Quality Indices. Transp. Res. Rec. J. Transp. Res. Board 2004, 1863, 81–87. [Google Scholar] [CrossRef]
- Austrian Standards Institute. EN 13848-5: Railway Applications-Track-Track Geometry Quality-Part 5: Geometrical Quality Levels-Plain Line, Switches and Crossings; Austrian Standards Institute: Vienna, Austria, 2017. [Google Scholar]
- Luber, B. Methode zur Bewertung von Gleislageabweichungen auf Basis von Fahrzeugreaktionen; Graz University of Technology: Graz, Austria, 2011. [Google Scholar]
- Hummitzsch, R. Zur Prognostizierbarkeit des Qualitätsverhaltens von Gleisen: Statistische Analyse des Gleisverhaltens zur Erstellung eines Prognosemodells; TU Graz: Graz, Austria, 2009. [Google Scholar]
- Mlinarić, T.J. Dugoročna Procjena Kvalitete Kolosiječne Geometrije s Ciljem Identificiranja Zahtjeva Održavanja; University of Zagreb: Zagreb, Croatia, 2002. [Google Scholar]
- Madejski, J.; Grabczyk, J. Continuous Geometry Measurement for Diagnostics of Tracks and Switches. In Proceedings of the International Conference on Swithches, Delft, The Netherlands, 19–22 March 2002. [Google Scholar]
- Andersson, M. Strategic Planning of Track Maintenance, Borlänge. 2002. Available online: http://www4.banverket.se/raildokuffe/pdf/MC0228.pdf (accessed on 23 October 2020).
- Jernbanekompetanse.no, Textbooks in Railway Technology. 2019. Available online: https://www.jernbanekompetanse.no/wiki/Tilstandskontroll (accessed on 28 October 2020).
- Berawi, A.R.B. Improving Railway Track Maintenance Using Power Spectral Density (PSD); University of Porto: Porto, Portugal, 2013. [Google Scholar]
- Ebersöhn, W.; Selig, E.T. Use of Track Geometry Measurements for Maintenance Planning. Transp. Res. Rec. J. Transp. Res. Board. 1994, 1470, 84–92. [Google Scholar]
- Yu-Jiang, P.; Zhang, P.; El-Sibaie, M.; Sung, L. FRA Track Quality Indices and Distribution Characteristics. In Proceedings of the AREMA Annual Conference, Nashville, TN, USA, 19–22 September 2004. [Google Scholar]
- Lichtberger, B. Track Compendium; Eurailpress Tetzlaff-Hestra GmbH & Co.: Hamburg, Germany, 2005. [Google Scholar]
- Austrian Standards Institute. EN 13803: Railway Applications-Track-Track Alignment Design Parameters-Track Gauges 1435 mm and Wider; Austrian Standards Institute: Vienna, Austria, 2017. [Google Scholar]
- Hansmann, F. Innovative Messdatenanalyse–ein Beitrag für ein Nachhaltiges Anlagenmanagement Gleis; Graz University of Technology: Graz, Austria, 2015; Available online: https://online.tugraz.at/tug_online/wbAbs.showThesis?pThesisNr=58734&pOrgNr=1228# (accessed on 3 November 2020).




| Parameter | Description |
|---|---|
| Longitudinal level | Deviation of the running table level from a smoothed vertical position (reference line) within defined wavelength ranges. |
| Alignment | Lateral deviation of the rail from a smoothed lateral position (reference line) within defined wavelength ranges. |
| Track gauge | Shortest distance of the inner flanks of the rail heads 0–14 mm below the rail surface. |
| Cross level | Difference in height of the adjacent running tables. |
| Twist | Difference between two cross levels divided by their distance apart. |
| Geometry Parameter | Intervention Limit |
|---|---|
| Longitudinal level (V ≤ 80 [kph], V ≤ 120 [kph]) | ±17 [mm], ±13 [mm] |
| Alignment (V ≤ 80 [kph], V ≤ 120 [kph]) | ±15 [mm], ±11 [mm] |
| Gauge positive, Gauge negative (V ≤ 120 kph) | +30 [mm], −9 [mm] |
| Cross level (V ≤ 120 kph) | ±20 [mm] |
| Twist (V ≤ 120 kph) | ±5 [mm] |
| Track Class | Speed [kph] | Vertical Geometry (sH) | Cross Level (σR) | Horizontal Geometry (σP) | Interaction (σS) |
|---|---|---|---|---|---|
| K0 | 145– | 1.1 | 0.9 | 1.1 | 1.6 |
| K1 | 125–140 | 1.3 | 1.0 | 1.2 | 1.7 |
| K2 | 105–120 | 1.5 | 1.2 | 1.3 | 1.9 |
| K3 | 75–100 | 1.9 | 1.4 | 1.7 | 2.4 |
| K4 | 40–70 | 2.4 | 1.8 | 2.0 | 3.1 |
| K5 | −35 | 2.9 | 2.2 | 2.4 | 3.6 |
| Parameter | SD New Track | SD Maintenance (Vmax > 105 [kph]) | SD Maintenance (Vmax < 105 [kph]) |
|---|---|---|---|
| Longitudinal level | 2.5 | 6.2 | 7.2 |
| Alignment | 1.5 | 3.0 | 3.0 |
| Gauge | 1.0 | 3.6 | 3.6 |
| Twist | 1.75 | 3.8 | 4.2 |
| (i) Basic Concept of the TQI | (ii) TQI Includes all Parameters | (iii) TQI Requires Adjustment Factors | |
|---|---|---|---|
| Isolated defects | threshold | n/a | no |
| CoSD | sd | no | yes |
| MDZ-a | miscellaneous | no | yes |
| Chinese TQI | sd | yes | no |
| CN’s TQI | sd | no | yes |
| J coefficient | sd | no | no |
| Q-value | sd | no | no |
| K-value | threshold (sd) | no | no |
| Netherlands Q | sd | n/a | no |
| TGI | sd | no | no |
| OTGI | sd (+miscellaneous) | no | yes |
| w5 | threshold | yes | no |
| R² | miscellaneous | no | no |
| FRA TQI | miscellaneous | no | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Offenbacher, S.; Neuhold, J.; Veit, P.; Landgraf, M. Analyzing Major Track Quality Indices and Introducing a Universally Applicable TQI. Appl. Sci. 2020, 10, 8490. https://doi.org/10.3390/app10238490
Offenbacher S, Neuhold J, Veit P, Landgraf M. Analyzing Major Track Quality Indices and Introducing a Universally Applicable TQI. Applied Sciences. 2020; 10(23):8490. https://doi.org/10.3390/app10238490
Chicago/Turabian StyleOffenbacher, Stefan, Johannes Neuhold, Peter Veit, and Matthias Landgraf. 2020. "Analyzing Major Track Quality Indices and Introducing a Universally Applicable TQI" Applied Sciences 10, no. 23: 8490. https://doi.org/10.3390/app10238490
APA StyleOffenbacher, S., Neuhold, J., Veit, P., & Landgraf, M. (2020). Analyzing Major Track Quality Indices and Introducing a Universally Applicable TQI. Applied Sciences, 10(23), 8490. https://doi.org/10.3390/app10238490






