A New Constrained State Estimation Method Based on Unscented H∞ Filtering
Abstract
Featured Application
Abstract
1. Introduction
2. Preliminaries
2.1. The Principle of the H-Infinity Filter
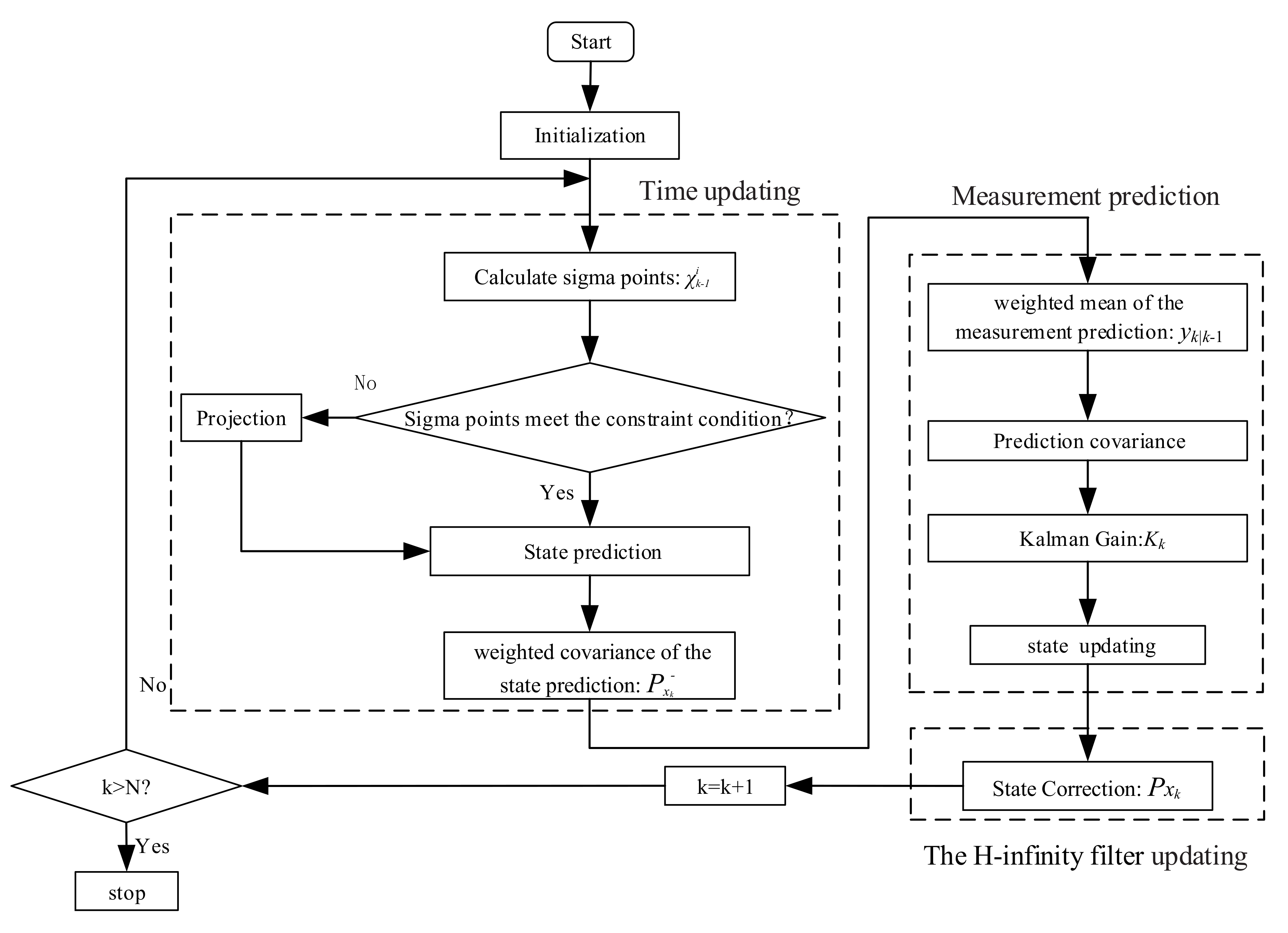
2.2. The Principle of the Unscented H∞ Filter
- (1)
- Initialization:where the and are the system process noise and measurement noise covariance. In the UKF, the effective vector of this augmented state is , the superscript “a” here means the new state is an “augmented” state. It consists of a target state vector, process noise and observation noise.To calculate the sigma points and weights:
- (a)
- Generate 2L+1 Sigma points:
- (b)
- The weights are determined as follows:where denotes the i-th column of the square root of the matrix [18]. λ is a compound scaling parameter,; L is the dimension of the state variable; α is a scale parameter, which is generally a small positive value and determines the distribution of the sigma points [19]; is a non-negative weighting term that affects the weight of the sigma points used for covariance calculations and can be set to 2; is a scale parameter, which is usually greater than or equal to 0 to ensure the positive definiteness of the covariance matrix. , are the weights of the state and covariance, respectively.
- (2)
- Time updating:
- (3)
- Measurement updating:
2.3. State Estimation under Constraints
3. Simulation Results
3.1. A Reversible Reaction Example
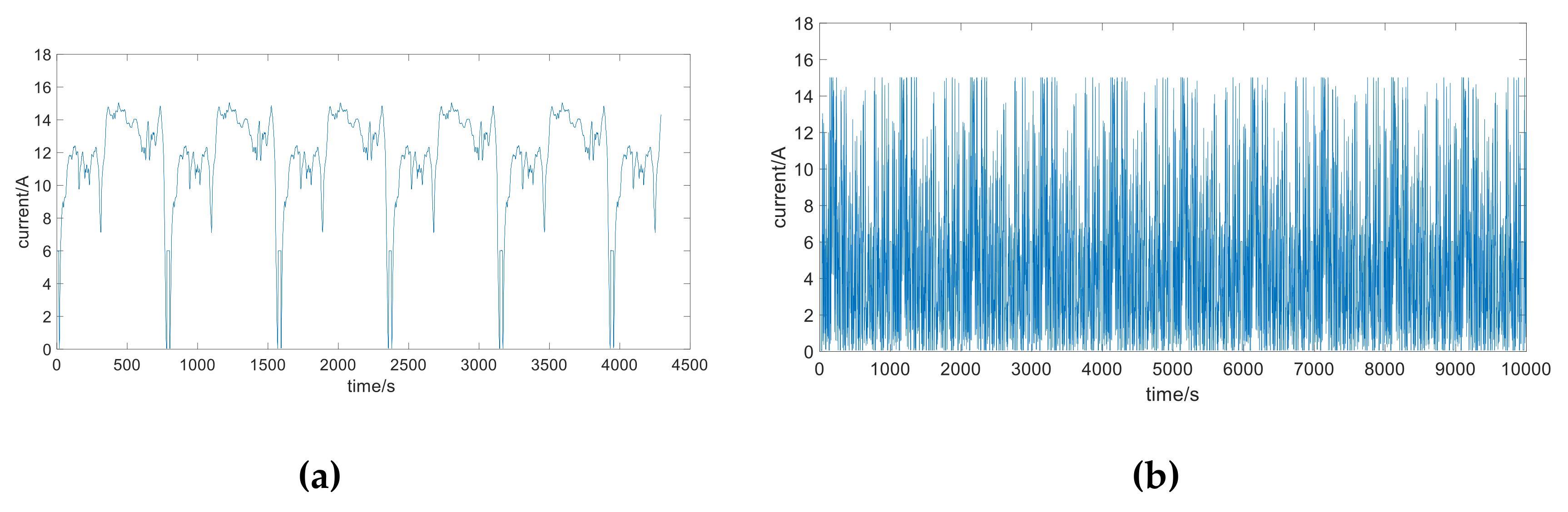
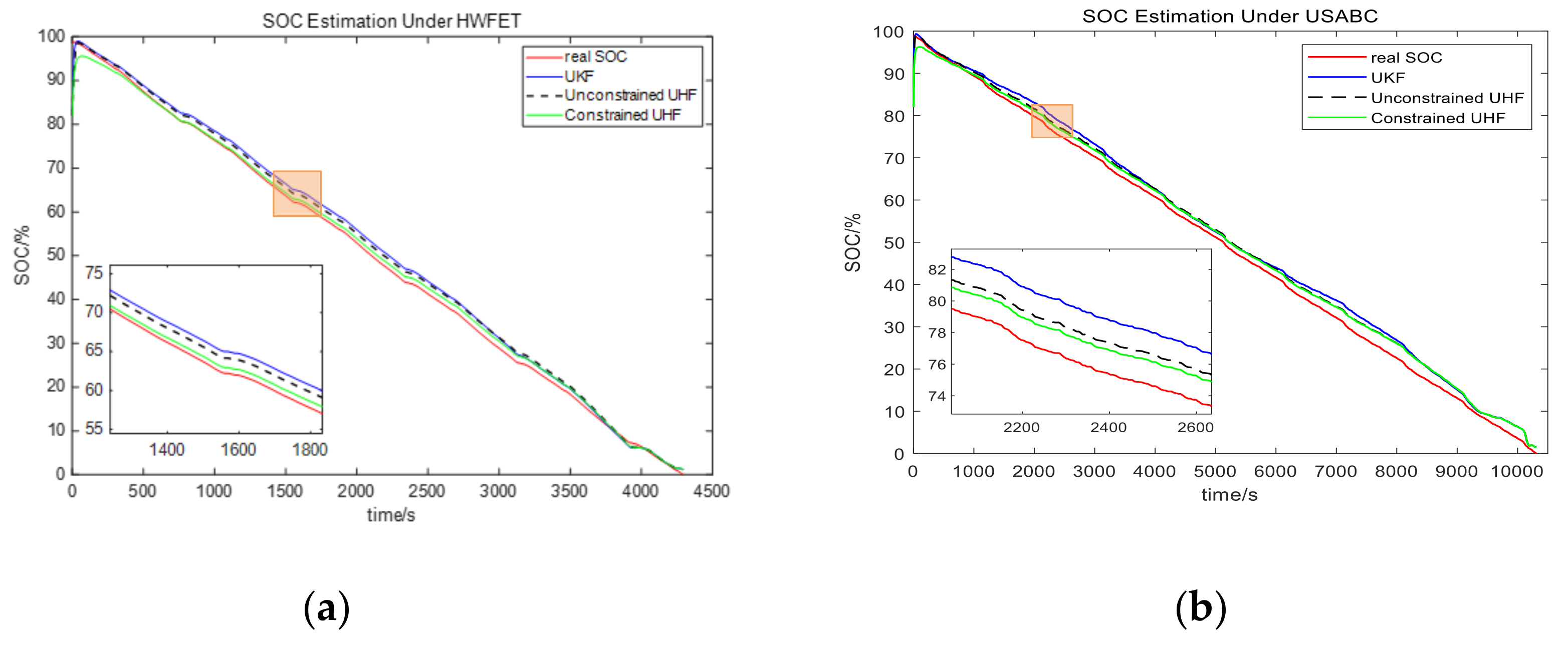
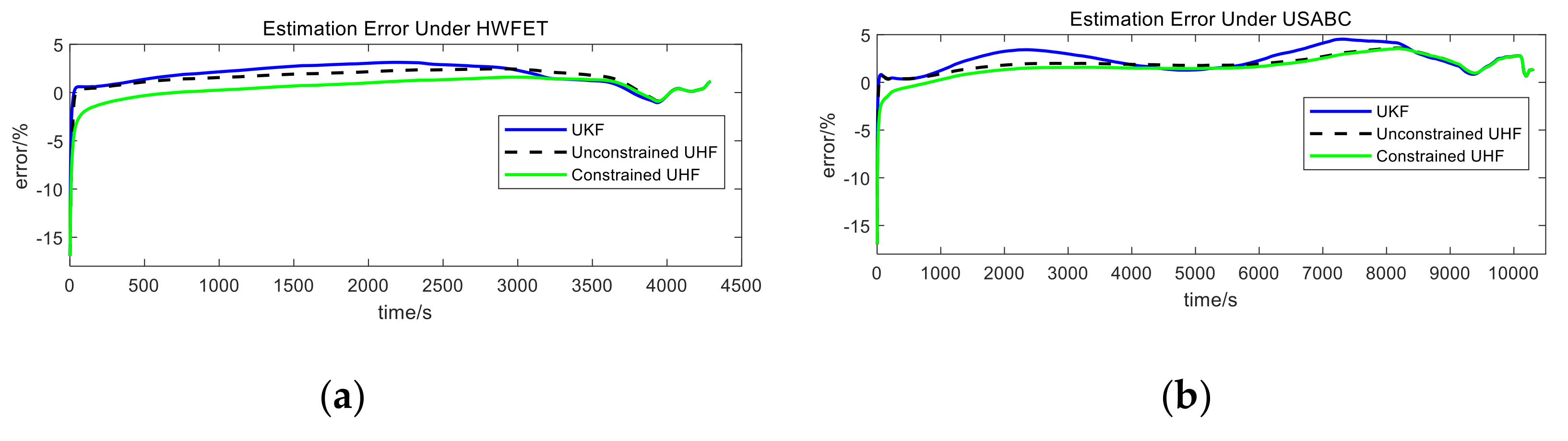
3.2. State of Charge Estimation for LITHIUM-Ion Batteries
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME D J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Costanzi, R.; Fanelli, F.; Meli, E.; Ridolfi, A.; Caiti, A.; Allotta, B. UKF-Based Navigation System for AUVs: Online Experimental Validation. IEEE J. Ocean. Eng. 2019, 44, 633–641. [Google Scholar] [CrossRef]
- Lee, D.; Liu, C.; Liao, Y.; Hedrick, J.K. Parallel Interacting Multiple Model-Based Human Motion Prediction for Motion Planning of Companion Robots. IEEE T. Autom. Sci. Eng. 2017, 14, 52–61. [Google Scholar] [CrossRef]
- Lou, T.; Yang, N.; Wang, Y.; Chen, N. Target Tracking Based on Incremental Center Differential Kalman Filter With Uncompensated Biases. IEEE Access 2018, 6, 66285–66292. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Tech. Rep. TR95041; Department of Computer Science University of North Carolina: Chapel Hill, NC, USA, 2000. [Google Scholar]
- Gao, M.; He, Z.; Liu, Y. Improved unscented kalman filter for bounded state estimation. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 2101–2104. [Google Scholar]
- Wang, Z.; Qin, Y.; Gu, L.; Dong, M. Vehicle System State Estimation Based on Adaptive Unscented Kalman Filtering Combing With Road Classification. IEEE Access 2017, 5, 27786–27799. [Google Scholar] [CrossRef]
- Bucy, R.S.; Senne, K. Digital Synthesis of Nonlinear Filters; Technical Report, SRL 70-0010; Frank J. Seiler Research Laboratory: Colorado Springs, CO, USA, June 1970. [Google Scholar]
- Van der Merwe, R.; Wan, E.A.; Julier, S.J. Sigma-point Kalman filters for nonlinear estimation and sensor-fusion-applications to integrated navigation. In Proceedings of the AIAA Guidance, Navigation, Control Conference, Providence, RI, USA, 16–19 August 2004. AIAA-2004-5120. [Google Scholar]
- Sahoo, H.K.; Dash, P.K. Robust estimation of power quality disturbances using unscented H∞ filter. Int. J. Electr. Power Energy Syst. 2015, 73, 438–447. [Google Scholar] [CrossRef]
- Havangi, R. Unscented H-infinity filtering based simultaneous localization and mapping with evolutionary resampling. J. Frankl. Inst. 2015, 352, 4801–4825. [Google Scholar] [CrossRef]
- Zhao, J. Dynamic State Estimation with Model Uncertainties Using H-infinity Extended Kalman Filter. IEEE Trans. Power Syst. 2018, 33, 1099–1100. [Google Scholar] [CrossRef]
- Zhao, J.; Mili, L. A Theoretical Framework of Robust H-infinity Unscented Kalman Filter and Its Application to Power System Dynamic State Estimation. IEEE Trans. Signal Process. 2019, 67, 2734–2746. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H∞ and Nonlinear Approaches; Wiley: Hoboken, NJ, USA, 2006; Chapter 11. [Google Scholar]
- Li, W.; Jia, Y. H-infinity filtering for a class of nonlinear discrete-time systems based on unscented transform. Signal Process. 2010, 90, 3301–3307. [Google Scholar] [CrossRef]
- Shao, X.; Huang, B.; Lee, J.M. Constrained Bayesian state estimation—A comparative study and a new particle filter based approach. J. Process Control 2010, 20, 143–157. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, B.; Rong, L. A robust unscented Kalman filter and its application in estimating dynamic positioning ship motion states. J. Mar. Sci. Technol. 2019, 24, 1265–1279. [Google Scholar] [CrossRef]
- Bruno, O.S.; Tôrres, L.A.B.; Aguirre, L.A.; Bernstein, D.S. On unscented Kalman filtering with state interval constraints. J. Process Control 2010, 20, 45–57. [Google Scholar]
- Teixeira, B.O.S.; Chandrasekar, J.; Tôrres, L.A.B.; Aguirre, L.A.; Bernstein, D.S. State estimation for linear and non-linear equality-constrained systems. Int. J. Control 2009, 82, 918–936. [Google Scholar] [CrossRef]
- Bhushan, K.K.K.; Bhartiya, S. Projection Based Constrained Nonlinear State Estimation Using Gaussian Sum Filters; IEEE: New York, NY, USA, 2016; pp. 444–449. [Google Scholar]
- Kandepu, R.; Imsland, L.; Foss, B. Constrained state estimation using the unscented kalman filter. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Corsica, France, 25–27 June 2008; pp. 1453–1458. [Google Scholar]
- Foss, S.K.A.; Schei, T.S. Constrained nonlinear state estimation based on the UKF approach. Comput. Chem. Eng. 2009, 33, 1386–1401. [Google Scholar] [CrossRef]
- Foss, S.K.A.; Schei, T.S. Noise modeling concepts in nonlinear state estimation. J. Process Control 2009, 19, 1111–1125. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Chen, S.; Kang, C.; Zhang, Z.; Zhu, H. A method for SOC estimation for lead-acid battery based on multi-model adaptive Extended Kalman Filtering estimation. In Proceedings of the Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016. [Google Scholar]


| Algorithm | Mean Square Error (PA) | Mean Square Error (PB) |
|---|---|---|
| unconstrained UHF | 0.5348 | 0.5326 |
| constrained UHF | 0.1922 | 0.1976 |
| K0 | R | K1 | K2 | K3 | K4 |
|---|---|---|---|---|---|
| 3.3738 | −0.0050 | 0.0000 | −0.1197 | 0.0935 | −0.0198 |
| Algorithm | Mean Square Error | Max Error | Time |
|---|---|---|---|
| UKF | 4.6758 × 10−4 | 3.13% | 0.957 s |
| Unconstrained UHF | 3.5107 × 10−4 | 2.46% | 0.853 s |
| Constrained UHF | 1.6079 × 10−4 | 1.60% | 0.847 s |
| Algorithm | Mean Square Error | Max Error | Time |
|---|---|---|---|
| UKF | 7.2030 × 10−4 | 4.53% | 1.5007 s |
| Unconstrained UHF | 4.6877 × 10−4 | 3.61% | 1.7334 s |
| Constrained UHF | 3.9919 × 10−4 | 3.55% | 1.7298 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fu, Y.; Lin, H.; Liu, J.; Gao, M.; He, Z. A New Constrained State Estimation Method Based on Unscented H∞ Filtering. Appl. Sci. 2020, 10, 8484. https://doi.org/10.3390/app10238484
Liu Y, Fu Y, Lin H, Liu J, Gao M, He Z. A New Constrained State Estimation Method Based on Unscented H∞ Filtering. Applied Sciences. 2020; 10(23):8484. https://doi.org/10.3390/app10238484
Chicago/Turabian StyleLiu, Yuanyuan, Yaqiong Fu, Huipin Lin, Jingbiao Liu, Mingyu Gao, and Zhiwei He. 2020. "A New Constrained State Estimation Method Based on Unscented H∞ Filtering" Applied Sciences 10, no. 23: 8484. https://doi.org/10.3390/app10238484
APA StyleLiu, Y., Fu, Y., Lin, H., Liu, J., Gao, M., & He, Z. (2020). A New Constrained State Estimation Method Based on Unscented H∞ Filtering. Applied Sciences, 10(23), 8484. https://doi.org/10.3390/app10238484






