Abstract
Mechanical brakes are essential for electric cranes when emergency braking occurs. This paper presents, for the first-time, a dynamic response analysis of emergency braking events of electrical cranes that has modelled crane components as flexible and rigid bodies. Based on the Hamilton principle, a nonlinear and non-smooth dynamic model is derived from a modified Lagrangian function and the virtual work of non-conservative forces. The dynamic responses of a 32-ton overhead travelling crane during the emergency braking process of its lifting mechanism with two service brakes determined by simulating realistic operations. The numerical results show that the loads acting on components of the crane during the braking process depend on the braking capacity and the action time of the mechanical brakes, as well as the magnitude and the initial position of the payload. When a dual-brake scheme of the lifting mechanism is adopted, the maximum load of the high-speed links and the maximum thermal power of the mechanical brake appear in the emergency braking process when one of the two brakes fails to work. In addition, it is found to be a false belief that the lower the initial speed, the lower the maximum loads acting on components of cranes become during the braking process.
1. Introduction
Braking is applied frequently during the operation of cranes. For electric cranes, there are two kinds of braking, referred to as normal braking and emergency braking respectively in this paper. Normal braking is applied during normal operations and when moderate faults occur, such as overheating of the electrical system. However, emergency braking is also unavoidable in some situations. For example, electric power is cut off suddenly, over-current occurs in a circuit of a driving motor, the load handling device comes into contact with the lever of the counter-weighted limit switch, or the emergency stop button is pressed [1], and so on.
A normal braking operation can be described as: at first the electrical braking is applied, then the mechanical brake is applied when the rotational speed of the motor gets to a specified low level, and subsequently the electric motor is switched off in less than a second. However, when emergency braking happens, the mechanism is stopped only by the mechanical brake, without the electrical braking process.
High safety is required in all cranes, and therefore the mechanical brake is one of the critical devices to ensure the safe operation of cranes. It has been accepted that a braking process by a mechanical brake causes energy dissipation and wear of the friction pairs [2], and it is vital to maintain a steady braking capacity for brakes. Therefore, some fundamental principles have to be followed when choosing brakes [3].
According to the report of Severin and Dörsch [4], the braking capacity of mechanical brakes in operation is related to the thermal load of brakes, the friction work, the friction power at the beginning of braking, and metal particles diffused into the friction linings. The mean friction coefficient of the friction pair basically remains invariant within the normal range of thermal loads, but it decreases sharply when the friction pairs overheat [4,5]. Meanwhile, Van Wittenberghe et al. [6] demonstrated that there were quite different thermal characteristics for different types of materials of friction pairs of brakes.
The safety of cranes is also much related to their dynamic responses during normal operations. Park et al. [7] analysed the dynamic factor of the rope of a floating crane during lifting based on flexible multi-body dynamics. Sun et al. [8] carried out the dynamic analysis of a lattice mobile crane during hoisting controlled by a hydraulic secondary control system with speed regulation. Posiadała [9] conducted a numerical simulation of a truck crane using a dynamic model considering the flexibility of the crane support system. Ju et al. [10] studied the dynamic response of the steel structure of a tower crane induced by the movement of a spherical pendulum and a planar pendulum (the payload and the rope are regarded as a single pendulum). Jerman [11] presented a new dynamic model of slewing cranes with a large swaying angle of the payload during slewing. Cibicik et al. [12] presented a dynamic model for luffing motion of a flexible knuckle boom crane. Yildirim and Esim [13] carried out a finite element dynamic analysis of the bridge of an overhead travelling crane while its traversing mechanism was in operation and introduced a kind of finite element subjected to a point load. Urbaś [14] built a dynamics model of a forest crane that considered the flexibility of connections between the crane and the ground, the flexibility of links and their drives based on the rigid finite element method. Adamiec-Wójcik et al. [15] implemented static and dynamic analyses of an offshore knuckle boom crane during the hoist acceleration or deceleration in a 3D dynamic model. Cibicik and Egeland [16] applied screw theory to formulate the dynamic model of an offshore knuckle crane with passive rotary joints and piston actuators and obtained dynamic reaction forces of the joints during jib luffing motion. Tomasz [17] presented a dynamic model of an overhead crane during lifting mechanism operation, which incorporated two steel rope system models, namely the Kelvin–Voigt model and Bouc–Wen model, to consider the influence of rope system parameters on dynamic factors due to the inertia effect of the cargo mass during the lifting mechanism operation.
To ensure the safety and efficiency of installation operations of a jack-up crane vessel, Zhao et al. [18] built a fully coupled aero-hydro-soil-elastic-mechanical dynamic model for the vessel, and studied the important dynamic responses of the vessel during installation of an offshore wind turbine blade. Cekus et al. [19] analysed the system response of a mobile crane during operations in a windy environment using a coupled kinematic and dynamic model. Furthermore, motion control strategies for cranes cannot be developed without a proper dynamic analysis [20,21,22,23,24,25].
Dynamic responses under unusual circumstances are the other factors related to the safety of cranes. Otani et al. [26] investigated the vertical seismic response of a 1/8-scale model of an overhead crane and carried out simulation of a nonlinear dynamic model of the crane excited by catastrophic ground motion with gap elements at the crane wheels/tracks interface. To simulate three-dimensional nonlinear seismic responses of container cranes, Kobayashi et al. [27] presented a model including the contact problem between the wheels and rails of cranes based on multi-body dynamics formulation. Feau et al. [28] carried out experimental and numerical investigations of the earthquake response of crane bridges. Huh et al. [29] compared the effects of three kinds of boundary conditions, which were used to respectively model the contact between wheels and rails as pin supports, gap elements and friction contact elements, on seismic responses of the container crane.
Today, emergency braking of cranes has recently emerged as a big concern [5,30,31]. Wang et al. [5] prepared the higher friction brake shoe material used for the emergency brake of an ultra-deep coal mine hoist and verified its tribological behaviour by means of the test designed by the uniform experimental design method. Chen et al. [30] proposed a control method for emergency braking of the traversing mechanism of overhead travelling cranes, which considered the payload swing suppression. Vöth [31] proposed a new emergency braking scheme for a coal handling gantry hoist to prevent high loads from appearing on the drive chains of the hoist, which was equipped with an additional safety brake on the rope drum. Streltsov et al. [32] investigated the stress–strain state of the steel frame of a gantry crane under the horizontal constrained forces of rails caused by the difference of the braking torques of the brakes located on the two sides of the gantry crane when braking.
Although emergency braking is a kind of unusual operation, during which the components of cranes may be subjected to the most unfavourable loads, especially for those controlled by speed control systems, because the dynamic loads during normal operations are now less serious after the adoption of the frequency control, electrical braking and command shaping technology [33,34,35]. Therefore, dynamic loads during emergency braking are added as critical design loads to ensure load-bearing capacity of components of cranes in the latest edition of design codes on cranes, but the dynamic effect is considered only crudely by an amplification factor [36,37]. However, the problems that design engineers care about most, the characteristic of dynamic responses under emergency braking operations and pertinent influence factors, remain unclear.
Given that the failure of the lifting mechanism is more dangerous than that of the travelling or traversing mechanism, accidents induced by braking of lifting mechanisms using mechanical brakes are not uncommon, and the test of the emergency braking is unrealistic or infeasible during product design. Thus, as it is impossible to determine the dynamic loads through experiments in the design phase, the prediction of dynamic loads during emergency braking becomes necessary for crane design.
To understand emergency braking operations, this paper focuses on the dynamic behaviour of electric cranes governed by frequency control systems during emergency braking of lifting or lowering operations. First, a theoretical approach to investigate the process is presented, and a nonlinear dynamic model and a numerical simulation algorithm of a general overhead travelling crane is established. Then, the effects on the dynamic response of the system under different parameters and braking schemes are to be discussed.
For simplicity, lifting or lowering emergency braking in this paper are referred to as braking hereinafter.
2. Dynamic Model
2.1. Physical Model and Assumption
In general, a real electric overhead travelling crane consists of a bridge, one or two trolleys and travelling mechanisms, as shown in Figure 1.
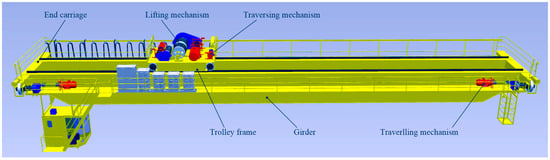
Figure 1.
Electric overhead travelling crane.
The bridge, which is composed of two identical girders and two identical end carriages, is a welded thin-walled steel structure. The girders and end carriages, whose height and width are much smaller than the crane span, have high torsional rigidity. The cross sections of the girders and the end carriages are unchanged except in a very small range at their two ends. The maximum deflection of the girders is less than L/1000–L/750 (L is the crane span) and is much larger than that of the end carriages. The bridge is supported on two crane rails by crane wheels with cylindrical tread. There is a certain curvature on the top surfaces of the rails and a side clearance from 20 mm to 30 mm between a rail and two flanges of all crane wheels.
A trolley is made up of one or two lifting mechanisms, a traversing mechanism and a trolley frame. If there are two lifting mechanisms in a trolley, they are referred to as the main and auxiliary lifting mechanisms respectively.
A typical lifting mechanism, as shown in Figure 2a, mainly consists of a 3-phase induction motor, a gear reducer, a mechanical brake (referred to as the service brake), a gear coupling with a brake drum (or a gear coupling without the brake drum, and a brake drum), a wire rope reeving system (including a rope drum, pulleys and one or two wire ropes) and a load handling device. The gear coupling is assembled on the high-speed shaft extension of the gear reducer and the shaft extension of the motor. To compensate for the misalignment between the axes of the motor shaft and the high-speed shaft of the reducer, a floating shaft is often adopted (item 5 in Figure 2b).
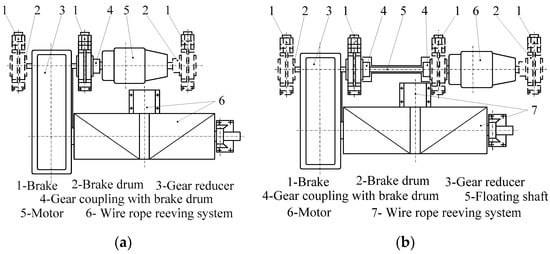
Figure 2.
A typical mechanical brake layout in lifting mechanism of an overhead crane. (a) The lifting mechanism without the floating shaft; (b) The lifting mechanism with the floating shaft.
The mechanical brake is used for not only holding the payload but also decelerating during braking. In general, when one service brake is used, the brake is assembled on a high-speed shaft extension of the gear reducer; when two service brakes are used, another brake may be assembled on another high-speed shaft extension of the gear reducer or one of the two motor shaft extensions, as shown in Figure 2b.
The traversing mechanism may include the wheels, driving motors, reducers, brakes, shafts and couplings and so on. As the support structure of the lifting mechanism and the traversing mechanism, the trolley frame, a high order statically indeterminate steel structure, has high bending and torsional rigidity.
In crane mechanisms, the moments of inertia of transmission shafts and rope sheaves are much smaller than those of other parts. The torsional deformation of the transmission shafts is much larger than those of other parts and the clearances between the transmission parts are small. The wire ropes are non-rotational, alternate lay wire ropes. That is, wires in each strand are arranged in the same helical direction while the strands are wound in opposite helical directions. When tensioning the wire rope, in theory, there is no rotation effect on the hung object and the wire rope itself is only subjected to a tensile force too. The payload undergoes only translational motion during lifting. Furthermore, when lifting height is less than 50 m, the mass of the steel rope is small relative to the mass of the lifted heavy object; the elastic modulus of the steel rope varies within a certain small range although it is a nonlinear variable which depends on the rope load, lubrication, etc.
In view of the above features of electric overhead cranes, some reasonable assumptions are made as follows:
- The two girders are treated as elastic Euler beams with the same small curvature, uniform damping and mass distributions.
- The wire rope is deemed to be a massless elastic body with a constant modulus of elasticity and viscous damping and can withstand only axial tension.
- The trolley frame, stators and rotors of motors, couplings, brake drums (or discs), the rope drums, gears, reducer housings, rope sheaves, steel wheels, and end carriages are considered rigid bodies. The payload (including the load handling device) is assumed to be a point mass.
- The clearances between transmission parts are negligible.
Based on the above assumptions and the mechanical brake layout of lifting mechanisms stated above, the physical model of a general electric overhead crane during braking of the lifting mechanism can be abstracted as the system shown in Figure 3.
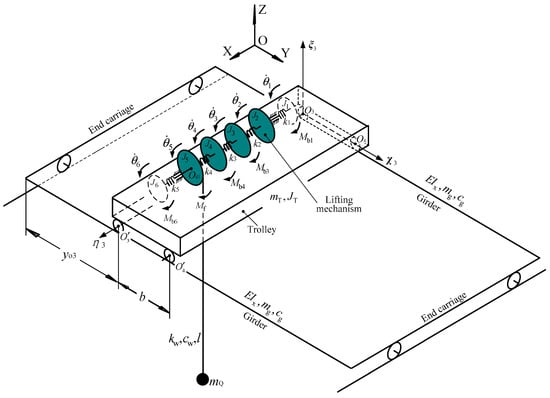
Figure 3.
Physical model of electric overhead crane under braking of lifting mechanism.
2.2. Energy of System
The energy of the crane includes the potential energy and kinetic energy T. The potential energy consists of the strain energy of the transmission shafts, the wire rope and two girders, and the gravitational potential energy of the trolley and the payload. The kinetic energy is composed of the kinetic energy of the two girders and the trolley due to the vibration, kinetic energy of the payload due to its translational movement in the vertical direction and kinetic energy of the rotational rigid bodies in lifting mechanism due to the rotation movement about their own axes.
As shown in Figure 3, an orthogonal coordinate system OXYZ is defined in the crane workspace, and another orthogonal coordinate system is fixed to the trolley. The displacement of a point in the two girders axis, whose Y coordinate is y, relative to its position under the dead weight of the girder is a function of y and time t:
where
Here, and n () are respectively the vector and the number of generalized coordinates used for describing elastic deformation of the girders along Z direction.
If the static equilibrium position of girders under their dead weight is defined as the zero position of the strain energy of girders and plane XOY is defined as the zero position of the gravitational potential energy of the system, then the potential energy of the crane can be expressed as;
with
Here, , l, and kw are used to describe respectively the tensile strain, the free length, and the total tensile force per unit strain of the wire rope segments hanging from the rope drum. and mQ are the masses of the trolley and lifted object (including the load-handling device) respectively. Ci (i = T, d) are the constants involved in the elastic deformation due to the dead weight, the camber and the geometrical sizes of the girder. is the angular displacement of rotating rigid body i in the lifting mechanism and is converted to quantities in reference to the rope drum axis. E and Ix are, respectively, the Young’s modulus of the girder material and the moment of inertia of the girder cross section with respect to its neutral axis, which is parallel to the X-axis. b is the wheel base of the trolley. is the Y coordinate of the points on the trolley wheels axis . is the coordinate of the points on the rope drum axis. is the coordinate of the gravity centre of the trolley. Rd is the wrapping radius of the wire rope on the rope drum. is the friction coefficient between the rope drum groove and the wire rope. ms is the reeving of the pulley block. ki (i = 1, 2,,5) is the torsional stiffness of the high-speed transmission shaft i in the lifting mechanism and is converted to quantities in reference to the rope drum axis.
The kinetic energy of the crane is
where
Here, mg is the mass of a girder, is the moment of inertia of the trolley about its centroid axis, which is parallel to -axis, is the moments of inertia of rotating rigid body i in the lifting mechanism and is converted to quantities in reference to the rope drum axis. For simplification, the rotating rigid body i with the moment of inertia is referred to as component hereafter.
2.3. Virtual Work of Non-Conservative Forces
In the overhead crane dynamic system, the non-conservative forces are the braking torques of the mechanical brakes, the resistance torque of the lifting mechanism, the damping forces in the elastic components of the crane system, and the friction force between the rope drum grooves and the wire rope wrapping around the rope drum.
Suppose the directions of , and as shown in Figure 3 are positive, and consider the damping forces in all elastic components viscous, then the virtual work of the non-conservative forces in the crane system can be formulated as
with
Here, cg, cs, and cw are the viscous damping coefficients of material of the girder, transmission shafts in the lifting mechanism and the wire rope respectively. and are the time function of the braking moment and the time function of the braking capacity of the brake i, which are all converted to quantities in reference to the rope drum axis. is the efficiency of the lifting mechanism.
2.4. Equation of Motion and Simulation Algorithm
The total free length of the wire rope (the sum of the original length of the rope segment wrapping on the rope drum and the original length of the rope segments hanging from the rope drum) remains invariable. Therefore, a constraint (expressed by Equation (26) in [38]), which gives the relationship between l, and , is incorporated into a modified Lagrangian function , in which is a Lagrange multiplier.
After applying Hamilton’s principle, ignoring higher order small quality and denoting , the equation of motion of the crane during braking of the lifting mechanism are derived as
where
Equation (5) is just a general equation of motion of the electric crane during braking of the lifting mechanism. There are all two kinds of motion states for every component during braking, that is, rotation state and non-rotation state. So if component is held by the mechanical brake and cannot rotate, the equation of motion (5) must be reduced according to the following two steps:
The first step is substituting vector by a new vector . Then, the equation of motion (5) becomes
where , is the angular displacement of component at this instant, is a column vector formed by the (n + i)-th column of .
The second step is deleting the (n + i)-th row of Equation (6) and the (n + i)-th column of matrixes , , and K. The resulting equation becomes the equation of motion when components are held
Just for the reasons mentioned above, the braking process consists of a set of these sub-processes governed by the different equations for the two motion states of component . Meanwhile, in order to switch correctly between these sub-processes, the motion states of component Jihave to be checked in every step in the numerical integration. This process is explained as follows:
- (1)
- When component Ji is in the rotation state initially, needs to be checked at the end of each step of the numerical integration. If , then Jiis still in the rotation state; once , must be calculated ( is an algebraic sum of all torques acting on component Ji except braking torque ). If , component Ji starts to go into the non-rotation state; otherwise, component Ji will continue to rotate after this time instant when the direction of rotation of component Ji changes.
- (2)
- When component Ji is in the non-rotation state initially, needs to be calculated at the end of each step of the numerical integration. Once and , component Ji will start to go into the rotation state. Otherwise, component Ji will still be in the non-rotation state.
Moreover, if there are no mechanical brakes assembled on components and/or , the (n + 1)-th and/or (n + 6)-th row of Equation (5), and the (n + 1)-th and/or (n + 6)-th column of matrixes ,and should be deleted, and (i = 1 and/or 5) in and should be set to zero.
In short, the equation of motion describing braking process of the lifting mechanism of the overhead travelling crane is nonlinear. Because Coulomb friction is adopted, the equation of motion is non-smooth as well. Additionally, damping and stiffness matrices of the motion equation vary with time, therefore the simulation of the braking process is quite complicated.
Matlab programs are coded to implement all the calculations. The flow chart of the simulation algorithm of the braking process of lifting mechanism in which service brakes are assembled on component 4 and 6 only is given in Figure 4. In Figure 4, [t0, tend] is the integral interval of the equation of motion. x0 and is the initial value, . t and y are the time instantaneous value at the end of each integration process and the corresponding solution of the equation respectively, . Case i (i = 1, 2, 3, 4) is a variable used for representing the motion state of component J4 and J6.
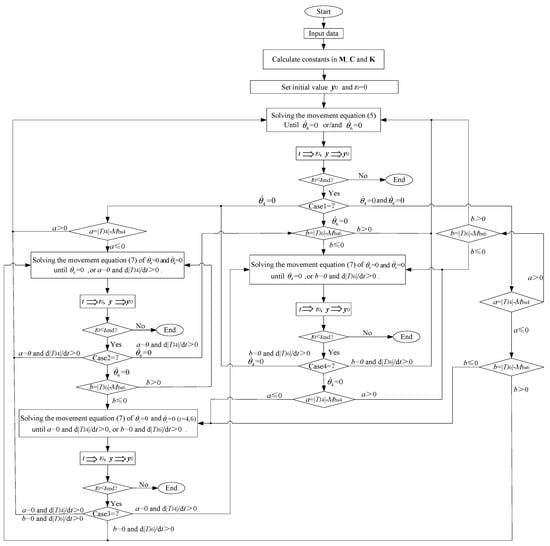
Figure 4.
The flow chart of simulation algorithm for braking process of lifting mechanism.
3. Simulation Parameters
To better understand the behaviour of cranes during the braking process, the dynamic responses during braking of the lifting mechanism which is equipped with two service brakes of a 32-ton overhead travelling crane are simulated. Before braking, the system is considered to be in a quasi-steady state and the electric motor of lifting mechanism is operating at a specified speed . The two service brakes, which are assembled on components J4 and J6 respectively, are assumed to be identical and actuated at the same time. Hereafter, the two service brakes assembled on components J4/J6 are referred to as brake 4/6, andis referred to as the initial speed.
According to the test report from manufacturers and those in [4], the dynamic friction coefficient of the friction pairs of the mechanical brake used in cranes is relatively invariable when the brake has a sufficient thermal capacity, and the difference between the static and dynamic friction coefficients is quite small, hence Coulomb friction with equal static and dynamic friction coefficients is adopted in this paper. Considering the mechanical and electro-magnetic delay, and the pressure variation on friction pairs in the initial braking stage, the variation of the braking capacity with time of the mechanical brake is idealized as the function shown in Figure 5. The braking capacity of the mechanical brake is the maximum friction torque between the brake linings and the brake drum.
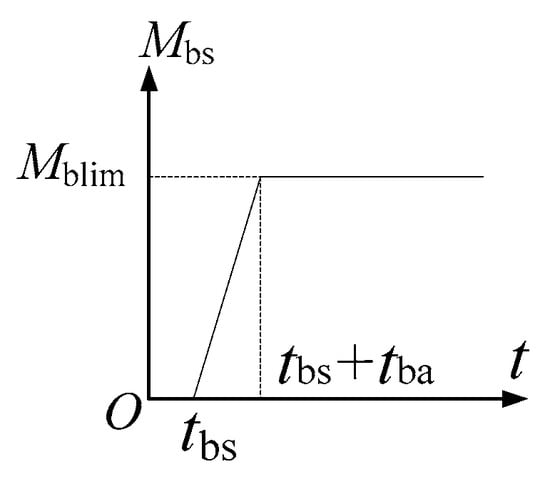
Figure 5.
Time function about braking capacity of mechanical brake.
In Figure 5, the origin of the time axis is the instant when the motor and the actuator of mechanical brake are switched off, and when the payload starts to get out of control. is the instant when the braking capacity of the brake starts to increase from zero. is the time interval when the braking capacity of the brake increases from zero to its maximum value.is the maximum braking capacity of the brakes converted to the corresponding quantity in reference to the axis of the rope drum.
The parameters of a 32-ton crane used in the simulation of two basic braking processes are given in Table 1. The data about the brake is from its manufacturer. The data about the steel rope is from the [39]. Some other date is calculated by the authors based on the machine elements of this actual crane. In subsequent analyses, a few parameters will be varied while other parameters remain unchanged when discussing their effects.

Table 1.
The data used for simulation
In Table 1, is the rated rotational speed of motor used for driving the lifting mechanism. are the damping ratios corresponding to respectively. are the free lengths of the rope hanging from the rope drum when the load-handling device is at its lower limit position and when the basic braking scenarios start, respectively. is the Y coordinate of the centres of wheels O3 and O3′ when wheels O4 and O4′ are located on the most unfavourable sections of the girders, respectively.
4. Time Histories of Two Basic Scenarios
When the two basic scenarios start, the rotating speed of driving motor is and the position of the payload is determined by the two parameters l0b and yo3b. The basic scenarios of are referred to as scenarios A and B respectively.
In the following simulation results, are the torques acting on the shaft used to connect components Ji and Ji+1 of the high-speed links in the lifting mechanism and calculated by ; Mbi (i = 4,6) is the calculated braking torques of the mechanical brake i (i = 4,6). These results about the high-speed links have been transformed back to the same kind of quantities in reference to the high-speed axis.
Figure 6 and Figure 7 show some time histories in scenarios A and B respectively. They describe torques acting on shafts of the high-speed links, the braking torques exerted by the two mechanical brakes, and the rotational speed (in rpm) of one of components J4 and J6, which stops first (expressed by red dashed lines). The time history of is omitted because it looks like , just its mean values in the first and second phases, and the amplitudes of its high frequency components in all phases being a little smaller.
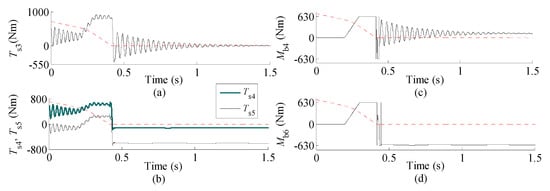
Figure 6.
Time histories of torques of high-speed links and braking torques of two brakes in scenario A. (a) Torque of the shaft connecting components J3 and J4; (b) Torque of the shaft connecting components Ji and Ji+1. (i = 4, 5); (c) Braking torque provided by the brake assembled on components J4; (d) Braking torque provided by the brake assembled on components J6.
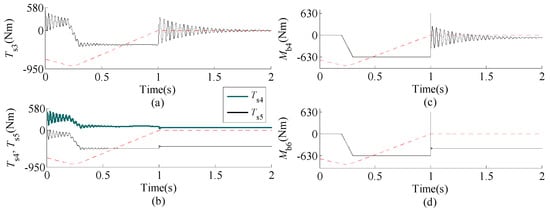
Figure 7.
Time histories of torques on high-speed links and braking torques of two brakes in scenario B. (a) Torque of the shaft connecting components J3 and J4; (b) Torque of the shaft connecting components Ji and Ji+1 (i = 4, 5); (c) Braking torque provided by the brake assembled on components J4; (d) Braking torque provided by the brake assembled on components J6.
From Figure 6a,b and Figure 7a,b, it is found that these histories are clearly divided into three phases, which successively correspond to the phase without brake application, deceleration phase due to application of the mechanical brakes, and the phase after completion of braking, respectively.
In the first and the third phases, all torque responses are time-varying with piecewise constant mean values, which implies that the crane system is being subjected to constant external forces during these phases. At the beginning of the second phase, the mean values of these responses undergo linear variations with the increase of the braking torque. In the end, these mean values will become constant once the braking torques increase to their limit values.
In the view of the traditional design theory on cranes, transmission shafts of lifting mechanisms are subjected to only a pulsating load per crane work cycle. However, it is noted that transmission shafts are subjected to time-varying loads in two opposite directions in scenarios A and B. Obviously, this kind of load is much more complex than the pulsating load whose minimum value is zero, and it is more harmful than that of a pulsating loading with zero minimum value from a fatigue strength point of view.
At the end of the third phase, the difference between and equals the difference between the torque about the rope drum axis due to weight of the payload and the resistance torque of the lifting mechanism, and is equal to zero which implies that no load acts on the floating shaft ultimately. These results satisfy the law of equilibrium.
As shown in Figure 6c,d and Figure 7c,d, after completion of braking, the payload is not supported evenly by the two brakes, although the two brakes are identical, actuate at the same time and supply almost equal amounts of friction work during braking. Meanwhile, from scenario A, there is stick-slip motion between the brake drums and the friction linings of brakes before the brake drums are stopped completely.
Figure 8a,c represent the time histories of the rope load in scenarios A and B, respectively. Figure 8b,d represent the time histories of the bending moments on the most unfavourable cross sections of girders in scenarios A and B, respectively. These time histories are also clearly divided into three phases, and the maximum values of the rope force and the bending moments of girders occur after the braking phase of hoisting/lowering process ends/starts.
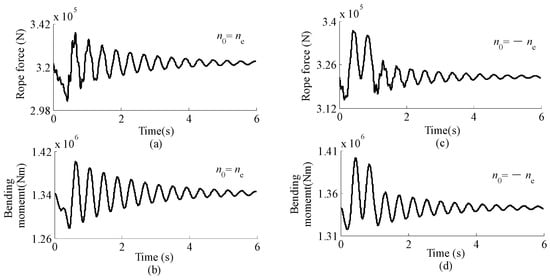
Figure 8.
Time histories of rope load and bending moment acting on the most unfavourable cross sections of girders in scenarios A and B. (a) Rope force at scenario A; (b) Bending moment in the most unfavourable cross section of the girder at scenario A; (c) Rope force at scenario B; (d) Bending moment in the most unfavourable cross section of the girder at scenario B.
5. Discussions
5.1. Time Histories of High-Speed Links
Based on numerical simulation, it is found that the torque time-histories of the high-speed links are affected not much by the position of the payload on girders, but much by the magnitude of the payload, the maximum braking capacity of the brakes and the time interval when the braking capacity of the brake increases from zero to its maximum values.
As shown in Figure 9, the torque peaks and maximum torque range occur when the crane is under the rated load or in no-load condition; in the third phase of the braking process, the amplitudes of the high frequency components of TS3 increase obviously when the crane is in no-load condition. This result, namely the maximum braking time of the lifting mechanism and the maximum braking distance of a payload are determined by the process of lowering a rated payload at full speed, is consistent with rigid dynamic analysis.
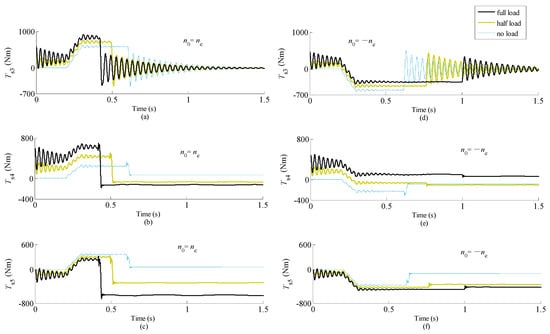
Figure 9.
Effect of payload magnitude on time histories of torques acting on the high-speed links. (a) The torque of the shaft connecting components J3 and J4 when braking starts at ne; (b) The torque of the shaft connecting components J4 and J5 when braking starts at ne; (c) The torque of the shaft connecting components J5 and J6 when braking starts at ne; (d) The torque of the shaft connecting components J3 and J4 when braking starts at −ne; (e) The torque of the shaft connecting components J4 and J5 when braking starts at −ne; (f) The torque of the shaft connecting components J5 and J6 when braking starts at −ne.
The effects of Mblim and on the torques of the high-speed links are shown in Figure 10. The yellow lines are about the histories of torques in the basic scenarios. For example, the larger and the shorter , the shorter the braking time of the lifting mechanism; the larger and the shorter , the higher peak torques and torque ranges; the larger , the larger amplitudes of the high frequency components of Ts3 in the beginning of the third phase; the shorter , the larger the amplitudes of the high frequency components of all torques in the beginning of the second phases. Besides, and will also influence the friction moment contributed to by each brake after completion of braking (Figure 11).
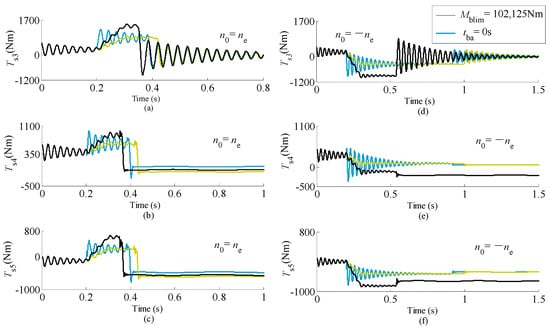
Figure 10.
Effects of Mblim and on time histories of torques acting on the high-speed links. (a) The torque of the shaft connecting components J3 and J4 when n0 =ne; (b) The torque of the shaft connecting components J4 and J5 when n0 = ne; (c) The torque of the shaft connecting components J5 and J6 when n0 =ne; (d) The torque of the shaft connecting components J3 and J4 when n0 = −ne; (e) The torque of the shaft connecting components J4 and J5 when n0 = −ne; (f) The torque of the shaft connecting components J5 and J6 when n0 = −ne.
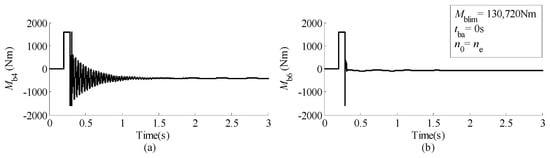
Figure 11.
Effects of and on friction moment of two brakes for holding payload. (a) Braking torque provided by the brake assembled on component J4; (b) Braking torque provided by the brake assembled on component J6.
Without doubt, the lower initial speed of lifting mechanism shortens the braking time, but the initial speed may not affect the peaks and ranges of torques acting on the high-speed links. As long as has reached its maximum value when braking ends, the peak torques and the torque ranges are almost the same as those under n0 = ne. Otherwise, the peak and range of torques decrease as shown in Figure 12. In addition, from Figure 12a–c, when the initial lifting speed is lower and the payload is bigger, a phenomenon is observed that at first the lifting mechanism is decelerated to zero speed by the payload, then accelerated in the opposite rotating direction till the braking torque is applied, finally stopped by the mechanical brake. This phenomenon can also be seen in practice.
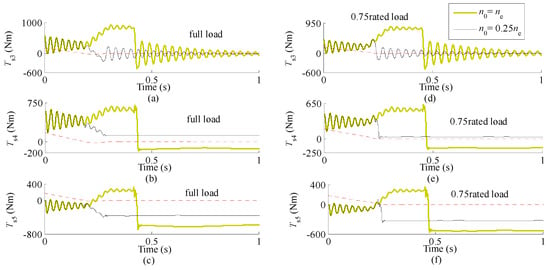
Figure 12.
Time histories of torques acting on high-speed links during braking for. (a) The torque of the shaft connecting components J3 and J4 at full load; (b) The torque of the shaft connecting components J4 and J5 at full load; (c) The torque of the shaft connecting components J5 and J6 at full load; (d) The torque of the shaft connecting components J3 and J4 at 75% rated load; (e) The torque of the shaft connecting components J4 and J5 at 75% rated load; (f) The torque of the shaft connecting components J5 and J6 at 75% rated load.
As for the dual-brake configuration, the greatest advantage is its redundancy function, that is, the safety of payload, equipment and workers around the payload is expected to be ensured if anyone of the two brakes fails to work. However, when only one brake works during braking of a lowering rated payload at full speed, the friction work of the mechanical brake and the braking distance of the payload would be several times higher than those when both brakes work (Figure 13a,b). This implies that a higher requirement for the thermal capacity of the brake should be taken into account to implement this function of the dual-brake scheme.
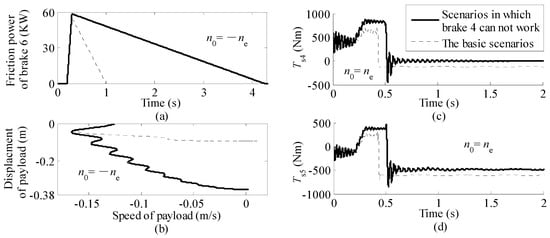
Figure 13.
Dynamic responses when brake 4 cannot work vs. those in basic scenarios. (a) Friction power in the brake assembled on component J6 during lowering braking; (b) Displacement of the payload during lowering braking; (c) The torque of the shaft to connect component J4 and J5 during lifting braking; (d) The torque of the shaft to connect component J5 and J6 during lifting braking.
Furthermore, the peak torque of the high-speed links is different when mechanical brakes 4 or 6 fails to work. For example, during braking of a hoisting rated payload at full speed, the peak torques of the two high-speed shaft extensions of the reducer are higher when brake 4 fails to work (Figure 13c,d). This indicates that the loads on the high-speed transmission shafts should be taken into careful consideration during design phase when dual-brake scheme is adopted.
5.2. Time History of Rope Force and Bending Moment of Girder
Obviously, the heavier the payload and the bigger Mblim, the bigger the maximum value and the variation range of the rope load. When the position of the trolley is at yo3 = 11.305 m and yo3 = 0.245 m respectively, the comparison of the time histories of the relative rope force (the ratio of the instant rope force with the gravity of the lifted object) during braking processes of the lifting mechanism equipped with dual-brakes, whose braking capacity increases from 630 Nm (Mblim= 51,471 Nm) to 1250 Nm (Mblim = 102,125 Nm), is shown in Figure 14.
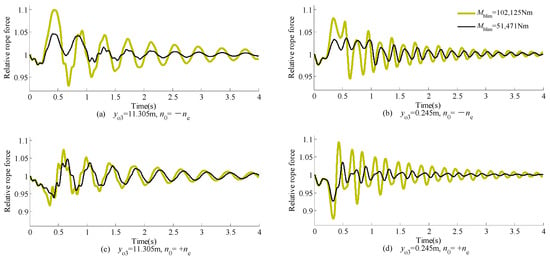
Figure 14.
Effects of Mblim on time histories of rope force. (a) The comparison of relative rope force when yo3 = 11.305 m and no = −ne; (b) The comparison of relative rope force when yo3 =0.245 m and no = −ne; (c) The comparison of relative rope force when yo3 = 11.305 m and no =ne; (d) The comparison of relative rope force when yo3 = 0.245 m and no =ne.
Moreover, the initial position of the payload and the initial speed of the lifting mechanism influence the maximum value of the rope force in each braking process as well, and the relationships are nonlinear as shown in Figure 15. The initial position of the payload is given by parameters l0 and yo3.
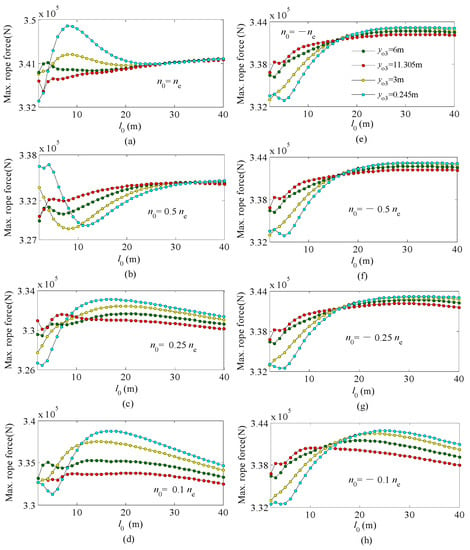
Figure 15.
Maximum rope force vs. initial length of hanging ropeat different yo3 and different n0. (a) The function relationship between Max. rope force and l0 when no = ne; (b) The function relationship between Max. rope force and l0 when no = 0.5ne; (c) The function relationship between Max. rope force and l0 when no = 0.25ne; (d) The function relationship between Max. rope force and l0 when no = 0.1ne; (e) The function relationship between Max. rope force and l0 when no = −ne; (f) The function relationship between Max. rope force and l0 when no = −0.5ne; (g) The function relationship between Max. rope force and l0 when no = −0.25ne; (h) The function relationship between Max. rope force and l0 when no = −0.1ne.
As shown in Figure 15, when changing yo3, the maximum rope force takes its biggest value at yo3 = 0.245 m (the limit position of the trolley in the crane span range). The variation range of the maximum rope force decreases when the trolley approaches the middle of the girder. In the view of the traditional design theory on cranes, the global peak of maximum rope force occurs when the trolley is in the middle of the girders and a payload is braked during lowering or is hoisted suddenly from its support surface. However, in this simulation, it is found that the global peak of the rope force may occur during braking of the lifting mechanism at full speed in hoisting direction when the trolley is in its limit position at the crane span end.
In order to understand better the effect of the initial speed on the maximum rope force, the results at yo3 = 0.245 m are reorganized to Figure 16 from Figure 15 (the relationship between the maximum rope force and at different n0 when yo3 = 0.245 m). It is found that the effect of the initial speed is completely different under braking processes of hoisting and lowering a payload. The maximum rope forces are very sensitive to the initial speed during braking processes of hoisting a payload; however, they are not so during braking processes of lowering a payload.
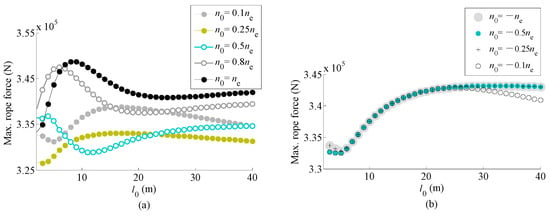
Figure 16.
Maximum rope force at yo3 = 0.245 m and different n0 vs. initial length of hanging rope (a) The function relationship between Max. rope force and l0 when braking of a lifting payload at different speed; (b) The function relationship between Max. rope force and l0 when braking of a lowering payload at different speed.
It is further observed that the maximum rope forces during braking of a hoisting payload do not increase monotonously with n0 under the same . Note that, when the lifting mechanism does not get braked by the mechanical brakes until after changing its direction of movement, and the braking torques still does not reach the maximum capacity when braking ends. Therefore, maybe the above results are jointly resulted in by the magnitude of the braking torque when braking ends and the motion states of the system when braking starts.
When lowering a payload at yo3 = 0.245 m, the relationships between and the maximum rope forces during braking at different n0 are almost the same except for that at . The difference between the relationship at and those at other n0 just occurs at lower and higher values of . The difference becomes bigger in the wider region of n0 and if the position of the trolley is closer to the middle of the crane span (Figure 17). The phenomena may be explained as the result of the effect of increasing vibration of the girders. In addition, there is a similar relationship for the bending moment at the cross sections of the girders.
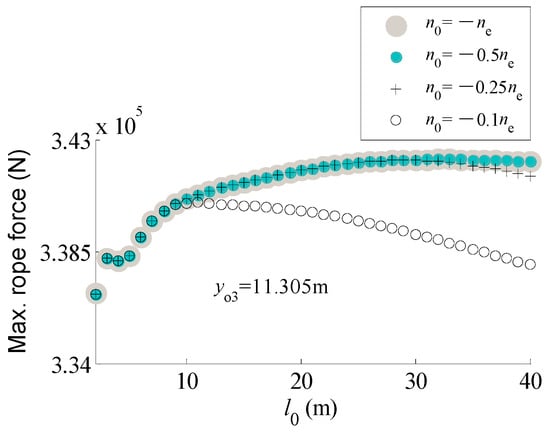
Figure 17.
Maximum rope forces during braking at yo3 = 11.305 m and different n0 vs. the initial length of hanging rope .
6. Conclusions
In this paper, based on the Hamilton principle, a nonlinear and non-smooth dynamic model of the payload-trolley-lifting mechanism-girders system has been derived from a modified Lagrangian function and the virtual work of non-conservative forces. The dynamic responses and effects of some parameters during braking of lifting mechanism with two mechanical brakes to halt a runaway payload have been investigated in detail. Some conclusions are drawn as follows:
- (1)
- The high-speed links in the lifting mechanism experience a fluctuating torque acting in two opposite directions with a non-zero mean during braking. This indicates that it is beneficial for increasing the working life of lifting mechanisms to avoid frequent emergency braking.
- (2)
- When a multi-brake scheme is adopted, the payload is unlikely to be supported equally by these brakes after completion of braking. The peak values of rope force and the bending moment of the girders may occur when braking a hoisting full-speed payload while the trolley is at the crane span end.
- (3)
- The magnitude of the payload, and the braking capacity and the action time of mechanical brakes are very important factors affecting the peak values and the range of internal forces acting on all components of the crane during braking. On the other hand, the position of the trolley mainly influences the internal forces acting on the steel rope and the girders.
- (4)
- The installation position of the mechanical brake and the action sequence when the multi-brake scheme is adopted may affect the loads acting on the high-speed links of the lifting mechanism. When the lifting mechanism with a dual-brake scheme is adopted, the load capacity of the high-speed links and the thermal capacity of friction pair of the brake are governed by the process when one of the two brakes ceases to work. In addition, the loads acting on components of cranes are higher if the braking capacity of the mechanical brakes is higher. Therefore, the two factors, i.e., the safety of cranes themselves and the capability of stopping and holding payloads safely, must be balanced when selecting the mechanical brakes.
- (5)
- The effect of the initial speed on the internal forces acting on the steel structure and the wire rope during braking of a hoisting payload is fairly different from that during braking of a lowering payload. Additionally, the peak values of the internal forces acting on the steel structure and the wire rope during braking process at a lower initial speed are not always smaller than those during braking at the full speed, i.e., as far as the steel structure and the wire rope of cranes are concerned, a braking process at a lower initial speed is not guaranteed to be safer than at full speed.
Author Contributions
Conceptualization, C.N.; methodology, C.N. and H.O.; software, C.N.; validation, C.N.; formal analysis, C.N.; investigation, C.N.; resources, C.N.; writing—original draft preparation, C.N.; writing—review and editing, C.N. and H.O.; visualization, C.N.; supervision, H.O.; project administration, H.O.; funding acquisition, H.O. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the National Natural Science Foundation of China, grant number 11672052.
Conflicts of Interest
The authors declare no conflict of interest.
Notation
| the vector of generalized coordinates used for describing elastic deformation of the girders along Z direction of the orthogonal coordinate system OXYZ | |
| b | the wheel base of the trolley |
| cg | the viscous damping coefficient of the material of the girder |
| cs | the viscous damping coefficient of transmission shafts in the lifting mechanism |
| cw | the viscous damping coefficient of the wire rope |
| kw | the total tensile force per unit strain of the wire rope segments hanging from the rope drum |
| ki | the torsional stiffness of the high-speed transmission shaft i in the lifting mechanism which is converted to a stiffness value in reference to the rope drum axis |
| l | the free length of the wire rope segments hanging from the rope drum |
| the free lengths of the rope hanging from the rope drum when the load-handling device is at its lower limit position | |
| the free lengths of the rope hanging from the rope drum when the basic braking scenario starts | |
| mg | the mass of a girder |
| ms | the reeving of the pulley block |
| the mass of the trolley | |
| mQ | the mass of the lifted object (including the load-handling device) |
| n | the number of generalized coordinates used for describing elastic deformation of the girders along Z direction of the orthogonal coordinate system OXYZ, |
| the rotating speed of driving motor in the lifting mechanism when braking starts | |
| the rated rotational speed of motor used for driving the lifting mechanism | |
| t0 | the starting instant of the integral interval of the equation of motion |
| the instant when the braking capacity of the brake starts to increase from zero | |
| the time interval when the braking capacity of the brake increases from zero to its maximum value | |
| tend | the ending instant of the integral interval of the equation of motion |
| the displacement of a point in the girder axis, whose Y coordinate in the orthogonal coordinate system OXYZ is y, relative to its position under the dead weight of the girder | |
| x0 | the initial value of the integration |
| the Y coordinate of the points on the trolley wheels axis | |
| the Y coordinate of the centres of wheels O3 and O3′ when wheels O4 and O4′ are located on the most unfavourable sections of the girders | |
| Ci | the constants involved in the elastic deformation due to the dead weight, the camber and the geometrical sizes of the girder, i=T, d |
| E | Young’s modulus of the girder material |
| Ix | the moment of inertia of the girder cross section with respect to its neutral axis, which is parallel to the X-axis of the orthogonal coordinate system OXYZ |
| the moment of inertia of the trolley with respect to its centroid axis, which is parallel to axis of the orthogonal coordinate system fixed to the trolley | |
| the moments of inertia of rotating rigid body i in the lifting mechanism which is converted to quantities in reference to the rope drum axis | |
| the modified Lagrangian function | |
| L | the span of the crane |
| the time function of the braking torque of the mechanical brake, which is converted to quantities in reference to the rope drum axis | |
| the maximum braking capacity of the brakes, which is converted to the corresponding quantity in reference to the axis of the rope drum | |
| the time function of the braking capacity of the brake i, which is converted to quantities in reference to the rope drum axis | |
| the resistance torque of the lifting mechanism | |
| Rd | the wrapping radius of the wire rope on the rope drum |
| T | the kinetic energy of the crane |
| the torque acting on the shaft used to connect components Ji and Ji+1 of the high-speed links in the lifting mechanism | |
| the potential energy of the crane | |
| the tensile strain of the wire rope segments hanging from the rope drum | |
| the efficiency of the lifting mechanism | |
| the angular displacement of rotating rigid body i in the lifting mechanism, which is converted to quantities in reference to the rope drum axis | |
| the Lagrange multiplier | |
| the friction coefficient between the rope drum groove and the wire rope | |
| the damping ratios corresponding to | |
| the damping ratios corresponding to | |
| the constraint which gives the relationship between l, and | |
| the coordinate of the points on the rope drum axis | |
| the coordinate of the gravity centre of the trolley |
References
- CEN. EN ISO13850 Safety of Machinery Emergency Stop Principles for Design; CEN: Brussels, Belgium, 2015. [Google Scholar]
- Olesiak, Z.; Pyryev, Y.; Yevtushenko, A. Determination of temperature and wear during braking. Wear 1997, 210, 120–126. [Google Scholar] [CrossRef]
- German Institute for Standardisation. DIN 15434-1-1989 Power Transmission Engineering—Principles for Drum- and Disc Brakes, Calculation; German Institute for Standardisation: Berlin, Germany, 1989. [Google Scholar]
- Severin, D.; Dörsch, S. Friction mechanism in industrial brakes. Wear 2001, 249, 771–779. [Google Scholar] [CrossRef]
- Wang, D.; Yin, J.; Zhu, Z.; Zhang, D.; Liu, D.; Liu, H.; Sun, F. Preparation of high friction brake shoe material and its tribological behaviors during emergency braking in ultra-deep coal mine hoist. Wear 2020, 458–459, 203391. [Google Scholar] [CrossRef]
- Wittenberghe, J.V.; Ost, W.; Baets, P.D. Testing the friction characteristics of industrial drum brake linings. Exp. Tech. 2012, 36, 43–49. [Google Scholar] [CrossRef]
- Park, K.P.; Cha, J.H.; Lee, K.Y. Dynamic factor analysis considering elastic boom effects in heavy lifting operations. Ocean Eng. 2011, 38, 1100–1113. [Google Scholar] [CrossRef]
- Sun, G.; Kleeberger, M.; Liu, J. Complete dynamic calculation of lattice mobile crane during hoisting motion. Mech. Mach. Theory 2005, 40, 447–466. [Google Scholar] [CrossRef]
- Posiadała, B. Influence of crane support system on motion of the lifted load. Mech. Mach. Theory 1997, 32, 9–20. [Google Scholar] [CrossRef]
- Ju, F.; Choo, Y.S.; Cui, F.S. Dynamic response of tower crane induced by the pendulum motion of the payload. Int. J. Solids Struct. 2006, 43, 376–389. [Google Scholar] [CrossRef]
- Jerman, B. An enhanced mathematical model for investigating the dynamic loading of a slewing crane. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 421–433. [Google Scholar] [CrossRef]
- Cibicik, A.; Pedersen, E.; Egeland, O. Dynamics of luffing motion of a flexible knuckle boom crane actuated by hydraulic cylinders. Mech. Mach. Theory 2020, 143, 103616. [Google Scholar] [CrossRef]
- Yildirim, Ş.; Esim, E. A new approach for dynamic analysis of overhead crane systems under moving loads. In CONTROLO 2016, Proceedings of the 12th Portuguese Conference on Automatic Control, Guimarães, Portugal, 14–16 September 2016; Garrido, P., Soares, F., Moreira, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 471–481. [Google Scholar]
- Urbaś, A. Computational implementation of the rigid finite element method in the statics and dynamics analysis of forest cranes. Appl. Math. Model. 2017, 46, 750–762. [Google Scholar] [CrossRef]
- Adamiec-Wójcik, I.; Drąg, Ł.; Metelski, M.; Nadratowski, K.; Wojciech, S. A 3D model for static and dynamic analysis of an offshore knuckle boom crane. Appl. Math. Model. 2019, 66, 256–274. [Google Scholar] [CrossRef]
- Cibicik, A.; Egeland, O. Dynamic modelling and force analysis of a knuckle boom crane using screw theory. Mech. Mach. Theory 2019, 133, 179–194. [Google Scholar] [CrossRef]
- Tomasz, H. Modeling the dynamics of cargo lifting process by overhead crane for dynamic overload factor estimation. J. Vibroeng. 2017, 19, 75–86. [Google Scholar]
- Zhao, Y.; Cheng, Z.; Sandvik, P.C.; Gao, Z.; Moan, T.; Van Buren, E. Numerical modeling and analysis of the dynamic motion response of an offshore wind turbine blade during installation by a jack-up crane vessel. Ocean Eng. 2018, 165, 353–364. [Google Scholar] [CrossRef]
- Cekus, D.; Gnatowska, R.; Kwiatoń, P. Impact of wind on the movement of the load carried by rotary crane. Appl. Sci. 2019, 9, 3842. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.I.; Lazim, I.M. Control strategies for crane systems: A comprehensive review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Tomczyk, J.; Cink, J.; Kosucki, A. Dynamics of an overhead crane under a wind disturbance condition. Autom. Constr. 2014, 42, 100–111. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.; Selamat, H.; Pota, H.R.; Zainal Abidin, M.S.; Fasih, S.M. Efficient control of a 3D overhead crane with simultaneous payload hoisting and wind disturbance: Design, simulation and experiment. Mech. Syst. Signal Process. 2020, 145, 106893. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, J. Distributed-mass payload dynamics and control of dual cranes undergoing planar motions. Mech. Syst. Signal Process. 2019, 126, 636–648. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Hua, L.; Xia, M. Dynamic analysis and time optimal anti-swing control of double pendulum bridge crane with distributed mass beams. Mech. Syst. Signal Process. 2020, 144, 106968. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Ji, B.; Ma, C.; Cheng, X. Adaptive sway reduction for tower crane systems with varying cable lengths. Autom. Constr. 2020, 119, 103342. [Google Scholar] [CrossRef]
- Otani, A.; Nagashima, K.; Suzuki, J. Vertical seismic response of overhead crane. Nucl. Eng. Des. 2002, 212, 211–220. [Google Scholar] [CrossRef]
- Kobayashi, N.; Kuribara, H.; Honda, T.; Watanabe, M. Nonlinear seismic responses of container cranes including the contact problem between wheels and rails. J. Press. Vessel Technol. 2004, 126, 59–65. [Google Scholar] [CrossRef]
- Feau, C.; Politopoulos, I.; Kamaris, G.; Mathey, C.; Chaudat, T.; Nahas, G. Experimental and numerical investigation of the earthquake response of crane bridges. Eng. Struct. 2015, 84, 89–101. [Google Scholar] [CrossRef]
- Huh, J.; Nguyen, V.B.; Tran, Q.H.; Ahn, J.-H.; Kang, C. Effects of boundary condition models on the seismic responses of a container crane. Appl. Sci. 2019, 9, 241. [Google Scholar] [CrossRef]
- Chen, H.; Xuan, B.; Yang, P.; Chen, H. A new overhead crane emergency braking method with theoretical analysis and experimental verification. Nonlinear Dyn. 2019, 98, 2211–2225. [Google Scholar] [CrossRef]
- Vöth, S. Emergency braking of fast running coal handling gantry hoists. In Proceedings of the XVII International Coal Preparation Congress, Saint-Petersburg, Russia, 28 June–1 July 2016; Litvinenko, V., Ed.; Springer: Cham, Switzerland, 2016; pp. 135–140. [Google Scholar]
- Streltsov, S.V.; Ryzhikov, V.A. Influence of uneven braking of running wheels on stress-strain state of crane metal structure. In Lecture Notes in Mechanical Engineering, Proceedings of the 4th International Conference on Industrial Engineering, Moscow, Russia, 15–18 May 2018; Radionov, A., Kravchenko, O., Eds.; Springer: Cham, Switzerland, 2018; pp. 2055–2062. [Google Scholar]
- Singer, N.C.; Seering, W.P. Preshaping command inputs to reduce system vibration. J. Dyn. Syst. Meas. Control 1990, 112, 76–82. [Google Scholar] [CrossRef]
- Singhose, W. Command shaping for flexible systems: A review of the first 50 years. Int. J. Precis. Eng. Manuf. 2009, 10, 153–168. [Google Scholar] [CrossRef]
- Manning, R.; Clement, J.; Kim, D.; Singhose, W.E. Dynamics and control of bridge cranes transporting distributed-mass payloads. J. Dyn. Syst. Meas. Control 2010, 132, 014505. [Google Scholar] [CrossRef]
- BSI. BS EN 13001-2-2004+A3-2009 Crane Safety-General Design Part 2: Load Actions; BSI: London, UK, 2009. [Google Scholar]
- BSI. BS EN 13001-1-2004+A1-2009 Crane Safety-General Design Part 1: General Principles and Requirements; BSI: London, UK, 2009. [Google Scholar]
- Niu, C.M.; Zhang, H.W.; Ouyang, H. A comprehensive dynamic model of electric overhead cranes and the lifting operations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 1484–1503. [Google Scholar] [CrossRef]
- Feyrer, K. Wire Ropes-Tension, Endurance, Reliability, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).