Three-Dimensional Combined Finite-Discrete Element Modeling of Shear Fracture Process in Direct Shearing of Rough Concrete–Rock Joints
Abstract
1. Introduction
2. GPGPU-Parallelized 3D Y-HFDEM IDE
3. Calibration of the Combined Finite-Discrete Element Method by Modeling UCS and BTS
4. 3D FDEM Modeling of Rough Concrete–Rock Joint Failure in a Direct Shear Test
4.1. Modelling Procedure
4.2. Results
5. Discussion
5.1. Direct Shearing of Concrete–Rock Joint with Different Asperity Roughness
5.2. Effect of Fiction Coefficient on Direct Shearing of Concrete–Rock Joint
6. Conclusions
- (1)
- The GPGPU-parallelized FDEM reproduced the asperity dilatation, sliding, and degradation on the direct shear test of the concrete–rock joint with rough saw-tooth triangular asperity. Compared with laboratory observation, the simulation result presented a good agreement on the bulk shear stress–horizontal displacement curve before the regime of residual shear resistance. However, the laboratory test results presented a continuous decrease of bulk shear stress unlike the numerical simulation result, which showed constant residual stress after shear softening. In this study, we concluded that the additional damages found in the experiment results induced a continuous stress drop and presented different behaviors in the numerical simulation in the regime of the constant residual stress statement.
- (2)
- The roughness of asperities in the concrete–rock joint affects the overall joint shear resistance, where the main fracture mechanism is asperity sliding in the smooth asperity and asperity degradation in the rough asperity. The smoother single asperity is freer from the bending moment, which was easy to induce in the tensile crack in concrete asperity base, than the rough single asperity. The only factor of the shear resistance in the smooth asperity is the friction between the concrete and rock joint interface. The effect of the increment of asperity roughness affects the shear strength increment and causes the asperity degradation, which presents the shear softening behavior after the peak bulk shear stress, while the smooth asperity roughness presents the residual stress statement immediately after the initial elastic behavior. In addition, when the direct shear test results are presented as Mohr–Coulomb criterion, the bulk internal friction angle was clearly increased with an increasing asperity angle. In this study, the effect of asperity roughness on the bulk internal friction angle follows the Patton’s theoretical model.
- (3)
- The friction coefficient is an important parameter for simulating the direct shearing of the concrete–rock joint. Especially, the friction coefficient was more effective on the internal friction angle in terms of the smooth joint than the rough joint. The asperity degradation was the main mechanism in the rough joint, the concrete asperity base was fractured, and the friction was applied at the macroscopic crack surface in the concrete asperity base. Thus, the internal friction angle in the vicinity of the rough concrete–rock joint may be independent of the friction coefficient between the rock and concrete. However, in the smooth joint, the main mechanism of shear resistance was sliding without fracturing, and the different friction coefficient was directly reflected to the friction force as well as the internal friction angle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Han, Y.; Liu, X.; Wei, N.; Li, D.; Deng, Z.; Wu, X.; Liu, D. A Comprehensive Review of the Mechanical Behavior of Suspension Bridge Tunnel-Type Anchorage. Adv. Mater. Sci. Eng. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- AASHTO, LFRD. Standard Specifications for Highway Bridges, 17th ed.; American Association of State Highway and Transportation: Washington, DC, USA, 2002. [Google Scholar]
- American Association of State Highway Transportation. Highway Safety Manual; Officials; AASHTO: Washington, DC, USA, 2010; Volume 1. [Google Scholar]
- Bond, A.; Harris, A. Decoding Eurocode 7; CRC Press: London, UK, 2006. [Google Scholar]
- Japan Road Association. Design Specifications of Highway Bridges, Part V Seismic Design; Maruzen: Tokyo, Japan, 2002. [Google Scholar]
- Korea Road and Transportation Association. Korea Bridge Design Code; Ministry of Land, Transport and Maritime Affairs: Seoul, Korea, 2012. [Google Scholar]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Jaeger, J.C. Friction of Rocks and Stability of Rock Slopes. Géotechnique 1971, 21, 97–134. [Google Scholar] [CrossRef]
- Ladanyi, B.; Archambault, G. Simulation of shear behavior of a jointed rock mass. In Proceedings of the 11th US Symposium on Rock Mechanics (USRMS), Berkeley, CA, USA, 16–19 June 1969. [Google Scholar]
- Patton, F.D. Multiple modes of shear failure in rock. In Proceedings of the 1st ISRM Congress, Lisbon, Portugal, 25 September–1 October 1966. [Google Scholar]
- Lam, T.S.K.; Johnston, I.W. Shear Behavior of Regular Triangular Concrete/Rock Joints—Evaluation. J. Geotech. Eng. 1989, 115, 728–740. [Google Scholar] [CrossRef]
- Johnston, I.W.; Lam, T.S.K. Shear Behavior of Regular Triangular Concrete/Rock Joints—Analysis. J. Geotech. Eng. 1989, 115, 711–727. [Google Scholar] [CrossRef]
- Barton, N. Shear strength criteria for rock, rock joints, rockfill and rock masses: Problems and some solutions. J. Rock Mech. Geotech. Eng. 2013, 5, 249–261. [Google Scholar] [CrossRef]
- Amadei, B.; Saeb, S. Constitutive models of rock joints. In Proceedings of the International Symposium on Rock Joints, Loen, Norway, 4–6 June 1990; pp. 581–594. [Google Scholar]
- Lee, H.; Park, Y.; Cho, T.; You, K. Influence of asperity degradation on the mechanical behavior of rough rock joints under cyclic shear loading. Int. J. Rock Mech. Min. Sci. 2001, 38, 967–980. [Google Scholar] [CrossRef]
- Hossaini, K.A.; Babanouri, N.; Nasab, S.K. The influence of asperity deformability on the mechanical behavior of rock joints. Int. J. Rock Mech. Min. Sci. 2014, 70, 154–161. [Google Scholar] [CrossRef]
- Plesha, M.E. Constitutive models for rock discontinuities with dilatancy and surface degradation. Int. J. Numer. Anal. Methods Gíomích. 1987, 11, 345–362. [Google Scholar] [CrossRef]
- Souley, M.; Homand, F.; Amadei, B. An extension to the Saeb and Amadei constitutive model for rock joints to include cyclic loading paths. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 101–109. [Google Scholar] [CrossRef]
- Maksimović, M. The shear strength components of a rough rock joint. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 769–783. [Google Scholar] [CrossRef]
- Haque, A.; Indraratna, B. Shear Behaviour of Rock Joints; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Olsson, R.; Barton, N. An improved model for hydromechanical coupling during shearing of rock joints. Int. J. Rock Mech. Min. Sci. 2001, 38, 317–329. [Google Scholar] [CrossRef]
- Serrano, A.; Olalla, C.; Galindo-Aires, R.Á. Micromechanical basis for shear strength of rock discontinuities. Int. J. Rock Mech. Min. Sci. 2014, 70, 33–46. [Google Scholar] [CrossRef]
- Indraratna, B.; Thirukumaran, S.; Brown, E.T.; Zhu, S.-P. Modelling the Shear Behaviour of Rock Joints with Asperity Damage Under Constant Normal Stiffness. Rock Mech. Rock Eng. 2014, 48, 179–195. [Google Scholar] [CrossRef]
- Hencher, S.R.; Richards, L.R. Assessing the Shear Strength of Rock Discontinuities at Laboratory and Field Scales. Rock Mech. Rock Eng. 2014, 48, 883–905. [Google Scholar] [CrossRef]
- Shrivastava, A.K.; Rao, K.S. Shear Behaviour of Rock Joints Under CNL and CNS Boundary Conditions. Geotech. Geol. Eng. 2015, 33, 1205–1220. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R.; Hebblewhite, B.K. Parametric Study of Smooth Joint Parameters on the Shear Behaviour of Rock Joints. Rock Mech. Rock Eng. 2014, 48, 923–940. [Google Scholar] [CrossRef]
- Kodikara, J.; Johnston, I. Shear behaviour of irregular triangular rock-concrete joints. Int. J. Rock Mech. Min. Sci. Geoomech. Abstr. 1994, 31, 313–322. [Google Scholar] [CrossRef]
- Gu, X.F.; Seidel, J.P.; Haberfield, C.M. Direct Shear Test of Sandstone-Concrete Joints. Int. J. Geomech. 2003, 3, 21–33. [Google Scholar] [CrossRef]
- Saiang, D.; Malmgren, L.; Nordlund, E. Laboratory Tests on Shotcrete-Rock Joints in Direct Shear, Tension and Compression. Rock Mech. Rock Eng. 2005, 38, 275–297. [Google Scholar] [CrossRef]
- Seidel, J.P.; Haberfield, C.M. A theoretical model for rock joints subjected to constant normal stiffness direct shear. Int. J. Rock Mech. Min. Sci. 2002, 39, 539–553. [Google Scholar] [CrossRef]
- Haberfield, C.; Johnston, I. A mechanistically-based model for rough rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 279–292. [Google Scholar] [CrossRef]
- Tian, H.M.; Chen, W.; Yang, D.S.; Yang, J.P. Experimental and Numerical Analysis of the Shear Behaviour of Cemented Concrete–Rock Joints. Rock Mech. Rock Eng. 2014, 48, 213–222. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B. Numerical direct shear tests to model the shear behaviour of rock joints. Comput. Geotech. 2013, 51, 101–115. [Google Scholar] [CrossRef]
- Park, J.-W.; Song, J.-J. Numerical simulation of a direct shear test on a rock joint using a bonded-particle model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Munjiza, A. Discrete Elements in Transient Dynamics of Fractured Media. Ph.D. Thesis, Swansea University, Swansea, UK, 1992. [Google Scholar]
- Munjiza, A.A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Munjiza, A.A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Munjiza, A.; Knight, E.E.; Rougier, E. Large Strain Finite Element Method: A Practical Course; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mahabadi, O.K.; Lisjak, A.; Munjiza, A.; Grasselli, G. Y-Geo: New Combined Finite-Discrete Element Numerical Code for Geomechanical Applications. Int. J. Geomech. 2012, 12, 676–688. [Google Scholar] [CrossRef]
- Yan, C.; Jiao, Y. A 2D fully coupled hydro-mechanical finite-discrete element model with real pore seepage for simulating the deformation and fracture of porous medium driven by fluid. Comput. Struct. 2018, 196, 311–326. [Google Scholar] [CrossRef]
- Yan, C.; Jiao, Y.-Y.; Zheng, H. A fully coupled three-dimensional hydro-mechanical finite discrete element approach with real porous seepage for simulating 3D hydraulic fracturing. Comput. Geotech. 2018, 96, 73–89. [Google Scholar] [CrossRef]
- Lisjak, A.; Mahabadi, O.; He, L.; Tatone, B.; Kaifosh, P.; Haque, S.; Grasselli, G. Acceleration of a 2D/3D finite-discrete element code for geomechanical simulations using General Purpose GPU computing. Comput. Geotech. 2018, 100, 84–96. [Google Scholar] [CrossRef]
- Rougier, E.; Bradley, C.R.; Broom, S.T.; Knight, E.E.; Munjiza, A.; Sussman, A.J.; Swift, R.P. The Combined Finite-Discrete Element Method Applied to the Study of Rock Fracturing Behavior in 3D; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2011. [Google Scholar]
- An, H.; Liu, H.Y.; Han, H.; Zheng, X.; Wang, X. Hybrid finite—discrete element modelling of dynamic fracture and resultant fragment casting and muck-piling by rock blast. Comput. Geotech. 2017, 81, 322–345. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kang, Y.M.; Lin, P. Hybrid finite—discrete element modeling of geomaterials fracture and fragment muck-piling. Int. J. Geotech. Eng. 2013, 9, 115–131. [Google Scholar] [CrossRef]
- Liu, H.Y.; Han, H.; An, H.M.; Shi, J.J. Hybrid finite-discrete element modelling of asperity degradation and gouge grinding during direct shearing of rough rock joints. Int. J. Coal Sci. Technol. 2016, 3, 295–310. [Google Scholar]
- Mohammadnejad, M.; Fukuda, D.; Liu, H.Y.; Dehkhoda, S.; Chan, A. GPGPU-parallelized 3D combined finite–discrete element modelling of rock fracture with adaptive contact activation approach. Comput. Part. Mech. 2019, 7, 849–867. [Google Scholar] [CrossRef]
- Mohammadnejad, M.; Dehkhoda, S.; Fukuda, D.; Liu, H.Y.; Chan, A. GPGPU-parallelised hybrid finite-discrete element modelling of rock chipping and fragmentation process in mechanical cutting. J. Rock Mech. Geotech. Eng. 2020, 12, 310–325. [Google Scholar] [CrossRef]
- Fukuda, D.; Mohammadnejad, M.; Liu, H.; Dehkhoda, S.; Chan, A.; Cho, S.; Min, G.; Han, H.; Kodama, J.; Fujii, Y. Development of a GPGPU-parallelized hybrid finite-discrete element method for modeling rock fracture. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1797–1824. [Google Scholar] [CrossRef]
- Fukuda, D.; Mohammadnejad, M.; Liu, H.-Y.; Zhang, Q.; Zhao, J.; Dehkhoda, S.; Chan, A.; Kodama, J.-I.; Fujii, Y. Development of a 3D Hybrid Finite-Discrete Element Simulator Based on GPGPU-Parallelized Computation for Modelling Rock Fracturing Under Quasi-Static and Dynamic Loading Conditions. Rock Mech. Rock Eng. 2019, 53, 1079–1112. [Google Scholar]
- Han, H.; Fukuda, D.; Liu, H.Y.; Salmi, E.F.; Sellers, E.; Liu, T.; Chan, A. Combined finite-discrete element modelling of rock fracture and fragmentation induced by contour blasting during tunnelling with high horizontal in-situ stress. Int. J. Rock Mech. Min. Sci. 2020, 127, 104214. [Google Scholar]
- Latham, J.-P.; Munjiza, A.; Lu, Y. On the prediction of void porosity and packing of rock particulates. Powder Technol. 2002, 125, 10–27. [Google Scholar] [CrossRef]
- Karami, A.; Stead, D. Asperity Degradation and Damage in the Direct Shear Test: A Hybrid FEM/DEM Approach. Rock Mech. Rock Eng. 2007, 41, 229–266. [Google Scholar]
- Tatone, B.; Grasselli, G. A combined experimental (micro-CT) and numerical (FDEM) methodology to study rock joint asperities subjected to direct shear. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Munjiza, A.; Andrews, K.R.F.; White, J.K. Combined single and smeared crack model in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Muralha, J.; Grasselli, G.; Tatone, B.; Blümel, M.; Chryssanthakis, P.; Yujing, J. ISRM Suggested Method for Laboratory Determination of the Shear Strength of Rock Joints: Revised Version. Rock Mech. Rock Eng. 2014, 47, 291–302. [Google Scholar] [CrossRef]
- Mahinroosta, R.; Sadaghiani, M.H.; Pak, A.; Saleh, Y. Rock joint modeling using a visco-plastic multilaminate model at constant normal load condition. Geotech. Geol. Eng. 2006, 24, 1449–1468. [Google Scholar]
- Cundall, P.J. Distinct element models of rock and soil structure. Anal. Comput. Methods Eng. Rock Mech. 1987, 1, 129–163. [Google Scholar]
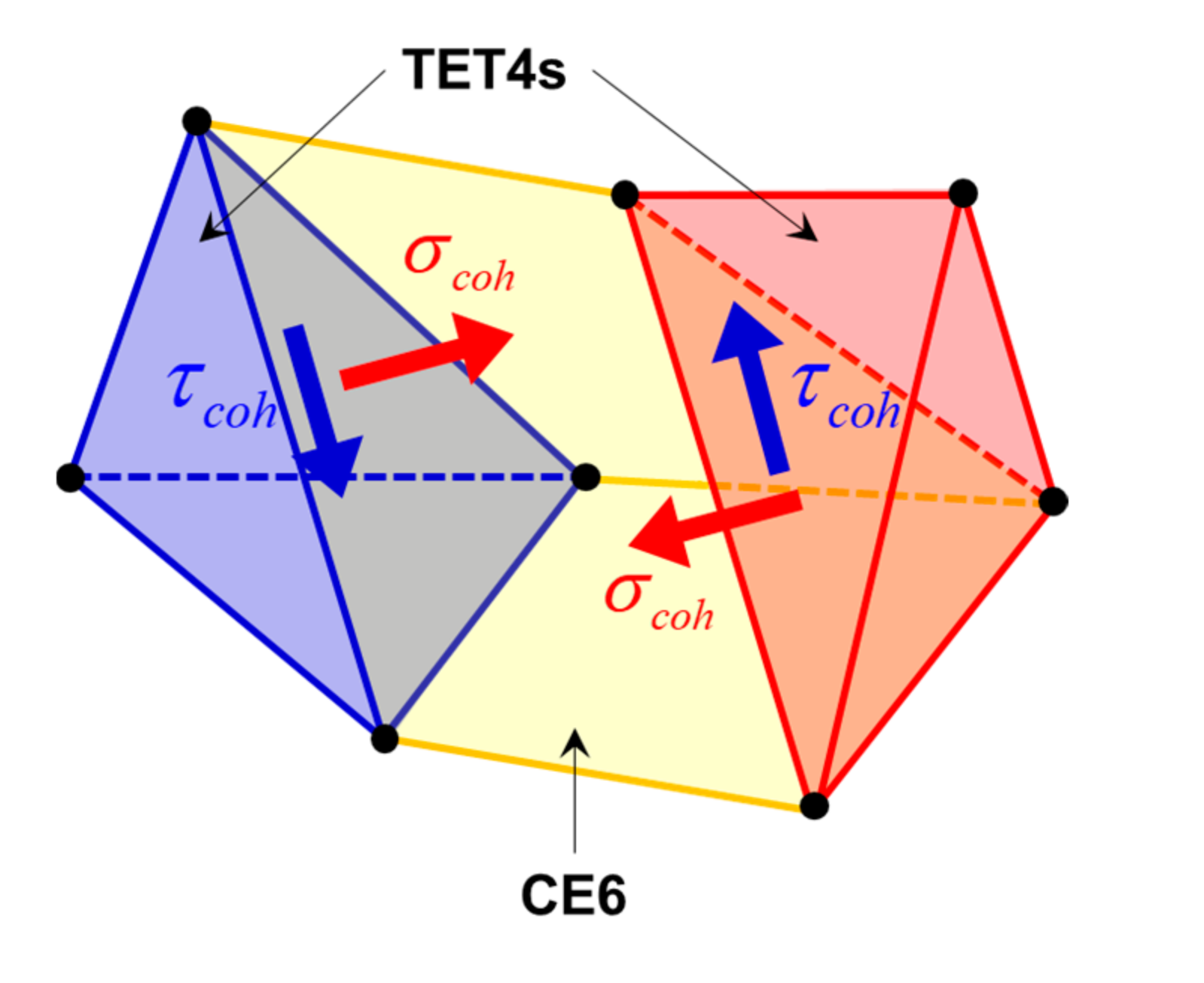















| Parameter | Unit | Value | |
|---|---|---|---|
| 35 MPa Concrete | Granite | ||
| Mass density | 2200 | 2700 | |
| Young’s modulus | 30.0 | 46.0 | |
| Poisson’s ratio | - | 0.20 | 0.21 |
| Tensile strength | 2.62 | 10.0 | |
| Cohesion | 7.87 | 26.0 | |
| Internal friction angle | Degrees | 35.0 | 58.1 |
| Uniaxial compressive strength | 35.0 | 202 | |
| Parameter | Unit | Value | |
|---|---|---|---|
| 35 MPa Concrete | Granite | ||
| Density () | 2200 | 2700 | |
| Young’s modulus () | 30.0 | 46.0 | |
| Poisson’s ratio () | - | 0.20 | 0.21 |
| Microscopic tensile strength () | 2.10 | 20.0 | |
| Microscopic cohesion () | 6.70 | 56.0 | |
| Microscopic internal friction angle () | Degrees | 35.0 | 59.0 |
| Microscopic mode I fracture energy () | 30.0 | 60.0 | |
| Microscopic mode II fracture energy () | 90.0 | 120.0 | |
| Artificial cohesive penalty (, ) | 3000 | 4600 | |
| Artificial cohesive penalty () | 30000 | 46000 | |
| Parameter | Unit | Value |
|---|---|---|
| Normal contact penalty between rock and rock surface () | 460.0 | |
| Normal contact penalty between concrete and concrete surface () | 300.0 | |
| Normal contact penalty between concrete and rock surface () | 300.0 | |
| Normal contact penalty between rock and platen surface () | 460.0 | |
| Normal contact penalty between concrete and platen surface () | 300.0 | |
| Friction coefficient between rock and rock surface () | - | 0.6 |
| Friction coefficient between concrete and concrete surface () | - | 0.6 |
| Friction coefficient between concrete and rock surface () | - | 0.6 |
| Friction coefficient between specimen and platen surface (, ) | - | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, G.; Fukuda, D.; Oh, S.; Kim, G.; Ko, Y.; Liu, H.; Chung, M.; Cho, S. Three-Dimensional Combined Finite-Discrete Element Modeling of Shear Fracture Process in Direct Shearing of Rough Concrete–Rock Joints. Appl. Sci. 2020, 10, 8033. https://doi.org/10.3390/app10228033
Min G, Fukuda D, Oh S, Kim G, Ko Y, Liu H, Chung M, Cho S. Three-Dimensional Combined Finite-Discrete Element Modeling of Shear Fracture Process in Direct Shearing of Rough Concrete–Rock Joints. Applied Sciences. 2020; 10(22):8033. https://doi.org/10.3390/app10228033
Chicago/Turabian StyleMin, Gyeongjo, Daisuke Fukuda, Sewook Oh, Gyeonggyu Kim, Younghun Ko, Hongyuan Liu, Moonkyung Chung, and Sangho Cho. 2020. "Three-Dimensional Combined Finite-Discrete Element Modeling of Shear Fracture Process in Direct Shearing of Rough Concrete–Rock Joints" Applied Sciences 10, no. 22: 8033. https://doi.org/10.3390/app10228033
APA StyleMin, G., Fukuda, D., Oh, S., Kim, G., Ko, Y., Liu, H., Chung, M., & Cho, S. (2020). Three-Dimensional Combined Finite-Discrete Element Modeling of Shear Fracture Process in Direct Shearing of Rough Concrete–Rock Joints. Applied Sciences, 10(22), 8033. https://doi.org/10.3390/app10228033






