Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation
Abstract
Featured Application
Abstract
1. Introduction
2. Experimental Procedures
2.1. Specimen Preparation
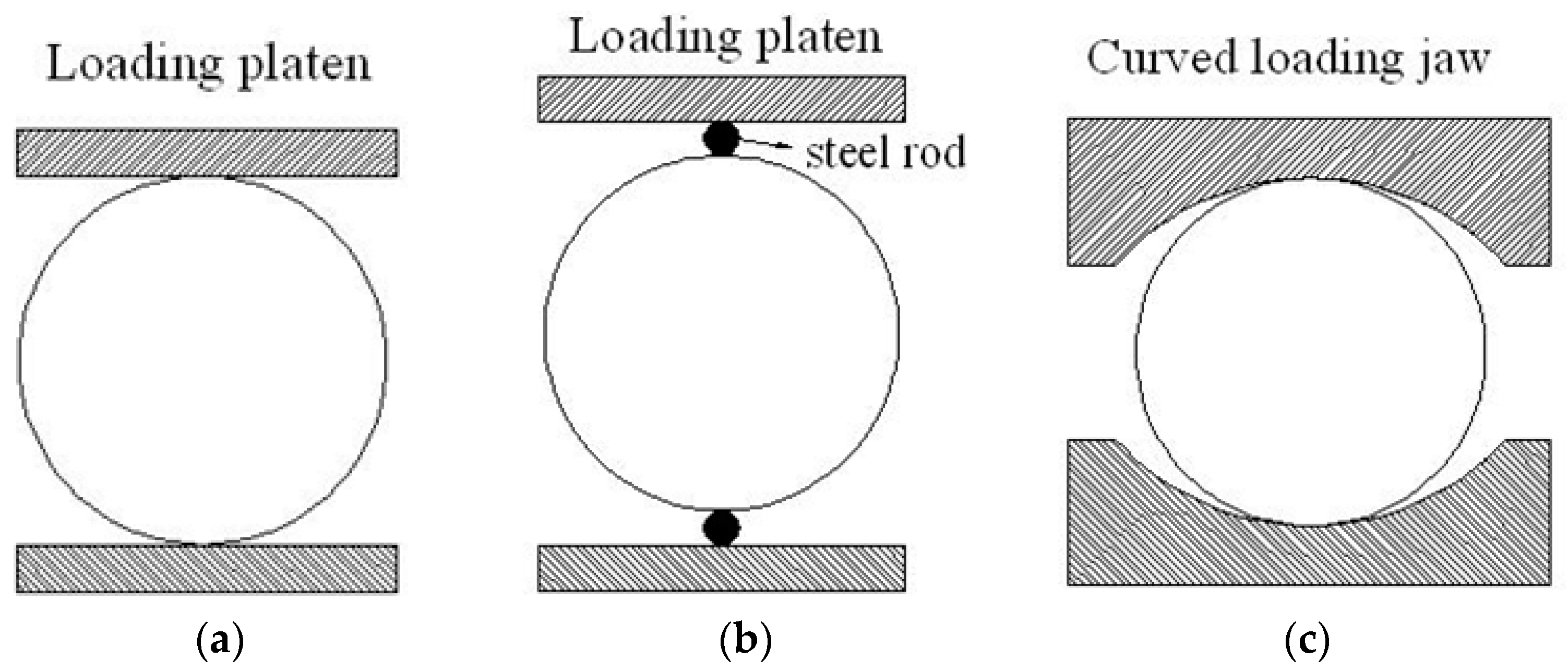
2.2. Experimental Setup and Testing Method
3. Results
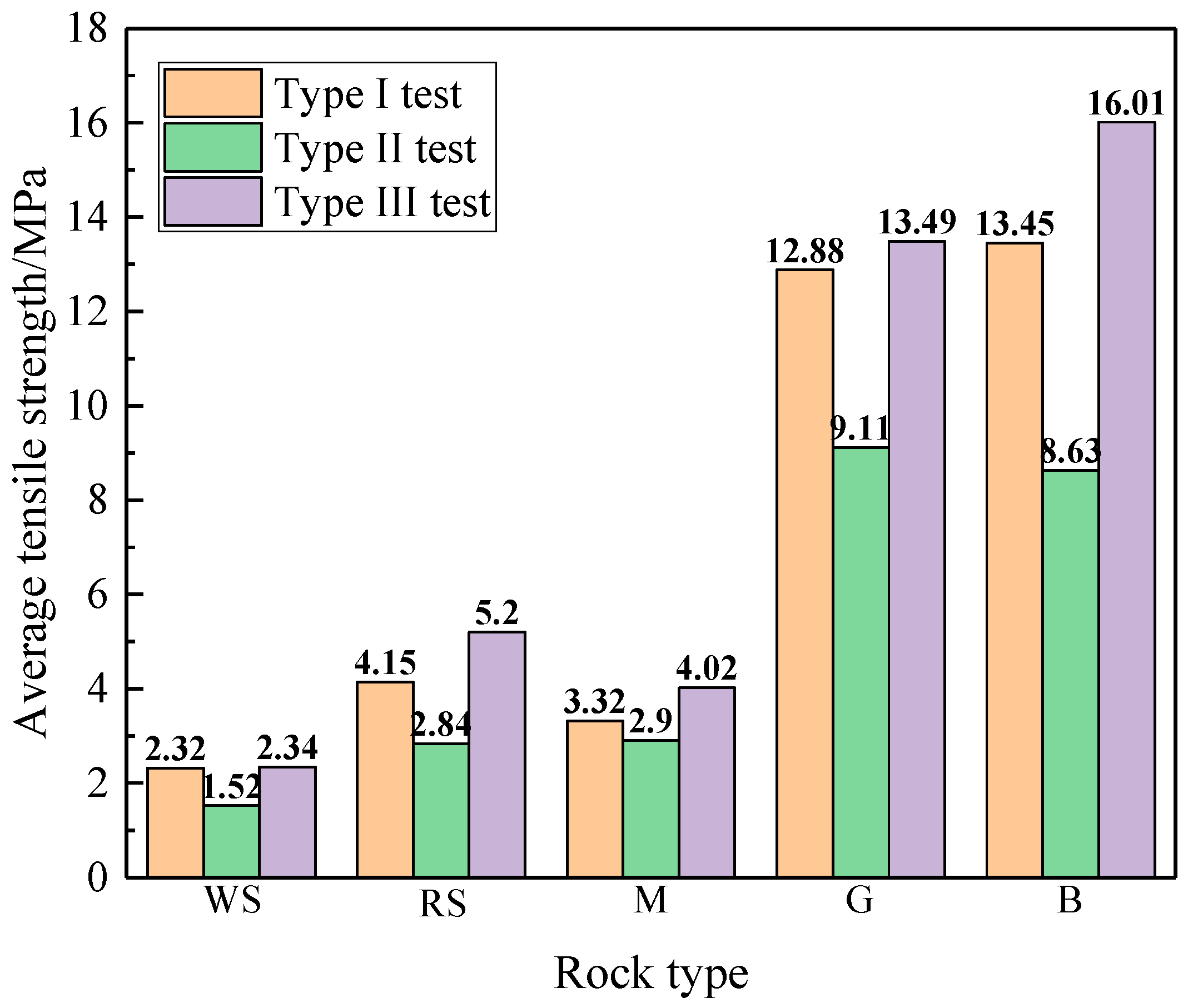
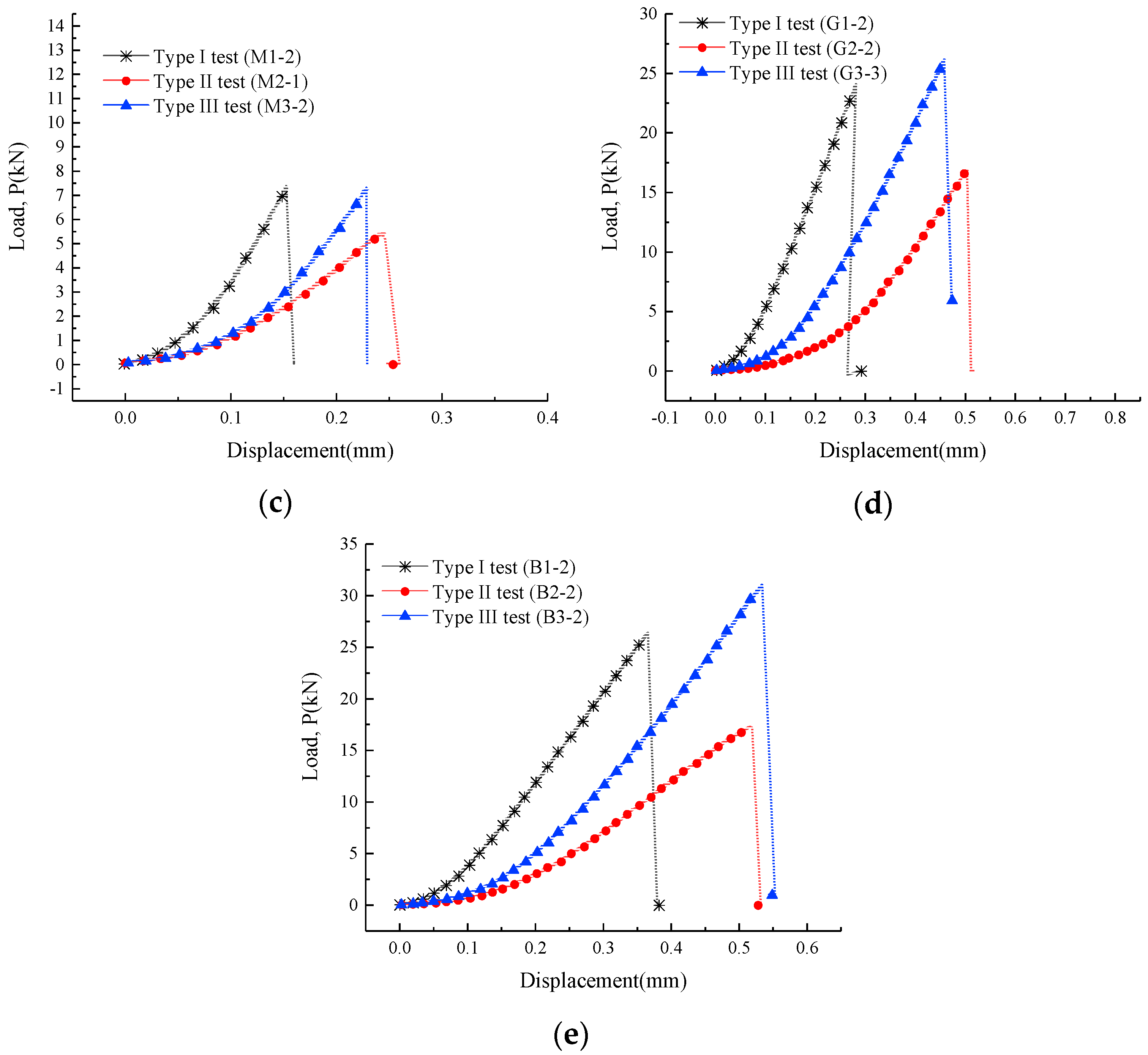
3.1. Tensile Strength and Deformation Characteristic
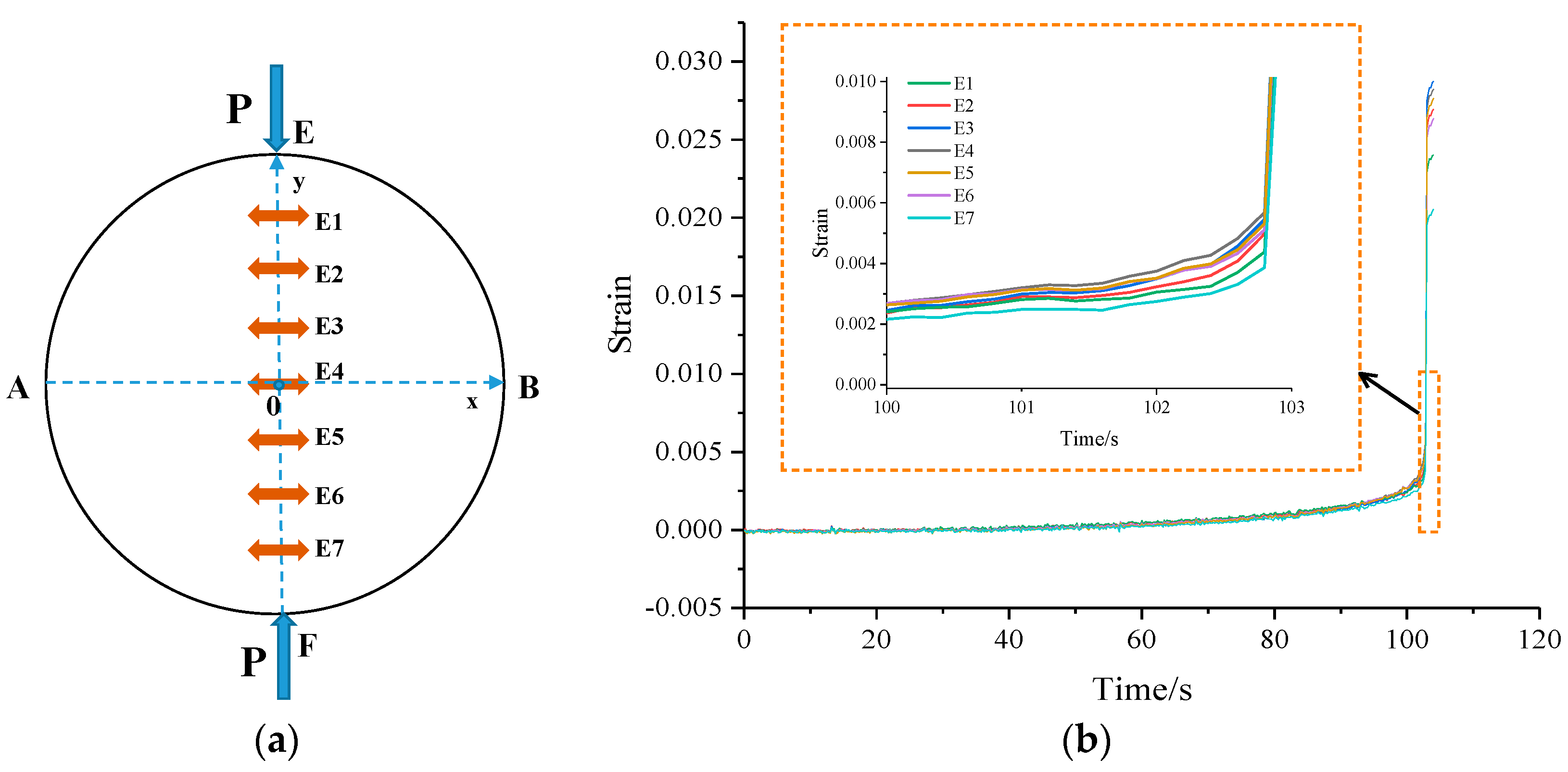
3.2. Failure Process Analysis
3.3. Failure Patterns
4. Discussion
5. Conclusions
- (1)
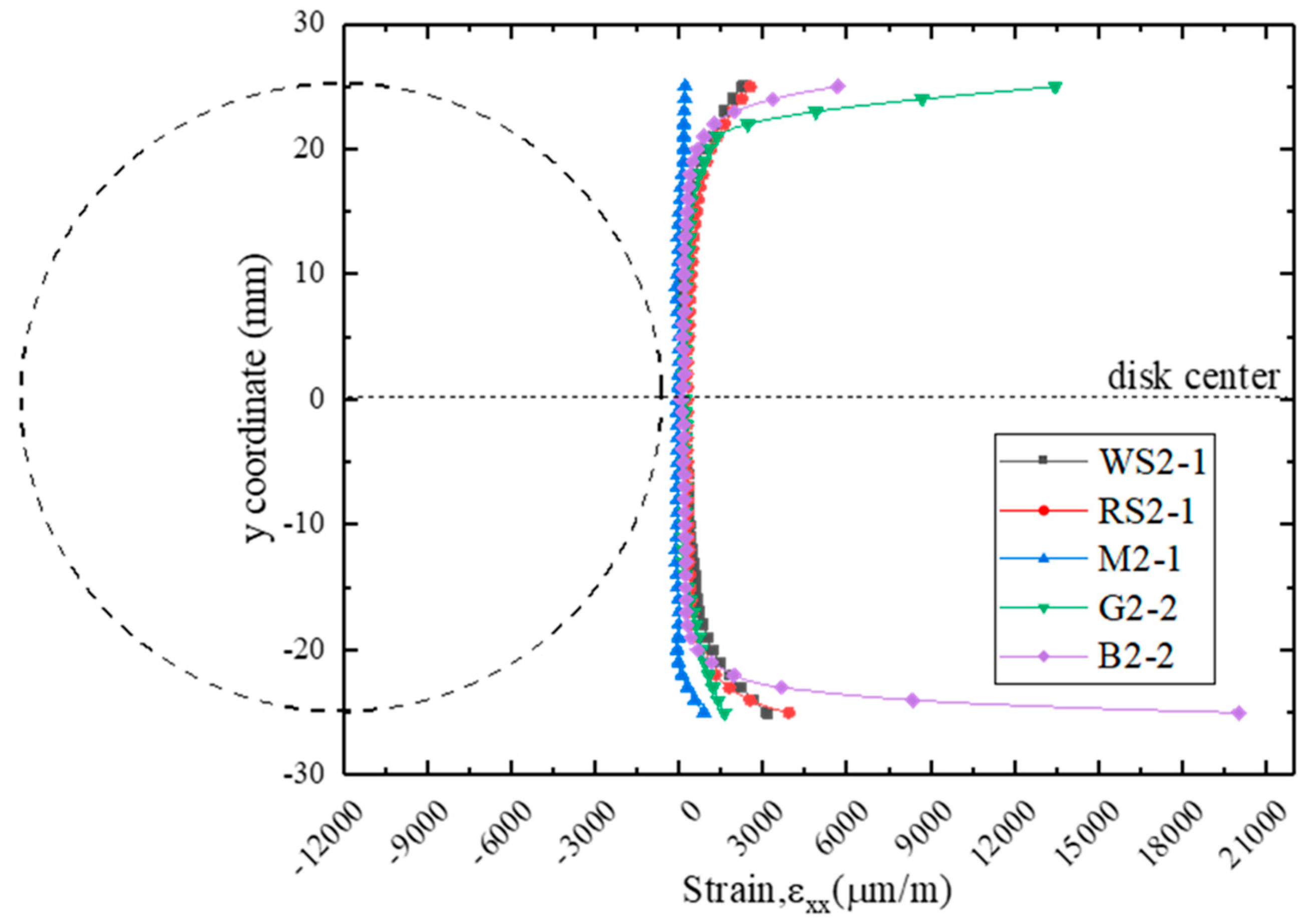
- The failure load and deformation of the Brazilian discs are strongly affected by the loading type. The average tensile strength determined by the Type III test is the highest among the three test types for all rock types, while the Type II test is the lowest. Additionally, the vertical deformation response to load of the disc specimens tested by Type II test specification is the largest, while the Type I test resulted in the lowest.
- (2)
- The Type II test is evidently not applicable to measuring the tensile strength of rocks. The other two testing methods may lead to an invalid failure mode for rock materials with high stiffness and tensile to compressive strength ratios. In this regard, other testing methods and rock types need to be further investigated, which is also the next research direction of this work.
- (3)
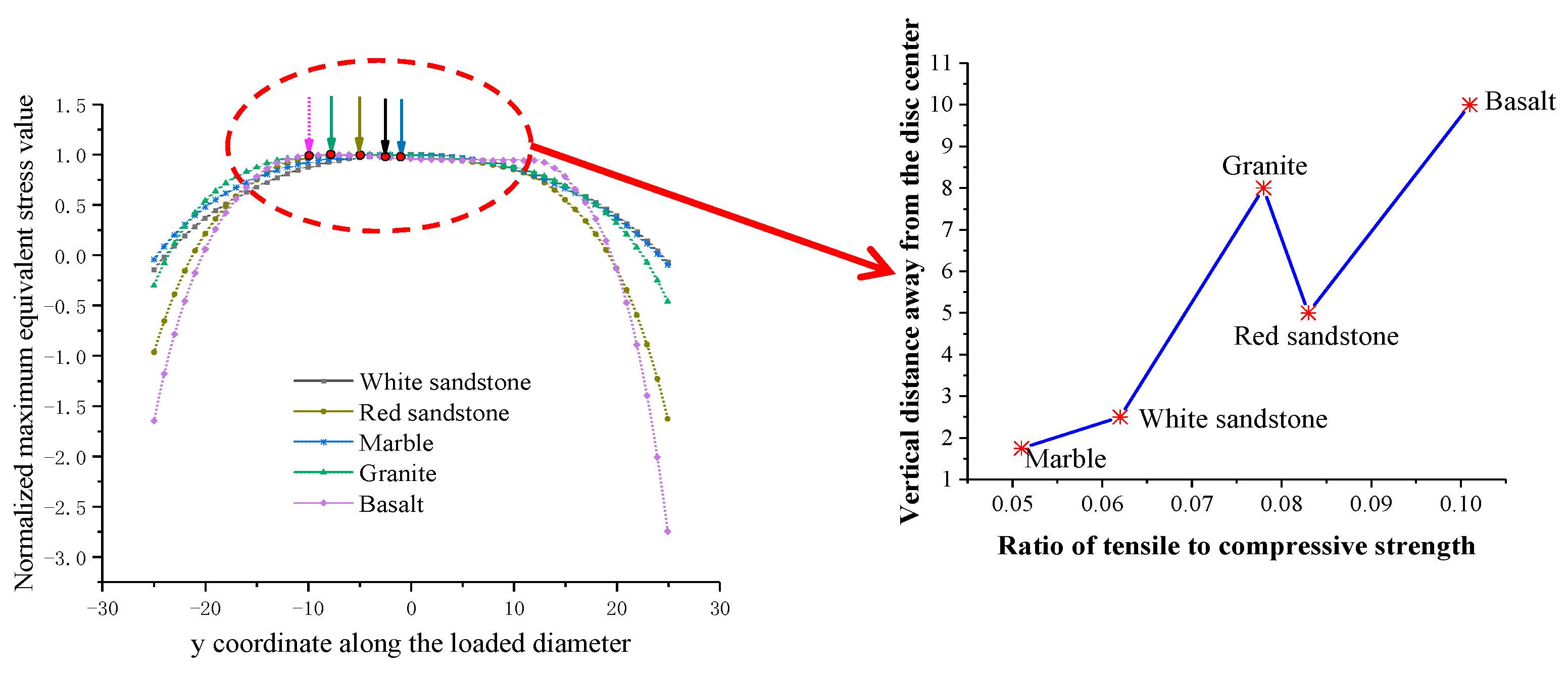
- In the Brazilian test with the ISRM standard specification, the maximum equivalent stress point (possible crack initiation point) based on the Mohr theory generally tends to occur further away from the disc center with the increasing ratio of tensile to compressive strength in rock specimens. Nevertheless, this is not absolute. It was found that the maximum equivalent stress of a disc specimen is co-controlled by the material stiffness and its tensile–compression ratio.
- (4)
- It is not recommendable to evaluate the validity of the Brazilian test only by visually observing the post-fracture pattern of the disc specimens. In fact, DIC can enable us to understand the damage evolution process and failure modes of the specimens.
Author Contributions
Funding
Conflicts of Interest
References
- Rehman, H.; Ali, W.; Naji, A.M.; Kim, J.-J.; Abdullah, R.A.; Yoo, H.-K. Review of Rock-Mass Rating and Tunneling Quality Index Systems for Tunnel Design: Development, Refinement, Application and Limitation. Appl. Sci. 2018, 8, 1250. [Google Scholar] [CrossRef]
- Fernandez-Gutierrez, J.D.; Perez-Acebo, H.; Mulone-Andere, D. Correlation between Bieniawski’s RMR index and Barton’s Q index in fine-grained sedimentary rock formations. Inf. Constr. 2017, 69, e205. [Google Scholar]
- Dan, D.; Konietzky, H.; Herbst, M. Brazilian tensile strength tests on some anisotropic rocks. Int. J. Rock Mech. Min. Sci. 2013, 58, 1–7. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.Q.; Yang, D.X.; Braun, A.; Han, Z.H. Investigation of the Quasi-Brittle Failure of Alashan Granite Viewed from Laboratory Experiments and Grain-Based Discrete Element Modeling. Materials 2017, 10, 835. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.Y.; Li, D.Y.; Zhou, T.; Zhu, Q.Q.; Ranjith, P.G. Experimental study of stress wave propagation and energy characteristics across rock specimens containing cemented mortar joint with various thicknesses. Int. J. Rock Mech. Min. Sci. 2020, 131, 104–352. [Google Scholar] [CrossRef]
- Li, D.Y.; Zhu, Q.Q.; Zhou, Z.L.; Li, X.B.; Ranjith, P.G. Fracture analysis of marble specimens with a hole under uniaxial compression by digital image correlation. Eng. Fract. Mech. 2017, 183, 109–124. [Google Scholar] [CrossRef]
- Zhu, Q.Q.; Li, D.Y.; Han, Z.Y.; Li, X.B.; Zhou, Z.L. Mechanical properties and fracture evolution of sandstone specimens containing different inclusions under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2019, 115, 33–47. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, Z.Y.; Sun, X.L.; Zhou, T.; Li, X.B. Dynamic Mechanical Properties and Fracturing Behavior of Marble Specimens Containing Single and Double Flaws in SHPB Tests. Rock Mech. Rock Eng. 2019, 52, 1623–1643. [Google Scholar] [CrossRef]
- International Society for Rock Mechanics. Suggested methods for determining tensile strength of rock materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 99–103. [Google Scholar] [CrossRef]
- Akazawa, T. New test method for evaluating internal stress due to compression of concrete: The splitting tension test. J. Jpn. Soc. Civ. Eng. 1943, 29, 777–787. [Google Scholar]
- Carneiro, F. A new method to determine the tensile strength of concrete. In Proceedings of the 5th Meeting of the Brazilian Association for Technical Rules, Rio de Janeiro, Brazil, 16 September 1943; pp. 126–129. [Google Scholar]
- Li, D.Y.; Wong, L. The Brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- American Society for Testing and Materials International (ASTM). Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens; ASTM D3967-16; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- National Standards Compilation Group of People’s Republic of China. Standard for Tests Method of Engineering Rock Masses; GB/T 50266-99; China Plan Press: Beijing, China, 1999.
- Fairhurst, C. On the validity of the ‘Brazilian’ test for brittle materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1964, 1, 535–546. [Google Scholar] [CrossRef]
- Hudson, J.A.; Brown, E.T.; Rummel, F. The controlled failure of rock discs and rings loaded in diametral compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1972, 9, 241–248. [Google Scholar] [CrossRef]
- Yu, Y. Questioning the validity of the Brazilian test for determining tensile strength of rocks. Chin. J. Rock Mech. Eng. 2005, 24, 1150–1157. (In Chinese) [Google Scholar]
- Hooper, J.A. The failure of glass cylinders in diametral compression. J. Mech. Phys. Solids 1971, 19, 179–200. [Google Scholar] [CrossRef]
- Mellor, M.; Hawkes, I. Measurement of tensile strength by diametral compression of discs and annuli. Eng. Geol. 1971, 5, 173–225. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W. Fundamentals of Rock Mechanics; Chapman and Hall: London, UK, 1976. [Google Scholar]
- Swab, J.; Yu, J.; Gamble, R.; Kilczewski, S. Analysis of the diametral compression method for determining the tensile strength of transparent magnesium aluminate spinel. Int. J. Fract. 1971, 172, 187–192. [Google Scholar] [CrossRef]
- Erarslan, N.; Williams, D.J. Experimental, numerical and analytical studies on tensile strength of rocks. Int. J. Rock Mech. Min. Sci. 2012, 49, 21–30. [Google Scholar] [CrossRef]
- Yanagidani, T.; Sano, O.; Terada, M.; Ito, I. The observation of cracks propagating in diametrically-compressed rock discs. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 225–235. [Google Scholar] [CrossRef]
- Steen, B.; Vervoort, A.; Napier, J.A.L. Observed and simulated fracture pattern in diametrically loaded discs of rock material. Int. J. Fract. 2005, 131, 35–52. [Google Scholar] [CrossRef]
- Zhu, W.C.; Tang, C.A. Numerical simulation of Brazilian disk rock failure under static and dynamic loading. Int. J. Rock Mech. Min. Sci. 2006, 43, 236–252. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K. Numerical simulation of the Brazilian test and the tensile strength of anisotropic rocks and rocks with pre-existing cracks. Int. J. Rock Mech. Min. Sci. 2004, 41, 450–451. [Google Scholar] [CrossRef]
- Yu, Y.; Yin, J.M.; Zhong, Z.W. Shape effects in the Brazilian tensile strength test and a 3D FEM correction. Int. J. Rock Mech. Min. Sci. 2006, 43, 623–627. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, J.X.; Zhang, J.C. A modified Brazilian disk tension test. Int. J. Rock Mech. Min. Sci. 2009, 46, 421–425. [Google Scholar] [CrossRef]
- Lavrov, A.; Vervoort, A. Theoretical treatment of tangential loading effects on the Brazilian test stress distribution. Int. J. Rock Mech. Min. Sci. 2002, 39, 275–283. [Google Scholar] [CrossRef]
- Markides, C.F.; Pazis, D.N.; Kourkoulis, S.K. Influence of friction on the stress field of the Brazilian tensile test. Rock Mech. Rock Eng. 2011, 44, 113–119. [Google Scholar] [CrossRef]
- Dorogoy, A.; Banks-Sills, L. Effect of crack face contact and friction on Brazilian disk specimens—A finite difference solution. Eng. Fract. Mech. 2005, 72, 2758–2773. [Google Scholar] [CrossRef]
- Markides, C.F.; Kourkoulis, S.K. The stress field in a standardized brazilian disc: The influence of the loading type acting on the actual contact length. Rock Mech. Rock Eng. 2012, 45, 145–158. [Google Scholar] [CrossRef]
- Markides, C.F.; Pazis, D.N.; Kourkoulis, S.K. Closed full-field solutions for stresses and displacements in the Brazilian disk under distributed radial load. Int. J. Rock Mech. Min. Sci. 2010, 7, 227–237. [Google Scholar] [CrossRef]
- Exadaktylos, G.E.; Kaklis, K.N. Applications of an explicit solution for the transversely isotropic circular disc compressed diametrically. Int. J. Rock Mech. Min. Sci. 2001, 38, 227–243. [Google Scholar] [CrossRef]
- Claesson, J.; Bohloli, B. Brazilian test: Stress field and tensile strength of anisotropic rocks using an analytical solution. Int. J. Rock Mech. Min. Sci. 2002, 39, 991–1004. [Google Scholar] [CrossRef]
- Tavallali, A.; Vervoort, A. Effect of layer orientation on the failure of layered sandstone under Brazilian test conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 313–322. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Zhao, G.F.; Russell, A.R. Crack development in transversely isotropic sandstone discs subjected to Brazilian tests observed using digital image correlation. Int. J. Rock Mech. Min. Sci. 2019, 119, 211–221. [Google Scholar] [CrossRef]
- Komurlu, E.; Kesimal, A. Jaw effects on indirect tensile strength test disc failure mechanism. In Proceedings of the 7th Asian Rock Mechanics Symposium, Seoul, Korea, 15–19 October 2012; pp. 624–637. [Google Scholar]
- Sgambitterra, E.; Lamuta, C.; Candamano, S.; Pagnotta, L. Brazilian disk test and digital image correlation: A methodology for the mechanical characterization of brittle materials. Mater. Struct. 2018, 51, 19. [Google Scholar] [CrossRef]
- Liu, J.F.; Chen, L.; Wang, C.P.; Man, K.; Wang, L.; Wang, J.; Su, R. Characterizing the mechanical tensile behavior of Beishan granite with different experimental methods. Int. J. Rock Mech. Min. Sci. 2014, 69, 50–58. [Google Scholar] [CrossRef]
- Stirling, R.A.; Simpson, D.J.; Davie, C.T. The application of digital image correlation to Brazilian testing of sandstone. Int. J. Rock Mech. Min. Sci. 2013, 60, 1–11. [Google Scholar] [CrossRef]
- Komurlu, E.; Kesimal, A. Evaluation of Indirect Tensile Strength of Rocks Using Different Types of Jaws. Rock Mech. Rock Eng. 2015, 48, 1723–1730. [Google Scholar] [CrossRef]
- Pan, B.; Li, K. A fast digital image correlation method for deformation measurement. Opt. Laser Eng. 2011, 49, 841–847. [Google Scholar] [CrossRef]
- Sutton, M.A.; Matta, F.; Rizos, D.; Ghorbani, R.; Rajan, S.; Mollenhauer, D.H.; Schreier, H.W.; Lasprilla, A.O. Recent Progress in Digital Image Correlation: Background and Developments since the 2013 W M Murray Lecture. Exp. Mech. 2017, 57, 1–30. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Zhou, X.P.; Lian, Y.J.; Wong, L.N.Y.; Berto, F. Understanding the fracture behavior of brittle and ductile multi-flawed rocks by uniaxial loading by digital image correlation. Eng. Fract. Mech. 2018, 199, 438–460. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.Y.; Song, H.P.; Kang, Y.L. Experimental investigation of deformation and failure mechanisms in rock under indentation by digital image correlation. Eng. Fract. Mech. 2012, 96, 667–675. [Google Scholar] [CrossRef]
- CorelatedSolutions. CSI Application Note AN-824; Correlated Solutions: Columbia, SC, USA, 2010; Available online: www.CorrelatedSolutions.com (accessed on 20 May 2020).
- CorelatedSolutions. Vic-3D 2010 Reference Manual; Correlated Solutions: Columbia, SC, USA, 2010; Available online: www.CorrelatedSolutions.com (accessed on 20 May 2020).
- Hucka, V.; Das, B. Brittleness determination of rocks by different methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 389–392. [Google Scholar] [CrossRef]
- Yang, S.; Yin, P.; Huang, Y. Experiment and discrete element modelling on strength, deformation and failure behaviour of shale under Brazilian compression. Rock Mech. Rock Eng. 2019, 52, 4339–4359. [Google Scholar] [CrossRef]
- Wang, C.; Li, S.Y.; Zhang, T.W.; You, Z.M. Experimental Study on Mechanical Characteristics and Fracture Patterns of Unfrozen/Freezing Saturated Coal and Sandstone. Materials 2019, 12, 992. [Google Scholar] [CrossRef]
- Bhavikatti, S.; Bhat, M.R.; Murthy, C.R.L. Fatigue crack growth monitoring in Ti-6Al-4V alloy using acoustic emission technique and digital image correlation. J. Nondestruct. Eval. 2011, 9, 4. [Google Scholar]
- Yu, Y.; Xu, Y. Method to determine tensile strength of rock using flattened Brazilian disk. Chin. J. Rock Mech. Eng. 2006, 25, 1457–1462. (In Chinese) [Google Scholar]
- Pandey, P.; Singh, D.P. Deformation of a rock in different tensile tests. Eng. Geol. 1986, 22, 281–292. [Google Scholar] [CrossRef]
- Efimov, V.P. The rock strength in different tension conditions. J. Min. Sci. 2009, 45, 569–575. [Google Scholar] [CrossRef]
- Fuenkajorn, K.; Klanphumeesri, S. Laboratory determination of direct tensile strength and deformability of intact rocks. Geotech. Test. J. 2011, 34, 103134. [Google Scholar]
- Ye, J.H.; Wu, F.Q.; Sun, J.Z. Estimation of the tensile elastic modulus using Brazilian disc by applying diametrically opposed concentrated loads. Int. J. Rock Mech. Min. Sci. 2009, 46, 568–576. [Google Scholar]







| Rock Type | Parameter | Mean Value | Standard Deviation |
|---|---|---|---|
| White sandstone | 37.7 | 0.6 | |
| (GPa) | 9.2 | 0.2 | |
| 0.15 | 0.01 | ||
| Red sandstone | 62.6 | 0.8 | |
| (GPa) | 14.8 | 0.6 | |
| 0.18 | 0.01 | ||
| Marble | 79.2 | 0.7 | |
| (GPa) | 43.7 | 0.6 | |
| 0.21 | 0.01 | ||
| Granite | 171.7 | 0.4 | |
| (GPa) | 72.2 | 0.9 | |
| 0.23 | 0.01 | ||
| Basalt | 158.4 | 3.3 | |
| (GPa) | 61.9 | 2.1 | |
| 0.25 | 0.01 |
| Specimens No. | D/mm | t/mm | Pmax/kN | σt/MPa | Mean/MPa | BI |
|---|---|---|---|---|---|---|
| WS1-1 1 | 48.98 | 25.09 | 4.54 | 2.35 | 2.32 | |
| WS1-2 | 49.08 | 25.09 | 4.26 | 2.20 | ||
| WS1-3 | 49.09 | 25.09 | 4.62 | 2.39 | ||
| WS2-1 | 49.02 | 25.11 | 2.94 | 1.52 | 1.52 | |
| WS2-2 | 49.05 | 25.10 | 3.00 | 1.55 | ||
| WS2-3 | 49.01 | 25.09 | 2.88 | 1.49 | ||
| WS3-1 | 49.06 | 25.09 | 4.96 | 2.57 | 2.34 | 16.11 |
| WS3-2 | 48.99 | 25.09 | 4.30 | 2.19 | ||
| WS3-3 | 48.98 | 25.06 | 4.36 | 2.26 | ||
| RS1-1 | 49.09 | 25.05 | 8.79 | 4.55 | 4.15 | |
| RS1-2 | 49.06 | 25.05 | 7.70 | 3.99 | ||
| RS1-3 | 49.07 | 25.02 | 7.52 | 3.90 | ||
| RS2-1 | 49.02 | 25.04 | 5.23 | 2.71 | 2.84 | |
| RS2-2 | 49.06 | 25.06 | 6.24 | 3.23 | ||
| RS2-3 | 49.02 | 25.03 | 4.96 | 2.57 | ||
| RS3-1 | 49.07 | 25.02 | 10.08 | 5.23 | 5.20 | 12.04 |
| RS3-2 | 49.03 | 25.02 | 10.10 | 5.24 | ||
| RS3-3 | 49.03 | 25.06 | 9.90 | 5.13 | ||
| M1-1 | 49.07 | 25.03 | 6.19 | 3.21 | 3.32 | |
| M1-2 | 49.05 | 25.08 | 7.35 | 3.81 | ||
| M1-3 | 49.05 | 25.01 | 5.66 | 2.94 | ||
| M2-1 | 49.05 | 25.08 | 5.40 | 2.80 | 2.90 | |
| M2-2 | 49.04 | 25.04 | 5.73 | 2.97 | ||
| M2-3 | 49.05 | 25.07 | 5.60 | 2.92 | ||
| M3-1 | 49.39 | 25.31 | 8.40 | 4.28 | 4.02 | 19.70 |
| M3-2 | 49.03 | 24.99 | 7.29 | 3.80 | ||
| M3-3 | 48.96 | 25.01 | 7.61 | 3.96 | ||
| G1-1 | 48.81 | 25.10 | 24.87 | 12.93 | 12.88 | |
| G1-2 | 48.86 | 25.08 | 23.86 | 12.40 | ||
| G1-3 | 48.84 | 25.10 | 25.62 | 13.31 | ||
| G2-1 | 48.89 | 25.07 | 17.45 | 9.07 | 9.11 | |
| G2-2 | 48.89 | 25.06 | 16.85 | 8.76 | ||
| G2-3 | 48.87 | 25.11 | 18.31 | 9.50 | ||
| G3-1 | 48.91 | 25.11 | 25.24 | 13.09 | 13.49 | 12.73 |
| G3-2 | 48.92 | 25.12 | 26.84 | 13.91 | ||
| G3-3 | 48.86 | 25.12 | 25.97 | 13.48 | ||
| B1-1 | 49.54 | 25.02 | 28.36 | 14.57 | 13.45 | |
| B1-2 | 49.56 | 24.99 | 26.26 | 13.50 | ||
| B1-3 | 49.56 | 24.98 | 23.89 | 12.29 | ||
| B2-1 | 49.54 | 25.00 | 16.85 | 8.67 | 8.63 | |
| B2-2 | 49.54 | 25.00 | 17.22 | 8.86 | ||
| B2-3 | 49.59 | 24.98 | 16.28 | 8.37 | ||
| B3-1 | 49.52 | 25.03 | 28.94 | 14.87 | 16.01 | 9.89 |
| B3-2 | 49.53 | 25.01 | 31.04 | 15.96 | ||
| B3-3 | 49.55 | 24.96 | 33.40 | 17.20 |
| Rock Type | Type I Test | Type II Test | Type III Test |
|---|---|---|---|
| White sandstone | 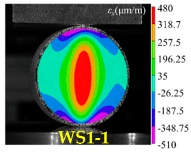 | 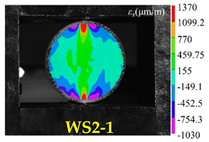 | 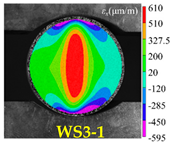 |
| Red sandstone | 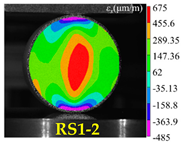 | 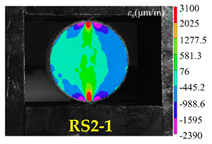 | 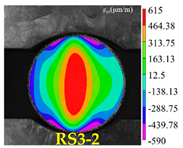 |
| Marble |  | 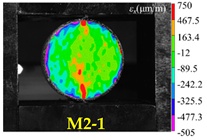 | 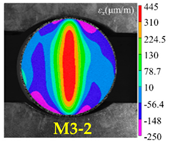 |
| Granite | 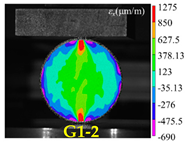 | 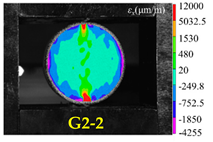 | 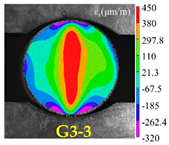 |
| Basalt | 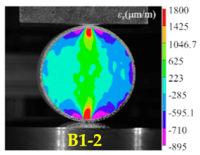 |  | 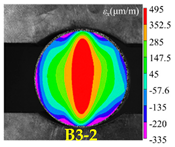 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Li, B.; Han, Z.; Zhu, Q. Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation. Appl. Sci. 2020, 10, 5513. https://doi.org/10.3390/app10165513
Li D, Li B, Han Z, Zhu Q. Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation. Applied Sciences. 2020; 10(16):5513. https://doi.org/10.3390/app10165513
Chicago/Turabian StyleLi, Diyuan, Bang Li, Zhenyu Han, and Quanqi Zhu. 2020. "Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation" Applied Sciences 10, no. 16: 5513. https://doi.org/10.3390/app10165513
APA StyleLi, D., Li, B., Han, Z., & Zhu, Q. (2020). Evaluation on Rock Tensile Failure of the Brazilian Discs under Different Loading Configurations by Digital Image Correlation. Applied Sciences, 10(16), 5513. https://doi.org/10.3390/app10165513








