Accelerating Emergence of Aerial Swarm

Abstract

Herein, we present a methodology and framework for exploiting certain interdisciplinary studies that can particularly benefit from integration. In this paper, rigorous derivation of control theory and statistical analysis of simulation results are organically unified for testifying and optimizing the emergence of order in aerial swarming scenarios under free boundary conditions. Each Unmanned Aerial Vehicle (UAV) is regulated by a simplified mathematical model, based on which a distributed flocking protocol is proposed as a feasible solution for aerial swarms. On condition that the initial interaction network is connected, the LaSalle–Krasovskii invariance principle is implemented to verify the effectiveness of the above algorithm. However, most existing results on flocking are far from being engineering applications. A basic challenge is how to present a low-cost energy and time saving solution on account of the limited flight capability of these UAVs and real-time operational requirements. As is well known, energy consumption can be reduced if unnecessary interactions among individuals are eliminated. Therefore, another contribution of this paper is to propose a precise optimization of an existing flocking algorithm for UAVs with respect to interaction requirements. Energy and time measurements, as well as scalability effects, are assessed in terms of statistical significance and strength. The results indicate that the flocking control protocol adopting the minimal interaction is the most promising swarm.

1. Introduction

Aerial swarm has been considered as one of the most challenging, exciting, and multidisciplinary fields of robotics in the last decades [1,2,3,4,5,6,7,8,9]. Compared with single-robot systems, aerial swarm systems are expected to be more robust to failure and own faster response capability to complete complex tasks, such as patrolling, exploration, and search and rescue in large areas. Flocking is a type of collective behavior emerging from a set of individuals that rely only on simple rules and local sensing. In recent years, flocking has been widely studied as an effective and low-cost solution to aerial swarm. However, the computation complexity and quantity will increase sharply following the expansion of the scale of the group. Therefore, it is necessary to discuss how to accelerate the emergence of flocking structures.

The literature on flocking can be summarized into two categories. One category is to discuss the flocking problem by using rigorous mathematical analysis [10,11,12,13,14]. There are mainly three basic elements to study the flocking behavior in this category, including model, interaction rules, and distributed control protocol. Prior studies on flocking are mainly based on either the simple first-order or second-order integrator model or a general dynamic model [15,16,17]. The nonlinear dynamics inherent in the system of Unmanned Aerial Vehicles (UAVs) remain sparse, which can, with a large probability, cause the failure of the proposed control algorithm to resolve the coordination control of UAVs. A kind of scale-dependent interaction rule is usually adopted, called the nearest-neighbor interaction rule [18]. The mechanism of the interaction network depends on communication radius. Inspired by natural starlings, a flocking algorithm with the combination of a consensus and artificial potential field has been proposed to reveal the underlying mechanism responsible for the emerging collective behaviors that a set of individuals move in unison while creating a dynamic formation pattern. The flocking control of wheeled mobile robots [19] and underwater robots [14,20] were dealt with, yet these studies just considered the two-dimensional motion of individuals. Jia et al. have studied the three-dimensional flocking of UAVs governed by a nonlinear dynamic model, but did not give any further analysis and discussion on how to accelerate the emergence of flocking behaviors and how to apply the proposed control algorithm to large-scale systems [21].

The second category uses a statistical method to analyze the simulation results. These simulations are designed mostly according to the real experimental data of flocks of animals. Ballerini et al. have tracked and analyzed the movements of these starling flocks [22]. In this study, they found that there is not any leader in the colony. Besides, the number of individual birds in a flock can be as many as thousands, although each bird just follows local rules and only interacts with six to seven neighbors. Generally speaking, bigger interaction networks (referring to more interactions) yield faster consensuses. However, starlings show fast and flexible dynamic aggregation relying only on small interaction networks. Therefore, a problem exists in how the scale of the interaction network influences the emergence behavior of a flock. As proposed by economists, Rybski et al. found a phenomenon called diminishing returns, which led by the increasing of the number of deployed robots [23]. Rosenfeld et al. also found that additional robots usually produce negative returns after a peak in performance when they focused on the scalability study of foraging tasks [24]. Besides, Timothy et al. have compared three strategies for aerial swarm deployment task according to the energy-time efficiency by using statistical analysis methods [25]. In this paper, a statistical method is applied to analyze whether the diminishing returns exist in the interaction network of an aerial swarm or not.

According to the above research results, rigorous theoretical analysis can offer rigorous mathematical proof, but these conclusions are always limited to some unreasonable hypothesis. At the same time, although simulation can be carried out as close as possible to realistic conditions, these conclusions are easily doubted and argued because of some special cases. Therefore, our goal here is to design a general methodology and framework for studying flocking behaviors by means of the combination of control theory and statistical method.

First, the UAV system is considered to be an egalitarian one with two basic properties: One is that every individual obeys the same control protocol to adjust its behavior during the entire process of flight, and the other is that each UAV uses the same communication radius to recognize its neighbors for information exchange. Thus, the communication radius can be regarded as the only factor to draw the scale of the interaction network. Second, a flocking protocol is proposed for each UAV to form a three-dimensional cohesive configuration in a consistent pattern. Instead of a simple first-order or second-order integrator, each UAV is simplified as a nonlinear dynamic model commonly used to describe the UAV in the existing literature [26,27]. According to the LaSalle–Krasovskii invariance principle [28], the UAV flocking will emerge as long as the initial interaction network is connected. During the evolutionary process, collision is carefully avoided among pairwise UAVs. Finally, energy/time costs are evaluated under different communication radii, and the scalability performance is examined by increasing the group size. A statistical method is applied to analyze the energy/time measurements and scalability effects. The results indicate that the flocking protocol adopting the minimally connected communication radius is considered as the most promising swarm from the perspective of energy savings and the rate of convergence. This conclusion tactfully echoes from the biological evidence that each starling interacts with only six or seven nearest-neighbors most often at the same time.

This paper is organized as follows. Materials and methods are given in Section 2. Section 3 illustrates the effectiveness of the proposed solution for UAV flocking. Section 4 shows the energy/time measurements and scalability effects in a quantitative way. Finally, this paper is concluded in Section 5.

2. Materials and Methods

2.1. UAV Model

A collective task is considered to be carried out by N homogeneous UAVs flying in three-dimensional space. Each UAV has the same hardware installment and software configuration, as well as owns the same communication capability. The communication capability of each UAV can be measured by its communication radius D (D is a positive constant). According to the existing literatures on UAVs, the dynamics of each UAV is described by the following differential equation [26,27],

$$\begin{array}{c}\stackrel{.}{x_i}\left(t\right)={\vartheta }_i\left(t\right)cos{\gamma }_i\left(t\right)cos{\psi }_i\left(t\right)\hfill \\ \stackrel{.}{y_i}\left(t\right)={\vartheta }_i\left(t\right)cos{\gamma }_i\left(t\right)sin{\psi }_i\left(t\right)\hfill \\ \stackrel{.}{h_i}\left(t\right)={\vartheta }_i\left(t\right)sin{\gamma }_i\left(t\right)\hfill \\ \stackrel{.}{{\vartheta }_i}\left(t\right)=g·(n_{ti}\left(t\right)-sin{\gamma }_i\left(t\right))\hfill \\ \stackrel{.}{{\psi }_i}\left(t\right)=g·n_{hi}\left(t\right)/({\vartheta }_i\left(t\right)cos{\gamma }_i\left(t\right))\hfill \\ \stackrel{.}{{\gamma }_i}\left(t\right)=g·(n_{vi}\left(t\right)-cos{\gamma }_i\left(t\right))/{\vartheta }_i\left(t\right),i=1,\cdots ,N\hfill \end{array}$$

(1)

where i denotes index for the ith UAV, $x_i\left(t\right)$ is the ith UAV’s downrange, $y_i\left(t\right)$ is the ith UAV’s crossrange, $h_i\left(t\right)$ is the ith UAV’s altitude, ${\vartheta }_i\left(t\right)>0$ is the ith UAV’s speed, ${\psi }_i\left(t\right)\in (-\frac{\pi }{2},\frac{\pi }{2})$ is the ith UAV’s heading angle, ${\gamma }_i\left(t\right)\in (-\frac{\pi }{2},\frac{\pi }{2})$ is the ith UAV’s flight path angle, $n_{hi}\left(t\right)$ is the ith UAV’s horizontal load factor, $n_{vi}\left(t\right)$ is the ith UAV’s vertical load factor, $n_{ti}\left(t\right)$ is the ith UAV’s tangential load factor, and g is the constant acceleration of gravity.

For brevity, the proposed simplified model (1) of UAV i is shown in Figure 1. Generally speaking, the behavior of UAV i is steered under four forces: lift force, drag force, weight, and thrust force. $T_i\left(t\right)$ is the magnitude of the thrust, $L_i\left(t\right)$ is the magnitude of the lift force, $D_i\left(t\right)$ is the magnitude of the drag force, and $W_i\left(t\right)$ is the magnitude of the gravity. Heading angle ${\psi }_i\left(t\right)$ describes whether the aircraft is turning left or right. Flight path angle ${\gamma }_i\left(t\right)$ describes whether the aircraft is climbing or descending. Bank angle ${\mu }_i\left(t\right)=arctan\frac{n_{hi}\left(t\right)}{n_{vi}\left(t\right)}$ describes whether the aircraft is rolling clockwise or counterclockwise. The three-dimensional aircraft model not only considers the longitudinal plane, but also the lateral plane, thus the control variable $[L_i\left(t\right),D_i\left(t\right),T_i\left(t\right)]$ is replaced with $[n_{ti}\left(t\right),n_{hi}\left(t\right),n_{vi}\left(t\right)]$ in this model (1).

Then, the state of UAV i at time t can be expressed by its position vector $p_i\left(t\right)={[x_i\left(t\right),y_i\left(t\right),h_i\left(t\right)]}^T$ and its velocity vector

$$q_i\left(t\right)=\left[\begin{array}{c}{\vartheta }_i\left(t\right)cos{\gamma }_i\left(t\right)cos{\psi }_i\left(t\right)\\ {\vartheta }_i\left(t\right)cos{\gamma }_i\left(t\right)sin{\psi }_i\left(t\right)\\ {\vartheta }_i\left(t\right)sin{\gamma }_i\left(t\right)\end{array}\right].$$

(2)

Thus, we have

$${\dot{q}}_i=\left[\begin{array}{c}{\dot{\vartheta }}_{i}cos{\gamma }_{i}cos{\psi }_i-{\dot{\gamma }}_i{\vartheta }_{i}sin{\gamma }_{i}cos{\psi }_i-{\dot{\psi }}_i{\vartheta }_{i}cos{\gamma }_{i}sin{\psi }_i\\ {\dot{\vartheta }}_{i}cos{\gamma }_{i}sin{\psi }_i-{\dot{\gamma }}_i{\vartheta }_{i}sin{\gamma }_{i}sin{\psi }_i+{\dot{\psi }}_i{\vartheta }_{i}cos{\gamma }_{i}cos{\psi }_i\\ {\dot{\vartheta }}_{i}sin{\gamma }_i+{\dot{\gamma }}_i{\vartheta }_{i}cos{\gamma }_i\end{array}\right].$$

(3)

Here, due to the space limitation, we use $q_i$, ${\vartheta }_i$, ${\gamma }_i$, and ${\psi }_i$ instead of $q_i\left(t\right)$, ${\vartheta }_i\left(t\right)$, ${\gamma }_i\left(t\right)$, and ${\psi }_i\left(t\right)$ for short. Put the last three equations of (1) into (3), one gets

$${\dot{q}}_i=g\left[\begin{array}{c}{n}_{ti}cos{\gamma }_{i}cos{\psi }_i-n_{hi}sin{\psi }_i-n_{vi}sin{\gamma }_{i}cos{\psi }_i\\ n_{ti}cos{\gamma }_{i}sin{\psi }_i+n_{hi}cos{\psi }_i\\ n_{ti}sin{\gamma }_i+n_{vi}cos{\gamma }_i-1\end{array}\right].$$

(4)

Let the control input of UAV i at time t is denoted as $u_i\left(t\right)={[n_{ti}\left(t\right),n_{hi}\left(t\right),n_{vi}\left(t\right)]}^T$. Then, Equation (4) can be rewritten as

$${\dot{q}}_i=g\left[\begin{array}{ccc}cos{\gamma }_{i}cos{\psi }_i\hfill & -sin{\psi }_i& -sin{\gamma }_{i}cos{\psi }_i\\ cos{\gamma }_{i}sin{\psi }_i\hfill & cos{\psi }_i& -sin{\gamma }_{i}sin{\psi }_i\\ sin{\gamma }_i\hfill & 0& cos{\gamma }_i\end{array}\right]\left[\begin{array}{c}{n}_{ti}\\ n_{hi}\\ n_{vi}\end{array}\right]-G,$$

(5)

where $G={[0,0,g]}^T$. Then, the simplified point-mass model of UAV i can be rewritten by

$$\begin{array}{c}\stackrel{.}{p_i}\left(t\right)=q_i\left(t\right)\hfill \\ \stackrel{.}{q_i}\left(t\right)=g{H}_i^T\left(t\right)u_i\left(t\right)-G,i=1,\cdots ,N\hfill \end{array}$$

(6)

where $H_i\left(t\right)={[t_i\left(t\right),n_i\left(t\right),h_i\left(t\right)]}^T$. The definitions of $t_i\left(t\right)$, $n_i\left(t\right)$, and $h_i\left(t\right)$ are, respectively,

$$t_i\left(t\right)=\left[\begin{array}{c}cos{\gamma }_i\left(t\right)cos{\psi }_i\left(t\right)\\ cos{\gamma }_i\left(t\right)sin{\psi }_i\left(t\right)\\ sin{\gamma }_i\left(t\right)\end{array}\right],$$

(7)

$$n_i\left(t\right)=\left[\begin{array}{c}-sin{\psi }_i\left(t\right)\\ cos{\psi }_i\left(t\right)\\ 0\end{array}\right],$$

(8)

and

$$h_i\left(t\right)=\left[\begin{array}{c}-sin{\gamma }_i\left(t\right)cos{\psi }_i\left(t\right)\\ -sin{\gamma }_i\left(t\right)sin{\psi }_i\left(t\right)\\ cos{\gamma }_i\left(t\right)\end{array}\right].$$

(9)

Obviously, $H_i\left(t\right)$ is an orthogonal matrix. $t_i\left(t\right)$, $n_i\left(t\right)$, and $h_i\left(t\right)$ are orthogonal unit vectors.

2.2. Interaction Mechanism

As mentioned above, the UAV system involved in this paper is supposed to be an egalitarian system. For egalitarian systems, the interaction between any two individuals is undirectional. Thus, the metric interaction network $\xi \left(t\right)$ of the UAV system is definitely a dynamic undirected graph consisting of a vertex set $\nu =\{1,\cdots ,N\}$ and a time-varying edge set $\epsilon \left(t\right)=\left\{(i,j)\right|(i,j)\in \nu \times \nu ,j\in N_i\left(t\right)\}$. Therein, each vertex denotes a UAV, while each edge denotes the pairwise–interaction relationship of two UAVs. $N_i\left(t\right)$ is defined as the neighbor set of UAV i at time t, $i=1,\cdots ,N$. The initial value of $N_i\left(t\right)$ is described by the following formula,

$$N_i\left(0\right)=\left\{j\right|\parallel p_{ij}\left(0\right)\parallel <D,j=1,\cdots ,N,j\ne i\},$$

(10)

where $p_{ij}\left(t\right)=p_i\left(t\right)-p_j\left(t\right)$, $\parallel •\parallel$ denotes the Euclidean norm. That is to say, each UAV is assumed to interact with its neighbor UAVs.

The interaction network $\xi \left(t\right)$ is supposed to switch at $t_p$, $p=1,2,\cdots$. Thus, $\xi \left(t\right)$ is fixed in each time-interval $[t_r,t_{r+1})$, where $r=0,1,\cdots$. $\xi \left(0\right)$ is assumed to be connected. During the whole evolution process, the switch condition satisfying the following hysteresis [29],

(1)

When $(i,j)\notin \epsilon \left(t^{-}\right)$, if $\parallel p_{ij}\left(t\right)\parallel <D-\zeta$, $\zeta \in (0,D)$, then $(i,j)\in \epsilon \left(t\right)$, for $t>0$;

(2)

When $(i,j)\in \epsilon \left(t^{-}\right)$, if $\parallel p_{ij}\left(t\right)\parallel <D$, then $(i,j)\in \epsilon \left(t\right)$, for $t>0$.

2.3. Control Protocol and Stability Analysis

In 1987, Reynolds developed a computer model mimicking animal aggregation and social cohesion in animal groups [30]. This model consists of three steering behaviors—collision avoidance, velocity alignment, and flocking cohesion, which describe how an individual agent maneuvers based on the relative positions and relative velocities of its nearby flock mates. Following this work, several variants on flocking model has been proposed [11,14,18,31,32], and led to derive decentralized controllers consisting of consensus algorithm and artificial potential field which provably give rise to these collective phenomena. According to the specific UAV model (1), the control protocol of each UAV i, $i=1,\cdots ,N$ is proposed as

$$\begin{array}{c}\begin{array}{c}{n}_{ti}\left(t\right)=-\frac{1}{g}{t}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}(q_i\left(t\right)-q_j\left(t\right))+\frac{1}{g}{t}_i^T\left(t\right)G-\frac{1}{g}{t}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}{\nabla }_{p_{ij}\left(t\right)}V(\parallel p_{ij}\left(t\right)\parallel )\hfill \end{array}\hfill \\ \begin{array}{c}{n}_{hi}\left(t\right)=-\frac{1}{g}{n}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}(q_i\left(t\right)-q_j\left(t\right))+\frac{1}{g}{n}_i^T\left(t\right)G-\frac{1}{g}{n}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}{\nabla }_{p_{ij}\left(t\right)}V(\parallel p_{ij}\left(t\right)\parallel )\hfill \end{array}\hfill \\ \begin{array}{c}{n}_{vi}\left(t\right)=-\frac{1}{g}{h}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}(q_i\left(t\right)-q_j\left(t\right))+\frac{1}{g}{h}_i^T\left(t\right)G-\frac{1}{g}{h}_i^T\left(t\right){\displaystyle \sum _{j\in N_i\left(t\right)}}{\nabla }_{p_{ij}\left(t\right)}V(\parallel p_{ij}\left(t\right)\parallel ).\hfill \end{array}\hfill \end{array}$$

(11)

There are three equations in control protocol (11). The first part of each equation is the consensus term, which aims at forcing all the UAVs fly with consistent velocities. The second part of each equation is the gravity term. The third part is the negative gradient of the potential function $V(\parallel p_{ij}\left(t\right)\parallel )$, which is used to adjust the relative positions between any two UAVs. The potential function can be divided into a repulsive item and an attractive item, whose definition is given as follows,

Definition 1. 

(Potential function):Potential $V(\parallel p_{ij}\left(t\right)\parallel )$ is a differentiable, non-negative, radially unbounded function of the distance $\parallel p_{ij}\left(t\right)\parallel$ between agents i and j, such that

(1) 

$V(\parallel p_{ij}\left(t\right)\parallel )\to \infty$ as $\parallel p_{ij}\left(t\right)\parallel \to 0$;

(2) 

$V(\parallel p_{ij}\left(t\right)\parallel )\to \infty$ as $\parallel p_{ij}\left(t\right)\parallel \to D$;

(3) 

$V(\parallel p_{ij}\left(t\right)\parallel )$attains its unique minimum when agents i and j are located at a desired distance between 0 and D.

Rule (1) of Definition 1 is related to the repulsive item, which forces the UAVs to avoid collision with each other. Rule (2) of Definition 1 is related to the attractive item, which mainly affects the flocking cohesion behavior of these UAVs. Rule (3) of Definition 1 decides the equilibrium distance among individuals. Then, the following theorem can be obtained.

Theorem 1. 

(Three-dimensional Cohesive Flocking):There exists a system consisting of N UAVs governed by (1). The behavior of each UAV is decided by the protocol (11). The interaction network of the proposed UAV system is assumed to be undirected and connected at the initial time. Then, the following conclusions hold.

1. 

Each UAV avoids collision with each other.

2. 

The metric interaction network is always connected.

3. 

The system asymptotically converge to a consistent configuration that each UAV owns the same speed, the same heading angle, and the same flight-path angle.

4. 

The system approaches a cohesive configuration that its total potential is minimized.

In short, we may ignore the time variable in the following proof process for these time-variant variables. For example, we may use $N_i$ instead of $N_i\left(t\right)$.

Proof of Theorem 1. 

From $u_i={[n_{ti},n_{hi},n_{vi}]}^T$ and $H_i={[t_i,n_i,h_i]}^T$, control protocol (11) can be rewritten as

$$\begin{array}{c}{u}_i=-\frac{1}{g}{H}_i{\displaystyle \sum _{j\in N_i}}(q_i-q_j)+\frac{1}{g}{H}_{i}G-\frac{1}{g}{H}_i^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )\hfill \end{array}$$

(12)

As $H_i$ is an orthogonal matrix, $H_i^T{H}_i=I$. From (6) and (12), one gets

$$\stackrel{.}{q_i}=-\sum _{j\in N_i}(q_i-q_j)-\sum _{j\in N_i}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel ),i=1,\cdots ,N$$

(13)

Let $p={[p_1^T,\cdots ,p_N^T]}^T$ and $q={[{q_1}^T,\cdots ,{q_N}^T]}^T$. According to (6) and (13), one gets

$$\begin{array}{c}\begin{array}{c}\dot{q}=-(L_N\otimes I_3)q-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )\hfill \end{array}\hfill \end{array}$$

(14)

where $I_3$ denotes the $3\times 3$ identity matrix, and $L_N\left(t\right)={\left[l_{ij}\right]}_{N\times N}$ is defined as $\xi \left(t\right)$’s Laplacian matrix.

Let $\psi ={[{\psi }_1^T,\cdots ,{\psi }_N^T]}^T$ and $\gamma ={[{{\gamma }_1}^T,\cdots ,{{\gamma }_N}^T]}^T$. Consider the following energy function as the common Lyapunov function

$$E(p,q)=\frac{1}{2}V+\frac{1}{2}{q}^{T}q.$$

(15)

Then the derivative of $E(p,q,\psi ,\gamma )$ w.r.t time $t\in [t_r,t_{r+1})$ is

$$\begin{array}{c}\frac{dE}{dt}=\frac{1}{2}{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{{\dot{p}}_{ij}}^T{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )+q^T\dot{q}\hfill \\ \begin{array}{c}={\displaystyle \sum _{i=1}^N}{\dot{p_i}}^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )+q^T(-(L_N\otimes I_3)q-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel ))\hfill \\ ={\displaystyle \sum _{i=1}^N}{q}_i^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )-q^T(L_N\otimes I_3)q-{\displaystyle \sum _{i=1}^N}{q}_i^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )\hfill \end{array}\hfill \\ =-q^T(L_N\otimes I_3)q.\hfill \end{array}$$

(16)

Undirected graph $\xi \left(t\right)$’s Laplacian matrix $L_N$ is symmetric and positive semi-definite, thus we have

$$dE/dt\le 0.$$

(17)

The potential energy of the system at initial time is finite, and the velocities and attitudes of all UAVs at initial time are also finite. Thus, $E\left(p\right(0),q(0\left)\right)$ (the energy of the system at initial time) is finite. Since $\frac{dE}{dt}\le 0$ on each time-interval $[t_r,t_{r+1})$, $r=0,1,\cdots$, the supremum of $E\left(t\right)$ is obviously its initial value $E\left(p\right(0),q(0\left)\right)$, for all t. Furthermore, both $V\left(t\right)={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}V(\parallel p_{ij}\parallel )$ and $V(\parallel p_{ij}\parallel )$ are bounded.

Definition 1’s rule (1) indicates that if $\parallel p_{ij}\parallel \to 0$, then we have $V(\parallel p_{ij}\parallel )\to \infty$, which violates the above conclusion ($V(\parallel p_{ij}\parallel )$ is bounded). Thus, one gets $\parallel p_{ij}\parallel >0$, that is, no collision happens between any two UAVs.

According to rule (2) of definition 1, if $\parallel p_{ij}\parallel \to D((i,j)\in \epsilon )$, then one gets $V(\parallel p_{ij}\parallel )\to \infty$, which is also not consistent with the above conclusion (that is, $V(\parallel p_{ij}\parallel )$ is bounded). Therefore, we have $\parallel p_{ij}\parallel <D$. A new edge $(i,j)\notin \epsilon$ is supposed to be added to $\epsilon$, then the associated potential $V(\parallel p_{ij}\parallel )$ remains finite because $\parallel p_{ij}\left(t\right)\parallel <D-\zeta$. Therefore, the new potential V is finite too. That is to say, the connectivity of the communication network is preserved.

Assume that there are $m_r\in \mathbb{N}$ new edges being added to the interaction network at switching time $t_r$, $r=1,2,\cdots$. The UAV system’s interaction topology at initial time is supposed to be connected. ${\xi }_1$ denotes the interaction topology of the system at the initial time, and ${\xi }_c$ denotes the set of undirected and connected graphs on the vertices. The sequence of switching topologies ${\xi }_{r+1}$ within $[t_r,t_{r+1})$ consists of such graphs that satisfy ${\xi }_{r+1}\in {\xi }_c$. ${\xi }_c$ is a finite set, since the number of vertices is finite. At most $M\in \mathbb{N}$ new edges are assumed can be added to the initial interaction topology ${\xi }_1$. It is clear that $0<m_r\le M$ and $r\le M$, that is, the number of switching time is finite. Consequently, $\xi \left(t\right)$ becomes fixed finally. Then, we are going to discuss in further restricted to the time interval $[t_f,\infty )$, where $t_f$ is the last switching time.

As the distance between neighbors is not longer than D, set $B=\{p,q|E(p,q)\le E\left(p\right(0),q(0\left)\right\}$ is positively invariant. One gets $\parallel p_{ij}\parallel <(N-1)D$ for all i and j, due to $G\left(t\right)$ is connected for all $t\ge 0$. According to $E(p,q)\le E\left(p\right(0),q(0\left)\right)$, we obtain that $q^{T}q\le 2E(p\left(0\right),q\left(0\right))$, that is, $\parallel q\parallel \le \sqrt{2E\left(p\right(0),q(0\left)\right)}$. Therefore, the set B is compact (bounded and closed). On the connected time interval $[t_f,\infty )$, the system (1) with control input (11) is an autonomous system. Therefore, the trajectories of the UAVs will converge to the invariant set $S=\{p,q|\frac{dE}{dt}=0\}$. Besides, $\frac{dE}{dt}=0$ if and only if $q_i=q_j$ for all $i\in \mathbb{N}$ and $j\in N_i$.

According to (2), $q_i=q_j$ is equivalent to

$$\left\{\begin{array}{c}{\vartheta }_{i}cos{\gamma }_{i}cos{\psi }_i={\vartheta }_{j}cos{\gamma }_{j}cos{\psi }_j\\ {\vartheta }_{i}cos{\gamma }_{i}sin{\psi }_i={\vartheta }_{j}cos{\gamma }_{j}sin{\psi }_j\\ {\vartheta }_{i}sin{\gamma }_i={\vartheta }_{j}sin{\gamma }_j.\end{array}\right.$$

(18)

that is, ${\vartheta }_i={\vartheta }_j$, ${\psi }_i={\psi }_j$, and ${\gamma }_i={\gamma }_j$.

With $p_{ij}=-p_{ji}$, one gets ${\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )=0$. From the control input (11) and $q_i=q_j$, one has

$$\begin{array}{c}\dot{\overline{q}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\dot{q}}_i\hfill \\ \begin{array}{c}=\frac{1}{N}(-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}(q_i-q_j)-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel ))\hfill \\ =\frac{1}{N}(-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel ))\hfill \end{array}\hfill \\ =0.\hfill \end{array}$$

(19)

Due to $q_1=\cdots =q_N=\overline{q}$, we have ${\dot{q}}_i=\dot{\overline{q}}=0$, that is, $g{H}_i^T{u}_i+G=0$, $i=1,\cdots ,N$. Thus, we obtain that $-{\displaystyle \sum _{j\in N_i}}(q_i-q_j)-{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )=0$ for $i=1,\cdots ,N$. With $q_i=q_j$, one gets ${\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )=0$. The minimum value of V is obtained by

$$\begin{array}{c}\frac{dV}{dt}={\displaystyle \sum _{i=1}^N}{\dot{p_{ij}}}^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )\hfill \\ =2{\displaystyle \sum _{i=1}^N}{\dot{p_i}}^T{\displaystyle \sum _{j\in N_i}}{\nabla }_{p_{ij}}V(\parallel p_{ij}\parallel )\hfill \\ =0.\hfill \end{array}$$

(20)

So far, the four conclusions of Theorem 1 are all proved. □

3. Results

Take 80 UAVs as an example, numerical simulations are carried out in MATLAB to verify the four conclusions of Theorem 1. Furthermore, flocking scenarios of these 80 UAVs under different interaction requirements are quantitatively analyzed and compared statistically from the point of energy and time savings. After that, the collective effects under different group sizes, that is, the scalability effects, are discussed in further.

3.1. Initial Conditions

N UAVs are supposed to fly under free boundary conditions. Each UAV is steered by (1). The initial position of each UAV is randomly generated in a cubic area with size L, and its initial speed is randomly generated from the interval $(0,0.5)$. Besides, its initial heading angle and flight-path angle are randomly generated from the interval $(-\frac{\pi }{2},\frac{\pi }{2})$.

To keep the continuity and comparability of simulation results under different group sizes, these UAV systems’ initial density $\rho =\frac{N}{L^3}$ should be a constant. That is to say, the scale of group size N directly proportional to the cube of the area size L. In the following simulations, the initial density $\rho =0.1$, and each experiment’s simulation time $T=100$ s.

The specific potential function in the control protocol (11) is given as [14]

$$V(\parallel p_{ij}\left(t\right)\parallel )=\frac{b}{\parallel p_{ij}{\left(t\right)\parallel }^2}-aln(D^2-\parallel p_{ij}\left(t\right){\parallel }^2)$$

(21)

where the first part is the repulsive potential item and the second part is the attractive potential item. Here, a is an attractive coefficient, and b is a repulsive coefficient. There exists a unique distance $\parallel d^{*}\parallel =\sqrt{\frac{\sqrt{b^2+4ab{D}^2}-b}{2a}}$, at which the attraction and repulsion balance. Without loss of generality, the parameters are chosen as $a=1$, $b=1$, and thus $\parallel d^{*}\parallel =\sqrt{\frac{\sqrt{1+4D^2}-1}{2}}\doteq \sqrt{D}$.

One of the most important initial conditions is that the initial communication network must be connected. To satisfy this condition, three steps should be carried out. First, the initial positions of these UAVs are generated randomly. Second, the connectivity of the communication network based on the above initial positions is checked. If the network is connected, then these UAVs implement the simulations under control protocol (11); otherwise, a new set of initial positions is randomly generated for these UAVs. Third, the above process is repeated until a connected initial communication network is found out.

3.2. Simulation Example

In order to validate the effectiveness of these conclusions of Theorem 1, $N=80$ UAVs are taken as an example to execute the cohesive flocking task. Each UAV governed by (1) adjusts its behavior under the control protocol (11). The communication radius D is 4 m.

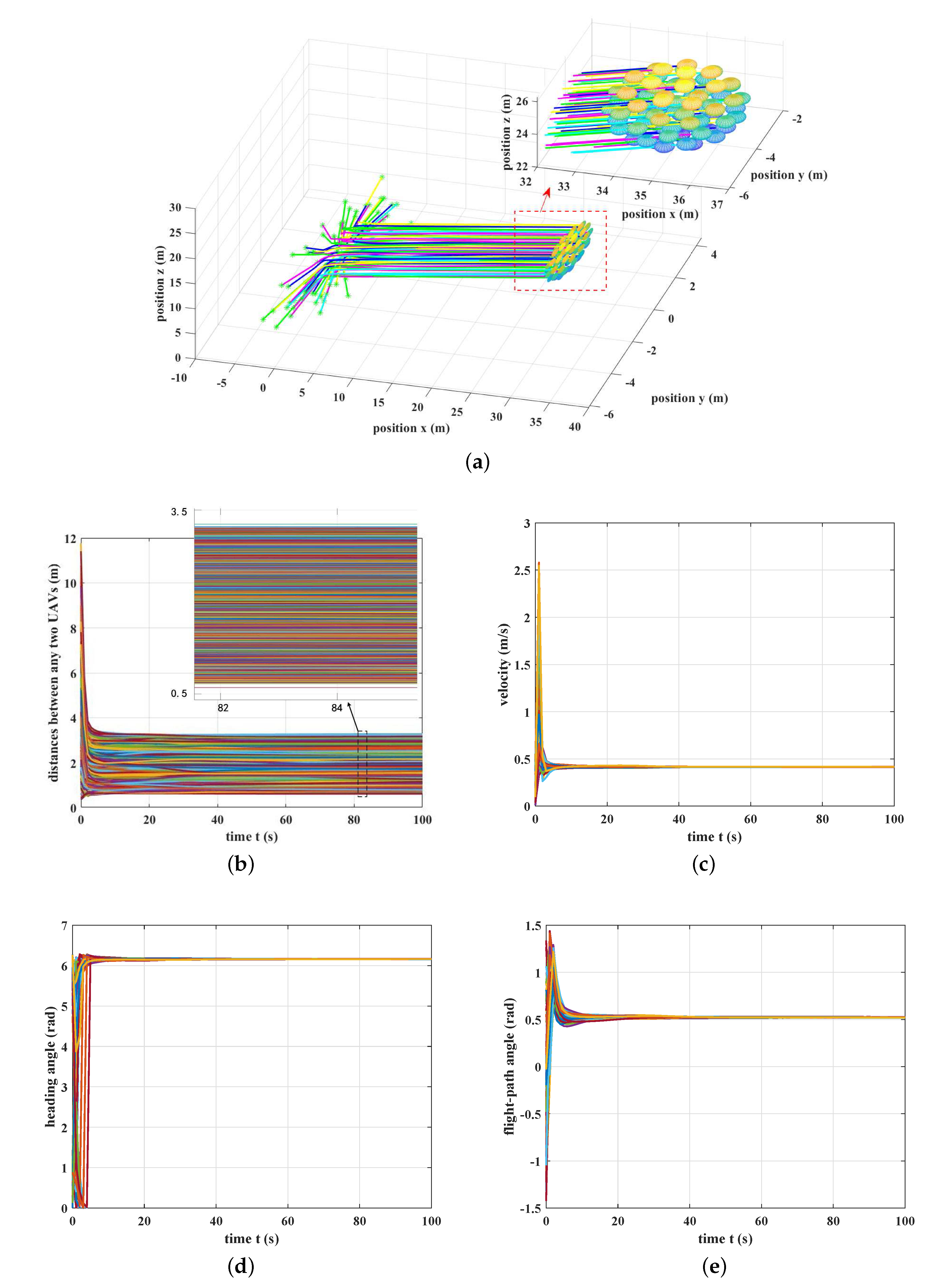
Figure 2 gives the readers a detailed intuition into the results of the proposed simulation. As shown in Figure 2a, 80 UAVs start flying from these green star points, and their final positions due to the simulation time $T=100$ s is expressed by these colorful balls. Each curve denotes the trajectory of one UAV. The curves with different colors denote the trajectories of different UAVs. Figure 2a has given a clear exhibition that 80 UAVs asymptotically converge to flying in a flock. Eighty UAVs are considered in this case, thus there are $\frac{N(N-1)}{2}=\frac{80\times 79}{2}=3160$ curves in Figure 2b. Each curve denotes the distance between two UAVs. According to the simulation result shown in Figure 2b, the distances between any two UAVs finally become stable. During the evolutionary process, the distances between any two UAVs are all larger than 0, that is to say, there is no collision between any two UAVs. More importantly, the interference among UAVs can be reduced in terms of adjusting the repulsive term, such as increasing the value of repulsive coefficient b. Figure 2c–e, respectively, gives the velocities, the heading angles, and the flight-path angles of 80 UAVs versus time.

The above simulation results have definitely proved that these UAVs will form a cohesive and consistent configuration without collisions between any two UAVs.

4. Discussion

According to the above analysis, we already know that the UAV system will converge to a flock finally, on condition that the initial interaction network is connected. Then, a more important question is coming, that is, how to accelerate the emergency of a flock. In the following paragraphs, the energy and time costs, as well as scalability effects of emerging a flock are evaluated from the point of statistical significance and strength quantitatively.

To guarantee that all of the UAVs will converge to cohesive flocking finally, one condition must be satisfied, that is, the initial interaction topology of the UAVs should be connected. As the nearest-neighbor interaction rules have been adopted and every UAV has the same communication radius, the common communication radius becomes the only factor that can change the network connectivity. The value of the communication radius decides the scale of the interaction network and also the neighbor number of each UAV.

The initial state of the UAV system is supposed to be given. Let $D_{min}$ denote the minimal value of the communication radius that forces the interaction network to be connected. For these connected communication radii $D\in [D_{min},\infty )$, a smaller value means fewer neighbors for each UAV. This situation further causes the decrease of computational complexity and calculated quantity of the whole system, as well as the reduction of energy consumption.

The distance between any two UAVs is one of the proper variables to draw the convergence speed of UAV flocking and also reflects the stability of the UAV system. If the distance between any two UAVs becomes stable, then the system becomes stable. Therefore, energy measurements can be evaluated simply by the following order parameter

$$EE\left(t\right)=\frac{{\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N{d}_{ij}\left(t\right)}{N(N-1)/2}.$$

(22)

where $d_{ij}\left(t\right)=\Vert p_i\left(t\right)-p_j\left(t\right)\Vert$, $i,j\in \nu$.

To assess the energy and time costs of a flock, numerical simulations of 80 UAVs are carried out under a series of connected communication radii. There are mainly three steps: First, the initial states of 80 UAVs are produced randomly. Second, connected communication radius’ sample values are linearly selected from the interval $[2.8,8]$. Finally, starting from the same initial states of 80 UAVs, the experiment is carried out under each sample communication radius. 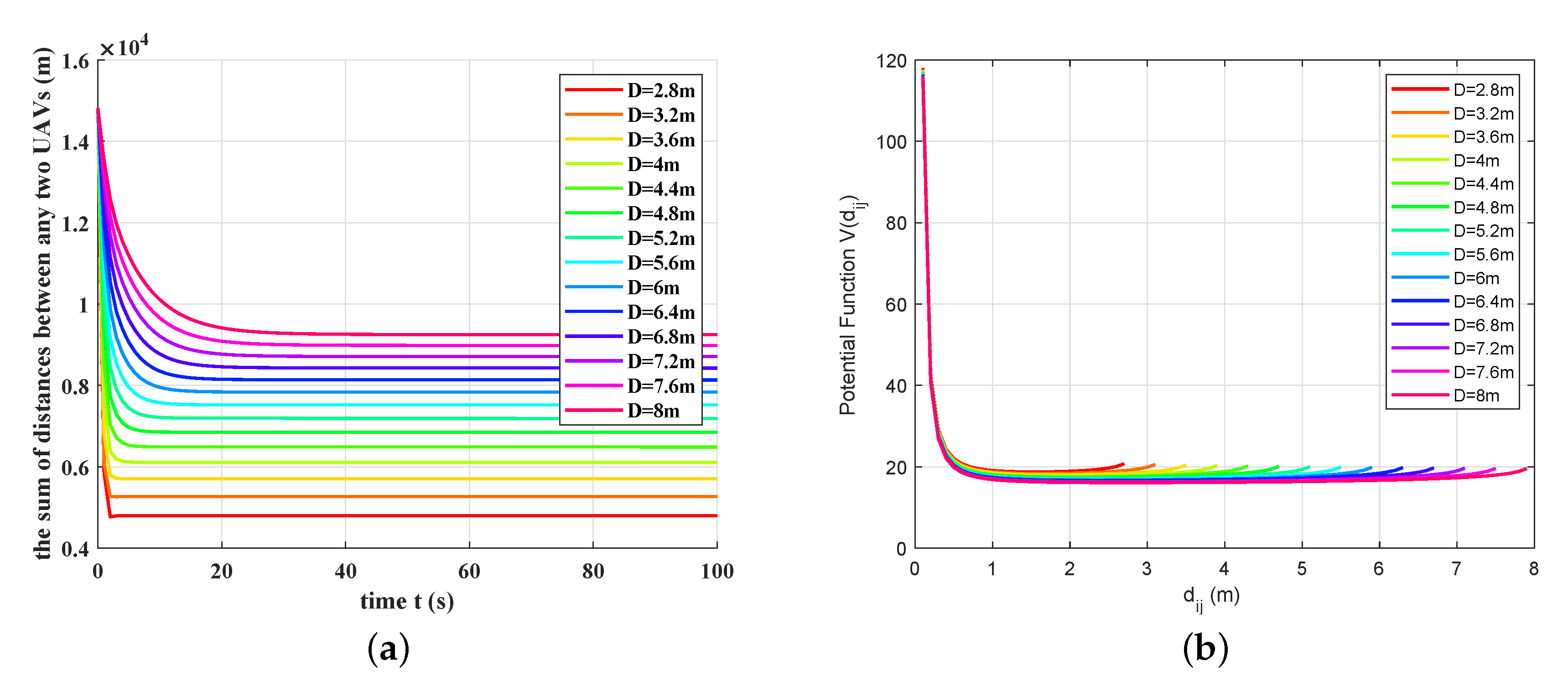Figure 3b shows the specific potential functions under these sample communication radii, and the simulation results are shown in Figure 3a. Different colors describe the simulation results under different sample communication radii. It is clear to see that the system converges to a flock faster under a smaller communication radius, although in which a longer journey (equaling to the initial individual distance minus the stable individual distance) should be covered to reach the stable individual distance $d^{*}=\sqrt{D}$.

Moreover, the above conclusion is obtained according to a fixed initial state and fixed group size. In order to make the conclusion more rigorous and more precise, each experiment is repeated over 100 trials that start with different initial states. Convergence time $t^c$ is adopted as the order parameter to evaluate the time cost of each experiment. The definition of convergence time $t^c$ is the minimal value of $t_k$, which satisfies the following constraint condition,

$$\frac{EE\left(t_k\right)-EE\left(T\right)}{EE\left(T\right)}\le K,$$

(23)

where $K=0.01$. The standard error bar is defined as

$$\sigma =\frac{1}{\sqrt{n}}{t}_c$$

(24)

where $n=100$ is the experiment number.

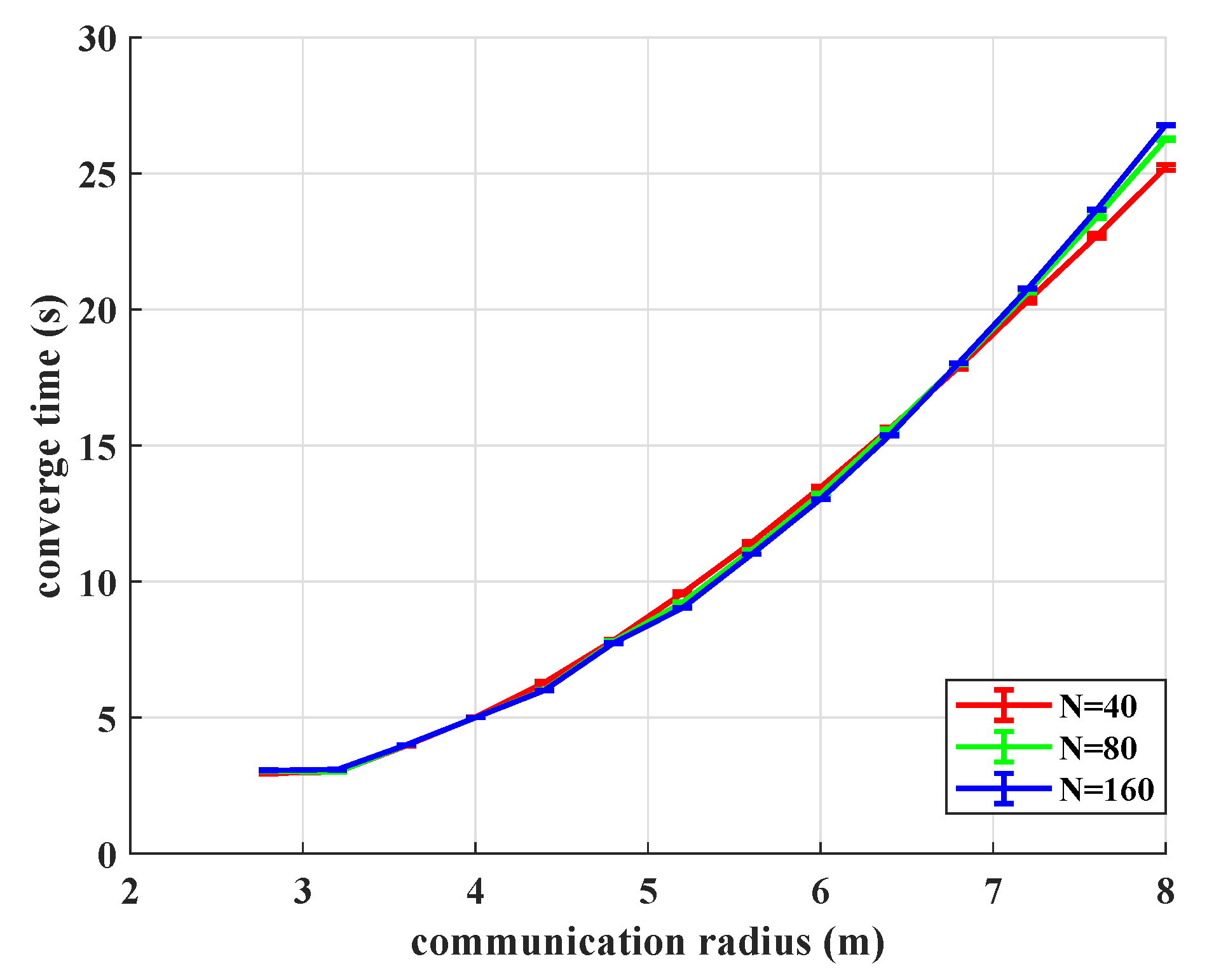
The relationships between convergence time and sample communication radius under different group sizes are shown in Figure 4. In all of these figures, the system converges to a flock within simulation time. For each given group size, the convergence time increases with the enlargement of communication radius most of the time when $D\ge D_{min}$. That is to say, under the premise that the initial communication network is undirected and connected, the minimal communication radius causes the largest convergent speed. The minimal communication radius means the minimal edge set of the connected interaction network of the UAV system, at the same time, requires minimal computation capability for each UAV during the whole evolutionary process. This conclusion can be easily used to extend the distributed control algorithm from small groups to large-scale groups of UAVs and to skillfully avoid the awkwardness of exponential growth caused by the increase in group size.

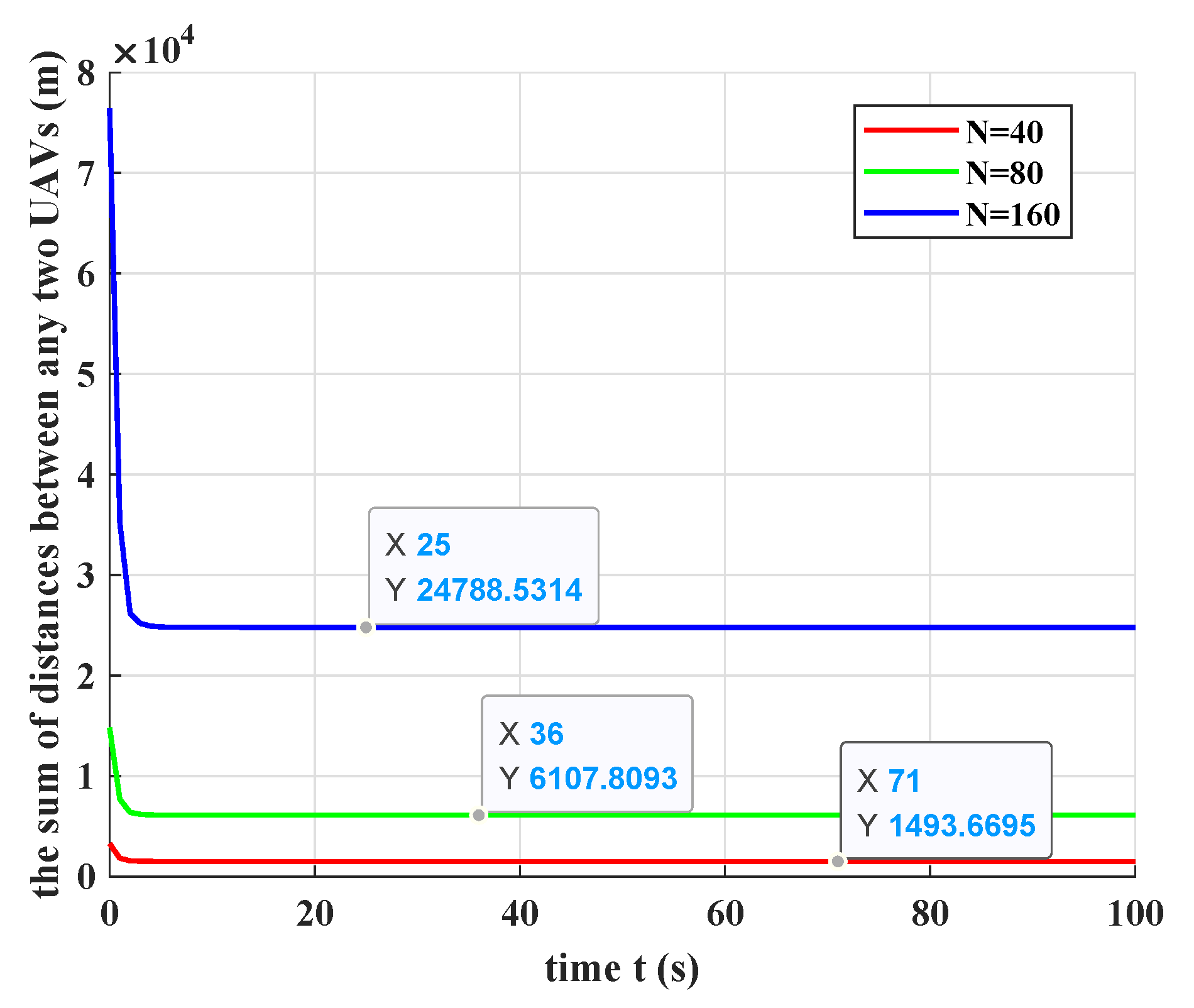
Scalability performance is examined by increasing the robot group size. In this case, communication radius D is fixed to 4 m. The energy cost $EE\left(t\right)$ is drawn versus time when the number of UAVs is double increased from 40 to 160. Figure 5 shows the good scalability performance of the flocking system (1) under control protocol (11), as the converge time almost the same following with the increase of group size. I have labeled the coordination value of three points on the three curves. There are $N(N-1)/2$ edges between any two UAVs for a system consisting of N UAVs. When $N=40$, then we have $N(N-1)/2=780$ edges, and the average distance between any two UAVs is $1493.6695/780=1.915\approx 2$. Similarly, when $N=80$, then we have $N(N-1)/2=3160$ edges, and the average distance between any two UAVs is $6107.8093/3160=1.93\approx 2$; when $N=160$, then we have $N(N-1)/2=12,720$ edges, and the average distance between any two UAVs is $24,788.5314/12,720=1.95\approx 2$. They all equal to the sqrt of communication radius D. Thus, Figure 5 have proved the conclusion that the stable individual distance $d^{*}=\sqrt{D}$. Furthermore, Figure 5 reinforces this conclusion that the converge times for different group sizes are almost the same when the value of the connected communication radius is small enough.

5. Conclusions

In conclusion, we have introduced a systematically and logically rigorous research methodology for studying these interdisciplinary topics, such as aerial swarms. In this paper, we mainly focus on combing the control theories and statistical analysis of simulation results to solve the optimization of the emergence of order in a flock. The UAV system is supposed to be an egalitarian system that obeys the nearest-neighbor interaction rules. Therein, each UAV is depicted by a simplified mathematical model with nonlinear constraints. Theoretical analysis of the UAV flocking steered by a distributed control algorithm is provided, as long as the initial communication network is connected. Communication radius is considered as the only scale to draw the interaction topology, a statistical method is therefore proposed to scrutinize the relationship between communication radius of each UAV and convergence speed of these UAVs based on the above theoretical framework. Convergence time serves as a criterion to evaluate the convergence effect in the flock. Statistical analysis of abundant simulation results is provided to optimize the emergence of collective behavior by evaluating energy/time measurements and scalability effects. Results show that smaller communication radius causes faster convergence of the aerial group. To some extent, this conclusion echoes from the biological evidence that each starling interacts with six or seven neighbors most often at the same time. More importantly, this conclusion offers empirical evidence on the transition from scale-dependent interaction to topology-dependent interaction.