Multi-Objective Electric Vehicles Scheduling Using Elitist Non-Dominated Sorting Genetic Algorithm

Featured Application

The proposed methodology can be used in the electric vehicles charging/discharging scheduling considering different multi-objective functions.

Abstract

The introduction of electric vehicles (EVs) will have an important impact on global power systems, in particular on distribution networks. Several approaches can be used to schedule the charge and discharge of EVs in coordination with the other distributed energy resources connected on the network operated by the distribution system operator (DSO). The aggregators, as virtual power plants (VPPs), can help the system operator in the management of these distributed resources taking into account the network characteristics. In the present work, an innovative hybrid methodology using deterministic and the elitist nondominated sorting genetic algorithm (NSGA-II) for the EV scheduling problem is proposed. The main goal is to test this method with two conflicting functions (cost and greenhouse gas (GHG) emissions minimization) and performing a comparison with a deterministic approach. The proposed method shows clear advantages in relation to the deterministic method, namely concerning the execution time (takes only 2% of the time) without impacting substantially the obtained results in both objectives (less than 5%).

1. Introduction

In recent years, policymakers have given significant importance to decrease the carbon footprint, mainly in the power system and road transport sectors [1]. Hence, large investments have been made in different types of distributed energy resources (DERs). This was the case of distributed generation based on natural sources, such as wind and solar. More recently, some countries are creating mechanisms to encourage the use of electric vehicles (EVs). The increased use of EVs can bring benefits to the power systems mainly when the bidirectional vehicle-to-grid (V2G) technology [2] is considered. In this case, EVs can increase the available storage level in the power system, thereby allowing better management of the system and creating some benefits to the EVs owners [3]. Note, however, that EVs may also create new challenges, particularly in distribution grids such as congestion problems or voltage stability [4].

Within this context, smart grids rapidly evolved from a visionary concept to be widely accepted by the involved players in power systems (i.e., academic and utilities). This concept ensures proper decentralized management of power systems to overcome the adverse effects of large-scale integration of DERs, e.g., the volatility of renewables and congestion problems [5]. Additionally, the concept of a DER aggregator entity, such as virtual power plants (VPPs) or fleet operators, has been put forward to ease the integration between the DERs and other entities operating in power systems, such as distribution system operators (DSOs) or transmission system operators (TSOs).

The literature has studied several ways to improve EVs integration in the power system by resorting to intelligent EV scheduling. In general, the studies have focused on the intelligent EVs coordination to mitigate their potential problems, e.g., power transformer congestions or voltage violations. The recommendation is to incorporate other objectives in the EV scheduling problem, instead of simply considering the economic perspective (i.e., minimizing cost or maximizing profit). We can consider the reduction of greenhouse gas (GHG) emissions as a relevant goal for EVs scheduling. Since these goals can conflict with each other, this leads to a multi-objective optimization approach. For example, the generation cost of a coal power plant can be lower than other technologies, but the CO₂ emissions costs are very significant. In this case, the goal is to obtain the Pareto front that contains all nondominated solutions [6], then EV aggregators can select the solution that best suits their interests using different techniques such as the fuzzy-based method proposed in the present paper. We can use a linear combination of objective functions with weight factors to determine the Pareto front as a single objective function. This is the most known classic method for handling multi-objective problems [4].

The elitist nondominated sorting genetic algorithm, also called NSGA-II [7], is used in this paper, as the literature points it out to be one of the best techniques for dealing with multi-objective problems [8]. Thus, this technique suits the multi-objective problems of this study because they are complex and demanding in terms of computational performance. However, a hybrid approach, which combines the NSGA-II with a deterministic technique, is better suited to obtain good results in an acceptable time. The main goal of the approach proposed in the present paper is to improve computational performance while not significantly degrading the energy resources scheduling solution.

The term deterministic technique is used to designate the group of analytical techniques, also called classical techniques, used in the field of operational research [9]. In this paper, the deterministic technique is used to generate an initial solution to each individual of the initial population. As proved in [10], the results of metaheuristics for single-objective functions are largely improved by using a good starting point that is determined by the deterministic approach. This hybrid approach helps the search for new solutions near to the optimal region, reducing the computational effort and solving some drawbacks related to evolutionary algorithms [11]. As an example, if the deterministic approach points to a solution where an electric vehicle is charging at maximum power, P_{EV_max}, the search interval in NSGA-II is reduced to an interval around this value, instead of the normal interval (−P_{EV_max} to P_{EV_max}). In [10], several tools were tested to determine a good initial solution to be used as a starting point in simulated annealing (SA) heuristic. SA is a local optimization model that considers only one objective function. In this paper is proposed the use of a relaxed deterministic approach, like the one used in [10], but considering a multi-objective function. Moreover, this initial solution is combined with NSGA-II heuristic allowing the definition of nondominated solutions in the Pareto-front curve.

The main contributions of this paper can be stated as (i) proposing an innovative hybrid NSGA-II combining the traditional NSGA-II with a deterministic technique, (ii) use the hybrid NSGA-II algorithm to handle multi-objective problems related to the EV’s integration not compromising the final solution and improving the execution-time, (iii) defining multi-objective functions that address both costs and environmental aspects, and considering the Alternate Current Optimal Power Flow (AC-OPF) in the formulation and (iv) compare the NSGA-II with a deterministic method for the same multi-objective problem.

This paper is structured as follows: Section 2 describes the proposed methodology and the adopted mathematical formulation to solve the multi-objective problem; Section 3 validates the proposed model based on a 37-bus distribution network considering realistic data and, finally, Section 4 presents the most important conclusions.

2. Optimization Problem and Methodology

The present section describes the methodologies used to achieve the goals defined in the introduction section. To facilitate the comprehension of the proposed methodology, this section is split into four subsections, namely, the description of the objective functions, the description of the considered constraints, the proposed hybrid NSGA-II algorithm and, finally, the fuzzy-based method used to determine the best compromise solutions.

2.1. Objective Functions

The considered objective functions intend to optimize the use of DER, in concerning cost optimization and GHG emissions minimization and, therefore, the overall distribution system operation. The most traditional objective function intends to reduce the operation costs considering the costs associated with the use of all types of DER, for instance, distributed generation (DG), the energy provided by external suppliers (ES), the costs associated with the charge and discharge of electric vehicles (EV) and electric storage systems (ESS). The costs associated with the activation of demand response programs were also considered for each generic load connected to the network. When the load does not have demand response (DR) contracts, the activation is limited to zero. Additionally, a penalization cost related to the service not supplied (SNS) is included. This service means that the aggregator is unable to provide services for grid users such as supply energy to the consumers and battery charging, as well as absorbing the energy injected by generators and battery discharge. These costs are depicted in Equation (1).

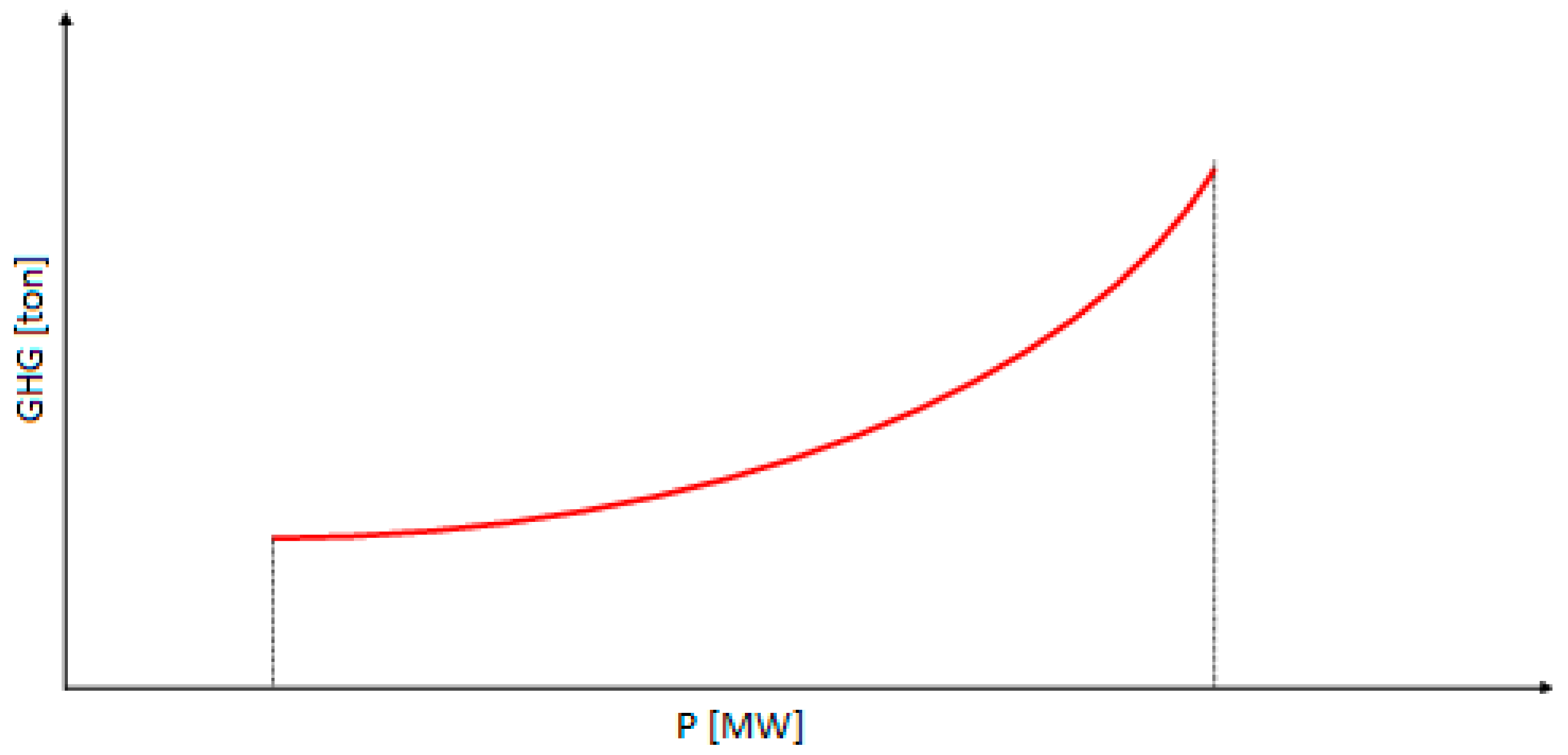
In addition to this objective function traditional approach, we considered a quadratic function to determine the GHG emission cost [12] (Equation (2)). It is important to mention that in the present study only the GHGs produced during the use of the resources are considered. The GHG emissions function is directly related to the fuel consumption by the generators. Therefore, we can build a graphic relating the GHC emissions and the output power of the plant, as shown in Figure 1.

The building and decommissioning emissions are not considered since these emissions are not dependent on the use and, consequently, should not be considered on the optimal resource scheduling (ORS) problem. Taking this approach in mind, only the emissions generated by the DG aggregated to a VPP and the emissions of the external suppliers are considered. The GHG emissions of EVs and storage systems are not considered in Equation (2), neither the DG based on natural resources, such as wind and sun.

$$F_{Cost}={\displaystyle \sum _{t=1}^T\left(\begin{array}{l}{\displaystyle \sum _{DG=1}^{N_{DG}}f\left(c_{\left(DG,t\right)}\times P_{\left(DG,t\right)}\right)}+{\displaystyle \sum _{EV=1}^{N_{EV}}f\left(c_{\left(EV,t\right)}\times P_{\left(EV,t\right)}\right)}+\\ {\displaystyle \sum _{ESS=1}^{N_{ESS}}f\left(c_{\left(ESS,t\right)}\times P_{\left(ESS,t\right)}\right)}+{\displaystyle \sum _{L=1}^{N_L}f\left(c_{\left(DR,t\right)}\times P_{\left(DR,t\right)}\right)}+\\ {\displaystyle \sum _{ES=1}^{N_{ES}}f\left(c_{\left(ES,t\right)}\times P_{\left(ES,t\right)}\right)}+{\displaystyle \sum _{SNS=1}^{N_{SNS}}f\left(c_{\left(SNS,t\right)}\times P_{\left(SNS,t\right)}\right)}\end{array}\right)}$$

(1)

$$\begin{array}{l}{F}_{GHG}={\displaystyle {\displaystyle \sum }_{t=1}^T}({\displaystyle {\displaystyle \sum }_{DG=1}^{N_{DG}}}{\alpha }_{\left(DG\right)}{X}_{\left(DG,t\right)}+{\beta }_{\left(DG\right)}{P}_{\left(DG,t\right)}+{\gamma }_{\left(DG\right)}{P}_{\left(DG,t\right)}^2\\ +{\displaystyle {\displaystyle \sum }_{ES=1}^{N_{ES}}}{\alpha }_{\left(ES\right)}{X}_{\left(ES,t\right)}+{\beta }_{\left(ES\right)}{P}_{\left(ES,t\right)}+{\gamma }_{\left(ES\right)}{P}_{\left(ES,t\right)}^2)\end{array}$$

(2)

2.2. Constraints

The problem constraints are modelled according to the characteristics of the distribution system and technologies. Taking this principle into account, the constraints are considered regardless of the multi-objective functions used in this study. A detailed description of these constraints can be seen in [10]. First, the multi-objective ORS problems consider an AC OPF to ensure that the results cause no technical constraints to the grid. The OPF allows congestion verification of balanced distribution grids, like voltage limits and line thermal limits. This means that the use of a full AC-OPF also improves the quality of the technical objective functions described in the previous section.

For a VPP in centralized management, it is not enough to have a scheduling solution since the VPP also has control over the network in the future paradigm. Thus, incorporation of the AC OPF is fundamental to ensure a feasible solution in terms of network operation. It can also represent an economical saving when compared to the coordination of DERs in the current operation that separates the ORS problem from the OPF [13,14]. For instance, a resource can be selected by the OPF to solve a constraint that was previously not scheduled, causing an extra cost. On the other hand, the proposed approach can optimize the cost of scheduling extra resources to solve congestion problems. The active and reactive power flow in each branch, and voltage magnitude and angle in each node are determined by the AC OPF.

The application of Kirchhoff’s current law in each bus leads to the following equations for the active (3) and reactive (4) power:

$$\begin{array}{l}{P}_{G\left(i,t\right)}-P_{D\left(i,t\right)}=G_{ii}\times V_{i(t)}^2+V_{i(t)}\times {\displaystyle \sum _{j\in T{L}^i}{V}_{j(t)}\times \left(G_{ij}\cos {\theta }_{ij(t)}+B_{ij}\sin {\theta }_{ij(t)}\right)}\\ P_{G\left(i,t\right)}={\displaystyle \sum _{DG=1}^{N_{DG}^i}\left(P_{\left(DG,t\right)}^i-P_{\left(SNS,t\right)}^i\right)}+{\displaystyle \sum _{ES=1}^{N_{ES}^i}{P}_{\left(ES,t\right)}^i}+{\displaystyle \sum _{EV=1}^{N_{EV}^i}{P}_{\left(EV,t\right)}^i}+{\displaystyle \sum _{ESS=1}^{N_{ESS}^i}{P}_{\left(ESS,t\right)}^i}\\ P_{D\left(i,t\right)}={\displaystyle \sum _{L=1}^{N_L^i}\left(P_{\left(L,t\right)}^i-P_{\left(DR,t\right)}^i\right)}\\ \forall t\in \left\{1,\dots ,T\right\};\forall i\in \left\{1,\dots ,N_{Bus}\right\};{\theta }_{ij\left(t\right)}={\theta }_{i\left(t\right)}-{\theta }_{j\left(t\right)}\end{array}$$

(3)

$$\begin{array}{l}{\displaystyle \sum _{DG=1}^{N_{DG}^i}\left(Q_{\left(DG,t\right)}^i-Q_{SNS\left(L,t\right)}^i\right)}+{\displaystyle \sum _{ES=1}^{N_{ES}^i}{Q}_{ES\left(ES,t\right)}^i}-{\displaystyle \sum _{L=1}^{N_L^i}{Q}_{\left(L,t\right)}^i}=V_{i(t)}\times {\displaystyle \sum _{j\in T{L}^i}{V}_{j(t)}\times \left(G_{ij}\sin {\theta }_{ij(t)}+B_{ij}\cos {\theta }_{ij(t)}\right)}-B_{ii}\times V_{i(t)}^2\\ \forall t\in \left\{1,\dots ,T\right\};\forall i\in \left\{1,\dots ,N_{Bus}\right\};{\theta }_{ij\left(t\right)}={\theta }_{i\left(t\right)}-{\theta }_{j\left(t\right)}\end{array}$$

(4)

For a feasible solution of AC power flow, it is necessary to keep the voltage magnitude (5) and angle (6) between a maximum and a minimum limit.

$$V_{Min}^i\le V_{i\left(t\right)}\le V_{Max}^i;\forall t\in \left\{1,\dots ,T\right\}$$

(5)

$${\theta }_{Min}^i\le {\theta }_{i\left(t\right)}\le {\theta }_{Max}^i;\forall t\in \left\{1,\dots ,T\right\}$$

(6)

A slack bus was previously selected, and both the reference voltage magnitude and angle are specified for it, typically 1 and 0, respectively. In the distribution network, the upper and lower bounds for voltage magnitude are typically 0.95 and 1.05, and for voltage angle are typically $-\pi /2$ and $\pi /2$.

A constraint regarding the power flow in the line (connecting bus i to bus j), that must be lower than a maximum limit (line thermal limit), is shown in (7).

$$\begin{array}{l}\left|\overline{V_{i(t)}}\times {\left[\overline{y_{ij}}\times \left(\overline{V_{i(t)}}-\overline{V_{j(t)}}\right)+\overline{y_{sh(i)}}\times \overline{V_{i(t)}}\right]}^{\ast }\right|\le S_{TL}^{max}\\ \forall t\in \left\{1,\dots ,T\right\};\forall i,j\in \left\{1,\dots ,N_{Bus}\right\};i\ne j;\forall TL\in \left\{1,\dots ,N_{TL}\right\}\end{array}$$

(7)

The power generation can be obtained from DG units, external suppliers, electric storage systems and electric vehicles. The minimum and maximum active (8) and reactive (9) power generation provided by the DG units and by external suppliers (ES) are formulated as:

$$P_{Min\left(DG,t\right)}\times X_{(DG,t)}\le P_{(DG,t)}\le P_{Max\left(DG,t\right)}\times X_{(DG,t)};\forall t\in \left\{1,\dots ,T\right\};\forall DG\in \left\{1,\dots ,N_{DG}\right\}$$

(8)

$$Q_{Min\left(DG,t\right)}\times X_{(DG,t)}\le Q_{(DG,t)}\le Q_{Max\left(DG,t\right)}\times X_{(DG,t)};\forall t\in \left\{1,\dots ,T\right\};\forall DG\in \left\{1,\dots ,N_{DG}\right\}$$

(9)

Energy storage systems and electric vehicles are modelled in the same way. When the electric vehicles are not connected to the network the maximum charge and discharge limits are defined as zero. The energy balance equation is defined as in Equation (10).

$$\begin{array}{l}{E}_{Stored}{}_{(EV,t)}=E_{Stored}{}_{(EV,t-1)}-E_{Trip}{}_{(EV,t)}+{\eta }_{c(EV)}\times \left(P_{Ch}{}_{(EV,t)}\right)-\frac{1}{{\eta }_{d(EV)}}\times \left(P_{Dch}{}_{(EV,t)}\right)\\ \forall t\in \left\{1,\dots ,T\right\};\forall EV\in \left\{1,\dots ,N_{EV}\right\}\end{array}$$

(10)

In the case of energy storage systems, the energy spent on the trips (E_Trip) is always zero. It is also important to mention that the variable P_(EV) is positive when the vehicle is charging and negative when the vehicle is injecting energy to the network. The variables P_Ch(EV,t) and P_Dch(EV,t) are used instead of P_(EV) to facilitate the comprehension of the constraints.

The energy stored in the batteries must be under a maximum and minimum energy limit for all periods as formulated in Equation (11):

$$E_{BatMin(EV,t)}\le E_{Stored}{}_{(EV,t)}\le E_{BatMax(EV,t)};\forall t\in \left\{1,\dots ,T\right\};\forall EV\in \left\{1,\dots ,N_{EV}\right\}$$

(11)

where, $E_{BatMax\left(EV,t\right)}$ corresponds to the battery capacity and $E_{BatMin\left(EV,t\right)}$ corresponds to the minimum amount of energy stored that the EV user demands, in a particular period or to the minimum technical limit of the battery so that to avoid fast degradation.

The power charge and discharge must be lower or equal to the power charge limit, as shown in Equations (12) and (13):

$$P_{Ch(EV,t)}\le P_{Ch\_\max (EV,t)};\forall t\in \left\{1,\dots ,T\right\};\forall EV\in \left\{1,\dots ,N_{EV}\right\}$$

(12)

$$P_{Dch(EV,t)}\le P_{Dch\_\max (EV,t)};\forall t\in \left\{1,\dots ,T\right\};\forall EV\in \left\{1,\dots ,N_{EV}\right\}$$

(13)

Concerning demand response, the load’s control can be discrete (14) or continuous (15) following the equations:

$$P_{\left(DR,t\right)}=P_{\max \left(DR,t\right)}\times X_{\left(DR,t\right)};\forall t\in \left\{1,\dots ,T\right\};\forall DR\in \left\{1,\dots ,N_{DR}\right\}$$

(14)

$$P_{\left(DR,t\right)}\le P_{\max \left(DR,t\right)};\forall t\in \left\{1,\dots ,T\right\};\forall DR\in \left\{1,\dots ,N_{DR}\right\}$$

(15)

2.3. Hybrid Evolutionary Algorithm

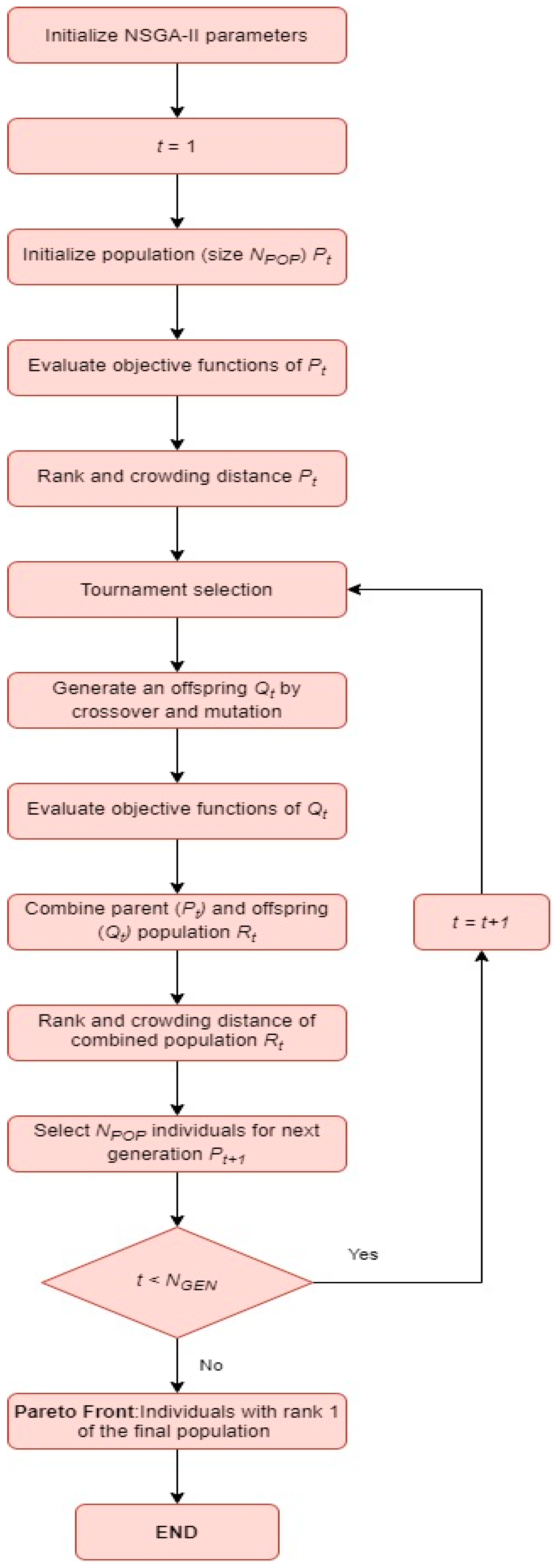
The evolutionary algorithm used in this paper (NSGA-II) was proposed by Deb et al. [7], and since then several authors have been using this algorithm to solve different multi-objective optimization problems [15], particularly in the power system field [8,16]. Figure 2 displays the flowchart of the NSGA-II algorithm.

The NSGA-II algorithm starts with the initialization of several parameters, namely the population size N_POP, the number of generations N_GEN, the crossover probability p_Cross and the mutation probability p_Mut. Then, the parent population P_t is generated based on the deterministic technique, which is further explained below. Each individual of P_t is evaluated for the two objective functions that compose the multi-objective function. The next step consists in ranking all individuals of P_t and determining the crowding distance among them using the methods described in [6]. The rank mechanism ranks all individuals (or solutions) based on nondomination levels: level 1 is the best one, level 2 is the second-best one, and so on. The crowding distance metric determines an estimate of the perimeter of the cuboid formed by using the nearest neighbours of the solution as the vertices. The idea is to assign a high crowding distance value for solutions located in a less crowded region.

A binary tournament selection with the crowded tournament operator, which uses the ranking and crowding distance, is used to select the best individuals of P_t. The first criterion is the selection of the individual with the lower rank (meaning it is better). Otherwise, if both individuals have the same rank, then the solution with a higher crowding distance is selected. The objective of this operator is to obtain a well-spread population for the next generation t + 1. Next, the crossover and mutation are performed to generate an offspring population Q_t with same size N_POP. Once again, all individuals of Q_t are evaluated for each objective function.

Thereafter, the two populations P_t and Q_t (i.e., parent and offspring, respectively) are combined creating a new population R_t with twice the size of the two populations; then, the combined population is ranked, and the crowding distance is also determined. The next step selects the best N_POP individuals of R_t based on the ranking and crowding distance, which creates the parent population (P_t + 1) for the next generation t + 1. The NSGA-II algorithm returns to the tournament selection block and continues the rest of the flowchart until t is equal to the number of generations N_GEN. However, the NSGA-II algorithm can also stop after some iterations when no significant improvement in the population occurs.

2.3.1. Decision Variables

In summary, this NSGA-II algorithm considers the following variables:

• V_i(t) and q_ij(t)—Voltage and power flows defined by AC optimal power flow (AC OPF)
• P_(ES,t) and Q_(ES,t)—Active and reactive power supplied by external suppliers
• P_(DG,t), Q_(DG,t) and P_GCP(DG,t)—Active and reactive power produced by DG units
• P_(SNS,t)—Active power of service not supplied. The SNS can be positive in case of load curtailment or negative in case of generation curtailment
• P_(ESS,t)—Active power charged in electric storage systems (negative values represent power discharge)
• P_(EV,t)—Active power charged in electric vehicles (negative values represent power discharge)
• P_DR(L,t)—Load demand curtailment under demand response programs

A numerical algorithm is used to determine the AC optimal power flow for a radial network [17]. In this study, it is assumed that the VPP operates in a radial distribution grid, which turns the said numerical algorithm suitable for this situation. This algorithm determines the V_i(t), q_ij(t) and power losses from the knowledge of the other variables. This process is run before each individual being evaluated for the two functions composing the multi-objective function.

2.3.2. Initial Solution

The NSGA-II algorithm uses the best strategy for the initial solution proposed in [10]. This heuristic has been adapted to find the best starting point for the multi-objective problem in this study. According to [10], this heuristic is a deterministic technique that solves a relaxed version of the ORS problem for minimizing the energy cost. This relaxed version does not consider the AC OPF, and the metaheuristics using mixed integer linear programming (MILP) heuristic show the best results. Thus, this heuristic was adapted for the NSGA-II algorithm. To perform an adequate modification, the MILP heuristic uses the weighted sum method for each individual, this being designated in this paper as WMILP (weighted sum method with MILP). The weighted sum method [18] converts the set of objective functions into a single-objective function through a linear combination of weights and functions. The sum of weights must be equal to 1, and each weight factor is between 0 and 1. Each individual of the initial population is well spread over the multi-objective functions space. The weight factor starts at zero for the first individual of the population size and ends up at one for the last individual. The step between weight factors is equal to 1 divided by the population size minus 1 (for an even distribution of weight values). For instance, in an initial population with five individuals, the first one has a weight equal to 0, the second one 0.25, in the third and fourth individuals the factors are equal to 0.5 and 0.75, respectively and the last one has a weight equal to 1.

2.3.3. Crossover and Mutation Operators

The crossover operator designated as simulated binary crossover (SBX) [19] is used in the proposed NSGA-II algorithm because this operator is one of the most suitable to deal with continuous variables. The crossover starts by selecting a pair of best individuals in the parent population P_t that were previously selected by the tournament selection. Next, it is decided if the two-parent individuals will be crossed or not to generate two offspring individuals. This is accomplished if a random number is lower or equal to the defined crossover probability p_Cross, otherwise the two selected individuals will be part of the offspring population Q_t. The next step is applying the SBX operator to cross the variables regarding EVs and storage units scheduling (P_ST(ST,t) and P_EV(EV,t)) from the two selected individuals. The SBX starts with the first EV and if the new solutions generated from the SBX violate the EV constraints they are rejected. These steps are applied to all EVs and storage units. After the SBX operator generates two offspring individuals, the heuristics implemented in [20] for neighbourhood solutions in metaheuristics are applied to improve the two offspring individuals.

The final step for generating the offspring population is the mutation operator, which is applied to each individual if a random number is lower or equal to the defined mutation probability (p_Mut). The polynomial mutation operator [21] is used to each EV and storage system because it is one of the most recommended operators to handle with a continuous variable. If the new solution generated from the polynomial mutation operator violates the EV or storage constraint it is rejected.

2.3.4. Stopping Criteria

The NSGA-II algorithm uses two criteria, the first being the maximum number of generations. The second one was changed for coping with the Pareto front characteristics of having multiple nondominated solutions (and not just one like the single-objective problems). For each generation, the mean value of each objective function, and the number of solutions with rank 1, are calculated. If the difference of any of these metrics during a certain number of generations is lower than a specific threshold, the algorithm stops searching for new solutions. For this study, the threshold and the number of iterations is 10⁻⁴ and 20, respectively.

2.4. Fuzzy-Based Method

After determining the Pareto front, the fuzzy set theory is used to choose the best candidate solution for the VPP [22,23]. The methodology has the following steps:

• Definition of the maximum and minimum values for each objective function.
• Definition of the membership function for each objective function (see Equation (16)).
• Definition of the normalized membership function (see Equation (17)).
• Order the Pareto solutions according to the normalized membership function.

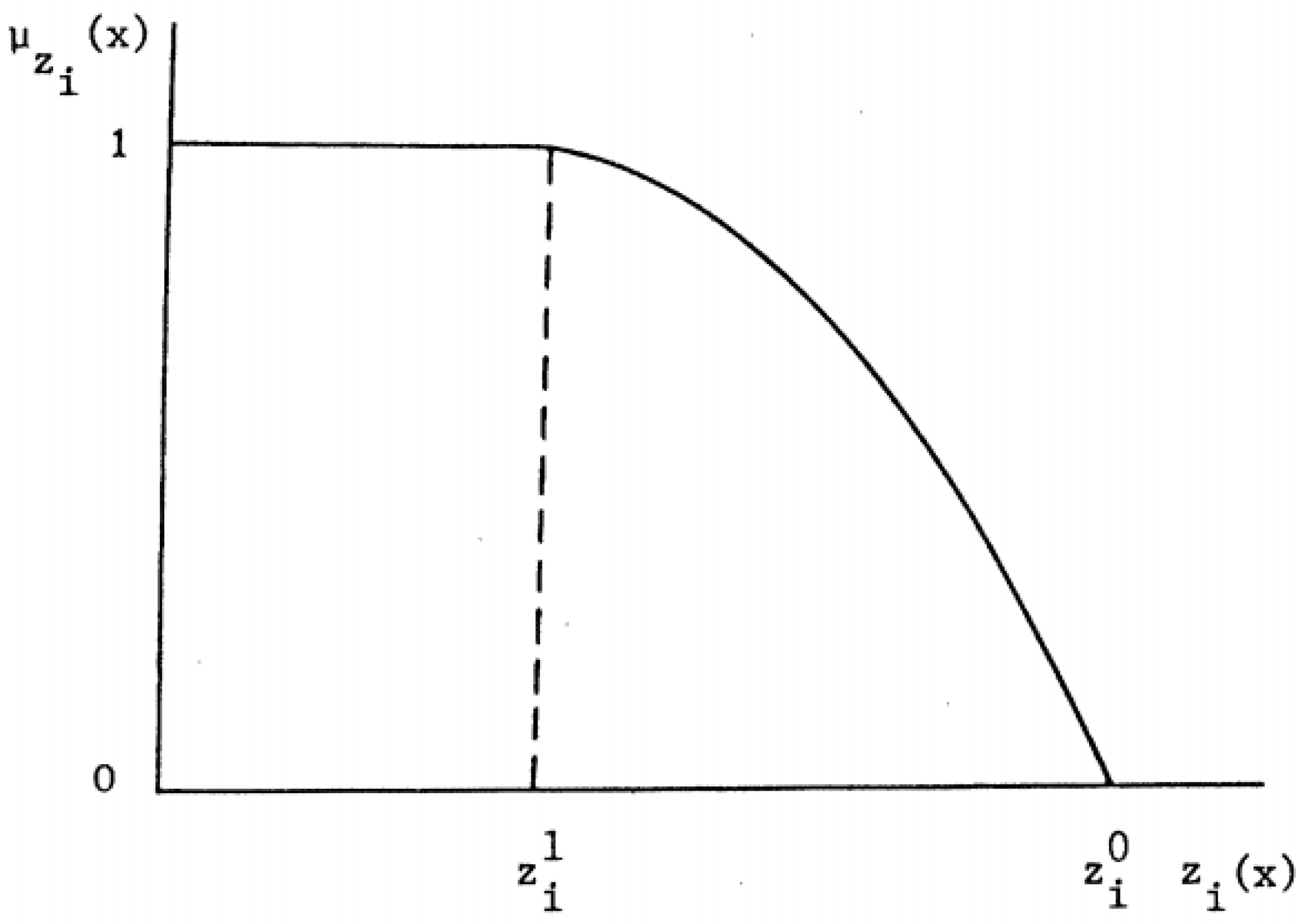
In Step 2, a membership function ${\mu }_o^S$ related to each objective function (represented by index ‘o’) of each solution ‘s’ in the Pareto front is calculated as

$${\mu }_o^S=\{\begin{array}{ll}1& ,F_o\le F_o^{min}\\ \frac{F_o^{max}-F_o}{F_o^{max}-F_o^{min}}& ,F_o^{max}<F_o<F_o^{min}\\ 0& ,F_o\ge F_o^{max}\end{array}$$

(16)

where, $F_o^{max}$ and $F_o^{min}$, defined in Step 1, are the maximum and minimum values of the objective function o, respectively. The membership function can be represented as exemplified in Figure 3.

In Step 3, for each nondominated solution s, the normalized membership function ${\mu }^s$ is calculated as:

$${\mu }^s=\frac{{\displaystyle \sum _{o=1}^{N_{obj}}{\mu }_o^S}}{{\displaystyle \sum _{s=1}^M{\displaystyle \sum _{o=1}^{N_{obj}}{\mu }_o^S}}}$$

(17)

where M and $N_{obj}$ are the total number of nondominated solutions and the total number of objective functions, respectively. The best compromise solution is the one with the maximum ${\mu }_o^S$ value. It is noted that, for the decision-maker, it would be interesting to arrange all Pareto solutions in descending order according to their membership function and having a priority list of Pareto solutions (Step 4).

3. Case Study

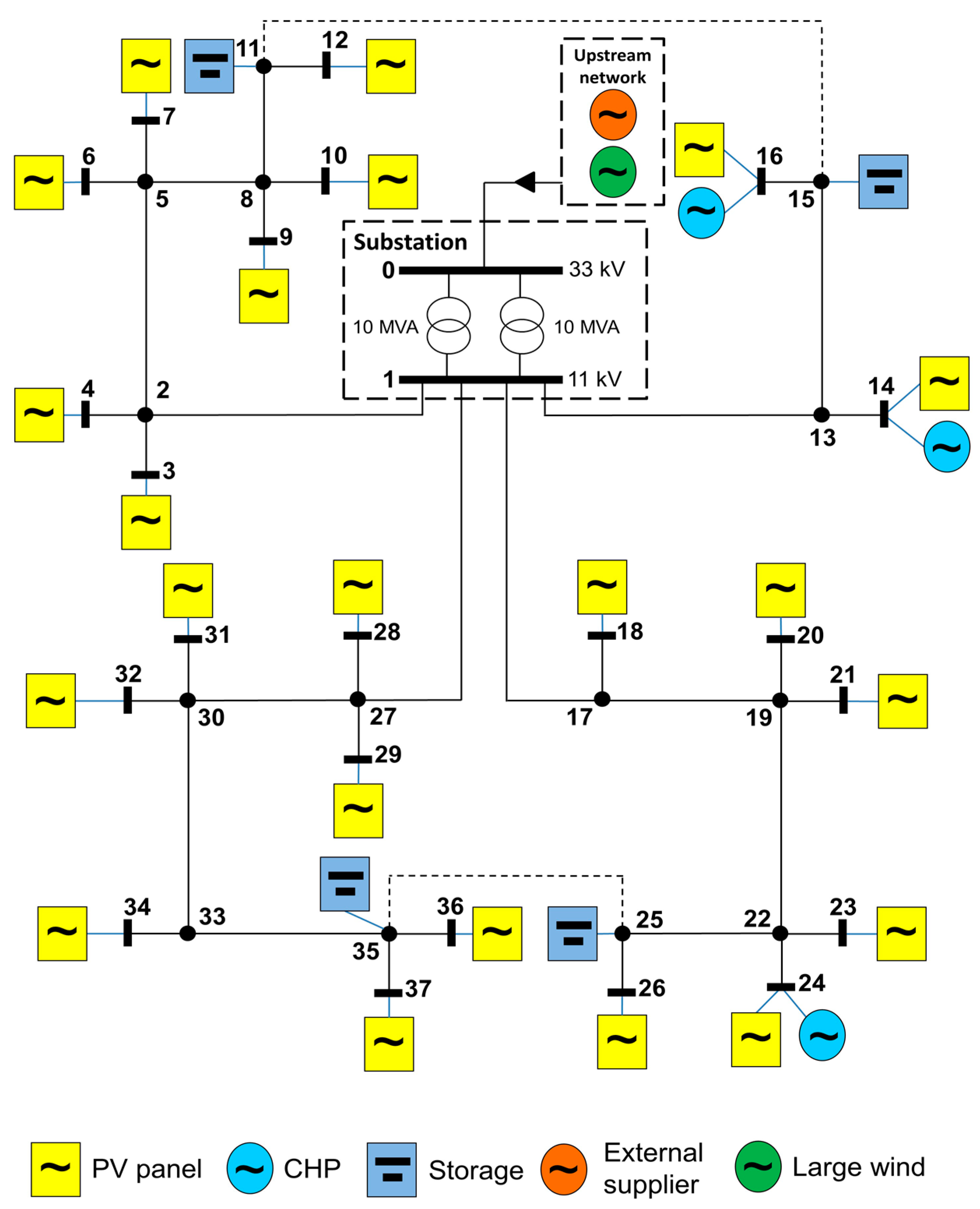
This section presents the results of the case study for illustrating the applicability and performance of the hybrid NSGA-II algorithm. The results of the case study intend to provide an optimal resource scheduling solution considering a balance between the minimum operating costs and minimum CO₂ emissions. The case study is composed of a distribution grid with 37 buses that are connected to the upstream network by two 10 MVA power transformers [24]. This case study contains 1908 consumers: 1850 domestic houses, two industries, 50 commerce stores, and six service buildings. These consumers are aggregated by buses resulting in 22 aggregated loads. All consumers have two direct load control DR programs: the maximum power reduction of DR_A and DR_B correspond to 3% and 2% of the power consumption in each period. The energy roadmap for 2050 proposed in [25], which takes into account the EU targets [26], was used to establish the scenario for the DG units’ capacity. This resulted in a DG penetration composed of photovoltaic (PV) panels with a total installed power of 8MW, three Combined Heat and Power (CHP) units with a total installed power of 1.5MW, and four storage systems with the capability of storing 750 kWh. The penetration of EVs is around 50% and has been established based on the study developed in [27], resulting in 2000 EVs connected to this distribution network. Figure 4 shows the scheme of the 37-bus distribution network considering the DER’s penetration, where the substation (bus 1) connects this network to the system. The substation is composed of two transformers, with a power capacity of 10 MVA each, in which the energy from the 10 external suppliers flows. The input data related to the distribution network and the distributed energy resources are attached to the paper, as Supplementary Materials.

The hybrid NSGA-II was implemented on MATLAB software. In Appendix A,

Table A1. Parameters used in the NSGA-II algorithm.

Parameters	NSGA-II
Population number—NPOP	30
Number of generations—NGEN	50
Crossover probability—pCross	0.9
Simulated Binary Crossover (SBX) distribution index	5
Mutation probability—pMut	0.2
Polynomial mutation index	2
Threshold	10−2
Threshold iterations	20

shows the NSGA-II parameters used. For comparison purposes, another weighted sum method is used in this study and is designed by WMINLP (weighted sum mixed-integer nonlinear programming method). This is the most known classical method for handling multi-objective problems [18]. This method was implemented on GAMS software. Both optimization algorithms were executed on a computer with two processors Intel^® Xeon^® E5-2620 v2 210 GHz, each one with two cores, 16 GB of random-access-memory.

3.1. Pareto front Result

In this simulation, the external suppliers and CHP units presented in Figure 4 are the ones producing GHG emissions.

Table A2. Parameters used in the NSGA-II algorithm.

Resource		Coefficients
Type	Bus	α [ton/h]	β [ton/kWh]	γ [ton/kWh2]
CHP	14	0.01	2.5 × 10−4	3.0 × 10−6
	16	0.03	5.0 × 10−3	7.0 × 10−6
	24	0.02	3.3 × 10−4	4.1 × 10−6
External Supplier	1	0.008	3.0 × 10−3	3.8 × 10−6
		0.01	3.2 × 10−3	4.0 × 10−6
		0.012	3.4 × 10−3	4.2 × 10−6
		0.014	3.6 × 10−3	4.4 × 10−6
		0.016	3.8 × 10−3	4.6 × 10−6
		0.018	4.0 × 10−3	5.0 × 10−6
		0.02	4.2 × 10−3	5.2 × 10−6
		0.022	4.4 × 10−3	5.4 × 10−6
		0.024	4.6 × 10−3	5.6 × 10−6
		0.026	4.8 × 10−3	5.8 × 10−6

of Appendix A contains the coefficients used in Equation (2). The NSGA-II algorithm executed 1000 run trials and the hypervolume measure was used to select the trial with the most suitable Pareto front. This measure determines the volume of the objective space dominated by a Pareto front of a certain trial. The trial that presents the highest hypervolume is selected as the best one. For the WMINLP, the weighted sum method solved the problem 21 times, and in each run, the weight factor changed from 0 to 1 with a step of 0.05.

Figure 5 depicts the Pareto front obtained by both algorithms. In the case of NSGA-II, the Pareto front (i.e., individuals with rank equal to 1) of the initial population is represented by a green line with triangles. The individuals that only minimize the operation cost or the GHG emissions are highlighted with purple and light blue circles, respectively. Each solution presented in the Pareto Front represents the scheduling (active and reactive power setpoints) of all the energy resources. The respective costs and CO2 emissions are obtained through the objective functions.

The WMINLP algorithm obtained a Pareto front containing 19 nondominated solutions, while the NSGA-II obtained a final Pareto front with 30 nondominated solutions. In this case, the initial population only had 13 nondominated solutions and the remaining individuals had a rank higher than 1. The fact of obtaining more solutions with a rank equal to 1 proves the effectiveness of the crossover and mutation operators used in the study. These operators helped to obtain a Pareto front well spread along with the objective functions space, as compared to the initial population. More precisely, the proposed NSGA-II method was able to find solutions close to the region near to the minimum GHG point.

As expected, the WMINLP found better solutions than the NSGA-II algorithm in most of the objective functions space. A small number of the WMINLP solutions are dominated by the Pareto front of NSGA-II; in particular, the ones close to the minimum GHG point. For this region, a small step of 0.01 was tested to find more nondominated solutions. This smaller step enabled the WMINLP to find nondominated solutions in a region where the WMINLP algorithm with 0.05 step was not able to find (but NSGA-II was). However, it increased the number of runs and implied more computation time. Moreover, the solution that minimizes GHG emissions is dominated by the last nondominated solution of the Pareto front obtained by the WMINLP algorithm (counting from left to right in the operation cost axis). This solution was obtained with a weight factor equal to 0.1, which obtains the same minimum GHG, but with a lower operation cost.

In terms of execution time, the NSGA-II achieved a mean time of around 779.39 s (i.e., around 13 min), and the initial population was obtained with a mean time around 624.75 s. On the other hand, the WMINLP algorithm solved the problem considering just the linear coefficient for the energy cost (1) and emissions (2) to have a faster response in each run. However, the WMINLP algorithm took a huge time (around 1,018,243.46 s), corresponding to 282.85 h (i.e., around 12 days). The mean time obtained for each run of the WMINLP method was around 48,487.78 s (13.47 h). A single run was made with the quadratic functions in (1) and (2), which resulted in a time around 26 h. This allows the conclusion that the proposed hybrid NSGA-II is the most suitable algorithm for this type of multi-objective problems. From these results, it is also possible to observe that the weighted sum method (WMINLP) needs an unrealistic execution time to produce a result for mixed-integer nonlinear programming problems in general. Thus, a future direction is to assess the performance of this NSGA-II algorithm with a parallel computing approach in a high-performance computer.

3.2. Best Compromise Solution

After determining the Pareto front by the NSGA-II algorithm, the fuzzy-based method was applied to determine the best compromise solutions taking into account the decision maker’s perspective. Before applying this fuzzy method, it is required to set the maximum and minimum limits that VPP admits for each objective function (presented on

Table 1. Limits in the objective functions allowing the virtual power plants (VPP) to select the best solution.

Objective Function	Limits	Scenario
Operation Cost	Max-Flmax	26,500
	Min-Flmin	24,500
GHG emissions	Max-Flmax	3400
	Min-Flmin	2800

). These parameters depend on the VPP strategy for the ORS problem. Therefore, a scenario was defined based on a balanced solution between the economic and environmental perspectives. This results in the limits shown in Table 1.

Afterwards, the fuzzy-based method was applied for the proposed scenario and the five best compromise solutions are depicted in

Table 2. Best compromise solutions.

Best Solution	Cost (m.u)	GHG (ton)
1	25,649.69	2808.86
2	25,689.80	2774.97
3	25,580.27	2832.88
4	25,297.04	2925.31
5	25,265.53	2947.30

.

It can be seen that the best solutions are around the minimum GHG of 2800 tons established for this scenario, and they represent a middle-term solution between the cost and GHG emissions for the VPP. The first three best solutions show close results in terms of cost and GHG emissions. The fourth and fifth-best solutions show a lower cost than the first three best solutions but achieve GHG emissions around 2900 tons. One of the first three best solutions could be used if the VPP is more interested in minimal GHG emissions, while the fourth and fifth solutions could be adopted for reaching a lower cost. For this scenario, the energy resource scheduling of the best compromise solution is shown in Figure 6.

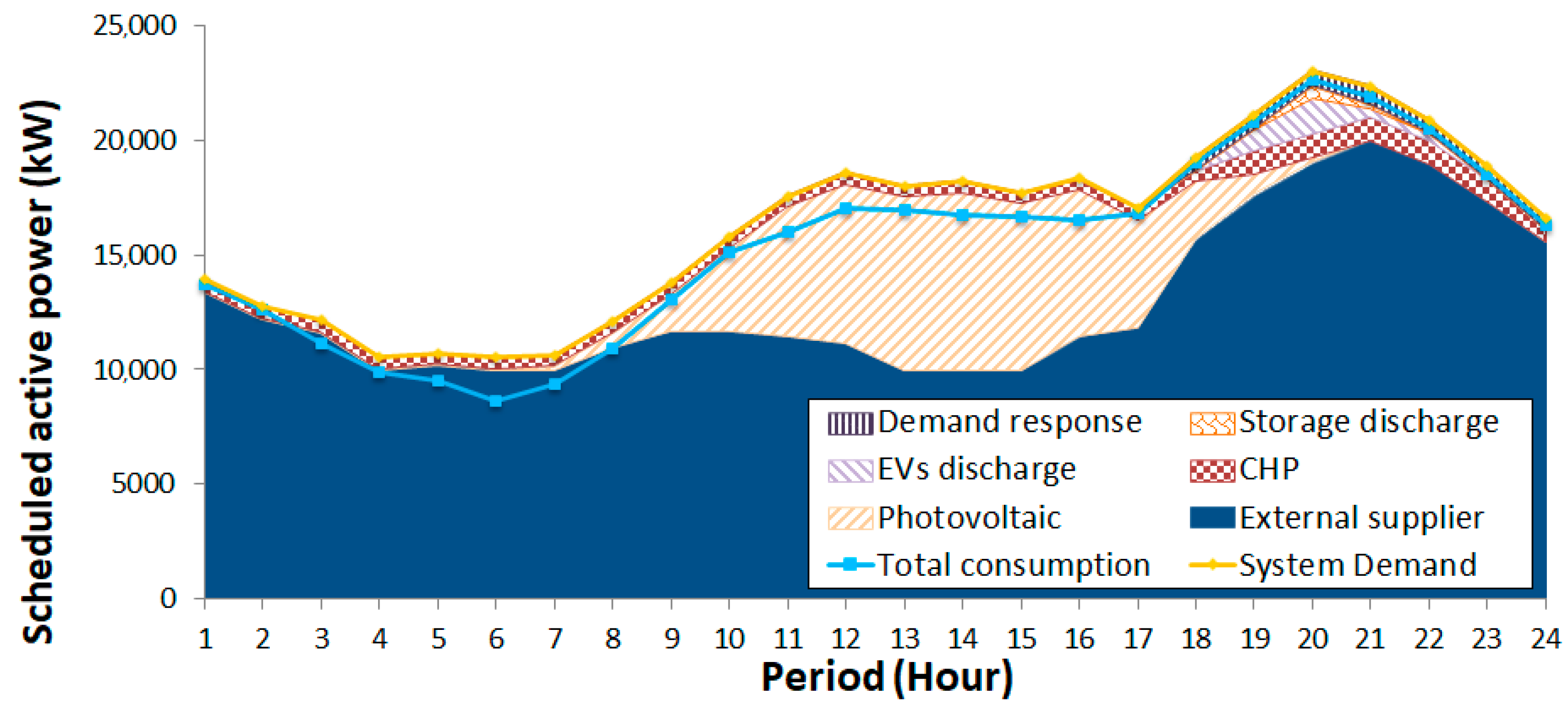
The scheduling, presented in Figure 6 only uses CHP units in the peak hours when the other resources are more expensive, trying to find a compromise solution between costs and emissions. The EVs discharge is also scheduled in these periods reaching a total energy scheduling of 3.2 MWh. It is important to mention that the cost and emissions of energy supplied by external suppliers are also dependent on the requested power. Looking at the total energy resources’ availability (optimization research space), it is possible to conclude that in peak hours only the demand response is not scheduled and the CHP is only partially scheduled.

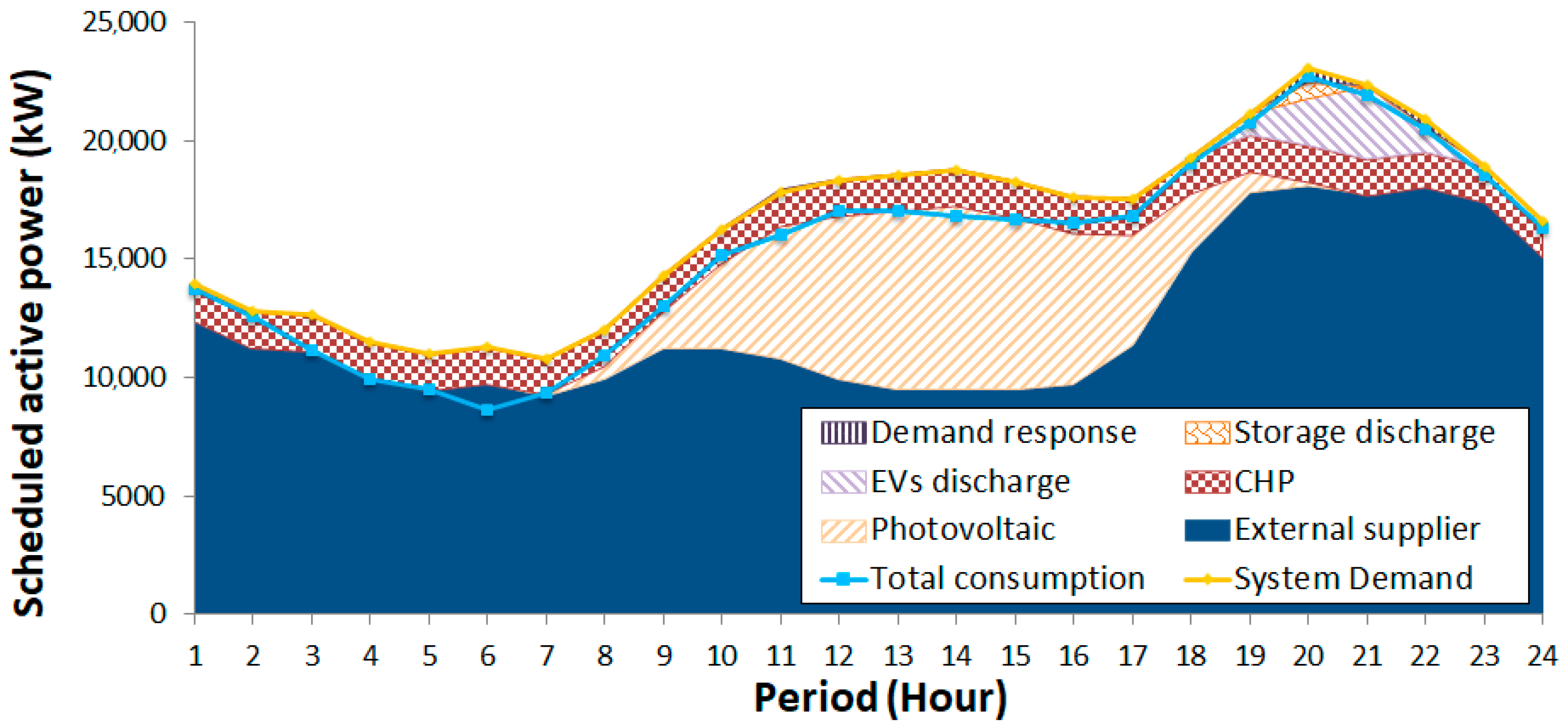
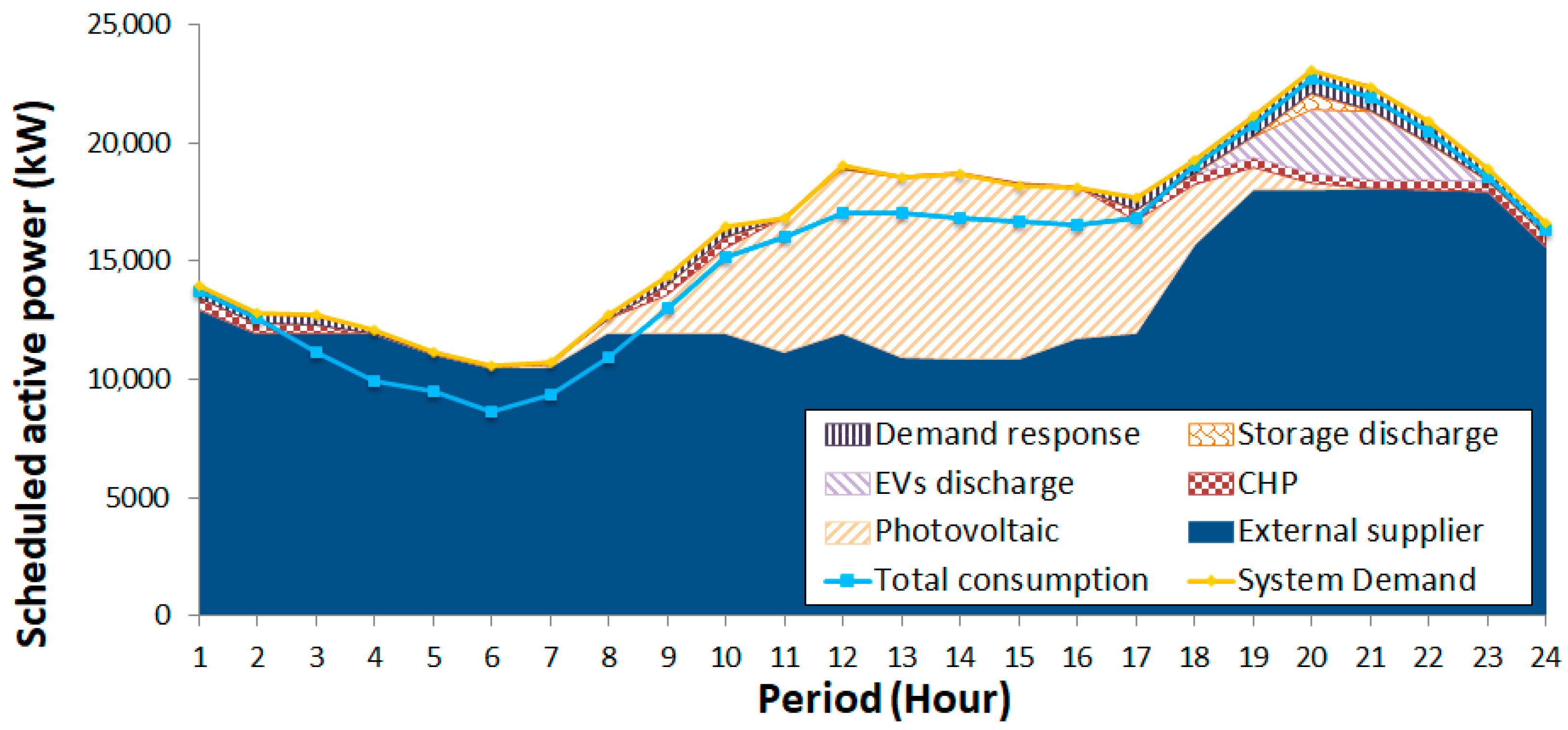
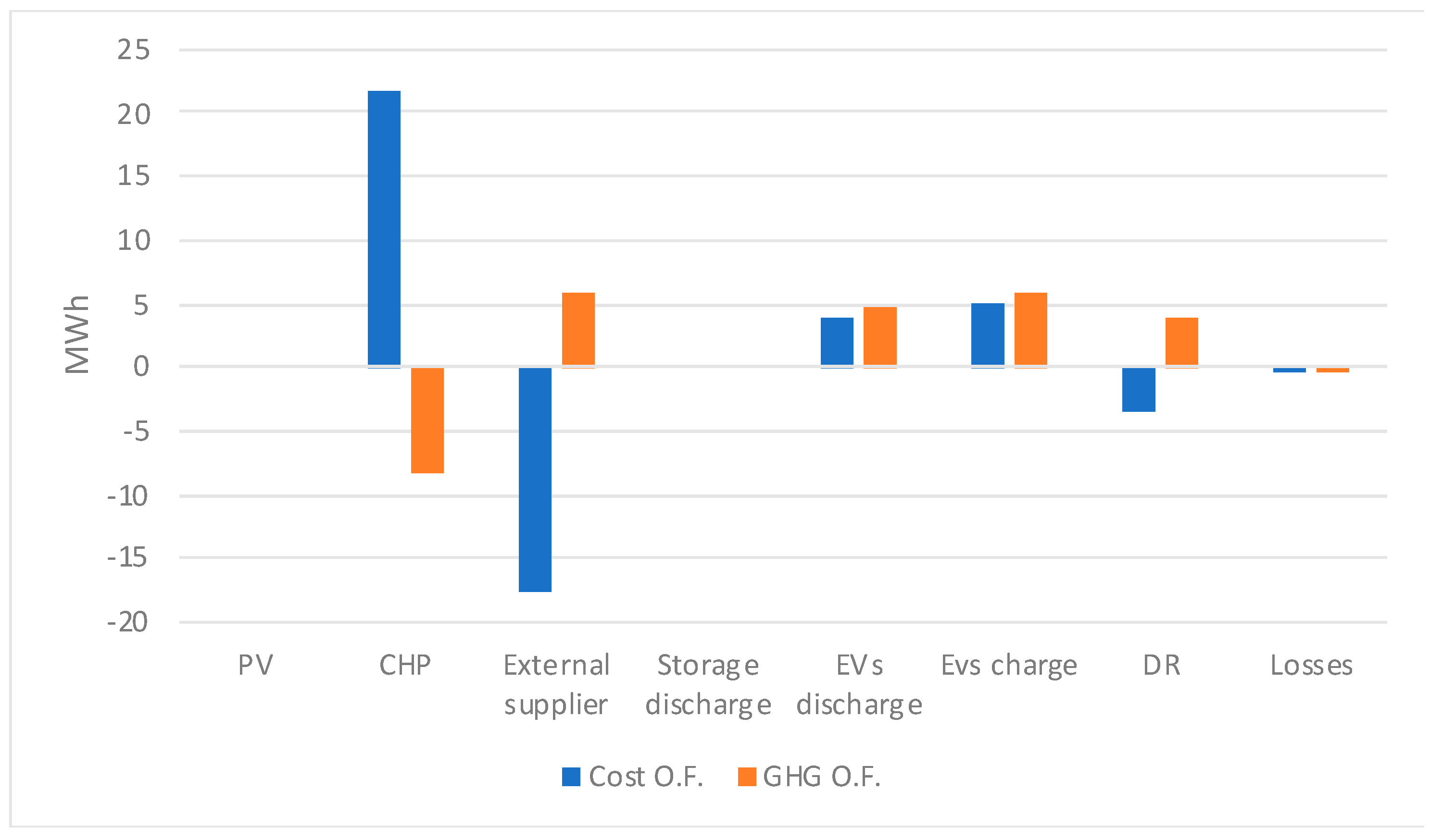
The compromise solution presented in Figure 6 is now compared to the solution considering only the single objective functions (extremes points in Figure 5). The obtained diagrams are presented in Figure 7 (minimization of only cost objective function) and Figure 8 (minimization of only GHG emissions objective function). Figure 9 presents the total difference in energy scheduling considering the different objective functions.

Comparing the best compromise solution (minimum of both cost and GHG emissions) and the minimum of only cost function (Figure 6, Figure 7 and Figure 9), it is possible to see that the main difference is the intensive use of the CHP, instead of external suppliers, when only the minimum cost is considered. As expected, the use of demand response is reduced in the minimum cost function approach due to the higher costs. The management of electric vehicles is also different with more charge/discharge cycles in the only cost minimization approach. Finally, it is important to mention that the power losses are minimal when only the cost function is minimized.

Concerning the comparison between the best compromise solution and the minimum GHG emissions objective function (Figure 6, Figure 8 and Figure 9), the main difference can be observed in the CHP and external suppliers scheduling. However, in this case, the use of CHP is replaced by external suppliers due to the lower emissions. Also, the reduction of consumption through DR programs is considered until its maximum limits. The reduction of consumption means negative GHG emissions, as this will replace generation technologies, thereby reducing power flow and, consequently, power losses. Moreover, some differences can be noticed in the management of electric vehicles.

4. Conclusions

A hybrid metaheuristic is proposed in this paper to solve the energy resources scheduling problem considering the high penetration of electric vehicles. The hybrid technique proposes the use of deterministic mixed-integer linear programming to determine the initial solution of the elitist nondominated sorting genetic algorithm (NSGA-II). The objective function of the optimal resource scheduling minimizes the operation cost and the greenhouse gas emissions of the available resources, including a high number of electric vehicles. These objective functions are strategic for the aggregators as well as for society in general.

The main contribution of this paper lies in the modifications of traditional NSGA-II so that it can produce better solutions compared to the traditional NSGA-II and show significantly lower computational time compared to the deterministic mixed-integer nonlinear programming approach. The significant reduction of the execution time allows wider use of the proposed methodology, allowing its integration in industrial decision support tools.

The case study proved the effectiveness of the proposed method to solve the scheduling problem. When compared to the deterministic approach, it is possible to conclude that both generated Pareto fronts are very close. Moreover, the NSGA-II execution time was around 13 min, whereas the deterministic approach tooks more than 13 h. Finally, a fuzzy method was used to select the best compromise solutions considering a predefined limit for the objective functions. The compromise solution can be parameterized according to the user’s strategy, giving more priority to the costs or the GHG emissions. However, according to the obtained results, it is possible to see that it is possible to reduce significantly GHG emissions while not penalising significantly the costs.

For future work, it is expected that the present methodology will be used to test other multi-objective problems considering the optimization of network operation security.