Optimizing HARQ and Relay Strategies in Limited Feedback Communication Systems ^†

Abstract

One of the key challenges for future communication systems is to deal with fast changing channels due to the mobility of users. Having a robust protocol capable of handling transmission failures in unfavorable channel conditions is crucial, but the feedback capacity may be greatly limited due to strict latency requirements. This paper studies the hybrid automatic repeat request (HARQ) techniques involved in re-transmissions when decoding failures occur at the receiver and proposes a scheme that relies on codeword bundling and adaptive incremental redundancy (IR) to maximize the overall throughput in a limited feedback system. In addition to the traditional codeword extension IR bits, this paper introduces a new type of IR, bundle parity bits, obtained from an erasure code across all the codewords in a bundle. The type and number of IR bits to be sent as a response to a decoding failure is optimized through a Markov Decision Process. In addition to the single link analysis, the paper studies how the same techniques generalize to relay and multi-user broadcast systems. Simulation results show that the proposed schemes can provide a significant increase in throughput over traditional HARQ techniques.

1. Introduction

Communication systems are naturally prone to varying channel conditions. Before the recent information explosion, it was common for systems to use conservative configurations which allowed them to operate in a wide range of conditions, but this came at the expense of performance. In order to accommodate the ever-growing traffic requirements of next generation communication devices, researchers are now using adaptive schemes to maximize bandwidth efficiency and squeeze as much throughput as possible in every situation. A significant amount of work has been devoted to designing algorithms for adapting physical layer parameters such as the transmit power, modulation and coding rate based on the channel state information [1,2,3,4,5], but there is not as much literature on adaptive retransmissions when failures occur despite it has been shown that they can provide significant gains in terms of both throughput [6,7,8] and outage probability [9,10].

Traditional automatic repeat request (ARQ) forces the receiver to send an acknowledgment (ACK) back to the transmitter for every packet it successfully decodes, and a negative-acknowledgment (NACK) otherwise. If the transmitter does not receive an ACK before the timeout expires, the entire packet will be resent, assuming that it is still within the latency limit. Retransmitting the whole packet is justified when the previous one has been completely lost, but in many cases, the received packet can be partially recovered, and it still contains useful information for the decoder, even if it cannot be entirely decoded. In those cases, it is more efficient if the receiver can recover the whole packet with the help of a few additional bits sent from the transmitter, referred to as incremental redundancy (IR). This is commonly known as Type-II hybrid automatic repeat request (Type-II HARQ) [11], and it is the focus of this paper.

The achievable data rate (throughput) with Type-II HARQ has been upper-bounded under the assumption of unlimited single bit IR and perfect feedback [6,12] and several methods have been proposed to construct IR bits [13,14] or optimize their block lengths under a finite number of retransmissions [15,16]. However, most of these works have focused on extending idealized error correcting codes (ECC) in known channels with either infinite or single-bit feedback. Some works have proposed more realistic models accounting for system-level constraints [17,18,19], bundling multiple packets in one resource block [8,20] and imperfect channel information [21]. The first part of this paper takes one step further in this direction by introducing a new type of IR bits and proposing frameworks to optimize the number and type of IR bits to be sent in scenarios with imperfect ECC, limited feedback, packet bundling, and overhead costs for each round of incremental redundancy. It models the problem as a Markov decision process (MDP) which minimizes the average cost per information bit delivered, relying on a code-specific Gaussian model for the probability of decoding failure as a function of signal-to-noise ratio (SNR) and code rate. By adjusting the relative costs associated to decoding and retransmissions, this method can be used to model practical constraints such as latency and hardware.

HARQ has been included and widely deployed in recent cellular networks such as Long-Term Evolution (LTE) [22,23] and 5G NR [24], and there are studies that evaluate its performance [25]. However, most standards proposed the use of fixed-length IRs due to practical constraints. LTE generally assigns one bit feedback per transport block, equivalent to one bit per codeword. The 5G NR standard includes multiple types of operations and is a little more flexible, but does not rise to the level that we propose in this paper. It still uses ACK or NACK and pre-fixed IR lengths. This paper shows that our proposed HARQ strategies can potentially achieve higher throughput by allowing even more flexibility than 5G NR in the types and lengths of IR retransmissions. In terms of channel coding, the punctured turbo codes in LTE have been replaced with low-density parity-check (LDPC) codes in 5G NR. Among other advantages, LDPC codes provide more flexible puncturing and rate adaptation, allowing for a nearly continuous number of IR bits. The ideas on this paper can be applied to any family of channel codes, but assume the use of LDPC codes by default.

Upcoming millimeter wave (mmWave) systems are likely to deploy dense networks of access points acting as relays between a base station and the end users, requiring HARQ strategies suitable for multi-hop architectures [26,27,28]. These relay nodes have to decide between using amplify-and-forward (AF) or decode-and-forward (DF) when passing on information. AF amplifies and retransmits incoming packets as they are received, signal and noise. It is faster and less complex but noise accumulates over multiple hops until the packet can become unrecoverable. DF decodes the received signal and reencodes it before retransmission. This provides noise reduction and early detection of failures, but the required processing increases latency, complexity, and power consumption. Previous literature has shown that DF generally has higher channel capacity than AF [29] and lower frame error rate (FER) with several HARQ protocols [30]. However, some of the practical benefits of AF, such as simpler hardware and lower latency, were not considered in those studies. Hybrid schemes between AF and DF, such as transcoding [31] or compress and forward [32], have been shown to reduce the latency in modern 5G relay systems. Those schemes address how information is processed by the relay in each transmission, but do not address how to proceed when decoding failures occur. The second part of this paper shows how the MDP framework initially proposed for a single link scenario can be easily extended to account for the complexities of a relay system, including optimizing the decision between AF and DF.

Finally, the third part of this paper addresses another very relevant scenario for modern and future networks: multi-user systems where a single base station is communicating with multiple recipients. Even if each recipient is only interested in some of the information, it makes sense for the base station to bundle several packets and broadcast the bundle to all the users. If multiple users suffer a small number of decoding failures, the base station does not need to send individual IR to everyone; instead, it can broadcast one additional piece of information—for example the XOR (i.e., bitwise modulo 2 addition) of the packets in the bundle—to help multiple users decode their failed codewords. This idea, commonly known as network coded (H)ARQ, dates back to the 1980s [33], but it has recently experienced a renewed interest from the research community due to its potential uses in the Internet of Things (IoT). Its maximal achievable throughput under idealized conditions was characterized in [34], and [35] extended that work with a deeper study of the practical overheads associated with various implementations. It showed that using general linear codes requires significantly more overhead than binary codes, since the transmitter not only needs to specify which packets are included in each linear combination, but also their coefficients. Hence, this paper only considers binary XOR packet combinations. The choice of packets to include is then a special case of the well-known index coding problem [36,37], but our framework also requires optimizing the number of bits to be sent, which further complicates the problem. Still, we show that it can be formulated in a relatively simple convex form. Numerical convex optimization algorithms can then be applied to solve for a good approximation to the optimum.

The main contributions of the paper can be summarized as follows. It introduces a new type of IR bit, bundle parity bits, computed across a bundle of codewords. It proposes an MDP model for the HARQ process over a point-to-point link, optimizing the type and number of IR bits to be sent when failures occur. It then shows how such HARQ scheme can be generalized and adapted to suit a two-hop relay network, where the relay node can be optimized to choose between AF and DF based on the channel state information. Finally, it considers a multi-user broadcast scenario and shows that the optimization of the HARQ can be formulated in a convex form. Numerical simulations verify the derivations, and show that the proposed methods achieve modest improvements against traditional schemes in all three scenarios.

The rest of the paper is organized as follows. Section 2 explains the system model and some notation to be used throughout the paper. Section 3 introduces the different types of IR bits being considered and how they can help in the decoding of a given bundle of codewords. Section 4 builds a single-link decision engine optimizing the type and number of IR bits to be sent as a function of the channel SNR, coding rate, and number of failed codewords in the bundle. Section 5 derives the decision engine for the relay, which decides between AF and DF relay strategies as a function of the SNRs on the two links and the code rate on the first link. Section 6 addresses the case of multi-user systems, proposing a combinatorial optimization algorithm for deciding how the failed codewords should be grouped for the generation of IR when failures occur. Finally, Section 7 illustrates the performance of our proposed policies through numerical simulations, and Section 8 concludes the paper.

2. System Model

This section introduces the system models used throughout the paper. It first presents a single link scenario (with a direct channel between the transmitter and receiver) describing the channel, modulation, ECC, and HARQ schemes. Then it extends this scenario to the dual-hop relay system depicted in Figure 1, where the base station (BS) can only reach the end user through an intermediate relay station (RS), and to a multi-user scenario where a single transmitter (possibly the relay) is communicating with multiple recipients. All the links in the relay and multi-user scenarios follow the same model as that in the single link scenario.

2.1. Channel and Modulation

Modern communication systems estimate the channel by periodically sending pilot signals, and use those estimates to adjust the modulation and coding schemes so as to maintain a certain frame error rate (FER). However, the unpredictable nature of channels and the blind period between channel sounding cycles make it impossible to achieve optimal adaptation for all codewords.

In this paper, channels are modeled as interference-free additive white Gaussian noise (AWGN). We assume that multiple codewords or packets (For simplicity, we assume that each packet consists of a single codeword and we refer to packets or codewords indistinctly. In a scenario where each packet consists of multiple codewords, we can either acknowledge codewords independently or treat each packet as a single unit which can either succeed or fail to decode. ) are bundled together into a single block, experiencing the same (often unknown) SNR at the receiver. All the IR bits requested in the same round also experience the same SNR, but this SNR is independent from that for the bundle and for previous rounds of IR (if any). This assumption is made in light of the fact that there is typically a delay between the transmissions of the original bundle and the IR, during which channel conditions could have changed.

In order to increase throughput, the transmitter uses high-order modulations with multiple bits per symbol for all but the noisiest channel conditions. Encoding these modulation symbols directly would increase the error correction capabilities [38], but would complicate significantly the encoding and decoding. Treating the bits in a modulation symbol as independent and using binary error correcting codes is significantly simpler computationally, especially in the case of LDPC codes, but the performance is slightly worse than with non-binary error correction codes. Still, it is the most common approach in practice. Therefore, this paper assumes the use of binary encoders and decoders which operate as if the bits came from independent BPSK modulations with constant SNR throughout each codeword, even if higher order modulations are actually being used [39].

2.2. Error Correction

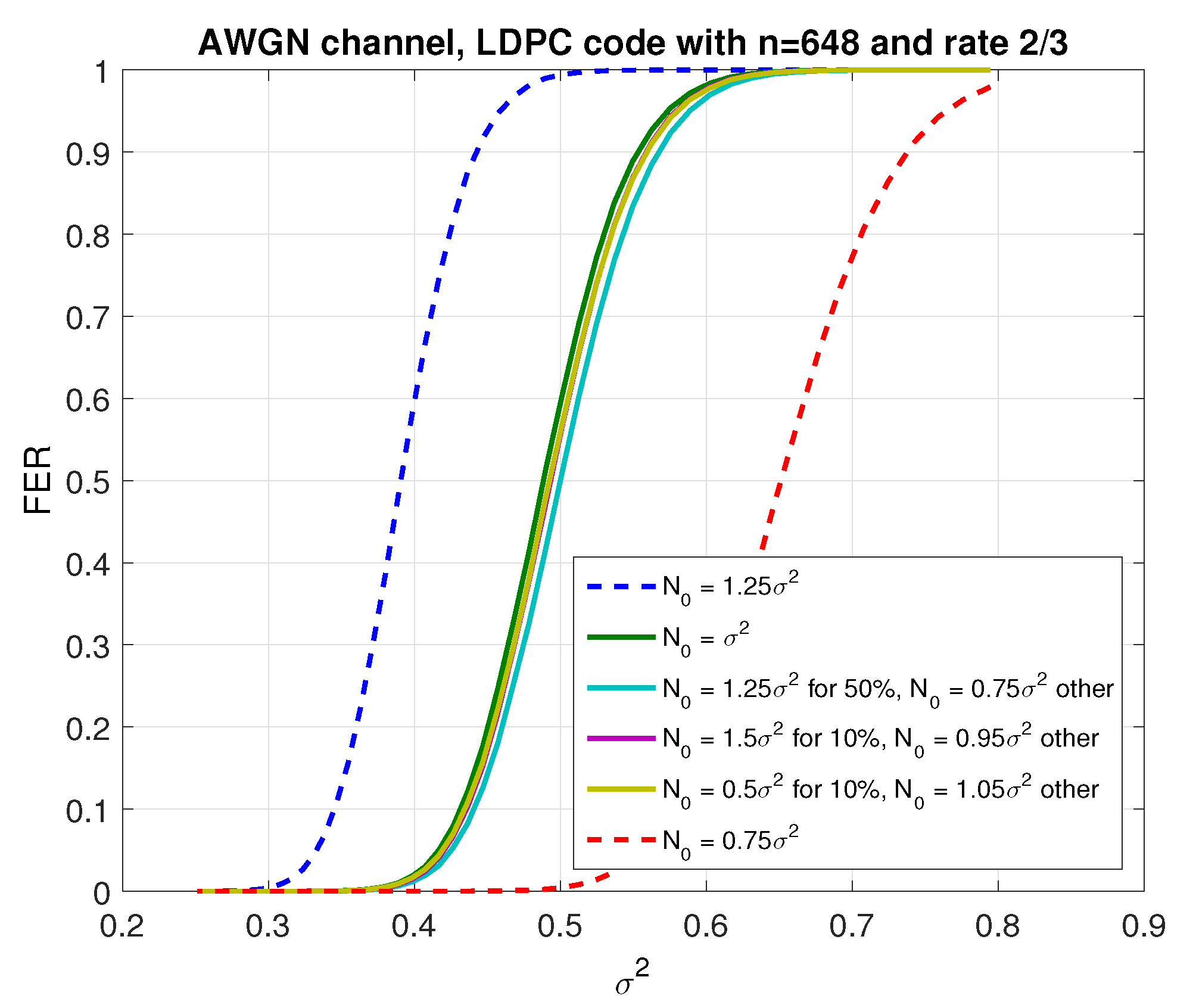
Several works (e.g., [15,40]) have shown that the FER of a finite length code can be well approximated by

$$P_e(R,SNR)=Q\left(\frac{\mu -R}{\sigma }\right),$$

(1)

where R represents the code rate (i.e., number of information bits divided by codeword length) and $\mu$ and $\sigma$ are code-specific parameters that depend on the SNR. We model such dependency as

$$\begin{array}{cc}\hfill \mu & =a_{\mu }·SN{R}^{-c_{\mu }}+b_{\mu },\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \sigma & =a_{\sigma }·SN{R}^{-c_{\sigma }}+b_{\sigma }.\hfill \end{array}$$

(3)

The techniques proposed in this paper could be applied to any code by adjusting the parameters ($a_{\mu }$, $b_{\mu }$, $c_{\mu }$, $a_{\sigma }$, $b_{\sigma }$, $c_{\sigma }$), but the numerical simulations in this paper will focus on the binary QC-LDPC code of length $n=648$ and $k=432$ (rate 2/3) proposed in the 3GPP standard for 802.11n [41], for illustrative purposes. Our prior work [42,43] showed that

$$\begin{array}{cccccc}\hfill a_{\mu }& =-0.2\hfill & \hfill b_{\mu }& =0.86\hfill & \hfill c_{\mu }& =1.74\hfill \end{array}$$

(4)

$$\begin{array}{cccccc}\hfill a_{\sigma }& =0.12\hfill & \hfill b_{\sigma }& =-0.08\hfill & \hfill c_{\sigma }& =0.42\hfill \end{array}$$

(5)

provide a good fit to this code when $SNR\in [0.5,2]$.

Binary QC-LDPC codes offer very efficient encoding and decoding using parallel shift registers [44,45]. This has made them the preferred option in 5G NR, over turbo codes such as the ones proposed in the LTE standard. Additionally, QC-LDPC codes can be flexibly punctured and extended for nearly continuous rate adaptation. A QC-LDPC code is uniquely defined by a sparse parity check matrix $H\in {\{0,1\}}^{(n-k)\times n}$, such that $Hx=0$ for all codewords x. Received channel values (i.e., matched filter outputs) are processed to obtain a log-likelihood ratio (LLR) for each individual bit b as

$$\ell =LLR\left(b\right|r)=log\frac{p(b=0|r)}{p(b=1|r)},$$

(6)

where $p\left(0\right|r)$ and $p\left(1\right|r)$ represent the conditional probability of $b=0$ and $b=1$, respectively, given the received value r. It is not hard to prove that for an AWGN channel with equiprobable and symmetric inputs, the LLR values are given by

$$\mathrm{LLR}\left(b\right|r)=2·SNR·r.$$

(7)

The decoding of LDPC codes is typically done through message-passing algorithms, which refine these LLR values iteratively until convergence or until a prefixed maximum number of iterations is reached. When the algorithm does converge, it is almost always to the right codeword. We thus assume that a codeword error occurs if and only if the LDPC decoder fails to converge.

2.3. Single Link System: Hybrid ARQ

This paper focuses on the optimization of HARQ protocols, abstracting some of the other practical complexities that are present in real world communication networks. For example, the paper assumes perfect synchronization between all the nodes and error-free, albeit limited-capacity, feedback links. Feedback links are assumed to offer no more than one bit of feedback per packet, allowing for 256 possible responses to a bundle of eight packets, for instance. However, most of the proposed HARQ strategies do not require that many feedback messages, so the required number of feedback bits can be lower.

It is also assumed that the receiver can request as many rounds of incremental redundancy as needed until the whole bundle is successfully decoded. Each round is penalized with an adjustable overhead cost of $c_R$ per link plus a decoding cost of $c_D$ for each codeword for which decoding is attempted.

2.4. Relay System: Amplify or Decode?

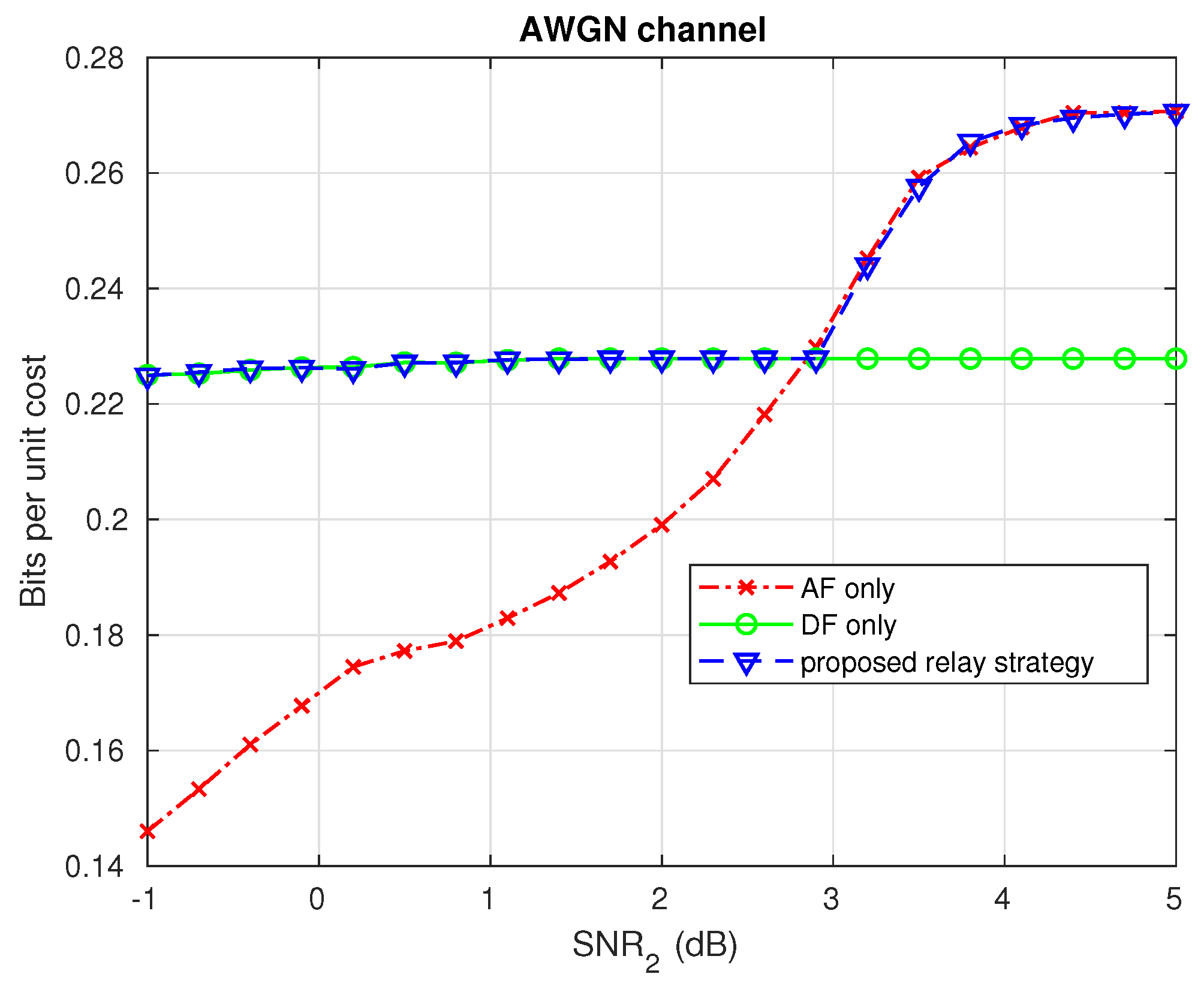
In the relay scenario, the intermediate node needs to decide whether to adopt an AF or DF strategy for each incoming bundle. It will base this decision on the channel SNR estimates and the code rate of the bundle. With DF, the system is equivalent to two separate links, which could be independently optimized using the same HARQ protocol as for the single link scenario. With AF, the HARQ problem is slightly more complex. When a bundle arrives, the relay will forward it without any processing, but we assume that it caches the LLR values temporarily. If the end user is successful in decoding the whole bundle, these LLR values can be discarded, but if the end user suffers any decoding failures, the relay reverts to DF. It decodes the bundle using its cached LLR values (employing HARQ if needed) and only after having succeeded it sends IR to the end user.

When employing AF, we assume unit transmit power at the base station and that the relay amplifies its received signal to invert the attenuation of the first channel. In other words, if the relay receives

$$y_1=g_{1}x+n_1,$$

where $g_1$ is the channel gain on the first link, x is the signal with $E\left[x^2\right]=1$ and $n_1$ is Gaussian noise with variance ${\sigma }_1^2$, the relay amplifies $y_1$ by a factor $1/g_1$ before forwarding it. Then, the received signal at the end user is

$$\begin{array}{cc}\hfill y_2& =g_2\frac{1}{g_1}{y}_1+n_2\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & =g_2\left(x+\frac{n_1}{g_1}+\frac{n_2}{g_2}\right),\hfill \end{array}$$

(9)

where $g_2$ is the gain over the second link. Since the noise components $n_1$ and $n_2$ are independent, the SNR at the end user with AF is

$$\begin{array}{c}\hfill SN{R}_{AF}=\frac{E\left[x^2\right]}{Var[\frac{n_1}{g_1}+\frac{n_2}{g_2}]}={(SN{R}_1^{-1}+SN{R}_2^{-1})}^{-1},\end{array}$$

(10)

where $E[·]$ and $Var[·]$ denote expectation and variance respectively, and $SN{R}_j=g_j^2/{\sigma }_j^2$ ($j=1,2$) is the SNR on the j-th link. Note that $SN{R}_{AF}$ is always lower than the SNR on either link.

2.5. Multi-User Systems

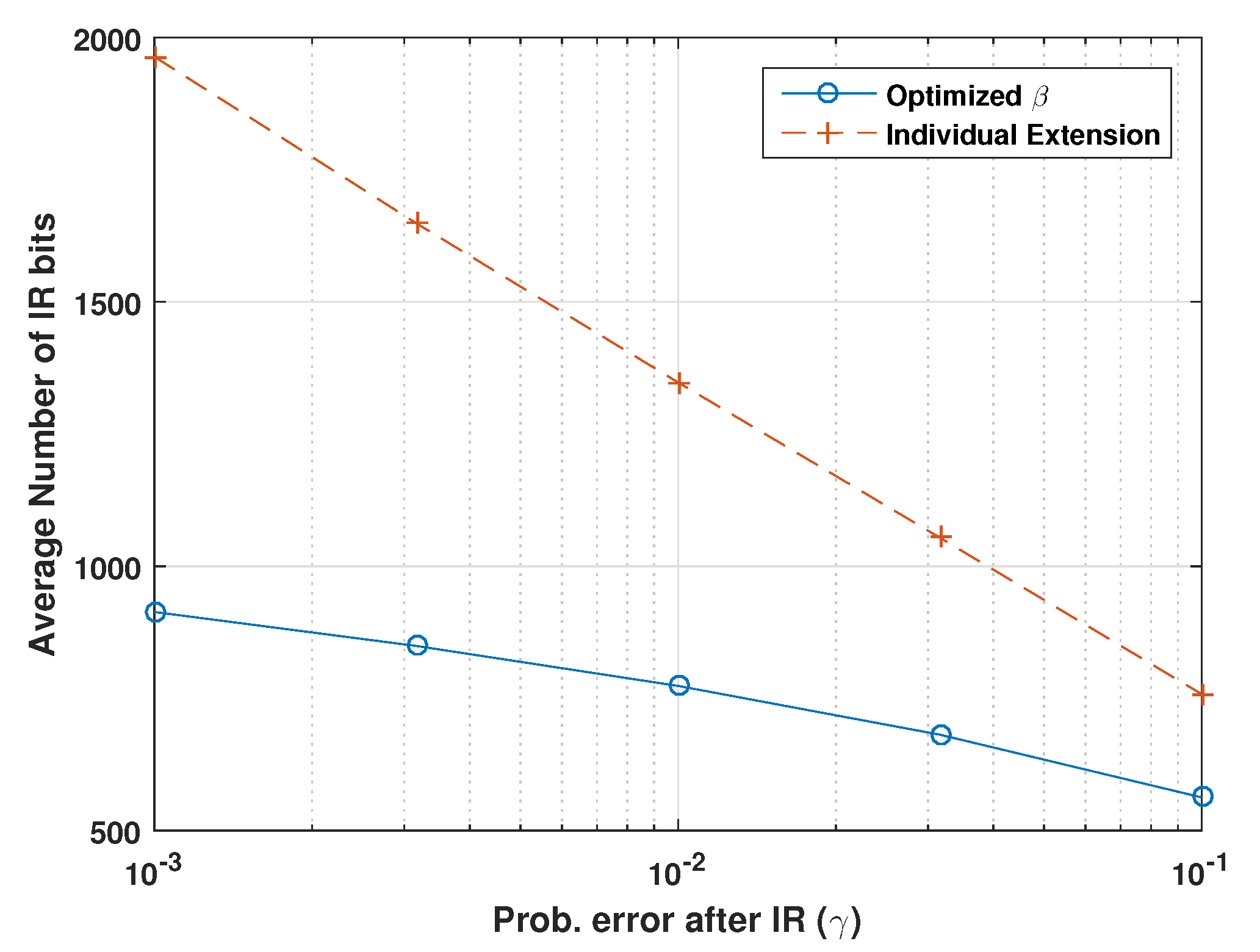
The last scenario studied in this paper is that of a single transmitter communicating with multiple recipients. Each recipient is only interested in a subset of the information being transmitted, but can overhear everything. Each receiver has its own data and feedback channel, with independent SNR and decoding process. When a receiver is unable to decode its desired information, it reports the failures to the transmitter and requests IR. The transmitter compiles the failure reports from all the receivers and uses the proposed algorithm to optimize the set of IR bits that should be broadcast in order to ensure that none of them suffers a probability of error above a pre-fixed value $\gamma$. This optimization is formulated as a convex optimization problem, albeit with the number of variables increasing exponentially with the number of failures reported. In any case, if the number of failures is too large, it is usually better to re-transmit the whole bundle anyway.

3. Incremental Redundancy

This paper uses the term “Incremental Redundancy” (IR) to denote all the bits transmitted with the objective of aiding in the recovery of one or more codewords whose decoding had previously failed. Figure 2 shows three different types of IR:

• Chase Combining [46]: the sequence of IR bits is identical to a subset of the bits previously sent. It is simple and computationally efficient, since the transmitter does not need to generate new bits and the decoder can just refine the previous LLRs using maximal ratio combining. However, some of the information transmitted might be redundant to the receiver, so it is a suboptimal approach.
• Bundle parity bits: the sequence of IR bits consists of a bit-wise erasure code over the previously transmitted codewords [47]. This paper uses the XOR of the codewords in a bundle, unless stated otherwise.
• Codeword parity (or extension) bits: the sequence of IR bits extends each of the previously transmitted codewords with either previously punctured bits or with completely new parity found by adding new rows and columns to the parity check matrix H.

We assume that the decoder can handle the decoding of a (possibly extended) codeword, but does not have enough memory to jointly decode all the codewords in a bundle. Each codeword is therefore decoded independently, although Chase Combining and bundle parity bits can be used to refine its LLR values.

We now study the effect that each of these types of IR bits has on the codewords. In a nutshell, Chase Combining and bundle parity bits increase the SNR for some bits in the failed codewords, and extension bits reduce the rate of the codeword. These improvements in SNR and rate can be translated into a lower probability of error using Equation (1).

3.1. Chase Combining

Let $r^{\left(0\right)}=b+n^{\left(0\right)}$ and $r^{\left(1\right)}=b+n^{\left(1\right)}$ be the received values corresponding to two transmissions of the same bit b with different $SN{R}_0$ and $SN{R}_1$, respectively. With Chase Combining, the receiver can combine both values into $r^{\left(0\right)}+r^{\left(1\right)}=2b+n^{\left(0\right)}+n^{\left(1\right)}$ resulting in an effective SNR of

$$SN{R}_{\mathrm{CC}}=\frac{4}{\frac{1}{SN{R}_0}+\frac{1}{SN{R}_{\mathrm{IR}}}},$$

(11)

for the retransmitted bits. Since $p\left(1\right|r^{\left(0\right)},r^{\left(1\right)})$ is proportional to $p\left(1\right|r^{\left(0\right)})p\left(0\right|r^{\left(1\right)})$ (the same applies for $b=0$), the decoder can just add the LLRs from the individual transmissions.

3.2. Bundle Parity

Similarly to Chase Combining, bundle parity bits can be used to increase the SNR for some of the bits in the failed codewords. Assume that a vector $\mathbf{b}=[b_1,b_2,\cdots ,b_n]$ of n bits from from different codewords is transmitted through an AWGN channel and that their XOR $x=b_1\oplus \cdots \oplus b_n$ is transmitted through another AWGN channel with possibly different SNR. Denoting the received values for $\mathbf{b}$ and x as $\mathbf{r}$ and $r_x$, respectively, the probability of a specific bit $b_k$ being 0 conditioned on these received values can be found as

$$p_k\left(0\right|\mathbf{r},r_x)=\sum _{\begin{array}{c}\mathbf{d}\in {\{0,1\}}^n\\ d_k=0\end{array}}\frac{\left({\displaystyle \prod _{j=1}^n}{p}_j\left(d_j\right|r_j)\right)p_x(⨁\mathbf{d}|r_x)}{{\displaystyle {\displaystyle \sum }_{\mathbf{v}\in {\{0,1\}}^n}}\left({\displaystyle \prod _{j=1}^n}{p}_j\left(v_j\right|r_j)\right)p_x(⨁\mathbf{v}|r_x)},$$

(12)

where ⨁ represents the XOR operator and $p_x(⨁\mathbf{v}|r_x)$ denotes the probability that $x=v_1\oplus \cdots \oplus v_n$ given the received value $r_x$. Equation (12) provides the exact probabilities required for the computation of the LLR values, but it is impractical to evaluate for large bundle sizes because the number of terms increases exponentially. Hence, we adopt a similar approximation to that used in Min-Sum LDPC decoders [48] and calculate the updated LLR for bit $b_k$ as

$${\ell }^{}{\mathrm{new}}_k={\ell }_k+\left(\prod _{\begin{array}{c}i=1\\ i\ne k\end{array}}^{n+1}sign\left({\ell }_i\right)\right)\underset{\begin{array}{c}i=1\cdots n+1\\ i\ne k\end{array}}{min}|{\ell }_i|,$$

(13)

where ${\ell }_{n+1}$ denotes the LLR value for $x=⨁\mathbf{b}$. The effect of this update can be modelled as an increase in the SNR of the bits using Equation (7). Specifically,

$$SN{R}_{\mathrm{new}}=\frac{E{\left[{\ell }^{}\mathrm{new}\right]}^2}{Var\left[{\ell }^{}\mathrm{new}\right]},$$

(14)

where ${\ell }^{}\mathrm{new}$ corresponds to the LLRs conditioned on $b=0$ being transmitted (The same formula would hold if $b=1$ is being transmitted). The two terms in Equation (13) are independent, so the moments of ${\ell }^{\mathrm{new}}$ can be found by adding their corresponding moments. Characterizing the mean and variance of the minimum value among a set of Gaussians is possible, but requires tedious equations that add little value to this paper. Instead, Figure 3 illustrates the $SN{R}_{\mathrm{new}}$ as a function of the number of failed codewords and the SNR of the original bits, assuming a SNR of 0 dB for the IR. In a practical setting, that table would be computed offline and saved in memory to be used in the optimizations described in subsequent sections.

LDPC decoders can occasionally fail to converge, but when they converge to a feasible codeword it is almost always the right one. Therefore, when the decoder fails to decode some of the codewords in a bundle, the receiver can set the LLR values for successfully decoded codewords to have infinite magnitude and update those for the failed codewords according to Equation (13) before attempting another decoding. If it succeeds in decoding any previously failed codewords, their LLRs can be scaled to have infinite magnitude and those for failed codewords can be updated again.

3.3. Codeword Extension

Finally, codeword extension bits reduce the rate of the code. The probability of a successful decoding with these extension bits is highly dependent on the specific code being used. The code specifications often characterize this probability, but only under the assumption that the original codeword and the extension bits are received with the same SNR. Unfortunately, this is generally not the case in practice.

In order to simplify our derivations, we define the effective SNR of a codeword as

$$SN{R}_{\mathrm{eff}}={\left(E\left[\frac{1}{SNR}\right]\right)}^{-1},$$

(15)

where the expectation is taken over the bits in the codeword. When all the bits in the codeword have the same energy $E_b$, $SN{R}_{\mathrm{eff}}$ is equivalent to dividing $E_b$ by the average noise power. Figure 4 illustrates the probability of decoding failure for different noise powers and distributions of signal strength within a codeword. Solid curves, which correspond to different distributions with the same $SN{R}_{\mathrm{eff}}$ are nearly identical, while dashed curves show the effect of a 25% variation in $SN{R}_{\mathrm{eff}}$. We therefore assume that the probability of failure mostly depends on $SN{R}_{\mathrm{eff}}$, not on the SNR variance within the codeword.

4. Decision Engine for Single Link

This section considers a point-to-point link, and proposes an optimization method where the requested number and type of IR bits can be chosen to minimize a cost function. We discretize the coding rate R and the SNR into a finite set of values so that practical numerical methods can be applied to the optimization problem. Since the feedback channel has limited capacity and only offers a few bits for each IR request, we constrain the number of IR bits to be requested to a small set of pre-defined values. A Markov Decision Process (MDP) can then be established to model the HARQ protocol as follows:

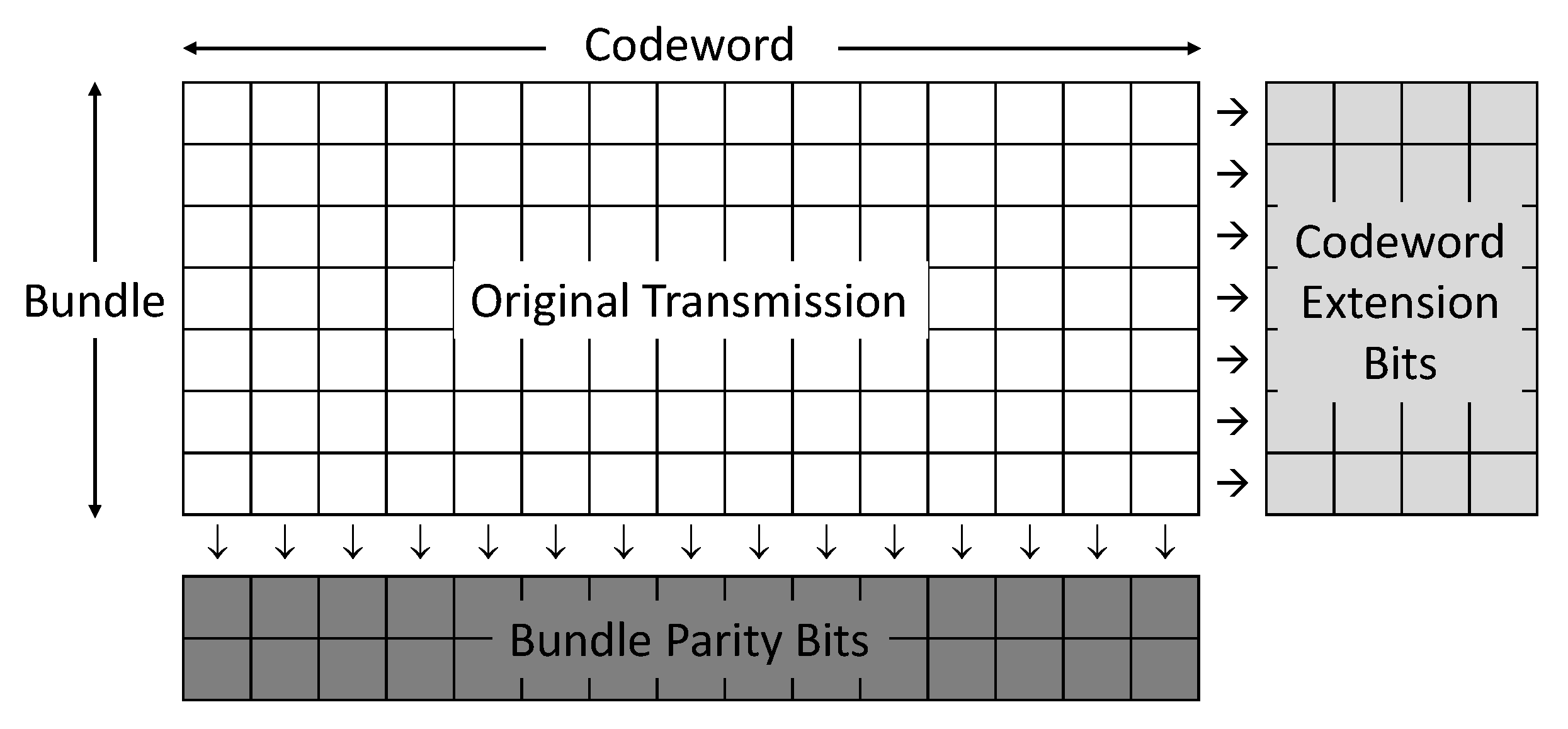
• State: $s=(f,SNR,R)$, where f denotes the number of decoding failures in the bundle, $SNR$ their effective SNR, and R their coding rate.
• Action: $A\left(s\right)=(\alpha ,\beta )$, where $\alpha$ and $\beta$ respectively represent the requested number of extension bits for every codeword in the bundle and the requested number of bundle parity bits. Chase Combining bits will not be used because for typical values of SNR and code rate, their performance is inferior compared to extension bits [46].
• Cost: $C=b\alpha +\beta +f{c}_D+c_R$, where b denotes the bundle size (i.e., number of codewords per bundle). Assuming that transmitting one bit costs one unit, $c_D$ denotes the cost to decode a single codeword, and $c_R$ denotes the overhead cost due to each round of IR accounting for hardware complexity, increased latency, feedback bits, etc. One possible interpretation for this cost is latency. In that case, $c_D$ would be the time required to decode a codeword and $c_R$ the time between retransmissions.

The objective is to find the actions that minimize the total expected cost until all codewords in the bundle are successfully decoded, i.e.,

$$A\left(s\right)=arg\underset{(\alpha ,\beta )}{min}E\left\{\mathrm{Total}\cos \mathrm{t}\right|s,\alpha ,\beta \},$$

(16)

for all s. By sending IR bits, $\alpha$ reduces the code rate and $\beta$ increases the SNR, transitioning from $s_0=(f_0,SN{R}_0,R_0)$ to a new state $s_1=(f_1,SN{R}_1,R_1)$, where $SN{R}_1$ and $R_1$ are deterministic and $f_1\le f_0$ follows a binomial distribution. They can be determined by the following equations:

$$\begin{array}{cc}\hfill & SN{R}_1={\left[\left(\frac{\alpha }{SN{R}_{IR}}+\frac{\beta }{SN{R}_{\mathrm{new}}}+\frac{k/R_0-\beta }{SN{R}_0}\right)\frac{1}{k/R_0+\alpha }\right]}^{-1}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & R_1=\frac{k}{k/R_0+\alpha }\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & P\left(f_1\right|s_0,\alpha ,\beta )=\left(\genfrac{}{}{0pt}{}{f_0}{f_1}\right)p^{f_1}{(1-p)}^{f_0-f_1},\hfill \end{array}$$

(19)

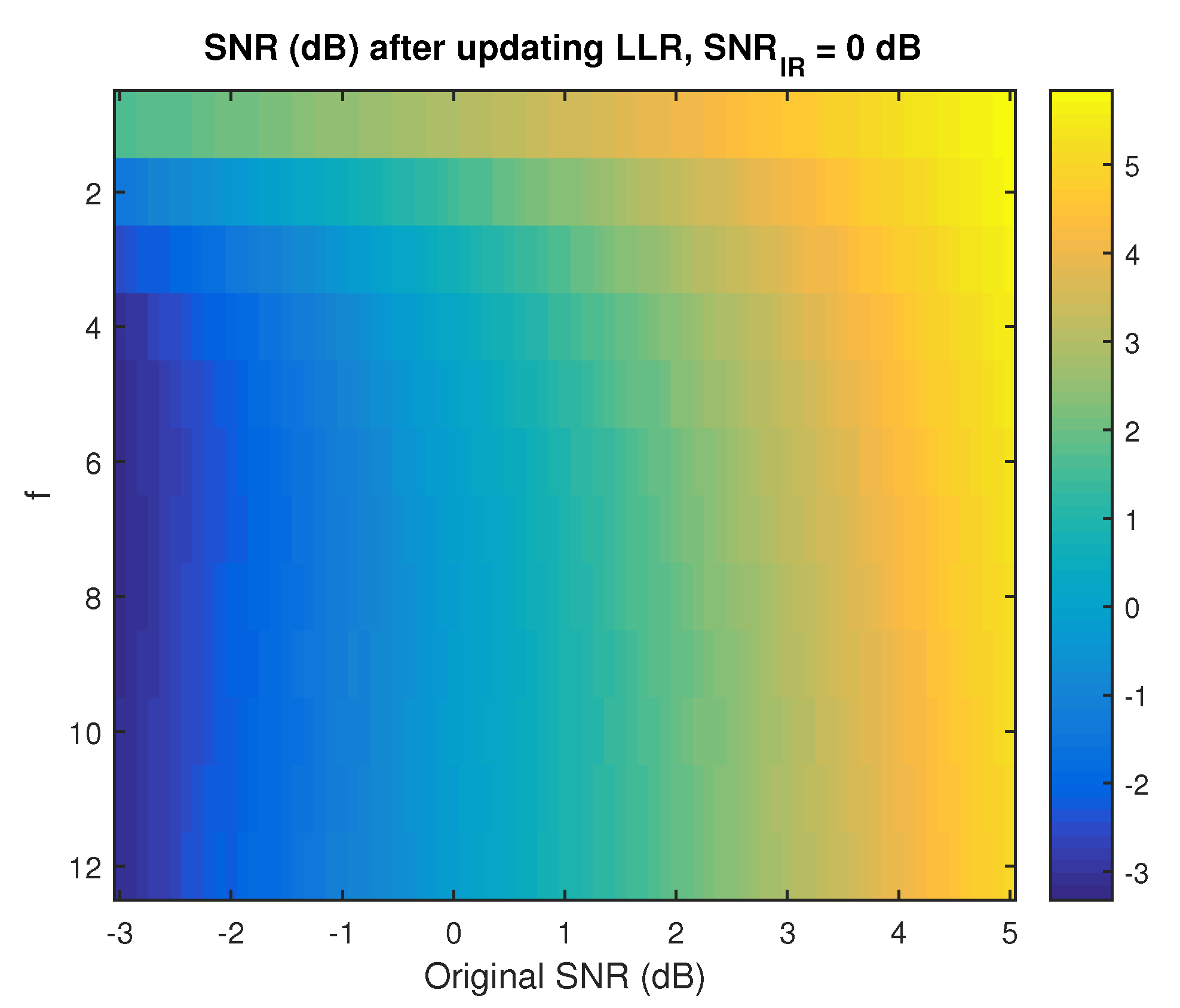
where k denotes the number of information bits per codeword and $SN{R}_{\mathrm{new}}$ denotes the increased SNR of the bits that participated in the bundle parity IR, as given by Equation (14) and illustrated in Figure 3. The formula for $SN{R}_1$ is obtained from Equation (15) by observing that every codeword in a bundle can be partitioned into three sections according to the SNR: the $\alpha$ bits of codeword extension have $SN{R}_{IR}$, the $\beta$ bits of overlapping part with bundle parity IR have $SN{R}_{\mathrm{new}}$ after updating their LLRs, and the remaining $k/R_0-\beta$ bits keep the same $SN{R}_0$ as before receiving the IR. The probability p in Equation (19) denotes the conditional probability that a codeword fails in state $s_1$ given that it failed in $s_0$, and can be computed using Equation (1) as

$$p=\frac{P_e(R_1,SN{R}_1)}{P_e(R_0,SN{R}_0)}.$$

(20)

For any state s and $SN{R}_{IR}$, the total expected future cost V and the optimal action A can be expressed recursively as follows:

$$\begin{array}{cc}\hfill V(s,SN{R}_{IR})& =E\left[\mathrm{Total}\cos \mathrm{t}\right|s,\alpha ,\beta ]\hfill \\ & =b\alpha +\beta +f{c}_D+c_R+\sum _{s^{\prime }}P\left(s^{\prime }\right|s,\alpha ,\beta )V(s^{\prime },SN{R}_{IR})\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill A(s,SN{R}_{IR})& =arg\underset{(\alpha ,\beta )}{min}V(s,SN{R}_{IR}),\hfill \end{array}$$

(22)

where the summation is taken over all possible states $s^{\prime }$ to which s can transition according to Equations (17)–(19) given that $(\alpha ,\beta )$ IR bits are sent. $P\left(s^{\prime }\right|s,\alpha ,\beta )$ denotes the state transition probability.

If we discretize the states and actions to take values from a finite set, the value iteration algorithm [49] can then be used to numerically find $V(s,SN{R}_{IR})$ and $A(s,SN{R}_{IR})$ for all s and $SN{R}_{IR}$. Essentially, value iteration initializes V with random values, and alternates between finding the optimal actions A according to Equation (22) and updating the value V according to Equation (21), until convergence. 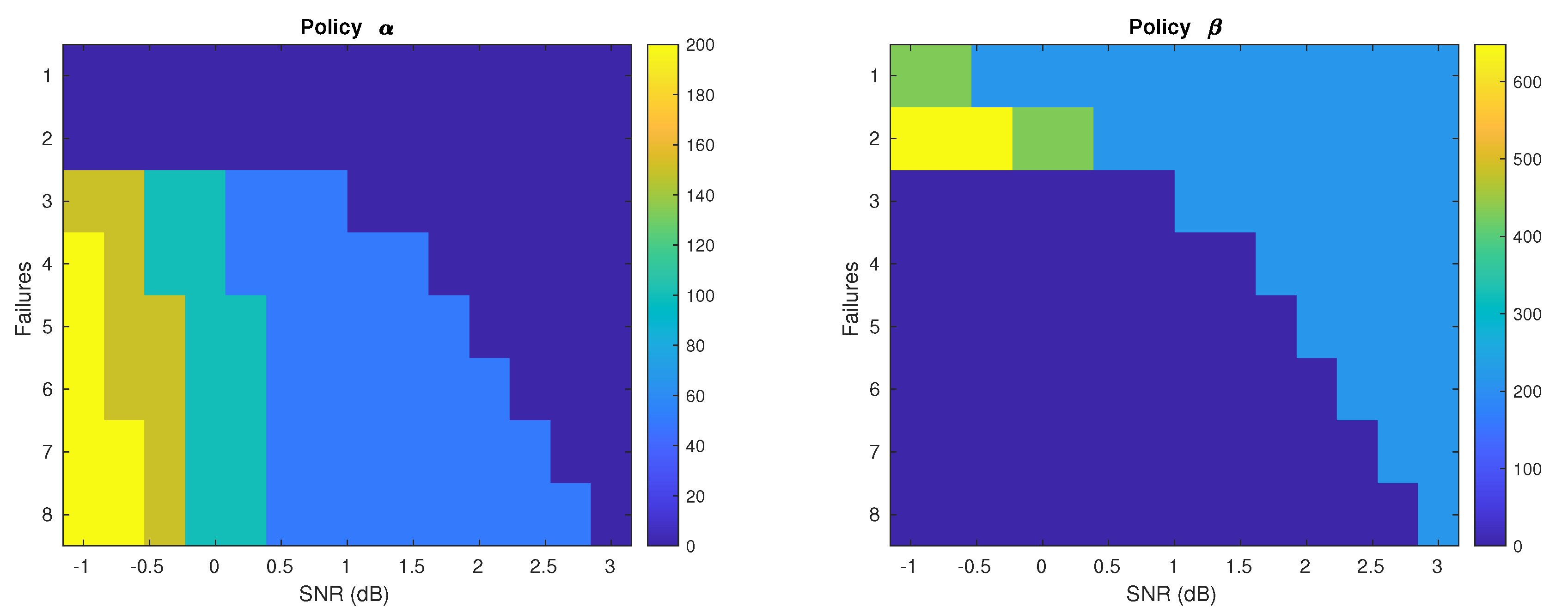At that point $A(s,SN{R}_{IR})$ stores the optimal policy to follow when the HARQ process is at state s expecting $SN{R}_{IR}$ for the IR, while $V(s,SN{R}_{IR})$ stores the total expected future cost until successfully decoding all codewords in the bundle at the receiver.

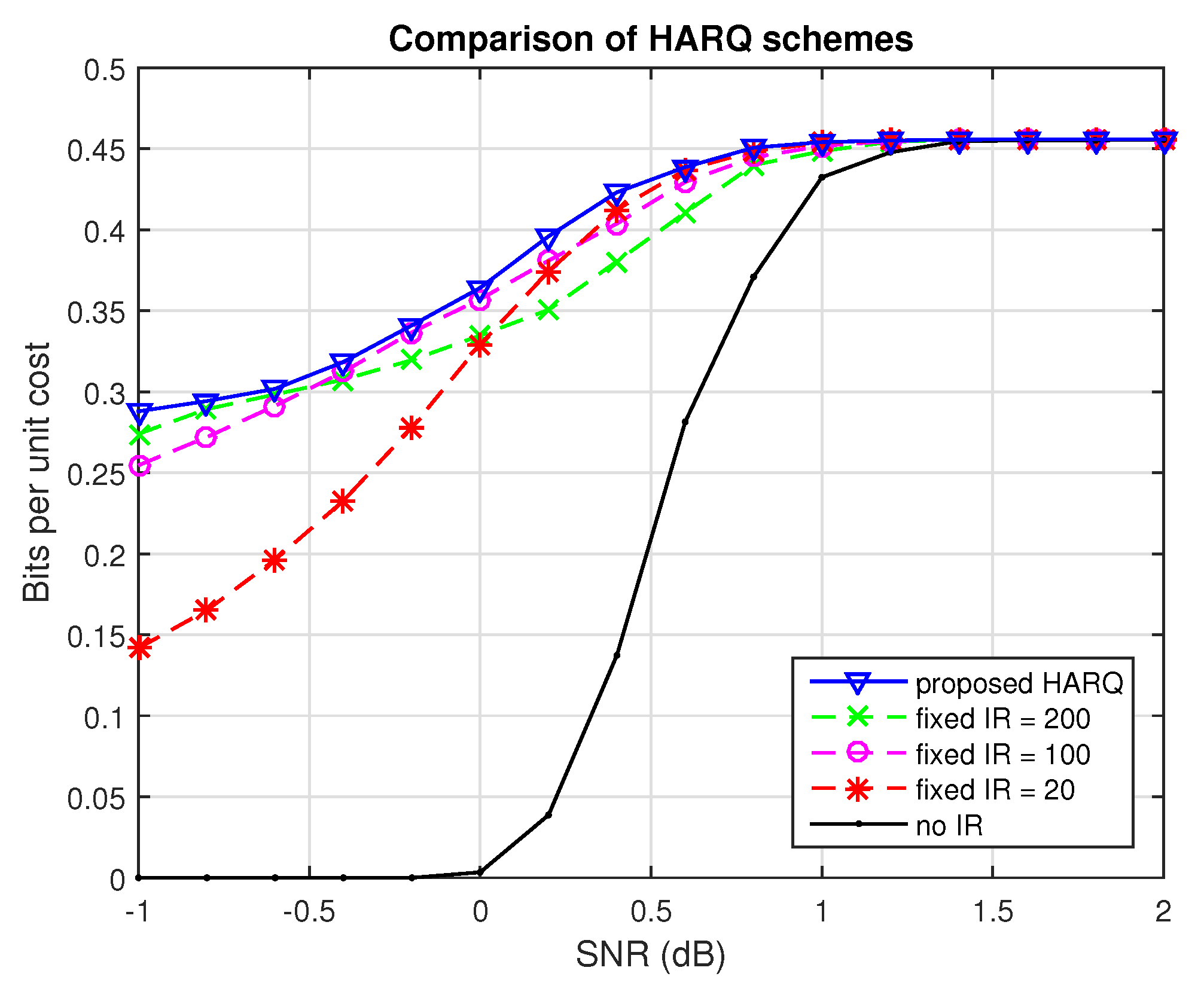
The single link scenario decision engine is specified by the policy A, and it can be readily extended to individual links in a multi-hop scenario as well. The receiver can estimate its state by computing the bundle’s relevant statistics when decoding failures occur, and it then follows A to request a combination of $(\alpha ,\beta )$ IR bits from the transmitter.

5. Decision Engine for Relay

This section extends the framework described in Section 4 to the two-hop scenario illustrated in Figure 1. On top of optimizing the type and number of IR bits to be transmitted, the intermediate station also has to decide between using an amplify and forward (AF) or decode and forward (DF) relay strategy. In order to compare both strategies, we propose a parametric cost model for each of them and a decision engine to minimize the average cost per successfully delivered information bit. Specifically, we model the cost of AF and DF ($c_{AF}$ and $c_{DF}$) as functions of the SNR on both links ($SN{R}_1$ and $SN{R}_2$) and the code rate in the first link ($R_1$). As in the single link decision engine, the decoding cost $c_D$ and the overhead cost $c_R$ are normalized by the cost of transmitting 1 bit of information over one link.

5.1. Cost of DF

With a DF relaying strategy, both links can be treated as independent. Thus, the cost of DF is decomposed as

$$c_{DF}=c_1+c_2,$$

(23)

where $c_j$ is the expected cost on the j-th link ($j=1,2$). We further decompose each $c_j$ as the sum of three terms: the number of bits sent on the j-th link, the cost of decoding the b codewords in the bundle, and the expected future cost in the case of decoding failures. Thus,

$$\begin{array}{c}\hfill c_j=\frac{bk}{R_j}+b{c}_D+\sum _{i=1}^b{P}_B(b,p_j,i){\delta }_j\left(i\right),\end{array}$$

(24)

where $P_B(b,p_j,i):=\left(\genfrac{}{}{0pt}{}{b}{i}\right)p_j^i{(1-p_j)}^{b-i}$ represents the probability of suffering i failures in the bundle and ${\delta }_j\left(i\right)$ represents the expected future cost on the j-th link when that happens. The probability of failure $p_j=P_e(R_j,SN{R}_j)$ is obtained from Equation (1) and

$$\begin{array}{c}\hfill {\delta }_j\left(i\right)=V((i,SN{R}_j,R_j),SN{R}_{IR,j})\end{array}$$

(25)

is given by Equation (21) from the single link scenario. The code rate on the second link $R_2$ should be chosen such that $c_2$ is minimized. For the sake of simplicity, we assume that the IR experiences the same SNR as the original codewords in the relay scenario, hence $SN{R}_{IR,j}=SN{R}_j$ for both links $j=1,2$.

5.2. Cost of AF

With an AF strategy, the relay is assumed to keep the code rate unchanged, i.e., $R_2=R_1$, so the same number of bits is sent over both links in the first transmission. Decoding the bundle at the end user costs $b{c}_D$ plus any cost associated to IR if failures occur. Thus, the cost of AF is decomposed as

$$\begin{array}{c}\hfill c_{AF}=2·\frac{bk}{R_1}+b{c}_D+\sum _{i=1}^b{P}_B(b,p_{AF},i){\delta }_{AF}\left(i\right),\end{array}$$

(26)

where $p_{AF}=P_e(R_1,SN{R}_{AF})$, $SN{R}_{AF}$ is taken from Equation (10), and ${\delta }_{AF}\left(i\right)$ denotes the expected future cost when i failures are present at the end user. If decoding failures do occur, the end user will request IR from the relay. We assume that the relay always reverts back to a DF strategy in this case, decoding the cached bundle with IR from the base station if necessary. If there are j failed codewords at the relay, decoding the entire bundle will cost $V((j,SN{R}_1,R_1),SN{R}_1)$. Once the relay has succeeded at decoding the whole bundle, it can generate and transmit the IR that the end user requested. This step costs another $V((i,SN{R}_{AF},R_2),SN{R}_2)$.

With AF, the noise accumulates over the two links. It is therefore very unlikely for a codeword that could not be decoded at the relay to be correctly decoded at the end user. Similarly, if a codeword was correctly decoded by the end user we assume that it will also be successfully decoded by the relay. The number of failures at the relay then follows a binomial distribution with i representing the number of failures at the end user and $p_R$ representing the conditional probability that a codeword fails at the relay conditioned on it failing at the end user. Hence,

$$\begin{array}{cc}\hfill {\delta }_{AF}\left(i\right)& =b{c}_D+V((i,SN{R}_{AF},R_2),SN{R}_2)\hfill \\ \hfill & +\sum _{j=1}^i{P}_B(i,p_R,j)V((j,SN{R}_1,R_1),SN{R}_1),\hfill \end{array}$$

(27)

where

$$p_R=\frac{P_e(R_1,SN{R}_1)}{P_e(R_1,SN{R}_{AF})}$$

follows from Bayes’ rule.

The values of $c_{DF}$ and $c_{AF}$ can now be computed for all discretized values of $SN{R}_1$, $SN{R}_2$, and $R_1$ using Equations (23) and (26). A decision map is then generated by specifying whether AF or DF provides lower expected cost. According to this decision map, the relay can make the AF or DF decision by estimating the SNR on the two links and finding the rate of the received codeword in a practical situation.

6. Decision Engine for Multi-User Systems

This section addresses a system where a single server (or base station) uses a broadcast link to deliver content to multiple users. The channels from the base station (BS) to each user experience different and independent SNR, so when the BS broadcasts a bundle of codewords, each user is able to decode some of them but not others. If all users are interested in decoding all codewords the problem is similar to that of a single link: it makes sense to focus on the user with the most failures and broadcast the corresponding IR bits, that all other users are also able to hear and use in their own data recovery. However, we analyze the more interesting case in which each user is only interested in a subset of the codewords but can overhear and attempt to decode those meant for other users. Furthermore, we assume that users can report the specific codewords that they succeeded in decoding. In this case, the BS can leverage that information and use network coding schemes to optimize the IR [35,36,50,51]. Since not all users are interested in all codewords, extension IR bits for any given codeword would only benefit a subset of the users, possibly a single one. Bundle parity bits obtained by taking the XOR of multiple codewords, however, have the potential to help multiple users decode their desired information. This section focuses on optimizing the choice of codewords in such combinations and the number of bundle parity bits to be sent for each of them.

Consider a bundle of codewords being broadcast to multiple users, so that user i is only interested in codeword i but overhears all the others. If user i can successfully decode codeword i, then it is done and does not require any IR. Our goal is to minimize the total number of IR bits sent while ensuring a minimal probability of success for all the users who failed to do so. Let b denote the number of users that fail to decode their corresponding codewords, and consider all the possible subsets of $\{1,\dots ,b\}$, indexed with numbers between 0 and $2^b-1$. A simple way of doing this would be to use the binary representation of the elements included in the subset. Let ${\mathsf{\Omega }}_k\subseteq \{1,\dots ,b\}$ represent the k-th such subset for $k=0,\dots ,2^b-1$, so that $j\in {\mathsf{\Omega }}_k$ if and only if $\lfloor k/2^{j-1}\rfloor$ is odd. Let ${\beta }_k$ represent the number of IR bits to be sent obtained from the XOR of the codewords in ${\mathsf{\Omega }}_k$. Then the problem that we are trying to solve is

$$\begin{array}{cc}\hfill \mathrm{minimize}& {\displaystyle \sum _{k=0}^{2^b-1}{\beta }_k}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& P_e^{\left(i\right)}\le \gamma ,i=1,\dots ,b\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\beta }_k\ge 0,k=0,\dots ,2^b-1\hfill \end{array}$$

(30)

where $P_e^{\left(i\right)}$ represents the probability of user i failing to decode after receiving the IR, conditioned on having failed without it, and $\gamma$ represents the highest such probability that we are willing to tolerate. The failure probability $P_e^{\left(i\right)}$ depends on $SN{R}_0^{\left(i\right)}$, the SNR of the original codeword, and on $SN{R}_{\mathrm{eff}}^{\left(i\right)}$, the effective SNR after IR defined in Equation (15). The latter is itself a function of $\mathbf{\beta }=({\beta }_1,{\beta }_2,\dots ,{\beta }_{2^b-1})$, as described below.

Let ${\chi }_i\in \{1,\dots ,b\}$ represent the indices of the codewords that user i failed to decode and assume that $i\in {\chi }_i$ (otherwise the user has received its information and is out of the picture). Receiving ${\beta }_k$ bits from the XOR of codewords in ${\mathsf{\Omega }}_k$ would help user i increase the SNR in ${\beta }_k$ of the bits from codeword i. Figure 3 provides the new SNR for those bits, denoted $SN{R}_{\mathrm{new}}$, as a function of $SN{R}_0^{\left(i\right)}$ and the number of failed codewords in the XOR, denoted $f_k^{\left(i\right)}=|{\chi }_i\cap {\mathsf{\Omega }}_k|$. Assuming that the IR updates do not overlap, the effective SNR for user i after IR would be

$$SN{R}_{\mathrm{eff}}^{\left(i\right)}\left(\mathbf{\beta }\right)={\left[\frac{1}{SN{R}_0^{\left(i\right)}}+\frac{1}{n}\sum _{\{k:i\in {\Omega }_k\}}{\beta }_k\left(\frac{1}{SN{R}_{\mathrm{new}}(f_k^{\left(i\right)},SN{R}_0^{\left(i\right)})}-\frac{1}{SN{R}_0^{\left(i\right)}}\right)\right]}^{-1}.$$

(31)

Equations (1)–(3) and (20) can be used to rewrite the error constraints in (29) as

$$\begin{array}{cc}\hfill {\lambda }_i{a}_{\sigma }{z}_i{\left(\beta \right)}^{c_{\sigma }}-a_{\mu }{z}_i{\left(\beta \right)}^{c_{\mu }}& \le {\theta }_i\hfill \end{array}$$

(32)

for $i=1,\dots ,b$, where

$$\begin{array}{cc}\hfill {\lambda }_i& :=Q^{-1}\left(\gamma P_e(R,SN{R}_0^{\left(i\right)})\right),\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\theta }_i& :=b_{\mu }-R-{\lambda }_i{b}_{\sigma },\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill z_i\left(\mathbf{\beta }\right)& :={\left(SN{R}_{\mathrm{eff}}^{\left(i\right)}\left(\mathbf{\beta }\right)\right)}^{-1}.\hfill \end{array}$$

(35)

In the above definitions $P_e(R,SN{R}_0^{\left(i\right)})$ denotes the probability of error before IR and R the coding rate, assumed to be identical for all codewords for the sake of simplicity. Using the numerical values in Equations (4) and (5), problem (28) becomes

$$\begin{array}{cc}\mathrm{minimize}\hfill & {\displaystyle \sum _{k=0}^{2^b-1}{\beta }_k}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & 0.2z_i{\left(\mathbf{\beta }\right)}^{1.74}+0.12{\lambda }_i{z}_i{\left(\mathbf{\beta }\right)}^{0.42}\le {\theta }_i,i=1,\dots ,b\hfill \\ \hfill & {\beta }_k\ge 0,k=0,\dots ,2^b-1.\hfill \end{array}$$

(36)

Observe that $z_i\left(\mathbf{\beta }\right)$ is a linear function of $\mathbf{\beta }$, as shown in Equation (31). Assuming that $z_i\left(\mathbf{\beta }\right)\ge 0.5$, since the model in Equation (1) is not valid outside of that range, the above problem is convex for $\gamma \ge \frac{2.3}{P_e(R,SN{R}_0)}·{10}^{-4}$ and can be solved by any of the many existing convex optimization methods [52]. The solution $\mathbf{\beta }=({\beta }_1,\dots ,{\beta }_{2^b-1})$, with all values rounded to the nearest integer, provides a good approximation to the optimal combination of IR bits to be sent so as to guarantee a probability of success above $1-\gamma$ for all users.

7. Numerical Results

We now simulate the proposed methods and show numerical results to evaluate their performance. All simulations assume a bundle size of $b=8$ codewords obtained from the QC-LDPC code of length $n=648$ and $k=432$ (rate 2/3) specified in [41]. Decoding and retransmission overhead costs are set to $c_D=300$ and $c_R=100$.

7.1. Single Link

This subsection simulates the method described in Section 4. As a reminder, the goal was to optimize the number and type of IR bits to be sent when there is a direct link between the transmitter and the receiver. Value iteration was applied to Equations (21) and (22) to yield a policy $A(f,SNR,R,SN{R}_{IR})$ specifying the number of extension bits ($\alpha$) and bundle parity bits ($\beta$) to be requested as a function of the number of failed codewords remaining in the bundle f and their effective $SNR$. We restrict the range of $\alpha$ and $\beta$ to be $[0,216]$ and $[0,648]$ respectively, so that the set of actions is finite. Figure 5 shows a slice of the policy for code rate $R=2/3$ and the IR having the same SNR as the original bundle, ($SN{R}_{IR}=SNR$). It can be seen that the sum of $\alpha$ and $\beta$ increases as the SNR decreases. This is because more IR bits are required to recover a highly corrupted bundle. In addition, our policy suggests that bundle parity bits are preferred over extension bits when there is a small number of failed codewords. This is worth noticing, since bundle parity is equivalent to Chase Combining when there is a single failure and extension bits generally offer better performance than Chase Combining [46]. However, the feedback limitations in our system prevent the receiver from conveying to the transmitter the specific codewords that failed; if extension bits were requested, the transmitter would have to send them for every codeword in the bundle, even for those that have already been successfully decoded. The policy illustrated in Figure 5 has less than 16 possible combinations of $(\alpha ,\beta )$, so it suffices to use 4 feedback bits to specify the request. This translates to only 1 bit of feedback per 2 codewords, which is half as much feedback as traditional fixed-length IR schemes with individual acknowledgements.

Figure 6 compares the number of information bits delivered per unit cost for different IR schemes. Each point in the plot is the result of averaging Monte Carlo simulations for 1000 bundles and unlimited rounds of IR until success. If we interpret the cost as delay, then the number of information bits delivered divided by the cost will be the throughput. It can be observed that our HARQ policy provides modest gains over those with a fixed IR length, regardless of what this fixed number is and the SNR of the channel. These gains would be even larger in a scenario with variable SNR where, unlike fixed IR schemes, the proposed HARQ protocol would be able to adapt the IR length to each individual bundle.

7.2. Relay

This subsection simulates the method described in Section 5. As a reminder, a relay between the transmitter and receiver has to decide between AF and DF, using the same policies as in the single link scenario when failures occurred. The costs $c_{DF}$ and $c_{AF}$, defined in Equations (23) and (26), are computed offline and compared to obtain the decision map. The relay estimates the SNR of both channels, finds the code rate of the received bundle, and looks up the decision map for whether or not to decode it. Figure 7 shows the decision map for $R_1=2/3$. It can be observed that AF is preferred when both $SN{R}_1$ and $SN{R}_2$ are high enough, since the resulting $SN{R}_{AF}$ is high and so AF removes the decoding cost at the relay, offsetting the small additional risk of decoding failure at the end user. Especially when $SN{R}_2>4.5$ dB, AF is the better choice regardless of $SN{R}_1$. The simulations also show that the AF region shifts to the right as the code rate $R_1$ increases. This makes sense because for higher code rates, the $SNR$ must be increased correspondingly so that the risk of decoding failure is maintained at a low level for AF to prevail as discussed earlier.

Monte Carlo simulations also verify that the proposed relay HARQ strategy provides higher throughput than existing ones. Again, we could interpret the cost as delay, and so the information bits delivered per unit cost would measure the average throughput. The simulations first use an AWGN channel with deterministic gain to show that the relay decision map in Figure 7 indeed chooses the forwarding scheme with a higher throughput. We then introduce stochastic channel gains to simulate a more practical scenario. Although the relay decision engine was derived based on the assumption of AWGN channels, we show that the smart relay using our proposed policy based on the measured channel side information (CSI) is also suitable in this scenario and outperforms a fixed AF or DF relay.

In order to perform a fair comparison all relays use the same HARQ strategy described earlier when it comes to the single-link regime. Figure 8 shows the average throughput using different relay strategies as a function of $SN{R}_2$, given a fixed $SN{R}_1=4$ dB and $R_1=2/3$. The relay decision map in Figure 7 predicts that AF is the better choice if $SN{R}_2>3$ dB, and indeed we see in the figure that AF results in higher throughput than DF when $SN{R}_1>3$ dB. The smart relay is programmed to take the strategy with higher throughput.

Using the decision map should provide an advantage against channel variations because the relay can measure the SNR of its received signal and adopt the appropriate strategy accordingly, whereas a relay with fixed forwarding scheme will fail to adapt to the time-varying channel. The received signal is modeled as $y=gx+n$ where we assume unit transmit power ($E\left[x^2\right]=1$) and additive Gaussian noise $n\sim \mathcal{N}(0,{\sigma }^2)$. The channel gain g is uniformly distributed over the range $[0.75,1.25]$, remaining constant within each bundle but changing across different bundles and links. Figure 9 shows the average throughput of the different relay strategies in the fading scenario as a function of $SN{R}_2$ for fixed $SN{R}_1=4$ dB and $R_1=2/3$. The smart relay exhibits a noticeable gain in throughput compared to AF or DF only relays. The gain is especially prominent in the region where AF and DF have similar performance, because our proposed hybrid relay strategy combines the advantages of both when neither of them significantly dominates the other.

7.3. Multi-User Systems

This subsection simulates the method described in Section 6. As a reminder, a single transmitter is delivering content to multiple receivers using a broadcast link. Each receiver is only interested in a subset of the codewords, but can overhear the others. Our goal is to minimize the number of IR bits to be broadcast in order to guarantee a certain probability of success for all users who suffered failures in decoding their desired information.

Figure 10 compares the average number of incremental redundancy bits resulting from Equation (36) with that required if we were to send extension bits for every codeword that failed decoding at its desired receiver. Each point in the plot is the result of 100 Monte Carlo simulations with rate $R=0.5$ broadcast to eight users experiencing random SNR uniformly distributed between $-2$ dB and $-1$ dB. According to Equation (1), that yields a probability of decoding failure between 0.1 and 0.9 per codeword at each user.

We used a logarithmic barrier method coupled with Newton descent to solve problem (36) and plotted the average ${\parallel \mathbf{\beta }\parallel }_1$ (number of IR bits) for different values of $\gamma$ (probability of error after receiving the IR). Then, we used Equation (1) to derive the number of extension bits that would be required to guarantee the same probability of error for all users. As it can be seen, our proposed method requires significantly fewer bits regardless of $\gamma$.

In most practical instances, the solution to problem (36) is not unique. There is a whole subspace of optimal values for $\mathbf{\beta }$. In order to obtain a sparse solution, we introduced a small random perturbation in the objective, minimizing ${\sum }_{k=0}^{2^b-1}(1+{ϵ}_k){\beta }_k$ instead of ${\sum }_{k=0}^{2^b-1}{\beta }_k$, where ${ϵ}_k$ are random noise variables distributed between 0 and ${10}^{-2}$. The result was that, in most cases, the number of non-zero entries in $\mathbf{\beta }$ was lower than the number of failed codewords. This means that, on top of requiring fewer IR bits, our method is also able to group them into fewer types than a pure extension approach, reducing the amount of overhead.

8. Conclusions

This paper addresses the problem of error correction in single link, relay, and broadcast systems. Specifically, it proposes techniques for optimizing the incremental redundancy (IR) bits sent by an HARQ protocol under the assumption that the feedback channel can only support a few bits of feedback per bundle of codewords (or packets). Apart from the traditional extension IR bits, consisting of a few additional bits for each codeword, this paper also considers bundle IR, consisting of encoded IR bits which the receiver can use to refine the LLRs in multiple codewords.

The allocation of IR bits in a single link is modelled as a Markov Decision Process seeking to minimize a pre-determined cost function. The paper describes how the problem should be formulated and solved, resulting in a set of policies parameterized by the number of failures per codeword bundle, effective SNR of the received codewords, and coding rate. It then extends this single link framework to a relay scenario, where an intermediate node has to decide whether to decode (DF) or just amplify (AF) incoming bundles before forwarding them on. Finally, the paper studies a multiuser scenario where a single source broadcasts information to multiple receivers with different interests. It proposes transmitting encoded IR bits that benefit multiple receivers and formulates a convex problem to optimize their number and encoding.

Numerical simulations show that the proposed methods provide a modest increase in throughput compared to traditional HARQ schemes with fixed-length codeword extension. The proposed policy for the relay outperforms fixed forwarding strategies and the proposed strategy for broadcast systems significantly reduces the total number of IR bits needed to guarantee a given probability of success, compared to sending individual extension bits for each codeword. The increased flexibility in requesting different numbers and types of IR bits and the ability to make decisions based on the measurement of the received signals display significant advantages in limited feedback communication systems.