1. Introduction
Communication systems are naturally prone to varying channel conditions. Before the recent information explosion, it was common for systems to use conservative configurations which allowed them to operate in a wide range of conditions, but this came at the expense of performance. In order to accommodate the ever-growing traffic requirements of next generation communication devices, researchers are now using adaptive schemes to maximize bandwidth efficiency and squeeze as much throughput as possible in every situation. A significant amount of work has been devoted to designing algorithms for adapting physical layer parameters such as the transmit power, modulation and coding rate based on the channel state information [
1,
2,
3,
4,
5], but there is not as much literature on adaptive retransmissions when failures occur despite it has been shown that they can provide significant gains in terms of both throughput [
6,
7,
8] and outage probability [
9,
10].
Traditional automatic repeat request (ARQ) forces the receiver to send an acknowledgment (ACK) back to the transmitter for every packet it successfully decodes, and a negative-acknowledgment (NACK) otherwise. If the transmitter does not receive an ACK before the timeout expires, the entire packet will be resent, assuming that it is still within the latency limit. Retransmitting the whole packet is justified when the previous one has been completely lost, but in many cases, the received packet can be partially recovered, and it still contains useful information for the decoder, even if it cannot be entirely decoded. In those cases, it is more efficient if the receiver can recover the whole packet with the help of a few additional bits sent from the transmitter, referred to as incremental redundancy (IR). This is commonly known as Type-II hybrid automatic repeat request (Type-II HARQ) [
11], and it is the focus of this paper.
The achievable data rate (throughput) with Type-II HARQ has been upper-bounded under the assumption of unlimited single bit IR and perfect feedback [
6,
12] and several methods have been proposed to construct IR bits [
13,
14] or optimize their block lengths under a finite number of retransmissions [
15,
16]. However, most of these works have focused on extending idealized error correcting codes (ECC) in known channels with either infinite or single-bit feedback. Some works have proposed more realistic models accounting for system-level constraints [
17,
18,
19], bundling multiple packets in one resource block [
8,
20] and imperfect channel information [
21]. The first part of this paper takes one step further in this direction by introducing a new type of IR bits and proposing frameworks to optimize the number and type of IR bits to be sent in scenarios with imperfect ECC, limited feedback, packet bundling, and overhead costs for each round of incremental redundancy. It models the problem as a Markov decision process (MDP) which minimizes the average cost per information bit delivered, relying on a code-specific Gaussian model for the probability of decoding failure as a function of signal-to-noise ratio (SNR) and code rate. By adjusting the relative costs associated to decoding and retransmissions, this method can be used to model practical constraints such as latency and hardware.
HARQ has been included and widely deployed in recent cellular networks such as Long-Term Evolution (LTE) [
22,
23] and 5G NR [
24], and there are studies that evaluate its performance [
25]. However, most standards proposed the use of fixed-length IRs due to practical constraints. LTE generally assigns one bit feedback per transport block, equivalent to one bit per codeword. The 5G NR standard includes multiple types of operations and is a little more flexible, but does not rise to the level that we propose in this paper. It still uses ACK or NACK and pre-fixed IR lengths. This paper shows that our proposed HARQ strategies can potentially achieve higher throughput by allowing even more flexibility than 5G NR in the types and lengths of IR retransmissions. In terms of channel coding, the punctured turbo codes in LTE have been replaced with low-density parity-check (LDPC) codes in 5G NR. Among other advantages, LDPC codes provide more flexible puncturing and rate adaptation, allowing for a nearly continuous number of IR bits. The ideas on this paper can be applied to any family of channel codes, but assume the use of LDPC codes by default.
Upcoming millimeter wave (mmWave) systems are likely to deploy dense networks of access points acting as relays between a base station and the end users, requiring HARQ strategies suitable for multi-hop architectures [
26,
27,
28]. These relay nodes have to decide between using amplify-and-forward (AF) or decode-and-forward (DF) when passing on information. AF amplifies and retransmits incoming packets as they are received, signal and noise. It is faster and less complex but noise accumulates over multiple hops until the packet can become unrecoverable. DF decodes the received signal and reencodes it before retransmission. This provides noise reduction and early detection of failures, but the required processing increases latency, complexity, and power consumption. Previous literature has shown that DF generally has higher channel capacity than AF [
29] and lower frame error rate (FER) with several HARQ protocols [
30]. However, some of the practical benefits of AF, such as simpler hardware and lower latency, were not considered in those studies. Hybrid schemes between AF and DF, such as transcoding [
31] or compress and forward [
32], have been shown to reduce the latency in modern 5G relay systems. Those schemes address how information is processed by the relay in each transmission, but do not address how to proceed when decoding failures occur. The second part of this paper shows how the MDP framework initially proposed for a single link scenario can be easily extended to account for the complexities of a relay system, including optimizing the decision between AF and DF.
Finally, the third part of this paper addresses another very relevant scenario for modern and future networks: multi-user systems where a single base station is communicating with multiple recipients. Even if each recipient is only interested in some of the information, it makes sense for the base station to bundle several packets and broadcast the bundle to all the users. If multiple users suffer a small number of decoding failures, the base station does not need to send individual IR to everyone; instead, it can broadcast one additional piece of information—for example the XOR (i.e., bitwise modulo 2 addition) of the packets in the bundle—to help multiple users decode their failed codewords. This idea, commonly known as network coded (H)ARQ, dates back to the 1980s [
33], but it has recently experienced a renewed interest from the research community due to its potential uses in the Internet of Things (IoT). Its maximal achievable throughput under idealized conditions was characterized in [
34], and [
35] extended that work with a deeper study of the practical overheads associated with various implementations. It showed that using general linear codes requires significantly more overhead than binary codes, since the transmitter not only needs to specify which packets are included in each linear combination, but also their coefficients. Hence, this paper only considers binary XOR packet combinations. The choice of packets to include is then a special case of the well-known index coding problem [
36,
37], but our framework also requires optimizing the number of bits to be sent, which further complicates the problem. Still, we show that it can be formulated in a relatively simple convex form. Numerical convex optimization algorithms can then be applied to solve for a good approximation to the optimum.
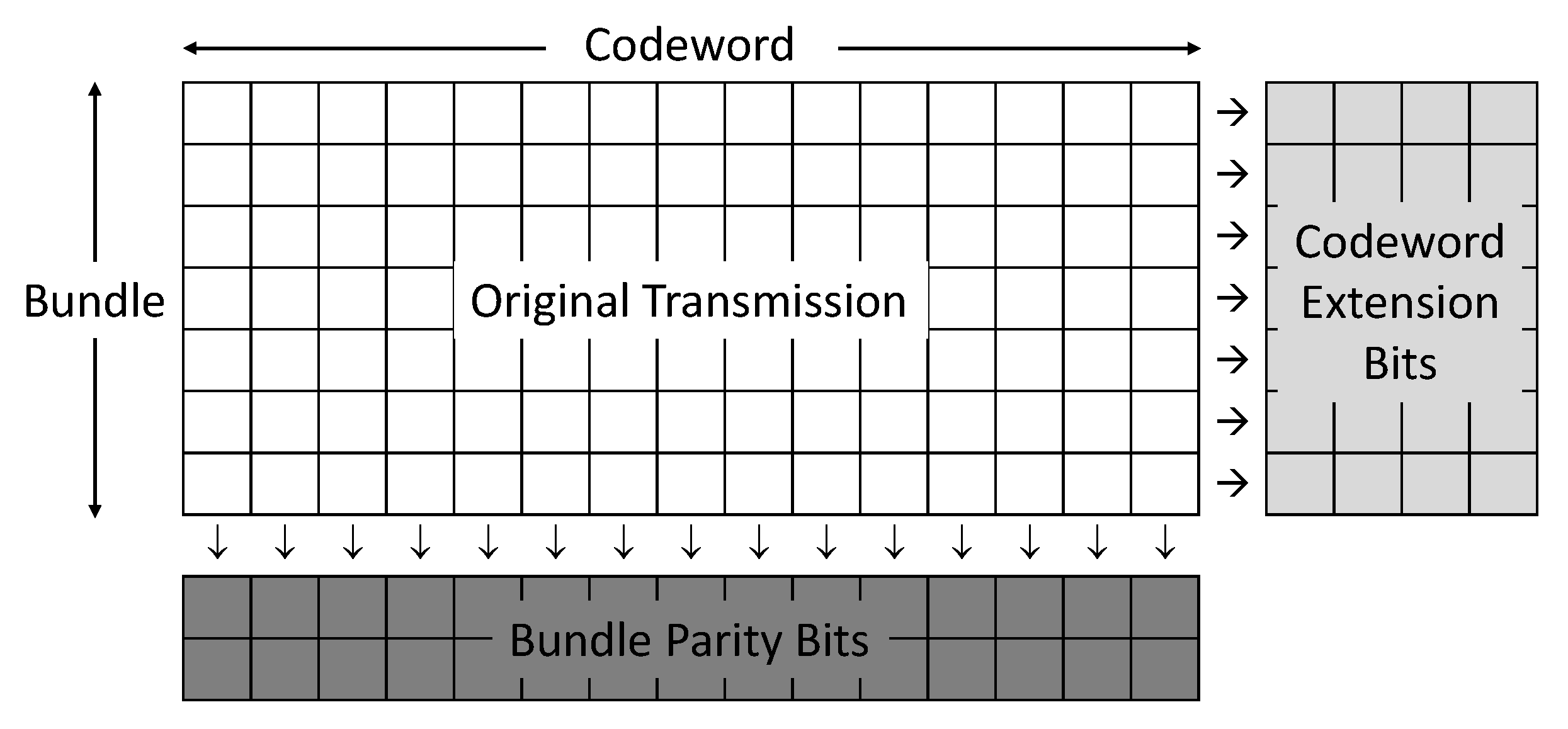
The main contributions of the paper can be summarized as follows. It introduces a new type of IR bit, bundle parity bits, computed across a bundle of codewords. It proposes an MDP model for the HARQ process over a point-to-point link, optimizing the type and number of IR bits to be sent when failures occur. It then shows how such HARQ scheme can be generalized and adapted to suit a two-hop relay network, where the relay node can be optimized to choose between AF and DF based on the channel state information. Finally, it considers a multi-user broadcast scenario and shows that the optimization of the HARQ can be formulated in a convex form. Numerical simulations verify the derivations, and show that the proposed methods achieve modest improvements against traditional schemes in all three scenarios.
The rest of the paper is organized as follows.
Section 2 explains the system model and some notation to be used throughout the paper.
Section 3 introduces the different types of IR bits being considered and how they can help in the decoding of a given bundle of codewords.
Section 4 builds a single-link decision engine optimizing the type and number of IR bits to be sent as a function of the channel SNR, coding rate, and number of failed codewords in the bundle.
Section 5 derives the decision engine for the relay, which decides between AF and DF relay strategies as a function of the SNRs on the two links and the code rate on the first link.
Section 6 addresses the case of multi-user systems, proposing a combinatorial optimization algorithm for deciding how the failed codewords should be grouped for the generation of IR when failures occur. Finally,
Section 7 illustrates the performance of our proposed policies through numerical simulations, and
Section 8 concludes the paper.
2. System Model
This section introduces the system models used throughout the paper. It first presents a single link scenario (with a direct channel between the transmitter and receiver) describing the channel, modulation, ECC, and HARQ schemes. Then it extends this scenario to the dual-hop relay system depicted in
Figure 1, where the base station (BS) can only reach the end user through an intermediate relay station (RS), and to a multi-user scenario where a single transmitter (possibly the relay) is communicating with multiple recipients. All the links in the relay and multi-user scenarios follow the same model as that in the single link scenario.
2.1. Channel and Modulation
Modern communication systems estimate the channel by periodically sending pilot signals, and use those estimates to adjust the modulation and coding schemes so as to maintain a certain frame error rate (FER). However, the unpredictable nature of channels and the blind period between channel sounding cycles make it impossible to achieve optimal adaptation for all codewords.
In this paper, channels are modeled as interference-free additive white Gaussian noise (AWGN). We assume that multiple codewords or packets (For simplicity, we assume that each packet consists of a single codeword and we refer to packets or codewords indistinctly. In a scenario where each packet consists of multiple codewords, we can either acknowledge codewords independently or treat each packet as a single unit which can either succeed or fail to decode. ) are bundled together into a single block, experiencing the same (often unknown) SNR at the receiver. All the IR bits requested in the same round also experience the same SNR, but this SNR is independent from that for the bundle and for previous rounds of IR (if any). This assumption is made in light of the fact that there is typically a delay between the transmissions of the original bundle and the IR, during which channel conditions could have changed.
In order to increase throughput, the transmitter uses high-order modulations with multiple bits per symbol for all but the noisiest channel conditions. Encoding these modulation symbols directly would increase the error correction capabilities [
38], but would complicate significantly the encoding and decoding. Treating the bits in a modulation symbol as independent and using binary error correcting codes is significantly simpler computationally, especially in the case of LDPC codes, but the performance is slightly worse than with non-binary error correction codes. Still, it is the most common approach in practice. Therefore, this paper assumes the use of binary encoders and decoders which operate as if the bits came from independent BPSK modulations with constant SNR throughout each codeword, even if higher order modulations are actually being used [
39].
2.2. Error Correction
Several works (e.g., [
15,
40]) have shown that the FER of a finite length code can be well approximated by
where
R represents the code rate (i.e., number of information bits divided by codeword length) and
and
are code-specific parameters that depend on the SNR. We model such dependency as
The techniques proposed in this paper could be applied to any code by adjusting the parameters (
,
,
,
,
,
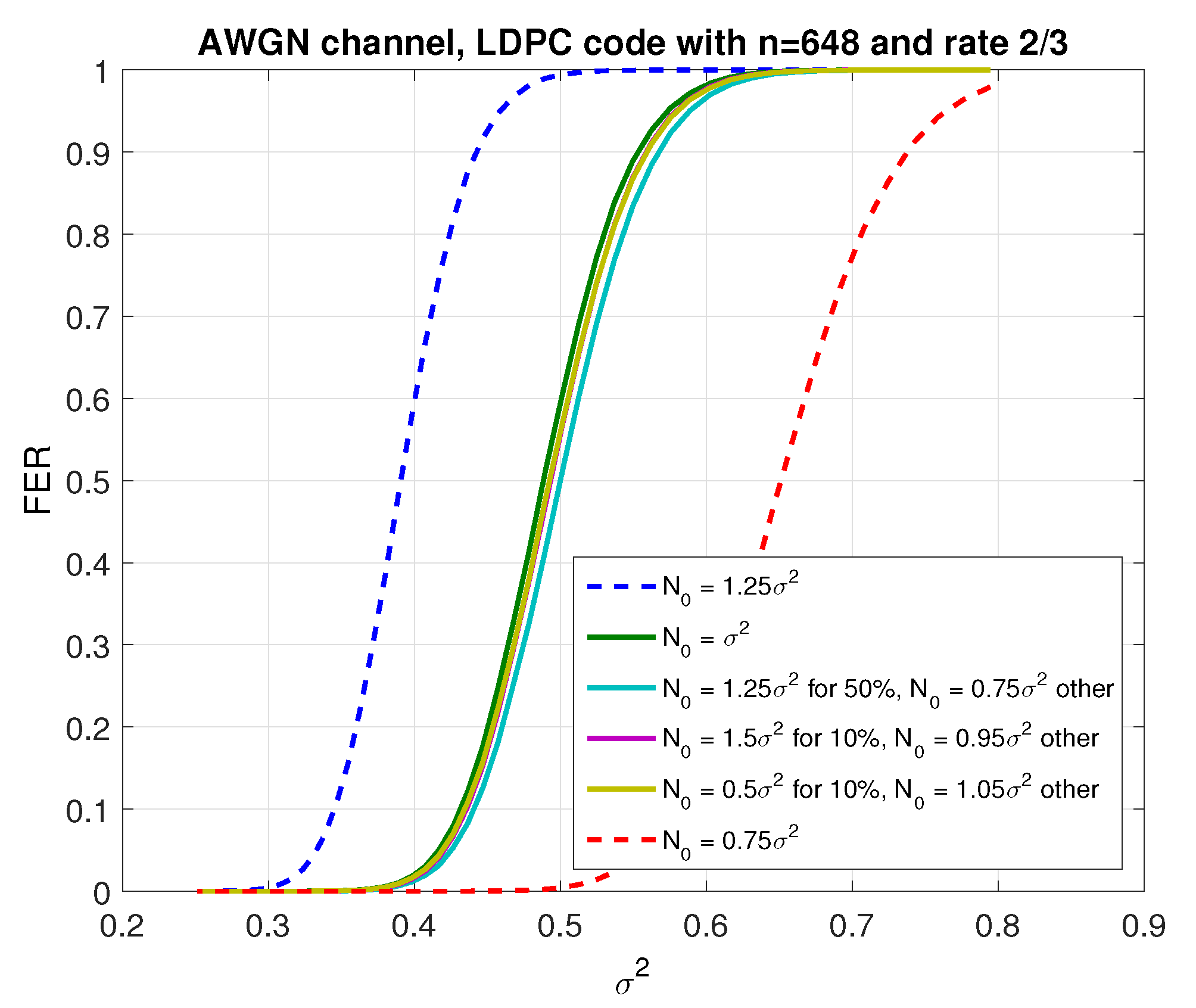
), but the numerical simulations in this paper will focus on the binary QC-LDPC code of length
and
(rate 2/3) proposed in the 3GPP standard for 802.11n [
41], for illustrative purposes. Our prior work [
42,
43] showed that
provide a good fit to this code when
.
Binary QC-LDPC codes offer very efficient encoding and decoding using parallel shift registers [
44,
45]. This has made them the preferred option in 5G NR, over turbo codes such as the ones proposed in the LTE standard. Additionally, QC-LDPC codes can be flexibly punctured and extended for nearly continuous rate adaptation. A QC-LDPC code is uniquely defined by a sparse parity check matrix
, such that
for all codewords
x. Received channel values (i.e., matched filter outputs) are processed to obtain a log-likelihood ratio (LLR) for each individual bit
b as
where
and
represent the conditional probability of
and
, respectively, given the received value
r. It is not hard to prove that for an AWGN channel with equiprobable and symmetric inputs, the LLR values are given by
The decoding of LDPC codes is typically done through message-passing algorithms, which refine these LLR values iteratively until convergence or until a prefixed maximum number of iterations is reached. When the algorithm does converge, it is almost always to the right codeword. We thus assume that a codeword error occurs if and only if the LDPC decoder fails to converge.
2.3. Single Link System: Hybrid ARQ
This paper focuses on the optimization of HARQ protocols, abstracting some of the other practical complexities that are present in real world communication networks. For example, the paper assumes perfect synchronization between all the nodes and error-free, albeit limited-capacity, feedback links. Feedback links are assumed to offer no more than one bit of feedback per packet, allowing for 256 possible responses to a bundle of eight packets, for instance. However, most of the proposed HARQ strategies do not require that many feedback messages, so the required number of feedback bits can be lower.
It is also assumed that the receiver can request as many rounds of incremental redundancy as needed until the whole bundle is successfully decoded. Each round is penalized with an adjustable overhead cost of per link plus a decoding cost of for each codeword for which decoding is attempted.
2.4. Relay System: Amplify or Decode?
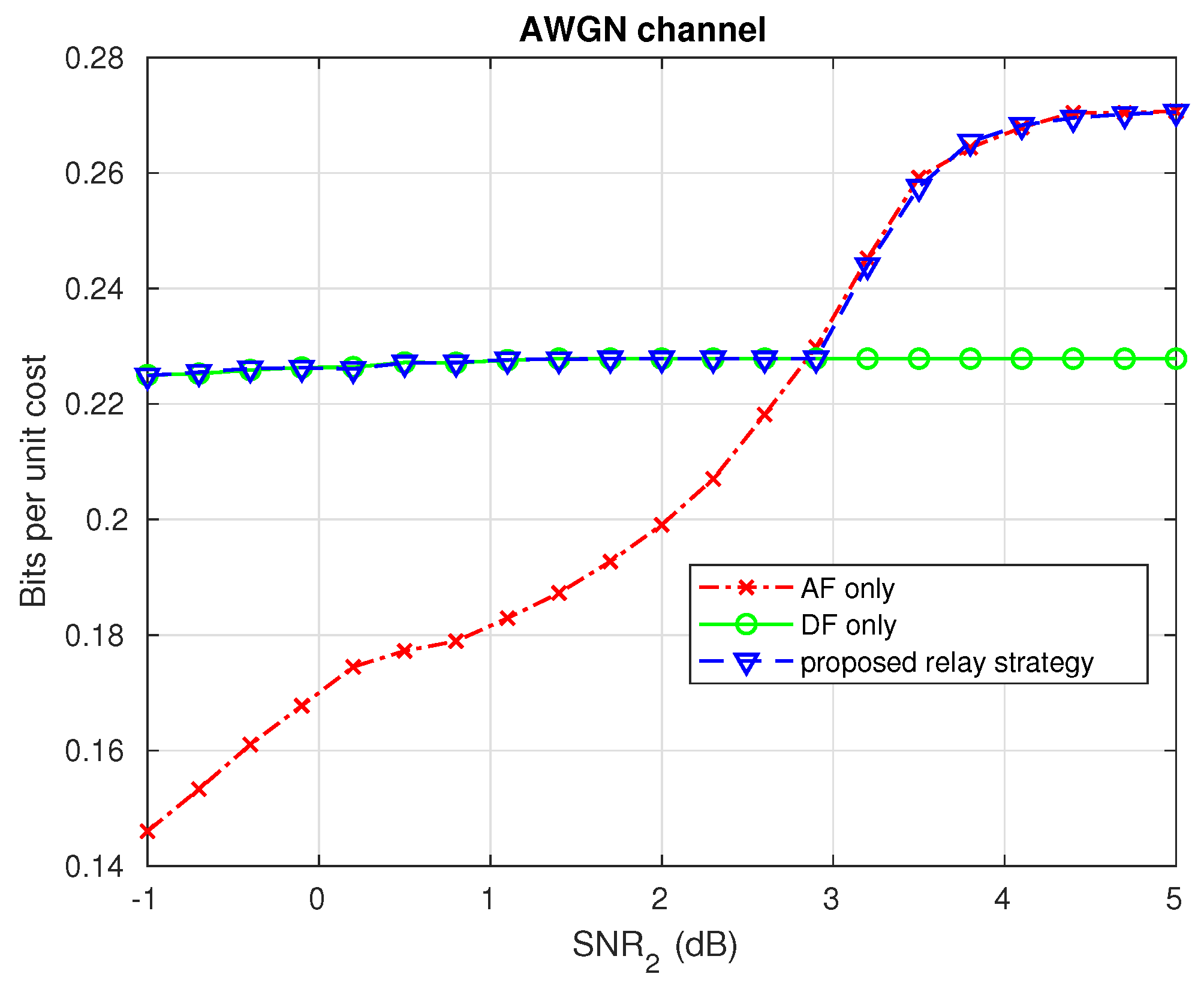
In the relay scenario, the intermediate node needs to decide whether to adopt an AF or DF strategy for each incoming bundle. It will base this decision on the channel SNR estimates and the code rate of the bundle. With DF, the system is equivalent to two separate links, which could be independently optimized using the same HARQ protocol as for the single link scenario. With AF, the HARQ problem is slightly more complex. When a bundle arrives, the relay will forward it without any processing, but we assume that it caches the LLR values temporarily. If the end user is successful in decoding the whole bundle, these LLR values can be discarded, but if the end user suffers any decoding failures, the relay reverts to DF. It decodes the bundle using its cached LLR values (employing HARQ if needed) and only after having succeeded it sends IR to the end user.
When employing AF, we assume unit transmit power at the base station and that the relay amplifies its received signal to invert the attenuation of the first channel. In other words, if the relay receives
where
is the channel gain on the first link,
x is the signal with
and
is Gaussian noise with variance
, the relay amplifies
by a factor
before forwarding it. Then, the received signal at the end user is
where
is the gain over the second link. Since the noise components
and
are independent, the SNR at the end user with AF is
where
and
denote expectation and variance respectively, and
(
) is the SNR on the
j-th link. Note that
is always lower than the SNR on either link.
2.5. Multi-User Systems
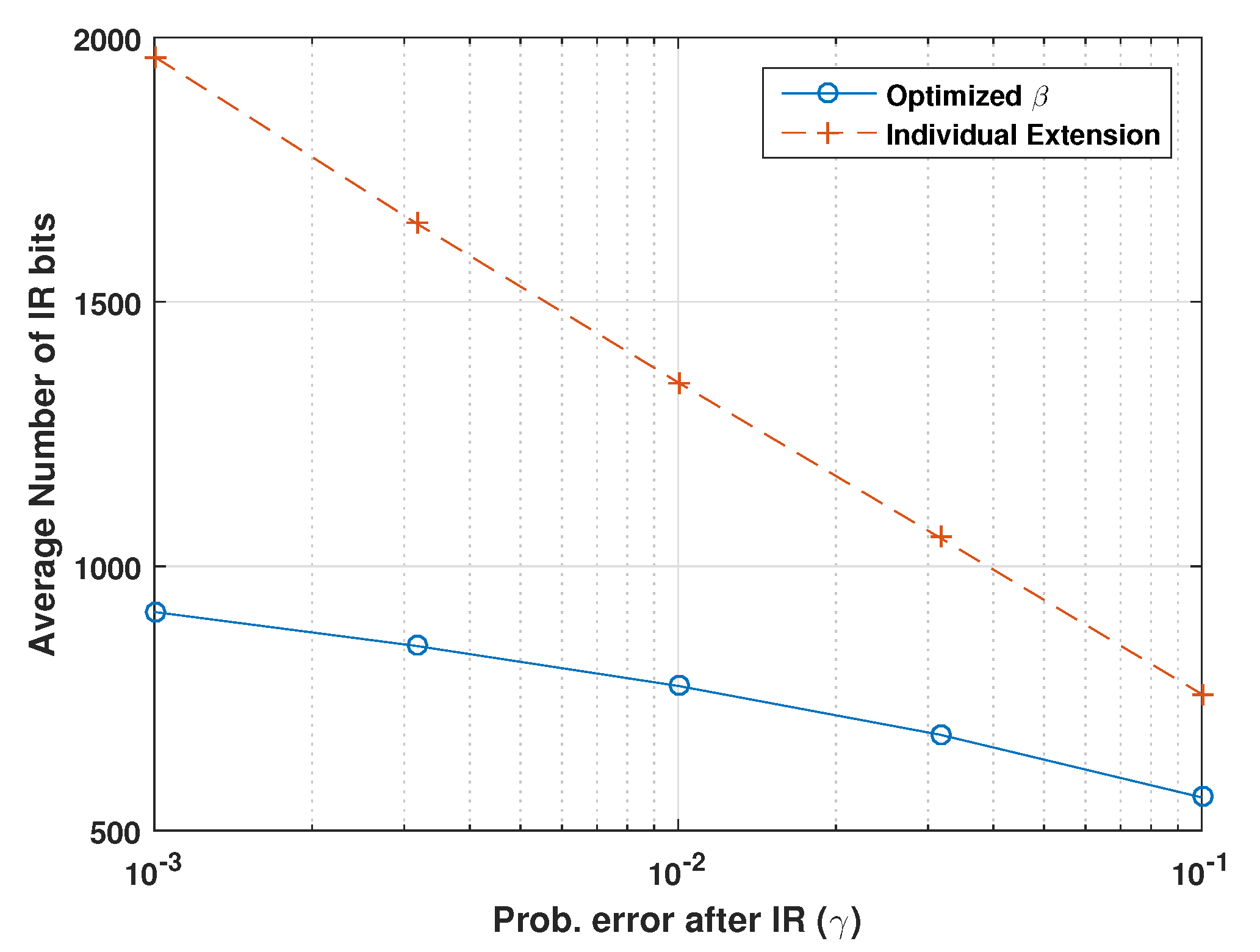
The last scenario studied in this paper is that of a single transmitter communicating with multiple recipients. Each recipient is only interested in a subset of the information being transmitted, but can overhear everything. Each receiver has its own data and feedback channel, with independent SNR and decoding process. When a receiver is unable to decode its desired information, it reports the failures to the transmitter and requests IR. The transmitter compiles the failure reports from all the receivers and uses the proposed algorithm to optimize the set of IR bits that should be broadcast in order to ensure that none of them suffers a probability of error above a pre-fixed value . This optimization is formulated as a convex optimization problem, albeit with the number of variables increasing exponentially with the number of failures reported. In any case, if the number of failures is too large, it is usually better to re-transmit the whole bundle anyway.
4. Decision Engine for Single Link
This section considers a point-to-point link, and proposes an optimization method where the requested number and type of IR bits can be chosen to minimize a cost function. We discretize the coding rate R and the SNR into a finite set of values so that practical numerical methods can be applied to the optimization problem. Since the feedback channel has limited capacity and only offers a few bits for each IR request, we constrain the number of IR bits to be requested to a small set of pre-defined values. A Markov Decision Process (MDP) can then be established to model the HARQ protocol as follows:
State: , where f denotes the number of decoding failures in the bundle, their effective SNR, and R their coding rate.
Action:
, where
and
respectively represent the requested number of extension bits for every codeword in the bundle and the requested number of bundle parity bits. Chase Combining bits will not be used because for typical values of SNR and code rate, their performance is inferior compared to extension bits [
46].
Cost: , where b denotes the bundle size (i.e., number of codewords per bundle). Assuming that transmitting one bit costs one unit, denotes the cost to decode a single codeword, and denotes the overhead cost due to each round of IR accounting for hardware complexity, increased latency, feedback bits, etc. One possible interpretation for this cost is latency. In that case, would be the time required to decode a codeword and the time between retransmissions.
The objective is to find the actions that minimize the total expected cost until all codewords in the bundle are successfully decoded, i.e.,
for all
s. By sending IR bits,
reduces the code rate and
increases the SNR, transitioning from
to a new state
, where
and
are deterministic and
follows a binomial distribution. They can be determined by the following equations:
where
k denotes the number of information bits per codeword and
denotes the increased SNR of the bits that participated in the bundle parity IR, as given by Equation (
14) and illustrated in
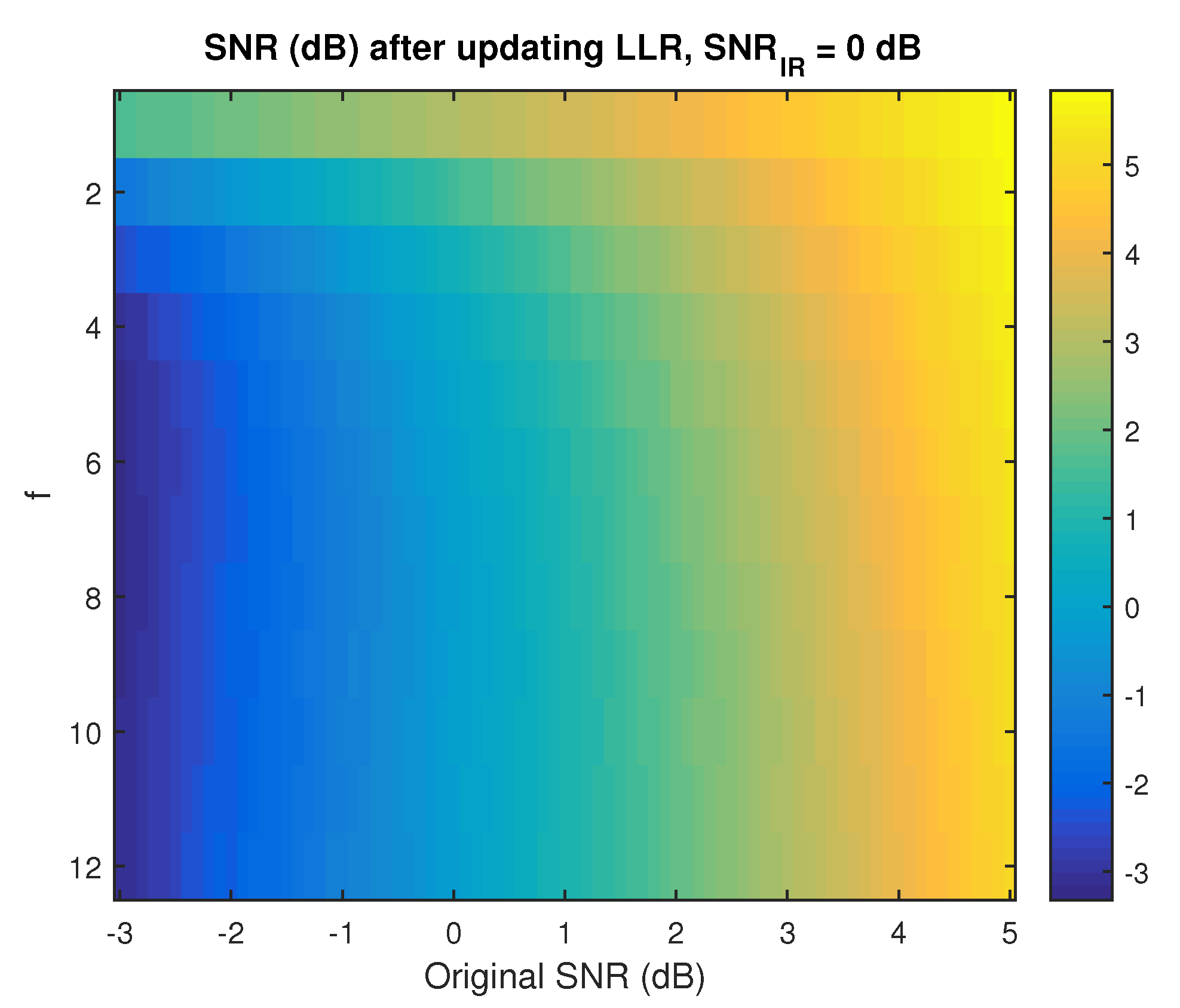
Figure 3. The formula for
is obtained from Equation (
15) by observing that every codeword in a bundle can be partitioned into three sections according to the SNR: the
bits of codeword extension have
, the
bits of overlapping part with bundle parity IR have
after updating their LLRs, and the remaining
bits keep the same
as before receiving the IR. The probability
p in Equation (19) denotes the conditional probability that a codeword fails in state
given that it failed in
, and can be computed using Equation (
1) as
For any state
s and
, the total expected future cost
V and the optimal action
A can be expressed recursively as follows:
where the summation is taken over all possible states
to which
s can transition according to Equations (
17)–(19) given that
IR bits are sent.
denotes the state transition probability.
If we discretize the states and actions to take values from a finite set, the value iteration algorithm [
49] can then be used to numerically find
and
for all
s and
. Essentially, value iteration initializes
V with random values, and alternates between finding the optimal actions
A according to Equation (22) and updating the value
V according to Equation (
21), until convergence. At that point
stores the optimal policy to follow when the HARQ process is at state
s expecting
for the IR, while
stores the total expected future cost until successfully decoding all codewords in the bundle at the receiver.
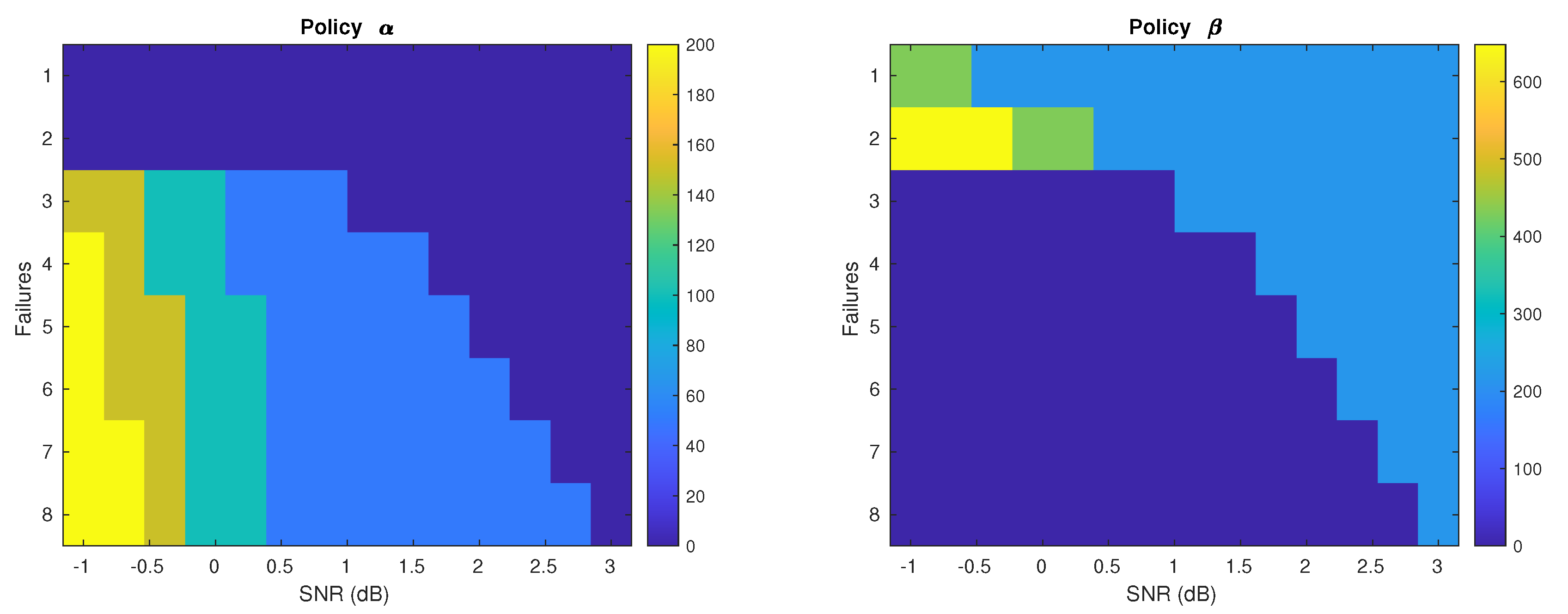
The single link scenario decision engine is specified by the policy A, and it can be readily extended to individual links in a multi-hop scenario as well. The receiver can estimate its state by computing the bundle’s relevant statistics when decoding failures occur, and it then follows A to request a combination of IR bits from the transmitter.
6. Decision Engine for Multi-User Systems
This section addresses a system where a single server (or base station) uses a broadcast link to deliver content to multiple users. The channels from the base station (BS) to each user experience different and independent SNR, so when the BS broadcasts a bundle of codewords, each user is able to decode some of them but not others. If all users are interested in decoding all codewords the problem is similar to that of a single link: it makes sense to focus on the user with the most failures and broadcast the corresponding IR bits, that all other users are also able to hear and use in their own data recovery. However, we analyze the more interesting case in which each user is only interested in a subset of the codewords but can overhear and attempt to decode those meant for other users. Furthermore, we assume that users can report the specific codewords that they succeeded in decoding. In this case, the BS can leverage that information and use network coding schemes to optimize the IR [
35,
36,
50,
51]. Since not all users are interested in all codewords, extension IR bits for any given codeword would only benefit a subset of the users, possibly a single one. Bundle parity bits obtained by taking the XOR of multiple codewords, however, have the potential to help multiple users decode their desired information. This section focuses on optimizing the choice of codewords in such combinations and the number of bundle parity bits to be sent for each of them.
Consider a bundle of codewords being broadcast to multiple users, so that user
i is only interested in codeword
i but overhears all the others. If user
i can successfully decode codeword
i, then it is done and does not require any IR. Our goal is to minimize the total number of IR bits sent while ensuring a minimal probability of success for all the users who failed to do so. Let
b denote the number of users that fail to decode their corresponding codewords, and consider all the possible subsets of
, indexed with numbers between 0 and
. A simple way of doing this would be to use the binary representation of the elements included in the subset. Let
represent the
k-th such subset for
, so that
if and only if
is odd. Let
represent the number of IR bits to be sent obtained from the XOR of the codewords in
. Then the problem that we are trying to solve is
where
represents the probability of user
i failing to decode after receiving the IR, conditioned on having failed without it, and
represents the highest such probability that we are willing to tolerate. The failure probability
depends on
, the SNR of the original codeword, and on
, the effective SNR after IR defined in Equation (
15). The latter is itself a function of
, as described below.
Let
represent the indices of the codewords that user
i failed to decode and assume that
(otherwise the user has received its information and is out of the picture). Receiving
bits from the XOR of codewords in
would help user
i increase the SNR in
of the bits from codeword
i.
Figure 3 provides the new SNR for those bits, denoted
, as a function of
and the number of failed codewords in the XOR, denoted
. Assuming that the IR updates do not overlap, the effective SNR for user
i after IR would be
Equations (
1)–(3) and (
20) can be used to rewrite the error constraints in (29) as
for
, where
In the above definitions
denotes the probability of error before IR and
R the coding rate, assumed to be identical for all codewords for the sake of simplicity. Using the numerical values in Equations (
4) and (5), problem (
28) becomes
Observe that
is a linear function of
, as shown in Equation (
31). Assuming that
, since the model in Equation (
1) is not valid outside of that range, the above problem is convex for
and can be solved by any of the many existing convex optimization methods [
52]. The solution
, with all values rounded to the nearest integer, provides a good approximation to the optimal combination of IR bits to be sent so as to guarantee a probability of success above
for all users.
8. Conclusions
This paper addresses the problem of error correction in single link, relay, and broadcast systems. Specifically, it proposes techniques for optimizing the incremental redundancy (IR) bits sent by an HARQ protocol under the assumption that the feedback channel can only support a few bits of feedback per bundle of codewords (or packets). Apart from the traditional extension IR bits, consisting of a few additional bits for each codeword, this paper also considers bundle IR, consisting of encoded IR bits which the receiver can use to refine the LLRs in multiple codewords.
The allocation of IR bits in a single link is modelled as a Markov Decision Process seeking to minimize a pre-determined cost function. The paper describes how the problem should be formulated and solved, resulting in a set of policies parameterized by the number of failures per codeword bundle, effective SNR of the received codewords, and coding rate. It then extends this single link framework to a relay scenario, where an intermediate node has to decide whether to decode (DF) or just amplify (AF) incoming bundles before forwarding them on. Finally, the paper studies a multiuser scenario where a single source broadcasts information to multiple receivers with different interests. It proposes transmitting encoded IR bits that benefit multiple receivers and formulates a convex problem to optimize their number and encoding.
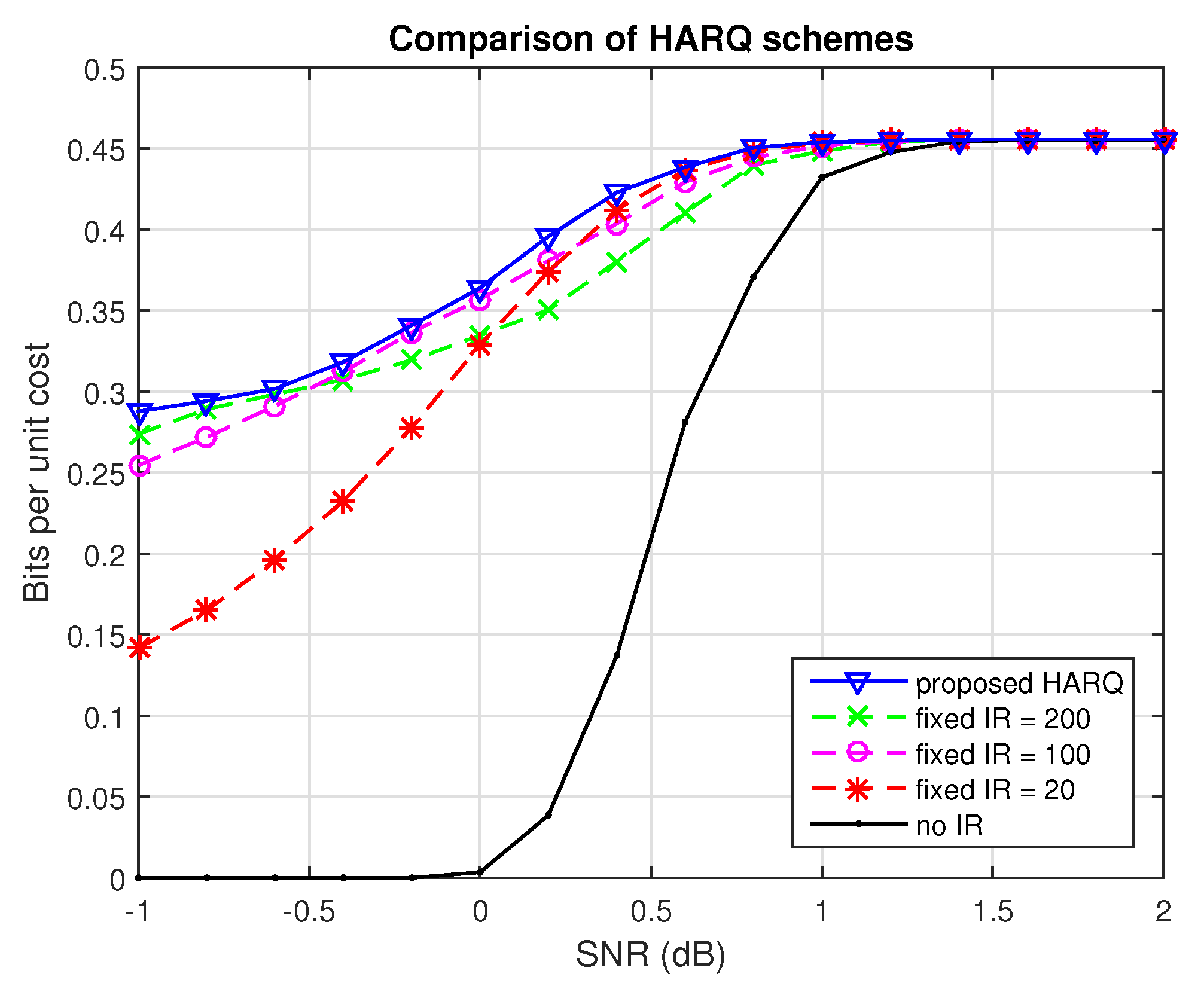
Numerical simulations show that the proposed methods provide a modest increase in throughput compared to traditional HARQ schemes with fixed-length codeword extension. The proposed policy for the relay outperforms fixed forwarding strategies and the proposed strategy for broadcast systems significantly reduces the total number of IR bits needed to guarantee a given probability of success, compared to sending individual extension bits for each codeword. The increased flexibility in requesting different numbers and types of IR bits and the ability to make decisions based on the measurement of the received signals display significant advantages in limited feedback communication systems.