1. Introduction
Every day, we face moments of decision-making where we must take into account more aspects at the same time. We need to consider more than one goal simultaneously, while some of them are often contradictory. The result is finding a solution that has compromise. We can find similar situations in many domains, such as engineering, business, or manufacturing. In production control, one can typically find many frequently appearing optimization tasks for different levels of production control, whether in scheduling operations [
1,
2], logistics [
3,
4,
5], or optimizing production objectives [
6]. Each of these problems internally includes the necessity of considering different features of a system’s performance. This type of problem is commonly referred to as a multi-objective or vector optimization problem (MOOP) [
7]. In contrast to a single objective optimization, to solve it is generally not trivial, because there is no unique optimal solution but rather a set of compromise solutions [
8]. Therefore, it demands applying multi-objective optimization methods to find acceptable optimal solutions.
A direct analytical approach for finding MOOP solutions can fail in the optimization of real-world systems due to difficulties caused by their performance complexity. In general, none or weakly analytically expressed information exists concerning the system dynamics of a relationship between a cause and a consequence. It means that we do not know the precise analytical relation between system inputs and outputs in a form of inputs–outputs transformation. Thus, the effect of decisions or applying specific design scenarios cannot be determined by direct calculation, but it must be studied by applying other methods, such as simulation or simulation-based optimization [
9,
10].
Both methods are important in the determination of system outputs or objective functions values, respectively. Computer simulation represents one of the most advanced and useful tools in the analysis of complex systems. It shows the true system behavior and offers a prediction of a future performance. Consequences of decisions and applying design scenarios in relation to the performance evaluation can be tested easily. Simulation-based optimization employs a simulation approach to evaluate unknown values of objective function during an optimization process. The method is time-consuming when exploring a large design space, mainly due to its high dimensionality.
Due to the complexity of manufacturing systems, and hand in hand with computational capabilities, one of the approaches to find solutions of an MOOP in this environment can be based on dealing with an explored system as a black box [
11,
12]. The black-box function represents mapping the design space to the space of responses as system outputs. Its direct application in the optimization via a method of simulation-based optimization is mostly computationally expensive [
13]. Many optimization strategies, including metaheuristics and simulation-based techniques, are mentioned in survey by Liu et al. [
14]. Despite the solutions that result from any of these methods most likely being suboptimal, metaheuristics perform well in practice [
8], even if they do not guarantee identifying a Pareto optimal solution.
The increasing requests for an automation of the manufacturing processes control demands solving an MOOP as fast as possible. To offer the suitable solution in a very short time is in contrast to the time-consuming NP-hard problem (NP stands for Non-deterministic Polynomial) solving, which constrained MOOP solving mostly represents with no doubt. The algorithmic complexity
O(
kn) of NP- hard problems is given by both the small velocity of finding and verifying the solution. They belong to the category of problems that cannot be generally solved in polynomial time but exponential time that depends on input size
n. As an alternative of metaheuristics, the way to deal with the MOOP can be through finding the adequate surrogate model of a costly evaluated function, which allows solving an MOOP with significant speed-up [
13,
15]. The challenge is to find a suitable compromise between calculation acceleration and model precision [
16].
As an example of an application of an idea of metamodeling-based optimization in manufacturing control, Azadeh and Maghsoudi [
17] employ a simulated Design of Experiments (DoE) and metaheuristic method Tabu Search in a single objective optimization. They conclude that the procedure is suitable for performance optimization in all types of discrete production systems. Conceptually inspired by this case study, in our work, we try to overcome the problem of a long-lasting process of MOOP solving connected to simulation-based optimization and to offer an alternative in which an approximate analytical approach is implemented. The intention of this work was to verify the possibility of finding approximate MOOP solutions that are close to Pareto optimal ones when applying a surrogate model of a simulation model for a batch production system. After derivation of the surrogate model for system input–output transformation in an analytical form and its employment in MOOP solving, we expected a substantial reduction of calculation time from several hours to minutes compared to simulation-based optimization with only an insignificant loss of solutions accuracy.
In this study, we adopted a scalarization technique with a priori defined preferences in the connection with simulation-based and surrogate-based multi-objective optimization. We employed the discrete-event simulation model of a batch production system to allow observing and predicting the system behavior and its response with respect to the external input parameters changes. It was a data source for acquiring the simulation outputs as further inputs to the DoE performance. It also served as an optimization model after completing it by the multi-objective function and by required constraints for simulation-based optimization. We used it for verification of the results of the surrogate-based optimization experiments.
The reminder of the paper is structured as follows. In
Section 2, a definition of the multi-objective optimization problem, modeling of surrogates, and applications related to an integration of both approaches are presented.
Section 3 introduces the steps of the proposed procedure for approximate solving of the MOOP when employing surrogate models in simultaneous optimizing production objectives. In
Section 4 and
Section 5, we present the obtained results and discuss the limitations.
Section 6 summarizes the work results and indicates a future research direction.
2. Background of Multi-Objective Optimization Based on a Surrogate Model
2.1. Multi-Objective Optimization Problem (MOOP)
In general, finding the solution of an MOOP can be presented as a procedure of simultaneous optimization of a set of
k individual objective functions under the constraints set. It can be defined in form given in Equation (1) referring to Marler and Arora [
7]:
The vector
x ∈
D, where the set
D is the feasible region in the design space, is constrained by its lower and upper limits
xL ≤
x ≤
xU. The vector
F(
x) ∈
Ek is the vector of objective functions
Fi(
x):
En →
E1 in feasible objective space
Z,
Z ⊂
Ek. Thus,
Z is the forward image of
D under the mapping
F [
8]. The value
m defines the number of inequalities, and
r defines the number of equalities for the constrained problem. If the objectives of
Fi are contradictory, there does not exist only one single optimal solution as a MOOP-solving result. This process leads to the set of tradeoffs that are completely equivalent in a mathematical sense.
Due to the obvious nonexistence of absolute ordering solutions in the space of objective functions [
18], an expert in the role of decision-maker is important as a support for the determination of the most appropriate solution [
7]. In general, multi-objective methods can be principally characterized with the respect to the involving decision-maker (DM) preferences, which play a significant role in the selection of an appropriate solution. The a priori defined preferences approach provides one single optimal solution dependent on the parameters specified by the DM. On the contrary, a posteriori defined preferences methods or interactive methods allow generating a set of many optimal solutions that are offered to the DM to select the most suitable one or influence the future direction of the optimization process, respectively [
7].
One of the broadly accepted concepts of identifying the optimal solution of an MOOP is an idea of Pareto optimality based on an idea of dominance in the sense of establishing the partial order of solutions. Yoshimura [
19] characterizes the Pareto optimum solutions set as a set of such feasible solutions in the objective (criterion) space, where no other feasible solutions for each of them exist that will yield an improvement in one objective without causing worsening in at least one other objective. All solutions in the objective space, which have the property of Pareto optimality mentioned above, are called nondominated solutions, and other solutions in objective space are dominated by them. For precise definitions of properties of dominance and Pareto optimality, we refer to [
15].
All Pareto optimal solutions form a so-called Pareto front in an objective space [
15,
16]. From the geometric point of view, the Pareto front represents a hypersurface in a
k-dimensional space of objective functions where all nondominated solutions are located. In case of a high-dimensional design space, the hypersurface can have a very complicated structure [
8]. Referring to Ehrgott [
20], the pre-images of the nondominated outcomes are called efficient solutions located in design space.
The concept of Pareto optimality implemented in a method called Pareto ranking is often combined in some modifications with evolutionary algorithms [
15] to increase the effectiveness of the computation of the entire set of Pareto optimal solutions.
An alternative for defining a partial order in objective space can be found in decomposition methods [
8]. It is a different but very natural and therefore a widely spread approach to handle with the MOOP solving by its decomposition to a set of single-objective optimization problems. This strategy transforms a complex multi-objective problem in a set of simple subproblems.
Decomposition methods utilize a scalarizing parametric function to aggregate all the objectives into a single scalar objective function [
8]. Different setting weight vectors and other parameters relating to the individual functions lead to yielding different optimal points belonging to a Pareto front. For the simple scalarization through the Weighted Sum Method (WSM) under an assumption of the convex constraints, it is proved that the solution is Pareto optimal if the value of the corresponding scalar multi-objective function is minimal [
7]. The known disadvantage of this method can be easily explained by the geometry point of view. A scalar multi-objective function is expressed as a linear combination of individual objective functions; therefore, it offers the capability of reaching the Pareto optimal solutions only in the convex part of the Pareto front.
2.2. Modeling of Surrogates and Their Application in a Multi-Objective Optimization
Metamodeling or surrogate modeling (through the following text) is a technique for the construction of “a model of the model” or “surrogates” to cover the essential features of the input–output system behavior [
16]. It approximates the black-box function analytically or generates a new model with better properties for further computation.
We can find plenty of works related to this field, focusing on optimization via metamodeling. Peitz and Dellnitz [
16] give an extensive survey of different types of surrogate models used for implementation in the objective function. Geometric models such as Response Surface Models generated by Response Surface Methodology (RSM) within the Design of Experiments technique, Radial Basis Function (RBF) models, statistical models such as Kriging or Gauss regression, and models based on Machine Learning methods—Artificial Neural Networks (ANN) or Support Vector Machines (SVM)—are among the most widespread. The authors also provide an overview of works when multi-objective optimization (MOO) and metamodeling are combined. Ky et al. [
11] discuss the most popular surrogate models being used in engineering designs suitable also for black-box optimization and the difficulties related to their application. They mention that polynomial models that are well-studied and employed in trust-region methods to provide approximation of the true function in local areas are unsuitable as global models for highly nonlinear multidimensional functions. The authors introduce models that are better performed in that sense, such as RBF and Kriging.
Knowles and Nakayama [
21] and Voutchkov and Keane [
22] particularly focus on metamodeling in multi-objective optimization. Zakerifar et al. [
23] pay attention to Kriging metamodeling in multi-objective simulation optimization. In a survey of Tabatabaei and Hakanen [
12], the authors introduce non-nature inspired methods for handling computationally expensive multi-objective optimization problems using surrogates. As for polynomial modeling, Barton et al. [
24] analyze the quality of fits in case of applying first- and second-order polynomials and other classes of metamodels in metamodel-based simulation optimization from the local and global fit point of view.
Regarding utilizing the surrogate-based optimization methods in engineering applications of real-world problems, one can find them mainly in the field of design of systems or product properties. Pillai et al. [
25] suggest a multi-objective optimization framework for offshore renewable energy mooring systems applying a random forest-based surrogate model coupled to a genetic algorithm. Park et al. [
26] compare the predictive cyclone models generated by response surface methodology, back propagation neural network, and group method of data-handling networks and apply them in multi-objective optimization of the cyclone separation performance via genetic algorithm, too. Chugh et al. [
27] compare the multi-objective optimization of an air intake ventilation system utilizing an evolutionary algorithm with and without a surrogate.
In particular, in the domain of designing manufacturing processes, the multi-objective optimization via metamodels coupled to simulation for machining and turning processes, respectively, is applied e.g., in Amouzgar et al. [
28] or Amouzgar et al. [
29]. For the optimization of a friction-drilling process, Bustillo et al. [
30] describe a novel strategy for real industrial conditions based on Adaboost ensembles. Regarding the results, this prediction model provided the highest accuracy and was more easily optimized than models that resulted from other machine learning techniques.
In relation to the manufacturing systems control, when the optimization of production objectives had been solved, we can observe a predominance of applying heuristic approaches, mainly evolutionary algorithms in the recent works. Um et al. [
31] presented the optimization problem of three production criteria: congestion, vehicle utilization, and the throughput via multi-objective nonlinear programming and simulation-based optimization using an Evolution Strategy for a flexible manufacturing system with an automated guided vehicle system. Azadeh and Maghsoudi [
17] suggested a robust procedure for the optimization of discrete production systems employing an integration of computer simulation, DoE, and Tabu search, and applied it in the case study for a large steelmaking workshop. Lughofer et al. [
32] propose an approach for the automated optimization of process parameters in manufacturing systems to automatically compensate possible downtrends in product quality using static predictive mappings and dynamic forecast models as surrogates within the evolutionary optimization process. As for RSM techniques, Durieux and Pierreval [
33] deal with regression metamodels applied in the design of an automated manufacturing system. For getting a wide overview of applications in the manufacturing system operations area, please see Liu et al. [
14].
2.3. Response Surface Models
Design of experiments within its techniques offers the possibility to generate and optimize regression models through many experimental designs. Particularly, one very known and widely used RSM methodology concerns mostly fitting and optimizing quadratic models. They are constructed as the approximation given by Equation (2) for the second-order model, referring e.g., to Khuri and Cornell [
34], where
and
are unknown regression coefficients,
xi,
xj are input variables that influence the response
y, and
ε denotes a random error (or a noise) observed in
y.
Box–Behnken Design (BBD) is used to build a quadratic model based on such an experimental structure in which we observe the responses at the midpoints of the edges of the experimental space [
35]. It does not ensure runs at the extreme combinations of all the factors. This disadvantage is compensated by having better prediction precision in the center of the experimental space. It requires at least three factors, and the effect of each of them is tested on three levels.
Face-Centered Design (FCD) represents a special case of a variety of Central Composite Designs (CCDs). CCDs are based on a two-level screening factorial design, which is augmented with center and axial points to fit quadratic models [
35]. Regular CCDs have five levels for each factor. The adaptation by choosing an axial distance α = ± 1 produces a Face-Centered, Central Composite Design with three levels per factor. The added axial points lay at the center of each face of the factorial space. FCD design is cuboidal rather than rotatable, which is the supposition for better prediction ability in the corners of the selected experimental space. We applied BBD and FCD designs for the construction of metamodel of a vector function of production goals within this study.
3. The Proposed Multi-Optimization Procedure Based on a Surrogate Model Implemented in Production Control
The designed procedure of surrogate-based MOOP solving is introduced in this section. We illustrate its application in a production environment. Firstly, the method of derivation of the surrogate models for the selected production goals of the batch manufacturing system via the integration of the simulation and DoE method is described. Secondly, we show how the best derived analytical models are applied in objective functions of MOOP solving to find such effective input system parameters that ensure the desired values of production objectives.
3.1. Procedure of Surrogate-Based MOOP Solving
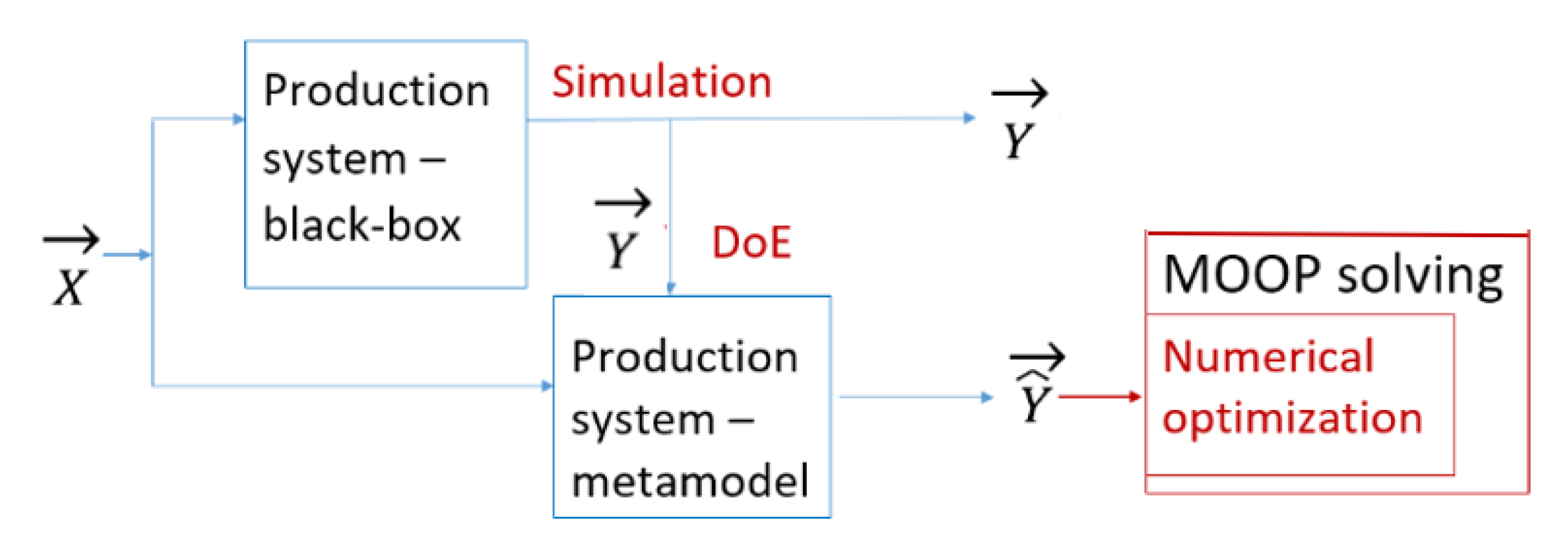
The scheme in
Figure 1 illustrates the procedure of a metamodel implementation to the MOOP solving in a production environment. Vector
represents system inputs that will be transformed to outputs
. The model structure and its configuration affect the system performance. Thus, mapping input parameters (production system loading) to outputs–production objectives, such as costs, flow time, or product quantities can be observed. Due to the fact that the direct analytical expression of this mapping is unknown, we consider the simulation model of a production system as a black box and the mapping of inputs to outputs as a black-box transformation. All the information about it can be gained from the simulation. The simulation model of a production system (production system black-box in
Figure 1) serves as a data source for building the surrogate model instead of a black-box function of the underlying simulation model. Simulation experiments need to consider the design of the experimental layout originated from DoE when evaluating the production objectives as outputs of the simulation runs. Once the production objectives have been evaluated, DoE adopts the observed production goals as responses
according to the suggested design of the planned experiment. The derived regression models (production system metamodel in
Figure 1) estimate the values of production goals
. These regression models by means of individual objective functions represent metamodels as analytically expressed transformations of inputs
for the selected simulation model of a production system.
The optimization of production means to find the effective configuration of input parameters for the black-box function to ensure the desired production performance. Therefore, metamodels for production objectives are incorporated into the scalar multi-objective function in the next step. It is subsequently minimized under specified constraints with respect to a priori defined preferences required by the selected MOO methods.
3.2. Simulation Model of Production System
The modeled production system was adapted from the work of Vazan et al. [
36]. It represented a job shop-type batch production system producing two different products, P1 and P2, with eight workstations using automated parallel working machines. Three of them demanded operators to set up for processing both products. Each of these products was finishing independently at the final phase of manufacturing. We considered all internal model parameters, such as the operation times for machines, setup times and costs for operators, machine setups, and storage as fixed; therefore, the simulation model was fully deterministic. It was built in a simulator Witness Horizon version 22 by Lanner Group Limited, Houston, TX, USA. We used it to obtain values of production objectives and validate the results of numerical calculation.
3.3. Simulation Experiments
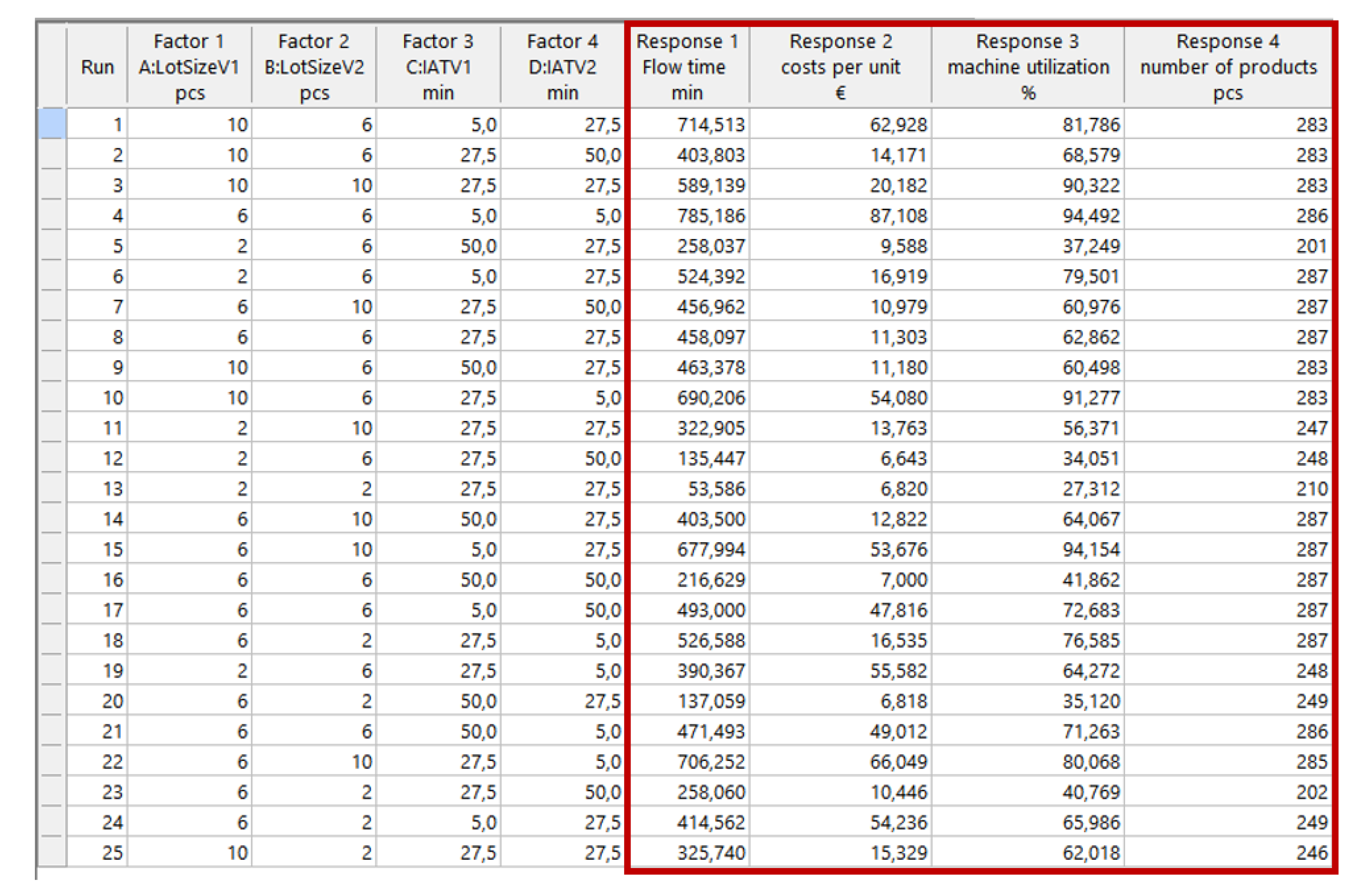
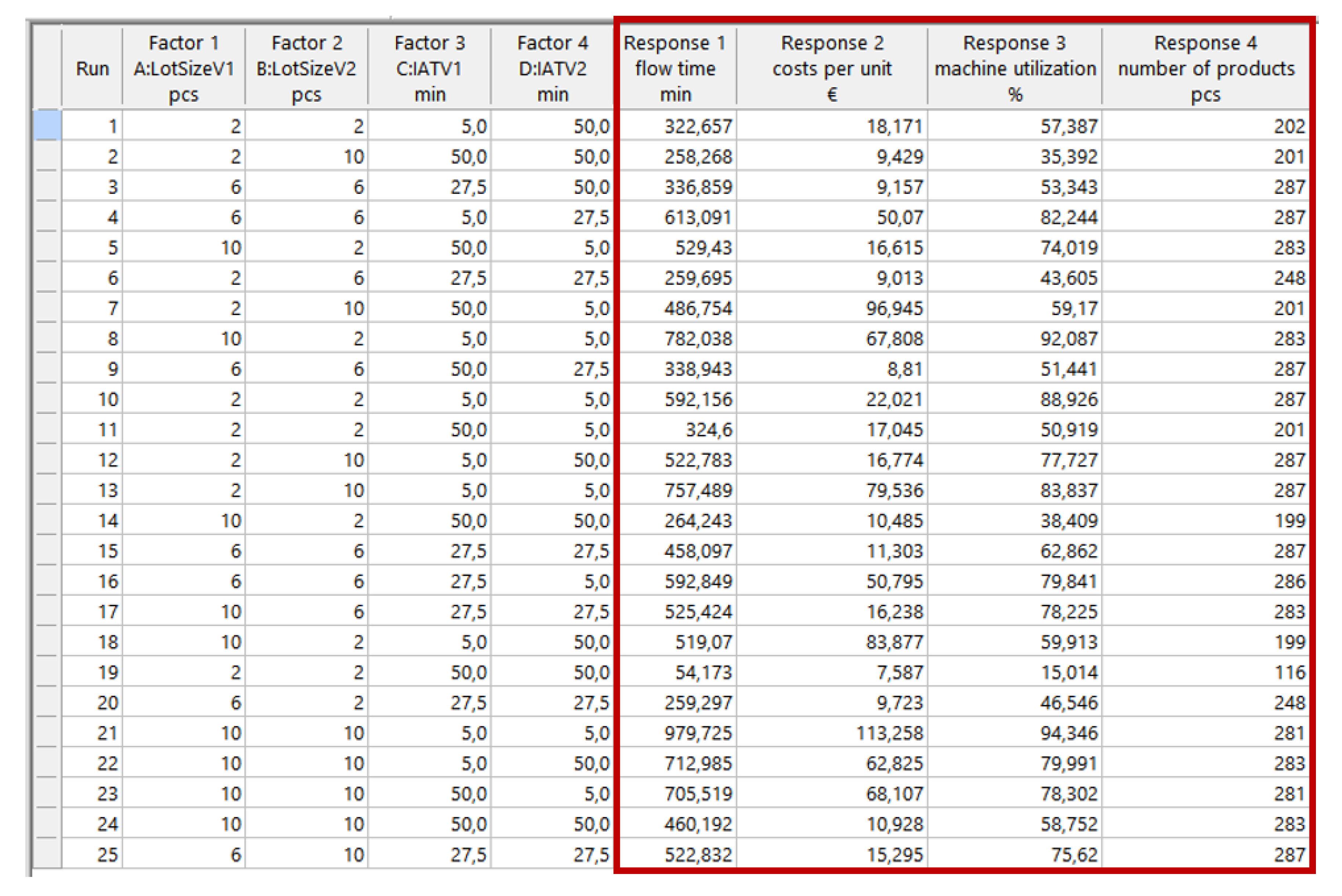
For all experiments performed on the simulation model in the Witness Horizon simulator (Lanner Group Limited, Houston, TX, USA), the inputs of the black-box function of the production system were four external input parameters—a lot size and an input arrival time for both manufacturing products. They represented loading the system. The design space was constrained by the lower and upper bounds between values 2 and 10 pcs for the lot size, and between 5 and 50 min for the supply arrival time for both products. The system outputs were four selected production objectives—a total number of products, an average flow time, an average machine utilization, and the average costs per part unit. The simulation experiments lasted 1440 min with a 100 min warm-up period. Each of the experimental designs for the BBD and FCD-type demanded the simulation of 25 scenarios according to the experimental schemes in
Figure 2 and
Figure 3, respectively.
3.4. DoE—Proposed Experimental Designs
To construct the metamodel of the production objectives, we were interested in two different experimental designs—the Box–Behnken Design (BBD) and Face-Centered Design (FCD). They were selected to explore and compare the suitability of both main types of spherical vs. cuboidal designs for the derivation of a metamodel of a simulation model. After screening experiments, we considered four factors on three levels (–1, 0, 1) in both types of experimental design and four responses
F1–
F4, representing the selected production goals (
Table 1). The factorial space was a four-dimensional domain, with lower and upper bounds between values 2 and 10 pcs for the lot size and between 5 and 50 min for the product arrival time of both products. As responses, four selected production performance indicators were considered: the total number of products, average flow time, average machine utilization, and average costs per part unit. Both designs required 25 simulation runs each. The values of responses in each of the experimental points were found by simulation in Witness Horizon by Lanner Group Limited, Houston, TX, USA (see
Figure 2 and
Figure 3, respectively). The BBD design layout for the actual values of the settings factors with the added responses that resulted from the simulation are shown in
Figure 2. Similarly,
Figure 3 depicts the experimental scheme with an added four responses for FCD.
3.5. The Particular MOOP Definition and Applied Scalar MOO Methods
The particular MOOP represents a task to design a set of four input parameters: the lot size and the input intervals for arriving supplies P1 and P2 within the specified ranges and production limitations while optimizing the production performance. Optimization involves minimizing the average costs per part unit and the average flow time and maximizing the total number of products and average machine utilization simultaneously.
To solve that, we applied two methods belonging to the class of scalarization methods with a priori defined preferences, referring to Marler and Arora [
7].
Firstly, we constructed the scalar multi-objective
U function in Equation (3) expressed through the Weighted Sum Method (WSM) as the linear combination of the normalized individual objectives
using the weight vector
w. All components
wi have the same value 0.25 to not prefer any production goal.
Secondly, we applied the Weighted Product Method (WPM) with the same settings of weights defined by Equation (4). In both cases, minimizing the scalar
U function leads to the single Pareto optimal solution finding.
There exist many possible transformations described e.g., by Marler and Arora [
37] to ensure dimensionless objectives
Fi entering the scalar multi-objective function. We employed a robust transformation given by Equation (5).
That relates to a component of a utopia point vector and a nadir point vector, which represent the unreachable solutions for individual production goals as the best one (utopia) and as the worst one (nadir). The utopia point vector
can be taken as the optimum of the single-criterion function according to the optimization goal regardless of other objectives.
is the vector created by the worst values of the production goals. It can be determined by expert preferences or obtained from single-optimization experiments, too.
Table 2 shows the applied values of these reference points. Value
Fi in Equation (5) is a component of the production goals (individual objectives) vector that resulted from experiments on a discrete-event driven simulation model.
For a numerical computation of the MOOP solution, we use the Evolutionary algorithm in MS Excel module Solver (by Microsoft, Redmond, WA, USA) to perform discrete global optimization.
The objective function employing WSM defined by Equation (3) and transformation in Equation (5) with the utopia and nadir points given by
Table 2 was expressed via regression models of production goals based on FCD in the following analytical form, and it was minimized:
Analogically, the minimized objective function designed on the base WPM with regression models that resulted from the FCD was expressed in the following form:
Both optimization models based on WSM and WPM multi-objective methods defined by Equations (6) and (7) included the constraints for the production goals listed in
Table 3. The objective functions domain was constrained by preliminary simulation experiments. The design space was constrained by lower and upper bounds in a range from 2 to 10 pcs for both supplies’ lot size, and 5 to 50 min for the time between the supplies’ arrivals.
3.6. Numerical Optimization via Maximizing Desirability Function
The second numerical approach is multi-response optimization based on the Desirability function maximization in software Design-Expert
® version 12 (by Stat-Ease, Minneapolis, MN, USA) where surrogate models for individual objective functions were built. Montgomery [
35] describes a multiple response method that employs an objective function
D, which is called the Desirability function. It reflects the desirable ranges for each individual response
di simultaneously. Equation (8) defines the value
di if the target
T for the response
y is a maximum value, and Equation (9) defines the value
di if the target
T is a minimum value, respectively.
Exponent
r determines how strictly the target value is desired. For
r = 1, the desirability function increases linearly toward
T; otherwise, the value
r causes a convex or concave function property. For
k transformed responses, the simultaneous objective function
D is a geometric mean (10) of all
di:
Numerical optimization via the
D function demands a range of factors, responses, and optimization goals in the settings. The applied settings of these parameters are listed in
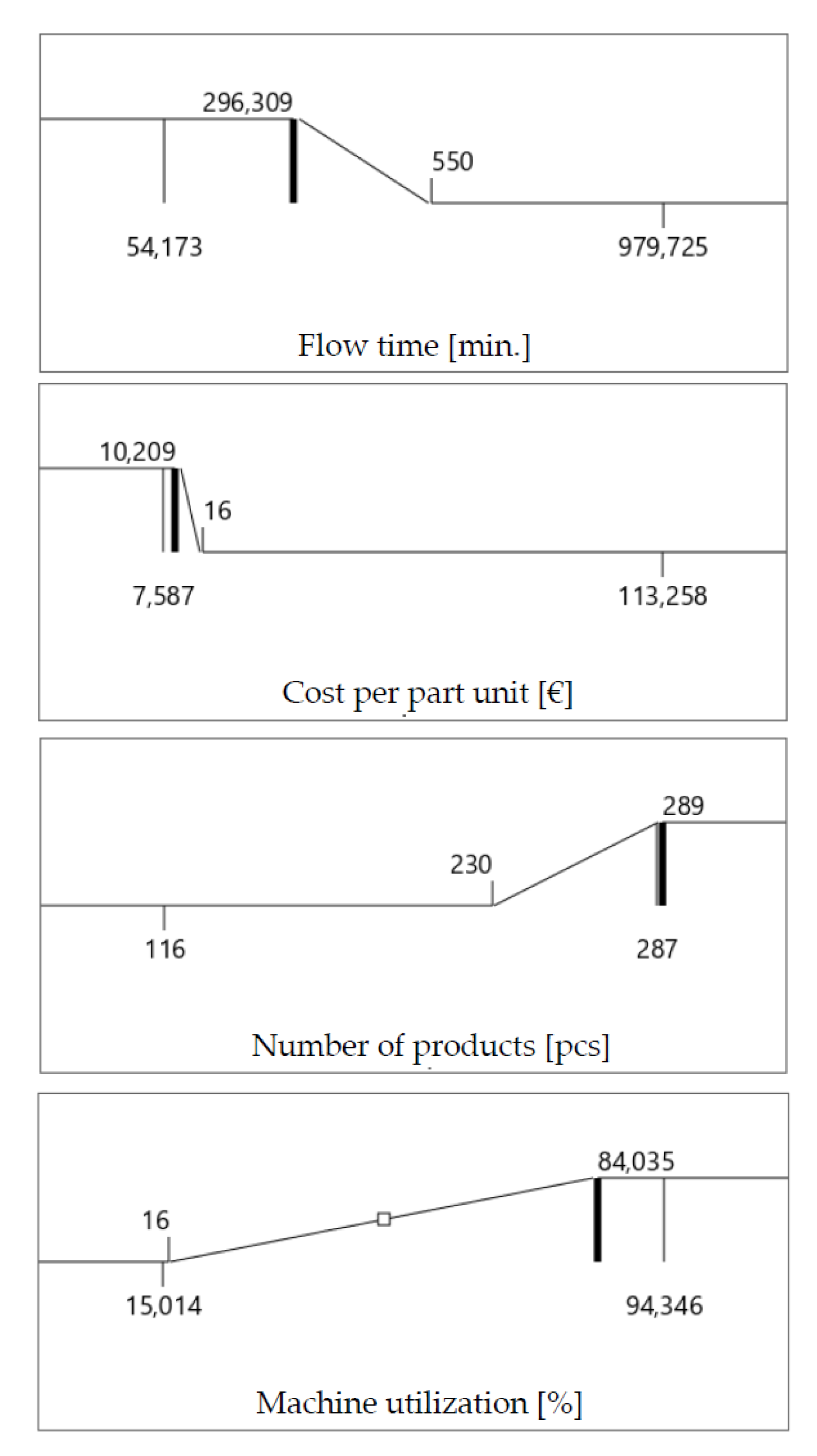
Table 4. The limits of functions in the form of ramps for individual responses
di are depicted in
Figure 4. It shows the graphs of
di functions in Equations (8) and (9) for specified limit values on individual intervals. Two of the notches on each ramp represent the minimum and maximum values of all response values within the experimental space, and two others are lower and upper limits for the given response. They correspond to
L and
U values in Equations (8) and (9), respectively (the lower and upper limit in
Table 4). At the same time, they correspond to the utopia and nadir points as reference points in other types of applied scalar multi-objective functions.
3.7. Validation of Proposed MOOP Solving Strategy
To validate the solutions calculated via proposed optimization models, we consequently performed simulation-based optimization of both
U functions applying metaheuristic (Adaptive Thermostatistical Simulated Annealing). In addition, the brute force algorithm All Combinations in the Witness module Experimenter (Lanner Group Limited, Houston, TX, USA) was performed in Advanced Mode under the same conditions, as previous numerical experiments were conducted. The design space was the same four-dimensional domain, with lower and upper bounds between values 2 and 10 pcs for the lot size and between 5 and 50 min for the supply arrival time for both products. The objective functions domain was constrained by the values listed in
Table 3. For all optimization experiments, the length of simulation was 1440 min with a 100 min warm-up period.
The WSM-derived scalar objective function employed Equation (3) and the transformation expressed by Equation (5). Utopia and nadir points are given in
Table 2. It was defined in an optimization model in the form shown in
Box 1.
Box 1. Definition of Weighted Sum Method (WSM)-based objective function in a simulator.
IF Number_of_products >= 230 AND Costs_per_part_unit <= 16 AND Flow_Time <= 550 AND Machine_Utilization >= 60
RETURN 0.25 * (Costs_per_part_unit − 10.209)/(16 − 10.209) + 0.25 * (Machine_Utilization − 84.035)/(60 − 84.035) + 0.25 * (Number_of_products − 289)/(230 − 289) + 0.25 * (Flow_Time − 296.309)/(550 − 296.309)
ELSE
RETURN 0.25 * (Costs_per_part_unit − 10.209)/(16 − 10.209) + 0.25 * (Machine_Utilization − 84.035)/(60 − 84.035) + 0.25 * (Number_of_products − 289)/(230 − 289) + 0.25 * (Flow_Time − 296.309)/(550 − 296.309) + 100
ENDIF
In the case of the WPM method, we used the definition of objective function body formulated in
Box 2.
Box 2. Definition of WPM-based objective function in the simulator.
IF Number_of_products >= 230 AND Costs_per_part_unit <= 16 AND Flow_Time <= 550 AND Machine_Utilization >= 60
RETURN ((Number_of_products − 289)/(230 − 289)) ** 0.25 * ((Costs_per_part_unit − 10.209)/(16 – 10.209)) ** 0.25 * ((Flow_Time − 296.309)/(550 − 296.309)) ** 0.25 * ((Machine_Utilization − 84.035)/(60 − 84.035)) ** 0.25
ELSE
RETURN ((Number_of_products − 289)/(230 − 289)) ** 0.25 * ((Costs_per_part_unit − 10.209)/(16 − 10.209)) **0.25 * ((Flow_Time − 296.309)/(550 − 296.309)) ** 0.25 * ((Machine_Utilization − 84.035)/(60 − 84.035)) ** 0.25 + 100
ENDIF
Due to minimization, when the conditions for the production goals’ constraints were not fulfilled, the value of the objective function was increased by 100.
4. Results
4.1. Derivation of Surrogate Models of Production Objectives
To fit the response surface, we performed DoE with two types of response surface designs, Face-Centered Design (FCD) and Box–Behnken Design (BBD) for four factors in Design-Expert® software by Stat-Ease (Minneapolis, MN, USA). It provided the polynomial regression models for four selected production objectives as models of the input–output behavior of the underlying simulation model. Based on the ANOVA analysis by F-test of the overall statistical significance of the model and t-tests of the statistical significance of individual regression coefficients, Equations (11)–(18) in terms of actual factors represent obtained response surface models for both types of design. The Lack of Fit test could not be performed due to no variance in the central point, because the applied simulation model has been deterministic.
As for BBD, the fitting model was linear for the average flow time and machine utilization responses according to Equations (11) and (13); others were reduced quadratic models for costs per part unit and number of products regarding to Equations (12) and (14).
The final equations in terms of the actual Equations (15)–(18) represent models with statistically significant coefficients based on FCD. Almost all the FCD-based models are reduced quadratic models, besides the model for machine utilization, which is linear with interactions.
The selected characteristics of analytical models for four production objectives, created via BBD and FCD designs, are shown in
Table 5 and
Table 6. With respect to the results of modeling, we apply only the better, FCD-based metamodel of a black-box function in the further surrogate-based optimization.
4.2. Results of Numerical Optimizations
The numerical optimization of scalar MOO functions involved two different approaches. We performed the global discrete minimization using the Evolutionary algorithm in the module Solver in MS Excel (by Microsoft, Redmond, WA, USA) for selected scalar MOO methods under the constraints specified in
Table 4. We implemented the FCD models defined by Equations (15)–(18) into
U functions only due to the better prediction ability of these models. Next, we found the solution via the Desirability function maximization for FCD models in the numerical optimization module of Design-Expert
® by Stat-Ease (Minneapolis, MN, USA). The results are presented in
Table 7,
Table 8 and
Table 9.
4.3. Validation of Approximate MOOP Solving Strategies
The comparison of results achieved by different numeric and simulation-based optimization methods for WSM and WPM is presented in
Table 7,
Table 8 and
Table 9. In addition, the table also includes the verification of results obtained via surrogate-based optimization by simulation.
5. Discussion
Having been inspired by [
17], we applied the DoE technique for the derivation of a surrogate model of a simulation model for a batch production system, namely Face-Centered Design (FCD) and Box–Behnken Design (BBD). Referring to Montgomery [
35], the designs chosen were two very frequently used ones with different properties regarding prediction ability.
With respect to the selected type of the response design, the results indicate that the FCD generated a very good regression model with better prediction precision for all four responses comparing to BBD. Therefore, only the analytical model derived on the base of FCD was applied in the objective functions when performing numerical multi-objective optimization.
As for FCD applied in optimization, in spite of its good characteristics, the analysis of results presented in
Table 7,
Table 8 and
Table 9 does not show a full consonance in the solutions found through different methods. The solutions, which resulted from simulation-based optimization via a brute force algorithm, have a very short Flow time component and they differ from surrogate-based solutions in this component significantly for both WSM and WPM methods. It implies that the Flow time function is very sensitive to the change of system loading, and the approximation of real values of this component by the FCD response surface model leads to results that are unacceptable for settings in a control process.
Despite this, if we look at the results in more detail, the match confirmed by the simulation is visible for three other components of the MOO solution vector in an objective space. The deviations for these three production objectives (the average costs per part unit, the total number of products, and the average machine utilization) are in an acceptable range (maximally 3.1%) other than the values that resulted directly from the maximization of Desirability function. The solutions that resulted from using this method are strongly influenced by the setting of method parameters. All substantial differences can be partially explained by an approximation error effect, parameters methods settings, and by the lack of guarantee to find a global solution using the heuristic method in case of an Evolutionary algorithm.
We also compare all numerically obtained MOOP solutions related to using metamodels to the values originated from simulation. All these solutions have offered such design variables that the corresponding production goals resulted from the simulation output are mostly dominated by solutions obtained by the All Combinations algorithm using simulation-based optimization. We can conclude that for a real practice, fast obtained solutions that originate from numerical optimization based on FCD are not so good in the sense of Pareto optimality. On the other hand, they can represent approximate values that are rather close enough to effective solutions in a design space for control purposes considering only production goals, which are not too sensitive to the change of input parameters. Regardless of the different locations of the points in design space, all applied surrogate-based multi-objective optimization methods provide similar solutions in terms of the components of the production objectives vector within the specific transformation and weight vector. When comparing this, all solutions verified by simulation are very close to each other in objective space.
The literature concerning metamodel-based solving MOOP [
11,
16] indicates that the utilization of valid metamodels can shorten the computational time needed for optimization processes, namely in the optimization of expensive black-box functions. We observed a significant shortness of calculation time when applying both numerical approaches in contrast to simulation-based optimization, but the time for searching for MOOP solutions strongly depended on the parameters of the applied methods. According to the authors’ best knowledge, there is no similar work that can be used for comparison conclusions due to the specifics of the underlying discrete-event driven simulation model.
To discuss the limitations of the presented MOOP solving procedure based on surrogates, the three main following limitations should be mentioned:
We assume that an adaptable simulation model of the production system must be built.
We assume that the controlled production system does not involve too fast inner parameters and structural changes. The inner parameters and structure can be flexible, but they need to be changed in hours, not in minutes. Even if the simulation model could reflect changes almost immediately, the steps of the designed MOOP procedure take some time to derive the surrogate model and consequently find the solutions.
We must consider that some of the production goals are too sensitive to the change of input parameters; therefore, the approximate solution is not satisfactory.
6. Conclusions and Future Work
In this paper, we presented the procedure for approximate MOOP solving via the surrogate model of a simulation model for the studied batch production system. The MOOP was focused on the simultaneous optimization of four selected production goals. We derived the surrogate model by applying an integration of simulation and DoE technique using Face-Centered Design (FCD) and Box–Behnken Design (BBD). The prediction ability of the model derived from the FCD was observed better than that from the BBD. Thus, only the model that originated from FCD was consequently applied for generating objective functions in the numerical solving of the MOOP.
We can conclude that for a real practice, the solutions that originated from the numerical optimization based on FCD can represent approximate values that are rather close enough to effective solutions in the design space for control purposes when we consider only production goals, which are not too sensitive to the change of input parameters. The advantage is that they are available much faster (in minutes) than solutions that resulted from the long-lasting simulation-based optimization process (in hours or days).
On the basis of the study results, we suppose that the obtained result of optimization is acceptable for control purposes for the studied production system. Of course, this conclusion cannot be generalized based on solutions corresponding to one specific simulation model. The potential wider applicability of the designed procedure in manufacturing control is limited by the results of another research study. When comparing the findings gathered within this study on other production systems, clearer conclusions can be pronounced for all systems that fulfill the assumptions outlined above.
From this point of view, the future interest can be focused on testing other types of surrogate models that could be able to increase the precision of numerical solving MOOP regarding the sense of closeness to Pareto optimal solutions. Additionally, the possibility of applying other multi-objective methods to find solutions in a nonconvex part of a Pareto front also can be investigated. After that, analogic experiments using stochastic models of production systems could be performed.
Author Contributions
Conceptualization, Z.Č., J.K. and P.V.; methodology, Z.Č., J.K. and P.V.; software, Z.Č. and P.V.; validation, Z.Č., J.K. and P.V.; investigation, Z.Č. and J.K.; writing—original draft preparation, Z.Č. and P.V.; writing—review and editing, Z.Č., B.J. and M.J.; supervision, P.V.; project administration, Z.Č., P.V., B.J. and M.J.; funding acquisition, P.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by VEGA agency, grant number 1/0232/18—“Using the methods of multi-objective optimization in production processes control”.
Acknowledgments
The authors thank editor and all anonymous reviewers for their valuable comments and suggestions how to improve the manuscript quality.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Pinedo, M.L. Scheduling—Theory, Algorithms, and Systems, 5th ed.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Zarandi, F.M.H.; Sadat, A.A.A.; Sotudian, S.; Castillo, O. A state of the art review of intelligent scheduling. Artif. Intell. Rev. 2020, 53, 501–593. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Z.; Lv, J.; Liu, Y. A Framework for Smart Production-Logistics Systems Based on CPS and Industrial IoT. IEEE Trans. Ind. Inform. 2018, 14, 4019–4032. [Google Scholar] [CrossRef]
- Zhang, N. Smart Logistics Path for Cyber-Physical Systems with Internet of Things. IEEE Access 2018, 6, 70808–70819. [Google Scholar] [CrossRef]
- Wang, L.; Guo, S.; Li, X.; Du, B.; Xu, W. Distributed manufacturing resource selection strategy in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2018, 94, 3375–3388. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D.; Sethi, S.P.; Sokolov, B. Scheduling in production, supply chain and Industry 4.0 systems by optimal control: Fundamentals, state-of-the-art and applications. Int. J. Prod. Res. 2019, 57, 411–432. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of Multi-Objective Optimization Methods for Engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Fleming, P.J. Methods for multi-objective optimization: An analysis. Inf. Sci. 2015, 293, 338–350. [Google Scholar] [CrossRef]
- Fu, M.C. Optimization via simulation: A review. Ann. Oper. Res. 1994, 53, 199–247. [Google Scholar] [CrossRef]
- Amaran, S.; Sahinidis, N.V.; Sharda, B.; Bury, S.B. Simulation optimization: A review of algorithms and applications. 4OR-Q. J. Oper. Res. 2014, 12, 301–333. [Google Scholar] [CrossRef]
- Ky, V.K.; D’Ambrosio, C.; Hamadi, Y.; Liberti, L. Surrogate-based methods for black-box optimization. Intl. Trans. Oper. Res. 2017, 24, 31. [Google Scholar]
- Tabatabaei, M.; Hakanen, J.; Hartikainen, M.; Miettinen, K.; Sindhya, K. A survey on handling computationally expensive multiobjective optimization problems using surrogates: Non- nature inspired methods. Struct. Multidiscip. Optim. 2015, 52, 25. [Google Scholar] [CrossRef]
- Akhtar, T.; Shoemaker, C.A. Multi objective optimization of computationally expensive multi-modal functions with RBF surrogate sand multi-rule selection. J. Glob. Optim. 2016, 64, 17–32. [Google Scholar] [CrossRef]
- Liu, R.; Xie, X.; Yu, K.Q.; Hu, Q. A survey on simulation optimization for the manufacturing system operation. Int. J. Model. Simul. 2018, 38, 11. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Brambila, S.G.; Gamboa, J.F.; Tapia, M.G.C.; Gómez, R.H. Survey and state of the art. Evolutionary multiobjective optimization: Open research areas and some challenges lying ahead. Complex. Intell. Syst. 2020, 6, 221–236. [Google Scholar] [CrossRef]
- Peitz, S.; Dellnitz, M. A Survey of Recent Trends in Multiobjective Optimal Control—Surrogate Models, Feedback Control and Objective Reduction. Math. Comput. Appl. 2018, 23, 30. [Google Scholar] [CrossRef]
- Azadeh, A.; Maghsoudi, A. Optimization of production systems through integration of computer simulation, design of experiment, and Tabu search: The case of a large steelmaking workshop. Int. J. Adv. Manuf. Technol. 2010, 48, 785–800. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science and Business Media: Berlin, Germany, 2012. [Google Scholar]
- Yoshimura, M. System Design Optimization for Product Manufacturing; Springer: London, UK, 2010. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Knowles, J.; Nakayama, H. Meta-Modeling in Multiobjective Optimization. In Multiobjective Optimization. Lecture Notes in Computer Science; Branke, J., Deb, K., Miettinen, K., Słowiński, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 245–284. [Google Scholar]
- Voutchkov, I.; Keane, A. Multi-Objective Optimization Using Surrogates. In Computational Intelligence in Optimization: Adaptation, Learning, and Optimization; Tenne, Y., Goh, C.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 7, pp. 155–175. [Google Scholar]
- Zakerifar, M.; Biles, W.; Evans, G. Kriging metamodeling in multi-objective simulation optimization. Simulation 2011, 87, 843–856. [Google Scholar] [CrossRef]
- Barton, R.; Meckesheimer, M. Chapter 18 Metamodel-Based Simulation Optimization. In Handbooks in Operations Research and Management Science; Henderson, S.G., Nelson, B.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 13, pp. 535–574. [Google Scholar]
- Pillai, A.C.; Thies, P.R.; Johanning, L. Mooring system design optimization using a surrogate assisted multi-objective genetic algorithm. Eng. Optim. 2019, 51, 1370–1392. [Google Scholar] [CrossRef]
- Park, D.; Cha, J.; Kim, M.; Go, J.S. Multi-objective optimization and comparison of surrogate models for separation performances of cyclone separator based on CFD, RSM, GMDH-neural network, back propagation-ANN and genetic algorithm. Eng. Appl. Comput. Fluid Mech. 2020, 14, 180–201. [Google Scholar] [CrossRef]
- Chugh, T.; Sindhya, K.; Miettinen, K.; Jin, Y.; Kratky, T.; Makkonen, P. Surrogate-assisted evolutionary multiobjective shape optimization of an air intake ventilation system. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), San Sebastian, Spain, 5–8 June 2017; IEEE: Washington, DC, USA, 2017. [Google Scholar]
- Amouzgar, K.; Bandaru, S.; Andersson, T.; Ng, A.H.C. A framework for simulation-based multi-objective optimization and knowledge discovery of machining process. Int. J. Adv. Manuf. Technol. 2018, 98, 2469–2486. [Google Scholar] [CrossRef]
- Amouzgar, K.; Bandaru, S.; Andersson, T.; Ng, A.H.C. Metamodel-based multi-objective optimization of a turning process by using finite element simulation. Eng. Optim. 2020, 52, 1261–1278. [Google Scholar] [CrossRef]
- Bustillo, A.; Urbikain, G.; Perez, J.M.; Pereira, O.M.; Lopez de Lacalle, L.N. Smart optimization of a friction-drilling process based on boosting ensembles. J. Manuf. Syst. 2018, 48, 108–121. [Google Scholar] [CrossRef]
- Um, I.; Cheon, H.; Lee, H. The simulation design and analysis of a Flexible Manufacturing System with Automated Guided Vehicle System. J. Manuf. Syst. 2009, 28, 115–122. [Google Scholar] [CrossRef]
- Lughofer, E.; Zavoianu, A.C.; Pratama, M.; Radauer, T. Automated Process Optimization in Manufacturing Systems Based on Static and Dynamic Prediction Models. In Predictive Maintenance in Dynamic Systems; Lughofer, E., Sayed-Mouchaweh, M., Eds.; Springer: Cham, Switzerland, 2019; pp. 485–531. [Google Scholar]
- Durieux, S.; Pierreval, H. Regression metamodeling for the design of automated manufacturing system composed of parallel machines sharing a material handling resource. Int. J. Prod. Econ. 2004, 89, 21–30. [Google Scholar] [CrossRef]
- Khuri, A.I.; Cornell, J.A. Response Surfaces: Designs an Analyses, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 10th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2019. [Google Scholar]
- Vazan, P.; Cervenanska, Z. Comparison of the Scalarization Approaches in Many-Objective Simulation-Based Optimization in Production System Control. In Proceedings of the 2018 IEEE 13th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT 2018), Lviv, Ukraine, 11–14 September 2018; IEEE: Washington, DC, USA, 2018. [Google Scholar]
- Marler, R.T.; Arora, J.S. Function-transformation methods for multi-objective optimization. Eng. Optim. 2006, 37, 551–570. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).