Mitigating Global Methane Emissions Using Metal-Organic Framework Adsorbents
Abstract
1. Introduction
2. Materials and Methods
3. Results
| MOF | VP (cm3 g−1) a | BET Surface Area (m2 g−1) | Lang. Surface Area (m2 g−1) | T (K) | P (bar) | Methane Uptake (mmol g−1) | Qst (kJ mol−1) | Ref. |
|---|---|---|---|---|---|---|---|---|
| UTSA-110a | 1.263 | 3241 | - | 273.15 | 1 | - | 14.5 | [56] |
| HKUST-1 | 0.78 | 1850 | - | 298 | 1 | 1.0 c | 17 | [57] |
| ATC-Cu | 0.23 | 600 | - | 298 | 1 | 2.8 c | 26.8 | [35] |
| NU-1501-Al | - | 7310 | - | 270 | 1 | - | - | [58] |
| Al-soc-MOF-1 | 2.3 | 5585 | - | 298 | 1 | 0.33 c | 10.5 | [59] |
| PCN-14 | 0.85 | 2170 | - | 298 | 1 | - | 17.6 | [32] |
| NJU-Bai 43 | 1.22 | 3090 | - | 298 | 1 | 0.20 c | 14.45 | [60] |
| PCN-61 | 1.36 | 3000 | - | 298 | 1 | - | - | [44] |
| MOF-950 | 1.3 | 3440 | - | 298 | 1 | 0.38 c | 11.9 | [61] |
| NJU-Bai 42 | 1.07 | 2830 | - | 298 | 1 | 0.80 c | 14.49 | [60] |
| Fe(bpd) | - | - | - | 298 | 1 | 0.1 c | - | [62] |
| NU-135 | 1.02 | 2530 | - | 298 | 1 | 0.9 c | 16.6 | [63] |
| NU-125 | 1.29 | 3120 | - | 298 | 1 | - | 15.5 | [64] |
| ZJU-25 | 1.183 | 2124 | - | 300 | 1 | - | 15.1 | [64] |
| MOF-519 | 0.938 | 2400 | - | 298 | 1 | 0.49 c | 14.6 | [65] |
| MOF-5 | 1.4 | - | - | 298 | 1 | - | 12.3 | [66] |
| NJU-Bai 19 | 1.063 | 2803 | - | 298 | 1 | 0.85 c | 14.8 | [67] |
| Cu-tbo-MOF-5 | 0.595 | 3971 | - | 298 | 1 | 1.29 c | 20.4 | [68] |
| MOF-905-Me2 | - | - | - | 298 | 1 | 0.47 b | - | [61] |
| MOF-905 | 1.34 | 3490 | 3770 | 298 | 1 | 0.33 b | 11.7 | [61] |
| MOF-905-Naph | 1.25 | 3310 | 3540 | 298 | 1 | 0.45 b | 11.3 | [61] |
| MOF-905-NO2 | 1.29 | 3380 | 3600 | 298 | 1 | 0.403 b | 10.7 | [61] |
| NJU-Bai-41 | 0.92 | 2370 | - | 298 | 1 | 0.969 c | 17.77 | [60] |
| Al4(OH)8(btec) MIL-120 | 0.11 | 308 | 432 | 303 | 10 | 1.7 d | 27 | [69] |
| Cu2(tdm) [PCN-26] | 0.84 | 1854 | 2545 | 298 | 1.07 | 1.1 d | - | [70] |
| Cu2(ebtc) | - | 1852 | 2844 | 273 | 1 | 0.6 c | - | [71] |
| Mg(tcpda) [SNU-25] | 0.368 | 795 | - | 298 | 1.01 | 0.4 c | - | [72] |
| Zn(Pur)2 [ZIF-20] | 0.27 | - | 800 | 273 | 1.01 | 0.7 b | - | [73] |
| Zn(bIm)(nIm) [ZIF-68] | - | - | 1090 | 298 | 1.01 | 0.4 b | - | [74] |
| Zn(cbIm)(nIm) [ZIF-69] | - | - | 950 | 298 | 1.01 | 0.6 b | - | [74] |
| Zn(Im)1.13(nIm)0.87 [ZIF-70] | - | - | 1730 | 298 | 1.01 | 0.4 b | - | [74] |
| Zn(nbIm)(nIm) [ZIF-78] | - | - | 620 | 298 | 1.01 | 0.6 b | - | [74] |
| Zn(mbIm)(nIm) [ZIF-79] | - | - | 810 | 298 | 1.01 | 0.5 b | - | [74] |
| Zn(bbIm)(nIm) [ZIF-81] | - | - | 760 | 298 | 1.1 | 0.5 b | - | [74] |
| Zn(cnIm)(nIm) [ZIF-82] | - | - | 1300 | 298 | 1.01 | 0.5 b | - | [74] |
| [H2O][Zn7(μ3-OH)3(bbs)6] | 0.24 | - | 649 | 273 | 1.01 | 0.6 d | - | [75] |
| Co3(2,4-pdc)2(μ3-OH)2 [CUK-1] | 0.26 | 630 | - | 298 | 1.01 | 0.4 d | - | [76] |
| Mn(2,6-ndc) | 0.068 | - | 191 | 273 | 1.01 | 0.8 d | - | [77] |
| Cu(tip) | 0.34 | 810 | 1063 | 298 | 1.01 | 1.0 d | - | [78] |
| Cu(bdc-OH) | 0.214 | - | 584 | 296 | 1.01 | 0.6 d | 18.5 | [79] |
| Zn5(bta)6(tda)2 | 0.24 | 414 | 607 | 295 | 1.01 | 0.4 d | - | [80] |
| Zn4(OH)2(1,2,4-btc) | 0.205 | 408 | 607 | 295 | 1.01 | 0.4 d | - | [81] |
| Co3(ndc)(HCOO)3(μ3-OH) | 0.58 | 1386 | 1434 | 298 | 1 | 0.7 d | 19.4 | [82] |
| Adsorbent | VP (cm3 g−1) a | BET Surface Area (m2 g−1) | Methane Uptake (mmol g−1) | T (K) | P (bar) | Qst (kJ mol−1) | Ref. |
|---|---|---|---|---|---|---|---|
| Carbonaceous materials | |||||||
| MW-CNTs@JUC32-2 | - | 146 | 0.75 c | 273 | 1 | 23.9 | [83] |
| KUA51751 | 1.48 | 3350 | 1.34 c | 298 | 1 | - | [84] |
| KUB41701 | 0.92 | 2123 | 1.32 c | 298 | 1 | - | [84] |
| Maxsorb-A | 1.38 | 3100 | 1.28 c | 298 | 1 | - | [84] |
| FELT 1 | 0.81 | 1741 | 1.34 c | 298 | 1 | - | [84] |
| LFC14 | 0.23 | 520 | 1.15 c | 298 | 1 | - | [84] |
| LFC30 | 0.41 | 930 | 1.22 c | 298 | 1 | - | [84] |
| CFC19 | 0.32 | 647 | 1.05 | 298 | 1 | - | [84] |
| CFC54 | 0.84 | 1859 | 1.09 | 298 | 1 | - | [84] |
| CFC74 | 0.92 | 2862 | 1.15 | 298 | 1 | - | [84] |
| Zeolites | |||||||
| NaX | 0.220 | 534 | 0.65 c | 303 | 1 | 20.1 | [55] |
| NaA | - | 473 | 0.65 c | 303 | 1 | - | [55] |
| CaA | 0.150 | 440 | 0.59 c | 303 | 1 | 29.0 | [55] |
| Polymers | |||||||
| p-Dichloroxylene (p-DCX) | 0.36 | 1307 | 0.73 c | 298 | 1 | 20.8 | [54] |
| BCMBP/p-DCX | 0.54 | 1904 | 0.72 c | 298 | 1 | - | [54] |
4. Discussion
Enhancing Volumetric Energy Density and Cyclability in MOFs for Global Methane Emissions Mitigation
5. Conclusions
Funding
Conflicts of Interest
References
- Etiope, G.; Schwietzke, S. Global geological methane emissions: An update of top-down and bottom-up estimates. Elem. Anthr. 2019, 7, 1–9. [Google Scholar] [CrossRef]
- Schiermeier, Q. Global Methane Levels Soar to Record High. Available online: https://www.nature.com/articles/d41586-020-02116-8 (accessed on 14 July 2020).
- Hiroko Tabuchi Global Methane Emissions Reach a Record High. Available online: https://www.nytimes.com/2020/07/14/climate/methane-emissions-record.html (accessed on 15 July 2020).
- Thurber, A.R.; Seabrook, S.; Welsh, R.M. Riddles in the cold: Antarctic endemism and microbial succession impact methane cycling in the Southern Ocean. Proc. R. Soc. B Biol. Sci. 2020, 287, 20201134. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.; Malik, N.S. No One Is Owning Up to Releasing Cloud of Methane in Florida. Available online: https://www.bloomberg.com/news/articles/2020-07-27/no-one-is-owning-up-to-releasing-cloud-of-methane-in-florida (accessed on 18 August 2020).
- Ferretti, D.F.; Miller, J.B.; White, J.W.C.; Etheridge, D.M.; Lassey, K.R.; Lowe, D.C.; MacFarling Meure, C.M.; Dreier, M.F.; Trudinger, C.M.; Van Ommen, T.D.; et al. Atmospheric science: Unexpected changes to the global methane budget over the past 2000 years. Science 2005, 309, 1714–1717. [Google Scholar] [CrossRef] [PubMed]
- Neef, L.; Van Weele, M.; Van Velthoven, P. Optimal estimation of the present-day global methane budget. Global Biogeochem. Cycles 2010, 24, 1–10. [Google Scholar] [CrossRef]
- Mitchell, L.E.; Brook, E.J.; Sowers, T.; McConnell, J.R.; Taylor, K. Multidecadal variability of atmospheric methane, 1000–1800 C.E. J. Geophys. Res. Biogeosci. 2011, 116, 1–16. [Google Scholar] [CrossRef]
- EPA’s Voluntary Methane Programs for the Oil and Natural Gas Industry. Available online: https://www.epa.gov/natural-gas-star-program (accessed on 8 February 2020).
- Consumers Energy Methane Reduction Plan. Available online: https://s2.q4cdn.com/027997281/files/doc_downloads/2019/11/CE-Methane-Report-2019-FINAL.PDF (accessed on 18 August 2020).
- Kate Abnett, S.N. EU’s Greenhouse Gas Strategy Fails to Plug Methane Hole. Available online: https://www.reuters.com/article/us-eu-energy-methane-insight/eus-greenhouse-gas-strategy-fails-to-plug-methane-hole-idUSKCN24I0IV (accessed on 19 August 2020).
- Bui, M.; Adjiman, C.S.; Bardow, A.; Anthony, E.J.; Boston, A.; Brown, S.; Fennell, P.S.; Fuss, S.; Galindo, A.; Hackett, L.A.; et al. Carbon capture and storage (CCS): The way forward. Energy Environ. Sci. 2018, 11, 1062–1176. [Google Scholar] [CrossRef]
- Schoedel, A.; Ji, Z.; Yaghi, O.M. The role of metal–organic frameworks in a carbon-neutral energy cycle. Nat. Energy 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Britt, D.; Furukawa, H.; Wang, B.; Glover, T.G.; Yaghi, O.M. Highly efficient separation of carbon dioxide by a metal-organic framework replete with open metal sites. Proc. Natl. Acad. Sci. USA 2009, 106, 20637–20640. [Google Scholar] [CrossRef]
- Li, J.R.; Ma, Y.; McCarthy, M.C.; Sculley, J.; Yu, J.; Jeong, H.K.; Balbuena, P.B.; Zhou, H.C. Carbon dioxide capture-related gas adsorption and separation in metal-organic frameworks. Coord. Chem. Rev. 2011, 255, 1791–1823. [Google Scholar] [CrossRef]
- Kim, E.J.; Siegelman, R.L.; Jiang, H.Z.H.; Forse, A.C.; Lee, J.-H.; Martell, J.D.; Milner, P.J.; Falkowski, J.M.; Neaton, J.B.; Reimer, J.A.; et al. Cooperative carbon capture and steam regeneration with tetraamine-appended metal–organic frameworks. Science 2020, 369, 392 LP–396. [Google Scholar]
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444-1–1230444–13. [Google Scholar] [CrossRef] [PubMed]
- Long, J.R.; Yaghi, O.M. The pervasive chemistry of metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1213–1214. [Google Scholar] [CrossRef] [PubMed]
- Yaghi, O.M.; O’Keeffe, M.; Ockwig, N.W.; Chae, H.K.; Eddaoudi, M.; Kim, J. Reticular synthesis and the design of new materials. Nature 2003, 423, 705–714. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.E.; Wheatley, P.S. Gas storage in nanoporous materials. Angew. Chem. Int. Ed. 2008, 47, 4966–4981. [Google Scholar] [CrossRef]
- Makal, T.A.; Li, J.-R.R.; Lu, W.; Zhou, H.-C.C. Methane storage in advanced porous materials. Chem. Soc. Rev. 2012, 41, 7761–7779. [Google Scholar] [CrossRef]
- He, Y.; Chen, F.; Li, B.; Qian, G.; Zhou, W.; Chen, B. Porous metal–organic frameworks for fuel storage. Coord. Chem. Rev. 2018, 373, 167–198. [Google Scholar] [CrossRef]
- He, Y.; Zhou, W.; Qian, G.; Chen, B. Methane storage in metal-organic frameworks. Chem Soc Rev 2014, 43, 5657–5678. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Xue, H.; Pang, H.; Xu, Q. Metal–organic frameworks as a platform for clean energy applications. EnergyChem 2020, 1, 100006. [Google Scholar] [CrossRef]
- Zhang, H.; Nai, J.; Yu, L.; Lou, X.W. (David) Metal-Organic-Framework-Based Materials as Platforms for Renewable Energy and Environmental Applications. Joule 2017, 1, 77–107. [Google Scholar] [CrossRef]
- Furukawa, H.; Ko, N.; Go, Y.B.; Aratani, N.; Choi, S.B.; Choi, E.; Yazaydin, A.Ö.; Snurr, R.Q.; O’Keeffe, M.; Kim, J.; et al. Ultrahigh porosity in metal-organic frameworks. Science 2010, 329, 424–428. [Google Scholar] [CrossRef]
- Perry, J.J.; Perman, J.A.; Zaworotko, M.J. Design and synthesis of metal-organic frameworks using metal-organic polyhedra as supermolecular building blocks. Chem. Soc. Rev. 2009, 38, 1400–1417. [Google Scholar] [CrossRef]
- Wang, C.; Liu, D.; Lin, W. Metal-organic frameworks as a tunable platform for designing functional molecular materials. J. Am. Chem. Soc. 2013, 135, 13222–13234. [Google Scholar] [CrossRef]
- Konstas, K.; Osl, T.; Yang, Y.; Batten, M.; Burke, N.; Hill, A.J.; Hill, M.R. Methane storage in metal organic frameworks. J. Mater. Chem. 2012, 22, 16698–16708. [Google Scholar] [CrossRef]
- Zhou, W. Methane storage in porous metal-organic frameworks: Current records and future perspectives. Chem. Rec. 2010, 10, 200–204. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, W.; Yildirim, T. High-capacity methane storage in metal-organic frameworks M2(dhtp): The important role of open metal sites. J. Am. Chem. Soc. 2009, 131, 4995–5000. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Krungleviciute, V.; Eryazici, I.; Hupp, J.T.; Farha, O.K.; Yildirim, T. Methane storage in metal-organic frameworks: Current records, surprise findings, and challenges. J. Am. Chem. Soc. 2013, 135, 11887–11894. [Google Scholar] [CrossRef] [PubMed]
- Getzschmann, J.; Senkovska, I.; Wallacher, D.; Tovar, M.; Fairen-Jimenez, D.; Düren, T.; Van Baten, J.M.; Krishna, R.; Kaskel, S. Methane storage mechanism in the metal-organic framework Cu 3(btc)2: An in situ neutron diffraction study. Microporous Mesoporous Mater. 2010, 136, 50–58. [Google Scholar] [CrossRef]
- Rosi, N.L.; Eckert, J.; Eddaoudi, M.; Vodak, D.T.; Kim, J.; O’Keeffe, M.; Yaghi, O.M. Hydrogen storage in microporous metal-organic frameworks. Science 2003, 300, 1127–1129. [Google Scholar] [CrossRef]
- Niu, Z.; Cui, X.; Pham, T.; Lan, P.C.; Xing, H.; Forrest, K.A.; Wojtas, L.; Space, B.; Ma, S. A Metal–Organic Framework Based Methane Nano-trap for the Capture of Coal-Mine Methane. Angew. Chem. Int. Ed. 2019, 58, 10138–10141. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Myers, A.L. Optimum conditions for adsorptive storage. Langmuir 2006, 22, 1688–1700. [Google Scholar] [CrossRef]
- Dauenhauer, P.J.; Abdelrahman, O.A. A Universal Descriptor for the Entropy of Adsorbed Molecules in Confined Spaces. ACS Cent. Sci. 2018, 4, 1235–1243. [Google Scholar] [CrossRef]
- Campbell, C.T.; Sellers, J.R. V The Entropies of Adsorbed Molecules. J. Am. Chem. Soc. 2012, 134, 18109–18115. [Google Scholar] [CrossRef]
- Liu, L.; Konstas, K.; Hill, M.R.; Telfer, S.G. Programmed pore architectures in modular quaternary metal-organic frameworks. J. Am. Chem. Soc. 2013, 135, 17731–17734. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Wu, H.; Srinivas, G.; Zhou, Y.; Xiang, S.; Chen, Z.; Yang, Y.; Zhou, W.; O’Keeffe, M.; Chen, B. A metal-organic framework with optimized open metal sites and pore spaces for high methane storage at room temperature. Angew. Chem. Int. Ed. 2011, 50, 3178–3181. [Google Scholar] [CrossRef] [PubMed]
- Kalidindi, S.B.; Nayak, S.; Briggs, M.E.; Jansat, S.; Katsoulidis, A.P.; Miller, G.J.; Warren, J.E.; Antypov, D.; Corà, F.; Slater, B.; et al. Chemical and structural stability of zirconium-based metal-organic frameworks with large three-dimensional pores by linker engineering. Angew. Chem. Int. Ed. 2015, 54, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Karagiaridi, O.; Bury, W.; Mondloch, J.E.; Hupp, J.T.; Farha, O.K. Solvent-assisted linker exchange: An alternative to the de novo synthesis of unattainable metal-organic frameworks. Angew. Chem. Int. Ed. 2014, 53, 4530–4540. [Google Scholar] [CrossRef]
- Stock, N.; Biswas, S. Synthesis of metal-organic frameworks (MOFs): Routes to various MOF topologies, morphologies, and composites. Chem. Rev. 2012, 112, 933–969. [Google Scholar] [CrossRef]
- Deng, H.; Doonan, C.J.; Furukawa, H.; Ferreira, R.B.; Towne, J.; Knobler, C.B.; Wang, B.; Yaghi, O.M. Multiple functional groups of varying ratios in metal-organic frameworks. Science 2010, 327, 846–850. [Google Scholar] [CrossRef]
- Moghadam, P.Z.; Fairen-Jimenez, D.; Snurr, R.Q. Efficient identification of hydrophobic MOFs: Application in the capture of toxic industrial chemicals. J. Mater. Chem. A 2015, 4, 529–536. [Google Scholar] [CrossRef]
- Casco, M.E.; Rey, F.; Jordá, J.L.; Rudić, S.; Fauth, F.; Martínez-Escandell, M.; Rodríguez-Reinoso, F.; Ramos-Fernández, E.V.; Silvestre-Albero, J. Paving the way for methane hydrate formation on metal-organic frameworks (MOFs). Chem. Sci. 2016, 7, 3658–3666. [Google Scholar] [CrossRef]
- Almeida Paz, F.A.; Klinowski, J.; Vilela, S.M.F.; Tomé, J.P.C.; Cavaleiro, J.A.S.; Rocha, J. Ligand design for functional metal–organic frameworks. Chem. Soc. Rev. 2012, 41, 1088–1110. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Timmons, D.J.; Yuan, D.; Zhou, H.C. Tuning the topology and functionality of metal-organic frameworks by ligand design. Acc. Chem. Res. 2011, 44, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Walecka, J.D. Introduction to Statistical Mechanics; World Scientific: Singapore, 2011; ISBN 9789814366229. [Google Scholar]
- Donnelly, P.; Ellis, R.S. Entropy, Large Deviations, and Statistical Mechanics. J. Am. Stat. Assoc. 1987, 82, 948–949. [Google Scholar] [CrossRef]
- Dudko, O.K. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Springer Nature: Cham, Switzerland, 2007. [Google Scholar]
- Lozano-Castelló, D.; Cazorla-Amorós, D.; Linares-Solano, A.; Quinn, D.F. Influence of pore size distribution on methane storage at relatively low pressure: Preparation of activated carbon with optimum pore size. Carbon N. Y. 2002, 40, 989–1002. [Google Scholar] [CrossRef]
- Policicchio, A.; MacCallini, E.; Agostino, R.G.; Ciuchi, F.; Aloise, A.; Giordano, G. Higher methane storage at low pressure and room temperature in new easily scalable large-scale production activated carbon for static and vehicular applications. Fuel 2013, 104, 813–821. [Google Scholar] [CrossRef]
- Wood, C.D.; Tan, B.; Trewin, A.; Su, F.; Rosseinsky, M.J.; Bradshaw, D.; Sun, Y.; Zhou, L.; Cooper, A.I. Microporous organic polymers for methane storage. Adv. Mater. 2008, 20, 1916–1920. [Google Scholar] [CrossRef]
- Li, Y.; Yi, H.; Tang, X.; Li, F.; Yuan, Q. Adsorption separation of CO2/CH4 gas mixture on the commercial zeolites at atmospheric pressure. Chem. Eng. J. 2013, 229, 50–56. [Google Scholar] [CrossRef]
- Wen, H.M.; Li, B.; Li, L.; Lin, R.B.; Zhou, W.; Qian, G.; Chen, B. A Metal–Organic Framework with Optimized Porosity and Functional Sites for High Gravimetric and Volumetric Methane Storage Working Capacities. Adv. Mater. 2018, 30, 1704792. [Google Scholar] [CrossRef]
- Moellmer, J.; Moeller, A.; Dreisbach, F.; Glaeser, R.; Staudt, R. High pressure adsorption of hydrogen, nitrogen, carbon dioxide and methane on the metal-organic framework HKUST-1. Microporous Mesoporous Mater. 2011, 138, 140–148. [Google Scholar] [CrossRef]
- Chen, Z.; Li, P.; Anderson, R.; Wang, X.; Zhang, X.; Robison, L.; Redfern, L.R.; Moribe, S.; Islamoglu, T.; Gómez-Gualdrón, D.A.; et al. Balancing volumetric and gravimetric uptake in highly porous materials for clean energy. Science 2020, 368, 297 LP–303. [Google Scholar] [CrossRef]
- Alezi, D.; Belmabkhout, Y.; Suyetin, M.; Bhatt, P.M.; Weseliński, L.J.; Solovyeva, V.; Adil, K.; Spanopoulos, I.; Trikalitis, P.N.; Emwas, A.H.; et al. MOF Crystal Chemistry Paving the Way to Gas Storage Needs: Aluminum-Based soc -MOF for CH4, O2, and CO2 Storage. J. Am. Chem. Soc. 2015, 137, 13308–13318. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Zhou, W.; Pham, T.; Forrest, K.A.; Liu, W.; He, Y.; Wu, H.; Yildirim, T.; Chen, B.; Space, B.; et al. Fine Tuning of MOF-505 Analogues To Reduce Low-Pressure Methane Uptake and Enhance Methane Working Capacity. Angew. Chem. Int. Ed. 2017, 56, 11426–11430. [Google Scholar] [CrossRef]
- Jiang, J.; Furukawa, H.; Zhang, Y.B.; Yaghi, O.M. High Methane Storage Working Capacity in Metal-Organic Frameworks with Acrylate Links. J. Am. Chem. Soc. 2016, 138, 10244–10251. [Google Scholar] [CrossRef]
- Mason, J.A.; Oktawiec, J.; Taylor, M.K.; Hudson, M.R.; Rodriguez, J.; Bachman, J.E.; Gonzalez, M.I.; Cervellino, A.; Guagliardi, A.; Brown, C.M.; et al. Methane storage in flexible metal-organic frameworks with intrinsic thermal management. Nature 2015, 527, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Tang, S.; Wang, C.; Lv, X.; Jiang, M.; Wu, H.; Zhao, X. High gas storage capacities and stepwise adsorption in a UiO type metal-organic framework incorporating Lewis basic bipyridyl sites. Chem. Commun. 2014, 50, 2304–2307. [Google Scholar] [CrossRef] [PubMed]
- Wilmer, C.E.; Farha, O.K.; Yildirim, T.; Eryazici, I.; Krungleviciute, V.; Sarjeant, A.A.; Snurr, R.Q.; Hupp, J.T. Gram-scale, high-yield synthesis of a robust metal–organic framework for storing methane and other gases. Energy Environ. Sci. 2013, 6, 1158–1163. [Google Scholar] [CrossRef]
- Gándara, F.; Furukawa, H.; Lee, S.; Yaghi, O.M. High methane storage capacity in aluminum metal-organic frameworks. J. Am. Chem. Soc. 2014, 136, 5271–5274. [Google Scholar] [CrossRef] [PubMed]
- Mason, J.A.; Veenstra, M.; Long, J.R. Evaluating metal-organic frameworks for natural gas storage. Chem. Sci. 2014, 5, 32–51. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, C.; Wang, Q.; Fu, W.; Huang, K.; Zhou, W. A metal-organic framework functionalized with piperazine exhibiting enhanced CH4 storage. J. Mater. Chem. A 2017, 5, 349–354. [Google Scholar] [CrossRef]
- Spanopoulos, I.; Tsangarakis, C.; Klontzas, E.; Tylianakis, E.; Froudakis, G.; Adil, K.; Belmabkhout, Y.; Eddaoudi, M.; Trikalitis, P.N. Reticular Synthesis of HKUST-like tbo-MOFs with Enhanced CH4 Storage. J. Am. Chem. Soc. 2016, 138, 1568–1574. [Google Scholar] [CrossRef]
- Volkringer, C.; Loiseau, T.; Haouas, M.; Taulelle, F.; Popov, D.; Burghammer, M.; Riekel, C.; Zlotea, C.; Cuevas, F.; Latroche, M.; et al. Occurrence of Uncommon Infinite Chains Consisting of Edge-Sharing Octahedra in a Porous Metal Organic Framework-Type Aluminum Pyromellitate Al4(OH)8[C10O8H2] (MIL-120): Synthesis, Structure, and Gas Sorption Properties. Chem. Mater. 2009, 21, 5783–5791. [Google Scholar] [CrossRef]
- Zhuang, W.; Yuan, D.; Liu, D.; Zhong, C.; Li, J.-R.; Zhou, H.-C. Robust Metal–Organic Framework with An Octatopic Ligand for Gas Adsorption and Separation: Combined Characterization by Experiments and Molecular Simulation. Chem. Mater. 2012, 24, 18–25. [Google Scholar] [CrossRef]
- Hu, Y.; Xiang, S.; Zhang, W.; Zhang, Z.; Wang, L.; Bai, J.; Chen, B. A new MOF-505 analog exhibiting high acetylene storage. Chem. Commun. 2009, 7551–7553. [Google Scholar] [CrossRef] [PubMed]
- Cheon, Y.E.; Park, J.; Suh, M.P. Selective gas adsorption in a magnesium-based metal–organic framework. Chem. Commun. 2009, 5436–5438. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, H.; Côté, A.P.; Furukawa, H.; O’Keeffe, M.; Yaghi, O.M. Zeolite A imidazolate frameworks. Nat. Mater. 2007, 6, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, R.; Furukawa, H.; Britt, D.; Knobler, C.; O’Keeffe, M.; Yaghi, O.M. Control of pore size and functionality in isoreticular zeolitic imidazolate frameworks and their carbon dioxide selective capture properties. J. Am. Chem. Soc. 2009, 132, 5578–5579. [Google Scholar] [CrossRef] [PubMed]
- Neofotistou, E.; Malliakas, C.D.; Trikalitis, P.N. Unprecedented sulfone-functionalized metal-organic frameworks and gas-sorption properties. Chem. A Eur. J. 2009, 15, 4523–4527. [Google Scholar] [CrossRef]
- Yoon, J.W.; Jhung, S.H.; Hwang, Y.K.; Humphrey, S.M.; Wood, P.T.; Chang, J.-S. Gas-Sorption Selectivity of CUK-1: A Porous Coordination Solid Made of Cobalt(II) and Pyridine-2,4- Dicarboxylic Acid. Adv. Mater. 2007, 19, 1830–1834. [Google Scholar] [CrossRef]
- Moon, H.R.; Kobayashi, N.; Suh, M.P. Porous Metal−Organic Framework with Coordinatively Unsaturated MnII Sites:Sorption Properties for Various Gases. Inorg. Chem. 2006, 45, 8672–8676. [Google Scholar] [CrossRef]
- Zhang, S.-M.; Chang, Z.; Hu, T.-L.; Bu, X.-H. New Three-Dimensional Porous Metal Organic Framework with Tetrazole Functionalized Aromatic Carboxylic Acid: Synthesis, Structure, and Gas Adsorption Properties. Inorg. Chem. 2010, 49, 11581–11586. [Google Scholar] [CrossRef]
- Chen, Z.; Xiang, S.; Arman, H.D.; Li, P.; Tidrow, S.; Zhao, D.; Chen, B. A microporous metal-organic framework with immobilized -OH functional groups within the pore surfaces for selective gas sorption. Eur. J. Inorg. Chem. 2010, 2010, 3745–3749. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiang, S.; Chen, Y.-S.; Ma, S.; Lee, Y.; Phely-Bobin, T.; Chen, B. A Robust Highly Interpenetrated Metal−Organic Framework Constructed from Pentanuclear Clusters for Selective Sorption of Gas Molecules. Inorg. Chem. 2010, 49, 8444–8448. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Xiang, S.; Rao, X.; Zheng, Q.; Fronczek, F.R.; Qian, G.; Chen, B. A rod packing microporous metal–organic framework with open metal sites for selective guest sorption and sensing of nitrobenzene. Chem. Commun. 2010, 46, 7205–7207. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Shi, W.; Zhao, K.; Niu, Z.; Chen, X.; Cheng, P. A Robust Porous Metal–Organic Framework with a New Topology That Demonstrates Pronounced Porosity and High-Efficiency Sorption/Selectivity Properties of Small Molecules. Chem. A Eur. J. 2012, 18, 5715–5723. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Xue, M.; Zhang, D.; Fan, L.; Pan, Y.; Qiu, S. Hybrid metal-organic framework nanomaterials with enhanced carbon dioxide and methane adsorption enthalpy by incorporation of carbon nanotubes. Inorg. Chem. Commun. 2015, 58, 79–83. [Google Scholar] [CrossRef]
- Lozano-Castelló, D.; Alcañiz-Monge, J.; De La Casa-Lillo, M.A.; Cazorla-Amorós, D.; Linares-Solano, A. Advances in the study of methane storage in porous carbonaceous materials. Fuel 2002, 81, 1777–1803. [Google Scholar] [CrossRef]
- Kubota, Y.; Takata, M.; Kitaura, R.; Matsuda, R.; Kobayashi, T.C.; Kitagawa, S. Hindered Rotation of Methane Molecules in the One-Dimensional Nanochannel of a Porous Coordination Polymer. J. Nanosci. Nanotechnol. 2009, 9, 69–76. [Google Scholar] [CrossRef]
- Chung, Y.G.; Camp, J.; Haranczyk, M.; Sikora, B.J.; Bury, W.; Krungleviciute, V.; Yildirim, T.; Farha, O.K.; Sholl, D.S.; Snurr, R.Q. Computation-ready, experimental metal-organic frameworks: A tool to enable high-throughput screening of nanoporous crystals. Chem. Mater. 2014, 26, 6185–6192. [Google Scholar] [CrossRef]
- Zhao, D.; Yuan, D.; Yakovenko, A.; Zhou, H.-C. A NbO-type metal–organic framework derived from a polyyne-coupled di-isophthalate linker formed in situ. Chem. Commun. 2010, 46, 4196–4198. [Google Scholar] [CrossRef] [PubMed]
- Park, H.J.; Cheon, Y.E.; Suh, M.P. Post-Synthetic Reversible Incorporation of Organic Linkers into Porous Metal–Organic Frameworks through Single-Crystal-to-Single-Crystal Transformations and Modification of Gas-Sorption Properties. Chem. A Eur. J. 2010, 16, 11662–11669. [Google Scholar] [CrossRef]
- Savage, M.; da Silva, I.; Johnson, M.; Carter, J.H.; Newby, R.; Suyetin, M.; Besley, E.; Manuel, P.; Rudić, S.; Fitch, A.N.; et al. Observation of Binding and Rotation of Methane and Hydrogen within a Functional Metal–Organic Framework. J. Am. Chem. Soc. 2016, 138, 9119–9127. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.J.; Bae, Y.S. Can metal-organic frameworks attain new DOE targets for on-board methane storage by increasing methane heat of adsorption? J. Phys. Chem. C 2014, 118, 19833–19841. [Google Scholar] [CrossRef]
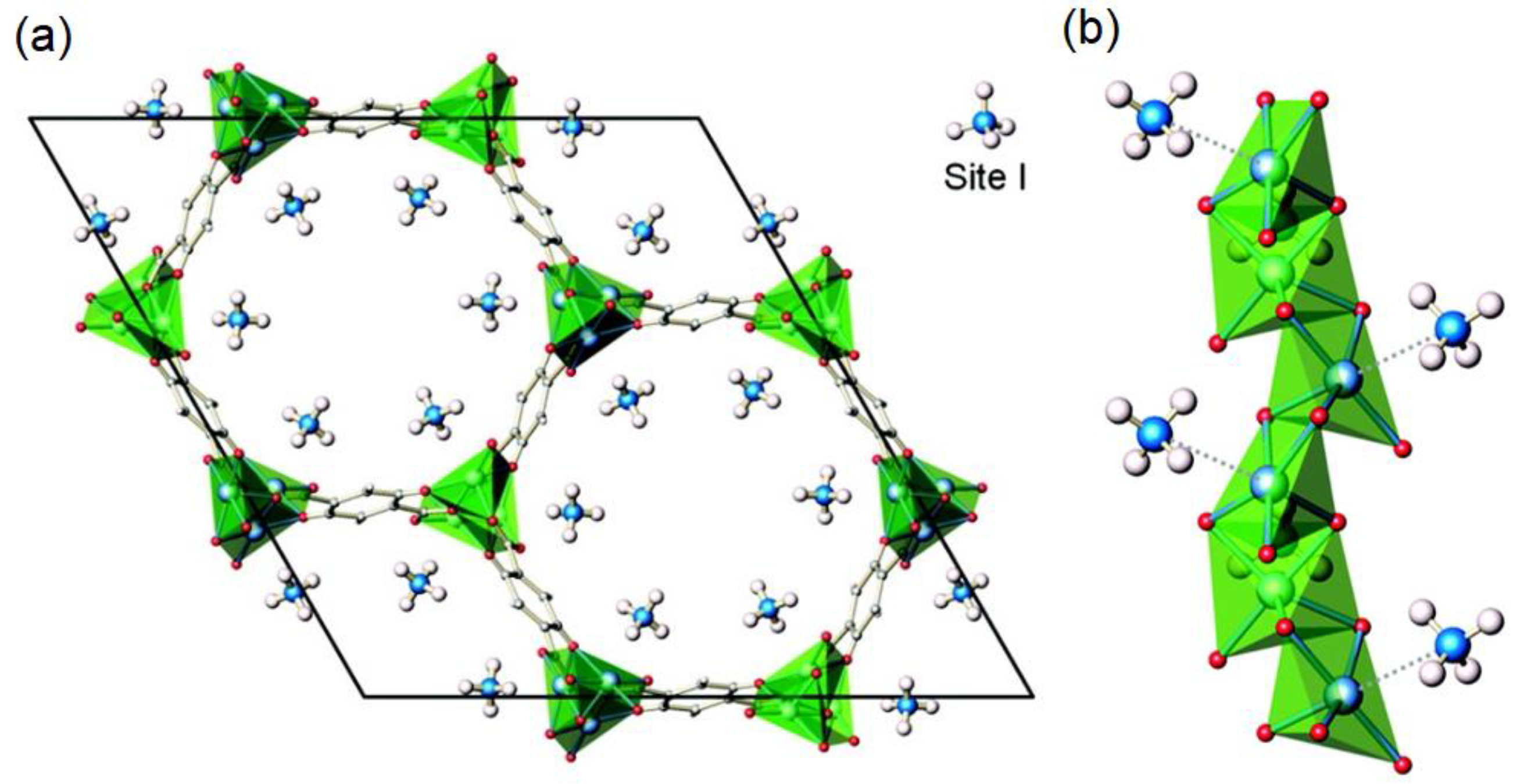
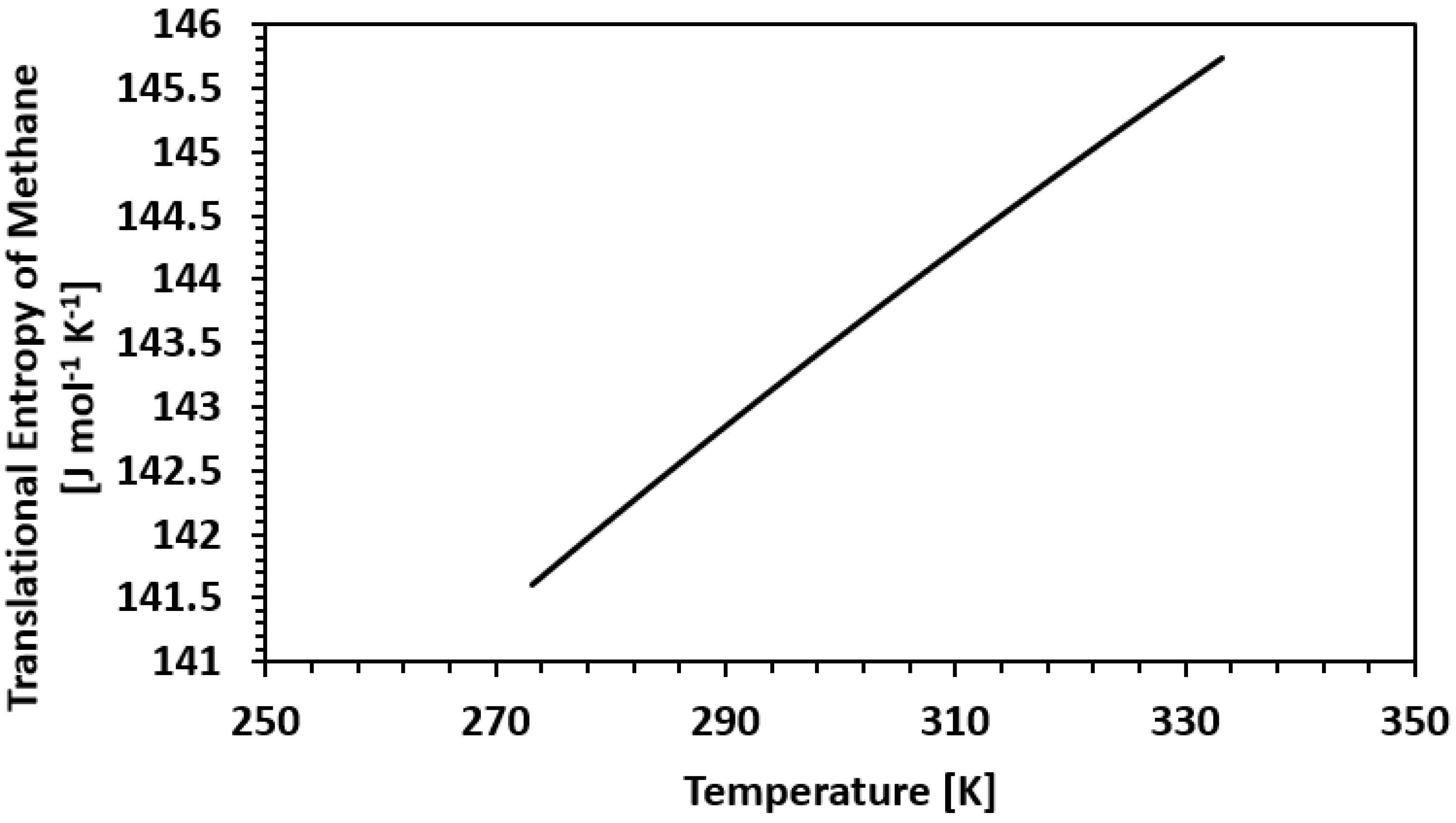
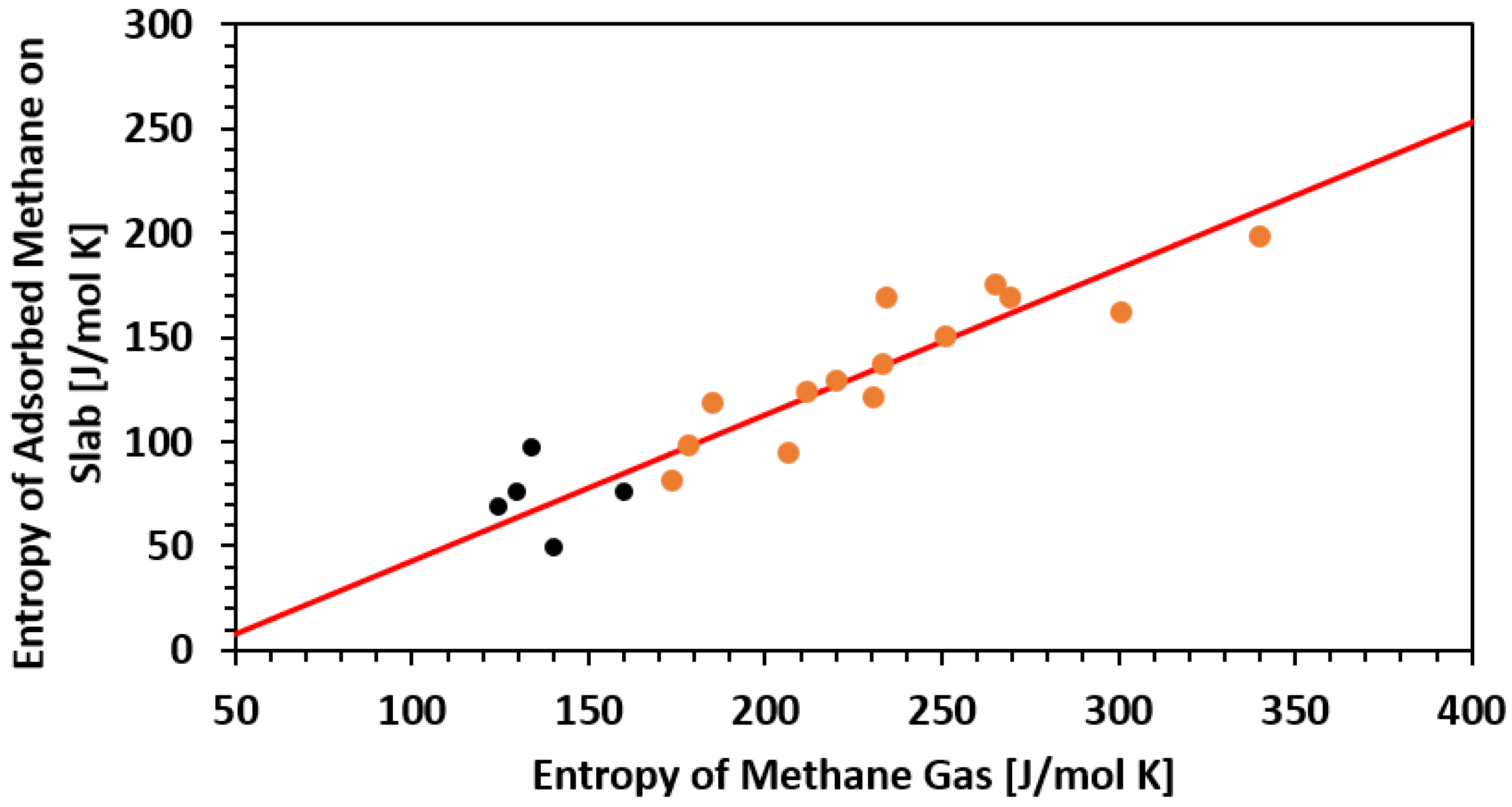
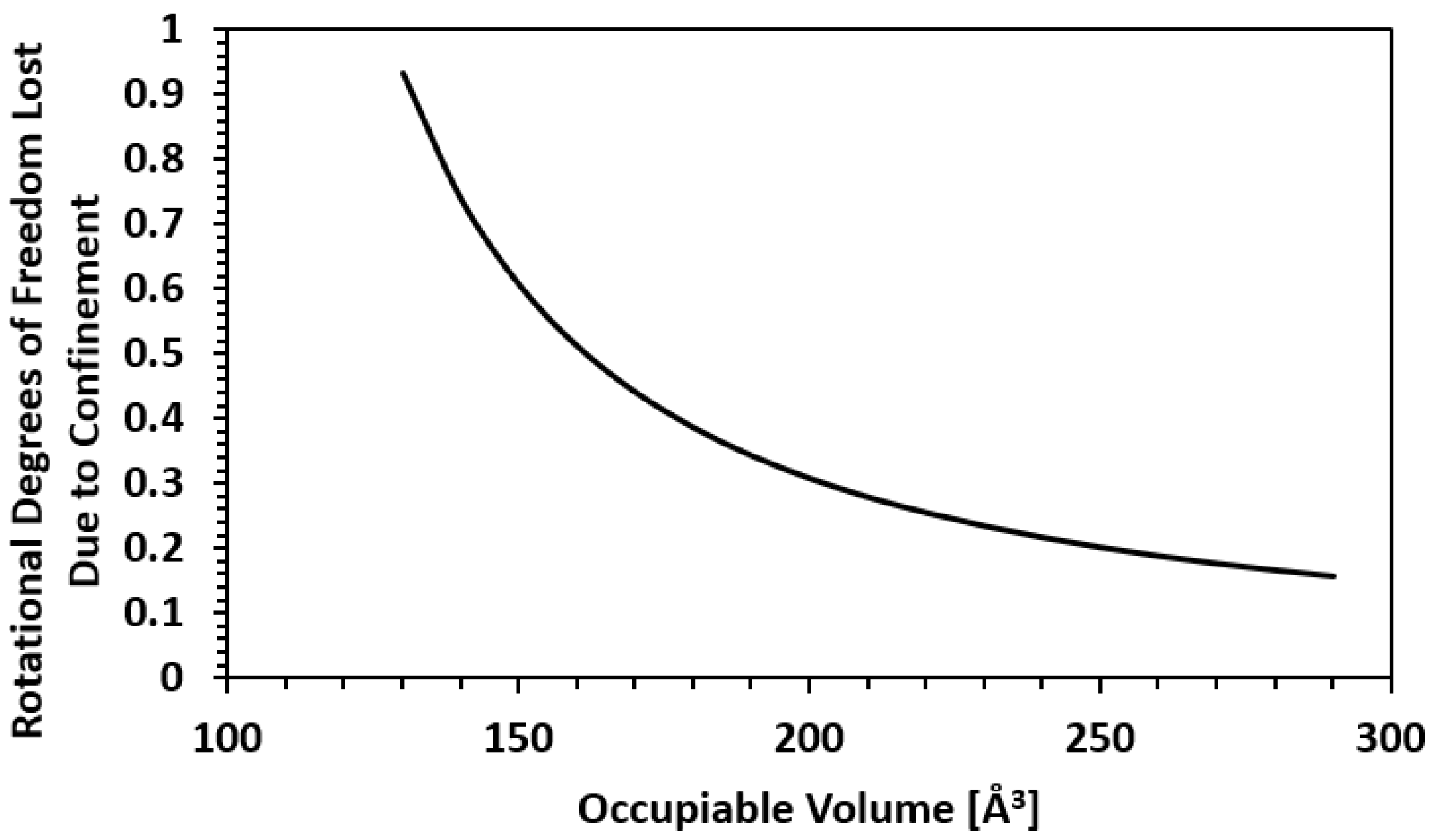
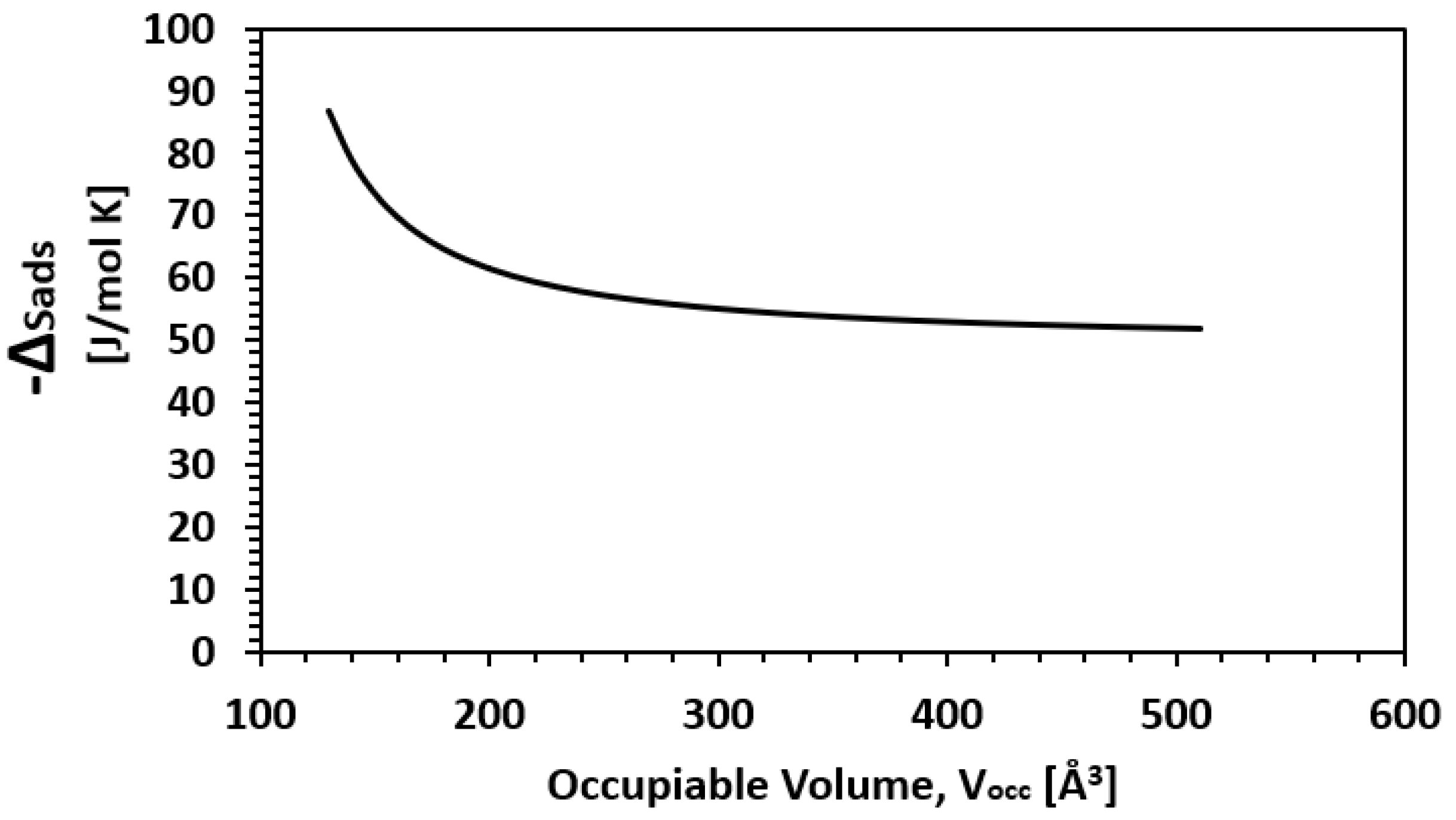
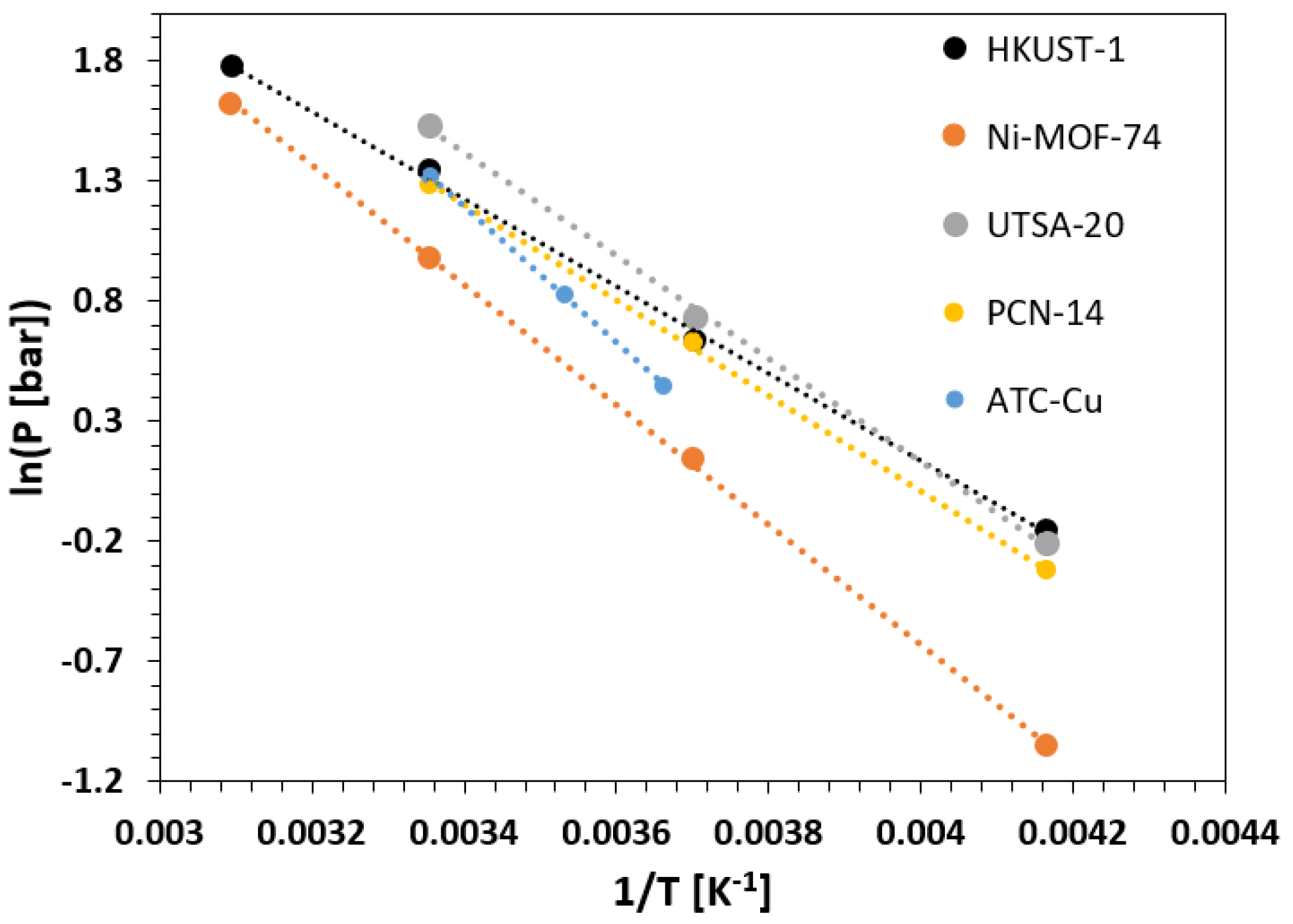
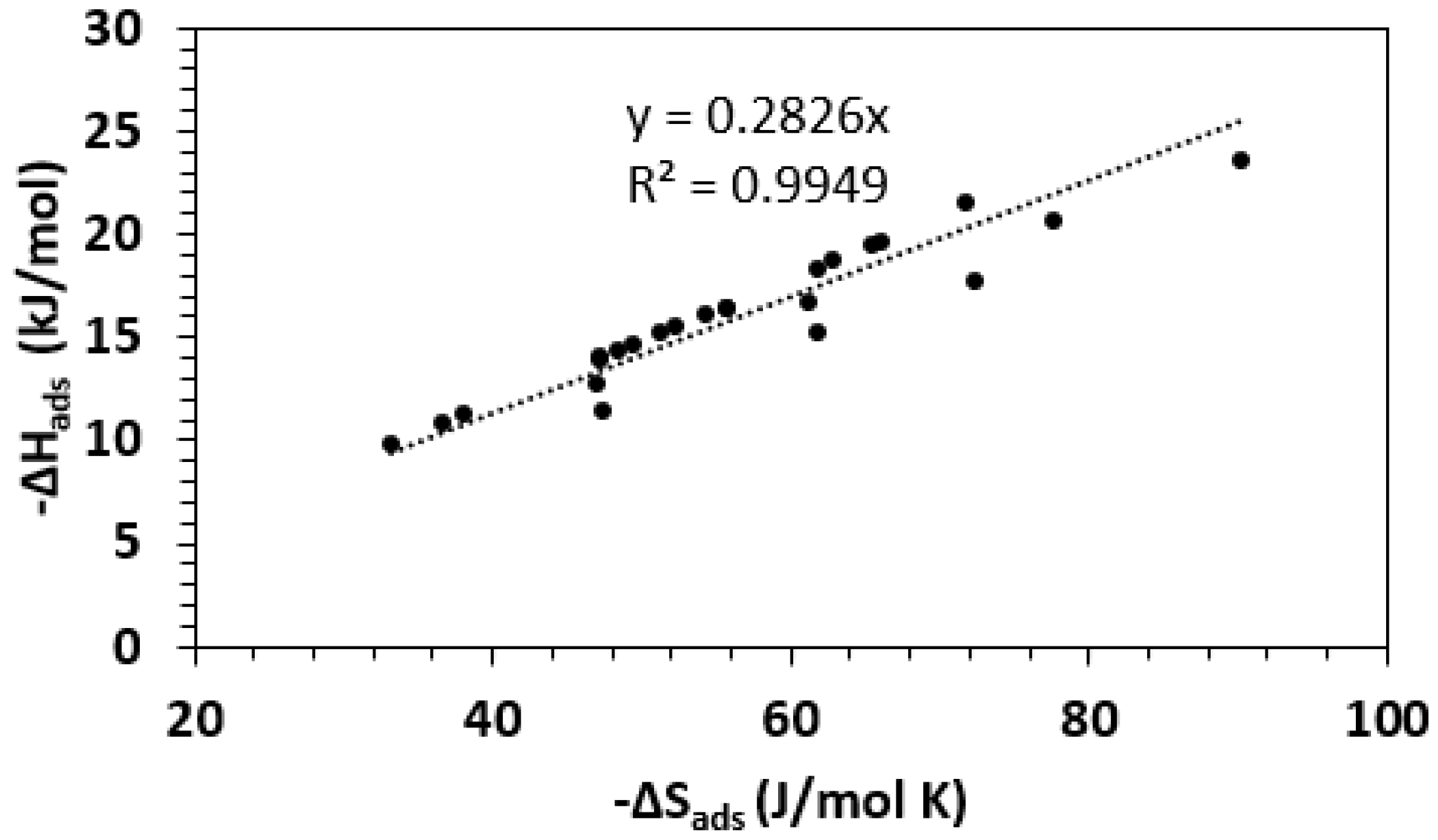
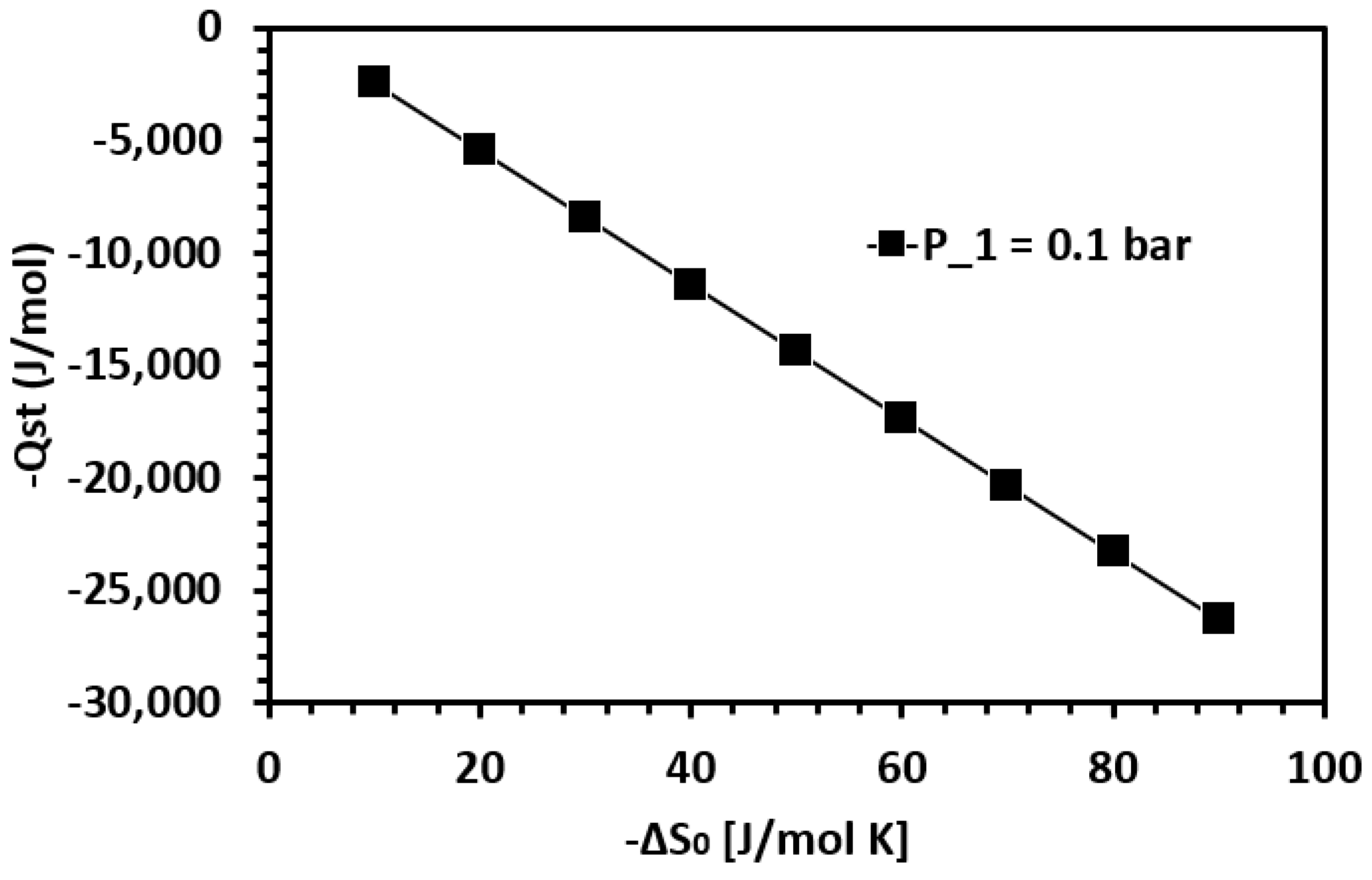
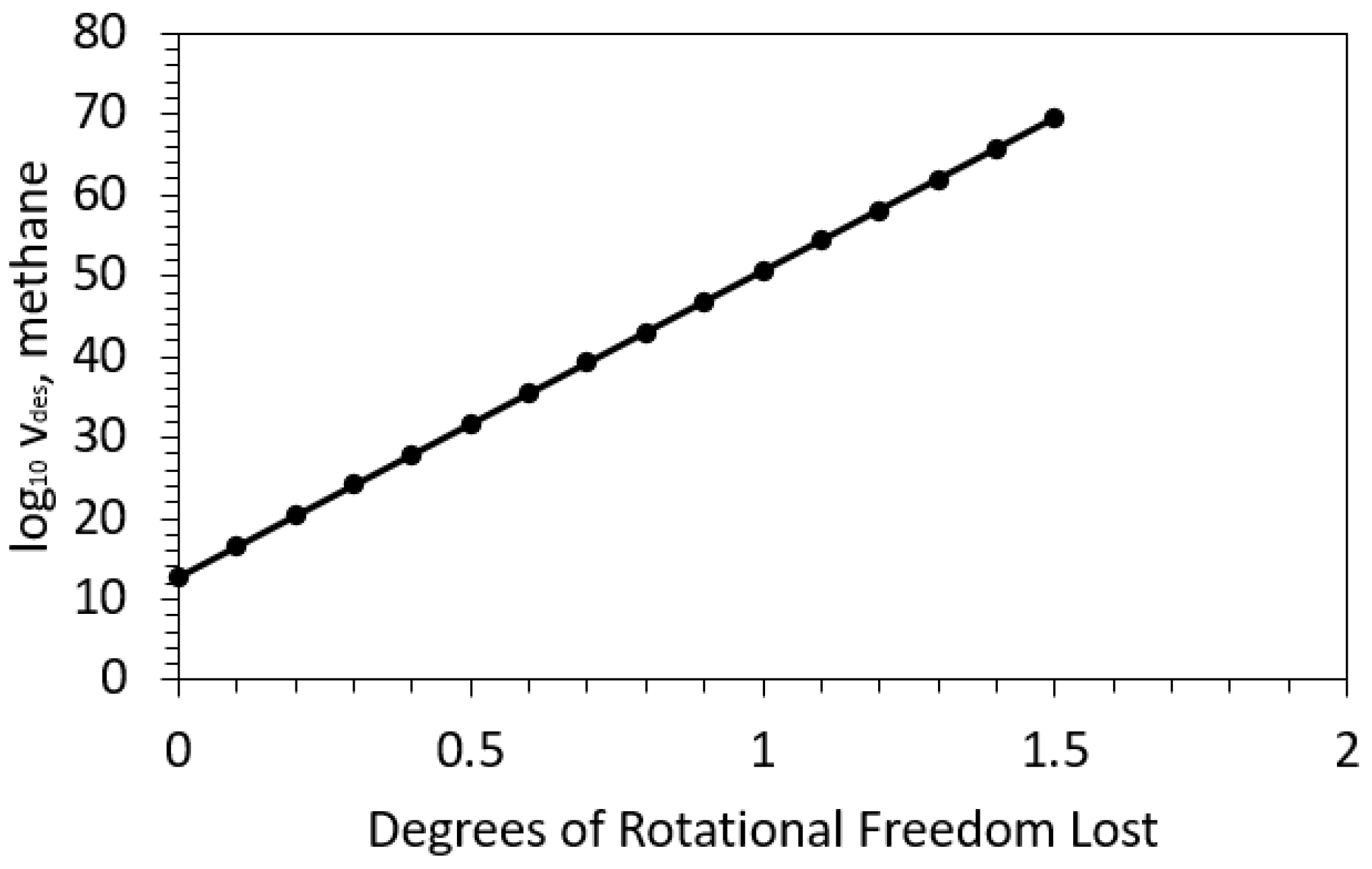
| Framework | Largest Cavity Diameter (Å) | Void Fraction of Accessible Probe-Occupiable Pore Volume | Ref. |
|---|---|---|---|
| HKUST-1 | 13.14982 | 0.67 | [57] |
| DUT-13 | 18.4908 | 0.81 | [85] |
| NU-125 | 19.37323 | 0.73 | [64] |
| PCN-46 | 12.05622 | 0.72 | [87] |
| PCN-61 | 18.70668 | 0.75 | [44] |
| SNU-30 | 14.9209 | 0.83 | [88] |
| UTSA-20 | 9.95246 | 0.57 | [40] |
| Framework | −∆Hads (kJ/mol) | −∆Sads (J/mol K) | Ref. |
|---|---|---|---|
| HKUST-1 | 15.2 | 61.7 | [32] |
| Ni-MOF-74 | 20.7 | 77.7 | [32] |
| UTSA-20 | 17.8 | 72.3 | [32] |
| PCN-14 | 11.4 | 47.39 | [32] |
| NJU-Bai-41 | 16.1 | 54.2 | [60] |
| MOF-905-Naph | 10.87 | 36.7 | [61] |
| MOF-905-NO2 | 9.86 | 33.2 | [61] |
| MFM-300 (In) | 16.49 | 55.66 | [89] |
| ATC-Cu | 23.6 | 90.2 | [35] |
| MOF-520 | 14.0 | 47.1 | [65] |
| Al-soc-MOF-1 | 15.3 | 51.2 | [59] |
| MOF-519 | 14.1 | 47.2 | [65] |
| ZIF-68 | 16.7 | 61.2 | [74] |
| ZIF-69 | 18.4 | 61.8 | [74] |
| Cu-tbo-MOF-5 | 21.6 | 71.8 | [68] |
| NJU-Bai-19 | 14.7 | 49.4 | [67] |
| NJU-Bai-42 | 12.8 | 46.9 | [60] |
| NJU-Bai-41 | 14.4 | 48.3 | [60] |
| MOF-950 | 11.3 | 38.1 | [61] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, E. Mitigating Global Methane Emissions Using Metal-Organic Framework Adsorbents. Appl. Sci. 2020, 10, 7733. https://doi.org/10.3390/app10217733
Mahmoud E. Mitigating Global Methane Emissions Using Metal-Organic Framework Adsorbents. Applied Sciences. 2020; 10(21):7733. https://doi.org/10.3390/app10217733
Chicago/Turabian StyleMahmoud, Eyas. 2020. "Mitigating Global Methane Emissions Using Metal-Organic Framework Adsorbents" Applied Sciences 10, no. 21: 7733. https://doi.org/10.3390/app10217733
APA StyleMahmoud, E. (2020). Mitigating Global Methane Emissions Using Metal-Organic Framework Adsorbents. Applied Sciences, 10(21), 7733. https://doi.org/10.3390/app10217733




