Abstract
The vision to manipulate and control magnetism with light is driven on the one hand by fundamental questions of direct and indirect photon-spin interactions, and on the other hand by the necessity to cope with ever growing data volumes, requiring radically new approaches on how to write, read and process information. Here, we present two complementary experimental geometries to access the element-specific magnetization dynamics of complex magnetic systems via ultrafast magneto-optical spectroscopy in the extreme ultraviolet spectral range. First, we employ linearly polarized radiation of a free electron laser facility to demonstrate decoupled dynamics of the two sublattices of an FeGd alloy, a prerequisite for all-optical magnetization switching. Second, we use circularly polarized radiation generated in a laboratory-based high harmonic generation setup to show optical inter-site spin transfer in a CoPt alloy, a mechanism which only very recently has been predicted to mediate ultrafast metamagnetic phase transitions.
1. Introduction
The absorption of a femtosecond laser pulse by a thin magnetic film induces a non-equilibrium and spin-dependent electron distribution that triggers a cascade of microscopic processes and causes a very rapid change in the magnetization [1,2]. Spin-orbit coupling mediates spin-flips in scattering events and leads to a local loss of the magnetization [3]. Magnon generation quenches the long-range magnetic order [4,5,6], and the spin-dependent transport properties of excited electrons trigger spin currents and redistribute spin angular momentum within the sample [7,8].
One of the most fascinating observations in the field of femtomagnetism is all-optical switching, which was first discovered in the rare earth-transition metal alloy, FeGd [9]. Upon optical excitation, the antiferromagnetically coupled Gd and Fe sites can be promoted into a transient ferromagnetic state, which mediates a reversal of macroscopic magnetization [10,11]. Microscopically, this is understood by a transient suppression of the inter-atomic exchange interaction due to ultrafast heating of the electrons, enabling an independent response of the rare earth and transition metal sublattices. Upon cooling, angular momentum exchange breaks the symmetry of the system and leads to magnetization switching. Because of the low specific heat of electrons, all-optical switching is inherently energy efficient with obvious potential for applications.
Very recently, a completely new mechanism to manipulate the magnetic structure has been put forward theoretically: laser pulse excitation induces an optical inter-site spin transfer (OISTR) in multi-element magnetic systems [12]. This spin manipulation is of a purely optical nature and is therefore one of the fastest ways to manipulate spins by light. The authors of this theoretical study also predicted that the spin-selective charge transfer between distinct sites can lead to a metamagnetic phase transition, switching the magnetic order from an antiferromagnetic to a transient ferromagnetic alignment. In the last two years, a number of experiments demonstrated signatures of OISTR, both in the optical [13,14] as well as in the extreme ultraviolet (XUV) [15,16,17,18] spectral range. The latter experiments were carried out with high harmonic generation (HHG) sources and exploited the element specificity of resonant core-to-valence state transitions. Here, the sensitivity to the local magnetic moment can be easily explained by a two step model [19]: if circularly polarized photons are absorbed by core level electrons with finite spin-orbit interaction the resulting photoelectrons become spin-polarized. Then, the helicity-dependent absorption strength in the material depends on the spin imbalance of the ferromagnet, with different numbers of available states for majority and minority electrons in the exchange-split valence band. Therefore, the observable, calculated as the difference of the transmitted light intensity for opposite circular polarization, is directly proportional to the magnetization and is called magnetic circular dichroism (MCD). More generally, the optical response around such a resonant transition in magnetic materials can be parameterized by a complex magneto-optical function.
While time resolved MCD measurements have been pioneered in the soft X-ray range at the L-edges of transition metals, in particular, at the femto-slicing beamline at BESSY, HZB, Germany [20], in the last decade a lot of effort has been devoted to transferring resonant probing techniques of magnetization to more shallow resonances in the XUV spectral range, both at free electron laser (FEL) facilities [21] and at laboratory-based HHG sources in reflection [22,23] or transmission geometry [24]. Research has focused on tracking laser-driven, ultrafast spin transport either using the transverse magneto-optical Kerr effect [25,26] or by exploiting the short wavelength of the XUV radiation in time-resolved small angle X-ray scattering experiments [27,28,29,30] as well as via ultrafast coherent imaging experiments [31]. Furthermore, the great potential of probing magnetization with resonant XUV radiation was convincingly demonstrated in a series of experiments, which showed that transient spectra can provide fingerprint signatures of microscopic processes responsible for ultrafast demagnetization, in particular differentiating Heisenberg type delocalized magnon or Stoner type spin-flip excitations [32,33,34].
In this contribution, we present two complementary experiments dedicated to an element-specific view of femtomagnetism based on ultrafast XUV spectroscopy of multi-component magnetic systems performed at the FEL facility, FLASH, DESY, Hamburg and at a HHG beamline at the Max Born Insitute, Berlin. At the FEL facility, we exploit the dispersive (real) part of the magneto-optical functions in a resonant Faraday rotation geometry to study the ultrafast response of an FeGd alloy and reveal decoupled dynamics of the two sublattices Gd and Fe. In the experiment using HHG radiation, we compare the ultrafast response of a Co film and a CoPt alloy by measuring the absorptive (imaginary) part of the magneto-optical functions in an MCD experiment. Here, we were able to demonstrate that OISTR between Pt and Co atoms in the two-component CoPt alloy dominates the early time dynamics and leads to a faster and more efficient demagnetization.
2. Results and Discussions
2.1. Static Magneto-Optical Functions
Before we discuss the time resolved experiments, we briefly review details on the complex magneto-optical function in the XUV spectral range, which allows us to probe the element-specific response of multi-component magnetic systems.
Linearly polarized electromagnetic radiation can be decomposed into two circularly polarized waves with opposite helicity and equal amplitude. Its propagation through a magnetized material is then characterized by the complex index of refraction:
and are the dispersive and absorptive parts of the electro-optical functions valid at the photon energy, E, and describe the interaction with non-magnetic materials. The effect of the magnetization is given by the magneto-optical functions and . The positive and negative sign refers to either parallel or antiparallel alignment of the magnetization with respect to the wave vector of the incident radiation. Equation (1) directly implies that the element specific magnetization can be accessed either via the dispersive or absorptive part of the magneto-optical function, leading to two possible experimental configurations in a transmission geometry, MCD and Faraday rotation.
The absorptive magnetic contribution, , leads to a difference in transmitted intensity, , between left and right circularly polarized light and is generally referred to as MCD. It is defined for a sample with thickness, d, as:
The dispersive magnetic contribution, , leads to a difference in the phase of the two oppositely polarized modes and rotates the plane of polarization of the incoming radiation. The corresponding rotation angle, , is called Faraday angle and can be expressed as:
This equation is valid for a normal incident geometry and an out-of-plane magnetization, such that refraction of the radiation at the sample interfaces does not need to be considered [24,35,36,37].
In Figure 1, we show the magneto-optical functions of an FeGd (15 nm thickness) alloy at the Gd resonance (4d→4f) around 150 eV and at the Fe (3p→3d) resonance around 55 eV. The measurements were performed at the UE112 beamline of the BESSY II synchrotron light source, HZB, Germany. We recorded and calculated the values of according to Equation (2). The corresponding dispersive part, , is determined via the Kramers–Kronig relation. Note that, because the magneto-optical functions are equal to zero away from the resonance, the connecting real or imaginary part of the complex response function can be computed with high accuracy [38]. We also show the deduced Faraday rotation, which reaches a maximum of ≈ 0.36 deg/nm for Gd around 149 eV and ≈ 0.07 deg/nm for Fe around 56 eV. Note that this is about an order of magnitude larger than in the visible spectral range.
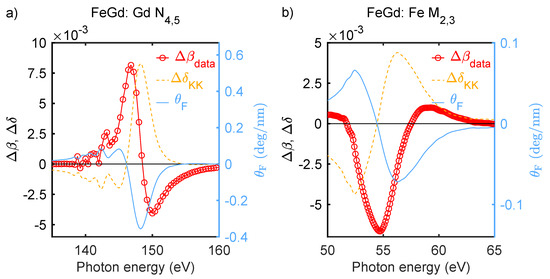
Figure 1.
Magneto-optical functions, and , of an FeGd alloy (a) at the Gd resonance around a photon energy of eV as well as (b) at the Fe resonance around a photon energy of eV. The dispersive part, , is retrieved by the Kramers–Kronig relation and is calculated according to Equation (3).
Co exhibits a magneto-optical function around its resonance with a similar shape and magnitude compared to Fe: the absorptive part reaches a maximum of at 60.3 eV. In a CoPt alloy, Co atoms induce a finite magnetic moment at their nearest neighbor Pt atoms with parallel aligned magnetic moments (cf. Figure 2e). In the spectral range between 45 and 72.5 eV, we can probe the local magnetization of Pt via the Pt and Pt resonances at 51.7, 65.3 and 71.2 eV, respectively [24,39]. For more details on the magneto-optical functions of the transition metals, as well as their ab initio description in a static and transient state, we refer to our recent works Willems et al. [38] and Dewhurst et al. [40].
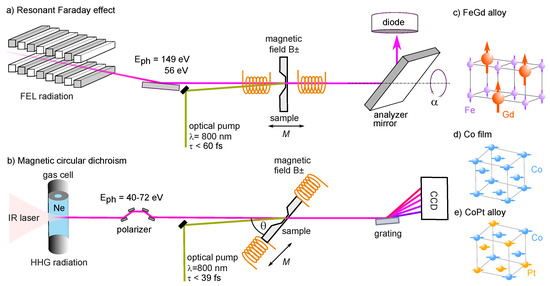
Figure 2.
(a) Scheme of a Faraday setup using single color FEL radiation. A linearly polarized XUV pulse is transmitted through the sample and the Faraday rotation is detected by a Rabniovitch polarimeter. (b) Scheme of an MCD setup using HHG radiation. The multiple emission peaks of the radiation are circularly polarized by a reflective phase-shifter, transmitted through the magnetic sample and detected by a spectrometer. In both setups, we realized a pump-probe geometry to measure optical driven ultrafast magnetization dynamics. Schematic depiction of (c) an out-of-plane magnetized FeGd alloy and of an in-plane magnetized (d) Co and (e) CoPt film.
2.2. Time Resolved Faraday Rotation
In this section, we present time resolved measurements based on the resonant Faraday Effect to demonstrate distinct ultrafast magnetization dynamics of the two magnetic sublattices of an FeGd ferrimagnetic alloy. The magnetic structure of the FeGd is schematically depicted in Figure 2c with Fe and Gd antiferromagnetically aligned in an out-of-plane direction. In panel (a) of Figure 2, we show the scheme of the experiment, as implemented at the beamline BL2 of the FEL facility FLASH, at DESY in Hamburg, Germany [41]. Linearly polarized pulses with a temporal duration between 50–80 fs are tuned to a photon energy resonant with either the Fe at ≈ 56 eV or with the Gd edge at ≈ 149 eV and impinge on the sample under normal incidence. The fluence of the XUV radiation is adjusted to remain below 1 mJ cm to avoid an influence of the probe pulses on the dynamics and to limit the risk of sample damage. The magnetization of FeGd (15 nm thickness) can be set with an external magnetic field to point parallel () or antiparallel () to the wave vector of the probe pulses. After transmission through the magnetic sample, the polarization of the XUV pulses is analyzed by a Rabinovitch polarimeter [42], consisting of a mirror aligned at the Brewster angle and an XUV sensitive photo diode. For Gd, the analyzer is a multilayer mirror (OptixFab GmbH, Jena) which has been optimized for a large contrast between the reflectance of s- and p-polarized light centered at 150 eV with a full width at half maximum of 10 eV. The reflectances, , of the multilayer mirror were determined by a calibration measurement at the light source of the German national metrology institute, PTB, Berlin, Germany, using 99.3% degree p-polarization. For Fe, we used a gold coated mirror. The polarizing power of the analyzer elements is defined as and listed with the respective reflectances in Table 1. The mirror–detector assembly can be rotated around the beam axis by the azimuthal angle . Pump pulses centered at a wavelength of 800 nm, with a pulse duration of fs and with a fluence of ≈ 5 mJ cm excite the sample in a collinear geometry to induce an ultrafast demagnetization. The time resolution is estimated to remain below 100 fs in all experiments, taking into account the temporal jitter of arrival times between optical and XUV pulses. Measurements are performed in a repetitive pump-probe scheme by averaging 100 shots at a 10 Hz repetition rate for each rotation angle or time delay. All data are normalized shot-to-shot by the photon numbers recorded by the gas monitor detector of the FLASH photon diagnostics.

Table 1.
Reflectances, , and polarizing power, , of the analyzer mirrors. The values for the ML mirror were determined at the Metrology Light source of PTB, Berlin, and the values for the Au mirror were calculated with a tabulated index of refraction at 56 eV [43]. The Brewster angles are measured in a grazing incidence geometry.
The XUV intensity recorded with the XUV photo diode is a function of the azimuthal rotation angle, , and is given by [36]:
where is the incident intensity, T the transmittance of the sample and takes into account the small effects due to an induced ellipticity of the beam after transmission through the magnetized sample.
In Figure 3a, we show the measured intensity for photon energies resonant at the Gd edge. The measurements before optical excitation at ps for two opposite magnetization directions of the sample are shifted by . We note that the rotation angle is smaller than the maximum value that is predicted according to the measurement shown in Figure 1. We attribute this to the uncertainty in determining the absolute photon energy combined with the difficulty to scan the photon energy with fixed undulator gaps at FLASH. The spectral bandwidth of the FEL radiation on the order of 1–2% also results in an effectively smaller value of . At 3 ps after optical excitation, we completely quench the magnetization and, consequently, the two measurements for opposite magnetization directions lie on top of each other and are centered around . In Figure 3b, we show the magnetic asymmetry calculated as . Before time delay zero, we observe a very large asymmetry of approximately 40 % at a rotation angle of , while 3 ps after optical excitation, the asymmetry is almost completely zero for all angles .
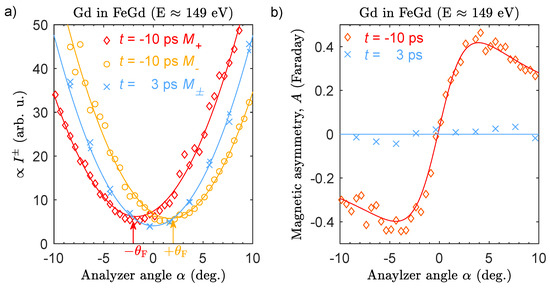
Figure 3.
(a) Detected intensity after reflection off the analyzer mirror as a function of rotation angle, , for eV, resonant at the edge of Gd. The two measurements before optical excitation at ps for two opposite directions of the sample magnetization, , are shifted by the Faraday angle . After optical excitation at ps, the Faraday angle is zero, , and the measurements are centered around , independent of the applied magnetic field. The lines are non-linear least square fits according to Equation (4). (b) Magnetic asymmetry before and after optical excitation is shown as a function of the analyzer angle. The maximum value reaches very large values of approximately % for .
In Figure 4a, we show the intensity measured at an angle of as a function of the time delay between the optical excitation and the XUV probe pulses. Upon excitation, we observe an ultrafast drop or increase in the intensity depending on the magnetization direction of the sample. For the approximation that and for , we can show that [37]:
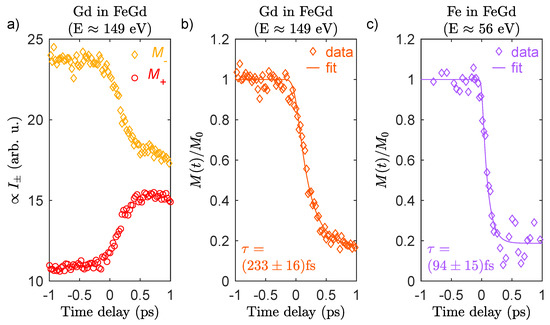
Figure 4.
(a) Measurements of for opposite magnetization directions, , as a function of the time delay at the Gd resonance at eV. Corresponding values of (b) for the Gd and (c) Fe sublattice determined according to Equation (5). Solid lines are non-linear least-square fit with a monoexponential function with a time constant fs and fs for Gd and Fe, respectively.
We normalize our observable, proportional to , to the average value before optical excitation, , and show the corresponding relative changes in the magnetization as a function of time delay in Figure 4b. A nonlinear least square fit of the data with a mono-exponential function convolved with the temporal resolution of the experiment yields a demagnetization amplitude of the Gd sublattice by approximately 80% with a corresponding time constant of fs. Analogously measured time resolved data at the Fe edge are shown in Figure 4c. While the amplitude of the demagnetization after 1 ps is comparable between the Fe and Gd sublattices, in Fe, we observe a significantly faster time constant of only fs. Distinct demagnetization times of the Gd and Fe sublattices in an FeGd alloy have been observed before in time resolved magnetic circular dichroism experiments. The microscopic origin has been explained by an ultrafast reduction in the interatomic exchange interaction due to the rapid heating of the electronic system close to, or even above the Curie temperature [10]. The demagnetization of the two sublattices is then allowed to proceed independently and scales with the very different magnetic moments of Fe () and Gd () [44]. As mentioned above, distinct sublattices with a different ultrafast magnetic response are a prerequisite for the formation of a transient ferromagnetic alignment of the two sublattices and, hence, for the occurrence of all-optical magnetic switching [45]. There are two more aspects which are noteworthy: first, as we qualitatively confirm the results of the FeGd demagnetization dynamics carried out with the established technique of MCD in the soft-X-ray range [10,44,46], we conclude that ultrafast Faraday rotation is indeed an accurate observable for the transient magnetization. Second, a lot of research in resonant XUV spectroscopy has recently been devoted to exploring a potential influence of transient changes in the electro-optical functions and to MCD signals [26,29,34,47,48,49]. Transient changes in the transmission, T [18], or reflection [50] at a core-valence band transition have been shown to be on the order of a few percent, and hence of a similar magnitude compared to the changes in MCD signals in the XUV spectral range [38]. This is different for the Faraday rotation. On the one hand, we observe very large asymmetries of up to 40% and, on the other hand, small relative changes in the transmission, T, have a negligible influence on for , as is easily verified by inspection of Equation (4). Therefore, non-equilibrium electron distributions are expected to have an insignificant effect on the extracted magnetization dynamics.
2.3. Time Resolved Magnetic Circular Dichroism and Helicity-Dependent Absorption
In the second part of this paper, we present recent results on the hypothesis that tailored chemical heterogeneities in magnetic systems can be used to enhance the ultrafast magnetic response after optical excitation. As outlined in the introduction, in multi-component magnetic systems with sites exhibiting a distinct number of available states above the Fermi energy, OISTR can become an important mechanism for ultrafast demagnetization. To this end, we have compared the ultrafast magnetization dynamics of an elemental Co film and CoPt alloy via MCD in transmission geometry [18], as schematically depicted in Figure 2b. We generate high harmonic radiation by focusing intense laser pulses into a neon-filled gas cell, leading to discrete harmonic emission peaks in the spectral range between ≈40–72 eV with a width of ≈200 meV. The state of polarization is controlled by a four-mirror phase-shifter [24,51,52], resulting in a high degree of circular polarization of >80% in the energy range between 50 and 65 eV. The broadband XUV spectrum is transmitted through the sample, energetically dispersed and measured by a charged coupled device (CCD). As both magnetic films, Co and CoPt, have their easy magnetization direction oriented in the sample plane (cf. schematic in Figure 2d,e), we mounted the sample at with respect to the incoming wave vector of the XUV light to ensure a finite projection onto the in-plane magnetization. The samples were excited in a collinear geometry with laser pulses centered at a wavelength of nm, a fluence of ≈15 mJ cm and a pulse length of 39 fs. The experiment is carried out at a 3 kHz repetition rate.
We measure the transmitted intensity, , for two opposite magnetization directions by toggling the external magnetic field, . Note that measurements with opposite magnetization directions of the sample but with a fixed helicity of the light is equivalent to measurements with opposite helicities but a fixed magnetization direction [19]. The magnetic asymmetry, A, is approximately proportional to the MCD contrast and is given by:
To increase the signal to noise ratio, we record the incoming spectrum with a second spectrometer and repeat the time delay scans up to 100 times. The total measurement time per sample amounts to about 4 h for each sample. For more details on the experimental details, we refer to Yao et al. [53].
In Figure 5, we show the magnetic asymmetry as a function of the time delay after optical excitation. The asymmetry for the elemental Co film measured at the Co edge is , which drops with a time constant fs by 20%. For the CoPt alloy, we follow the element-specific response by recording the respective sublattices at the Co edge as well as at the Pt and edge independently in the same measurement. Here, the asymmetries are smaller and remain below 1%. Note that the small asymmetries in XUV MCD compared to Faraday rotation measurements require a significantly better noise management. The rms value for A before fs corresponds to , yielding an excellent signal to noise ratio of our data. Non-linear least square fits (solid lines) reveal an equivalent response with a demagnetization amplitude of 80% and time constants of fs, fs, fs. A priori, identical local demagnetization times for Co and Pt are an unexpected result, because it is generally assumed that an important process responsible for ultrafast demagnetization relies on spin-flip scattering processes, which are mediated by spin-orbit interaction. With an approximately 10-times larger spin-orbit coupling in Pt compared to Co, we would anticipate a larger demagnetization rate localized at the Pt sites. This is, however, not what we observe. Additionally, we recall that CoPt compared to Co exhibits a significantly higher demagnetization rate and efficiency. This strongly suggests that an additional demagnetization channel is active in the two-component alloy CoPt. In the following section, we will demonstrate that this process can be identified as OISTR.
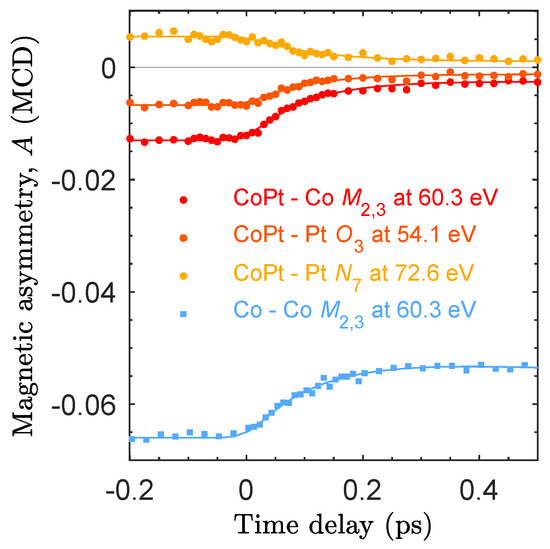
Figure 5.
The magnetic asymmetry, A (MCD), of the Co film and the CoPt alloy as a function of the time delay for three different photon energies corresponding to the Co edge at 60.3 eV and to the Pt and edge at 54.1 eV and 72.6 eV, respectively. The lines are non-linear least square fits. The rms value for values before fs corresponds to < yielding an excellent signal to noise ratio in spite of small asymmetry values.
In Figure 6, we show a calculation of the laser-driven spin-dependent electron occupation, around the Fermi energy of Co in the CoPt alloy and of the elemental Co film. The simulations are performed using a fully non-collinear version of TD-DFT as implemented within the Elk code [54]. Upon laser pumping, electrons are excited to available states above the Fermi energy. Because the density of states of the spin-split band of Co is dominated by available minority states, minority electrons are reshuffled more efficiently. In elemental Co, we observe a small loss of majority electrons (spin up) and a small increase in minority electrons (spin down), which we can attribute to spin-flips, leading to the observed loss of magnetization. However, much more prominent is the very large gain in minority electrons in CoPt above the Fermi energy, significantly exceeding the loss of minority electrons below the Fermi energy (red dashed line). It is worth also noting that this is much more pronounced compared to the minority response of elemental Co (blue dashed line). The additional minority electrons stem from the Pt sublattice and are transferred in an optical transition between the respective d minority states.
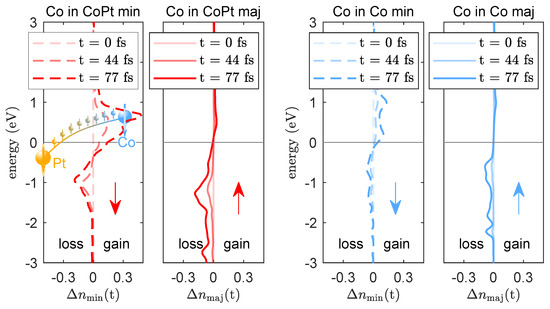
Figure 6.
We show a calculation of the laser induced changes in the spin-dependent electron occupations in the band, around the Fermi energy for Co in the CoPt alloy (red lines) and for elemental Co (blue lines). Laser excitation promotes electrons from occupied states below the Fermi energy to available states above the Fermi energy. Minority states (spin down) of Co in the CoPt alloy are filled much more efficiently than in the elemental Co, indicating a transfer of minority states from Pt to Co states, significantly increasing the efficiency of the demagnetization dynamics. This is schematically indicated in the left panel with minority electrons transferred from Pt to Co.
To experimentally demonstrate that the minority states of Co in CoPt are indeed efficiently filled in an OISTR process, we examine the helicity-dependent absorption channels individually. We calculate the absorption as , neglecting the small reflectance in the XUV spectral range. We show the normalized result in Figure 7 as a function of time delay between −50 fs and 100 fs: in the left panels, we plot the experimental data for Co and CoPt; in the right panels are the corresponding theoretically calculated values. Importantly, careful theoretical analysis shows that we can associate the transient absorption changes measured with opposite magnetization directions and with transitions predominantly into the majority and minority states, respectively.
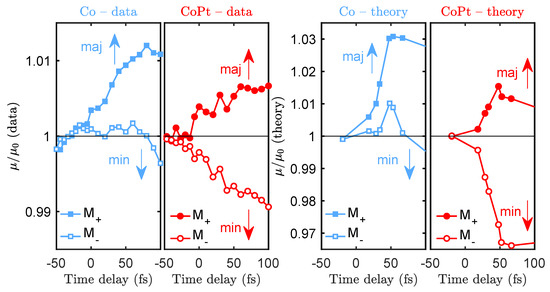
Figure 7.
Normalized helicity-dependent absorption, as a function of time delay for Co (blue squares) and CoPt (red circles). In the left panels, we show data measured at the Co resonance at 60 eV; in the right panel are the corresponding calculations. A positive magnetic field, , predominantly probes changes in majority occupations (spin up) and a negative magnetic field, , predominantly probes changes of the minority occupations (spin down). In CoPt we can clearly see that the absorption into minority states very rapidly decreases, which we interpret as the efficient filling of minority states by OISTR—i.e., transitions of Pt to Co minority states.
The most apparent differences of between the elemental Co and CoPt alloy is the response of the absorption for a sample magnetized in direction (open symbols in Figure 7): in Co, the absorption slightly increases or stays constant while in CoPt the absorption drops immediately after optical excitation. The interpretation is now straightforward and can be linked with the transient occupation changes, , shown in Figure 6: efficient filling of Co minority states above the Fermi energy by OISTR from Pt reduces the available final states for transitions, leading to an ultrafast drop of absorption. In elemental Co, this is not observed, again consistent with the transient occupations shown in Figure 6. The theoretical calculation of the exact same observable, , reproduces our experimental finding very well [18].
Finally, we remark that the distinct response between the absorption measured with different magnetization directions of the sample (or opposite helicities), as observed in the experiment, further strongly supports the theoretical finding that helicity-dependent absorption measures the spin-resolved transient changes of the occupations around the Fermi level of a specific element for early times after optical excitation (≈100 fs).
3. Conclusions
As optically induced functionalities of magnetic materials are closely linked to the ultrafast interplay of different elements within a magnetic system, access to element-specific observables is a necessity for progress on the path from a fundamental understanding to potential applications. We have demonstrated that resonant XUV spectroscopy in conjunction with state-of-the-art theory is indeed capable of providing a detailed picture of the microscopic processes responsible for macroscopic magnetization.
We demonstrated this by two complementary experimental realizations probing either the dispersive or the absorptive part of the magneto-optical functions in a Faraday rotation and an MCD experiment, respectively. In the first experiment, the polarization plane of transmitted photons tuned to the respective core-to-valence band transition in an FeGd alloy yielded large Faraday rotation angles and allowed us to reveal decoupled ultrafast magnetization dynamics of the Gd and Fe sublattices. Three advantages of Faraday rotation measurements are noteworthy: first, they yield large magnetic asymmetries; second, they do not require polarization control of the XUV radiation, which has remained challenging in HHG and is not (yet) always available at free-electron laser facilities; finally, the intrinsic contrast of Faraday measurements is only based on a phase difference and is therefore not detrimentally affected by strong absorption losses at the resonance of the probed element.
In the second experiment, we employed MCD contrast to reveal an efficient inter-site spin transfer in the two-component CoPt alloy. As the strength and direction of such spin-selective charge flow is determined by the available states above the Fermi energy of the involved elements [55], we envisioned to tailor the ultrafast magnetic response and work towards realizing a metamagnetic phase transition on the fastest time scale. While MCD experiments in the XUV spectral range require circularly polarized radiation and are technically very demanding because of very small magnetic asymmetries, they offer the great potential to analyze the energy and helicity-dependent transient absorption in order to differentiate the ultrafast occupation changes of minority and majority electrons after optical excitation.
Finally, we remark that, with our recent successful efforts to extend the photon range of HHG sources beyond the water window [56], we expect, in the very near future, the first experiments with photon energies around the giant N resonances of rare earth elements, as well as around L resonances of transition metals in laboratory based experiments.
4. Materials and Methods
The thin magnetic films, Co, CoPt and GdFe were grown by DC magnetron sputtering. The FeGd alloy with a thickness of 15 nm was grown on a free standing DMC (diamond like carbon) membrane. Its magnetization pointed out of the sample plane with a coercive field of 50 mT. The Co and CoPt films with a thickness of 15 nm were deposited on freestanding 20 nm thick SiN and 200 nm thick Al membranes, respectively. They exhibit an in-plane anisotropy and were consequently mounted under a grazing angle of 45 degrees for a finite projection of the k-vector of the circularly polarized XUV pulses onto the magnetization of the sample. They exhibit a square hysteresis loop with a coercive field below 10 mT.
Author Contributions
C.v.K.S., S.E., F.W., I.R. and S.S. conceived the experiments, C.v.K.S., M.H., I.R., C.S., V.S., J.B., G.H., K.B., J.V., B.M., S.G., S.D., E.J., B.V. and J.L. performed the experiment at FLASH. J.L. programmed and implemented the data acquisition software for the FLASH experiment. F.W., K.Y., D.S., C.S. and C.v.K.S. performed the HHG experiments. D.S. programmed and implemented the data acquisition software for the HHG experiment. S.S. performed the ab initio calculations. D.W.E. grew the samples. C.v.K.S., F.W., S.S., S.E., K.Y., M.B. and I.R. interpreted and discussed the results. C.v.K.S. prepared the figures and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by DFG through TRR227 project A02 and A04. The authors are grateful for financial support of the CNRS-PICS program.
Acknowledgments
We kindly acknowledge the invaluable help by the different support groups at FLASH, Desy in Hamburg.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CCD | charged coupled device |
| FEL | free electron laser |
| HHG | high harmonic generation |
| MCD | magnetic circular dichroism |
| OISTR | optical inter-site spin transfer |
| XUV | extreme ultraviolet |
References
- Beaurepaire, E.; Merle, J.C.; Daunois, A.; Bigot, J.Y. Ultrafast Spin Dynamics in Ferromagnetic Nickel. Phys. Rev. Lett. 1996, 76, 4250–4253. [Google Scholar] [CrossRef] [PubMed]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731–2784. [Google Scholar] [CrossRef]
- Koopmans, B.; Malinowski, G.; Dalla Longa, F.; Steiauf, D.; Fähnle, M.; Roth, T.; Cinchetti, M.; Aeschlimann, M. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 2010, 9, 259–265. [Google Scholar] [CrossRef]
- Schmidt, A.B.; Pickel, M.; Donath, M.; Buczek, P.; Ernst, A.; Zhukov, V.P.; Echenique, P.M.; Sandratskii, L.M.; Chulkov, E.V.; Weinelt, M. Ultrafast Magnon Generation in an Fe Film on Cu(100). Phys. Rev. Lett. 2010, 105, 197401. [Google Scholar] [CrossRef]
- Carpene, E.; Hedayat, H.; Boschini, F.; Dallera, C. Ultrafast demagnetization of metals: Collapsed exchange versus collective excitations. Phys. Rev. B 2015, 91, 174414. [Google Scholar] [CrossRef]
- Eich, S.; Plötzing, M.; Rollinger, M.; Emmerich, S.; Adam, R.; Chen, C.; Kapteyn, H.C.; Murnane, M.M.; Plucinski, L.; Steil, D.; et al. Band structure evolution during the ultrafast ferromagnetic-paramagnetic phase transition in cobalt. Sci. Adv. 2017, 3, e1602094. [Google Scholar] [CrossRef] [PubMed]
- Malinowski, G.; Dalla Longa, F.; Rietjens, J.H.H.; Paluskar, P.V.; Huijink, R.; Swagten, H.J.M.; Koopmans, B. Control of speed and efficiency of ultrafast demagnetization by direct transfer of spin angular momentum. Nat. Phys. 2008, 4, 855–858. [Google Scholar] [CrossRef]
- Battiato, M.; Carva, K.; Oppeneer, P.M. Superdiffusive Spin Transport as a Mechanism of Ultrafast Demagnetization. Phys. Rev. Lett. 2010, 105, 027203. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Tsukamoto, A.; Kimel, A.V.; Hansteen, F.; Kirilyuk, A.; Itoh, A.; Rasing, T. Subpicosecond Magnetization Reversal across Ferrimagnetic Compensation Points. Phys. Rev. Lett. 2007, 99, 217204. [Google Scholar] [CrossRef] [PubMed]
- Radu, I.; Vahaplar, K.; Stamm, C.; Kachel, T.; Pontius, N.; Dürr, H.A.; Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 2011, 472, 205–208. [Google Scholar] [CrossRef] [PubMed]
- Ostler, T.; Barker, J.; Evans, R.; Chantrell, R.; Atxitia, U.; Chubykalo-Fesenko, O.; El Moussaoui, S.; Le Guyader, L.; Mengotti, E.; Heyderman, L.; et al. Ultrafast heating as a sufficient stimulus for magnetization reversal in a ferrimagnet. Nat. Commun. 2012, 3, 666. [Google Scholar] [CrossRef] [PubMed]
- Dewhurst, J.K.; Elliott, P.; Shallcross, S.; Gross, E.K.U.; Sharma, S. Laser-Induced intersite Spin Transfer. Nano Lett. 2018, 18, 1842–1848. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Bovensiepen, U.; Eschenlohr, A.; Müller, T.; Elliott, P.; Gross, E.K.U.; Dewhurst, J.K.; Sharma, S. Competing Spin Transfer and Dissipation at Co/Cu(001) Interfaces on Femtosecond Timescales. Phys. Rev. Lett. 2019, 122, 067202. [Google Scholar] [CrossRef]
- Steil, D.; Walowski, J.; Gerhard, F.; Kiessling, T.; Ebke, D.; Thomas, A.; Kubota, T.; Oogane, M.; Ando, Y.; Otto, J.; et al. Efficiency of ultrafast optically induced spin transfer in Heusler compounds. Phys. Rev. Res. 2020, 2, 023199. [Google Scholar] [CrossRef]
- Siegrist, F.; Gessner, J.A.; Ossiander, M.; Denker, C.; Chang, Y.P.; Schröder, M.C.; Guggenmos, A.; Cui, Y.; Walowski, J.; Martens, U.; et al. Light-wave dynamic control of magnetism. Nature 2019, 571, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Tengdin, P.; Gentry, C.; Blonsky, A.; Zusin, D.; Gerrity, M.; Hellbrück, L.; Hofherr, M.; Shaw, J.; Kvashnin, Y.; Delczeg-Czirjak, E.K.; et al. Direct light–induced spin transfer between different elements in a spintronic Heusler material via femtosecond laser excitation. Sci. Adv. 2020, 6, eaaz1100. [Google Scholar] [CrossRef]
- Hofherr, M.; Häuser, S.; Dewhurst, J.K.; Tengdin, P.; Sakshath, S.; Nembach, H.T.; Weber, S.T.; Shaw, J.M.; Silva, T.J.; Kapteyn, H.C.; et al. Ultrafast optically induced spin transfer in ferromagnetic alloys. Sci. Adv. 2020, 6, eaay8717. [Google Scholar] [CrossRef]
- Willems, F.; von Korff Schmising, C.; Strüber, C.; Schick, D.; Engel, D.W.; Dewhurst, J.K.; Elliott, P.; Sharma, S.; Eisebitt, S. Optical inter-site spin transfer probed by energy and spin-resolved transient absorption spectroscopy. Nat. Commun. 2020, 11, 871. [Google Scholar] [CrossRef]
- Stöhr, J.; Siegmann, H.C. Magnetism: From Fundamentals to Nanoscale Dynamics; Springer: Berlin/Heidelberg, Germany, 2006; Volume 152, pp. 1–822. [Google Scholar] [CrossRef]
- Stamm, C.; Kachel, T.; Pontius, N.; Mitzner, R.; Quast, T.; Holldack, K.; Khan, S.; Lupulescu, C.; Aziz, E.F.; Wietstruk, M.; et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 2007, 6, 740–743. [Google Scholar] [CrossRef]
- Gutt, C.; Streit-Nierobisch, S.; Stadler, L.M.; Pfau, B.; Günther, C.M.; Könnecke, R.; Frömter, R.; Kobs, A.; Stickler, D.; Oepen, H.P.; et al. Single-pulse resonant magnetic scattering using a soft x-ray free-electron laser. Phys. Rev. B 2010, 81, 100401. [Google Scholar] [CrossRef]
- La-O-Vorakiat, C.; Siemens, M.; Murnane, M.M.; Kapteyn, H.C.; Mathias, S.; Aeschlimann, M.; Grychtol, P.; Adam, R.; Schneider, C.M.; Shaw, J.M.; et al. Ultrafast Demagnetization Dynamics at the M Edges of Magnetic Elements Observed Using a Tabletop High-Harmonic Soft X-Ray Source. Phys. Rev. Lett. 2009, 103, 257402. [Google Scholar] [CrossRef] [PubMed]
- Mathias, S.; La-O-Vorakiat, C.; Grychtol, P.; Granitzka, P.; Turgut, E.; Shaw, J.M.; Adam, R.; Nembach, H.T.; Siemens, M.E.; Eich, S.; et al. Probing the timescale of the exchange interaction in a ferromagnetic alloy. Proc. Natl. Acad. Sci. USA 2012, 109, 4792–4797. [Google Scholar] [CrossRef] [PubMed]
- Willems, F.; Smeenk, C.T.L.; Zhavoronkov, N.; Kornilov, O.; Radu, I.; Schmidbauer, M.; Hanke, M.; von Korff Schmising, C.; Vrakking, M.J.J.; Eisebitt, S. Probing ultrafast spin dynamics with high-harmonic magnetic circular dichroism spectroscopy. Phys. Rev. B 2015, 92, 220405. [Google Scholar] [CrossRef]
- Rudolf, D.; La-O-Vorakiat, C.; Battiato, M.; Adam, R.; Shaw, J.M.; Turgut, E.; Maldonado, P.; Mathias, S.; Grychtol, P.; Nembach, H.T.; et al. Ultrafast magnetization enhancement in metallic multilayers driven by superdiffusive spin current. Nat. Commun. 2012, 3, 1037. [Google Scholar] [CrossRef] [PubMed]
- Turgut, E.; La-o vorakiat, C.; Shaw, J.M.; Grychtol, P.; Nembach, H.T.; Rudolf, D.; Adam, R.; Aeschlimann, M.; Schneider, C.M.; Silva, T.J.; et al. Controlling the Competition between Optically Induced Ultrafast Spin-Flip Scattering and Spin Transport in Magnetic Multilayers. Phys. Rev. Lett. 2013, 110, 197201. [Google Scholar] [CrossRef]
- Vodungbo, B.; Gautier, J.; Lambert, G.; Sardinha, A.B.; Lozano, M.; Sebban, S.; Ducousso, M.; Boutu, W.; Li, K.; Tudu, B.; et al. Laser-induced ultrafast demagnetization in the presence of a nanoscale magnetic domain network. Nat. Commun. 2012, 3, 999. [Google Scholar] [CrossRef] [PubMed]
- Pfau, B.; Schaffert, S.; Müller, L.; Gutt, C.; Al-Shemmary, A.; Büttner, F.; Delaunay, R.; Düsterer, S.; Flewett, S.; Frömter, R.; et al. Ultrafast optical demagnetization manipulates nanoscale spin structure in domain walls. Nat. Commun. 2012, 3, 1100. [Google Scholar] [CrossRef]
- Weder, D.; von Korff Schmising, C.; Günther, C.M.; Schneider, M.; Engel, D.; Hessing, P.; Strüber, C.; Weigand, M.; Vodungbo, B.; Jal, E.; et al. Transient magnetic gratings on the nanometer scale. Struct. Dyn. 2020, 7, 054501. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.; Pfau, B.; Günther, C.M.; von Korff Schmising, C.; Weder, D.; Geilhufe, J.; Perron, J.; Capotondi, F.; Pedersoli, E.; Manfredda, M.; et al. Ultrafast Demagnetization Dominates Fluence Dependence of Magnetic Scattering at Co M Edges. Phys. Rev. Lett. 2020, 125, 127201. [Google Scholar] [CrossRef]
- von Korff Schmising, C.; Pfau, B.; Schneider, M.; Günther, C.M.; Giovannella, M.; Perron, J.; Vodungbo, B.; Müller, L.; Capotondi, F.; Pedersoli, E.; et al. Imaging Ultrafast Demagnetization Dynamics after a Spatially Localized Optical Excitation. Phys. Rev. Lett. 2014, 112, 217203. [Google Scholar] [CrossRef]
- Turgut, E.; Zusin, D.; Legut, D.; Carva, K.; Knut, R.; Shaw, J.M.; Chen, C.; Tao, Z.; Nembach, H.T.; Silva, T.J.; et al. Stoner versus Heisenberg: Ultrafast exchange reduction and magnon generation during laser-induced demagnetization. Phys. Rev. B 2016, 94, 1–6. [Google Scholar] [CrossRef]
- Zusin, D.; Tengdin, P.M.; Gopalakrishnan, M.; Gentry, C.; Blonsky, A.; Gerrity, M.; Legut, D.; Shaw, J.M.; Nembach, H.T.; Silva, T.J.; et al. Direct measurement of the static and transient magneto-optical permittivity of cobalt across the entire M-edge in reflection geometry by use of polarization scanning. Phys. Rev. B 2018, 97, 024433. [Google Scholar] [CrossRef]
- Jana, S.; Malik, R.S.; Kvashnin, Y.O.; Locht, I.L.M.; Knut, R.; Stefanuik, R.; Di Marco, I.; Yaresko, A.N.; Ahlberg, M.; Åkerman, J.; et al. Analysis of the linear relationship between asymmetry and magnetic moment at the M edge of 3d transition metals. Phys. Rev. Res. 2020, 2, 013180. [Google Scholar] [CrossRef]
- Kuneš, J.; Oppeneer, P.M.; Mertins, H.C.; Schäfers, F.; Gaupp, A.; Gudat, W.; Novák, P. X-ray Faraday effect at the L2,3 edges of Fe, Co, and Ni: Theory and experiment. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 64, 1–10. [Google Scholar] [CrossRef]
- Valencia, S.; Gaupp, A.; Gudat, W.; Mertins, H.C.; Oppeneer, P.M.; Abramsohn, D.; Schneider, C.M. Faraday rotation spectra at shallow core levels: 3p edges of Fe, Co, and Ni. New J. Phys. 2006, 8. [Google Scholar] [CrossRef]
- Alves, C.; Lambert, G.; Malka, V.; Hehn, M.; Malinowski, G.; Hennes, M.; Chardonnet, V.; Jal, E.; Lüning, J.; Vodungbo, B. Resonant Faraday effect using high-order harmonics for the investigation of ultrafast demagnetization. Phys. Rev. B 2019, 100, 144421. [Google Scholar] [CrossRef]
- Willems, F.; Sharma, S.; v. Korff Schmising, C.; Dewhurst, J.K.; Salemi, L.; Schick, D.; Hessing, P.; Strüber, C.; Engel, W.D.; Eisebitt, S. Magneto-Optical Functions at the 3 p Resonances of Fe, Co, and Ni: Ab initio Description and Experiment. Phys. Rev. Lett. 2019, 122, 217202. [Google Scholar] [CrossRef]
- Willems, F.; von Korff Schmising, C.; Weder, D.; Günther, C.M.; Schneider, M.; Pfau, B.; Meise, S.; Guehrs, E.; Geilhufe, J.; Merhe, A.E.D.; et al. Multi-color imaging of magnetic Co/Pt heterostructures. Struct. Dyn. 2017, 4, 014301. [Google Scholar] [CrossRef]
- Dewhurst, J.K.; Willems, F.; Elliott, P.; Li, Q.Z.; Schmising, C.V.K.; Strüber, C.; Engel, D.W.; Eisebitt, S.; Sharma, S. Element Specificity of Transient Extreme Ultraviolet Magnetic Dichroism. Phys. Rev. Lett. 2020, 124, 077203. [Google Scholar] [CrossRef]
- Tiedtke, K.; Azima, A.; von Bargen, N.; Bittner, L.; Bonfigt, S.; Düsterer, S.; Faatz, B.; Frühling, U.; Gensch, M.; Gerth, C.; et al. The soft x-ray free-electron laser FLASH at DESY: Beamlines, diagnostics and end-stations. New J. Phys. 2009, 11, 023029. [Google Scholar] [CrossRef]
- Rabinovitch, K.; Canfield, L.R.; Madden, R.P. A Method for Measuring Polarization in the Vacuum Ultraviolet. Appl. Opt. 1965, 4, 1005. [Google Scholar] [CrossRef]
- Henke, B.; Gullikson, E.; Davis, J. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Radu, I.; Stamm, C.; Eschenlohr, A.; Radu, F.; Abrudan, R.; Vahaplar, K.; Kachel, T.; Pontius, N.; Mitzner, R.; Holldack, K.; et al. Ultrafast and Distinct Spin Dynamics in Magnetic Alloys. Spin 2015, 5, 1–10. [Google Scholar] [CrossRef]
- Davies, C.; Janssen, T.; Mentink, J.; Tsukamoto, A.; Kimel, A.; van der Meer, A.; Stupakiewicz, A.; Kirilyuk, A. Pathways for Single-Shot All-Optical Switching of Magnetization in Ferrimagnets. Phys. Rev. Appl. 2020, 13, 024064. [Google Scholar] [CrossRef]
- Hennecke, M.; Radu, I.; Abrudan, R.; Kachel, T.; Holldack, K.; Mitzner, R.; Tsukamoto, A.; Eisebitt, S. Angular Momentum Flow during Ultrafast Demagnetization of a Ferrimagnet. Phys. Rev. Lett. 2019, 122, 1–10. [Google Scholar] [CrossRef] [PubMed]
- La-O-Vorakiat, C.; Turgut, E.; Teale, C.A.; Kapteyn, H.C.; Murnane, M.M.; Mathias, S.; Aeschlimann, M.; Schneider, C.M.; Shaw, J.M.; Nembach, H.T.; et al. Ultrafast Demagnetization Measurements Using Extreme Ultraviolet Light: Comparison of Electronic and Magnetic Contributions. Phys. Rev. X 2012, 2, 011005. [Google Scholar] [CrossRef]
- Vodungbo, B.; Gautier, J.; Lambert, G.; Zeitoun, P.; Lüning, J. Comment on “Ultrafast Demagnetization Measurements Using Extreme Ultraviolet Light: Comparison of Electronic and Magnetic Contributions”. Phys. Rev. X 2013, 3, 038001. [Google Scholar] [CrossRef]
- Yao, K.; Willems, F.; von Korff Schmising, C.; Radu, I.; Strüber, C.; Schick, D.; Engel, D.; Tsukamoto, A.; Dewhurst, J.K.; Sharma, S.; et al. Distinct spectral response in M-edge magnetic circular dichroism. Phys. Rev. B 2020, 102, 100405. [Google Scholar] [CrossRef]
- Tengdin, P.; You, W.; Chen, C.; Shi, X.; Zusin, D.; Zhang, Y.; Gentry, C.; Blonsky, A.; Keller, M.; Oppeneer, P.M.; et al. Critical behavior within 20 fs drives the out-of-equilibrium laser-induced magnetic phase transition in nickel. Sci. Adv. 2018, 4, 1–9. [Google Scholar] [CrossRef]
- Vodungbo, B.; Barszczak Sardinha, A.; Gautier, J.; Lambert, G.; Valentin, C.; Lozano, M.; Iaquaniello, G.; Delmotte, F.; Sebban, S.; Lüning, J.; et al. Polarization control of high order harmonics in the EUV photon energy range. Opt. Express 2011, 19, 4346. [Google Scholar] [CrossRef]
- von Korff Schmising, C.; Weder, D.; Noll, T.; Pfau, B.; Hennecke, M.; Strüber, C.; Radu, I.; Schneider, M.; Staeck, S.; Günther, C.M.; et al. Generating circularly polarized radiation in the extreme ultraviolet spectral range at the free-electron laser FLASH. Rev. Sci. Instrum. 2017, 88, 053903. [Google Scholar] [CrossRef]
- Yao, K.; Willems, F.; Schmising, C.V.K.; Engel, D.; Strüber, C.; Hessing, P.; Pfau, B.; Schick, D.; Eisebitt, S.; Schneider, M. A tabletop setup for ultrafast helicity- dependent and element-specific absorption spectroscopy and scattering in the extreme ultraviolet spectral range A tabletop setup for ultrafast helicity-dependent and element-specific absorption spectroscopy and scattering in the extreme ultraviolet spectral range. Rev. Sci. Instrum. 2020, 91, 093001. [Google Scholar] [CrossRef]
- Dewhurst, J.K. The Elk Code 2018. Available online: http://elk.sourceforge.net/ (accessed on 26 October 2020).
- Borchert, M.; Schmising, C.v.K.; Schick, D.; Engel, D.; Sharma, S.; Eisebitt, S. Manipulation of Ultrafast Demagnetization Dynamics by Optically Induced intersite Spin Transfer in Magnetic Compounds with Distinct Density of States. 2020, pp. 1–10. Available online: https://arxiv.org/abs/2008.12612 (accessed on 26 October 2020).
- Feng, T.; Heilmann, A.; Bock, M.; Ehrentraut, L.; Witting, T.; Yu, H.; Stiel, H.; Eisebitt, S.; Schnürer, M. 27 W 21 μm OPCPA system for coherent soft X-ray generation operating at 10 kHz. Opt. Express 2020, 28, 8724. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).