Wavelet-Based Optimum Identification of Vehicle Axles Using Bridge Measurements
Abstract
1. Introduction
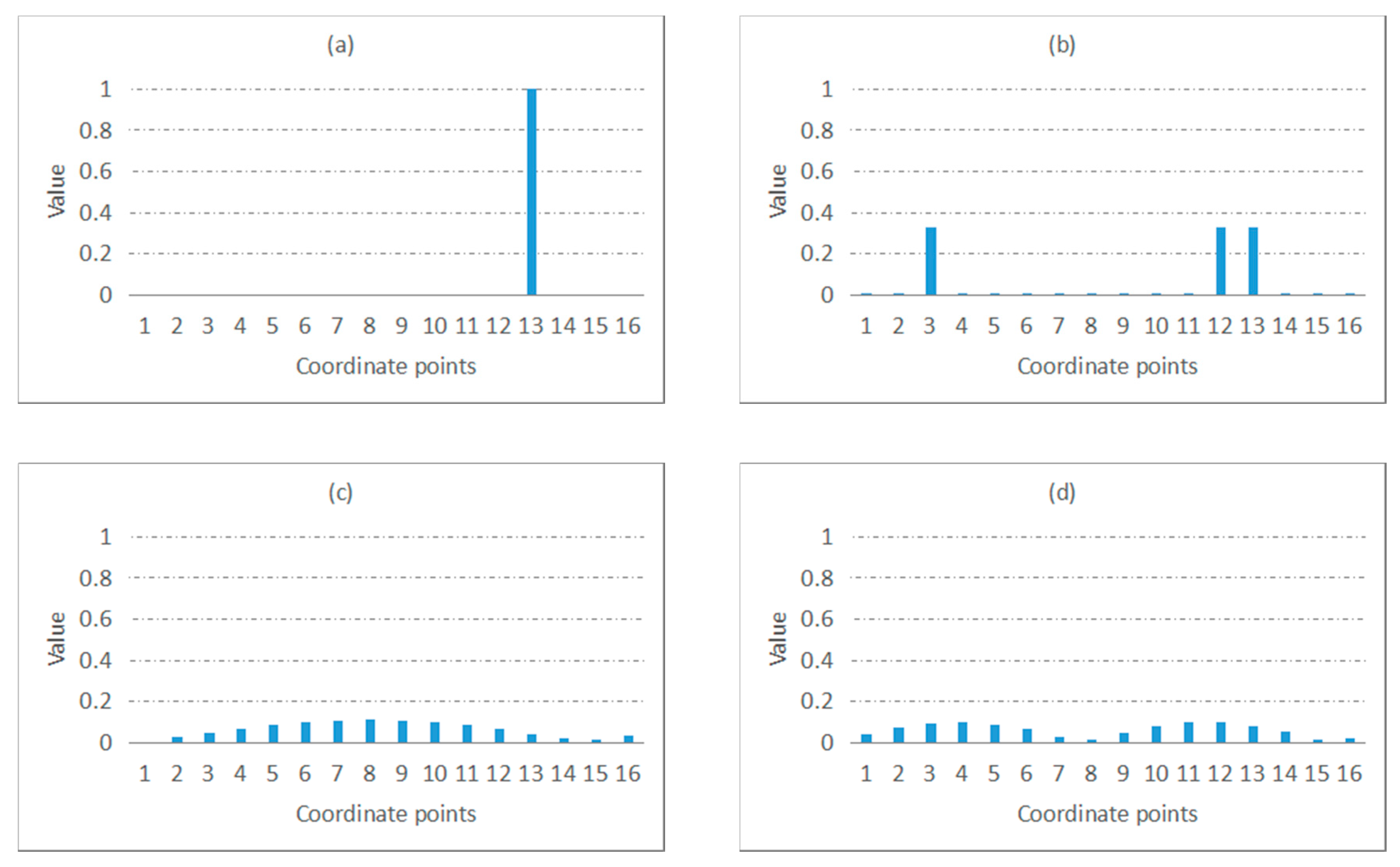
2. Shannon Entropy
3. Wavelet Theory
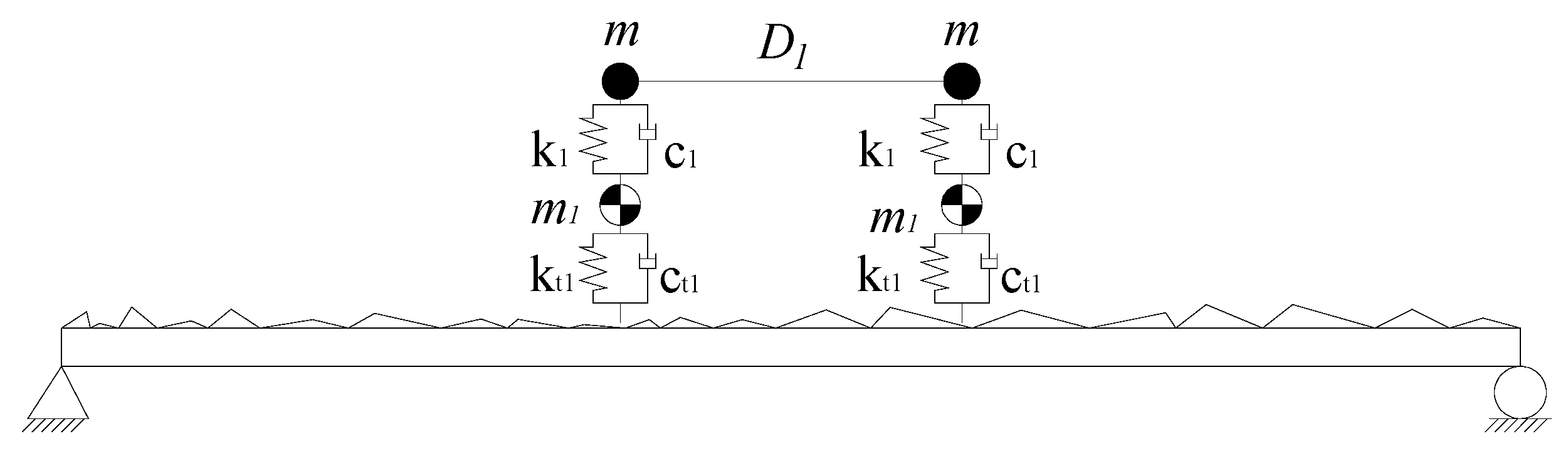
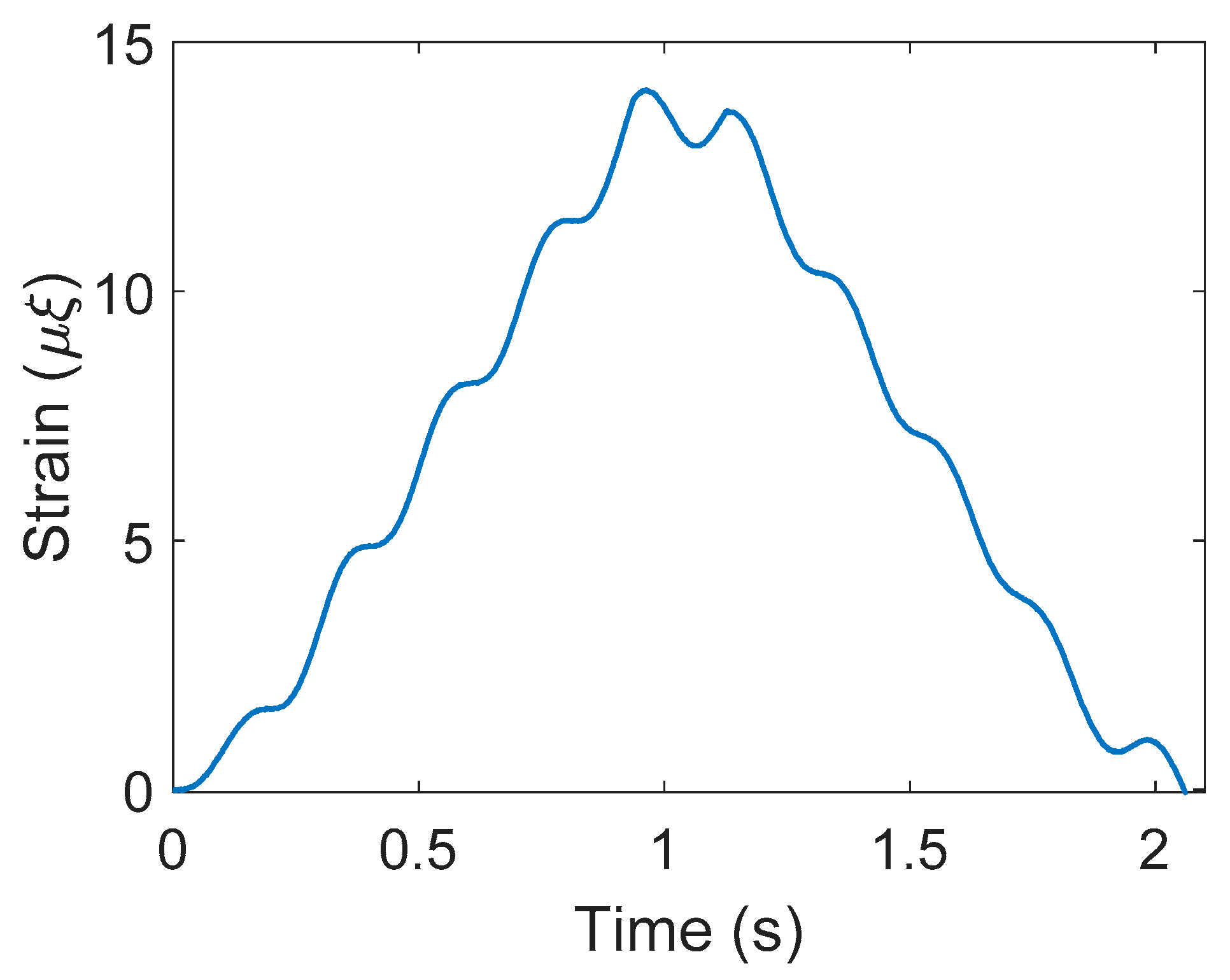
4. Numerical Simulation
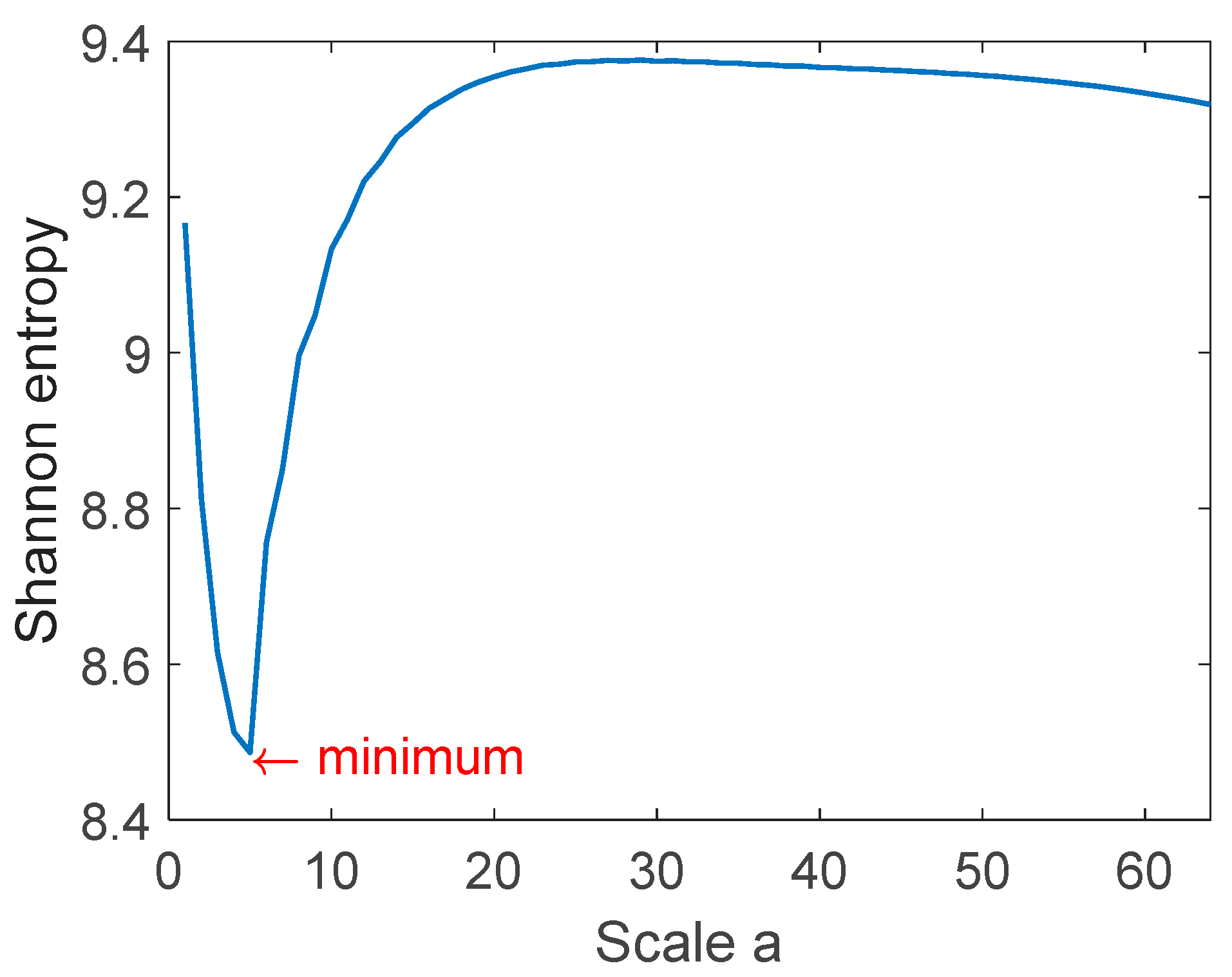
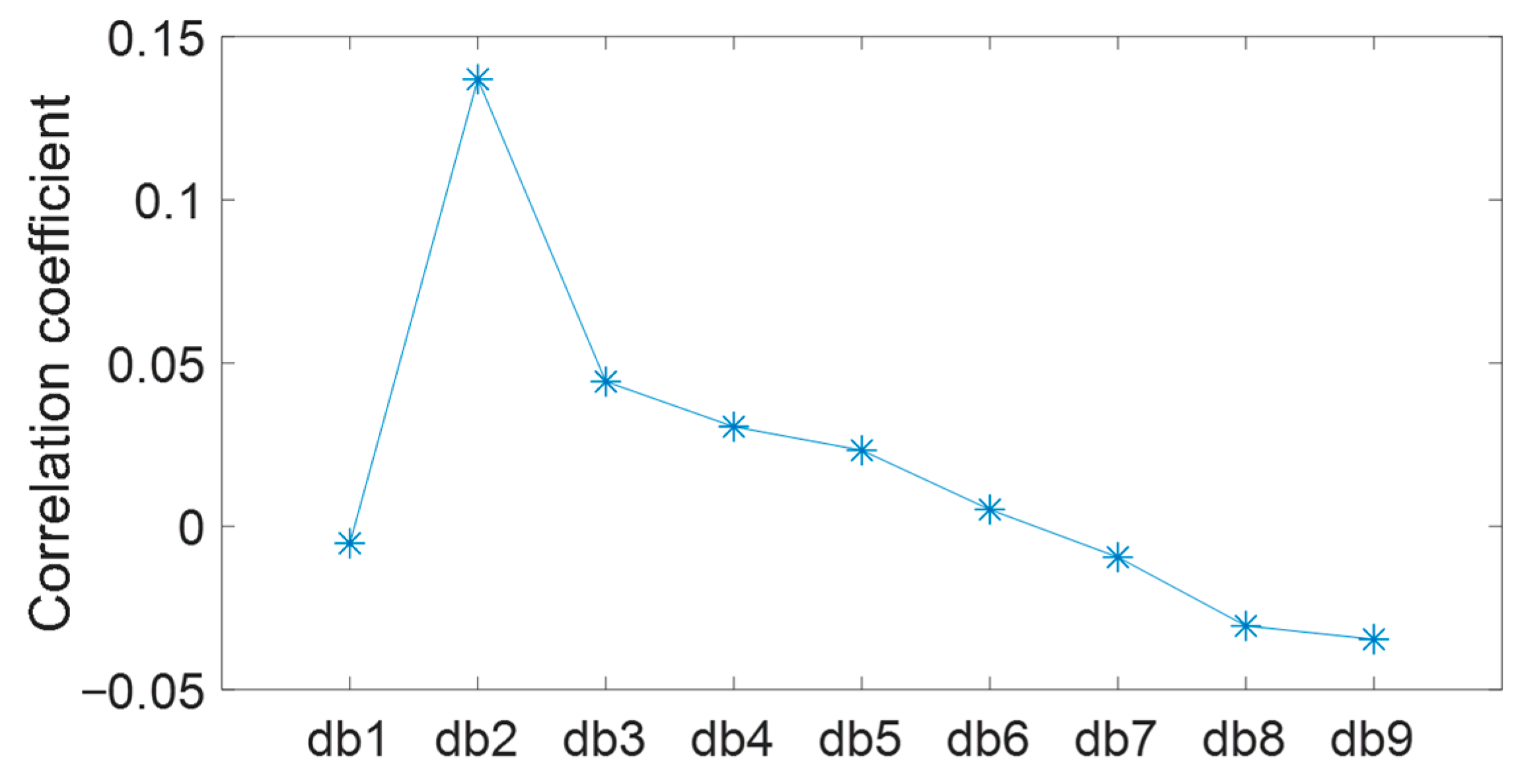
5. The Selection of Mother Wavelet
6. Field Test of Fifth Wushui Bridge, China
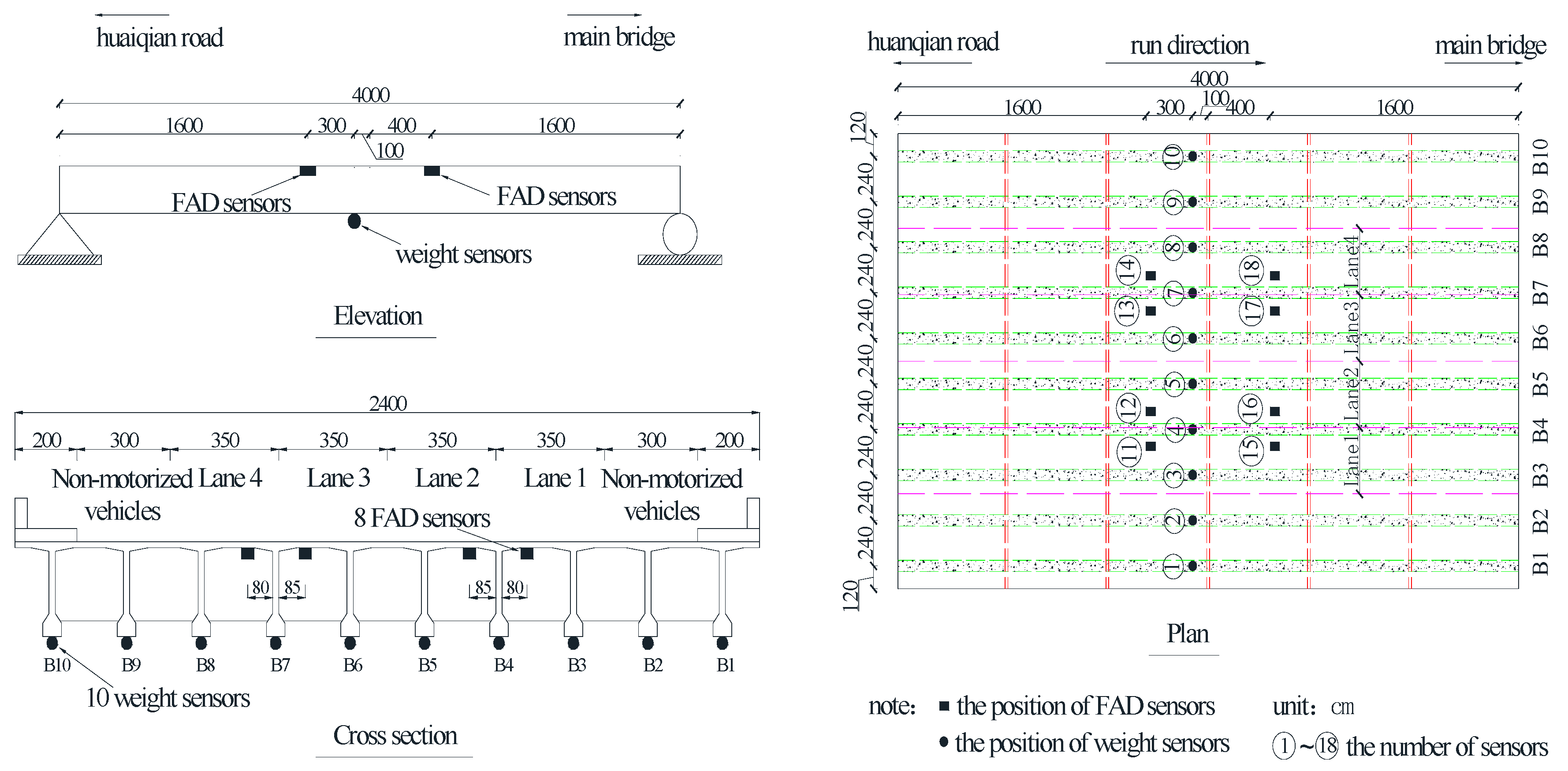
6.1. Introduction to Field Test
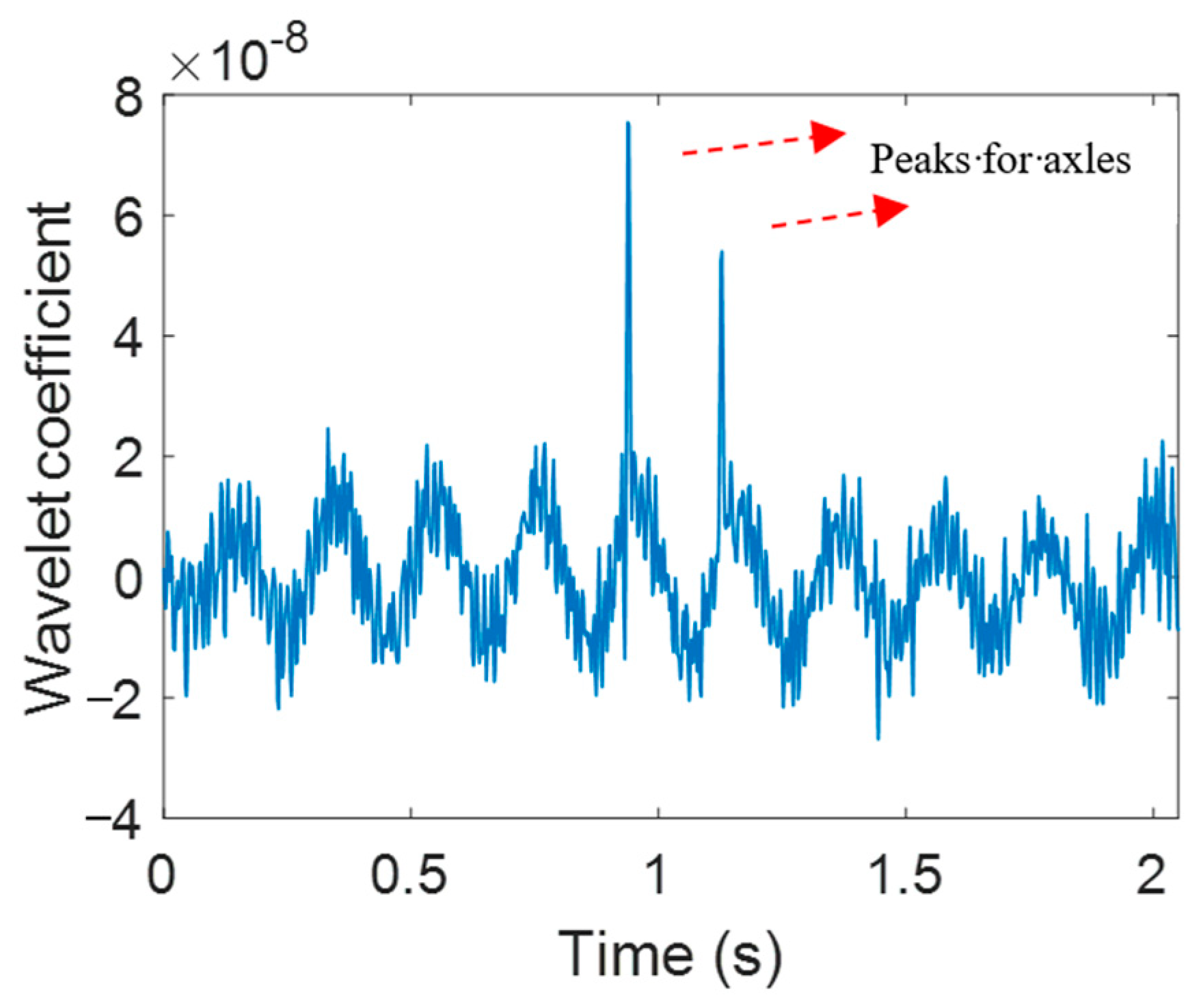
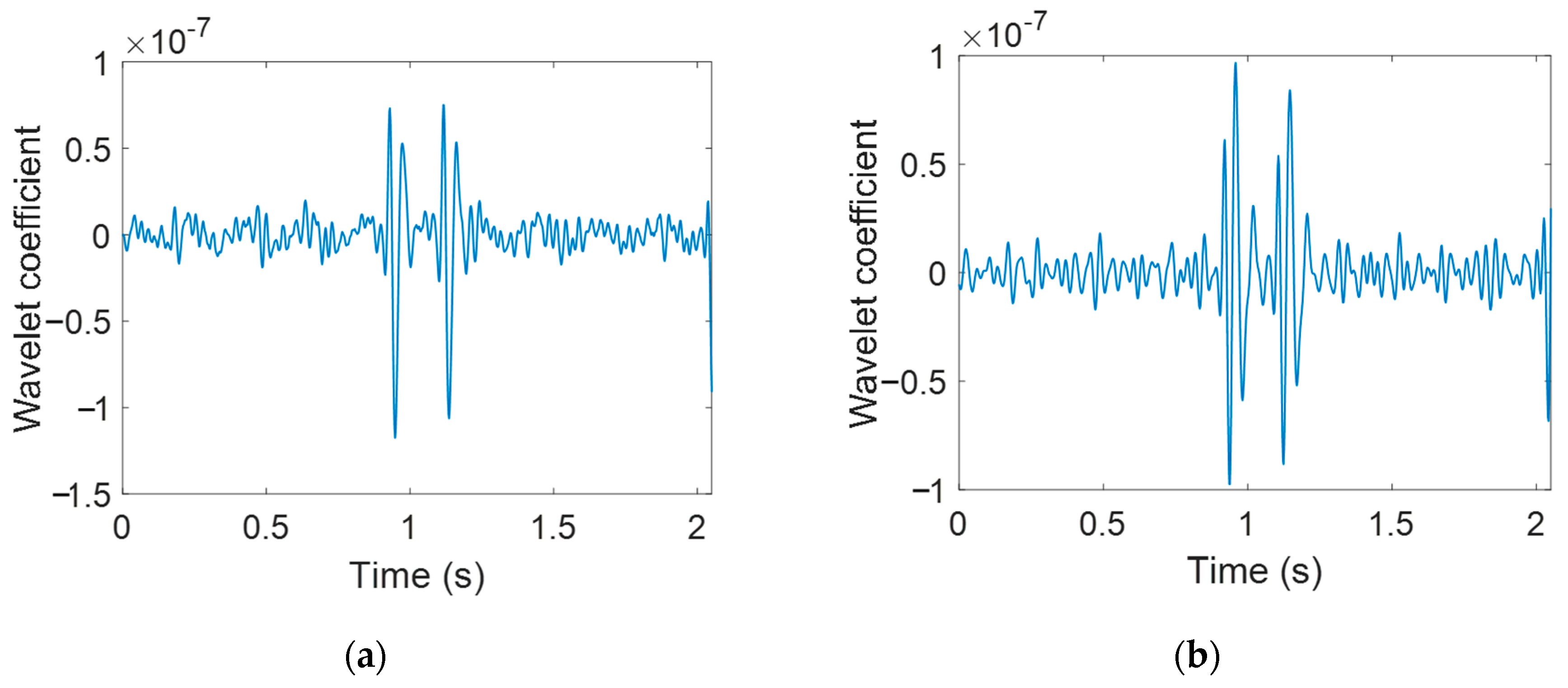
6.2. Wavelet Analysis of Test Results for Single Truck Crossing
6.3. Wavelet Analysis of Test Results with Multiple Presence
7. Field Test on a Simply Supported Stiff Concrete Bridge
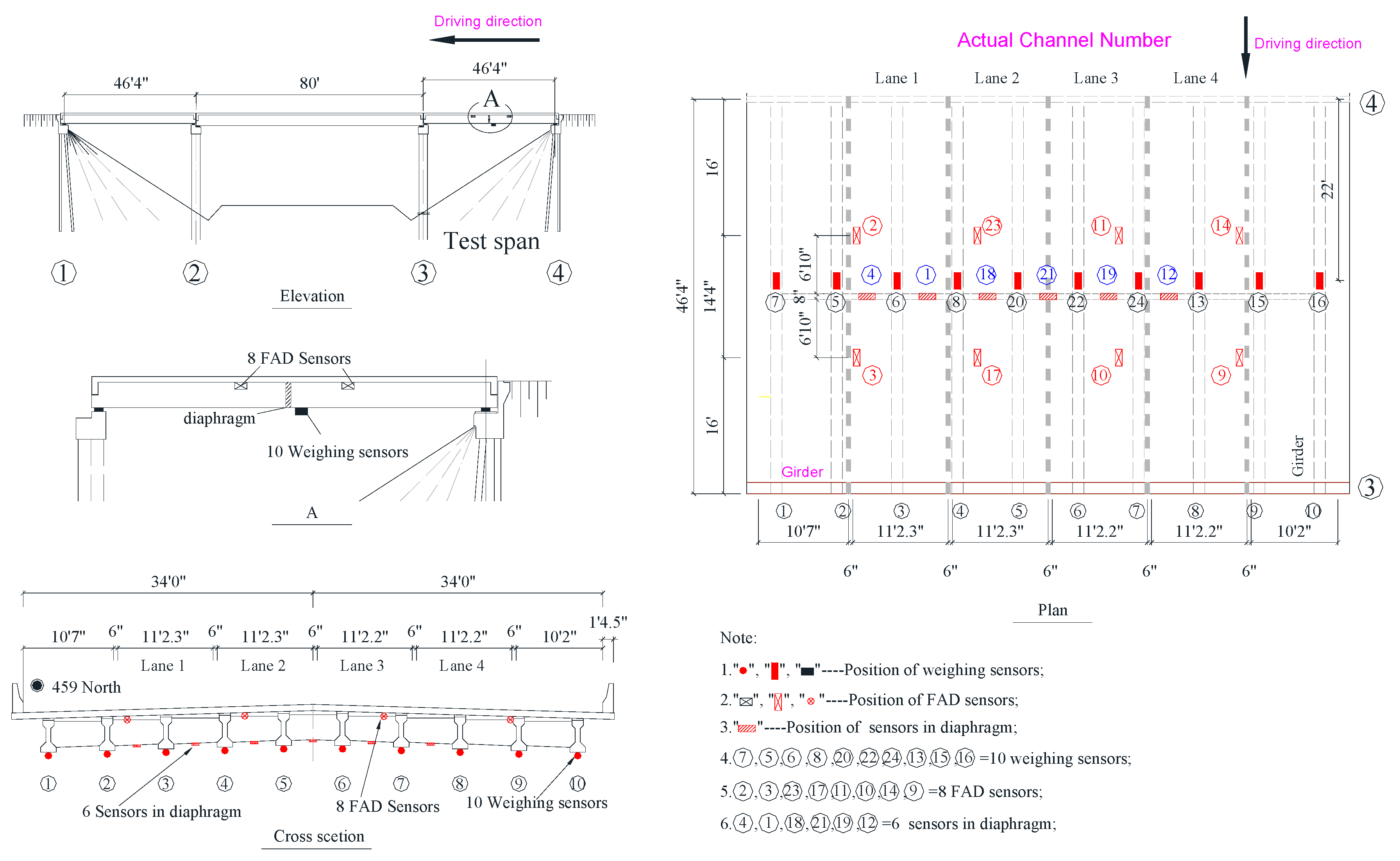
7.1. Test Bridge and Instrumentation
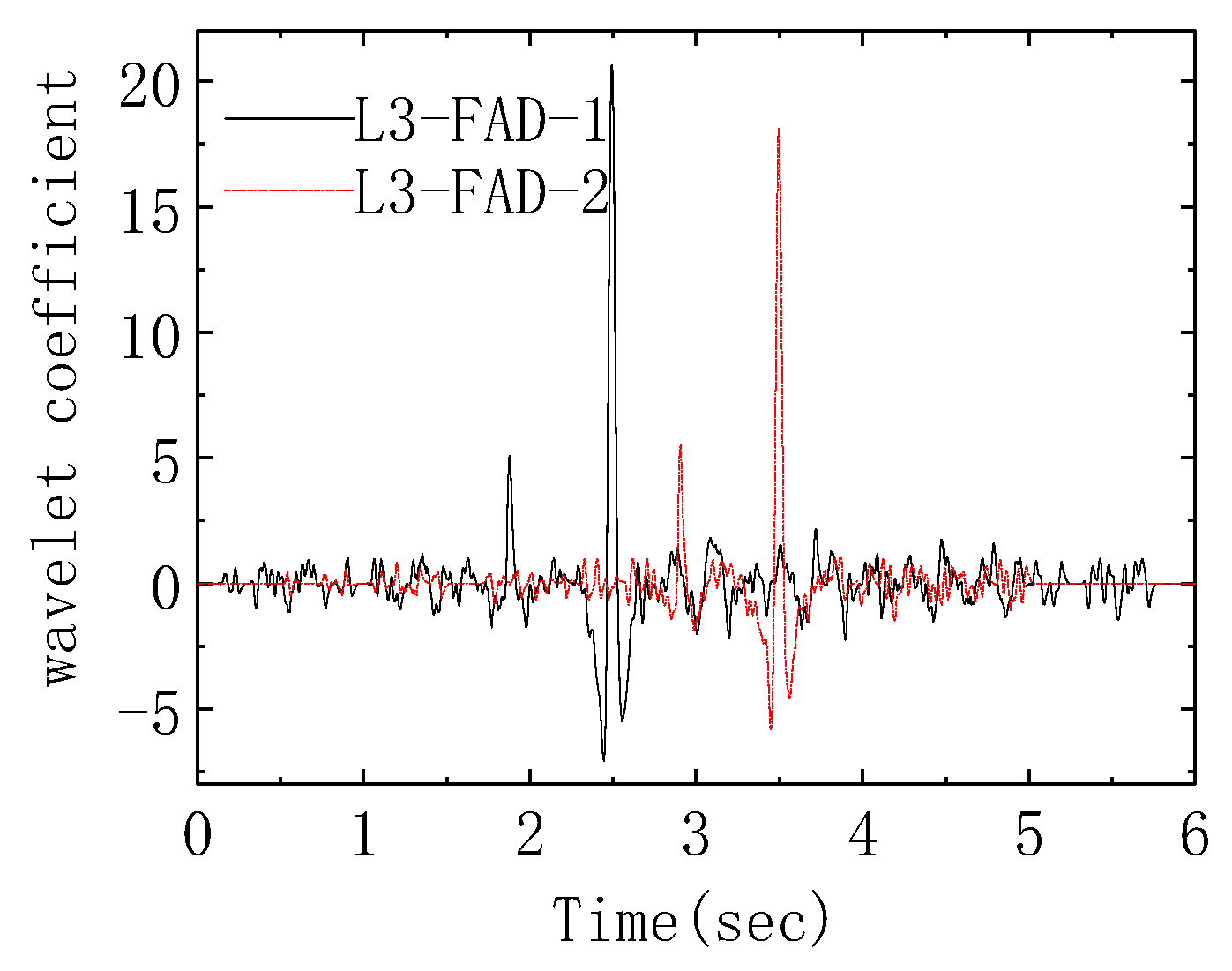
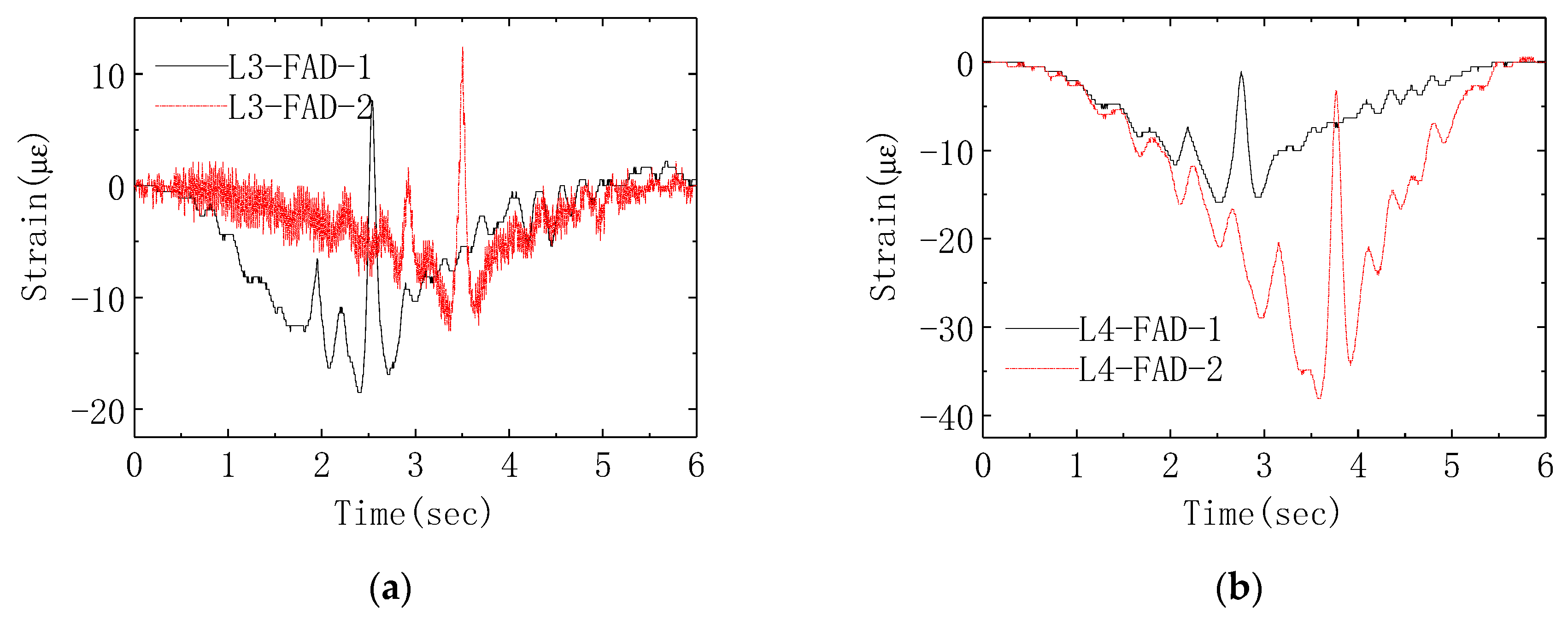
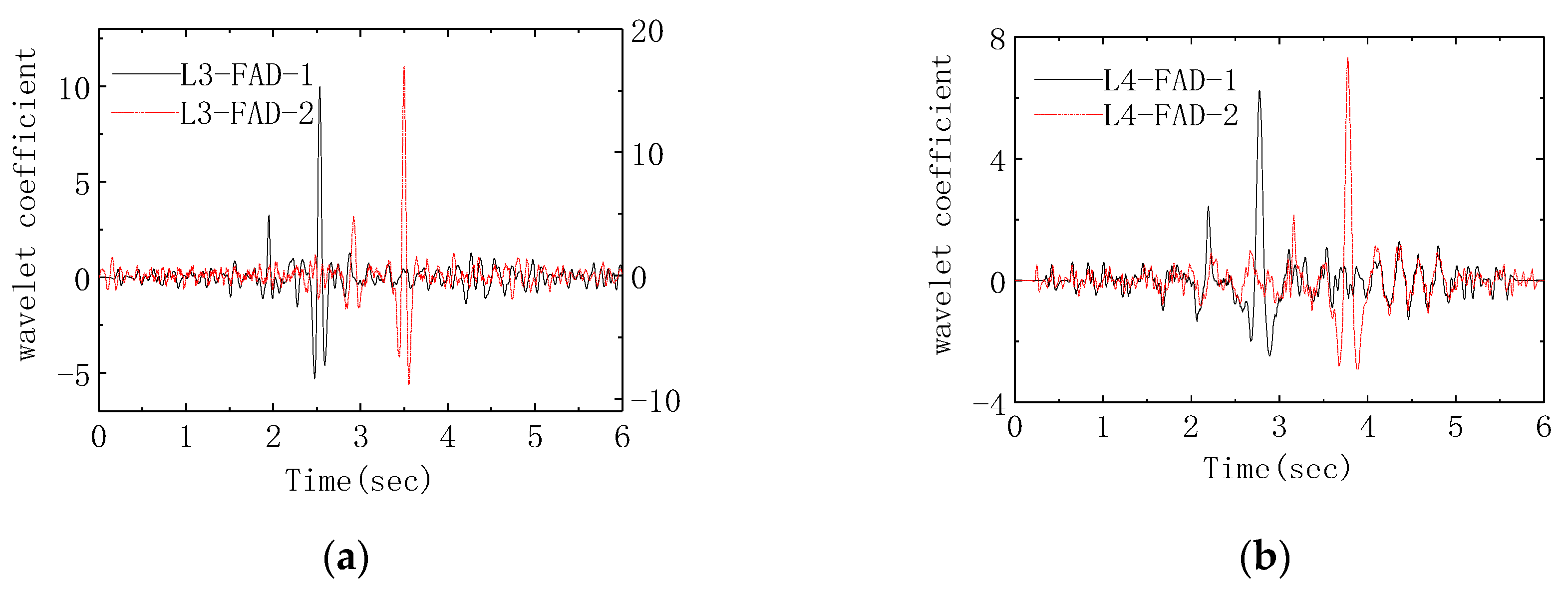
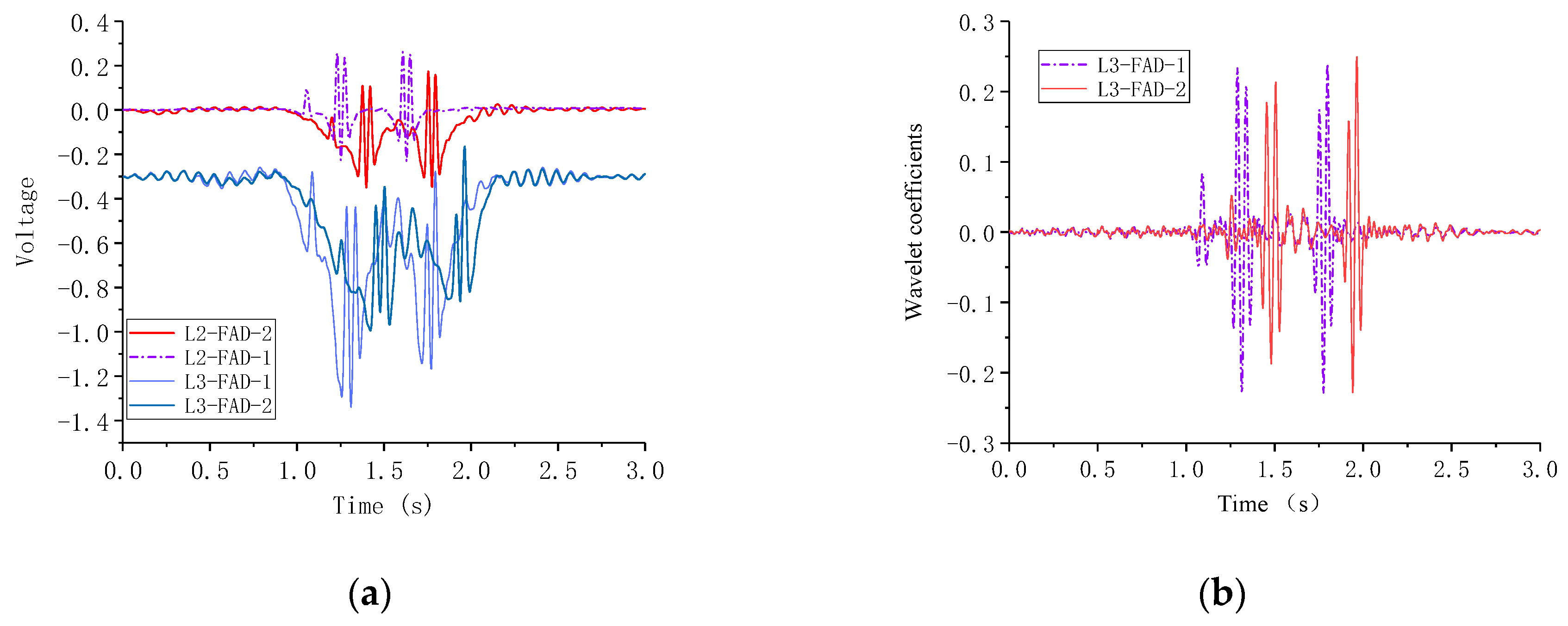
7.2. Improved Axle Detection for Multiple Presence Loading Events
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ASCE. 2017 Infrastructure Report Card; Technical Report; ASCE: Reston, VA, USA, 2017. [Google Scholar]
- Yau, J.D.; Yang, J.P.; Yang, Y.B. Wave number-based technique for detecting slope discontinuity in simple beams using moving test vehicle. Int. J. Struct. Stab. Dyn. 2017, 17, 1750060. [Google Scholar] [CrossRef]
- Cantero, D.; González, A. Bridge Damage Detection Using Weigh-in-Motion Technology. J. Bridge Eng. 2015, 20, 04014078. [Google Scholar] [CrossRef]
- Ono, R.; Ha, T.M.; Fukada, S. Analytical study on damage detection method using displacement influence lines of road bridge slab. J. Civ. Struct. Health Monit. 2019, 9, 565–577. [Google Scholar] [CrossRef]
- Hester, D.; Brownjohn, J.; Huseynov, F.; OBrien, E.; Gonzalez, A.; Casero, M. Identifying damage in a bridge by analysing rotation response to a moving load. Struct. Infrastruct. Eng. 2020, 16, 1050–1065. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yang, J.P. State-of-the-art review on modal identification and damage detection of bridges by moving test vehicles. Int. J. Struct. Stab. Dyn. 2018, 18, 1850025. [Google Scholar] [CrossRef]
- Yang, Y.B.; Yang, J.P.; Zhang, B.; Wu, Y. Vehicle Scanning Method for Bridges; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Gonzalez, A.; Dowling, J.; O’Brien, E.; Znidaric, A. Testing of a Bridge Weigh-in-Motion Algorithm Utilising Multiple Longitudinal Sensor Locations. J. Test. Eval. 2012, 40, 961–974. [Google Scholar] [CrossRef]
- Moses, F. Weigh-in-motion system using instrumented bridges. Transp. Eng. 1979, 3, 233–249. [Google Scholar]
- Moses, F.; Ghosn, M. Weighing Trucks-in-Motion Using Instrumented Highway Bridges: Final Report; Case Western University: Cleveland, OH, USA, 1981. [Google Scholar]
- OBrien, E.J.; Quilligan, M.J.; Karoumi, R. Calculating an influence line from direct measurements. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2006; Volume 159, pp. 31–34. [Google Scholar]
- Yamaguchi, E.; Kawamura, S.-I.; Matuso, K.; Matsuki, Y.; Naito, Y. Bridge-Weigh-In-Motion by Two-Span Continuous Bridge with Skew and Heavy-Truck Flow in Fukuoka Area, Japan. Adv. Struct. Eng. 2009, 12, 115–125. [Google Scholar] [CrossRef]
- Lydon, M.; Robinson, D.; Taylor, S.E.; Amato, G.; OBrien, E.J.; Uddin, N. Improved axle detection for bridge weigh-in-motion systems using fiber optic sensors. J. Civ. Struct. Health Monit. 2017, 7, 325–332. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wu, G.; Feng, D.C. Development of a bridge weigh-in-motion method considering the presence of multiple vehicles. Eng. Struct. 2019, 191, 724–739. [Google Scholar] [CrossRef]
- Oskoui, E.A.; Taylor, T.; Ansari, F. Method and sensor for monitoring weight of trucks in motion based on bridge girder end rotations. Struct. Infrastruct. Eng. 2020, 16, 481–494. [Google Scholar] [CrossRef]
- Alamandala, S.; Prasad, R.S.; Kumar, P.R.; Kumar, M.R. Damage Detection in Bridge-Weigh-In-Motion Structures using Fiber Bragg Grating Sensors. In Laser Science (pp. JW3A-103); Optical Society of America: Washington, DC, USA, 2018. [Google Scholar]
- Moses, F. Instrumentation for Weighing Trucks-in-Motion for Highway Bridge Loads; Final Report; National Technical Information Service: Springfield, WV, USA, 1983.
- Znidaric, A.; Dempsey, A.; Lavric, I.; Baumgaertner, W. Bridge WIM Systems without Axle Detectors; Hermes Science: Paris, France, 1999; pp. 101–110. [Google Scholar]
- Znidaric, A.; Lavric, I.; Kalin, J. Bridge WIM Measurements on Short Slab Bridges; Hermes Science: Paris, France, 1999; pp. 217–225. [Google Scholar]
- Zhang, L. An Evaluation of the Technical and Economic Performance of Weigh-In-Motion Sensing Technology. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2007. [Google Scholar]
- Kalin, J.; Žnidarič, A.; Lavrič, I. Practical implementation of nothing-on-the-road bridge weigh-in-motion system. In International Symposium on Heavy Vehicle Weights and Dimensions. 2006. Available online: https://hvttforum.org/wp-content/uploads/2019/11/Practical-Implementation-of-Nothing-on-the-Road-Bridge-Weigh-In-Motion-System-Kalin.pdf (accessed on 27 September 2020).
- Peters, R.J. Axway-A system to obtain vehicle axle weights. Victoria. In Australian Road Research; Australian Road Research Board (ARRB): Victoria, Australia, 1984; Volume 12, pp. 10–18. [Google Scholar]
- Peters, R.J. Culway-An unmanned and undetectable highway speed vehicle weighing system. In Australian Road Research; Australian Road Research Board (ARRB): Victoria, Australia, 1986; Volume 13, pp. 70–83. [Google Scholar]
- Brown, A.J. Bridge Weigh-in-Motion Deployment Opportunities in Alabama; Jones, S., Richardson, J., Lindly, J., Weber, J., Eds.; ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2011. [Google Scholar]
- Kalhori, H.; Makki Alamdari, M.; Zhu, X.; Samali, B. Nothing-on-Road Axle Detection Strategies in Bridge-Weigh-in-Motion for a Cable-Stayed Bridge: Case Study. J. Bridge Eng. 2018, 23, 05018006. [Google Scholar] [CrossRef]
- OBrien, E.J.; Zhang, L.; Zhao, H.; Hajializadeh, D. Probabilistic bridge weigh-in-motion. Can. J. Civ. Eng. 2018, 45, 667–675. [Google Scholar] [CrossRef]
- He, W.; Ling, T.; OBrien, E.J.; Deng, L. Virtual Axle Method for Bridge Weigh-in-Motion Systems Requiring No Axle Detector. J. Bridge Eng. 2019, 24, 04019086. [Google Scholar] [CrossRef]
- Chatterjee, P.; OBrien, E.; Li, Y.; Gonzáilez, A. Wavelet domain analysis for identification of vehicle axles from bridge measurements. Comput. Struct. 2006, 84, 1792–1801. [Google Scholar] [CrossRef]
- Hitchcock, W.A.; Uddin, N.; Sisiopiku, V.; Salama, T.; Kirby, J.; Zhao, M.H.; Toutanji, H.; Richardson, J. Bridge Weigh-in-Motion (B-WIM) System Testing and Evaluation; UTCA Project (07212); University Transportation Center for Alabama: Tuscaloosa, AL, USA, 2012. [Google Scholar]
- Dunne, D.; O’Brien, E.J.; Basu, B.; Gonzalez, A. Bridge WIM systems with Nothing on the Road (NOR). In Proceedings of the 4th International Conference on Weigh-In-Motion, Taipei, Taiwan, 20–23 February 2005; National Taiwan University: Taipei, Taiwan, 2005; p. 9. [Google Scholar]
- Yu, Y.; Cai, C.S.; Deng, L. Vehicle axle identification using wavelet analysis of bridge global responses. J. Vib. Control. 2017, 23, 2830–2840. [Google Scholar] [CrossRef]
- Blackburn, S. The Oxford Dictionary of Philosophy; OUP Oxford: Oxford, UK, 2005. [Google Scholar]
- Saviotti, P.P. Information, variety and entropy in technoeconomic development. Res. Policy 1988, 17, 89–103. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM Sigmobile Mobile Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- de Oliveira, H.M.; de Souza, D.F. Wavelet analysis as an information processing technique. In 2006 International Telecommunications Symposium; IEEE: New York, NY, USA, 2006. [Google Scholar]
- Bulusu, K.V.; Plesniak, M.W. Shannon entropy-based wavelet transform method for autonomous coherent structure identification in fluid flow field data. Entropy 2015, 17, 6617–6642. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling sampling theory; Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Cebon, D. Handbook of Vehicle-Road Interaction; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Yang, J.P.; Sun, J.Y. Pitching effect of a three-mass vehicle model for analyzing vehicle-bridge interaction. Eng. Struct. 2020, 224, 111248. [Google Scholar] [CrossRef]
- Gao, R.X.; Yan, R. Selection of Base Wavelet; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Harris, N.K.; OBrien, E.J.; González, A. Reduction of bridge dynamic amplification through adjustment of vehicle suspension damping. J. Sound Vib. 2007, 302, 471–485. [Google Scholar] [CrossRef]
- ISO. Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data; International Organization for Standardization: Geneva, Switzerland, 1995. [Google Scholar]

| Vehicle Properties | Bridge Properties | ||
|---|---|---|---|
| D1 | 1.5 m | Span | 15 m |
| m | 5000 kg | Density | 4800 kg/m3 |
| k1 | 3500 kN/m | Second moment of area of cross-section | 0.365 m4 |
| c1 | 10 kN s/m | Modulus of elasticity | 3.5 × 1010 N/m2 |
| m1 | 750 kg | Damping ratio | 0.01 |
| kt1 | 350 kN/m | Breadth | 6 m |
| ct1 | 0 | Depth | 0.9 m |
| Axle 1 | Axle 2 | ||
|---|---|---|---|
| Truck A | Axle spacing (m) | 4.7 | |
| Axle weight (tonnes) | 5.8 | 24.5 | |
| Truck B | Axle spacing (m) | 4.7 | |
| Axle weight (tonnes) | 7.4 | 21.1 | |
| Vehicle No. | Axle Weight (Kips) | Axle Spacing (Inches) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GVW | 1st axle | 2nd axle | 3rd axle | 4th axle | 5th axle | A1-A2 | A2-A3 | A3-A4 | A4-A5 | |
| 1 | 80.1 | 21.5 | 29.7 | 28.9 | 223 | 56 | ||||
| 2 | 41.1 | 20.0 | 10.8 | 10.3 | 223 | 56 | ||||
| 3 | 79.8 | 10.5 | 15.4 | 16.4 | 18.6 | 18.9 | 172 | 52 | 438 | 52 |
| 4 | 41.1 | 10.7 | 7.8 | 7.7 | 7.4 | 7.5 | 172 | 52 | 438 | 52 |
| Item | Axle Spacing | Run 1 | Run 2 | Run 3 | Run 4 | Run 5 | Run 6 | Run 7 | Run 8 | Run 9 | Run 10 | Mean | SD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Truck no. | 3 | 3 | 3 | 3 | 4 | 2 | 2 | 2 | 1 | 1 | / | / | |
| Lane | 1 | 1 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 2 | / | / | |
| Speed (m/s) | 30.5 | 30.5 | 29.9 | 30.5 | 30.1 | 27.7 | 28.2 | 27.8 | 28.2 | 28.2 | |||
| Error in axle spacing (relative to static measurement) | A1-A2 | −0.50% | −1.10% | −1.00% | −1.80% | −0.30% | −3.80% | −3.70% | −3.10% | −2.00% | −0.60% | −1.79% | 1.26% |
| A2-A3 | 3.60% | 0% | −2.70% | −2.40% | −6.40% | 4.70% | 4.50% | 3.40% | 4.70% | 5.10% | 1.45% | 4.00% | |
| A3-A4 | −0.40% | −0.80% | −0.30% | 0% | 0.60% | / | / | / | / | / | −0.18% | 0.47% | |
| A4-A5 | −5.40% | −0.20% | −7.20% | −7.00% | −6.40% | / | / | / | / | / | −5.24% | 2.60% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Tan, C.; OBrien, E.J.; Uddin, N.; Zhang, B. Wavelet-Based Optimum Identification of Vehicle Axles Using Bridge Measurements. Appl. Sci. 2020, 10, 7485. https://doi.org/10.3390/app10217485
Zhao H, Tan C, OBrien EJ, Uddin N, Zhang B. Wavelet-Based Optimum Identification of Vehicle Axles Using Bridge Measurements. Applied Sciences. 2020; 10(21):7485. https://doi.org/10.3390/app10217485
Chicago/Turabian StyleZhao, Hua, Chengjun Tan, Eugene J. OBrien, Nasim Uddin, and Bin Zhang. 2020. "Wavelet-Based Optimum Identification of Vehicle Axles Using Bridge Measurements" Applied Sciences 10, no. 21: 7485. https://doi.org/10.3390/app10217485
APA StyleZhao, H., Tan, C., OBrien, E. J., Uddin, N., & Zhang, B. (2020). Wavelet-Based Optimum Identification of Vehicle Axles Using Bridge Measurements. Applied Sciences, 10(21), 7485. https://doi.org/10.3390/app10217485






