Assessment of Terrorism Risk to Critical Infrastructures: The Case of a Power-Supply Substation
Abstract
1. Introduction
2. Literature Review
2.1. Vulnerability Assessment of Critical Infrastructures
2.2. Strategies for Protecting Critical Infrastructures against Terrorist Attacks
2.3. Game Theory and Terrorism Risk Assessment in Critical Infrastructures
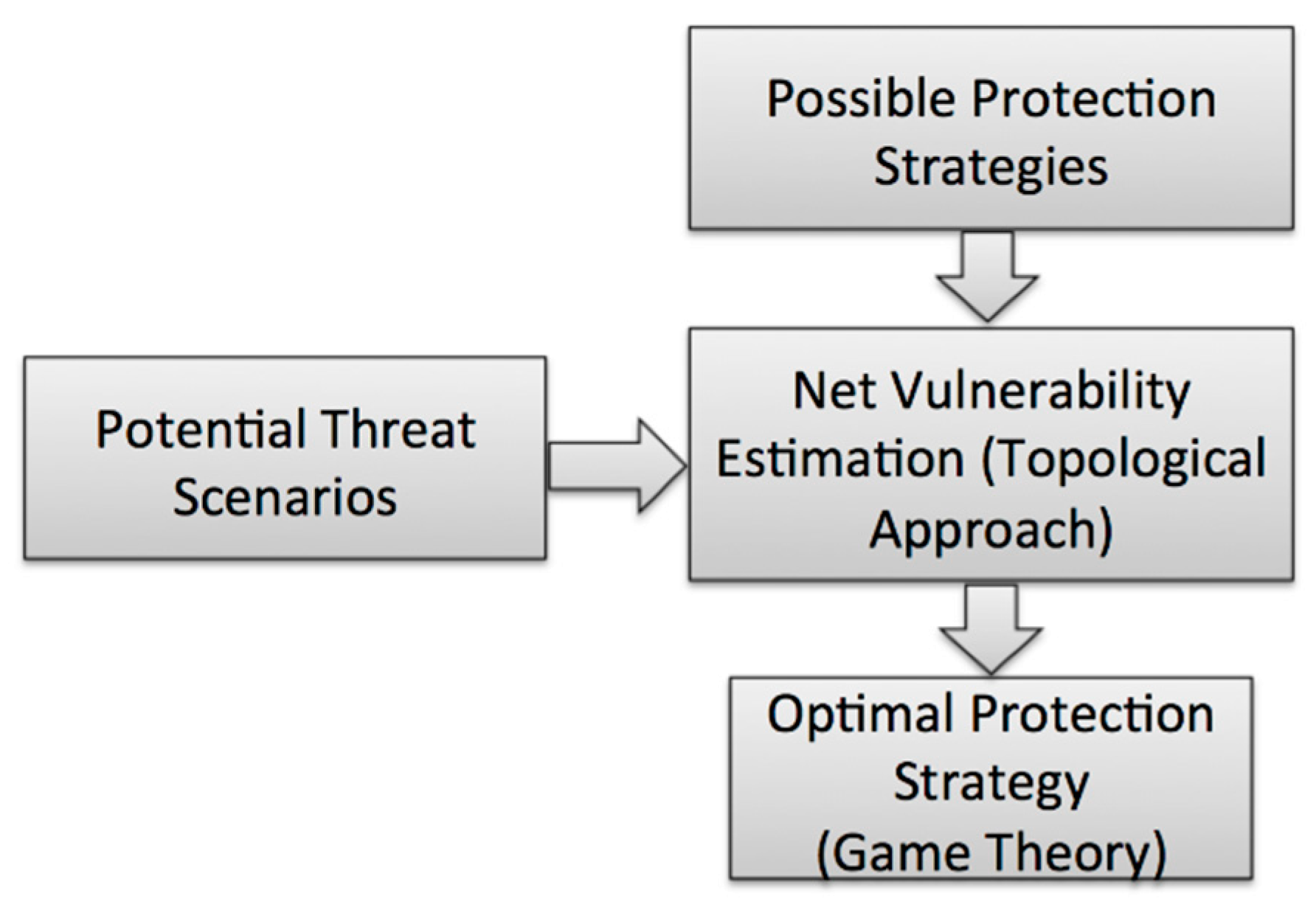
3. Methodology
3.1. Analysis Framework
3.2. Critical Infrastructure Modeling
3.3. Terrorist Attack Loss Modeling
3.3.1. Direct Loss Estimation
3.3.2. Indirect Loss Estimation
4. Strategy Analysis
Optimizing Protection Strategy Using Game Theory
5. Case Study
5.1. Substation Network Modeling
5.2. Terrorist Attack Damage Estimation
5.2.1. Attacking Weapon Used
5.2.2. Estimating Damage
5.3. Terrorist Attack Loss Estimation
5.3.1. Direct Loss Estimation
5.3.2. Indirect Loss Estimation
5.4. Protection Method Specifications
5.4.1. Improving Substation Component Robustness
5.4.2. Improving Substation Component Redundancy
5.5. Protection Strategy Analysis
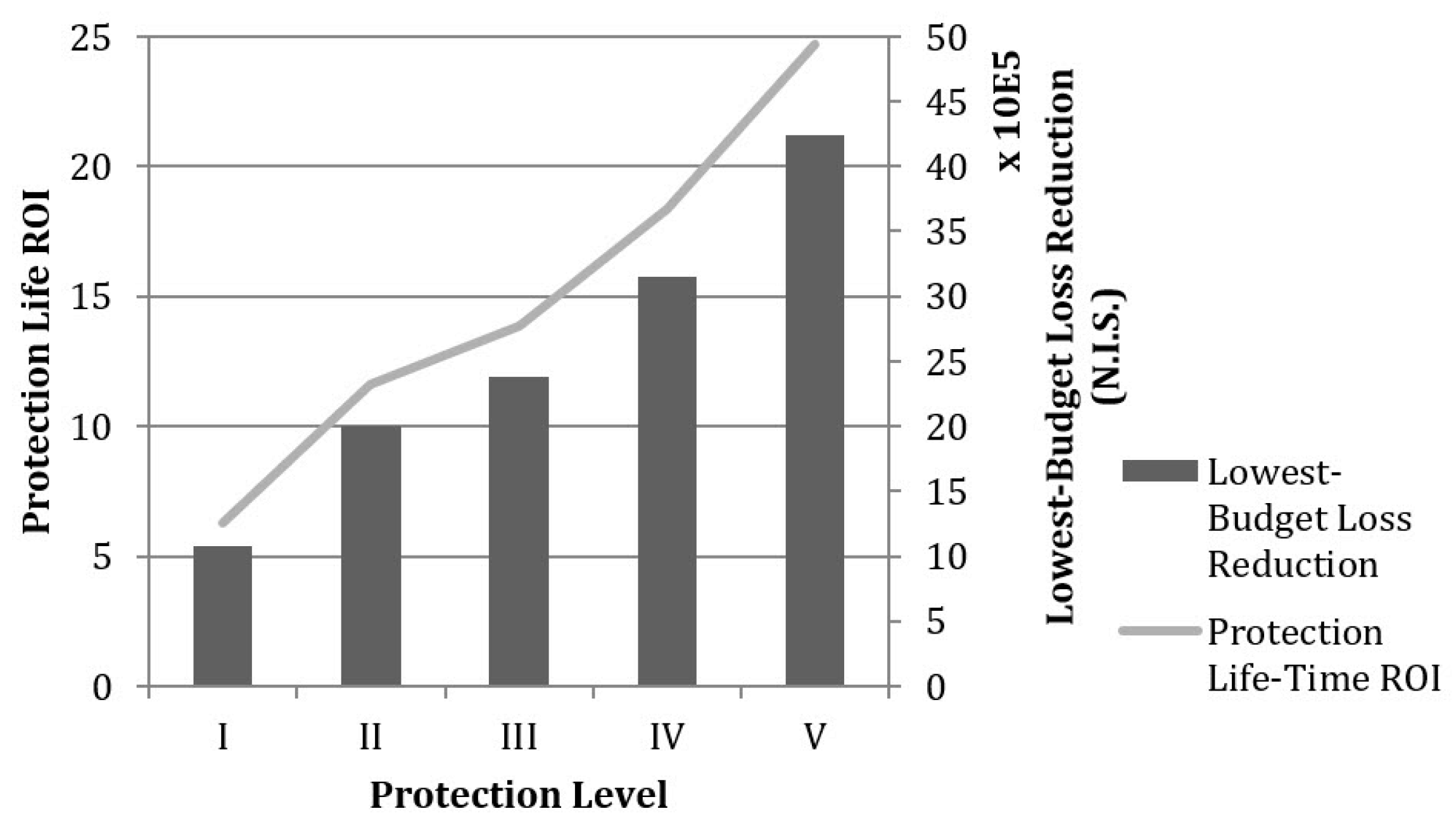
5.5.1. Protection Strategy Analysis: Improving Robustness
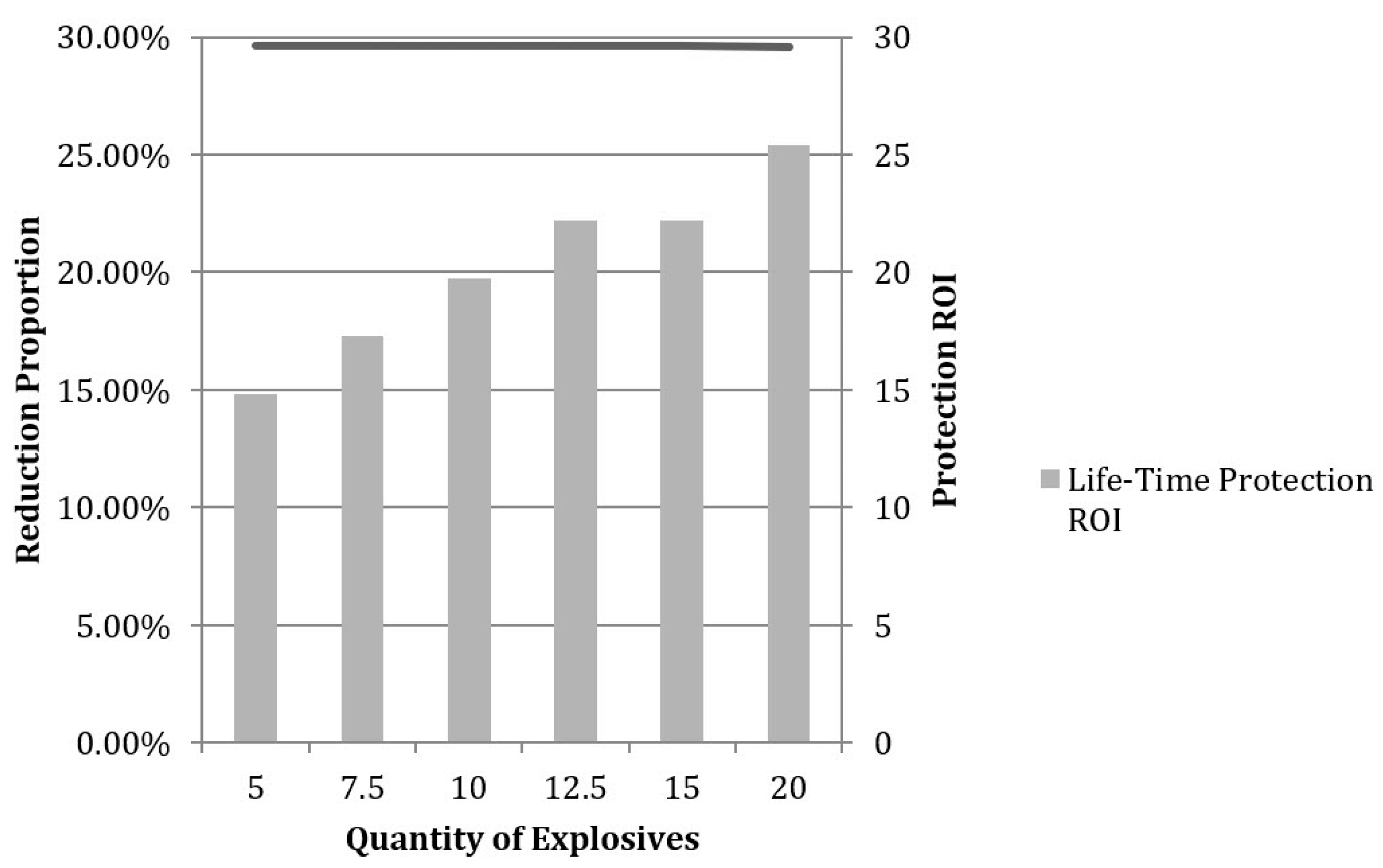
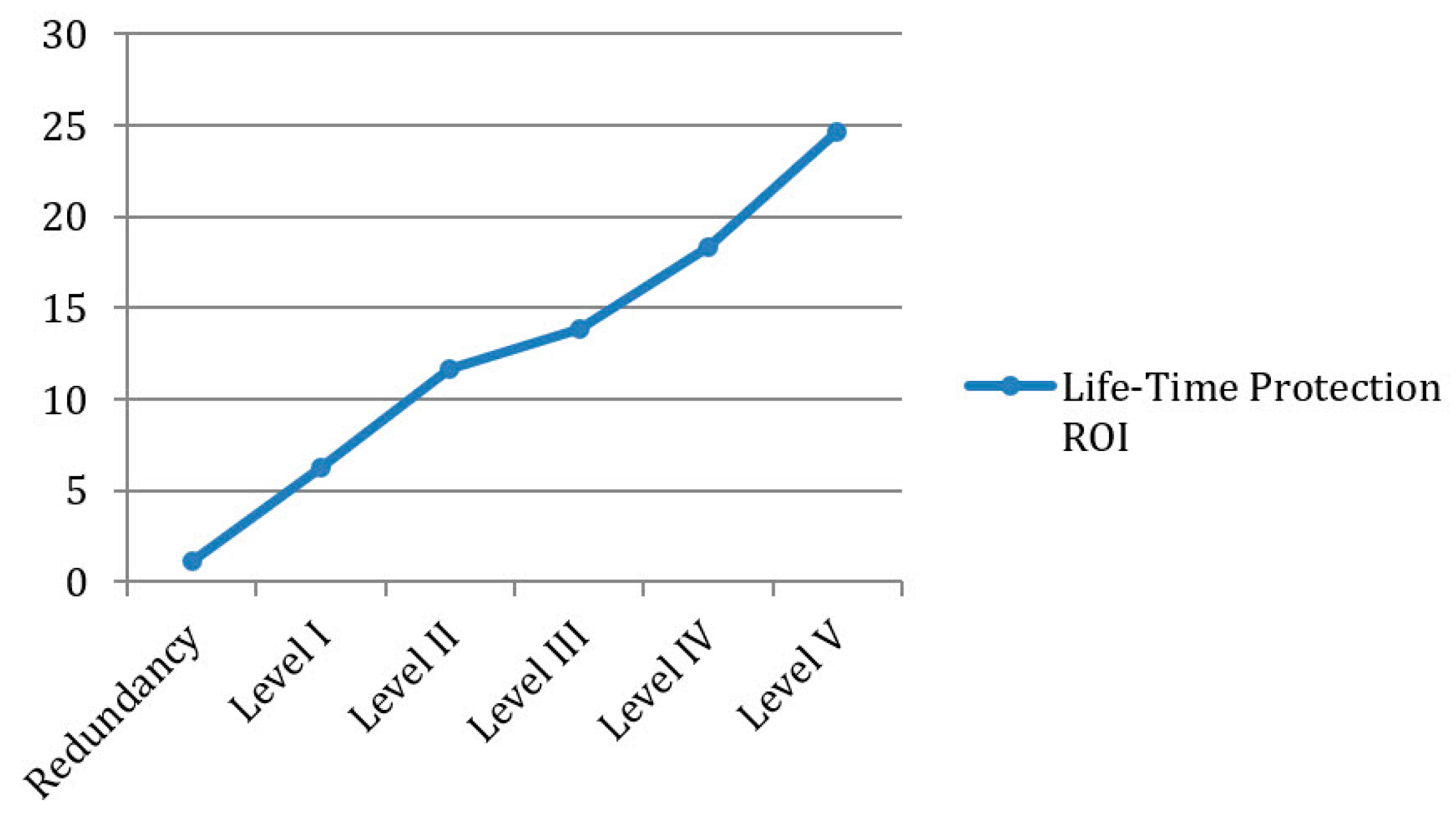
5.5.2. Protection Strategy: Improving Redundancy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mifflin, H. The American Heritage Dictionary; Turtleback School & Library Binding: San Diego, CA, USA, 2001. [Google Scholar]
- Moteff, J.; Parfomak, P. Critical Infrastructure and Key Assets: Definition and Identification; The Library of Congress, Congressional Research Service: Washington, DC, USA, 2004. [Google Scholar]
- O’Rourke, T.D. Critical Infrastructure, Interdependencies, and Resilience; National Emergency Training Center: Emmitsburg, MD, USA, 2007. [Google Scholar]
- Zimmerman, R. Social implications of infrastructure network interactions. J. Urban Technol. 2001, 8, 97–119. [Google Scholar] [CrossRef]
- Minkel, J.R. The 2003 Northeast Blackout—Five years later. Scientific American, 13 August 2008. [Google Scholar]
- Mueller, J.; Stewart, M.G. Terror, Security, and Money: Balancing the Risks, Benefits, and Costs of Homeland Security; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- IEP. 2014 Global Terrorism Index Report—Vision of Humanity; Institute of Economics & Peace (IEP): Sydney, Australia, 2014. [Google Scholar]
- University of Maryland. Global Terrorism Database; University of Maryland: College Park, MD, USA, 2014. [Google Scholar]
- Elkabets, S.M.; Shohet, I.M. “Triple R”—A quantitative model for critical infrastructures to withstand extreme events. In Proceedings of the Creative Construction Conference, Prague, Czech Republic, 21–24 June 2014. [Google Scholar]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, understanding, and analyzing critical infrastructure interdependencies. IEEE Control Syst. Mag. 2001, 21, 11–25. [Google Scholar]
- Dudenhoeffer, D.D.; Permann, M.R.; Manic, M. CIMS: A framework for infrastructure interdependency modeling and analysis. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 478–485. [Google Scholar]
- Yusta, J.M.; Correa, G.J.; Lacal-Arántegui, R. Methodologies and applications for critical infrastructure protection: State-of-the-art. Energy Policy 2011, 39, 6100–6119. [Google Scholar] [CrossRef]
- Haimes, Y.Y. Systems-based guiding principles for risk modeling, planning, assessment, management, and communication. Risk Anal. Int. J. 2012, 32, 1451–1467. [Google Scholar] [CrossRef] [PubMed]
- Eusgeld, I.; Nan, C.; Dietz, S. “System-of-systems” approach for interdependent critical infrastructures. Reliab. Eng. Syst. Saf. 2011, 96, 679–686. [Google Scholar] [CrossRef]
- Trucco, P.; Cagno, E.; De Ambroggi, M. Dynamic functional modelling of vulnerability and interoperability of Critical Infrastructures. Reliab. Eng. Syst. Saf. 2012, 105, 51–63. [Google Scholar] [CrossRef]
- Oh, E.H.; Deshmukh, A.; Hastak, M. Disaster impact analysis based on inter-relationship of critical infrastructure and associated industries. Int. J. Disaster Resil. Built Environ. 2010. [Google Scholar] [CrossRef]
- White, T.; Ariaratnam, S.T.; Michael, J. Subterranean infrastructure reconnaissance for manmade and natural hazards and disasters. Int. J. Disaster Resil. Built Environ. 2012. [Google Scholar] [CrossRef]
- McEntire, D.; Crocker, C.G.; Peters, E. Addressing vulnerability through an integrated approach. Int. J. Disaster Resil. Built Environ. 2010. [Google Scholar] [CrossRef]
- Min, H.-S.J.; Beyeler, W.; Brown, T.; Son, Y.J.; Jones, A.T. Toward modeling and simulation of critical national infrastructure interdependencies. IIE Trans. 2007, 39, 57–71. [Google Scholar] [CrossRef]
- Rehan, R.; Unger, A.J.; Knight, M.A.; Haas, C.T. Financially sustainable management strategies for urban wastewater collection infrastructure–Implementation of a system dynamics model. Tunn. Undergr. Space Technol. 2014, 39, 102–115. [Google Scholar] [CrossRef]
- Cavallini, S.; D’Alessandro, C.; Volpe, M.; Armenia, S.; Carlini, C.; Brein, E.; Assogna, P. A system dynamics framework for modeling critical infrastructure resilience. In Proceedings of the International Conference on Critical Infrastructure Protection, Arlington, VA, USA, 17–19 March 2014; pp. 141–154. [Google Scholar]
- Bompard, E.; Wu, D.; Xue, F. Structural vulnerability of power systems: A topological approach. Electr. Power Syst. Res. 2011, 81, 1334–1340. [Google Scholar] [CrossRef]
- Wang, S.; Hong, L.; Ouyang, M.; Zhang, J.; Chen, X. Vulnerability analysis of interdependent infrastructure systems under edge attack strategies. Saf. Sci. 2013, 51, 328–337. [Google Scholar] [CrossRef]
- Hines, P.; Cotilla-Sanchez, E.; Blumsack, S. Do topological models provide good information about electricity infrastructure vulnerability? Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 033122. [Google Scholar] [CrossRef]
- Bentes, I.; Afonso, L.; Varum, H.; Pinto, J.; Varajão, J.; Duarte, A.; Agarwal, J. A new tool to assess water pipe networks vulnerability and robustness. Eng. Fail. Anal. 2011, 18, 1637–1644. [Google Scholar] [CrossRef]
- Bono, F.; Gutiérrez, E. A network-based analysis of the impact of structural damage on urban accessibility following a disaster: The case of the seismically damaged Port Au Prince and Carrefour urban road networks. J. Transp. Geogr. 2011, 19, 1443–1455. [Google Scholar] [CrossRef]
- Wang, S.; Hong, L.; Chen, X. Vulnerability analysis of interdependent infrastructure systems: A methodological framework. Phys. A Stat. Mech. Appl. 2012, 391, 3323–3335. [Google Scholar] [CrossRef]
- Mousavizadeha, S.; Ghanizadeh Bolandi, T.; Haghifama, M.R.; Moghimic, M.; Luc, J. Resiliency analysis of electric distribution networks: A new approach based on modularity concept. Electr. Power Syst. Res. 2020, 117, 105669. [Google Scholar] [CrossRef]
- Federation of American Scientists. Al Qaeda Training Mannual; Federation of American Scientists: Washington, DC, USA, 2006. [Google Scholar]
- Elkabets, S.M.; Shohet, I.M. Resilience Modeling (TRA) for critical infrastructures to withstand extreme events-sensitivity analyses. In Proceedings of the Creative Construction Conference, Krakow, Poland, 21–24 June 2015. [Google Scholar]
- Brown, G.G.; Carlyle, W.M.; Salmeron, J.; Wood, K. Analyzing the vulnerability of critical infrastructure to attack and planning defenses. In Emerging Theory, Methods, and Applications; Informs: Catonsville, MD, USA, 2005; pp. 102–123. [Google Scholar]
- Brown, G.; Carlyle, M.; Salmerón, J.; Wood, K. Defending critical infrastructure. Interfaces 2006, 36, 530–544. [Google Scholar] [CrossRef]
- Jenelius, E.; Westin, J.; Holmgren, Å.J. Critical infrastructure protection under imperfect attacker perception. Int. J. Crit. Infrastruct. Prot. 2010, 3, 16–26. [Google Scholar] [CrossRef]
- Dwivedi, A.; Yu, X. A maximum-flow-based complex network approach for power system vulnerability analysis. IEEE Trans. Ind. Inform. 2011, 9, 81–88. [Google Scholar] [CrossRef]
- Schneider, C.M.; Moreira, A.A.; Andrade, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 108, 3838–3841. [Google Scholar] [CrossRef]
- Cox, L.A., Jr. Some Limitations of “Risk = Threat × Vulnerability × Consequence” for Risk Analysis of Terrorist Attacks. Risk Anal. 2008, 28, 1749–1761. [Google Scholar] [CrossRef] [PubMed]
- Bier, V.M.; Kosanoglu, F. Target-oriented utility theory for modeling the deterrent effects of counterterrorism. Reliab. Eng. Syst. Saf. 2015, 136, 35–46. [Google Scholar] [CrossRef]
- Talarico, L.; Reniers, G.; Sörensen, K.; Springael, J. MISTRAL: A game-theoretical model to allocate security measures in a multi-modal chemical transportation network with adaptive adversaries. Reliab. Eng. Syst. Saf. 2015, 138, 105–114. [Google Scholar] [CrossRef]
- Feng, Q.; Cai, H.; Chen, Z.; Zhao, X.; Chen, Y. Using game theory to optimize allocation of defensive resources to protect multiple chemical facilities in a city against terrorist attacks. J. Loss Prev. Process Ind. 2016, 43, 614–628. [Google Scholar] [CrossRef]
- Hausken, K.; He, F. On the Effectiveness of Security Countermeasures for Critical Infrastructures. Risk Anal. 2016, 36, 711–726. [Google Scholar] [CrossRef]
- Napolitano, P.; Rossi, G.; Lombardi, M.; Garzia, F.; Ilariucci, M.; Forino, G. Threats Analysis and Security Analysis for Critical Infrastructures: Risk Analysis vs. Game Theory. In Proceedings of the IEEE 2018 International Carnahan Conference on Security Technology, Montreal, QC, Canada, 22–25 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Jaspersen, J.G.; Montibeller, G. On the learning patterns and adaptive behavior of terrorist organizations. Eur. J. Oper. Res. 2020, 282, 221–234. [Google Scholar] [CrossRef]
- Jeon, D.; Kim, K.; Han, S. Modified equation of shock wave parameters. Computation 2017, 5, 41. [Google Scholar] [CrossRef]
- Remennikov, A.M. A review of methods for predicting bomb blast effects on buildings. J. Battlef. Technol. 2003, 6, 5. [Google Scholar]
- Federal Emergency Management Agency. Risk Management Series: Primer to Design Safe School Projects in Case of Terrorist Attacks; Federal Emergency Management Agency: Washington, DC, USA, 2003.
- Haimes, Y.Y. On the complex quantification of risk: Systems-based perspective on terrorism. Risk Anal. 2011, 31, 1175–1186. [Google Scholar] [CrossRef] [PubMed]
- Shohet, I.M.; Elkabets, S.M.; Ornai, D.; Kivity, Y.; Gilad, E.; Levy, R.; Shany, G.; Levi-Tzedek, M.; Tavron, B.; Ben-Dor, G. A methodology for risk assessment and management for nuclear power plant SMR hit by high explosive warheads. In Proceedings of the Creative Construction Conference, 28 June–1 July 2020; pp. 50–55. [Google Scholar] [CrossRef]
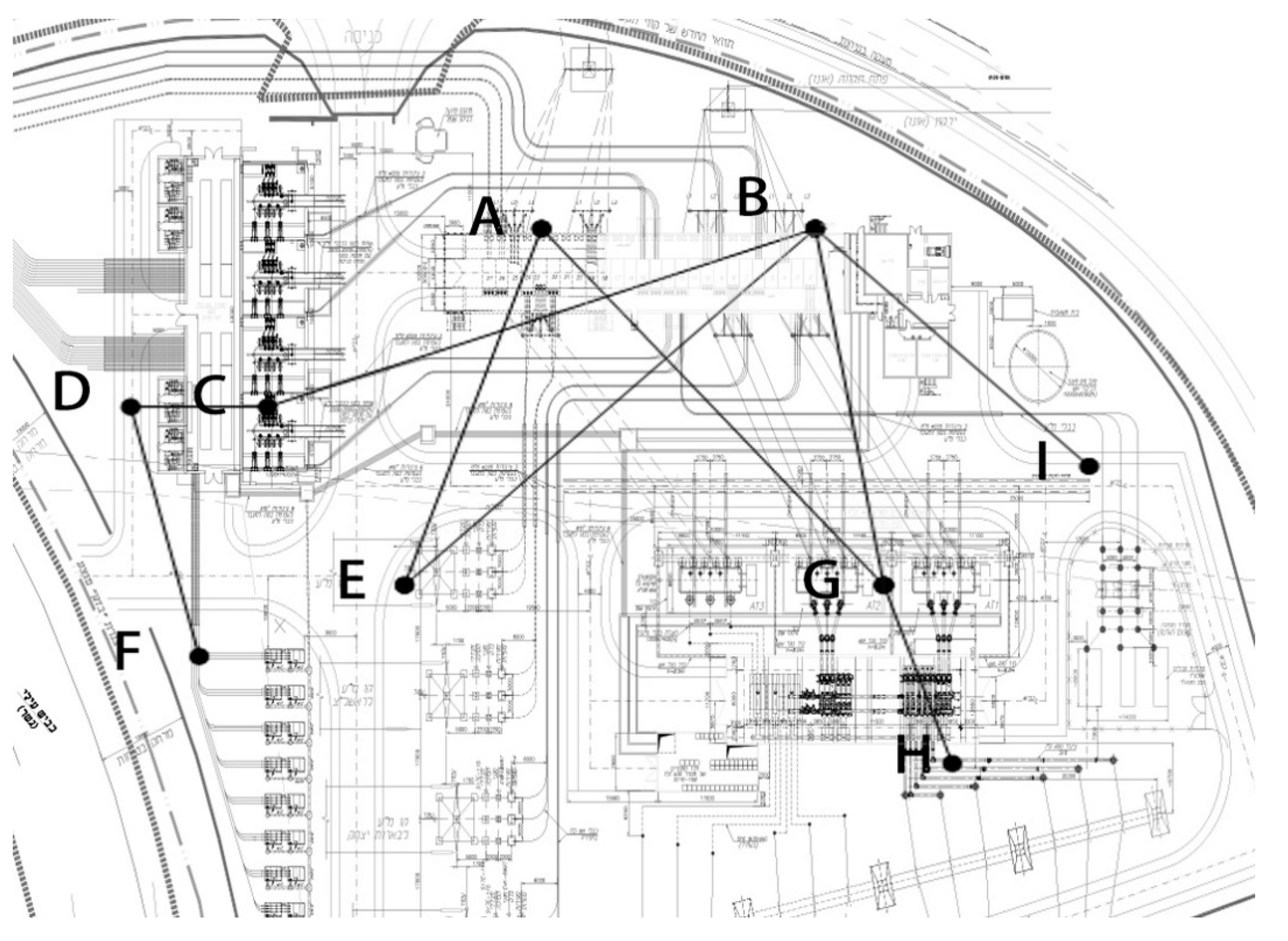
| Component Type | Number of Functioning Units |
|---|---|
| A | 10 |
| B | 17 |
| C | 4 |
| D | 4 |
| E | 4 |
| F | 8 |
| G | 3 |
| H | 2 |
| I | 1 |
| Connecting Edge | Number of Transmission Lines |
| AE | 2 |
| AG | 1 |
| BC | 4 |
| BE | 2 |
| BG | 2 |
| BI | 1 |
| CD | 2 |
| DF | 1 |
| GH | 2 |
| Component Type | Number of Failed Units |
|---|---|
| A | 10 |
| B | 10 |
| C | 2 |
| D | 2 |
| E | 1 |
| F | 4 |
| G | 1 |
| H | 1 |
| I | 1 |
| Connecting Edge | Number of Failed Transmission Lines |
| AE | 2 |
| AG | 1 |
| BC | 2 |
| BE | 2 |
| BG | 2 |
| BI | 1 |
| CD | 1 |
| DF | 1 |
| GH | 1 |
| Loss Factor | Amount of Loss (N.I.S.) |
|---|---|
| Damage to Equipment and Facility | 11,000,000 (2,773,613 USD) |
| Casualties | 19,803,000 (5,000,000 USD) |
| Total Direct Loss | 30,803,000 (7,773,613 USD) |
| Loss Causing Factor | Quantity |
|---|---|
| Total indirect loss of the substation | 25,000 N.I.S./h (6,304 USD/h) |
| Interruption to the power-supply network | 75,000 N.I.S./h (18,911 USD/h) |
| Estimated time to recovery | 10 d |
| Total indirect loss | 24,000,000 N.I.S. (6,059,688 USD) |
| Level of Protection | Protective Solution | |
|---|---|---|
| I | Steel construction | 99% |
| II | Reinforced concrete construction | 90% |
| III | Burial of critical components | 65% |
| IV | Partitioning reinforced concrete walls | 55% |
| V | Secured space | 35% |
| Level of Protection | Protection Allocation to Each Component | Expected Total Loss (N.I.S.) | Percentage Reduction in Loss | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | |||
| None | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 14,291,300 | 0% |
| I | 0.42 | 0.58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6,153,747 | 59% |
| II | 0.41 | 0.59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6,702,103 | 53% |
| III | 0.35 | 0.65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8,103,435 | 43% |
| IV | 0.31 | 0.69 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8,834,589 | 38% |
| V | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10,053,180 | 30% |
| Intensity of Terrorist Attack (kg TNT) | Protection Allocation to Each Component | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | |
| 5 | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7.5 | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12.5 | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0.15 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0.15 | 0.86 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, X.; Wei, H.-H.; Shohet, I.M.; Skibniewski, M.J. Assessment of Terrorism Risk to Critical Infrastructures: The Case of a Power-Supply Substation. Appl. Sci. 2020, 10, 7162. https://doi.org/10.3390/app10207162
Yao X, Wei H-H, Shohet IM, Skibniewski MJ. Assessment of Terrorism Risk to Critical Infrastructures: The Case of a Power-Supply Substation. Applied Sciences. 2020; 10(20):7162. https://doi.org/10.3390/app10207162
Chicago/Turabian StyleYao, Xijun, Hsi-Hsien Wei, Igal M. Shohet, and Miroslaw J. Skibniewski. 2020. "Assessment of Terrorism Risk to Critical Infrastructures: The Case of a Power-Supply Substation" Applied Sciences 10, no. 20: 7162. https://doi.org/10.3390/app10207162
APA StyleYao, X., Wei, H.-H., Shohet, I. M., & Skibniewski, M. J. (2020). Assessment of Terrorism Risk to Critical Infrastructures: The Case of a Power-Supply Substation. Applied Sciences, 10(20), 7162. https://doi.org/10.3390/app10207162






