Frequency Response of Optically Pumped Magnetometer with Nonlinear Zeeman Effect

Abstract

Optically pumped alkali atomic magnetometers based on measuring the Zeeman shifts of the atomic energy levels are widely used in many applications because of their low noise and cryogen-free operation. When alkali atomic magnetometers are operated in an unshielded geomagnetic environment, the nonlinear Zeeman effect may become non-negligible at high latitude and the Zeeman shifts are thus not linear to the strength of the magnetic field. The nonlinear Zeeman effect causes broadening and partial splitting of the magnetic resonant levels, and thus degrades the sensitivity of the alkali atomic magnetometers and causes heading error. In this work, we find that the nonlinear Zeeman effect also influences the frequency response of the alkali atomic magnetometer. We develop a model to quantitatively depict the frequency response of the alkali atomic magnetometer when the nonlinear Zeeman effect is non-negligible and verify the results experimentally in an amplitude-modulated Bell–Bloom cesium magnetometer. The proposed model provides general guidance on analyzing the frequency response of the alkali atomic magnetometer operating in the Earth’s magnetic field. Full and precise knowledge of the frequency response of the atomic magnetometer is important for the optimization of feedback control systems such as the closed-loop magnetometers and the active magnetic field stabilization with magnetometers. This work is thus important for the application of alkali atomic magnetometers in an unshielded geomagnetic environment.

1. Introduction

Highly resolving measurements of weak signals in the Earth’s magnetic field are very important for applications that involve measurement of faint magnetic-field signals, such as geophysical exploration [1,2,3,4], bio-magnetic field detection in an unshielded geomagnetic environment [5,6], and ultralow-field nuclear magnetic resonance [7,8]. One way to measure the small amplitude signals within the Earth’s magnetic field is using optically pumped magnetometers (OPMs) [9], which are based on detecting the Zeeman shifts of the atomic energy levels, such as those of the alkali ground states [10,11,12,13,14,15] or the He${}^4$ metastable state [16,17,18,19]. An alkali atom-based OPM is attractive for its low noise which can reach around $\mathrm{fT}/\sqrt{\mathrm{Hz}}$ (1 fT = 10${}^{-15}$ T) [20,21,22], and the cryogen-free operation. However, in the Earth’s field, alkali atoms based OPMs suffer from the nonlinear Zeeman (NLZ) effect [23,24,25]. The NLZ effect is caused by the nonzero nuclear spin of the alkali atoms and its coupling to the electron spin and as a consequence makes the Zeeman shifts of the atomic energy levels of the ground states become nonlinear dependent of the strength of the magnetic field. The NLZ effect becomes non-negligible in the Earth’s field range of about 20 $\mathsf{\mu }$T to 70 $\mathsf{\mu }$T (1 $\mathsf{\mu }$T = 10${}^{-6}$ T). It broadens and distorts the magnetic resonance lineshape which degrades the magnetometer’s noise specification [26] and generates a heading error [24,27].

We find that the frequency response of alkali atoms based OPM is also influenced by the NLZ effect. Full and precise knowledge about the OPM’s frequency response is important for parameter adjusting in control systems that involve the OPM, such as the closed-loop operation of the OPM [28], or the magnetic-field stabilization with OPM [29]. In the case of a small amplitude of the magnetic field, the NLZ effect is much smaller than the magnetic resonance linewidth and the frequency response of the OPM is typically a first-order Butterworth low-pass filter [28,30]. However, when the magnetic field amplitude increases and the NLZ effect is comparable with the magnetic resonance linewidth, the OPM’s frequency response deviates from that of the first-order low-pass filter.

In this work, we theoretically analyze the frequency response of the alkali atomic magnetometer for a non-negligible NLZ effect and experimentally verify the theoretical predictions with an amplitude-modulated Bell–Bloom cesium OPM. The frequency response of the Bell–Bloom cesium OPM is measured when the biasing magnetic field is 50 $\mathsf{\mu }$T or 70 $\mathsf{\mu }$T and the results are coincident with the theoretical predictions.

2. Experiment Setup

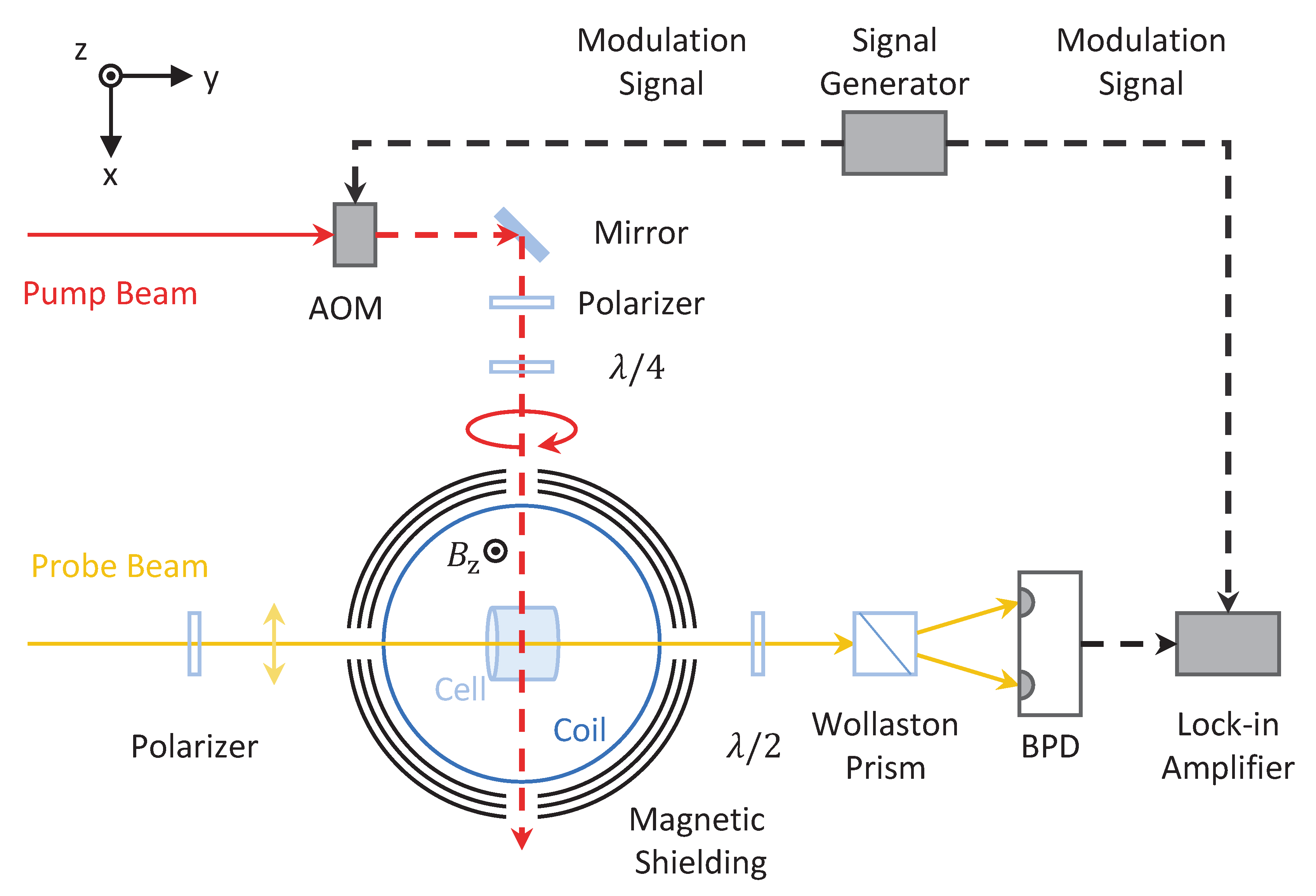
The overall scheme of our Bell–Bloom cesium magnetometer is shown in Figure 1. The cesium atoms are contained in a cylindrical paraffin-coated vapor cell with a diameter and length of 25 mm. The paraffin coating preserves the atomic polarization when the alkali atoms collide with the cell wall [31], which helps to prolong the lifetime of the ground-state Zeeman coherence and leads to a narrow magnetic resonance with a half width at half maximum of about 2 Hz in a small magnetic field (1.15 $\mathsf{\mu }$T). The vapor cell is kept at room temperature during the experiment and is placed in a cylindrical magnetic shielding with seven layers of mu-metal. The magnetic shielding prevents the external magnetic field from entering its inner space and provides a residual magnetic field ∼nT (1 nT = 10${}^{-9}$ T) inside the shielding. A magnetic coil, with a field-current constant of ∼0.115 $\mathsf{\mu }$T/mA, is placed inside the magnetic shielding to control the inner magnetic field along the axial direction (the z-direction). The strength of the magnetic field can be set to any value below 115 $\mathsf{\mu }$T by adjusting the current applied to the magnetic coil. The biasing magnetic field $B_z$ in our setup is set along the axial direction, or the z-axis. The magnetic coil used in our experiment is a cylindrical commercial magnetic coil which is composed of eight circular coils connected in series. Figure 1 is only a schematic and is not drawn to scale. The diameter of the coil is about 30 cm and the number of turns and the position of each circular coil are optimized to minimize the magnetic field gradient. There are four holes on the lateral side of the coil to let the beams pass and no circular coil passes through these holes. To estimate the broadening of the magnetic resonance due to the magnetic inhomogeneity, we measure the distribution of the biasing magnetic field $B_z$ along the z-axis and along the x-axis with a fluxgate. The result shows that the relative magnetic field inhomogeneity in the central ±1.25 cm is about 0.067%, which is limited by the inhomogeneity along the z axis. The magnetic resonance broadening induced by this magnetic field inhomogeneity in the evacuated cesium vapor cell is estimated to be 4.3 (8.5) Hz for 50 (70) $\mathsf{\mu }$T biasing field (the broadening will be larger if the vapor cell is not exactly placed in the center of the coil) [32], which is about 5 times smaller than the experimental measured overall magnetic resonance linewidth for the corresponding biasing field. Consequently, the broadening due to the magnetic field inhomogeneity is not the main reason for linewidth broadening in our setup.

During the experiment, we use a circularly-polarized pump laser beam with a $1/e^2$ diameter of ∼5 mm (e is the base of the natural logarithms. The light intensity falls to $1/e^2\approx 0.135$ times the maximum value at the edge of the $1/e^2$ diameter) to polarize the cesium atoms inside the vapor cell. Although the pump beam enters the vapor cell through the lateral cylindrical wall, which is curved, the distortions of the beam shape and the polarization are negligible because the beam diameter is much smaller than the cell diameter and the wall where the pump beam passes through is relatively flat. The pump laser is resonant with the cesium D1 transition (from $6{}^2{S}_{1/2}F=3$ to $6{}^2{P}_{1/2}{F}^{\prime }=4$, where F and $F^{\prime }$ are the total angular momentum numbers). Its amplitude is modulated with an acoustic-optical modulator (AOM) about the Larmor frequency of cesium atoms and a modulation duty cycle is 20%. The average power of the pump beam is $\sim 50\mu$W. The macroscopic magnetic moment produced by the pump beam precesses at the modulation frequency of the pump beam and is monitored with a linearly polarized probe laser which propagates along the axis of the cylindrical vapor cell. The probe laser is positively detuned by ∼400 MHz from the D2 transition (from $6{}^2{S}_{1/2}F=4$ to $6{}^2{P}_{3/2}{F}^{\prime }=5)$. The $1/e^2$ diameter of the probe laser is ∼2 mm and the average power of the probe laser is ∼10 $\mathsf{\mu }\mathrm{W}$ in the experiment with $B_z\approx$ 1.15 $\mathsf{\mu }$T and is ∼50 $\mathsf{\mu }\mathrm{W}$ in the experiment with $B_z\approx 50\mathsf{\mu }\mathrm{T}$ or 70 $\mathsf{\mu }$T. The precession of the atomic magnetic moment causes periodical optical rotation of the probe beam, which is analyzed with a polarimeter. The output signal from the polarimeter is demodulated with an SR865A lock-in amplifier (LIA). When the modulation frequency is tuned to the Larmor frequency, the in-phase component of the LIA is proportional to the difference between the modulation frequency and the Larmor frequency. As a result, when the modulation frequency is set to a fixed value in the nearby of the Larmor frequency, the variation of the in-phase component directly reflects the variation of the magnetic field to be measured. This is the so-called open loop mode operation of the magnetometer.

The OPM’s frequency response describes how its readout responds to magnetic-field signals with different frequencies. To extract the frequency response of the OPM, we apply a sinusoidal magnetic-field modulation with a typical amplitude of tens of pT along the z-direction and record the readout of the OPM. The OPM readout thus contains a sinusoidal component oscillating at the modulation frequency. In the ideal situation that the magnetometer could record the magnetic-field signal without time delay and distortion, this oscillating component in the OPM readout should have the same amplitude and phase as the modulated magnetic-field signal. In practice, however, there may be some amplitude scaling and phase shift between the readout of the magnetometer and the applied magnetic-field signal. The changes of the amplitude scaling factor and the phase shift with respect to the modulation frequency are the amplitude and phase frequency responses of the magnetometer, respectively, or in brief the frequency response.

3. Theory

In this work, we use the density matrix to model the cesium atomic states in the magnetometer. A complete description of the atomic states should involve both, the ground and excited states. Considering the fact that both, the pump and probe laser, are weak in our experiment, i.e., the light power densities of the pump and probe laser beams are so low that the rate at which atoms in the ground states are optically pumped to the excited states is much slower than the rate of the spontaneous emission which brings atoms in the excited states to the ground states, most of the cesium atoms lay in the ground states. As a consequence, we only model the evolution of the ground states. The ground states of cesium atoms are composed of two hyperfine states, i.e., $F=4$ and $F=3$. There are altogether 16 different Zeeman sublevels in the ground states. As a result, the density matrix $\rho$ describing both these two hyperfine states is a $16\times 16$ matrix. When the density matrix is expressed in the coupled basis, the terms corresponding to the coherence between the two different hyperfine states are fast oscillating and averaged to zero. So the only non-zero terms are the matrix blocks corresponding to the $F=4$ hyperfine state, or ${\rho }^{F_1}$, and that corresponding to the $F=3$ hyperfine state, or ${\rho }^{F_2}$. In our experiment, we are probing the magnetic resonance in the $F=4$ hyperfine state. Only ${\rho }^{F_1}$ has thus a direct influence on the probe signal. As a result, we can use the matrix block corresponding to the $F=4$ hyperfine state, i.e., ${\rho }^{F_1}$, to describe the evolution of the atomic state.

The evolution of ${\rho }^{F_1}$ follows the following Liouville equation

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\rho }^{F_1}}{\mathrm{d}t}=-\frac{\mathrm{i}}{ħ}[H,{\rho }^{F_1}]+\frac{{\mathrm{d}}^{\left(1\right)}{\rho }^{F_1}}{\mathrm{d}t}+\frac{{\mathrm{d}}^{\left(2\right)}{\rho }^{F_1}}{\mathrm{d}t},\end{array}$$

(1)

in which the square brackets denote the commutator, H is the Hamiltonian of the magnetic-field interaction that includes the linear Zeeman effect and the NLZ effect. The term $({\mathrm{d}}^{\left(1\right)}/\mathrm{d}t){\rho }^{F_1}$ describes the optical pumping and $({\mathrm{d}}^{\left(2\right)}/\mathrm{d}t){\rho }^{F_1}$ is the relaxation term which involves the contributions from the wall-collision relaxation, power broadening due to the pump and probe beams, broadening due to the magnetic field gradient, and et al. It should be noticed that, for the more general case where the spatial distribution and diffusion of the density matrix are taken into consideration, the partial derivations should be used in this Liouville equation. In our experiment, we use an anti-relaxation-coated evacuated vapor cell in which cesium atoms traverse the cell within their ground-state Zeeman coherence lifetime. As a result, the atomic polarization is uniformly distributed in the vapor cell. Consequently, we can neglect the non-uniform distribution of the density matrix and simplify the partial derivations to the absolute derivations. We choose the quantization axis along the direction of the magnetic field $B_z$ and extract the second-order Taylor expansion of the Breit–Rabi formula [33], so that H is a diagonal matrix in the coupled basis, with

$$H_{\alpha \beta }={\delta }_{\alpha ,\beta }ħ(\alpha {\omega }_{\mathrm{L}}-{\alpha }^2{\omega }_{\mathrm{NLZ}}/2+8{\omega }_{\mathrm{NLZ}}),$$

(2)

wherein $\alpha$ and $\beta$ are the magnetic quantum numbers ranging from −4 to 4, ${\omega }_{\mathrm{L}}=\gamma B_z$ is the Larmor frequency, where $\gamma$ is the gyromagnetic ratio, $B_z$ is the strength of the magnetic field, and ${\omega }_{\mathrm{NLZ}}\approx 2{\omega }_{\mathrm{L}}^2/{\omega }_{\mathrm{HF}}$ is the splitting of the magnetic resonance induced by the NLZ effect in the Earth’s field range, with ${\omega }_{\mathrm{HF}}=2\pi \times 9.19\mathrm{GHz}$ being the ground state hyperfine splitting of cesium atoms.

According to Equations (1) and (2), the evolution of the density matrix element ${\rho }_{\alpha \beta }^{F_1}$ due to the magnetic field is

$$-\frac{\mathrm{i}}{ħ}{[H,{\rho }^{F_1}]}_{\alpha \beta }=-\frac{\mathrm{i}}{ħ}(H_{\alpha \alpha }-H_{\beta \beta })\times {\rho }_{\alpha \beta }^{F_1}=-\mathrm{i}(\alpha -\beta )[{\omega }_{\mathrm{L}}-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2]\times {\rho }_{\alpha \beta }^{F_1},$$

(3)

which means that ${\rho }_{\alpha \beta }^{F_1}$ tends to oscillate at frequency $-(\alpha -\beta )[{\omega }_{\mathrm{L}}-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2]$.

During the optical pumping process, as the pump laser is resonant with the $6{}^2{S}_{1/2}F=3$ to $6{}^2{P}_{1/2}{F}^{\prime }=4$ transition, the atoms on the $F=3$ ground state are pumped into the $F^{\prime }=4$ excited state, and then decay into both the $F=4$ and $F=3$ ground states through the spontaneous emission. Atomic polarizations are generated in both, the $F=4$ and $F=3$ ground states, during this process. The atomic polarization in the ground states are generated in two ways, i.e., the depopulation pumping and the repopulation pumping [34]. The depopulation pumping originates from the different coupling strength between different ground Zeeman sublevels and makes the sublevels be pumped out at different rates and causes population imbalance [34]. The repopulation pumping is caused by the decay of the excited states to the ground states during which the atomic polarization in the excited state is transferred into the ground states [34]. In our experiment, the atomic polarization in the $F=3$ ground hyperfine state is generated from both, the depopulation pumping and the repopulation pumping, while the polarization in the $F=4$ ground hyperfine state is generated only from the repopulation pump, as the $F=4$ state is not directly coupled with the pump laser. The magnetic resonance in the $F=4$ state is thus less affected by the power broadening induced by the depopulation pump [35], which helps achieve higher sensitivity of the OPM. As a result, we use a linearly polarized probe laser beam, which is positively detuned by ∼400 MHz from $6{}^2{S}_{1/2}F=4$ to $6{}^2{P}_{3/2}{F}^{\prime }=5$ transition to detect the magnetic resonance in the $F=4$ state. The frequency of the probe laser beam is optimized to get the largest magnetic resonance signal. The evolution of ${\rho }^{F_1}$ due to the repopulation pump is described by Equation (4) as

$$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{\left(1\right)}{\rho }_{\alpha \beta }^{F_1}}{\mathrm{d}t}=A\left(t\right)P_{\alpha \beta },\end{array}$$

(4)

in which $A\left(t\right)$ is a real number which is related to the pump rate and P is a matrix determined by the density matrix of the $F=3$ ground hyperfine state, i.e., ${\rho }^{F_2}$, and the polarization of the pump beam. Since the difference between the gyromagnetic ratio of $F=3$ and $F=4$ states is about $2\pi \times 11$ Hz/$\mathsf{\mu }$T, the difference between the Larmor frequency of $F=3$ and $F=4$ states in the Earth’s field is several hundreds of Hertz, which is much larger than the magnetic resonance linewidth. As we are detecting the magnetic resonance of the $F=4$ state, the modulation frequency of the pump beam is resonant with the Larmor frequency of the $F=4$ state in our experiment. The modulation frequency is thus far off-resonant with the Larmor frequency of the $F=3$ ground state, indicating that the transverse atomic polarization of the $F=3$ ground state is not synchronized by the modulated pump beam. As a result, when it comes to the steady state, the $F=3$ state is almost unaffected by the modulation frequency of the pump beam and the transverse atomic polarization of $F=3$ state decays to 0, which means that ${\rho }^{F_2}$ is a constant diagonal matrix. In this case, if we ignore the phase shift due to the Larmor precession of the excited states, one can show that the matrix P induced by the circularly polarized pump beam that transmits along the x-direction is a constant matrix and each of its matrix elements is a real number. The pump beam is amplitude modulated at frequency ${\omega }_{\mathrm{M}}$ in an on-off manner in our experiment, so we can assume that $A\left(t\right)$ is also modulated by a square wave. The Fourier expansion of $A\left(t\right)$ is as follows

$$A\left(t\right)=\sum _{m=-\infty }^{\infty }{A}^{\left(m\right)}{e}^{\mathrm{i}m{\omega }_{\mathrm{M}}t},$$

(5)

in which $A^{\left(m\right)}$ is the amplitude of the m-th order expansion. We can choose a proper initial phase so that each $A^{\left(m\right)}$ is a real number and $A^{\left(m\right)}=A^{(-m)}$.

The relaxation of each density matrix element can be assumed to be an exponential decay as

$$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{\left(2\right)}{\rho }_{\alpha \beta }^{F_1}}{\mathrm{d}t}=-{\mathsf{\Gamma }}_{\alpha \beta }({\rho }_{\alpha \beta }^{F_1}-{\delta }_{\alpha ,\beta }/16),\end{array}$$

(6)

in which ${\mathsf{\Gamma }}_{\alpha \beta }$ is a real number describing the relaxation rate of the density matrix element ${\rho }_{\alpha \beta }^{F_1}$. The final value to which the matrix element decays is ${\delta }_{\alpha ,\beta }/16$. The diagonal elements of ${\rho }^{F_1}$ eventually decay to $1/16$, which is the population of each Zeeman sublevels when the atoms are in the unpolarized state. The off-diagonal elements decay to 0, which corresponds to no coherence in the unpolarized state. As the density matrix ${\rho }^{F_1}$ is Hermitian, ${\mathsf{\Gamma }}_{\alpha \beta }$ can be assumed to be equal to ${\mathsf{\Gamma }}_{\beta \alpha }$.

After substituting Equations (3)–(6) into Equation (1), we will get the equation depicting the overall evolution of density matrix ${\rho }^{F_1}$ as

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\rho }_{\alpha \beta }^{F_1}}{\mathrm{d}t}=-\mathrm{i}(\alpha -\beta )[{\omega }_{\mathrm{L}}-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2]\times {\rho }_{\alpha \beta }^{F_1}+P_{\alpha \beta }\sum _{m=-\infty }^{\infty }{A}^{\left(m\right)}{e}^{\mathrm{i}m{\omega }_{\mathrm{M}}t}-{\mathsf{\Gamma }}_{\alpha \beta }({\rho }_{\alpha \beta }^{F_1}-{\delta }_{\alpha ,\beta }/16).\end{array}$$

(7)

In the detection of atomic polarization, the Faraday rotation angle for the near-resonant linearly polarized probe light is proportional to the atomic polarization along the propagating direction of the probe beam [36], which is

$$\begin{array}{c}\hfill {\langle F_y\rangle }^{F1}=\sum _{\alpha =-3}^4\frac{1}{2\mathrm{i}}\left({\rho }_{\alpha \alpha -1}^{F_1}-{\rho }_{\alpha -1\alpha }^{F_1}\right)\times C_{\alpha }.\end{array}$$

(8)

Therein, $C_{\alpha }$ is a real number. In the case of an optically thin medium, the output signal from the polarimeter is proportional to the Faraday rotation angle, which is also proportional to ${\langle F_y\rangle }^{F1}$ in Equation (8).

To make it easier to solve the evolution of the density matrix ${\rho }^{F_1}$, we transfer ${\rho }^{F_1}$ into a rotating frame whose rotation frequency is the modulation frequency ${\omega }_{\mathrm{M}}$. The rotation direction is the same as the direction of the Larmor precession. The relation between the density matrix in the Lab frame, i.e., ${\rho }^{F_1}$, and that in the rotating frame, i.e., ${\tilde{\rho }}^{F_1}$, is

$${\tilde{\rho }}_{\alpha \beta }^{F_1}={\rho }_{\alpha \beta }^{F_1}{e}^{\mathrm{i}(\alpha -\beta ){\omega }_{\mathrm{M}}t}.$$

(9)

The evolution of ${\tilde{\rho }}^{F_1}$ is

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{\tilde{\rho }}_{\alpha \beta }^{F_1}}{\mathrm{d}t}=& -\mathrm{i}(\alpha -\beta )[{\omega }_{\mathrm{L}}-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2-{\omega }_{\mathrm{M}}]\times {\tilde{\rho }}_{\alpha \beta }^{F_1}\hfill \\ \hfill & +P_{\alpha \beta }\sum _{m=-\infty }^{\infty }{A}^{\left(m\right)}{e}^{\mathrm{i}m{\omega }_{\mathrm{M}}t}{e}^{\mathrm{i}(\alpha -\beta ){\omega }_{\mathrm{M}}t}\hfill \\ \hfill & -{\mathsf{\Gamma }}_{\alpha \beta }({\tilde{\rho }}_{\alpha \beta }^{F_1}-{\delta }_{\alpha ,\beta }/16).\hfill \end{array}$$

(10)

In the contributions from the optical-pumping process, or $P_{\alpha \beta }{\sum }_{m=-\infty }^{\infty }{A}^{\left(m\right)}{e}^{\mathrm{i}m{\omega }_{\mathrm{M}}t}{e}^{\mathrm{i}(\alpha -\beta ){\omega }_{\mathrm{M}}t}$, the terms with $m+\alpha -\beta \ne 0$ have fast oscillations. Their effects cancel out and the net effect is negligible. After ignoring these fast oscillating terms, the evolution of ${\tilde{\rho }}_{\alpha \beta }^{F_1}$ is

$$\begin{array}{c}\hfill \frac{\mathrm{d}{\tilde{\rho }}_{\alpha \beta }^{F_1}}{\mathrm{d}t}\approx -\mathrm{i}(\alpha -\beta )[{\omega }_{\mathrm{L}}-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2-{\omega }_{\mathrm{M}}]\times {\tilde{\rho }}_{\alpha \beta }^{F_1}+P_{\alpha \beta }{A}^{(\beta -\alpha )}-{\mathsf{\Gamma }}_{\alpha \beta }({\tilde{\rho }}_{\alpha \beta }^{F_1}-{\delta }_{\alpha ,\beta }/16).\end{array}$$

(11)

To measure the frequency response of the magnetometer, we typically add a small sinusoidal modulation component $B_{\mathrm{S}}cos\left({\omega }_{\mathrm{S}}t\right)$ to the steady biasing field $B_0$, and the overall magnetic field is $B_z=B_0+B_{\mathrm{S}}cos\left({\omega }_{\mathrm{S}}t\right)$. As a result, the Larmor frequency is ${\omega }_{\mathrm{L}}=\gamma B_0+\gamma B_{\mathrm{S}}cos\left({\omega }_{\mathrm{S}}t\right)$. The influence of the modulation on ${\omega }_{\mathrm{NLZ}}$ is small and can be neglected so that ${\omega }_{\mathrm{NLZ}}=2{\omega }_{\mathrm{L}}^2/{\omega }_{\mathrm{HF}}\approx 2{\left(\gamma B_0\right)}^2/{\omega }_{\mathrm{HF}}$. The response of the magnetometer to the modulation is also a sinusoidal component with the same frequency in the Bell–Bloom OPM readout signal. By extracting the amplitude scaling and phase shift of the magnetometer readout, we will derive the frequency response. We can express the frequency response as a complex function of the frequency whose amplitude indicates the amplitude scaling factor, and phase indicates the phase shift. To simplify the deduction, we could replace the modulation $B_{\mathrm{S}}cos\left({\omega }_{\mathrm{S}}t\right)$ with $B_{\mathrm{S}}exp\left(\mathrm{i}{\omega }_{\mathrm{S}}t\right)$. After the replacement, there is an error-prone place that should be taken into consideration. Generally speaking, the density matrix ${\rho }^{F_1}$ is the Hermitian conjugate of itself and ${\rho }_{\alpha \alpha -1}^{F_1}-{\rho }_{\alpha -1\alpha }^{F_1}$ in Equation (8) can be thus simplified as $2\mathrm{i}\times \mathrm{Im}\left({\rho }_{\alpha \alpha -1}^{F_1}\right)$, in which $\mathrm{Im}\left(Q\right)$ means the imaginary part of a number Q. But if we replace the modulated biasing magnetic field with a complex quantity $B_{\mathrm{S}}exp\left(\mathrm{i}{\omega }_{\mathrm{S}}t\right)$, the density matrix is no more the Hermitian conjugate of itself. ${\rho }_{\alpha \alpha -1}^{F_1}-{\rho }_{\alpha -1\alpha }^{F_1}$ in Equation (8) should not be simplified and may otherwise produce wrong results.

We could perturbatively expand the ${\tilde{\rho }}_{\alpha \beta }^{F_1}$ with $\gamma B_{\mathrm{S}}/{\mathsf{\Gamma }}_{\alpha \beta }$ as

$${\tilde{\rho }}_{\alpha \beta }^{F_1}=\sum _{n=0}^{+\infty }{\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)},$$

(12)

in which ${\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)}$ means the n-th order expansion. Substituting Equation (12) and the expression of ${\omega }_{\mathrm{L}}$ and ${\omega }_{\mathrm{NLZ}}$ into Equation (11), we will get the equation for every single ${\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)}$ as

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)}}{\mathrm{d}t}=& -\mathrm{i}(\alpha -\beta )[\gamma B_0-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2-{\omega }_{\mathrm{M}}]\times {\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)}-{\mathsf{\Gamma }}_{\alpha \beta }\times {\tilde{\rho }}_{\alpha \beta }^{F_1\left(n\right)}\hfill \\ \hfill & -\mathrm{i}(\alpha -\beta )(1-{\delta }_{0,n})\gamma B_{\mathrm{S}}{e}^{\mathrm{i}{\omega }_{\mathrm{S}}t}\times {\tilde{\rho }}_{\alpha \beta }^{F_1(n-1)}\hfill \\ \hfill & +{\delta }_{0,n}{P}_{\alpha \beta }{A}^{\left(\beta -\alpha \right)}+{\mathsf{\Gamma }}_{\alpha \beta }{\delta }_{0,n}{\delta }_{\alpha ,\beta }/16.\hfill \end{array}$$

(13)

The steady state solutions of the first two orders of expansion are

$${\tilde{\rho }}_{\alpha \beta }^{F_1\left(0\right)}=\frac{P_{\alpha \beta }{A}^{(\beta -\alpha )}+{\mathsf{\Gamma }}_{\alpha \beta }{\delta }_{\alpha ,\beta }/16}{\mathrm{i}(\alpha -\beta )\delta {\omega }_{\alpha \beta }+{\mathsf{\Gamma }}_{\alpha \beta }},$$

(14)

in which $\delta {\omega }_{\alpha \beta }=\gamma B_0-(\alpha +\beta ){\omega }_{\mathrm{NLZ}}/2-{\omega }_{\mathrm{M}}$, and

$$\begin{array}{cc}\hfill {\tilde{\rho }}_{\alpha \beta }^{F_1\left(1\right)}& =\frac{-\mathrm{i}(\alpha -\beta )\gamma B_{\mathrm{S}}\exp \left(\mathrm{i}{\omega }_{\mathrm{S}}t\right)}{\mathrm{i}{\omega }_{\mathrm{S}}+\mathrm{i}(\alpha -\beta )\delta {\omega }_{\alpha \beta }+{\mathsf{\Gamma }}_{\alpha \beta }}\times {\tilde{\rho }}_{\alpha \beta }^{F_1\left(0\right)}\hfill \\ \hfill & =\frac{-\mathrm{i}(\alpha -\beta )\gamma B_{\mathrm{S}}\exp \left(\mathrm{i}{\omega }_{\mathrm{S}}t\right)}{\mathrm{i}{\omega }_{\mathrm{S}}+\mathrm{i}(\alpha -\beta )\delta {\omega }_{\alpha \beta }+{\mathsf{\Gamma }}_{\alpha \beta }}\times \frac{P_{\alpha \beta }{A}^{(\beta -\alpha )}+{\mathsf{\Gamma }}_{\alpha \beta }{\delta }_{\alpha ,\beta }/16}{\mathrm{i}(\alpha -\beta )\delta {\omega }_{\alpha \beta }+{\mathsf{\Gamma }}_{\alpha \beta }}.\hfill \end{array}$$

(15)

According to Equation (8), the output signal from the polarimeter is

$$\begin{array}{cc}\hfill {\langle F_y\rangle }^{F1}=& \sum _{\alpha =-3}^4\frac{1}{2\mathrm{i}}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(0\right)}{e}^{-\mathrm{i}{\omega }_{\mathrm{M}}t}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(0\right)}{e}^{\mathrm{i}{\omega }_{\mathrm{M}}t}+{\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(1\right)}{e}^{-\mathrm{i}{\omega }_{\mathrm{M}}t}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(1\right)}{e}^{\mathrm{i}{\omega }_{\mathrm{M}}t}\right)\times C_{\alpha }\hfill \\ \hfill =& \sum _{\alpha =-3}^4\frac{1}{2\mathrm{i}}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(0\right)}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(0\right)}+{\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(1\right)}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(1\right)}\right)\times C_{\alpha }\cos {\omega }_{\mathrm{M}}t\hfill \\ \hfill & -\sum _{\alpha =-3}^4\frac{1}{2}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(0\right)}+{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(0\right)}+{\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(1\right)}+{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(1\right)}\right)\times C_{\alpha }\sin {\omega }_{\mathrm{M}}t.\hfill \end{array}$$

(16)

After demodulating the output signal at ${\omega }_{\mathrm{M}}$ with the LIA, the in-phase component (the term proportional to $\cos {\omega }_{\mathrm{M}}t$) is composed of the steady part

$$\begin{array}{c}\hfill Ou{t}_{\mathrm{In}}^{\left(0\right)}=\sum _{\alpha =-3}^4\frac{1}{2\mathrm{i}}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(0\right)}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(0\right)}\right)\times C_{\alpha }=-\sum _{\alpha =-3}^4\frac{\delta {\omega }_{\alpha \alpha -1}}{\delta {\omega }_{\alpha \alpha -1}^2+{\mathsf{\Gamma }}_{\alpha \alpha -1}^2}\times C_{\alpha }{P}_{\alpha \alpha -1}{A}^{(-1)},\end{array}$$

(17)

and the oscillating part

$$\begin{array}{cc}\hfill Ou{t}_{\mathrm{In}}^{\left(1\right)}\left(t\right)=& \sum _{\alpha =-3}^4\frac{1}{2\mathrm{i}}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(1\right)}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(1\right)}\right)\times C_{\alpha }\hfill \\ \hfill =& -\sum _{\alpha =-3}^4\frac{C_{\alpha }{P}_{\alpha \alpha -1}{A}^{(-1)}\gamma B_{\mathrm{S}}{e}^{\mathrm{i}{\omega }_{\mathrm{S}}t}}{2\left(\mathrm{i}{\omega }_{\mathrm{S}}+\mathrm{i}\delta {\omega }_{\alpha \alpha -1}+{\mathsf{\Gamma }}_{\alpha \alpha -1}\right)\times \left(\mathrm{i}\delta {\omega }_{\alpha \alpha -1}+{\mathsf{\Gamma }}_{\alpha \alpha -1}\right)}\hfill \\ \hfill & -\sum _{\alpha =-3}^4\frac{C_{\alpha }{P}_{\alpha \alpha -1}{A}^{(-1)}\gamma B_{\mathrm{S}}{e}^{\mathrm{i}{\omega }_{\mathrm{S}}t}}{2\left(\mathrm{i}{\omega }_{\mathrm{S}}-\mathrm{i}\delta {\omega }_{\alpha \alpha -1}+{\mathsf{\Gamma }}_{\alpha \alpha -1}\right)\times \left(-\mathrm{i}\delta {\omega }_{\alpha \alpha -1}+{\mathsf{\Gamma }}_{\alpha \alpha -1}\right)}.\hfill \end{array}$$

(18)

The steady part Equation (17) corresponds to the conventional magnetic resonance signal, which is a sum of eight Lorentz dispersive curves with different central frequencies. The oscillating part, which is expressed as Equation (18), is the OPM’s response to the magnetic-field modulation, oscillating at the magnetic modulation frequency ${\omega }_{\mathrm{S}}$ with an amplitude proportional to the magnetic modulation $B_{\mathrm{S}}$. It is also a sum of the response from the eight individual Lorentz peaks. If we have $\delta {\omega }_{\alpha \alpha -1}=0$ for some $\alpha$, then its corresponding contribution on $Ou{t}_{\mathrm{In}}^{\left(1\right)}\left(t\right)$ is

$$\begin{array}{cc}\hfill Ou{t}_{\mathrm{In}}^{\left(1\right)}{\left(t\right)}_{\alpha }{|}_{\delta {\omega }_{\alpha \alpha -1}=0}=& \frac{1}{2\mathrm{i}}\left({\tilde{\rho }}_{\alpha \alpha -1}^{F_1\left(1\right)}-{\tilde{\rho }}_{\alpha -1\alpha }^{F_1\left(1\right)}\right)\times C_{\alpha }{|}_{\delta {\omega }_{\alpha \alpha -1}=0}\hfill \\ \hfill =& -\frac{C_{\alpha }{P}_{\alpha \alpha -1}{A}^{(-1)}\gamma B_{\mathrm{S}}{e}^{\mathrm{i}{\omega }_{\mathrm{S}}t}}{{\mathsf{\Gamma }}_{\alpha \alpha -1}^2}\times \frac{{\mathsf{\Gamma }}_{\alpha \alpha -1}}{\mathrm{i}{\omega }_{\mathrm{S}}+{\mathsf{\Gamma }}_{\alpha \alpha -1}},\hfill \end{array}$$

(19)

in which the magnetic-field modulation frequency ${\omega }_{\mathrm{S}}$ related term ${\mathsf{\Gamma }}_{\alpha \alpha -1}/(\mathrm{i}{\omega }_{\mathrm{S}}+{\mathsf{\Gamma }}_{\alpha \alpha -1})$ is exactly a first-order Butterworth low-pass filter with bandwidth ${\mathsf{\Gamma }}_{\alpha \alpha -1}$, coincident with the common sense about OPM’s frequency response.

Typically, when we operate the OPM in the open-loop mode, we will make sure that $\gamma B_0\approx {\omega }_{\mathrm{M}}$. Under this condition, we can get the frequency response $FR\left({\omega }_{\mathrm{S}}\right)$ of the OPM by normalizing the oscillating amplitude of $Ou{t}_{\mathrm{In}}^{\left(1\right)}\left(t\right)$ with the oscillating amplitude at the limit that ${\omega }_{\mathrm{S}}$ approaches 0 as

$$\begin{array}{cc}\hfill FR\left({\omega }_{\mathrm{S}}\right)& =\frac{Ou{t}_{\mathrm{In}}^1\left(t\right)e^{-\mathrm{i}{\omega }_{\mathrm{S}}t}{|}_{\gamma B_0={\omega }_{\mathrm{M}}}}{Ou{t}_{\mathrm{In}}^1\left(t\right)e^{-\mathrm{i}{\omega }_{\mathrm{S}}t}{|}_{\gamma B_0={\omega }_{\mathrm{M}},{\omega }_{\mathrm{S}}\to 0}}.\hfill \end{array}$$

(20)

To predict the frequency response of the OPM, we could first fit the magnetic resonance curves with Equation (17), which gives parameters $C_{\alpha }{P}_{\alpha \alpha -1}{A}^{(-1)}$ and ${\mathsf{\Gamma }}_{\alpha \alpha -1}$ for each $\alpha$ ranging from $-3$ to 4. Afterward, we can use these parameters to calculate the frequency response of the OPM according to Equation (18) and Equation (20).

4. Results and Discussions

The response of the OPM to the magnetic-field modulation shown in Equation (18) is composed of the contributions from eight Lorentz peaks with different detuning $\delta {\omega }_{\alpha \alpha -1}$. We firstly examine the influence of the modulation detuning on the response from a single Lorentz peak. To do so, we set the biasing magnetic field to be around 1.15 $\mathsf{\mu }$T, where the NLZ effect is negligible and the magnetic resonance can be viewed as a single Lorentz peak, and then measure the response of the OPM to magnetic-field modulations when the detuning $\delta \omega =\gamma B_0-{\omega }_{\mathrm{M}}$ is set to a different value. 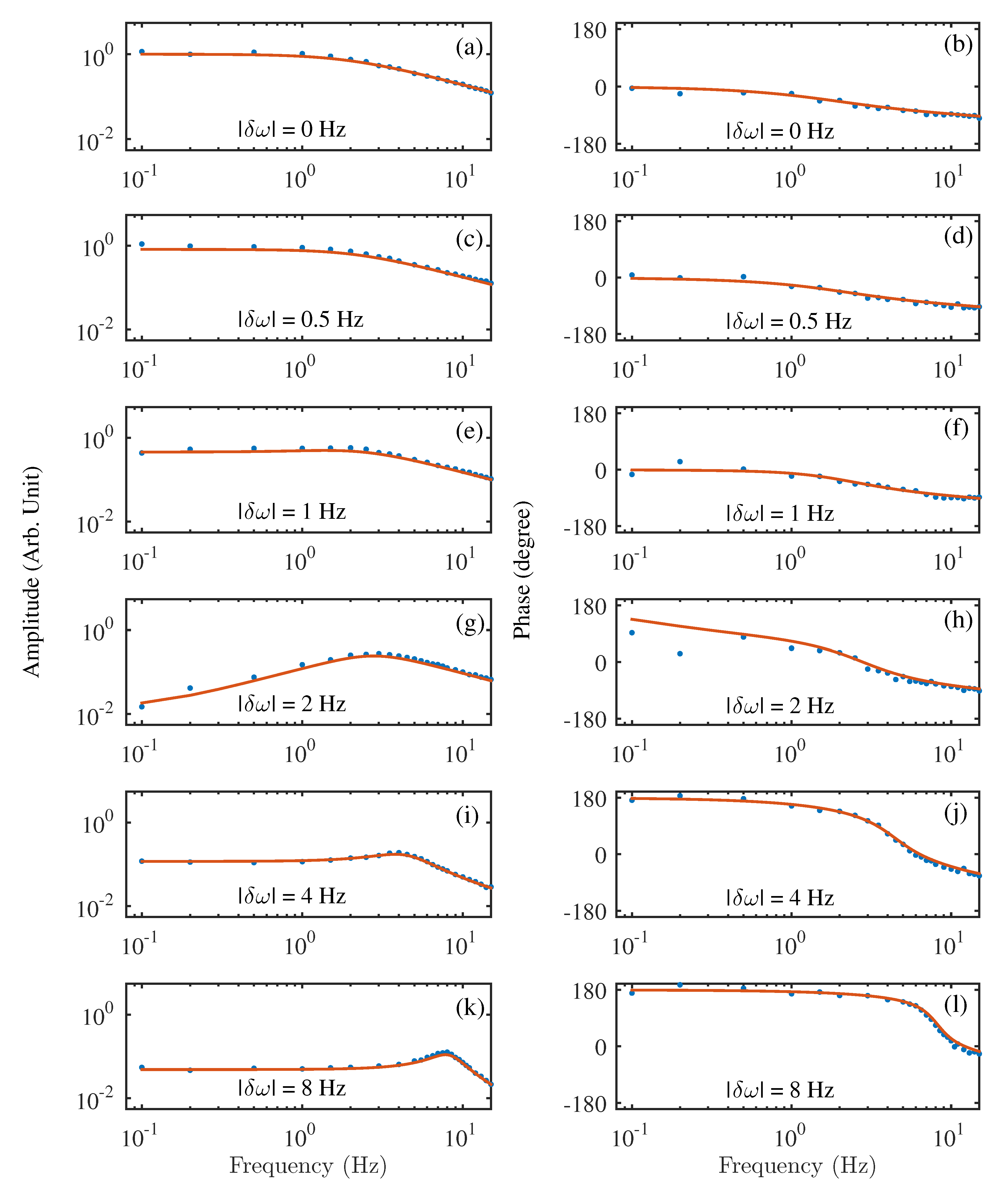Figure 2 compares the experimental and simulated frequency responses of the Bell–Bloom cesium OPM at 1.15 $\mathsf{\mu }$T with different detunings. To get the simulated frequency responses, we scan the magnetic resonance signal and fit it with a single Lorentz peak for deriving its amplitude and linewidth (about 2 Hz). Subsequently, we use these fitting parameters to predict the OPM’s response to magnetic-field modulation with the help of Equation (18). The figures in the left (right) column in Figure 2 indicate the amplitude (phase)-frequency responses. From the top to the bottom, the modulation detuning increases. All these curves are normalized by OPM’s response to magnetic-field modulation at the low-frequency limit when the detuning $\delta \omega$ equals 0. It is clear for a detuning frequency of 0, the frequency response is a Butterworth low-pass filter and the magnetometer has hence a larger response to the magnetic-field signals with lower frequencies. When the detuning $\delta \omega$ increases, the overall response of the magnetometer decreases. But the range for which the magnetometer has the largest response changes towards higher frequencies.

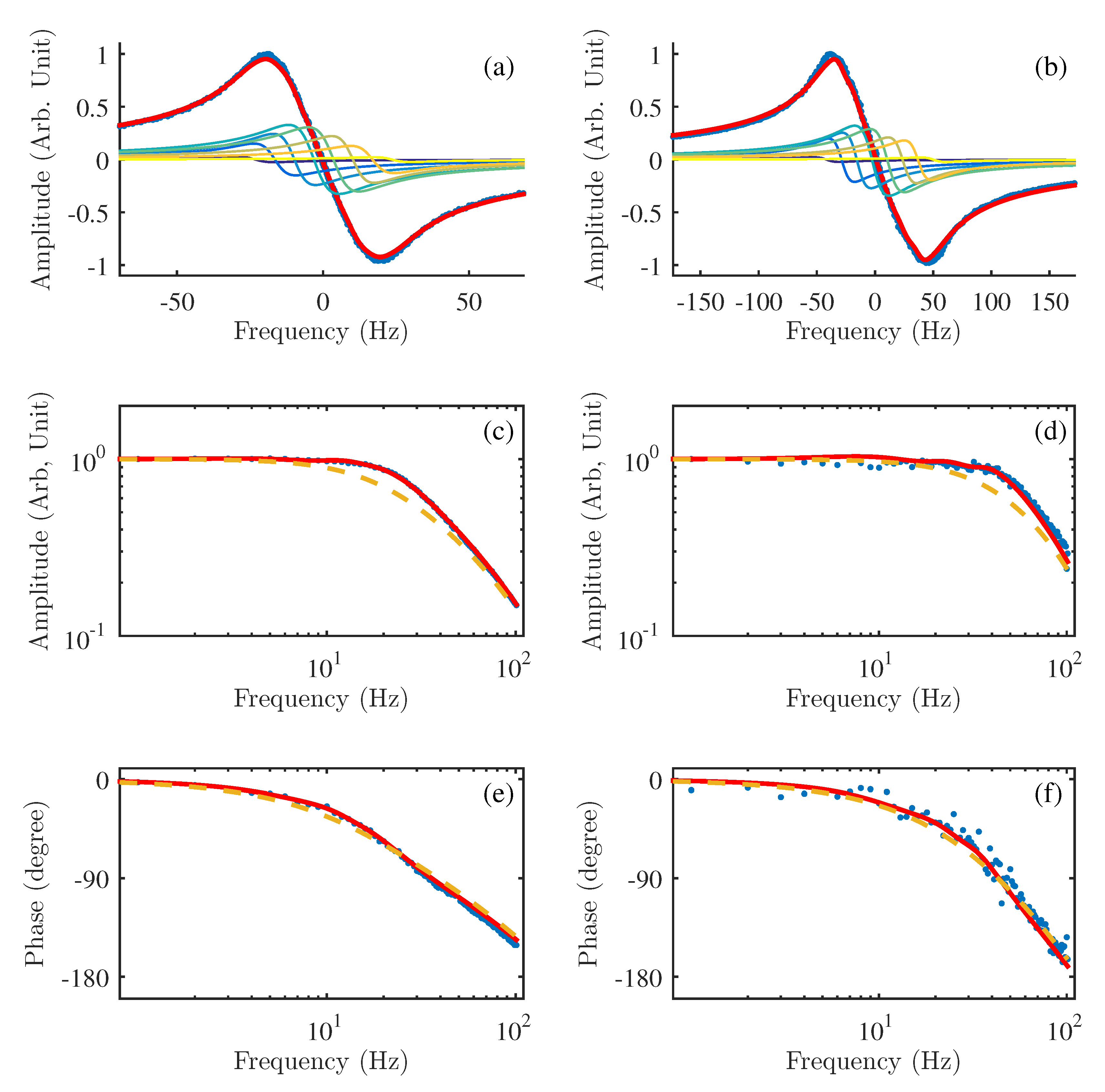
We also check our model when the NLZ effect is non-negligible in the Bell–Bloom OPM operated in the Earth’s magnetic field. The magnetic resonances and frequency responses of the OPM with biasing field $B_0$ of 50 $\mathsf{\mu }$T and 70 $\mathsf{\mu }$T are shown in Figure 3. We firstly fit the magnetic resonances with Equation (17) to get the central frequency, the amplitude, and the linewidth of each Lorentz curve. The fitted linewidth and amplitude of each Lorentz curve are listed in

Table 1. Fitted linewidth and amplitude of each Lorentz curve in the magnetic resonances of the Bell–Bloom cesium OPM at a biasing magnetic field of 50 $\mathsf{\mu }$T and 70 $\mathsf{\mu }$T.

Resonance No.	50 $\mathsf{\mu }$T		70 $\mathsf{\mu }$T
	Linewidth (Hz)	Amplitude (Arb. Unit)	Linewidth (Hz)	Amplitude (Arb. Unit)
1	6.5	0.058	11.1	0.050
2	7.2	0.38	11.2	0.46
3	7.2	0.62	12.4	0.66
4	8.7	1.0	14.9	1.0
5	8.7	0.93	14.9	0.90
6	7.3	0.57	12.4	0.54
7	7.5	0.34	11.7	0.45
8	6.5	0.053	11.1	0.048

(from lower central frequency ones to higher central frequency ones). The fitted linewidth with a biasing field of 70 $\mathsf{\mu }$T is larger than that with a biasing field of 50 $\mathsf{\mu }$T and both of them are larger than the 2 Hz linewidth with 1.15 $\mathsf{\mu }$T biasing field. The broadening of each Lorentz curve at a larger biasing field is mainly due to the increased magnetic gradient. The linewidth of a single Lorentz curve is about 3 times smaller than the experimental measured overall magnetic resonance linewidth for the corresponding biasing field, which is about 20 (40) Hz with a biasing field of 50 (70) $\mathsf{\mu }$T (${\omega }_{\mathrm{NLZ}}$ at 50 and 70 $\mathsf{\mu }$T biasing field are about 6.7 and 13.1 Hz, respectively). This suggests that the broadening of the overall magnetic resonance is mainly due to the NLZ effect, rather than the magnetic field inhomogeneity. Finally, we use these fitting results to calculate the theoretical frequency responses according to Equation (20) which is then compared with the experimental results. During the experiment, the low-pass filter in the lock-in amplifier for 50 (70) $\mathsf{\mu }$T experiment is a second (third)-order Butterworth low-pass filter with a time constant of 1 ms, which is taken into consideration in the calculation of the simulated frequency responses. It is shown that the calculated results coincide with the experimental results for both the amplitude- and the phase-frequency responses. We also calculate the frequency responses according to the first-order Butterworth low-pass filter and present the results in Figure 3 (the yellow dashed lines), which have large deviations from the experimental results in the amplitude-frequency responses. It proves that the model proposed in this work is more precise to characterize the frequency response of the magnetometer in a large magnetic field, within which the non-linear Zeeman effect is non-negligible.

5. Conclusions and Outlook

In this work, we present a quantitative model to describe the influence of the NLZ effect on the frequency response of the OPM and experimentally verify this model with a Bell–Bloom cesium OPM. While it is known that the magnetic resonance signal with an NLZ effect is a linear superposition of multiple Lorentz curves, we find that the frequency response of the Bell–Bloom magnetometer influenced by the NLZ effect is also the same linear superposition of contributions from these multiple Lorentz curves. This model can be extended to the OPMs based on other alkali atomic species by updating the gyromagnetic ratio $\gamma$, the ground state hyperfine splitting ${\omega }_{\mathrm{HF}}$, and the total angular momentum quantum number F.

Our work is important for analyzing the frequency response of the alkali atomic magnetometer operated in an unshielded geomagnetic environment. Full and precise knowledge of the frequency response of the OPM can help to automatically optimize parameters of the closed-loop operation of the OPM and thus help to extend the bandwidth of the OPM without losing its sensitivity, or to improve the identity between the frequency responses of different OPMs to improve the noise rejection ratio of the gradiometer [26]. As closed-loop magnetic-noise-compensation setups require adequate knowledge of the system response, our work can also help to improve the performance of the active magnetic-field stabilization operated in the Earth’s field [29,37] which is attractive for ultralow-field nuclear magnetic resonance [7] and for recording bio-magnetic signals from human brain activities in unshielded environments [26,38].