Parameter Optimization for Ship Antiroll Gyros
Abstract
1. Introduction
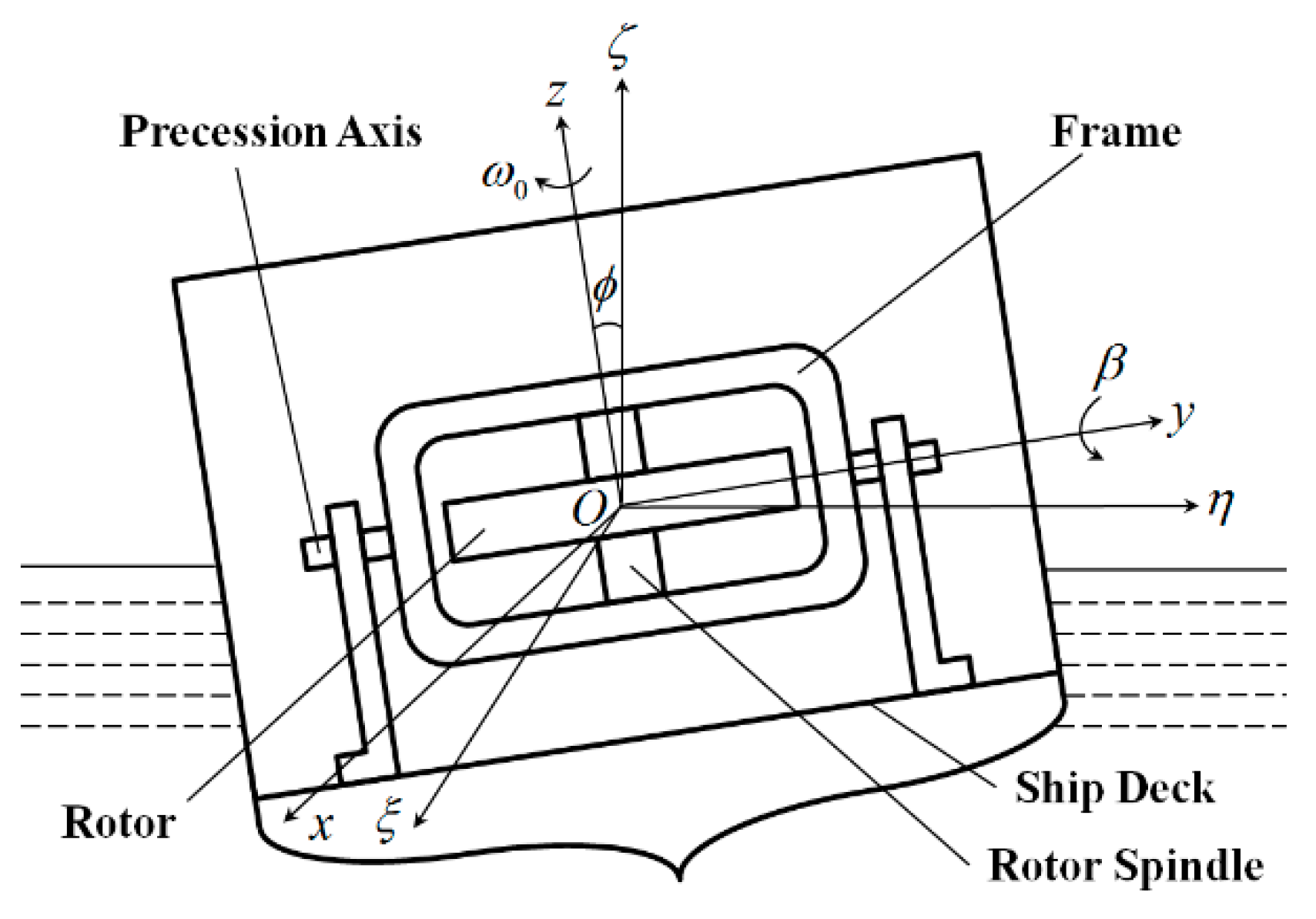
2. Dynamical Model of Ship’s Antiroll Gyro
2.1. Mathematical Model of Random Waves
2.2. Ship Rolling Mathematical Model under Random Wave Excitation
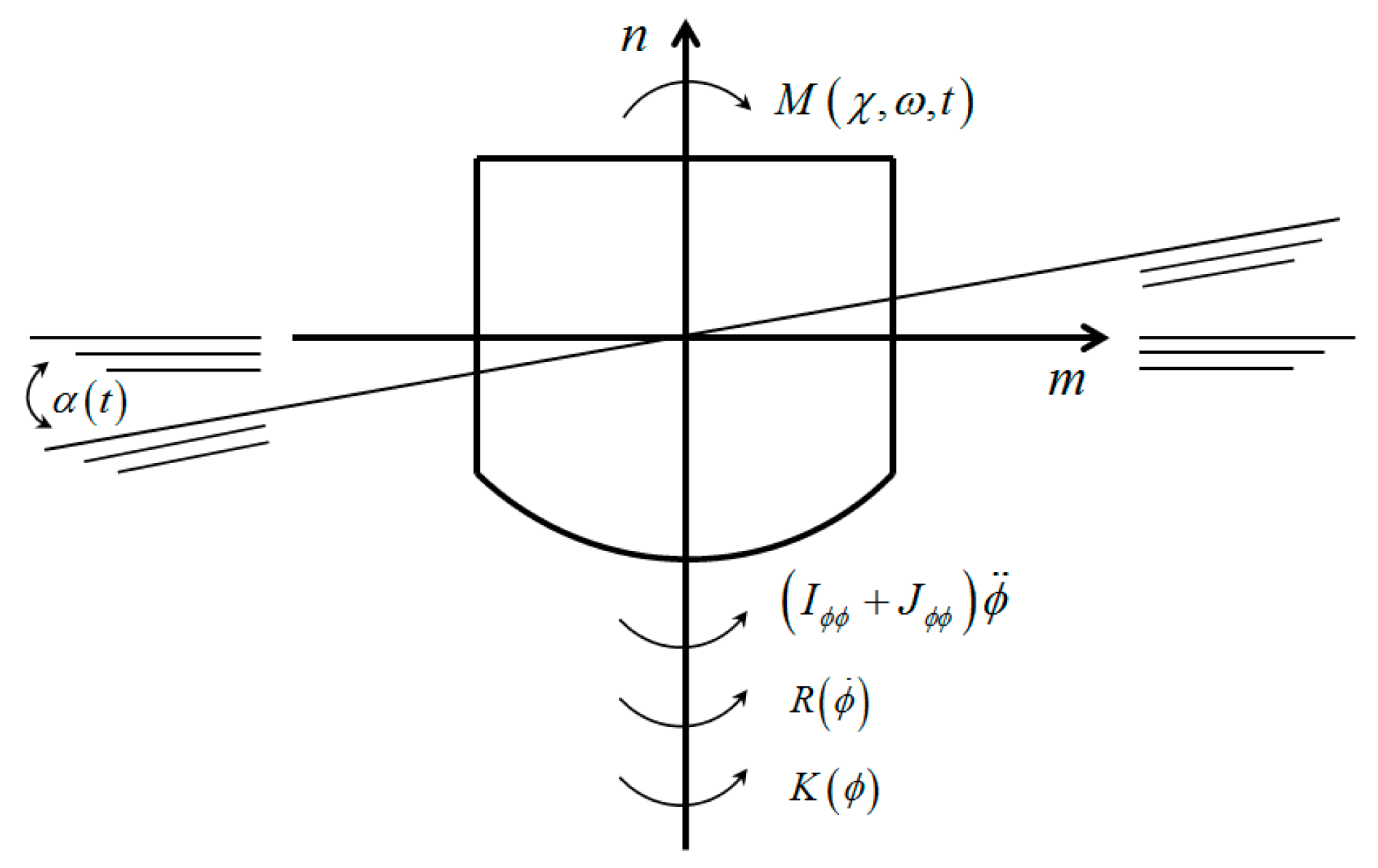
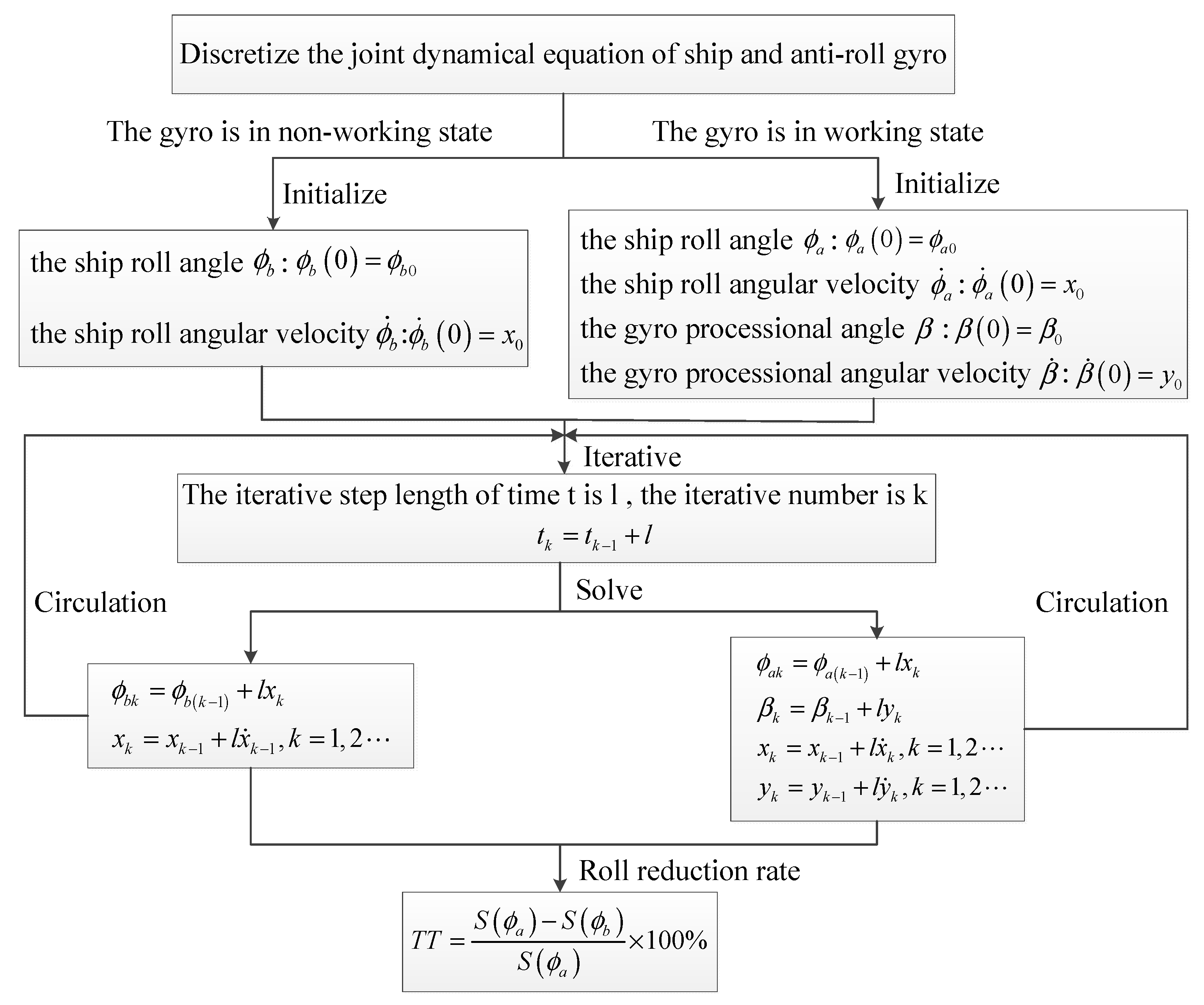
2.3. Joint Dynamical Equation of Ship and Antiroll Gyro
3. Study of the Antirolling Characteristics of the Gyro
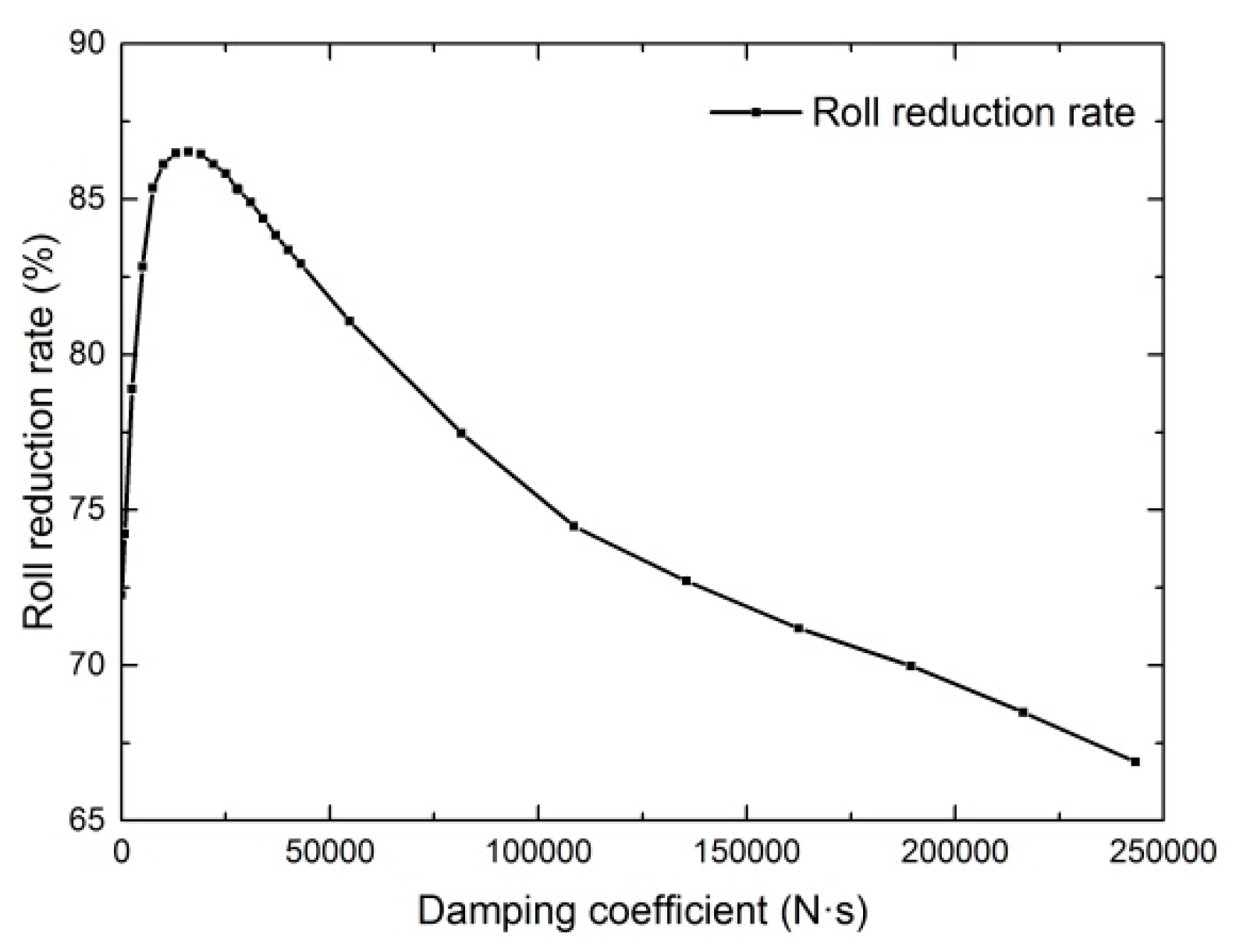
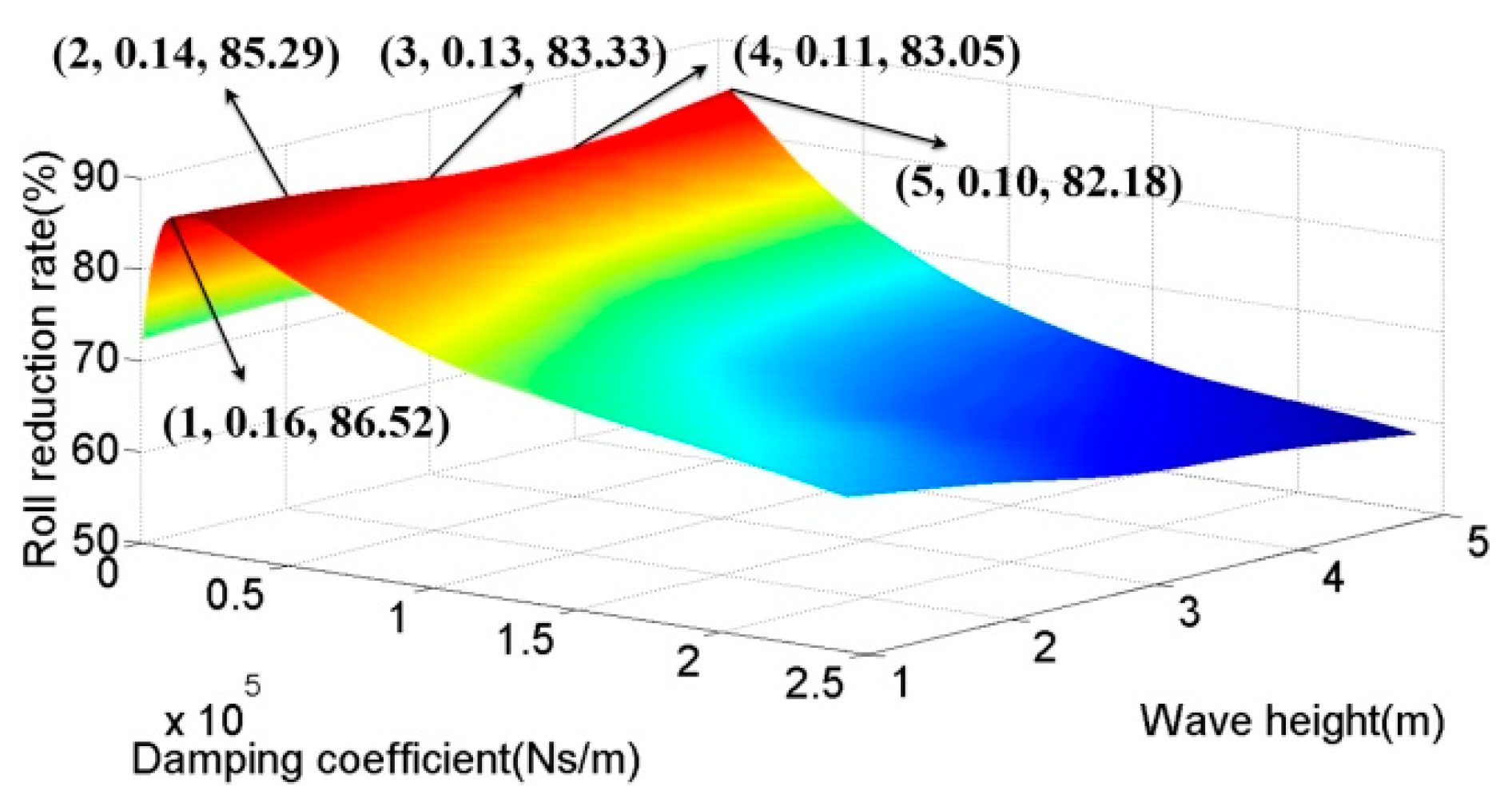
3.1. Influence of Gyro’s Damping Coefficient on Roll Reduction Rate
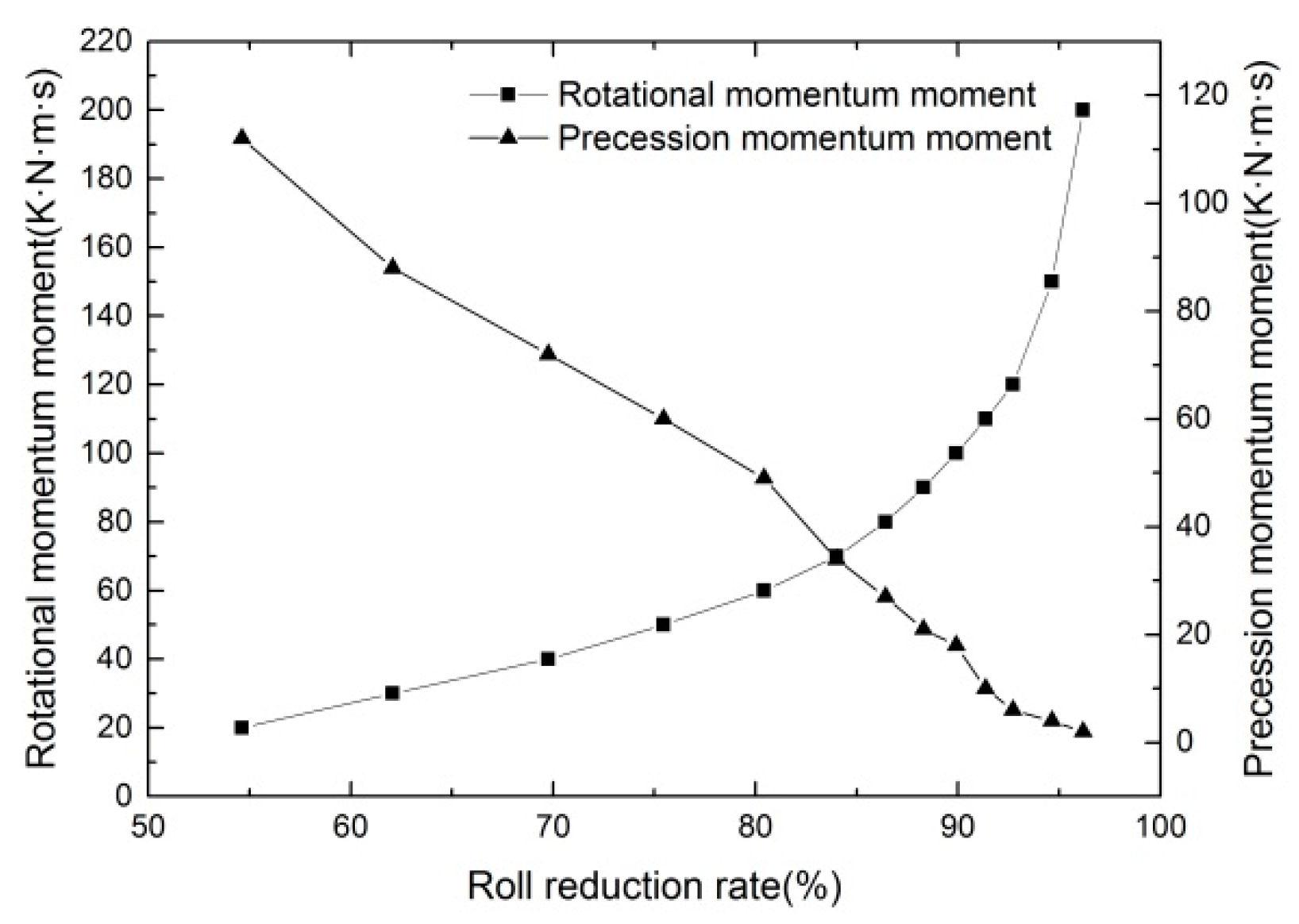
3.2. Influence of Rotational and Precession Momentum Moment on Roll Reduction Rate
4. Mathematical Model for Parameter Optimization of Antiroll Gyro
4.1. Establishing the Mathematical Model of the Ship Roll Reduction Rate
Expression of Ship Roll Reduction Rate
4.2. Objective Functions
4.3. Constraint Conditions
5. Comparative Analysis of Parameter Optimization Results
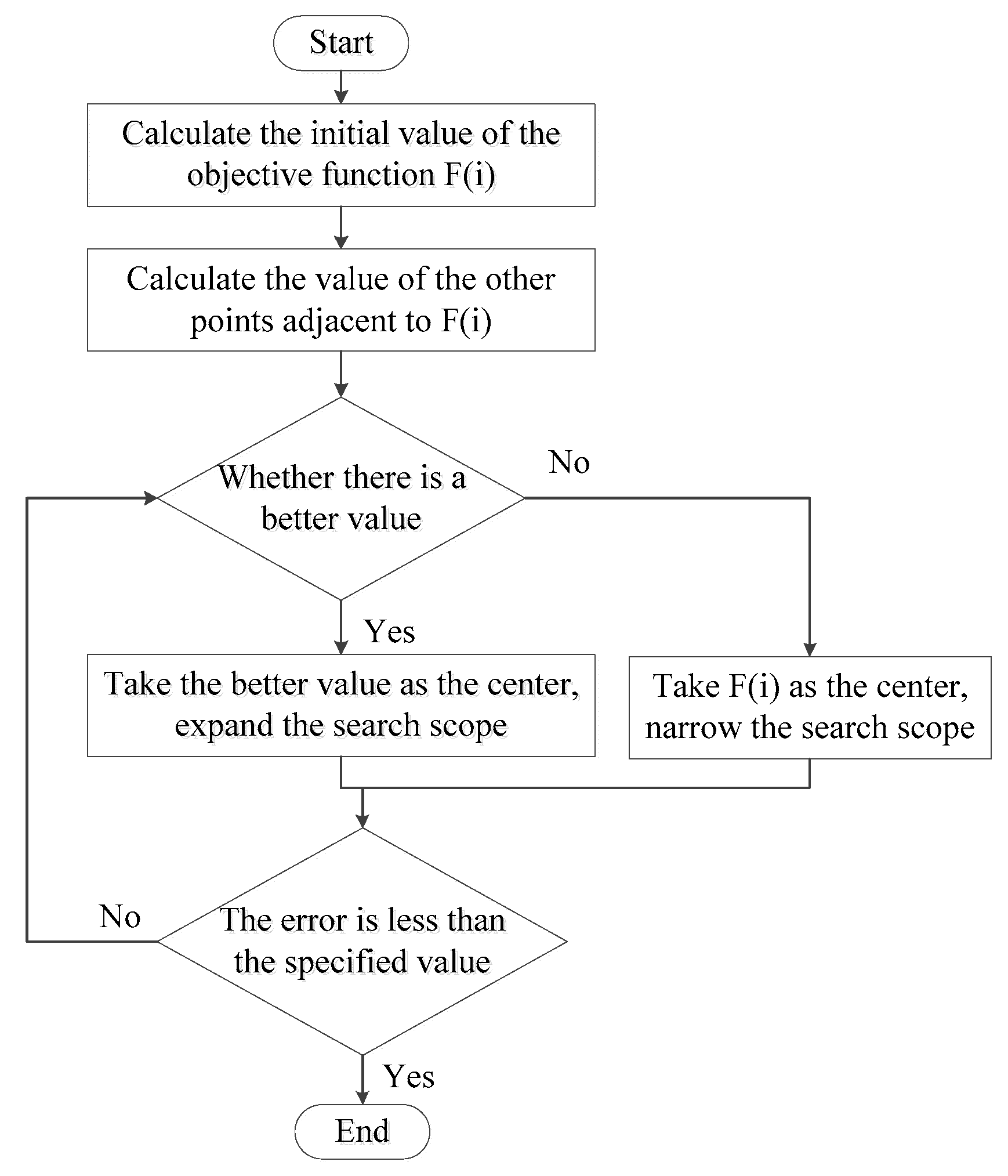
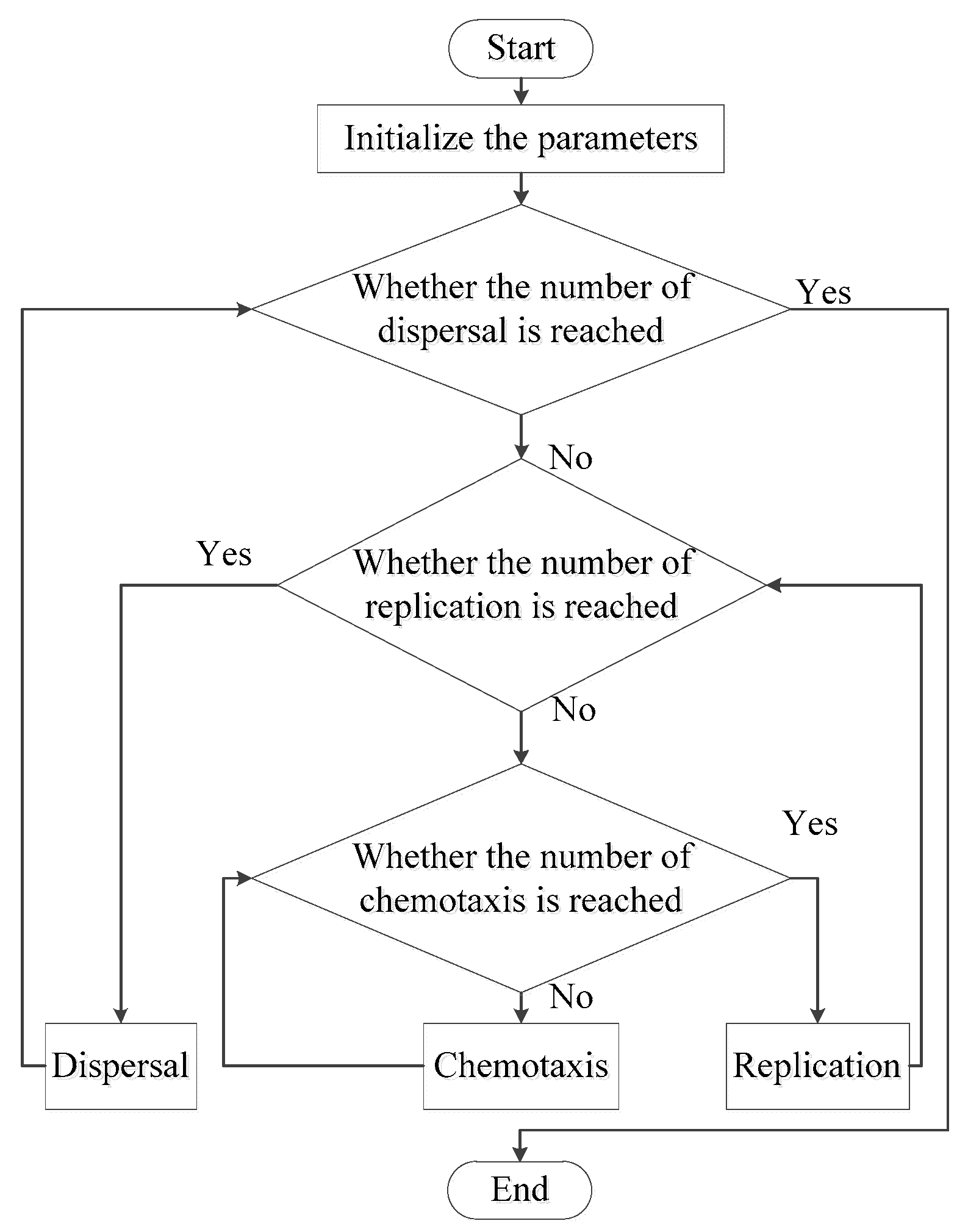
5.1. Principles of PSOA and BFOA
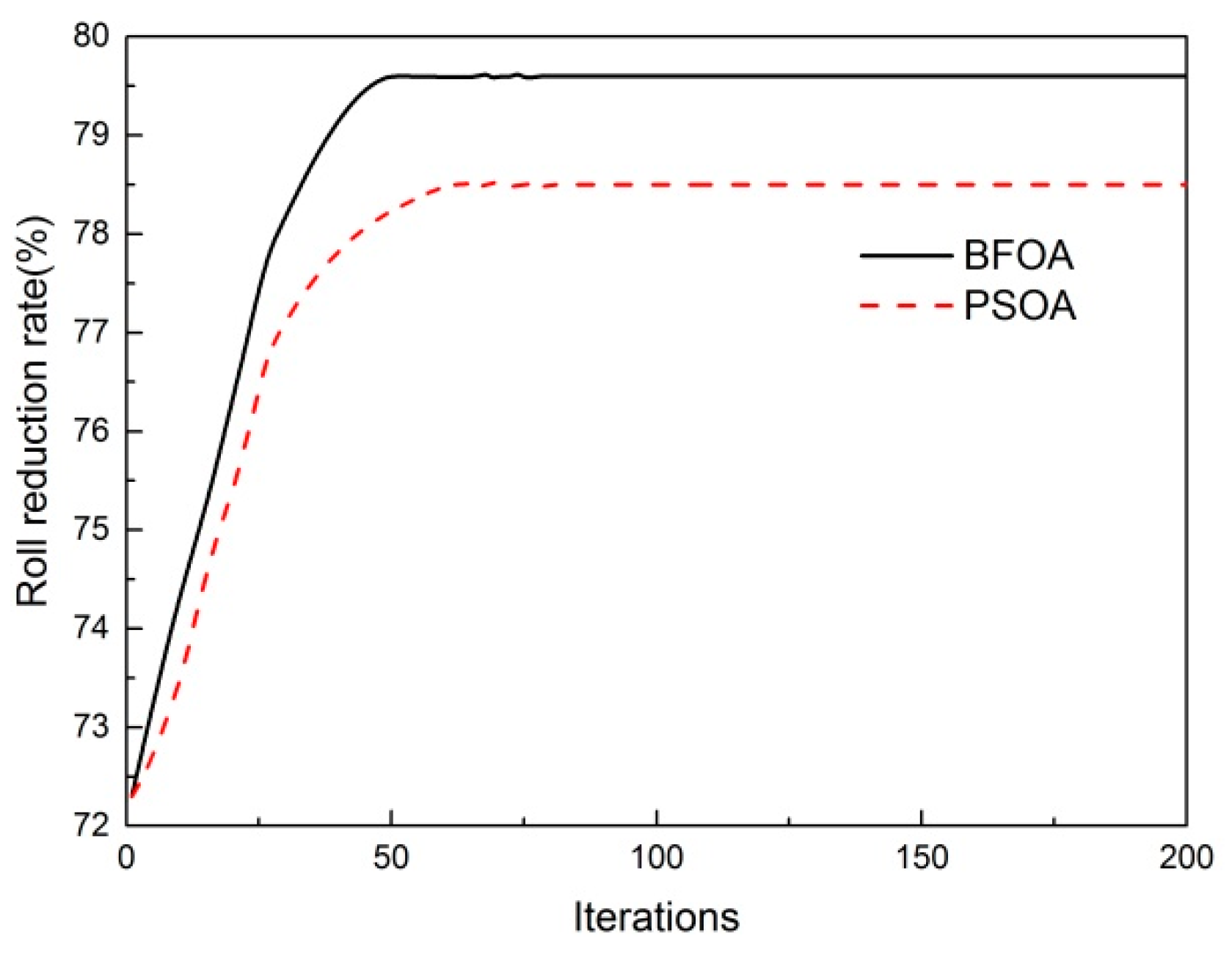
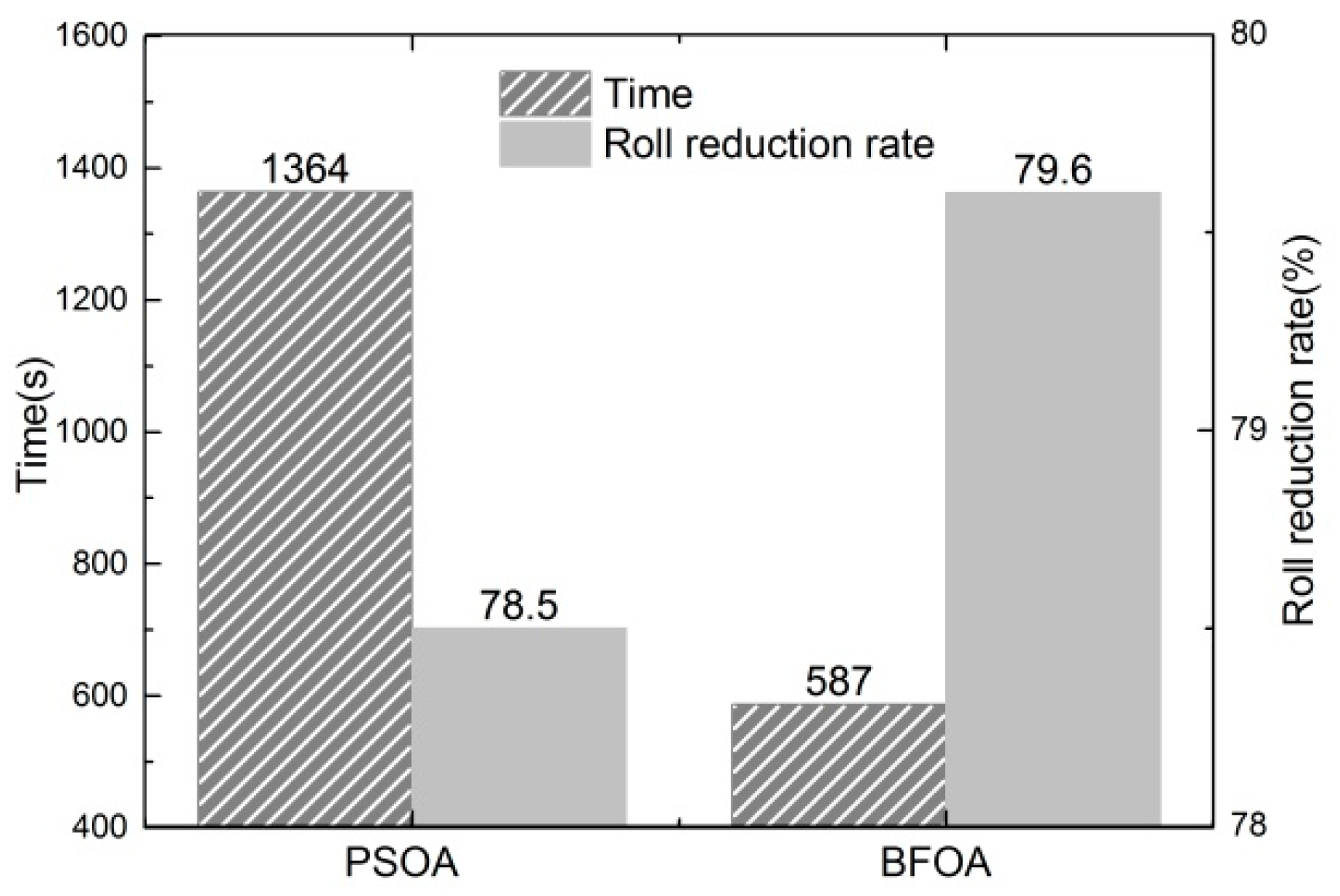
5.2. Results and Analysis of the Highest Roll Reduction Rate
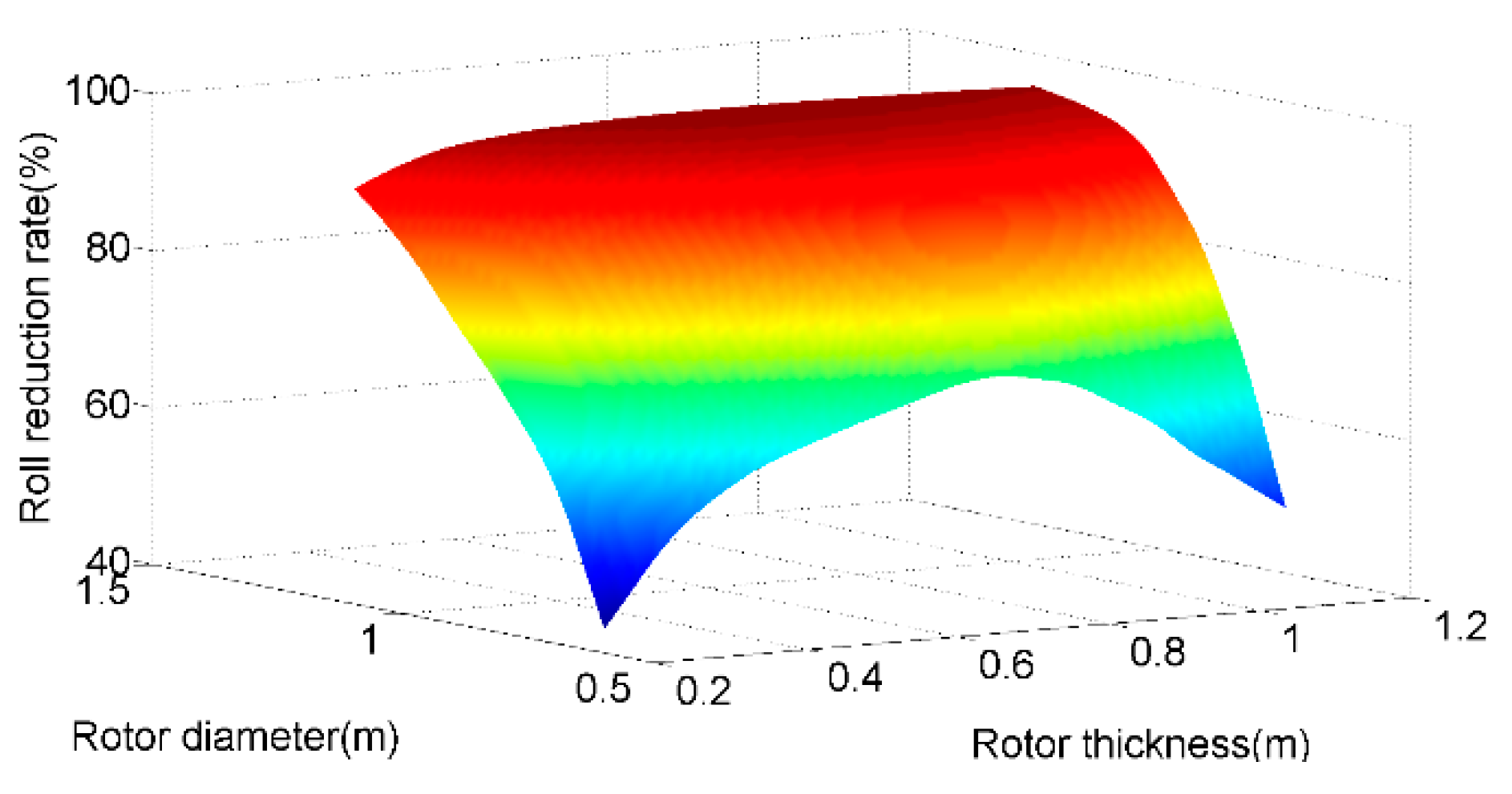
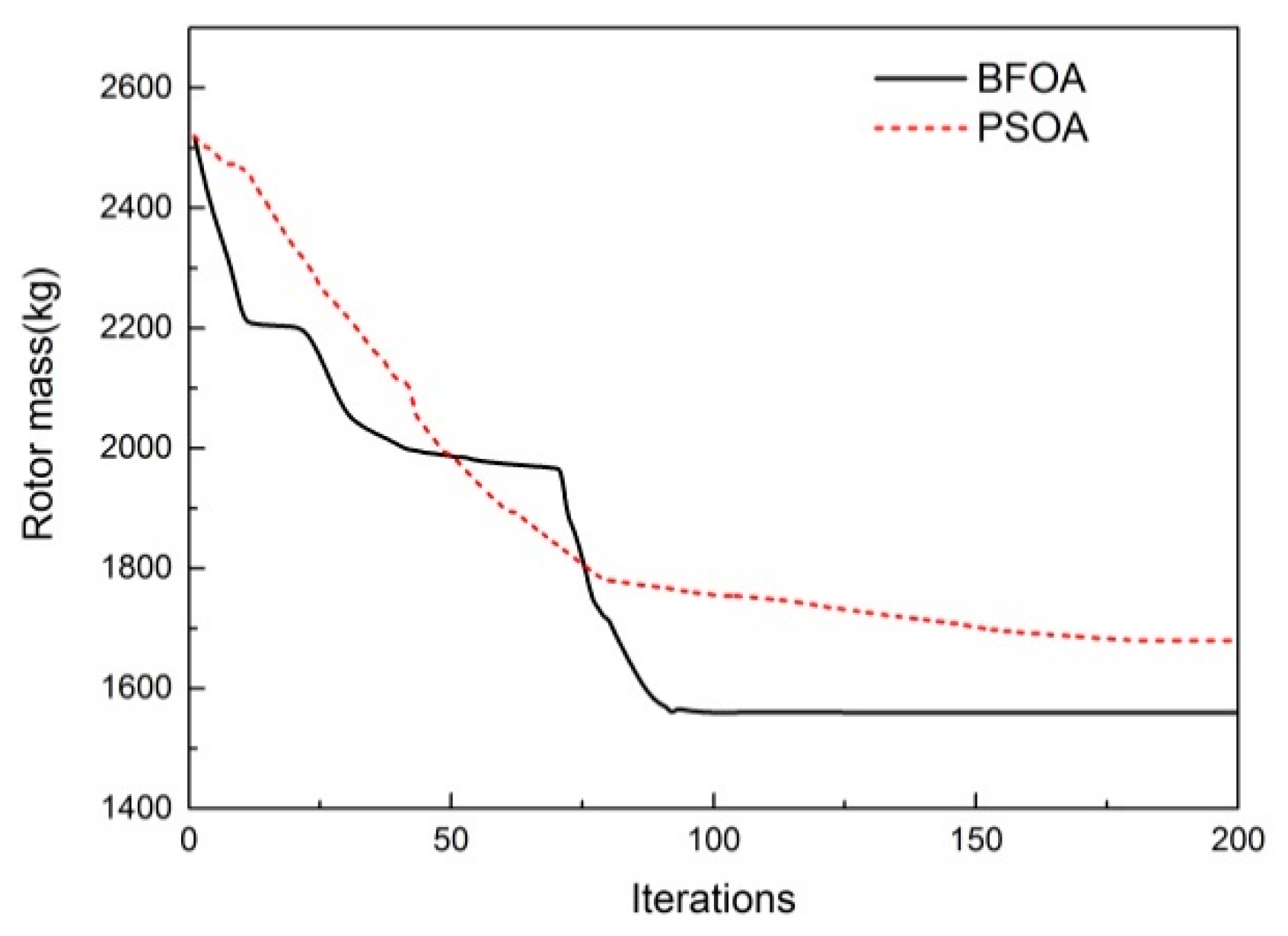
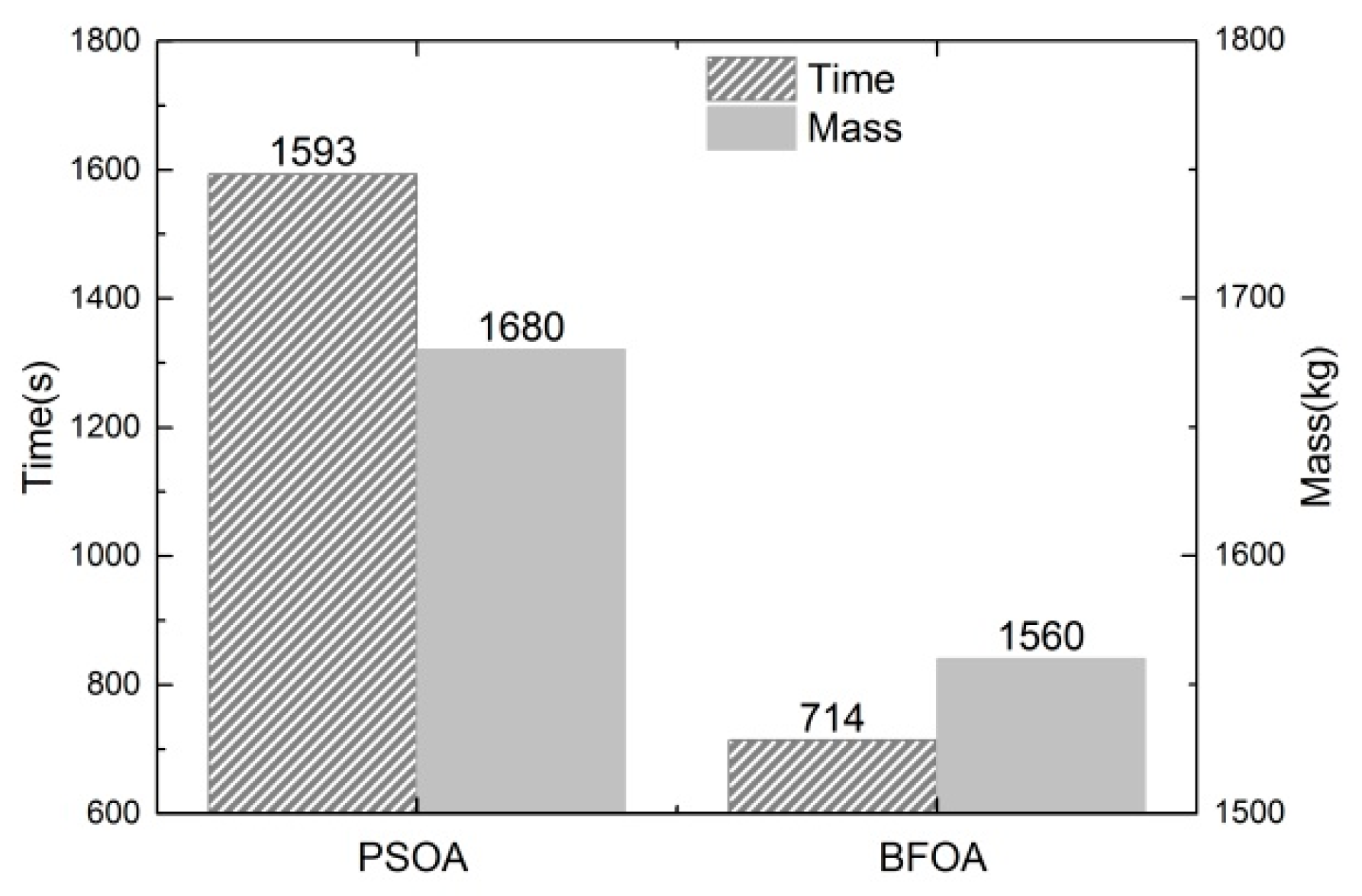
5.3. Results and Analysis of the Minimum Rotor Mass
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, L.; Zhao, P.; Zhang, S.; Ji, M.; Yuan, J. Simulation analysis of fin stabilizer on ship roll control during turning motion. Ocean Eng. 2018, 164, 733–748. [Google Scholar]
- Perez, T.; Blanke, M. Ship roll damping control. Annu. Rev. Control 2012, 36, 129–147. [Google Scholar] [CrossRef]
- Poh, K.B.; Tang, H.H.; Kang, H.S. Gyroscopic stabilisation of rolling motion in simplified marine hull model. In Proceedings of the IEEE International Conference on Underwater System Technology: Theory & Applications, Kuala Lumpur, Malaysia, 18–20 December 2017. [Google Scholar]
- Schlick, E.O. Device for Minimizing the Oscillatory Movements of Ships. U.S. Patent 769,493, 6 September 1904. [Google Scholar]
- Norden, C.L. Gyroscope Stabilizer. U.S. Patent 1,236,204, 7 August 1917. [Google Scholar]
- Thompson, H.H. Controlling and Braking Device for Ship’s Gyroscopes. U.S. Patent 1,558,720, 27 October 1925. [Google Scholar]
- Perez, T.; Steinmann, P. Advances in Gyro-Stabilisation of Vessel Roll Motion. In Proceedings of the International Maritime Conference, Sydney, Australia, 29–31 January 2008; Royal Institution of Naval Architects (RINA): London, UK, 2008; pp. 682–692. [Google Scholar]
- Perez, T.; Steinmann, P. Analysis of ship roll gyrostabiliser control. IFAC Proc. Vol. 2009, 42, 310–315. [Google Scholar] [CrossRef]
- Donaire, A.; Perez, T. Energy-based Nonlinear Control of Ship Roll Gyro-stabiliser with Precession Angle Constraints. IFAC Proc. Vol. 2013, 46, 328–333. [Google Scholar] [CrossRef]
- Lavieri, R.S.; Getschko, N.; Tannuri, E.A. Roll Stabilization Control System by Sliding Mode. IFAC Proc. Vol. 2012, 45, 447–452. [Google Scholar] [CrossRef]
- Townsend, N.C.; Murphy, A.J.; Shenoi, R.A. A new active gyrostabiliser system for ride control of marine vehicles. Ocean Eng. 2007, 34, 1607–1617. [Google Scholar] [CrossRef]
- Pourzeynali, S.; Salimi, S.; Kalesar, H.E. Robust multi-objective optimization design of TMD control device to reduce tall building responses against earthquake excitations using genetic algorithms. Sci. Iran. 2013, 20, 207–221. [Google Scholar]
- Siami, A.; Karimi, H.R.; Cigada, A. Parameter optimization of an inerter-based isolator for passive vibration control of Michelangelo’s Rondanini Pietà. Mech. Syst. Signal Process. 2018, 98, 667–683. [Google Scholar] [CrossRef]
- Jin, X.; Xie, S.; He, J. Optimization of tuned mass damper parameters for floating wind turbines by using the artificial fish swarm algorithm. Ocean Eng. 2018, 167, 130–141. [Google Scholar] [CrossRef]
- Choi, S.J.; Lee, D.; Kim, I.K. Trajectory optimization for a lunar orbiter using a pattern search method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 1325–1337. [Google Scholar] [CrossRef]
- Kumar, M.S.; Mahadevan, K. A novel methodology based on bacterial foraging technique in paper industry and marine application. Indian J. Mar. Sci. 2016, 45, 1372–1376. [Google Scholar]
- Gao, J.; Dai, L.; Zhang, W. Improved genetic optimization algorithm with subdomain model for multi-objective optimal design of spmsm. CES Trans. Electr. Mach. Syst. 2018, 2, 160–165. [Google Scholar]
- Tan, X.D.; Kong, L.H.; Li, D.R. Research on intelligent optimization algorithm for the hot press insulation of generator stator bar. Appl. Mech. Mater. 2017, 868, 265–270. [Google Scholar] [CrossRef]
- Ya, L.; Zekun, C.; Qinqin, N. Dynamic response of pile-cap structure under random sea wave action. Procedia Eng. 2015, 116, 1027–1035. [Google Scholar] [CrossRef][Green Version]
- Kubo, T.; Umeda, N.; Izawa, S.; Matsuda, A. Total Stability Failure Probability of a Ship in Beam Wind and Waves: Model Experiment and Numerical Simulation: Risk of Capsizing. In Contemporary Ideas on Ship Stability; Springer: New York, NY, USA, 2019; Volume 35, pp. 591–603. [Google Scholar]
- Allievi, A.; Soudack, A. Ship stability via the mathieu equation. Int. J. Control 1990, 51, 139–167. [Google Scholar] [CrossRef]
- Hou, X.R.; Zou, Z.J. Parameter identification of nonlinear roll motion equation for floating structures in irregular waves. Appl. Ocean Res. 2016, 55, 66–75. [Google Scholar] [CrossRef]
- Roe, P.L. Characteristic-based schemes for the euler equations. Annu. Rev. Fluid Mech. 2003, 18, 337–365. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Total length (m) | 44.8 | Ship’s roll-damping coefficient (Ns/m) | 843 |
| Molded breadth (m) | 8.9 | Ship’s roll-damping coefficient (Ns/m) | 6589 |
| Molded depth (m) | 4 | Roll-restoring moment coefficient (Ns2/m) | 10,791 |
| Displacement (t) | 594 | Roll-restoring moment coefficient (Ns2/m) | –9284 |
| Initial metacentric height (m) | 1.09 | Roll-restoring moment coefficient (Ns2/m) | 894 |
| Total moment of inertia (Nms2) | 6 × 106 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
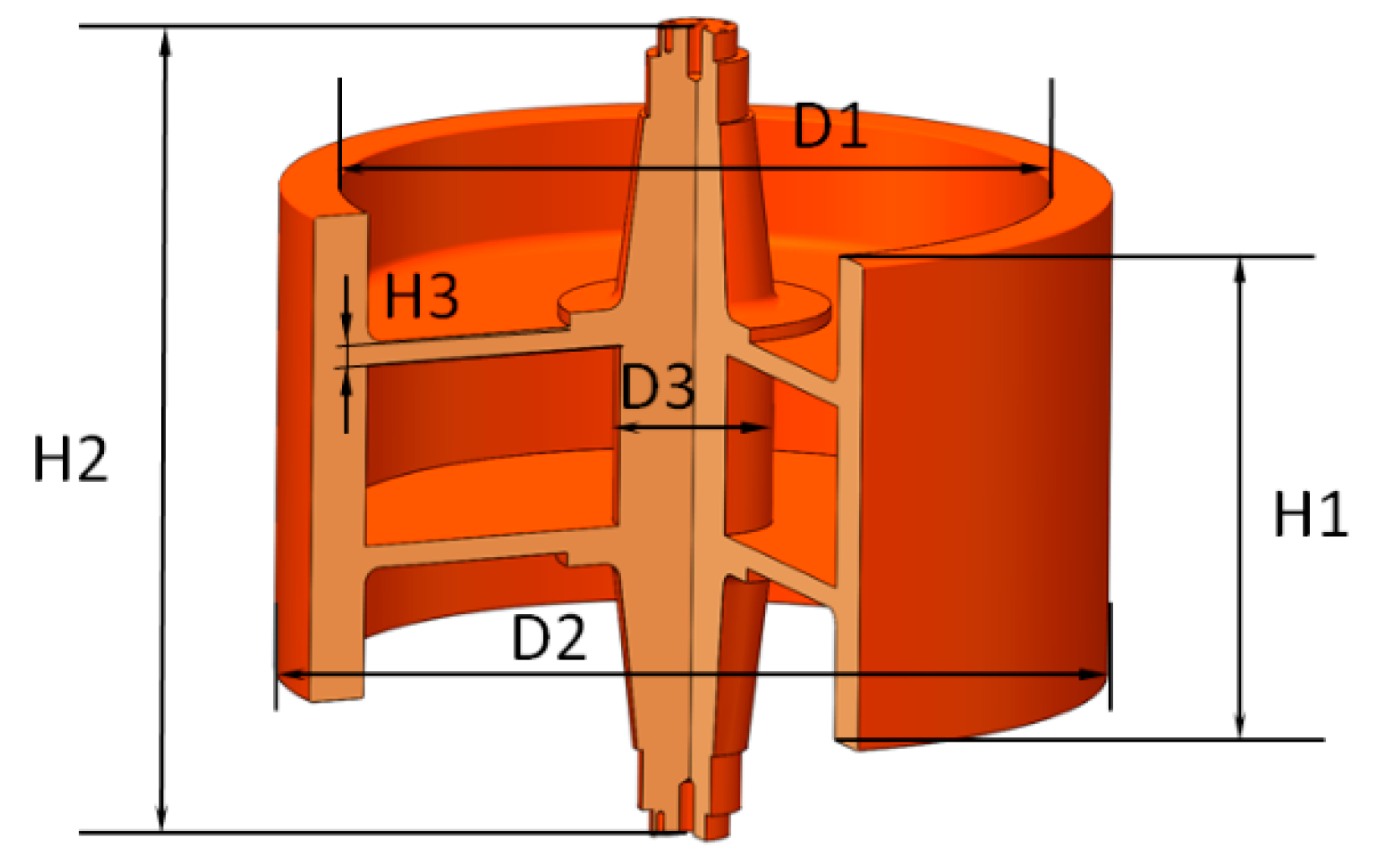
| Rotor inner diameter (m) | 1.07 | Gyro’s damping coefficient (Ns/m) | 25,300 |
| Rotor outer diameter (m) | 1.24 | Motor speed (r/min) | 1255 |
| Rotor shaft diameter (m) | 0.18 | Rotor material density (kg/m3) | 7850 |
| Rotor thickness (m) | 0.70 | Rotational momentum moment (Nms) | 104,100 |
| Shaft length (m) | 1.05 | Precession momentum moment (Nms) | 25,100 |
| Ribbed plate thickness (m) | 0.05 |
| Parameter | Before Optimization | After Optimization | Variation | Changing Rate |
|---|---|---|---|---|
| Inner diameter (m) | 1.070 | 1.104 | +0.034 | +3.2% |
| Outer diameter (m) | 1.240 | 1.233 | −0.007 | −0.6% |
| Shaft diameter (m) | 0.180 | 0.176 | −0.004 | −2.2% |
| Rotor thickness (m) | 0.700 | 0.718 | +0.018 | +2.6% |
| Ribbed plate thickness (m) | 0.050 | 0.045 | −0.005 | −10.0% |
| Gyro’s damping coefficient (Ns/m) | 25,300 | 28,648 | +3348 | +13.2% |
| Motor speed (r/min) | 1255 | 1300 | +45 | +3.6% |
| Mass (kg) | 2520 | 2000 | −520 | −20.6% |
| Roll reduction rate (%) | 73.7 | 79.6 | +5.9 | +8.0% |
| Parameter | Before Optimization | After Optimization | Variation | Changing Rate |
|---|---|---|---|---|
| Inner diameter (m) | 1.070 | 1.200 | +0.130 | +12.1% |
| Outer diameter (m) | 1.240 | 1.263 | +0.023 | +1.9% |
| Shaft diameter (m) | 0.180 | 0.150 | −0.030 | −16.7% |
| Rotor thickness (m) | 0.700 | 0.500 | −0.200 | −28.6% |
| Ribbed plate thickness (m) | 0.050 | 0.058 | +0.008 | +16.0% |
| Gyro’s damping coefficient (Ns/m) | 25,300 | 27,419 | +2119 | +8.4% |
| Motor speed (r/min) | 1255 | 1300 | +45 | +3.6% |
| Mass (kg) | 2520 | 1560 | −960 | −38.1% |
| Roll reduction rate (%) | 73.7 | 75.1 | +1.4 | +1.9% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Su, S.; Qian, Y.; Chen, Y.; Tang, W. Parameter Optimization for Ship Antiroll Gyros. Appl. Sci. 2020, 10, 661. https://doi.org/10.3390/app10020661
Zhu Y, Su S, Qian Y, Chen Y, Tang W. Parameter Optimization for Ship Antiroll Gyros. Applied Sciences. 2020; 10(2):661. https://doi.org/10.3390/app10020661
Chicago/Turabian StyleZhu, Yuanyuan, Shijie Su, Yuchen Qian, Yun Chen, and Wenxian Tang. 2020. "Parameter Optimization for Ship Antiroll Gyros" Applied Sciences 10, no. 2: 661. https://doi.org/10.3390/app10020661
APA StyleZhu, Y., Su, S., Qian, Y., Chen, Y., & Tang, W. (2020). Parameter Optimization for Ship Antiroll Gyros. Applied Sciences, 10(2), 661. https://doi.org/10.3390/app10020661





