Recent Advances in Non-Traditional Elastic Wave Manipulation by Macroscopic Artificial Structures
Abstract
1. Introduction
2. Elastic Metamaterials
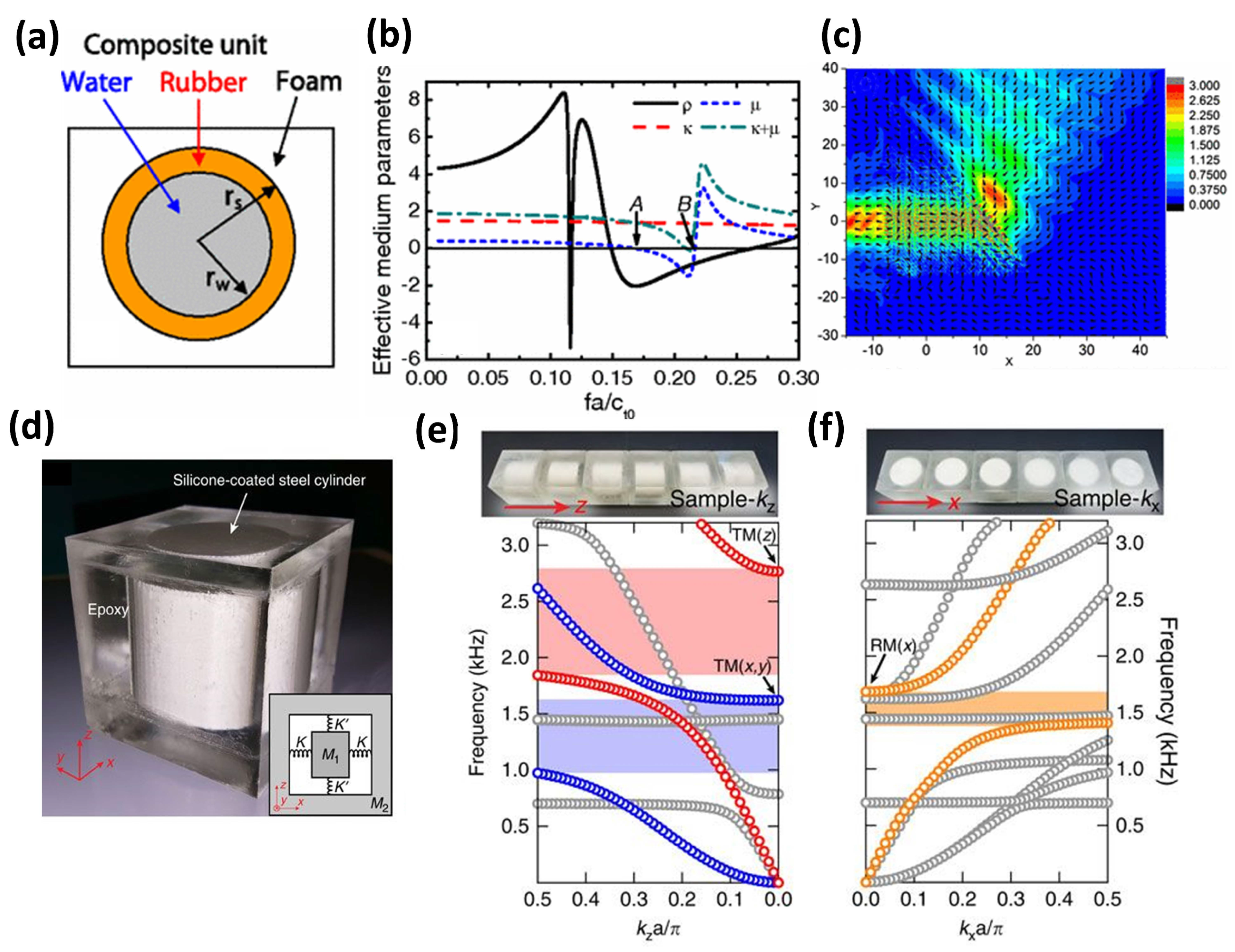
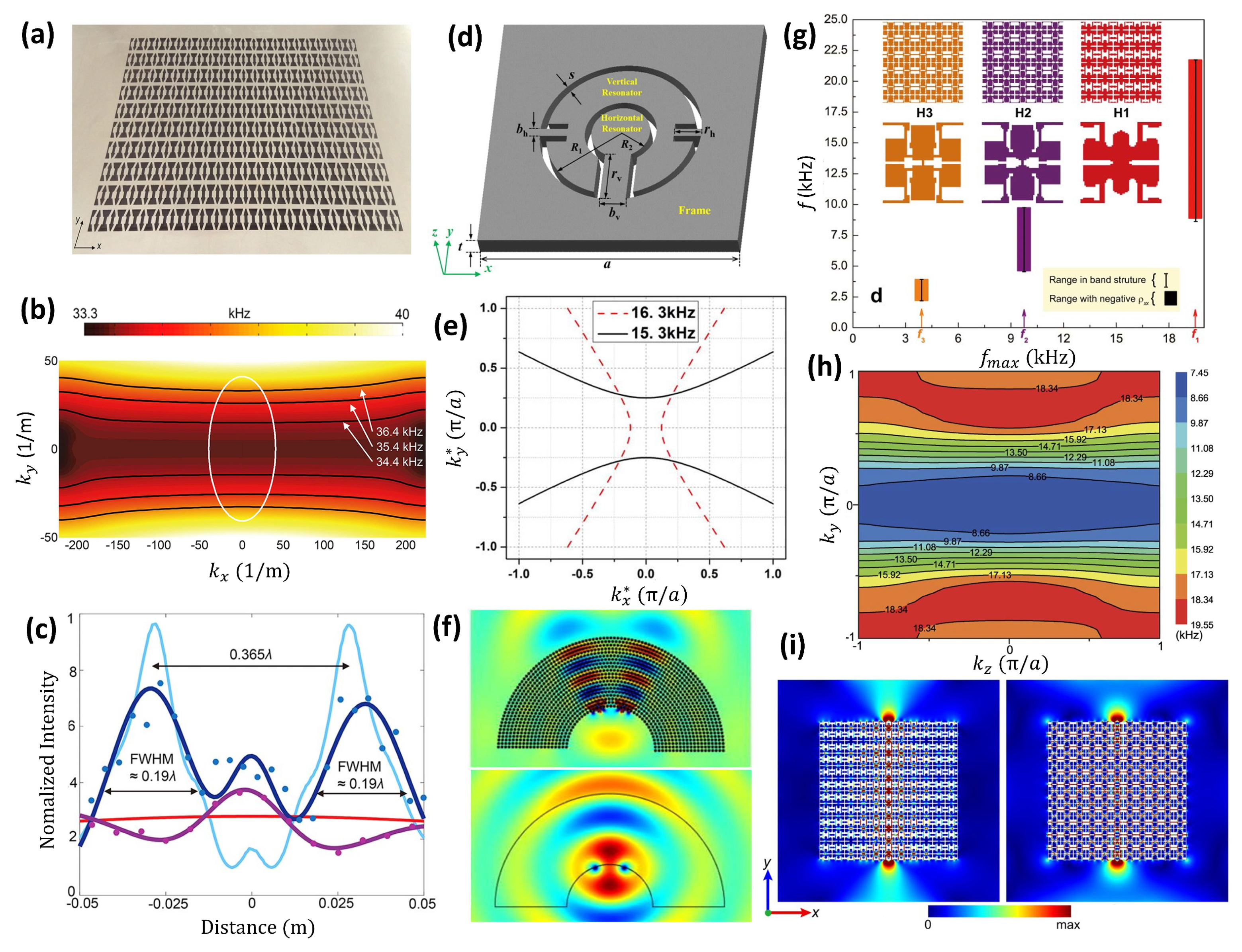
2.1. Representative Studies of Locally Resonant Elastic Metamaterials
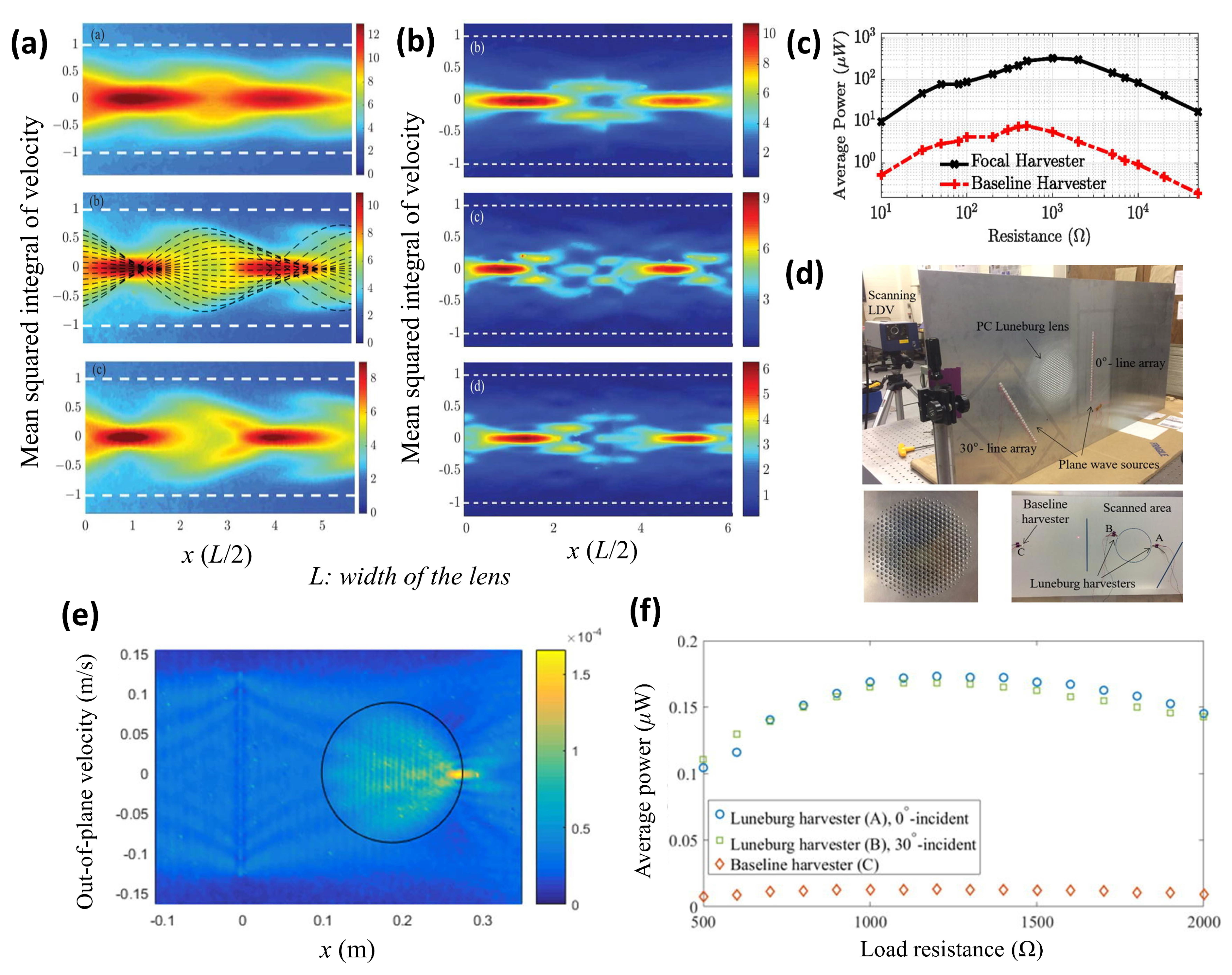
2.2. Elastic Gradient-Index Lens Using Phononic Crystals
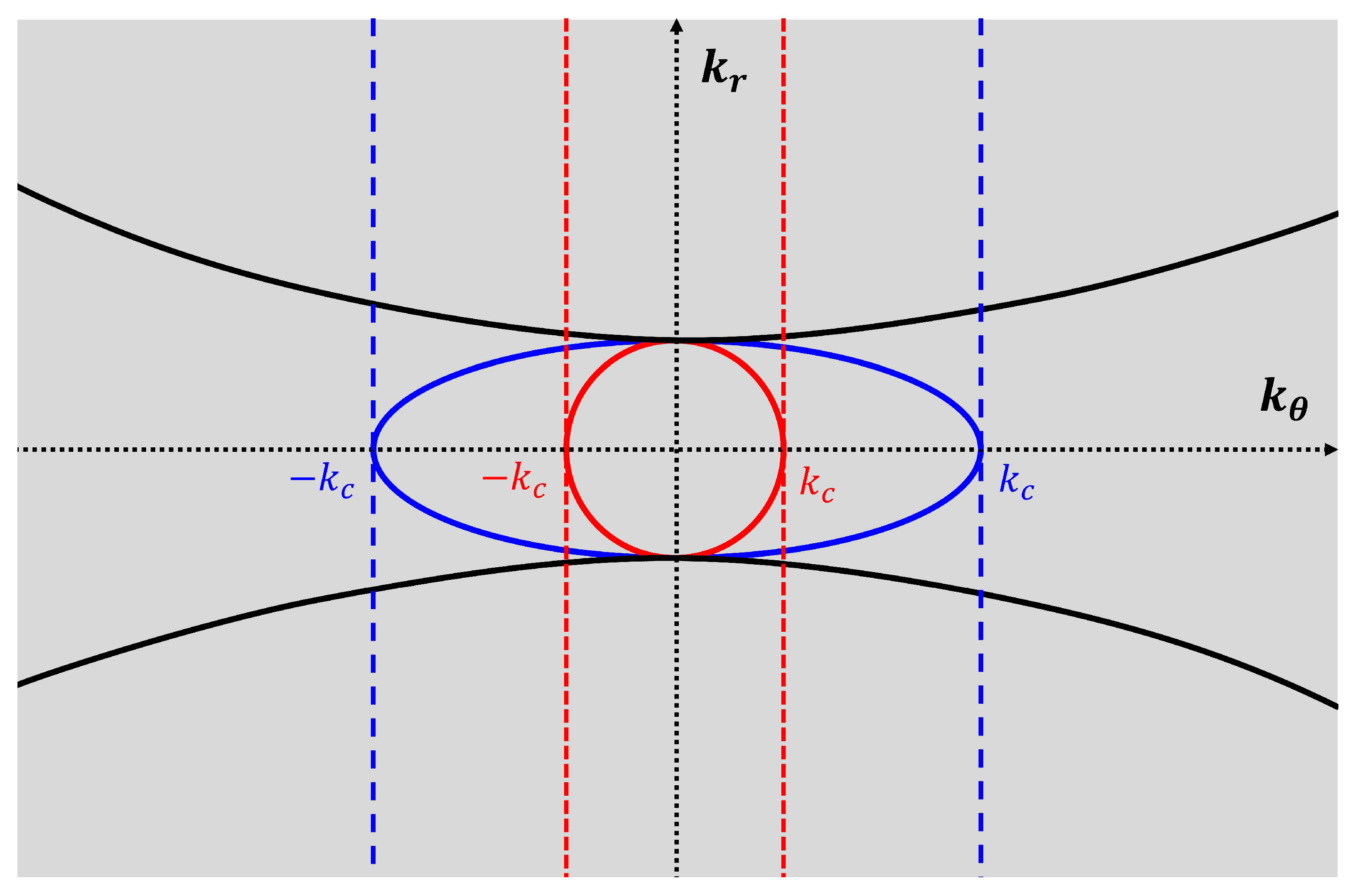
2.3. Elastic Hyperlens
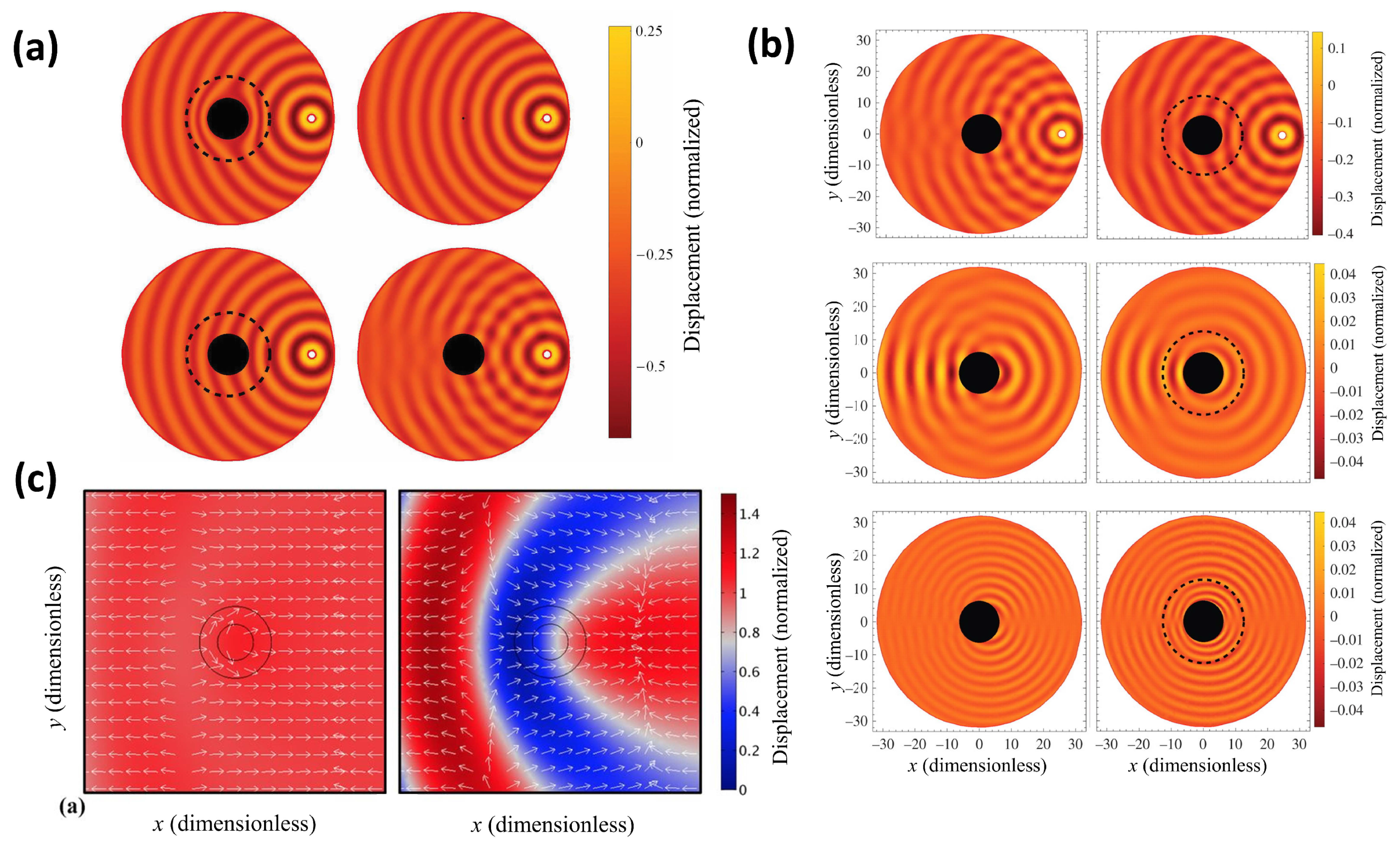
2.4. Cloaking Elastic Waves
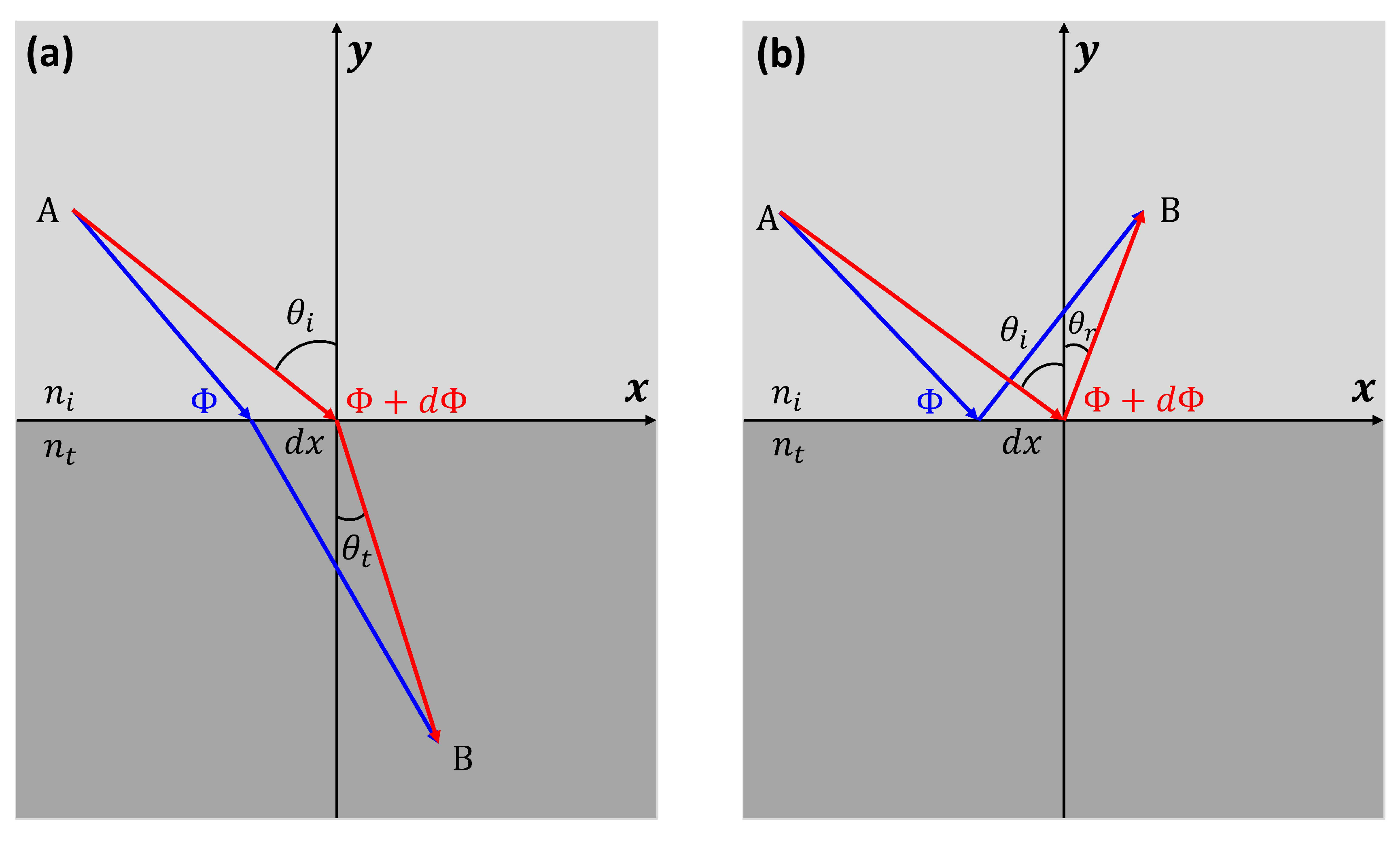
3. Elastic Metasurfaces
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veselago, V. Electrodynamics of substances with simultaneously negative and. Usp. Fiz. Nauk 1967, 92, 517. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.; Stewart, W.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76, 4773. [Google Scholar] [CrossRef]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub–diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z. Superlenses to overcome the diffraction limit. Nat. Mater. 2008, 7, 435. [Google Scholar] [CrossRef]
- Rogers, E.T.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224. [Google Scholar] [CrossRef]
- Li, J.; Pendry, J.B. Hiding under the carpet: A new strategy for cloaking. Phys. Rev. Lett. 2008, 101, 203901. [Google Scholar] [CrossRef]
- Valentine, J.; Li, J.; Zentgraf, T.; Bartal, G.; Zhang, X. An optical cloak made of dielectrics. Nat. Mater. 2009, 8, 568. [Google Scholar] [CrossRef]
- Lal, S.; Link, S.; Halas, N.J. Nano-optics from sensing to waveguiding. Nat. Photonics 2007, 1, 641. [Google Scholar] [CrossRef]
- O’Hara, J.F.; Singh, R.; Brener, I.; Smirnova, E.; Han, J.; Taylor, A.J.; Zhang, W. Thin-film sensing with planar terahertz metamaterials: Sensitivity and limitations. Opt. Express 2008, 16, 1786–1795. [Google Scholar] [CrossRef]
- Kabashin, A.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.; Atkinson, R.; Pollard, R.; Podolskiy, V.; Zayats, A. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742–2765. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Nguyen, D.M.; Rho, J. Acoustic wave science realized by metamaterials. Nano Converg. 2017, 4, 3. [Google Scholar] [CrossRef]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, X.; Hu, G.; Yuan, F.; Huang, G. Microstructural designs of plate-type elastic metamaterial and their potential applications: A review. Int. J. Smart Nano Mater. 2015, 6, 14–40. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Ardito, R.; Braghin, F.; Corigliano, A. Low frequency 3D ultra-wide vibration attenuation via elastic metamaterial. Sci. Rep. 2019, 9, 8039. [Google Scholar] [CrossRef]
- Oh, J.H.; Assouar, B. Quasi-static stop band with flexural metamaterial having zero rotational stiffness. Sci. Rep. 2016, 6, 33410. [Google Scholar] [CrossRef]
- Chen, Y.; Qian, F.; Zuo, L.; Scarpa, F.; Wang, L. Broadband and multiband vibration mitigation in lattice metamaterials with sinusoidally-shaped ligaments. Extreme Mech. Lett. 2017, 17, 24–32. [Google Scholar] [CrossRef]
- Nobrega, E.; Gautier, F.; Pelat, A.; Dos Santos, J. Vibration band gaps for elastic metamaterial rods using wave finite element method. Mech. Syst. Signal Proc. 2016, 79, 192–202. [Google Scholar] [CrossRef]
- Baravelli, E.; Ruzzene, M. Internally resonating lattices for bandgap generation and low-frequency vibration control. J. Sound Vibr. 2013, 332, 6562–6579. [Google Scholar] [CrossRef]
- Sugino, C.; Ruzzene, M.; Erturk, A. Merging mechanical and electromechanical bandgaps in locally resonant metamaterials and metastructures. J. Mech. Phys. Solids 2018, 116, 323–333. [Google Scholar] [CrossRef]
- Attarzadeh, M.; Nouh, M.; Al Ba’ba’a, H. Experimental evaluation of structural intensity in two-dimensional plate-type locally resonant elastic metamaterials. J. Appl. Mech. 2018, 85, 4. [Google Scholar]
- Al Ba’ba’a, H.; Callanan, J.; Nouh, M. Emergence of Pseudo-Phononic Gaps in Periodically Architected Pendulums. Front. Mater. 2019, 6, 119. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, G.; Sun, C. Band gap control in an active elastic metamaterial with negative capacitance piezoelectric shunting. J. Vib. Acoust. 2014, 136, 061008. [Google Scholar] [CrossRef]
- Nouh, M.A.; Aldraihem, O.J.; Baz, A. Periodic metamaterial plates with smart tunable local resonators. J. Intell. Mater. Syst. Struct. 2016, 27, 1829–1845. [Google Scholar] [CrossRef]
- Zhu, R.; Chen, Y.; Barnhart, M.; Hu, G.; Sun, C.; Huang, G. Experimental study of an adaptive elastic metamaterial controlled by electric circuits. Appl. Phys. Lett. 2016, 108, 011905. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, G. Active elastic metamaterials for subwavelength wave propagation control. Acta Mech. Sin. 2015, 31, 349–363. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, R.; Huang, G.; Yuan, F.G. Focusing guided waves using surface bonded elastic metamaterials. Appl. Phys. Lett. 2013, 103, 121901. [Google Scholar] [CrossRef]
- Chen, J.S.; Su, W.J.; Cheng, Y.; Li, W.C.; Lin, C.Y. A metamaterial structure capable of wave attenuation and concurrent energy harvesting. J. Intell. Mater. Syst. Struct. 2019, 30, 2973–2981. [Google Scholar] [CrossRef]
- Gonella, S.; To, A.C.; Liu, W.K. Interplay between phononic bandgaps and piezoelectric microstructures for energy harvesting. J. Mech. Phys. Solids 2009, 57, 621–633. [Google Scholar] [CrossRef]
- Hussein, M.I.; Frazier, M.J. Metadamping: An emergent phenomenon in dissipative metamaterials. J. Sound Vibr. 2013, 332, 4767–4774. [Google Scholar] [CrossRef]
- Pope, S.A.; Daley, S. Viscoelastic locally resonant double negative metamaterials with controllable effective density and elasticity. Phys. Lett. A 2010, 374, 4250–4255. [Google Scholar] [CrossRef]
- Brûlé, S.; Javelaud, E.H.; Enoch, S.; Guenneau, S. Experiments on seismic metamaterials: Molding surface waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef]
- Palermo, A.; Krödel, S.; Marzani, A.; Daraio, C. Engineered metabarrier as shield from seismic surface waves. Sci. Rep. 2016, 6, 39356. [Google Scholar] [CrossRef]
- Achaoui, Y.; Antonakakis, T.; Brule, S.; Craster, R.; Enoch, S.; Guenneau, S. Clamped seismic metamaterials: Ultra-low frequency stop bands. New J. Phys. 2017, 19, 063022. [Google Scholar] [CrossRef]
- Colombi, A.; Roux, P.; Guenneau, S.; Gueguen, P.; Craster, R.V. Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 2016, 6, 19238. [Google Scholar] [CrossRef]
- Colombi, A.; Colquitt, D.; Roux, P.; Guenneau, S.; Craster, R.V. A seismic metamaterial: The resonant metawedge. Sci. Rep. 2016, 6, 27717. [Google Scholar] [CrossRef]
- Colquitt, D.; Colombi, A.; Craster, R.; Roux, P.; Guenneau, S. Seismic metasurfaces: Sub-wavelength resonators and Rayleigh wave interaction. J. Mech. Phys. Solids 2017, 99, 379–393. [Google Scholar] [CrossRef]
- Brûlé, S.; Enoch, S.; Guenneau, S. Emergence of seismic metamaterials: Current state and future perspectives. Phys. Lett. A 2020, 384, 126034. [Google Scholar] [CrossRef]
- Lee, D.; Oh, J.H.; Kang, I.S.; Rho, J. Seismic phononic crystals by elastodynamic Navier equation. Phys. Rev. E 2019, 100, 063002. [Google Scholar] [CrossRef]
- Bacquet, C.L.; Ba’ba’a, H.A.; Frazier, M.J.; Nouh, M.; Hussein, M.I. Metadamping: Dissipation Emergence in Elastic Metamaterials. In Advances in Crystals and Elastic Metamaterials, Part 1; Hussein, M.I., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; Volume 51, pp. 115–164. [Google Scholar]
- Wang, Y.F.; Wang, Y.S.; Laude, V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 2015, 92, 104110. [Google Scholar] [CrossRef]
- Attarzadeh, M.; Nouh, M. Non-reciprocal elastic wave propagation in 2D phononic membranes with spatiotemporally varying material properties. J. Sound Vibr. 2018, 422, 264–277. [Google Scholar] [CrossRef]
- Nassar, H.; Chen, H.; Norris, A.N.; Haberman, M.R.; Huang, G.L. Non-reciprocal wave propagation in modulated elastic metamaterials. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2017, 473, 20170188. [Google Scholar] [CrossRef]
- Attarzadeh, M.; Callanan, J.; Nouh, M. Experimental Observation of Non-reciprocal Waves in a Resonant Metamaterial Beam. arXiv 2019, arXiv:1910.08765. [Google Scholar]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef]
- Attarzadeh, M.A.; Maleki, S.; Crassidis, J.L.; Nouh, M. Non-reciprocal wave phenomena in energy self-reliant gyric metamaterials. J. Acoust. Soc. Am. 2019, 146, 789–801. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological Phononic Crystals with One-Way Elastic Edge Waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.Q. Effective medium theory for elastic metamaterials in two dimensions. Phys. Rev. B 2007, 76, 205313. [Google Scholar] [CrossRef]
- Torrent, D.; Pennec, Y.; Djafari-Rouhani, B. Effective medium theory for elastic metamaterials in thin elastic plates. Phys. Rev. B 2014, 90, 104110. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, H.S.; Ma, P.S.; Kim, Y.Y. Effective material parameter retrieval of anisotropic elastic metamaterials with inherent nonlocality. J. Appl. Phys. 2016, 120, 104902. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, Y.; Sheng, P.; Zhang, Z.Q. Hybrid elastic solids. Nat. Mater. 2011, 10, 620. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lai, Y.; Zhang, Z.Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Liu, X.; Hu, G.; Sun, C.; Huang, G. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 2014, 5, 5510. [Google Scholar] [CrossRef]
- Ma, G.; Fu, C.; Wang, G.; Del Hougne, P.; Christensen, J.; Lai, Y.; Sheng, P. Polarization bandgaps and fluid-like elasticity in fully solid elastic metamaterials. Nat. Commun. 2016, 7, 13536. [Google Scholar] [CrossRef]
- Lucklum, R. Phononic Crystals and Metamaterials–Promising New Sensor Platforms. Procedia Eng. 2014, 87, 40–45. [Google Scholar] [CrossRef]
- Lu, M.H.; Feng, L.; Chen, Y.F. Phononic crystals and acoustic metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Lucklum, R.; Li, J. Phononic crystals for liquid sensor applications. Meas. Sci. Technol. 2009, 20, 124014. [Google Scholar] [CrossRef]
- Lucklum, R.; Ke, M.; Zubtsov, M. Two-dimensional phononic crystal sensor based on a cavity mode. Sens. Actuator B-Chem. 2012, 171, 271–277. [Google Scholar] [CrossRef]
- Zubtsov, M.; Lucklum, R.; Ke, M.; Oseev, A.; Grundmann, R.; Henning, B.; Hempel, U. 2D phononic crystal sensor with normal incidence of sound. Sens. Actuator A-Phys. 2012, 186, 118–124. [Google Scholar] [CrossRef]
- Oseev, A.; Zubtsov, M.; Lucklum, R. Gasoline properties determination with phononic crystal cavity sensor. Sens. Actuator B-Chem. 2013, 189, 208–212. [Google Scholar] [CrossRef]
- Khelif, A.; Deymier, P.A.; Djafari-Rouhani, B.; Vasseur, J.; Dobrzynski, L. Two-dimensional phononic crystal with tunable narrow pass band: Application to a waveguide with selective frequency. J. Appl. Phys. 2003, 94, 1308–1311. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 2004, 69, 046608. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, Z.; Mei, J.; Shi, J. Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals. Appl. Phys. Lett. 2005, 87, 104101. [Google Scholar] [CrossRef]
- Khelif, A.; Choujaa, A.; Benchabane, S.; Djafari-Rouhani, B.; Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl. Phys. Lett. 2004, 84, 4400–4402. [Google Scholar] [CrossRef]
- Sun, J.H.; Wu, T.T. Propagation of surface acoustic waves through sharply bent two-dimensional phononic crystal waveguides using a finite-difference time-domain method. Phys. Rev. B 2006, 74, 174305. [Google Scholar] [CrossRef]
- Vasseur, J.; Hladky-Hennion, A.C.; Djafari-Rouhani, B.; Duval, F.; Dubus, B.; Pennec, Y.; Deymier, P.A. Waveguiding in two-dimensional piezoelectric phononic crystal plates. J. Appl. Phys. 2007, 101, 114904. [Google Scholar] [CrossRef]
- Lin, S.C.S.; Huang, T.J.; Sun, J.H.; Wu, T.T. Gradient-index phononic crystals. Phys. Rev. B 2009, 79, 094302. [Google Scholar] [CrossRef]
- Wu, T.T.; Chen, Y.T.; Sun, J.H.; Lin, S.C.S.; Huang, T.J. Focusing of the lowest antisymmetric Lamb wave in a gradient-index phononic crystal plate. Appl. Phys. Lett. 2011, 98, 171911. [Google Scholar] [CrossRef]
- Zhao, J.; Marchal, R.; Bonello, B.; Boyko, O. Efficient focalization of antisymmetric Lamb waves in gradient-index phononic crystal plates. Appl. Phys. Lett. 2012, 101, 261905. [Google Scholar] [CrossRef]
- Chiou, M.J.; Lin, Y.C.; Ono, T.; Esashi, M.; Yeh, S.L.; Wu, T.T. Focusing and waveguiding of Lamb waves in micro-fabricated piezoelectric phononic plates. Ultrasonics 2014, 54, 1984–1990. [Google Scholar] [CrossRef]
- Jin, Y.; Torrent, D.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Simultaneous control of the S 0 and A 0 Lamb modes by graded phononic crystal plates. J. Appl. Phys. 2015, 117, 244904. [Google Scholar] [CrossRef]
- Zhao, J.; Bonello, B.; Becerra, L.; Boyko, O.; Marchal, R. Focusing of Rayleigh waves with gradient-index phononic crystals. Appl. Phys. Lett. 2016, 108, 221905. [Google Scholar] [CrossRef]
- Climente, A.; Torrent, D.; Sánchez-Dehesa, J. Gradient index lenses for flexural waves based on thickness variations. Appl. Phys. Lett. 2014, 105, 064101. [Google Scholar] [CrossRef]
- Colombi, A. Resonant metalenses for flexural waves in plates. J. Acoust. Soc. Am. 2016, 140, EL423–EL428. [Google Scholar] [CrossRef]
- Kim, S.H. Retroreflector approximation of a generalized Eaton lens. J. Mod. Opt. 2012, 59, 839–842. [Google Scholar] [CrossRef][Green Version]
- Lee, D.; Cho, C.; Mun, J.; Park, N.; Rho, J. Demonstration of steering acoustic waves by generalized Eaton lens. Appl. Phys. Lett. 2018, 113, 161904. [Google Scholar] [CrossRef]
- Tol, S.; Degertekin, F.; Erturk, A. Gradient-index phononic crystal lens-based enhancement of elastic wave energy harvesting. Appl. Phys. Lett. 2016, 109, 063902. [Google Scholar] [CrossRef]
- Zareei, A.; Darabi, A.; Leamy, M.J.; Alam, M.R. Continuous profile flexural GRIN lens: Focusing and harvesting flexural waves. Appl. Phys. Lett. 2018, 112, 023901. [Google Scholar] [CrossRef]
- Tol, S.; Degertekin, F.; Erturk, A. Phononic crystal Luneburg lens for omnidirectional elastic wave focusing and energy harvesting. Appl. Phys. Lett. 2017, 111, 013503. [Google Scholar] [CrossRef]
- Rho, J.; Ye, Z.; Xiong, Y.; Yin, X.; Liu, Z.; Choi, H.; Bartal, G.; Zhang, X. Spherical hyperlens for two-dimensional sub-diffractional imaging at visible frequencies. Nat. Commun. 2010, 1, 143. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Liu, Z. Hyperlenses and metalenses for far-field super-resolution imaging. Nat. Commun. 2012, 3, 1205. [Google Scholar] [CrossRef] [PubMed]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948. [Google Scholar] [CrossRef]
- Jacob, Z.; Alekseyev, L.V.; Narimanov, E. Optical hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express 2006, 14, 8247–8256. [Google Scholar] [CrossRef]
- Li, J.; Fok, L.; Yin, X.; Bartal, G.; Zhang, X. Experimental demonstration of an acoustic magnifying hyperlens. Nat. Mater. 2009, 8, 931. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.W.; Kim, Y.Y. Far-field subwavelength imaging for ultrasonic elastic waves in a plate using an elastic hyperlens. Appl. Phys. Lett. 2011, 98, 241912. [Google Scholar] [CrossRef]
- Oh, J.H.; Min Seung, H.; Young Kim, Y. A truly hyperbolic elastic metamaterial lens. Appl. Phys. Lett. 2014, 104, 073503. [Google Scholar] [CrossRef]
- Colombi, A.; Craster, R.V.; Colquitt, D.; Achaoui, Y.; Guenneau, S.; Roux, P.; Rupin, M. Elastic wave control beyond band-gaps: Shaping the flow of waves in plates and half-spaces with subwavelength resonant rods. Front. Mech. Eng. 2017, 3, 10. [Google Scholar] [CrossRef]
- Lee, H.; Oh, J.H.; Seung, H.M.; Cho, S.H.; Kim, Y.Y. Extreme stiffness hyperbolic elastic metamaterial for total transmission subwavelength imaging. Sci. Rep. 2016, 6, 24026. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Chen, Y.; Wang, Y.; Hu, G.; Huang, G. A single-phase elastic hyperbolic metamaterial with anisotropic mass density. J. Acoust. Soc. Am. 2016, 139, 3303–3310. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.W.; Zhao, S.D.; Wang, Y.S.; Zhang, C. Broadband single-phase hyperbolic elastic metamaterials for super-resolution imaging. Sci. Rep. 2018, 8, 2247. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Greenleaf, A.; Lassas, M.; Uhlmann, G. On nonuniqueness for Calderon’s inverse problem. Math. Res. Lett. 2003, 10, 685–693. [Google Scholar] [CrossRef]
- Milton, G.W.; Briane, M.; Willis, J.R. On cloaking for elasticity and physical equations with a transformation invariant form. New J. Phys. 2006, 8, 248. [Google Scholar] [CrossRef]
- Chen, H.; Chan, C. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 2007, 91, 183518. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, C.; Fang, N. Broadband Acoustic Cloak for Ultrasound Waves. Phys. Rev. Lett. 2011, 106, 024301. [Google Scholar] [CrossRef]
- Farhat, M.; Guenneau, S.; Enoch, S.; Movchan, A.B. Cloaking bending waves propagating in thin elastic plates. Phys. Rev. B 2009, 79, 033102. [Google Scholar] [CrossRef]
- Farhat, M.; Guenneau, S.; Enoch, S. Ultrabroadband elastic cloaking in thin plates. Phys. Rev. Lett. 2009, 103, 024301. [Google Scholar] [CrossRef] [PubMed]
- Stenger, N.; Wilhelm, M.; Wegener, M. Experiments on elastic cloaking in thin plates. Phys. Rev. Lett. 2012, 108, 014301. [Google Scholar] [CrossRef] [PubMed]
- Brun, M.; Guenneau, S.; Movchan, A.B. Achieving control of in-plane elastic waves. Appl. Phys. Lett. 2009, 94, 061903. [Google Scholar] [CrossRef]
- Norris, A.N.; Shuvalov, A.L. Elastic cloaking theory. Wave Motion 2011, 48, 525–538. [Google Scholar] [CrossRef]
- Parnell, W.J. Nonlinear pre-stress for cloaking from antiplane elastic waves. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2011, 468, 563–580. [Google Scholar] [CrossRef]
- Parnell, W.J.; Norris, A.N.; Shearer, T. Employing pre-stress to generate finite cloaks for antiplane elastic waves. Appl. Phys. Lett. 2012, 100, 171907. [Google Scholar] [CrossRef]
- Norris, A.N.; Parnell, W.J. Hyperelastic cloaking theory: Transformation elasticity with pre-stressed solids. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2012, 468, 2881–2903. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Bağcı, H.; Enoch, S.; Guenneau, S.; Alu, A. Platonic scattering cancellation for bending waves in a thin plate. Sci. Rep. 2014, 4, 4644. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Colombi, A.; Roux, P.; Guenneau, S.; Rupin, M. Directional cloaking of flexural waves in a plate with a locally resonant metamaterial. J. Acoust. Soc. Am. 2015, 137, 1783–1789. [Google Scholar] [CrossRef]
- Willis, J. Variational principles for dynamic problems for inhomogeneous elastic media. Wave Motion 1981, 3, 1–11. [Google Scholar] [CrossRef]
- Marqués, R.; Medina, F.; Rafii-El-Idrissi, R. Role of bianisotropy in negative permeability and left-handed metamaterials. Phys. Rev. B 2002, 65, 144440. [Google Scholar] [CrossRef]
- Milton, G.W.; Willis, J.R. On modifications of Newton’s second law and linear continuum elastodynamics. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2007, 463, 855–880. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Srivastava, A. Overall dynamic constitutive relations of layered elastic composites. J. Mech. Phys. Solids 2011, 59, 1953–1965. [Google Scholar] [CrossRef]
- Srivastava, A.; Nemat-Nasser, S. Overall dynamic properties of three-dimensional periodic elastic composites. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2012, 468, 269–287. [Google Scholar] [CrossRef]
- Norris, A.N.; Shuvalov, A.L.; Kutsenko, A.A. Analytical formulation of three-dimensional dynamic homogenization for periodic elastic systems. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2012, 468, 1629–1651. [Google Scholar] [CrossRef]
- Sieck, C.F.; Alù, A.; Haberman, M.R. Dynamic Homogenization of Acoustic Metamaterials with Coupled Field Response. Phys. Proc. 2015, 70, 275–278. [Google Scholar] [CrossRef][Green Version]
- Muhlestein, M.B.; Sieck, C.F.; Alù, A.; Haberman, M.R. Reciprocity, passivity and causality in Willis materials. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2016, 472, 20160604. [Google Scholar] [CrossRef]
- Xiang, Z.; Yao, R. Realizing the Willis equations with pre-stresses. J. Mech. Phys. Solids 2016, 87, 1–6. [Google Scholar] [CrossRef]
- Nassar, H.; Xu, X.; Norris, A.; Huang, G. Modulated phononic crystals: Non-reciprocal wave propagation and Willis materials. J. Mech. Phys. Solids 2017, 101, 10–29. [Google Scholar] [CrossRef]
- Koo, S.; Cho, C.; Jeong, J.h.; Park, N. Acoustic omni meta-atom for decoupled access to all octants of a wave parameter space. Nat. Commun. 2016, 7, 13012. [Google Scholar] [CrossRef] [PubMed]
- Muhlestein, M.B.; Sieck, C.F.; Wilson, P.S.; Haberman, M.R. Experimental evidence of Willis coupling in a one-dimensional effective material element. Nat. Commun. 2017, 8, 15625. [Google Scholar] [CrossRef] [PubMed]
- Sieck, C.F.; Alù, A.; Haberman, M.R. Origins of Willis coupling and acoustic bianisotropy in acoustic metamaterials through source-driven homogenization. Phys. Rev. B 2017, 96, 104303. [Google Scholar] [CrossRef]
- Li, J.; Shen, C.; Díaz-Rubio, A.; Tretyakov, S.A.; Cummer, S.A. Systematic design and experimental demonstration of bianisotropic metasurfaces for scattering-free manipulation of acoustic wavefronts. Nat. Commun. 2018, 9, 1342. [Google Scholar] [CrossRef] [PubMed]
- Quan, L.; Ra’di, Y.; Sounas, D.L.; Alù, A. Maximum Willis Coupling in Acoustic Scatterers. Phys. Rev. Lett. 2018, 120, 254301. [Google Scholar] [CrossRef] [PubMed]
- Quan, L.; Sounas, D.L.; Alù, A. Nonreciprocal Willis Coupling in Zero-Index Moving Media. Phys. Rev. Lett. 2019, 123, 064301. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, A.; Chiang, Y.K.; Quan, L.; Oberst, S.; Alù, A.; Marburg, S.; Powell, D. Acoustic meta-atom with experimentally verified maximum Willis coupling. Nat. Commun. 2019, 10, 1–7. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Zhu, J.; Xia, L.; Mondain-Monval, O.; Brunet, T.; Alù, A.; Li, J. Willis Metamaterial on a Structured Beam. Phys. Rev. X 2019, 9, 011040. [Google Scholar] [CrossRef]
- Ni, X.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband light bending with plasmonic nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef]
- Sun, S.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.; Kung, W.T.; Guo, G.Y.; et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef]
- Zhu, H.; Cheung, S.; Chung, K.L.; Yuk, T.I. Linear-to-circular polarization conversion using metasurface. IEEE Trans. Antennas Propag. 2013, 61, 4615–4623. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Xiao, S.; Cai, B.; He, Q.; Cui, T.J.; Zhou, L. Flat metasurfaces to focus electromagnetic waves in reflection geometry. Opt. Lett. 2012, 37, 4940–4942. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Kats, M.A.; Yu, N.; Blanchard, R.; Gaburro, Z.; Capasso, F. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 2012, 12, 4932–4936. [Google Scholar] [CrossRef] [PubMed]
- West, P.R.; Stewart, J.L.; Kildishev, A.V.; Shalaev, V.M.; Shkunov, V.V.; Strohkendl, F.; Zakharenkov, Y.A.; Dodds, R.K.; Byren, R. All-dielectric subwavelength metasurface focusing lens. Opt. Express 2014, 22, 26212–26221. [Google Scholar] [CrossRef]
- Zheng, G.; Mühlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308. [Google Scholar] [CrossRef]
- Li, Z.; Kim, I.; Zhang, L.; Mehmood, M.Q.; Anwar, M.S.; Saleem, M.; Lee, D.; Nam, K.T.; Zhang, S.; Luk’yanchuk, B.; et al. Dielectric Meta-Holograms Enabled with Dual Magnetic Resonances in Visible Light. ACS Nano 2017, 11, 9382–9389. [Google Scholar] [CrossRef]
- Yoon, G.; Lee, D.; Nam, K.T.; Rho, J. Pragmatic metasurface hologram at visible wavelength: The balance between diffraction efficiency and fabrication compatibility. ACS Photonics 2017, 5, 1643–1647. [Google Scholar] [CrossRef]
- Ansari, M.A.; Kim, I.; Lee, D.; Waseem, M.H.; Zubair, M.; Mahmood, N.; Badloe, T.; Yerci, S.; Tauqeer, T.; Mehmood, M.Q.; et al. A Spin-Encoded All-Dielectric Metahologram for Visible Light. Laser Photon. Rev. 2019, 13, 1900065. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Zhu, H.; Semperlotti, F. Anomalous Refraction of Acoustic Guided Waves in Solids with Geometrically Tapered Metasurfaces. Phys. Rev. Lett. 2016, 117, 034302. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Lu, Z.; Norris, A.N. Elastic metasurfaces for splitting SV- and P-waves in elastic solids. J. Appl. Phys. 2018, 123, 091701. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Cao, L.; Yang, Z.; Zhou, X. Steering of SH wave propagation in electrorheological elastomer with a structured meta-slab by tunable phase discontinuities. AIP Adv. 2017, 7, 095114. [Google Scholar] [CrossRef]
- Shen, X.; Sun, C.T.; Barnhart, M.V.; Huang, G. Elastic wave manipulation by using a phase-controlling meta-layer. J. Appl. Phys. 2018, 123, 091708. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Liu, F.; Diba, O.; Lamb, A.; Li, J. Source Illusion Devices for Flexural Lamb Waves Using Elastic Metasurfaces. Phys. Rev. Lett. 2017, 119, 034301. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y. Steering elastic SH waves in an anomalous way by metasurface. J. Sound Vibr. 2018, 418, 1–14. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y.; Assouar, B. Deflecting flexural wave with high transmission by using pillared elastic metasurface. Smart Mater. Struct. 2018, 27, 075051. [Google Scholar] [CrossRef]
- Palermo, A.; Marzani, A. Control of Love waves by resonant metasurfaces. Sci. Rep. 2018, 8, 7234. [Google Scholar] [CrossRef]
- Li, S.; Xu, J.; Tang, J. Tunable modulation of refracted lamb wave front facilitated by adaptive elastic metasurfaces. Appl. Phys. Lett. 2018, 112, 021903. [Google Scholar] [CrossRef]
- Lee, H.; Lee, J.K.; Seung, H.M.; Kim, Y.Y. Mass-Stiffness substructuring of an elastic metasurface for full transmission beam steering. J. Mech. Phys. Solids 2018, 112, 577–593. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Lee, D.; Rho, J. Recent Advances in Non-Traditional Elastic Wave Manipulation by Macroscopic Artificial Structures. Appl. Sci. 2020, 10, 547. https://doi.org/10.3390/app10020547
Park J, Lee D, Rho J. Recent Advances in Non-Traditional Elastic Wave Manipulation by Macroscopic Artificial Structures. Applied Sciences. 2020; 10(2):547. https://doi.org/10.3390/app10020547
Chicago/Turabian StylePark, Jeonghoon, Dongwoo Lee, and Junsuk Rho. 2020. "Recent Advances in Non-Traditional Elastic Wave Manipulation by Macroscopic Artificial Structures" Applied Sciences 10, no. 2: 547. https://doi.org/10.3390/app10020547
APA StylePark, J., Lee, D., & Rho, J. (2020). Recent Advances in Non-Traditional Elastic Wave Manipulation by Macroscopic Artificial Structures. Applied Sciences, 10(2), 547. https://doi.org/10.3390/app10020547





