Abstract
In this paper, an e-Learning toolbox based on a set of fuzzy logic data mining techniques is presented. The toolbox is mainly based on the fuzzy inductive reasoning (FIR) methodology and two of its key extensions: (i) the linguistic rules extraction algorithm (LR-FIR), which extracts comprehensible and consistent sets of rules describing students’ learning behavior, and (ii) the causal relevance approach (CR-FIR), which allows to reduce uncertainty during a student’s performance prediction stage, and provides a relative weighting of the features involved in the evaluation process. In addition, the presented toolbox enables, in an incremental way, detecting and grouping students with respect to their learning behavior, with the main goal to timely detect failing students, and properly provide them with suitable and actionable feedback. The proposed toolbox has been applied to two different datasets gathered from two courses at the Latin American Institute for Educational Communication virtual campus. The introductory and didactic planning courses were analyzed using the proposed toolbox. The results obtained by the functionalities offered by the platform allow teachers to make decisions and carry out improvement actions in the current course, i.e., to monitor specific student clusters, to analyze possible changes in the different evaluable activities, or to reduce (to some extent) teacher workload.
1. Introduction
E-Learning involves the use of electronic devices for learning, including the delivery of content via electronic media such as Internet/intranet/extranet, audio or video, satellite broadcast, interactive TV, and so on. E-Learning gives several advantages to students: cost effectiveness, timely content, and access flexibility [1,2]. E-Learning systems, such as virtual campus environments, have gradually established themselves as a plausible alternative to, and a complement of, traditional distance education models. It is a helping and useful tool in the process of teaching and learning.
However, experience has shown that the teacher considerably increases the workload in the virtual environment. They must carry out continuous feedback tasks to virtual students and correct a fairly high number of evaluable activities [3,4,5]. This issue has a greater relevance when we move from training to undergraduate and graduate courses, where competencies are closely related to higher thinking skills. By their very nature, timely and constant feedback is essential in these courses, increasing the workload of teachers. It should also be borne in mind that the assessment task that the teacher must carry out is arduous and takes a long time. Since collaborative resources are the most used in distance education tools, the formula for calculating the final grade is made up of many factors that have little weight and hinder a clear and well-defined evaluation process.
This topic is a relevant and challenging line of work in the area of e-Learning. The analysis, using data mining techniques (DM), of the data generated in the environment of e-Learning systems can be a good strategy to identify the most relevant evaluable activities, allowing to attack the correction overload problem from another less cumbersome prospect for the teacher.
It is possible to find in the literature interesting works where different DM methods are developed or used to improve some particular aspect of e-Learning systems. In [6], an analysis of the state of the art on Educational Data Mining (EDM) in higher education is presented. The authors conclude that EDM discipline is growing and new contributions are needed to be more useful, fully operative, and available for all users. Peña-Ayala [7] analyzed a large amount of EDM research works in the literature and stated that the evolution of DM tools and their application is mainly oriented to facilitate data processing, simplify the feature selection stage, provide learning support to students, and enhance the collaboration between students and teacher. Some of the most popular Learning Management Systems (LMSs) are AlfaNet [8,9], AHA! [10,11], LON-CAPA [12,13], ATutor [14], LExIKON [15], Blackboard [16], ELM-ART [17,18] and Moodle [19].
From all of the previously mentioned LMSs, Moodle is probably the most known (and used) open source platform [19]. In recent years, several plugins have been developed for Moodle that make use of DM techniques to improve the e-Learning process. An example is Moodle’s Engagement Analytics Plugin (MEAP+) [20], which analyses gradebook data, assessments submissions, and forum interactions to prepare personalized e-mails for students.
MoodleMiner is another Moodle plugin, used to perform basic data mining analysis, such as grouping students by their levels of interaction, determining at-risk students, and identifying important features that impact student academic performance [21]. MoodleMiner applies classification algorithms to predict student academic performance and cluster analysis to group similar students.
The Graphical Interactive Student Monitoring Tool for Moodle (GISMO) provides a visualization of student activities. GISMO generates graphical representations about the tracking behavior of the participants enrolled in a course. For instance, it is possible to obtain information about the students’ accesses to the course, the number of accesses made by the students to the resources of the course, and a graph reporting the submission of assignments and quizzes [22].
In [23], learning analytics are applied for the early prediction of students’ final academic performance in a calculus course delivered in a blended way. Principal component regression is used to forecast the students’ performance, by using different kind of variables like: out-of-class practice behaviors, homework and quiz scores, video-viewing behaviors, and after-school tutoring.
In [24], four classification methods: J48, PART, Random Forest and Bayes Network, are applied to analyze data from socio-economic, demographic and academic information in order to identify the student performance and to prevent drop out. The authors apply WEKA [25] as a data mining tool.
Juhanak, et al. apply process-mining methods to analyze students’ interactions when they take online quizzes. The objective is to identify specific types of interaction sequences that show the strategies used by students when they take quizzes [26].
In [27] an ensemble based tree model classifier is proposed for predicting students’ performance. The features used to perform the forecasting are: exams marks, labs tests, class tests, students’ demographics, education information, and family behaviors.
An educational DM platform that extracts patterns by using association rule mining from educational datasets is presented in [28]. The platform also applies the clustering k-means algorithm to group the survey answers of the participants.
Jayapradha et al. propose the use of DM techniques to help the student choose the most suitable career for him within the field of engineering. To perform these predictions, SVM, Random Forest, and Naïve Bayes classifiers are applied. The features involved in the classification are taken from the admission process like demographic features, the profession of their parents and his/her previous high school and higher secondary records [29].
After analyzing the literature, we can see that the existing tools are specialized in some particular aspect of e-Learning, such as the interaction between students, the prediction of student performance, the grouping of students based on similar behaviors, etc.
In this sense, the e-Learning toolbox presented in this work has the peculiarity and advantage over previous works that it integrates a set of useful functionalities for teachers, students, and modelers in a single platform.
To the best of our knowledge, this is the first time that an e-Learning toolbox uses as DM approaches, methodologies based on fuzzy logic and fuzzy modeling. All the functionalities developed in the platform are based on fuzzy logic and on reasoning under uncertainty. We consider that the approach we propose in this article is novel and relevant in the area of e-Learning, since the information derived from the students’ learning process invariably contains partial knowledge, uncertainty, and/or incomplete information. The use of fuzzy logic based methodologies allows to incorporate this uncertainty into the model. Fuzzy rule models enable to mimic the logic of human thought, are expressive, easy to understand and suitable for approximate reasoning. The works in e-Learning that are closest to our research are the approaches based on rule models, specifically the association rules [24,28], and the random forest algorithms [30]. Association rules are not as expressive and easy to understand as fuzzy rules, due to the fact that the consequence of an association rule includes input features. In the case of random forests, they generate decision trees comparable with learning rules; however, they are not as expressive and interpretable for the user.
The tool that we propose in this article offers different utilities that help teachers and provides useful information to the student. The main functionalities, which will be described in more detail in Section 3, are the identification of models of student learning behavior, the prediction of their final grade in a dynamic way, the determination of the most relevant features involved in the assessment process (as well as the relative weight of each of them), and the extraction of logical rules that allow a better understanding of the student’s learning process.
In the next section, the DM algorithms designed and used within the toolbox are briefly introduced. Section 3 presents the foundation and functionalities of the e-Learning toolbox. The experiments performed applying the proposed toolbox to two courses of the Latin American Institute for Educational Communication, are shown, analyzed, and discussed in Section 4. Conclusions and future works are presented in Section 5 of this paper.
2. Materials and Methods
The data mining methodologies designed and used in this research are mainly based on fuzzy inductive reasoning (FIR) methodology. Therefore, a brief description of this approach and its main developments are presented in this section. FIR is a modeling and simulation methodology derived from Klir’s General Systems Problem Solver (GSPS) [31]. It is a tool for general system analysis that allows studying the conceptual modes of behavior of dynamical systems.
FIR models are non-parametric models based on fuzzy logic. Unlike other widely used soft computing techniques, such as neural networks (NN), which perform a network training process from a data set in order to obtain a model, FIR performs a model synthesis process from the data set, which is less costly in time. Moreover, in this process FIR extracts the behavioral patterns from the data and represents them in the form of fuzzy rules. Therefore, the rules represent the knowledge associated with the data. In contrast, NN use the data to train a model by fitting a set of weights so that it approximates a function. Once the model is obtained, the data is discarded and not used in the prediction process. This implies that a NN will always predict something while a FIR model will only predict if it is possible to validate its prediction on the available data set. This ensures that the model never predicts if the available data are not sufficient to support the prediction.
FIR methodology consists of four main processes, namely: fuzzification, qualitative model identification, fuzzy forecast, and defuzzification.
The conversion of the quantitative data available from the system under study to qualitative data is performed within the fuzzification module. The fuzzification function converts a single quantitative value into a qualitative triple consisting of class, membership, and side values for each quantitative element.
The qualitative model identification process is responsible to obtain the best model that represents the behavior of the system. To this end, it is necessary to find the temporal and causal relationships between the input and output variables. An example of input–output relationship is presented in Equation (1). In this multivariate time series example, we have two input variables, i.e., Inp1 and Inp2, and an output variable, i.e., Out. Previous values in time (t-xδt), of the input and output variables may be relevant to predict the output value at current time (t).
Equation (1) shows the causal and temporal relation between the inputs and the output, i.e., it defines the model structure, which, in the FIR methodology, is called mask. In the example, the value of the output variable at time t, is obtained taking into account the values of the Inp1 and Out variables two time steps back into the past and the value of the Inp2 variable one time step back into the past.
A FIR model is composed of a mask and a pattern rule base (set of rules). The mask (see example in Equation (1)), represents the structure of the model, i.e., it selects those variables that best capture the behavior of the system. The optimal mask is obtained performing a feature selection process by means of the Shannon entropy measure, using either a mechanism of exhaustive search of exponential complexity, or by a suboptimal search strategy of polynomial complexity. The pattern rule base is the set of rules obtained from the training data when the mask is used to extract the set of patterns that describe the behavior of the system.
The next process is the prediction process, which, in the FIR methodology, is called fuzzy forecast. This inference process is based on the k-nearest neighbor technique. From the set of pattern rules obtained in the previous step, it is possible to identify the k nearest neighbors that will allow inferring the output of the new input pattern, by means of a distance measure. Finally, we have the defuzzification process that performs the conversion of the qualitative data obtained from the fuzzy forecast process to quantitative data. In other words, it performs the reverse process of fuzzification. This conversion to quantitative values is useful when the prediction obtained is part of the input of another quantitative submodel or is used for decision-making tasks.
For a deeper and more detailed insight into the FIR methodology, the reader is referred to [32,33].
2.1. Logical Rules Extraction from FIR Models: LR-FIR
The idea behind LR-FIR algorithm is to obtain interpretable, realistic, and efficient rules, describing students’ learning behavior. LR-FIR performs an iterative process that suitable compact the pattern rule base obtained by FIR. In order to obtain a set of rules congruent with the model previously identified by FIR, LR-FIR is based on its initial discretization, the mask features obtained and the pattern rule base identified. The algorithm can be summarized by the following ordered steps:
- Basic compaction. The main goal of this step is to transform the pattern rule base, into a reduced set of rules. It consist on an iterative step that evaluates one at a time, all of the rules, and each of their premises in the pattern rule base. A specific subset of rules can be transformed in the form of a compacted rule when all premises but one, as well as the consequence share the same values. If the subset contains all legal values, all these rules can be replaced by a single rule that has a value of −1 in that premise, and if no conflicts exists the compacted rule is accepted. Conflicts occur when the extended rules have the same values in all its premises, but different values in the consequence. The reduced set of rules includes all the rules compacted in previous iterations and those that cannot be compacted in this step.
- Improved compaction. This step extends the pattern rule base to cases that had not been previously used to build the model. In this compaction, a consistent minimal ratio of the legal values should be present in the candidate subset in order to compact it in the form of a single rule. In this case, assumed beliefs are incorporated to the set of compacted rules to some extent, not compromising the model previously identified by FIR. The obtained set of rules is subjected to a number of refinement steps: removal of duplicate rules and conflicting rules, unification of similar rules, etc. For a deeper insight into LR-FIR, the reader is referred to [34].
2.2. Causal Relevance Approaches: CR-FIR
The idea behind causal relevance (CR) can be addressed through the following question: how much does each input variable influence the prediction of the output? If it is possible to quantify the importance of each input variable with respect to the output, it becomes easier to obtain good predictions, closest to the best that can be obtained for a specific set of training data.
Equation (2) describes the Rdis formula used to compute the influence of each input variable, i, that conforms a FIR mask, on the prediction of the output.
Epi stands for the Mean Square Error in percentage (MSE) obtained when the mask that contains only the output and the ith input is used to predict the validation data set. Epm is the MSE obtained when the optimal mask, identified by FIR, is used to predict the validation data set. ∆Inf is a factor that helps to preserve the consistency of the model identified by FIR by given a low value to Rdis i when the prediction error obtained by the sub-optimal mask without the ith input is lower than the prediction error obtained by the optimal mask.
Equation (3) presents the MSE formulae used in this study. yvar stands for the variance, y(t) is the real output value and ŷ(t) is the predicted output value.
Once obtained, Rdis allows to compute a weighted Euclidean distance measure taking into account all the relevant input variables, to find better quality neighbors. Remember that the prediction process of FIR methodology is based on the k-nearest neighbor technique. For a deeper and detailed description of CR-FIR the reader is referred to [35].
3. The Toolbox
To deal with the previously stated objectives, the toolbox offers mechanisms to discover relevant learning behavior patterns from students’ interaction with the educational materials. The knowledge obtained can be used by teachers to design courses in a more effective way and to timely detect students with learning difficulties. It can also be helpful for students, allowing them to know their own learning performance. All of the toolbox functionalities are implemented as a MATLAB toolkit, and are exploited by forefront, efficient, and standard technologies, i.e., Java applet, JavaScript, Java Servlets, Java Server Pages, Apache Web Server, and Dynamic HMTL. The toolbox should work on all systems that support MATLAB, Java, and the Apache Web Server. The toolbox connects to the MATLAB algorithms developed with Stefan Müller’s Java Wrapper Class called JMatLink [36]. A general view of the toolbox is presented in Figure 1.
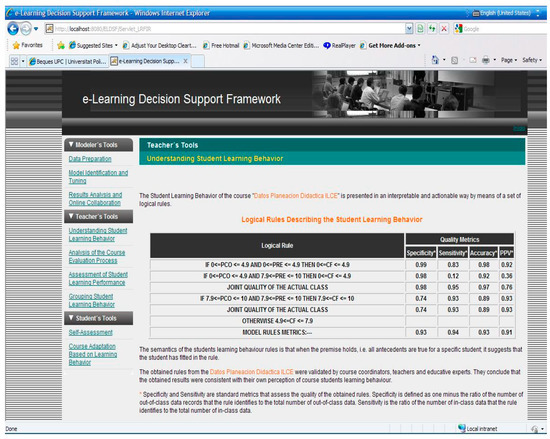
Figure 1.
The e-Learning toolbox framework.
3.1. Modeler
The modeler is the responsible for identifying all models of a specific course (representing different times within the course) by using the DM algorithms included in the toolbox, i.e., FIR, LR-FIR, and CR-FIR. Therefore, should be a person that has previous knowledge about the methodologies involved. She/he performs several actions, such are the preparation of the data, the modeling, and refinement of the models obtained, and moderates the online analysis of the results obtained, performed by the qualified teachers. These actions are grouped in three functionalities: data preparation (DP); model identification and tuning (MIT); and result analysis and online collaboration (RAOC), as can be seen on the upper left hand side in Figure 1.
In the DP option, the data gathered from different sources, such are student portfolios, their interactions with the e-Learning environment, and the course database is loaded in a specific format. There is available, at this moment, a plug-in for LMS Moodle data.
Using the MIT option, the modeler obtains the model that best represents the analyzed course. This option involves the identification of good model parameters. Notice, that only the users that have the role of modeler are allowed to perform this task. In the RAOC option, the accredited teachers analyze the knowledge obtained and its usefulness to improve the course. This is done in an online collaborative way together with the qualified teachers and with the modeler, being the moderator of the discussion. Once they consider that the results are coherent, valid, and represent the real behavior of the analyzed course, the corresponding models become available to the teacher and student platforms.
3.2. Teacher
Teachers have several options available to help them better understand student learning behavior and the usefulness of the assessment process. These options are: assessment of students’ learning performance (ASLP), grouping of students’ learning behavior (GSLB), understanding students’ learning behavior (USLB), and analysis of the course evaluation process (ACEP); see left hand side of Figure 1.
The ASLP option provides a continuous evaluation of students during course development. This is done by performing a prediction of the student’s final grade using a FIR model. That means that students’ learning behavior can be obtained and analyzed at any time through the course and after the end of it, giving teachers the possibility to offer efficient and on time feedback to students in order to improve their course performance. The platform offers teachers the possibility of sending automatic feedback to clusters of students, i.e., the set of students with failing grades predictions. The teacher decides the content of the automatic feedback and to which clusters of students should be applied. For example, the teacher decides that a message is sent automatically at a certain moment of the course to the cluster of students who are not obtaining good results, telling them that they are not on the right track, and announcing a virtual class to clarify concepts and answer questions about the topics covered so far. This option is accomplished by using the FIR methodology, described briefly in Section 2. The GSLB option provides, in a dynamic and incremental way, students’ clustering based on the prediction of their final marks. For instance, in the first month of the course, only information about the navigability, usability and the first test results are available; however, at the last part of the course richer information is accessible, such as different tests grades, homework marks, partial projects marks, collaborative resources marks, etc. In turn, a better model identification and, of course, more reliable prediction results can be accomplished.
The USLB tool provides an interpretable and comprehensible way to describe students’ learning behavior, by means of linguistic rules. The rules are automatically mined from the data gathered from the course and students’ interaction within the e-Learning platform. This allows knowing the course performance patterns and, therefore, using this knowledge in future courses design or for decision support. Mined rules reveal interesting and valuable knowledge, which can be applied in educational contexts to improve the learning experience. This functionality is accomplished by means of the LR-FIR algorithm (see Section 2).
The ACEP option identifies the most relevant features (i.e., input variables) involved in the evaluation process. This knowledge allows teachers to focus on the relevant variables (e.g., confer more weight) and take concrete actions related to the less relevant variables (e.g., not spend much time grading those items or delegate correction to an assistant). The results of the ACEP can be useful for teachers and course coordinators to analyze the way the course is being evaluated and, if necessary, modify it. This functionality is performed through the CR-FIR algorithm, described briefly in Section 2.
Figure 2 describes graphically the dynamic strategy for all the functionalities. For a given course, different time periods are defined by the educators (teachers and course coordinators). For each time period, a FIR model is identified using as input only those parameters that are available at that point in time. For example, FIR model 1 is obtained before course starts, so only initial student’s information data are available. The goal is to find patterns, if exists, that allow to predict the final grade of the student based on their initial information. FIR model 2 uses additional features, already related to the course, such are some evaluation tests, exercises, etc. since these features are already available at this time. Notice that all these models are identified from the data gathered in previous editions of the same course. Therefore, a FIR model in each defined time period is already available when the course starts.
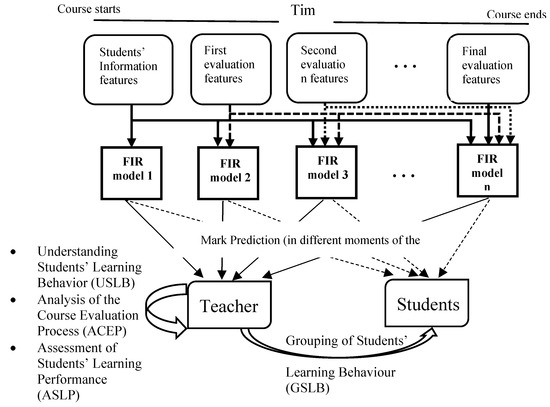
Figure 2.
Dynamic strategy of ASLP, GSLB, USLB, and ACEP functionalities. FIR = fuzzy inductive reasoning.
The main goal of identifying incremental and dynamic models is to find important didactic and educational checkpoints that could timely detect students’ learning difficulties, and provide realistic, reliable, and reasonable feedback to them in order to reach their educational and learning goals. Therefore, it is of major importance to obtain reliable predictions on time in order to give feedback to students as soon as possible.
3.3. Student
Students can obtain feedback related to their performance during the course by consulting the self-assessment (SA) option that allow them to know their final mark prediction at each checkpoint. The self-evaluation can be very useful if the student performs the learning actions needed in order to obtain a better course exploitation.
4. Results and Discussion
The Latin American Institute for Educational Communication (ILCE) virtual campus [37] offers continuous education and postgraduate courses to Latin-American students. Students have access to a wide variety of resources such as collaborative tools, i.e., e-mail, forums, chats, etc., personal tools, i.e., agenda, news system, etc., as well as virtual classrooms, digital library, interactive tutorials.
In the next subsections, didactic planning and the introductory ILCE courses are studied using the developed toolbox. All of the obtained results were evaluated and validated by five ILCE educative experts. For the sake of clarity and compaction, the results are presented by means of tables, instead of showing them by using the toolbox user interface. As explained above, before the execution of the teachers and students’ toolbox functionalities, it is compulsory to identify the FIR models that best represent the analyzed course from the prediction accuracy point of view.
4.1. Didactic Planning Course
Didactic planning is a course aimed at high school teachers who teach different subjects, such as Spanish reading and writing, chemistry, mathematics, companies’ management, computer science, Mexican history, and ethics and values. A total of 722 students who have taken this course (all high school teachers), were available to carry out the experiments. The objective of this course is for students to acquire new skills and techniques to plan their classes so that they are dynamic and engaging. All of the activities that students carry out throughout this course are centered on a document called a “class plan”. The purpose of this document is to develop a planning of the classes given by the secondary school teachers, incorporating all of the knowledge, methods, and strategies they acquire during the didactic planning course.
The data features available for this study are detailed on Table 1. It is interesting to pay special attention to two of the variables presented in this table, i.e., co-evaluation and experience report. These two features are not common in distance education settings. Co-evaluation means that a student evaluates a classmate’s “class plan”, and this evaluation is graded by the teacher. The experience report means that a student evaluates his/her own learning process, by means of a document where he/she describes his/her learning experience.

Table 1.
Data features collected for the didactic planning course.
The goal of this set of experiments is threefold. First, the idea is to prove that FIR models are capable of capturing the evolution of students and predicting their performance. A second objective is to identify those characteristics that have the most influence on student performance and are, therefore, more relevant. The last goal is to discover students’ learning behavior patterns. As stated before, all experiments have been performed in a dynamic and incremental way (refer to Figure 2), based on the educational scheduling of each course and using the information available at each moment. To this end, a test set composed of 132 samples and a training set of 540 samples are stated. To perform an evaluation of the relative relevance of the features involved in the evaluation process a validation dataset of 50 samples is used.
Based on the educational scheduling of the didactic planning course, teachers and course coordinators identified four models that incrementally describe the dynamic learning behavior of students along the course. In the next sections, a detailed analysis of each model is presented, discussing the toolbox functionalities.
4.1.1. Time 1 Model
This model is identified before starting the course, when only initial student’s information is available, i.e., AGE, EXP, G, STD, and POS (see Table 1). The goal is to study if there is any pattern between students’ initial data and their final grade. Human factors, such as personal attributes are of considerable importance, when it comes to forming an organizational group, therefore, in an educational context, we want to assess the importance of personal characteristics within students’ learning behavior.
The results are summarized in Table 2. The ACEP shows the features identified as relevant by the FIR model and the relative relevance of each one of them. Notice that the FIR model is obtained using the training set, i.e., using 540 students. The model is then used to extract a set of linguistic rules by means of the USLB functionality. These rules describe the relation between the relevant features and the final mark. Once the rules are available, they are used to evaluate the behavior of each of the 132 students that conform the test set, i.e., the mark of each student is inferred from the set of rules. As a result, the specificity, sensitivity and accuracy for each of the three classes that define the final mark, i.e., fail, pass and excellent are obtained, together with the overall macro and micro average precision of the whole set of rules when used to infer the students of the test set.

Table 2.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 1 of the didactic planning course. The MARK variable was discretized into three classes: fail (from 0–6), pass (from 6.1–8.9), and excellent (from 9–10). AGE variable was discretized into two classes: young (up to 35) and mature (more than 35). The rest of the variables are discrete, so each value corresponds to a class. Spec., Sen. and Acc. stand for specificity, sensitivity, and accuracy, respectively.
At the top of Table 2, the outcomes of the ACEP functionality are shown, i.e., the relative relevance of each feature selected by the model. Notice that, from the five features available, i.e., AGE, EXP, G, STD and POS, the FIR methodology has selected only two as relevant features, i.e., EXP and AGE. Moreover, in this case the relevance is distributed in such a way that both features have almost the same level of relevance, i.e., have the same influence on the predicted output.
With respect the set of rules obtained by the LR-FIR algorithm, two rules define the class fail and one defines the class excellent. It is interesting to notice that the specificity of the class fail is very high meaning that if the result of the inference for a given student is that he/she will not fail it is quite certain that the student will get a pass or an excellent grade. However, the sensitivity is, really, very low, meaning that with the current rules if the inference is a fail for a given student, it is uncertain that he/she will really fail at the end of the course. The macro and micro average precision are very low, meaning that the set of rules obtained from model 1 is not very reliable. In this case, the students’ initial information available does not contain relevant information related to their learning behavior.
At the bottom of Table 2, the results of the ASLP and GSLB toolbox options are shown. Model 1 is used to predict the final mark of the 132 students of the test set. The model, at this time, cannot successfully forecast the failing students, obtaining an overall mean square error (MSE) of 1.28, which is quite high. Regarding the prediction of fail, pass and excellent clusters only one student out of 20 has been correctly predicted as a student who will fail the course, 15 out of 39 and 42 out of 73 have been correctly predicted as pass and excellent students, respectively.
4.1.2. Time 2 Model
Model 2 is identified using the same set of five features available for model 1, plus the initial class plan feature, IC, which can take two possible values, i.e., delivered and not delivered. The results for model 2 are presented in Table 3.

Table 3.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 2 of the didactic planning course. The MARK variable was discretized into three classes: fail (from 0–6), pass (from 6.1–8.9), and excellent (from 9–10). AGE variable was discretized into two classes: young (up to 35) and mature (more than 35). IC variable was discretize, also, into two classes: delivered and not delivered. Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
As a result of the ACEP functionality it can be seen that when a variable directly related to the evaluation process, such as initial class plan (IC), is available, the FIR methodology chooses it as a relevant feature. In this case, the model choses only two features, i.e., IC and AGE, being the first one much more relevant than the second one, i.e., 0.65 vs. 0.35. Notice that this new model has a better prediction performance, with a MSE of 1.04 (see Table 3), lower than the one obtained with the first model of 1.28. Moreover, the classification metrics obtained when the set of rules are used to infer the final mark of the 132 students of the test set are also much better, mainly for the fail and excellent marks. The rules model obtained by the LR-FIR approach defines only one rule for the fail class and another rule for the excellent class. Notice that the specificity is very high, 0.98, meaning that there are very few false positives, i.e., all of the predicted, as non-fail students, at this moment, will not fail at the end of the course, except only two students. On the other hand, the sensitivity is very low, 0.15, meaning that there is a considerable number of students, 17, that at this moment are predicted as non-fail students but they will have a fail mark at the end of the course. Therefore, it is a reminder that they have to keep working throughout the course if they want to get a good mark. The improvement of the prediction performance of model 2 with respect model 1 is significant if we take into account the amount of information available. Notice that the new model added only the first evaluation feature of the course with only two possible values, i.e., delivered or not delivered.
4.1.3. Time 3 Model
To identify the FIR model at time 3, all of the features used in previous models, plus co-evaluation (COEV) and final class plan (FC), are made available. The meaning of each variable for the didactic planning course is presented in Table 1. The toolbox results for this model are summarized in Table 4. As expected, the ACEP results demonstrate that the FIR model selects as the most relevant variables to predict students’ course performance those related to homework marks, i.e., COEV, FC, and IC. All of them have a similar influence in the prediction, with the following relative relevancies: COEV = 0.3638, FC = 0.3000, and IC = 0.3362.

Table 4.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 3 of the didactic planning course. The MARK variable was discretized into three classes: fail (from 0–6), pass (from 6.9–8.9), and excellent (from 9–10). FC and COEV were discretized into three classes: low (from 0–5), medium (from 5.1–7.9), and high (from 8–10). IC variable was discretize, also, into two classes: delivered and not delivered. Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
The rules obtained by the USLB functionality have significant and reasonable meaning. As a result, quite good macro-average and micro-average precision metrics have been reached when used to infer the final mark of the students’ test set. An important enhancement in sensitivity, specificity, and accuracy evaluation metrics are also reached with respect the same metrics obtained by model 2.
The learning performance prediction is considerably better than the previous model, with an MSE of 0.32, much lower than the 1.04 obtained by model 2. The current model is able to identify 12 fail (out of 20), 25 pass (out of 39), and 59 excellent (out of 73) students. This is a very interesting result, since this model can be used, already, in the third month of the course, time enough to give feedback to students and for students to react in order to accomplish the course requirements.
4.1.4. Time 4 Model
The model at time 4 corresponds to the end of the course. At this point, the complete set of 13 features are available (see Table 1) and are used to obtain the last FIR model. The results for this model are presented in Table 5. As can be seen from the ACEP results, the variables with the most influence on the prediction of a student’s final mark are the co-evaluation (COEV), the initial class plan (IC), and the experience report (ER), with relevance values of 0.32, 0.33, and 0.35, respectively. These three variables alone account for 50% of the evaluation of the final grade. It is important to mention, that although variables FC (final class plan) and BR (work performed in the branch) constitute a 35% of the final grade, the FIR optimal model has not selected them as relevant. From these results, it can be concluded that they are highly correlated with COEV, IC, and ER, meaning that they contain redundant information.

Table 5.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 4 of the didactic planning course. The MARK variable was discretized into three classes: fail (from 0–6), pass (from 6.9–8.9), and excellent (from 9–10). COEV was discretized into three classes: low (from 0–5), medium (from 5.1–7.9) and high (from 8–10). IC was discretize into two classes: delivered and not delivered. ER was also discretized into two classes: low (from 0–8) and high (from 9–10). Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
As highlighted in the introduction, the evaluation process is, probably, the most time-consuming task for the teacher. The results obtained by the ACEP option can be used by the advisors to analyze and, if necessary, adapt the evaluation events that make up the final grade. The redundancy identified by the FIR model in some assessment events allows teachers to better organize the correction load, e.g., delegate the correction of the redundant evaluation acts to an assistant.
The set of rules obtained by the USLB option are simple, comprehensive, and are validated by teachers and course coordinator during the modeling phase. The rules are used to infer the final mark for the 132 students of the test set, obtaining high values of sensitivity, specificity, and accuracy. Moreover, macro and micro-average precisions are, also, quite high and have similar values, meaning good precision at, both, class and instance levels. Remember that macro-average gives equal weight to each class, whereas micro-average gives equal weight to each instance. In our case, where the multi-class classification problem is imbalanced, the micro-average precision is a more relevant metric.
It can be seen that the model obtains a high level of accuracy since the MSE has been reduced to a value of 0.09. This model is able to predict 16 failing students (out of 20), 28 pass students (out of 39), and 67 excellent students (out of 73).
The four students that failed, and were not predicted by the model as failing students, were predicted as pass students, and none of them were predicted as excellent students. Moreover, there are no false positives in the failing class, as the specificity shows, meaning that none of the pass or excellent students have been predicted as failing. Therefore, the model is quite consistent since the prediction errors are limited to jumps between adjacent classes.
4.1.5. Using the Toolbox in the Next Course
In the previous sections, the design and extraction of student behavior models at different times throughout the didactic planning course has been described. These models have been obtained from data from students who had taken this course in previous editions. The results of the functionalities offered by the toolbox, i.e., ACEP, USLB, ASLP, and GSLB, are useful for monitoring the new edition of the course, as well as for the analysis and possible adjustments of the features that are part of the course and its evaluation.
The Time 1 model, i.e., before the start of the course, does not provide useful information neither the teacher nor the students. However, Time 2 model, which corresponds to the first month of the course, is already becoming an interesting tool for both actors. Firstly, the results obtained (see Table 3) indicate that feedback can be given to students whose predictions point to a final fail or pass result. In this sense, the obtained rules tell us that those students who did not deliver the IC task have high possibilities of failing the course. This is a quite evident conclusion, if the student does not work in the course, he will not pass it. However, the rule that has as a consequent the pass grade gives us much more information. In this case, the students have delivered the IC homework; however, they are mature students, and for some reason the prediction is that they will not get an excellent, only a pass. The five teachers involved in the course endorsed this rule, since they themselves found that mature students find it more difficult to understand the concept of initial class plan (IC) and the use of new technologies to carry it out. As a consequence, the teachers decided to send an e-mail to the fail and pass clusters, explaining that understanding the IC concept is fundamental to carry out the course successfully, and an online reinforcement class was added to clarify all the doubts that the students can had about it.
On the other hand, analyzing the relative relevance of the FIR model features (ACEP functionality), it can be seen that the IC feature appears in Time 2, Time 3 and Time 4 models. In all of these models, the IC task has a very important relevance regarding the final grade of the course. As described previously (Section 4.1), all of the activities that students do throughout this course are centered on a document called a “class plan”. Therefore, it makes sense that the initial class plan that the students carry out has a substantial weight in the subject and is a fundamental task within the course. At the third month of the course, the teachers have a model (Time 3 model) that defines, in a quite precise way, the evolution of the different students. It is clear to them, seeing the rules of this model (see Table 4), that it is necessary to act on those students who had delivered the IC homework, but they have worked little in the tasks COEV and FC, or that they did not deliver the IC, and they have not made too much effort in the rest of tasks. Therefore, the five teachers decided to automatically send a weekly e-mail to all the students in the fail cluster, requesting a report of their progress related to the new homework they have to do, with the aim of trying to continuously follow-up with these students. This follow-up did not imply more correction burden, since it was only about making the student aware that he/she had to work regularly on the tasks to be able to finish the course successfully. Finally, analyzing the Time 4 model, the teachers realized that several evaluation features, such as BR (work performed in the branch), FC (final class plan), FCP (forum class plan), F (forum participation), and MAIL (activities sent by e-mail) do not influence the final mark in a relevant way or contain redundant information regarding the variables COEV, IC and RC (as previously discussed in Section 4.1.4). Due to this, they decided to delegate the correction of the features with less influence to an assistant, and they make a quick review of this correction. It should also be noted that, at any time, students can consult the prediction of their final grade, in order to be aware of their learning behavior.
4.2. Introductory Course
The second study is based on the data of the introductory course. This course is mandatory for all students who want to be enrolled in any of the masters offered by the ILCE. The main objective of this course is to provide a general background about the main topics offered by the different master courses, as well as to develop a set of competencies and skills related with communication, computation, and critical thinking. A set of 146 students enrolled in the introductory course is used in this study. From these, 100 students were used as a training set; the test set contains 30 students and the validation set consists of 16 students. The set of features available for this study are presented in Table 6.

Table 6.
Data features collected from the introductory course.
As in the previous study (Section 4.1), all experiments have been performed in a dynamic and incremental way (refer to Figure 2), based on the educational scheduling of each course and using the information available at each moment. Four models are also identified in this case by teachers and course coordinators, which incrementally describe the dynamic learning behavior of students along the course. In the next sections a detailed analysis of the results obtained by these FIR models is performed.
4.2.1. Time 1 Model
The first model is scheduled when students have done their first homework (H1 feature), since not much general information of the student is available in this course. In fact, only the GROUP where the student is enrolled is a feature not related to a grade.
Table 7 presents the results of the toolbox functionalities. The FIR model chose both input variables, i.e., GROUP and H1, as part of the prediction model, since no more information is available at this time. However, ACEP founds that H1 has a much higher relevance than the GROUP feature for the final mark prediction. H1 has as twice of the relevance than GROUP. This make sense, since H1 has a direct incidence in the course evaluation process.

Table 7.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 1 of the introductory course. The MARK variable was discretized into three classes: fail (from 0–60), pass (from 61–80), and excellent (from 81–100). H1 was also discretized into three classes: low (from 0–6), medium (from 6.1–8.9) and high (from 9–10). The GROUP is a discrete variable and can take seven different values; therefore, it is discretized into seven classes. Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
With respect the set of rules obtained, defining students’ learning behavior (USLB), there are three rules that define the class pass and two that defines the class excellent. It is interesting to notice that when the set of rules are used to infer the students of the test set, the sensitivity of the excellent class is quite high (0.81), meaning that if the result of the inference for a given student is that he/she will get an excellent, it is quite certain that the student will get this mark. However, we have to take into account that, as in the case of the didactic planning course, we are working with an imbalanced dataset. Therefore, the micro-average precision is the metric that gives as more information related to the precision of model at time 1. This metric has a value of 0.57, which is quite low, but at the same time is an expected result, since, clearly, not enough information is available yet to be able to infer a good prediction model.
As can be seen at the bottom of Table 7, only three students (out of 9) have been predicted correctly as students who will fail the course. For the categories pass and excellent, 1 and 13 students have been correctly predicted, out of 5 and 16, respectively. It is quite clear that the model, at this time, cannot successfully forecast the failing students, obtaining an overall mean square error (MSE) of 1.16, which is quite high. However, it is pretty good predicting excellent students. Therefore, it is a model that already helps teachers to give specific feedback to the set of students that, at this point of the course, are predicted as fail or pass students (i.e., non-excellent students).
4.2.2. Time 2 Model
At this time of the course, the data available is the one used by model 1 (i.e., GROUP and H1), plus the mark obtained by the student in the second homework, H2. The toolbox results obtained for this model are summarized in Table 8.

Table 8.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 2 of the introductory course. The MARK variable was discretized into three classes: fail (from 0–60), pass (from 61–80), and excellent (from 81–100). H2 was also discretized into three classes: low (from 0–6), medium (from 6.1–8.9), and high (from 9–10). Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
The FIR model has found that the input variable more causally related with the final mark is the second homework (H2) submitted by the students. As a result of the ACEP functionality, it is clearly seen that the H2 feature makes the difference; it is a really key factor to pass the course. That is why the relative relevance of H2 is 1. The MSE of this model is really low, with respect the error obtained by the previous model, i.e., 0.15 vs. 1.16. The rules model derived from the LR-FIR approach define only one rule for the fail class and another rule for the excellent class. Moreover, the classification metrics have increased heavily with respect the ones obtained by the Time 1 model, mainly for the fail class that has its maximum value for the three metrics.
The current model is able to identify 9 fail (out of 9), 4 pass (out of 5), and 12 excellent (out of 16) students. This is a very interesting result, since this model can be used from the third month of the course. From the first rule, it can be stated that if the student has a low mark in the second homework, will fail the whole course. This information is extremely valuable for the teacher from two different perspectives. On the one hand, he/she can propose specific actions for this set of students in order not to give them up for lost and help overcome their limitations. On the other hand, this information will make the teacher reflect on the evaluation method designed for the course. The fact that the second task of the course is so decisive is perhaps not a good strategy from the point of view of the learning objective.
4.2.3. Time 3 Model
To identify the model at time 3, all of the features used in the previous models, plus the mark of the didactic problem forum (DPF), and the mark of the co-evaluation (COEV), are available. The toolbox results for this model are summarized in Table 9.

Table 9.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 3 of the introductory course. The MARK variable was discretized into three classes: fail (from 0–60), pass (from 61–80), and excellent (from 81–100). H2 and COEV were also discretized into three classes: low (from 0–6), medium (from 6.1–8.9), and high (from 9–10). Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
The ACEP results demonstrate that the FIR model selects as the most relevant variables, H2 (which has been identified as crucial in the previous model) and COEV. Remember that COEV was also a relevant feature in the didactic planning course. H2 has more influence in the final mark prediction than COEV, since the relative relevancies are 0.64 and 0.36, respectively. As expected, the same rule obtained in model 2, which defines the failing students, is identified in model 3. Notice, however, that the rules that describe excellent students incorporate the COEV feature. These rules are then used to infer the final mark of the students that conform the test set. As seen in Table 9, the sensitivity for the excellent class is increased from 0.75 to 0.81 and the specificity from 0.83 to 0.86. However, notice that the micro-average precision remains the same.
The ASLP is better than the previous model, with a MSE of 0.094. The current model is able to identify all (9) failing students, 3 out of 5 pass students and 13 out of 16 excellent students. The results derived from this model can again be very useful as the teacher can focus on fail and pass clusters (i.e., not excellent students). This effort can have positive results considering that there are still two months left to the end of the course and several evaluation works pending.
4.2.4. Time 4 Model
The last model has available all the features described in Table 6. The toolbox results obtained for this model are summarized in Table 10. As can be seen from the ACEP results, the co-evaluation (COEV) and the final report of the didactic problem (FRDP) are the main assessment events to predict the course performance for each student, with relative relevance values of 0.55 and 0.45, respectively.

Table 10.
ACEP, USLB, ASLP, and GSLB toolbox results for the model 4 of the introductory course. The MARK variable was discretized into three classes: fail (from 0–60), pass (from 61–80), and excellent (from 81–100). COEV was discretized into three classes: low (from 0–6), medium (from 6.1–8.9), and high (from 9–10). FRDP was discretized into three classes: low (from 0–20), medium (from 21–30), and high (from 31–40). Spec., Sen., and Acc. stand for specificity, sensitivity, and accuracy, respectively.
Notice that the rule that represents the set of failing students is based only on the FRDP feature, obtaining a sensitivity, specificity, and accuracy values of 1. Therefore, this rule predicts correctly all the students that fail de course, as already did the first rule of models 2 and 3, using the H2 feature. Therefore, both variables (H2 and FRDP) describe completely this class, providing redundant information. The two rules that describe excellent students obtain better sensitivity and accuracy metrics than the previous models, when applied to the students of the test set. Moreover, the micro-average precision has also slightly increased. The set of rules obtained by the USLB option is simple, comprehensive, and provides new knowledge of the course to teachers and course coordinator. It has also been found in this study, that forum features do not appear in any of the models. Forum activities imply, usually, a significant workload. Teachers and course coordinators can use these results to revise the equation that computes the final mark to obtain a better representation of the knowledge acquired by the students. As shown in Table 10, the reduced MSE of 0.025 demonstrates that the proposed toolbox is capable of accurately capturing students’ performance. As previously mentioned, all the failing students are predicted correctly using model 4. For the categories pass and excellent, 2 and 15 students have been correctly predicted, out of 5 and 16, respectively.
4.2.5. Using the Toolbox in the Next Course
The models developed and validated for the introductory course using data from students who had taken the course in previous editions, were analyzed, and used by five teachers in the new edition of the same course.
As in the previously analyzed course, the Time 1 model, due to the fact that the course has just started, does not provide useful knowledge for the teachers who are carrying out the new edition of the course. However, Time 2 model is very useful for teachers. Firstly, analyzing the rules, it is concluded that it is possible to predict quite accurately (MSE of 0.15) the final grade of the student using only homework 2 (H2), independently of the grade the student had obtained in homework H1. The five teachers involved in the course were very surprised about this. They considered the H1 assignment to be important in the learning process and decided that they would study how to make it more relevant, both in content and in its role in the final grade formula. Secondly, they decided to send an e-mail to the cluster of fail students, offering them a review and questions class regarding the H2 task. It is important that students understand very well the concepts associated to H2 in order that they can consolidate the knowledge of the rest of the course, since in Time 3 model H2 feature still is a key factor of students’ learning behavior. Notice that in model 3, the mark of the co-evaluation (COEV) plays also an important role. Teachers, at this point in time (third month from the beginning of the course), decided to give a stricter follow-up to students who obtained low evaluation in the H2 homework. A weekly message is sent to the students asking them to report the work done that week. The rules model at Time 4 tells us that if students do a good job in the final report of the didactic problem (FRDP) they will pass the course. Therefore, the objective of teachers is to try to ensure that students carry out a continuous and quality work in the rest of the tasks that remain to finish the course, and for that reason they propose a more personalized follow-up measure to this cluster of students.
Finally, the five teachers of the current course analyzed the fact that homework 3 (H3) was not relevant in the prediction model. They considered that this task was just as important, from the point of view of knowledge acquisition, as H2, and that, therefore, they should study how to give it greater weight in the final grade. Notice that at any time students can consult the prediction of their final grade, in order to be aware of their learning behavior.
5. Conclusions
In this paper, an e-Learning toolbox is presented, whose main goal is to improve the e-Learning experience, and reduce the workload of teachers. Using the toolbox, the teachers and course coordinators can analyze the interaction of students with the e-Learning environment. The soft computing methodologies (FIR, LR-FIR, and CR-FIR), which are the data mining core of the toolbox, are able to offer valuable knowledge to both teachers and students that can be used to enhanced course performance.
One of the most critical challenges in web-based distance education systems is the personalization of the e-Learning process. The characterization of students’ online behavior would benefit, in terms of students’ mark prediction from two perspectives. First, as a tool capable of determining the relevance of the features involved in the analyzed data set. Second, as a method to extract interpretable rules describing students’ learning behavior.
As highlighted previously, the evaluation process is, probably, the most time-consuming task for teachers, due to the fact that, many evaluative acts are involved in this type of course. Therefore, the influence of all these factors in the final mark is not always well defined and/or analyzed. To this end, the toolbox proposed in this research is very useful to discover features that are highly relevant for the evaluation of groups (clusters) of students. In this way, it is possible for teachers to provide feedback to students, on their learning activity, online, and in real time, in a more effective way than if they tried to do it individually. This option, using clustering methods, can reduce teachers’ workload.
The experimental results have shown that the proposed toolbox is able to predict students’ learning performance; to determine the most relevant features involved in the evaluation process, and their relative weight; and to extract linguistic rules that are easily understandable by experts in an educative domain and that may expose problems with the data itself. This knowledge could be used for real time student guidance, and to help teachers in finding patterns of student behavior.
Currently, the e-Learning toolbox presented is working solely on the ILCE intranet; however, in the near future, several plug-ins will be implemented to allow the connection with the most known e-Learning platforms. Some security considerations will have to be taken into account in a future version. Right now, the implementation of the toolbox servlets makes it possible to execute all code on the host computer. Access to the servlets should be restricted to users on a password basis in order to reduce the security hazards. Moreover, it is necessary to include secure RMI (Remote Method Invocation) and web service features to the toolbox in order to maintain a high confidentiality of sensible information.
Author Contributions
Conceptualization, À.N. and F.M.; methodology, À.N., F.M., F.C.; software, F.C.; validation, À.N., F.M. and F.C.; formal analysis, À.N.; investigation, À.N., F.M. and F.C.; resources, F.C.; data curation, F.C.; writing—original draft preparation, F.C.; writing—review and editing, À.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors want to acknowledge the ILCE institution, which provided the data sets analyzed in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arkorful, V.; Abaidoo, N. The role of e-learning, advantages and disadvantages of its adoption in higher education. Int. J. Instr. Technol. Distance Learn. 2015, 12, 29–42. [Google Scholar]
- Dwivedi, S.K.; Rawat, B. An Architecture for Recommendation of Courses in e-Learning. Int. J. Inf. Technol. Comput. Sci. 2017, 4, 39–47. [Google Scholar] [CrossRef]
- Vellido, A.; Castro, F.; Nebot, A. Clustering educational data. In Handbook of Educational Data Mining; Chapman & Hall/CRC Press: London, UK, 2011; pp. 75–92. ISBN 9781439804575. [Google Scholar]
- Abu-Naser, S.; Ahmed, A.; Al-Masri, N.; Deeb, A.; Moshtaha, E.; Abu-Lamdy, M. An Intelligent Tutoring System for Learning Java Objects. Int. J. Artif. Intell. Appl. 2011, 2, 68–77. [Google Scholar] [CrossRef]
- Zorrilla, M.E.; Garcia, D.; Álvarez, E. A decision support system to improve e-learning environments. In Proceedings of the 2010 EDBT/ICDT Workshops, Lausanne, Switzerland, 22–26 March 2010; pp. 1–8. [Google Scholar]
- Hegazi, M.O.; Abugroon, M.A. The State of the Art on Educational Data Mining in Higher Education. Int. J. Comput. Trends Technol. 2016, 31, 46–56. [Google Scholar] [CrossRef]
- Peña Ayala, A. Educational Data Mining: A survey and Data Mining-based analysis. Expert Syst. Appl. 2014, 41, 1432–1462. [Google Scholar] [CrossRef]
- Santos, O.C.; Barrera, C.; Boticario, J.G. An Overview of aLFanet: An Adaptive iLMS based on standards. In Adaptive Hypermedia and Adaptive Web-Based Systems; De Bra, P.M.E., Nejdl, W., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3137. [Google Scholar]
- aLFanet. Available online: http://adenu.ia.uned.es/alfanet/ (accessed on 13 May 2020).
- Romero, C.; Ventura, S.; Delgado, J.A.; De Bra, P. Personalized Links Recommendation Based on Data Mining in Adaptive Educational Hypermedia Systems. In Proceedings of the second European Conference on Technology Enhanced Learning, EC-TEL, Crete, Greece, 17–20 September 2007; Springer LNCS: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- AHA. Available online: http://aha.win.tue.nl (accessed on 13 May 2020).
- Kortemeyer, G. LON-CAPA–An Open-Source Learning Content Management and Assessment System. In Proceedings of the ED-MEDIA -World Conference on Educational Multimedia, Hypermedia & Telecommunications, Honolulu, HI, USA, 22 June 2009; pp. 1515–1520. [Google Scholar]
- LON-CAPA. Available online: https:/loncapa.msu.edu/adm/login (accessed on 13 May 2020).
- ATutor. Available online: https://atutor.github.io/ (accessed on 13 May 2020).
- LExIKON. Available online: https://www.dfki.de/web/forschung/edtec/ (accessed on 13 May 2020).
- Blackboard. Available online: http://www.blackboard.com/index.html (accessed on 13 May 2020).
- Weber, G.; Brusilovsky, P. ELM-ART—An Interactive and Intelligent Web-Based Electronic Textbook. Int. J. Artif. Intell. Educ. 2016, 26, 72–81. [Google Scholar] [CrossRef]
- ELM-ART. Available online: http://art2.ph-freiburg.de/Lisp-Course (accessed on 13 May 2020).
- Moodle, Learning Analytics. Available online: https://moodle.com/ (accessed on 13 May 2020).
- Liu, D.Y.T.; Froissard, J.C.; Richards, D.; Atif, A. An enhanced learning analytics plugin for Moodle: Student engagement and personalised intervention. In Proceedings of the ASCILITE 2015–Australasian Society for Computers in Learning and Tertiary Education, Conference Proceedings, Perth, Australia, 30 November–3 December 2019; pp. 180–189. [Google Scholar]
- Akcapinar, G.; Bayasit, A. MoodleMiner: Data Mining Analysis Tool for Moodle Learning Management System. Elem. Educ. Online 2019, 18, 406–415. [Google Scholar] [CrossRef]
- GISMO. Available online: http://gismo.sourceforge.net (accessed on 10 September 2020).
- Lu, O.H.T.; Huang, A.Y.Q.; Huang, J.C.H.; Lin, A.J.Q.; Ogata, H.; Yang, S.J.H. Applying Learning Analytics for the Early Prediction of Students’ Academic Performance in Blended Learning. Educ. Technol. Soc. 2018, 21, 220–232. [Google Scholar]
- Hussain, S.; Dahan, N.A.; Ba-Alwi, F.M.; Ribata, N. Educational Data Mining and Analysis of Students’ Academic Performance Using WEKA. Indones. J. Electr. Eng. Comput. Sci. 2018, 9, 447–459. [Google Scholar] [CrossRef]
- WEKA. Available online: https://www.cs.waikato.ac.nz/ml/weka/ (accessed on 13 September 2020).
- Juhanak, L.; Zounek, J.; Rohlikova, L. Using process mining to analyze students’ quiz-taking behavior patterns in a learning management system. Comput. Hum. Behav. 2019, 92, 496–506. [Google Scholar] [CrossRef]
- Almasri, A.; Celebi, E.; Alkhawaldeh, R.S. EMT: Ensemble Meta-Based Tree Model for Predicting Student Performance. Sci. Program. Hindawi 2019, 2019, 3610248. [Google Scholar] [CrossRef]
- Aung, T.H.; Kham, N.S.M. Cloud Based Teacher’s Assessment Data in Educational Data Mining. In Proceedings of the 9th International Workshop on Computer Science and Engineering, WCSE, Hong Kong, China, 15–17 June 2019; pp. 159–164. [Google Scholar]
- Jayapradha, J.; Kumar, K.J.J.; Deka, B. Educational Data Classification and prediction using Data Mining Algorithms. Int. J. Recent Technol. Eng. 2019, 8, 8674–8678. [Google Scholar]
- Abubakar, Y.; Bahiah, N.; Ahmad, H. Prediction of Students’ Performance in E-Learning Environment Using Random Forest. Int. J. Innov. Comput. 2016, 7, 1–5. [Google Scholar]
- Klir, G.; Elias, D. Architecture of Systems Problem Solving, 2nd ed.; Plenum Press: New York, NY, USA, 2002. [Google Scholar]
- Nebot, A.; Mugica, F. Fuzzy Inductive Reasoning: A consolidated approach to data-driven construction of complex dynamical systems. Int. J. Gen. Syst. 2012, 41, 645–665. [Google Scholar] [CrossRef]
- Vellido, A.; Castro, F.; Etchells, T.A.; Nebot, A.; Mugica, F. Data Mining of Virtual Campus Data. In Evolution of Teaching and Learning Paradigms in Intelligent Environment. Studies in Computational Intelligence; Jain, L.C., Tedman, R.A., Tedman, D.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; p. 62. [Google Scholar]
- Castro, F.; Nebot, A.; Múgica, F. On the extraction of decision support rules from fuzzy predictive models. Appl. Soft Comput. 2011, 11, 3463–3475. [Google Scholar] [CrossRef]
- Nebot, A.; Mugica, F.; Castro, F. Causal Relevance to Improve the Prediction Accuracy of Dynamical Systems using Inductive Reasoning. Int. J. Gen. Syst. 2009, 38, 331–358. [Google Scholar] [CrossRef]
- Müller, S. JMatLink Library. Available online: http://jmatlink.sourceforge.net/ (accessed on 28 September 2020).
- ILCE. Available online: http://cecte.ilce.edu.mx/ (accessed on 13 May 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).