Towards Fully Jitterless Applications: Periodic Scheduling in Multiprocessor MCSs Using a Table-Driven Approach

Abstract

In mixed criticality systems (MCSs), the time-triggered scheduling approach focuses on a special case of safety-critical embedded applications which run in a time-triggered environment. Sometimes, for these types of MCSs, perfectly periodical (i.e., jitterless) scheduling for certain critical tasks is needed. In this paper, we propose FENP_MC (Fixed Execution Non-Preemptive Mixed Criticality), a real-time, table-driven, non-preemptive scheduling method specifically adapted to mixed criticality systems which guarantees jitterless execution in a mixed criticality time-triggered environment. We also provide a multiprocessor version, namely, P_FENP_MC (Partitioned Fixed Execution Non-Preemptive Mixed Criticality), using a partitioning heuristic. Feasibility tests are proposed for both uniprocessor and homogenous multiprocessor systems. An analysis of the algorithm performance is presented in terms of success ratio and scheduling jitter by comparing it against a time-triggered and an event-driven method in a non-preemptive context.

1. Introduction

Safety-critical systems are ubiquitous in our everyday life, from medical equipment and smart vehicles to military applications. These types of systems usually imply, on the one hand, a real-time response due to direct interaction with the environment and, on the other hand, the inclusion of several critical functionalities. Providing a real-time response while carefully managing resources and providing temporal and spatial isolation for the critical applications imposes the need for carefully tailored real-time scheduling approaches.

In a special category of safety-critical applications which run in a time-triggered environment, perfectly periodical (i.e., jitterless) scheduling for certain critical tasks is needed. This need can appear from message synchronization problems [1], from signal processing applications [2,3,4,5], or simply from conditions imposed by different types of certifications [6]. Moreover, jitterless execution is desired for certain tasks in any embedded control system, as jitter only introduces difficulties in control loops [6]. As stated in [7], computer-controlled systems are designed assuming periodical sampling and zero or negligible jitter. In practice, the only jitter that can be relatively easily eliminated is sampling jitter, by using dedicated hardware. Input–output jitter is influenced by the scheduling policy. Guaranteeing the performance and stability of the controller in target systems also implies, besides a bounded response time, a guarantee that the input–output jitter is bounded within a so-called jitter margin [7].

Dealing with task execution in a time-triggered environment for classical real-time systems is done using time-triggered (clock-driven) scheduling techniques, among which the static table-driven approach stands out.

The table-driven approach is based on static schedulability analysis, generating a scheduling table that is used at run time to decide the moment when each task instance (also called a job) must begin its execution [8]. A special case of real-time systems is represented by the mixed criticality systems (MCSs), where tasks with different criticalities, categorized based on a finite set of criticality levels, share the same hardware [9]. The system is considered to run in a number of criticality modes, each mode giving a certain degree of execution time assurance [9].

While the classical real-time approach implies the construction of a single scheduling table, in MCSs, things become more complex due to the number of criticality modes. The change from one criticality mode to another corresponds to a transition from one precomputed scheduling table to another. Thus, in MCSs, there is one scheduling table per criticality level [10].

MCSs are a suitable variant that can be used with respect to providing a real-time response, while isolating the critical functionalities. If we analyze safety-critical systems in the case of MCSs, there are certain advantages of such table-driven approaches over event-driven scheduling: easier certification, given by the fact that table-driven schedulers are completely deterministic [10]; easier synchronization between tasks [1]; easier power management, as each power-mode corresponds to a criticality level, and each level uses its own table; and easier adaptation of real-time applications from different fields like automotive, avionics, etc., which already use table-driven approaches [11].

In this paper we propose an adaptation of a real-time, table-driven, non-preemptive scheduling method for MCSs which guarantees jitterless execution in a mixed criticality time-triggered environment for both uniprocessor and homogenous multiprocessor systems. We also provide a partitioning heuristic for this scheduling method for multiprocessor systems.

The main contributions of this paper are as follows:

• A mixed criticality scheduling algorithm, FENP_MC (Fixed Execution Non-Preemptive Mixed Criticality), is proposed for jitterless task execution in a time-triggered environment;
• An adaptation of the FENP_MC for homogenous multiprocessor systems, P_FENP_MC, is provided;
• Feasibility tests are proposed for both uniprocessor and homogenous multiprocessor systems;
• The algorithm performance is analyzed using the success ratio against the utilization of the task sets;
• The proposed algorithm performance is compared against a time-triggered and an event-driven scheduling method in a non-preemptive context: Time-Triggered Merge (TT-Merge)/Energy-efficient Time-Triggered Merge (Energy-efficient TT-Merge) [12] and Earliest Deadline First with Virtual Deadlines (EDF-VD) [13], a non-preemptive variant.

The rest of this paper is structured as follows: In Section 2 we briefly present the state of the art regarding scheduling in a mixed criticality time-triggered environment. In Section 3, we describe our proposed scheduling algorithm for uniprocessor mixed criticality systems, while in Section 4, we propose an adaptation for homogenous multiprocessor MCSs. In Section 5, we analyze the performance of the proposed algorithm in terms of success ratio and compare it against a popular one, namely, EDF-VD NP (EDF-VD in its non-preemptive form). We conclude our paper in Section 6, where we also propose some future research and development directions.

2. Related Work

Since Vestal’s first mixed criticality model formalization [14], MCSs have attracted particular attention that has materialized in a set of scheduling algorithms that can be classified based on their scheduling points (i.e., the moments in time when scheduling decisions are made) into three categories: event-driven, time-triggered, and hierarchical scheduling approaches.

An extensive survey on scheduling in MCSs [9] shows that, until recently, the scheduling problem was mainly focused on event-driven scheduling algorithms, despite the fact that there are also important endeavors regarding time-triggered and hybrid approaches. In event-driven schedulers, the scheduling points are defined by task completion and task arrival events. Examples of event-driven schedulers were introduced in [15,16,17,18,19]. A popular event-driven scheduling algorithm in MCSs is Earliest Deadline First with Virtual Deadlines (EDF-VD) for two criticality levels (Hi—high criticality and Lo—low criticality) [13]. The algorithm computes a virtual deadline for every Hi-criticality task if the system is in Lo mode. In Hi mode, Hi-criticality tasks are scheduled according to their real deadlines. This is done in order to balance the schedulability on different criticality levels, which results in better schedulability and run-time performance.

Due to their predictability, time-triggered approaches have become increasingly popular in the last couple of years, but the relevant works are still limited and much more could be expected in the future. Time-triggered schedulers make their scheduling decisions at predetermined points in time. Few papers tackling MC scheduling in time-triggered environments appeared only in the last decade [6,10,12,20,21]. In [20], a heuristic for constructing scheduling tables in a time-triggered environment was presented. The algorithm relies on backtracking to guide the search in a tree-based structure, and it consists of two heuristics: one for constructing the scheduling tables and the other for backtracking. Another method for constructing scheduling tables based on priority ordering is described in [10]. The technique incorporates “mode-change”, which increases flexibility and system performance. In [21], a time-triggered scheduling algorithm for both independent and dependent MC jobs on an identical multiprocessor platform is proposed. Two separate scheduling tables are constructed for each processor to schedule dual-criticality tasks. Furthermore, the schedule is global, which means that jobs can be preempted in one processor and resume their execution in another processor. While the algorithms mentioned before are focused on predictability, the main goal of the algorithm proposed in [6] is to provide a low-jitter periodic schedule for mixed criticality messages in a time-triggered non-preemptive environment. Additionally, the algorithm introduced in [12] is meant to reduce the energy consumption. However, none of the algorithms mentioned above are focused on guaranteeing jitterless execution in a mixed criticality system, for all the active tasks, regardless of the system criticality mode. This is obviously a requirement for many safety-critical systems and represents the gap we aim to fill in this paper.

Hierarchical approaches combine both scheduling tables and event-driven scheduling methods, but the research on such systems is still in its preliminary stage. A hierarchical algorithm was introduced in [22] for scheduling MC real-time tasks on multiprocessor platforms. The method provides temporal isolation among tasks of different criticalities while allowing slack to be redistributed across different criticality levels. The same algorithm was implemented and tested on a standard real-time operating system (RTOS) in [23]. The experimental results showed that RTOS-related overheads are maintained at acceptable levels and the system is robust with respect to breaches of optimistic execution time assumptions.

3. FENP_MC: Fixed Execution Non-Preemptive Mixed Criticality

In this section we propose a scheduling algorithm for MCSs running in a time-triggered non-preemptive environment in response to the demand for jitterless task execution, with applicability to tasks used in signal processing, different types of synchronizations, control loops, etc. [1,6,7,24].

3.1. Perfectly Periodical Task Model

In real-time mixed criticality systems, periodical task execution models are based on the model originally proposed by Liu and Layland in 1973 [25]. This model imposes periodical behavior only regarding the release time. In most of the systems based on this periodical task model, the actual execution starting time is pseudo periodical [26].

Another type of model, not very different from the one proposed by Liu and Layland, but focused on this special case of periodical real-time tasks, was firstly proposed in [24]. In this paper, the tasks are called FModXs (fixed execution executable modules). Starting from this model, we propose a simplified version of a perfectly periodical task model for real-time systems:

$$M_i=\left\{T_i,D_i,C_i,S_i\right\}$$

(1)

where $T_i$ represents the period of periodical task i, $D_i$ is the time by which any job execution needs to complete, relative to its release time, $C_i$ represents the computation time, and $S_i$ gives the execution start time, relative to its release time.

Following Vestal’s approach to extend Liu and Layland’s model to mixed criticality systems [14], we propose the following perfectly periodical task model for MCSs:

$$M_i=\left\{T_i,D_i,L_i,\left\{C_{i,L_j}\right|j\in 1\dots l\},\{S_{i,L_j}|j\in 1,\dots ,l\}\right\}$$

(2)

where $M_i$ is a mixed criticality fixed execution task (MC-FModX), l represents the number of criticality levels, $T_i$ is the period for periodical tasks, $D_i$ is the time by which any job execution needs to complete, relative to its release time, $L_i$ represents the criticality level (1 being the lowest level), $C_{i,L_j}$ is the computation time, and $S_{i,L_j}$ is a vector of values—one per criticality level, for levels lower than or equal to the criticality level $L_i$. C expresses the worst-case execution time (WCET) for each criticality level and S the execution start time, relative to its release time, for each level of criticality lower than or equal to the task criticality level $L_i$.

A task consists of a series of jobs, with each job inheriting the set of parameters of the task, ($T_i,D_i,L_i)$, to which it adds its own parameters [27]. Thus, the kth job of task ${\tau }_i$ is characterized as

$$J_{i,k}=\left\{a_{i,k},d_{i,k},c_{i,k},s_{i,k} T_i,D_i,L_i\right\}$$

(3)

where $a_{i,k}$ represents the arrival time ($a_{i,k+1}-a_{i,k}\ge T_i$), $d_{i,k}$ is the absolute deadline ($d_{i,k+1}=a_{i,k}+D_i$), C represents the execution time allocated by the system, which is dependent on the criticality mode of the system (for $L_j$, $C_{i,k}=C_{i,L_j}$), $s_{i,k}$ gives the absolute execution start time of job k of task i which is also dependent on the criticality mode of the system, and $T_i,D_i,L_i$ have the same meaning as in the task model.

3.2. Perfectly Periodical Task Execution Model

Definition 1.

We say that the execution of task i is perfectly periodical if for each job k of task i,$J_{i, k}$, the difference between the absolute start times of jobs k and k − 1 is constant:

$$s_{i,1}-s_{i,0}=s_{i,2}-s_{i,1}=\dots =s_{i,n}-s_{i,n-1}=T_i.$$

(4)

In order to exemplify a perfectly periodical execution algorithm, let us consider the task set presented in Table 1 that needs to be scheduled on a single-processor system, with two criticality levels (Low—Lo and High—Hi). In Table 1, $T_i$ is the period of task i, $D_i$ represents the deadline, $L_i$ is the criticality level, $C_{i,L_{Lo}}$ expresses the computation time for the Lo-criticality mode and $C_{i,L_{Hi}}$ is the computation time for the Hi-criticality mode $C_{i,L_{Hi}}$.

Table 1. Three-task set example.

Task	${\mathit{T}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	${\mathit{L}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{L}\mathit{o}}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{H}\mathit{i}}}$
$M_1$	10	10	Lo	3	-
$M_2$	20	20	Hi	2	4
$M_3$	30	30	Hi	5	6

The start times of the tasks for the Lo-criticality case are depicted in Figure 1.

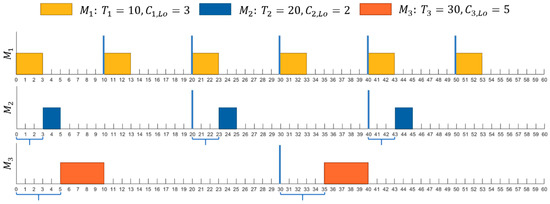
Figure 1. Start times for the three-task set example in Lo-criticality mode.

In an MCS, Equation (4) must be true for all the criticality modes of the system (i.e., for all criticality levels), as shown in Figure 2, where $P{0}_{Lo}$ represents low criticality and $P{0}_{Hi}$ represents the high criticality level.

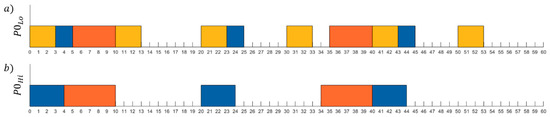
Figure 2. Scheduling the three-task set example in (a) Lo-criticality mode and (b) Hi-criticality mode.

In MCSs, different tasks with different criticality requirements share the same hardware; thus, in these systems, missing a deadline varies in severity from task to task [14]. In order to protect critical tasks from the interference of less critical ones, different levels of criticality are assigned to each task and different levels of assurance are provided for tasks running in different running scenarios, called criticality modes.

As explained in [9], the classical model implies that the MCS starts in the lowest criticality mode. If all jobs behave according to the level of assurance imposed by this mode, then the system stays in that mode. On the other hand, if they attempt to execute for a longer time, then a criticality mode change occurs to a higher level of assurance.

Next, we present an example where this mode change must occur and how FENP_MC treats the situation. Let us consider the task set presented in Table 2.

Table 2. Four-task set example.

Task	${\mathit{T}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	${\mathit{L}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{L}\mathit{o}}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{H}\mathit{i}}}$
$M_1$	8	8	Lo	2	-
$M_2$	12	12	Hi	2	6
$M_3$	16	16	Lo	2	-
$M_4$	24	24	Hi	1	5

In Figure 3a, two scheduling tables are provided for two criticality modes ($P{0}_{Lo}$ for the Lo-criticality mode and $P{0}_{Hi}$ for the Hi-criticality mode, where Lo < Hi). The system starts in the Lo-criticality mode, using the $P{0}_{Lo}$ scheduling table, but at Moment 4, task $M_2$ exceeds its time budget allocated for the Lo-criticality mode, and that causes a criticality mode switch (see Figure 3b). The system continues to run according to the $P{0}_{Hi}$ scheduling table, starting with the zeroth time instance. In this Hi mode, all Lo-criticality tasks are dropped, and only Hi-criticality tasks are scheduled according to their Hi level of assurance computation time.

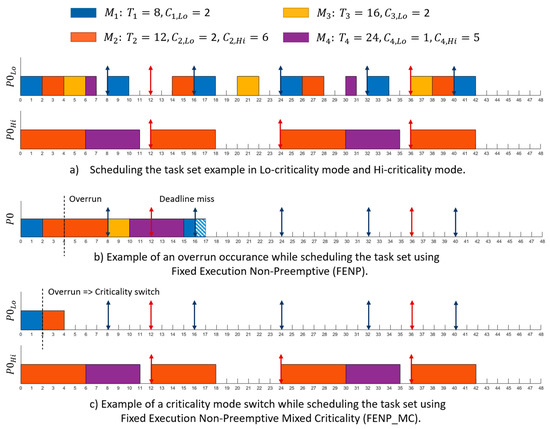
Figure 3. Example of a criticality mode switch.

3.3. Feasibility Analysis

3.3.1. Theoretical Aspects

Next, we present an exact feasibility test for perfectly periodical execution in a non-preemptive context. We call this type of execution Fixed Execution Non-Preemptive (FENP). The test is analogous with that provided in [24].

Let $M=\{M_1, M_2, \dots , M_n\}$ be a set of n independent MC fixed execution tasks (MC-FModXs), sorted in nondecreasing order of their periods. The MC tasks are characterized by the same parameters as those in Equation (2); thus,

$$\begin{array}{c}{M}_k\equiv \left\{T_k,D_k,L_k,\left\{C_{k,L_j}\right|j\in 1,\dots ,l\},\{S_{k,L_j}| j\in 1,\dots ,l\}\right\}, \mathrm{where} \mathrm{for} \mathrm{any} \mathrm{task} i,\\ T_i\le T_k \mathrm{for} i<k.\end{array}$$

(5)

Definition 2.

The task set M is FENP schedulable in a mixed criticality system if, and only if, the task set M is FENP schedulable for each criticality level$L_j$, where$j\in 1,\dots ,l$.

Definition 3.

The task set M is FENP schedulable in a mixed criticality system for criticality level$L_j$if all the tasks in the set M with criticality equal to or higher than$L_j$are FENP schedulable using the next feasibility test. Only the parameters for level$L_j$($C_{k,L_j}$and$S_{k,L_j}$) are considered in this case.

The feasibility tests are based on an execution mapping function, which is defined next.

Definition 4.

A fixed-execution mapping of task$M_k$over the period of task$M_i$is a function of the form:

$$\begin{array}{c}{\Delta }_{M_i/M_k}:\left\{0, 1,\dots , T_i-1\right\}\to \left\{0, 1\right\}\\ {\Delta }_{M_i/M_k}\left(\tau \right)=\underset{x=0}{\overset{\frac{1}{GCD\left(T_i,T_k\right)} · T_k-1}{{\displaystyle \cup }}}{M}_k\left(\tau +x·T_i\right)\end{array}$$

(6)

where τ represents a discrete time function with values between 0 and$T_i$, $GCD\left(T_i,T_k\right)$computes the greatest common divisor of the periods of tasks$M_i$and$M_k$, and$M_k\left(\tau +x·T_i\right)$represents the execution function of$M_k$:

$$M_k:N\to \left\{0,1\right\}, M_k\left(\mathsf{\tau }\right)= \mathsf{\sigma } \left(t mod T_k-S_k\right)- \mathsf{\sigma } \left(t mod T_k-S_k-C_k\right)$$

(7)

where mod is the modulo operator and σ is the unity step function:

$$Z\to \left\{0,1\right\}, \mathsf{\sigma }=\{\begin{array}{c}1,x\ge 0,\\ 0,x<0.\end{array}$$

(8)

For a certain criticality level $L_j$, Equation (7) becomes

$$M_k:N\to \left\{0,1\right\}, M_k\left(\mathsf{\tau }\right)= \mathsf{\sigma } \left(t mod T_k-{\mathrm{S}}_{\mathrm{k},{\mathrm{L}}_{\mathrm{j}}}\right)- \mathsf{\sigma } \left(t mod T_k-{\mathrm{S}}_{\mathrm{k},{\mathrm{L}}_{\mathrm{j}}}-{\mathrm{C}}_{\mathrm{k},{\mathrm{L}}_{\mathrm{j}}}\right).$$

(9)

Feasibility test: For a given criticality level $L_j$, a subset $M_{L_j}$ of tasks with criticality level $L_k\ge L_j$ are schedulable if, and only if,

$$\begin{array}{c}\forall M_k\in M_{L_j},M_k\equiv \left\{T_k,D_k,L_k,C_{k,L_j},S_{k,L_j}\right\},\\ \exists t_q\in \left\{0, 1,\dots , T_k-C_{k,L_j}\right\} \mathrm{so} \mathrm{that} {{\displaystyle \cup }}_{\tau =t_0}^{t_q+C_{k,L_j}-1}{{\displaystyle \cup }}_{i=1}^{k-1}{\Delta }_{M_k/M_i\left(\tau \right)}=0\end{array}$$

(10)

where $t_q$ is a discrete time instant between 0 and the latest possible start time of task $M_k$ and ${\Delta }_{M_i/M_k\left(\tau \right)}$ is defined by Equation (6).

3.3.2. Execution Examples

For a better understanding, the execution mapping function for the task set example in Table 1 is depicted in Figure 4 for a system with two criticality modes.

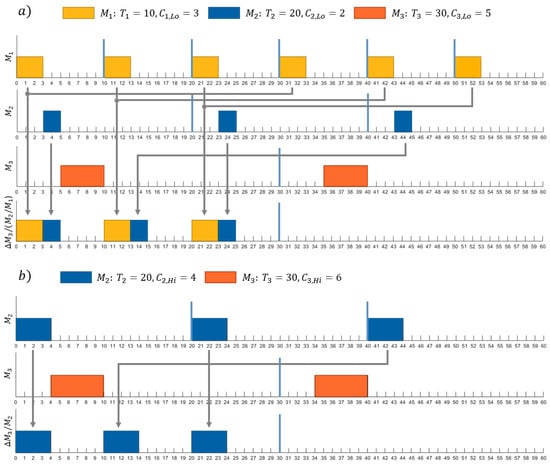
Figure 4. The execution mapping function for the task set example in Table 1 in (a) Lo-criticality mode and (b) Hi-criticality mode.

3.3.3. Implementation Guidelines

Algorithm 1 represents the pseudocode form of the feasibility test, which is an adaptation of [24] for MCSs.

Algorithm 1 Feasibility_test

Input:${\mathsf{\Gamma }}_q \left(the scheduling table of processor q\right), critLevel \left(the system criticality mode\right)$ Output:$FAILURE for a negative feasibility test, SUCCESS otherwise$ 1 sort ${\mathsf{\Gamma }}_q$ according to $T_i$ in a non-decreasing order 2 for$i=1;i<size of{ \mathsf{\Gamma }}_q;i++$do 3 for$j=0;j<i;j++$do 4 $gcd\leftarrow greatest common divisor of T_i and T_j$ 5 if$critLevel=Lo \mathrm{and} C_{i,critLevel}+C_{j,critLevel}>gcd$then 6 return$FAILURE$ 7 end if 8 if$critLevel=Hi and L_i=Hi \mathrm{and} L_j=Hi \mathrm{and} C_{i,critLevel}+C_{j,critLevel}>gcd$then 9 return$FAILURE$ 10 end if 11 end for 12 end for 13 return$SUCCESS$

3.4. FENP_MC

3.4.1. Theoretical Aspects

While event-driven scheduling approaches can only guarantee pseudo periodical execution, a carefully designed time-triggered approach can offer a solution for perfectly periodical tasks if we ignore the small jitter introduced by the criticality mode switch.

Next, we propose an adaptation to MCSs of the real-time table-driven scheduling algorithm FENP [24] for single processors and its partitioned P_FENP [28] variation for multicore systems.

The Fixed Execution Non-Preemptive (FENP) algorithm has been designed to provide maximum predictability for the execution of perfectly periodical tasks (FModXs) in a non-preemptive context.

Because the FENP algorithm follows Equation (4), each start time of job $J_{i,k}$ of task i can be determined knowing the start time of the previous job $J_{i,k-1}$:

$$s_{i,k}=s_{i,k-1}+T_i.$$

(11)

Moreover, $s_k$ can be statically determined in a direct manner:

$$s_{i,k}=s_{i,k-1}+k·T_i.$$

(12)

By designing a static scheduler based on Equations (11) and (12), we obtain jitterless task execution.

The FENP_MC scheduler creates, in an offline phase, a dispatch table for each criticality level of the system based on Equation (11) and on the feasibility tests firstly proposed in [24] for real-time operation and further developed and presented in the next section for mixed criticality systems.

The dispatch table is represented by an array of structures:

$${\mathsf{\Gamma }}_q=\left\{TaskID; StartTime\right\}$$

(13)

where ${\mathsf{\Gamma }}_q$ is sorted in nondecreasing order of start time for each job in the system for a scheduling period.

3.4.2. Execution Examples

Table 3 and Table 4 illustrate the Lo-criticality mode dispatch table and the Hi-criticality mode dispatch table, respectively, for the task set presented in Table 1:

Table 3. Lo-criticality mode dispatch table for the task set example in Table 1.

TaskID	StartTime
1	0
2	3
3	5

Table 4. Hi-criticality mode dispatch table for the task set example in Table 1.

TaskID	StartTime
2	0
3	4

3.4.3. Implementation Guidelines

The execution mapping function, presented in Algorithm 2 is used by the function for computing start times in Algorithm 3. Both algorithms are adaptations of [24] for MCSs.

Algorithm 2 MFunc

Input: $i \left(task index\right), t \left(time instance\right), critLevel \left(the system criticality mode\right)$ Output: $\Delta sigma=sigma1-sigma2$ 1 $temp\leftarrow mod\left(t,T_i\right)-S_{i, critLevel}$ 2 if$temp<0$then 3 $sigma1\leftarrow 0$ 4 else 5 $sigma1\leftarrow 1$ 6 end if 7 if$temp-C_{i, critLevel}<0$then 8 $sigma2\leftarrow 0$ 9 else 10 $sigma2\leftarrow 1$ 11 end if 12 return$sigma1-sigma2$

Algorithm 3 Start_Time_calculation

Input:${\mathsf{\Gamma }}_q \left(the scheduling table of processor q\right), critLevel \left(the system criticality mode\right)$ Output:$FAILURE to calculate the start times, SUCCESS otherwise$ 13 for$i=1;i<size of {\mathsf{\Gamma }}_q;i++$do 14 $schedulable\leftarrow 0$ 15 $count\leftarrow 0$ 16 $gcd\leftarrow 1$ 17 $StartTime\leftarrow -1$ 18 for$t=0;t\le T_i;t++$do 19 $delta\leftarrow 0$ 20 for$j=0;j<i;j++$do 21 if$delta\ne 0$then 22 break 23 end if 24 $gcd\leftarrow greatest common divisor of T_i and T_j$ 25 for$k=0;k<T_j/gcd;k++$do 26 if$delta\ne 0 or MFunc\left(j,t+k*T_i,critLevel\right)\ne 0$then 27 $delta\leftarrow 1$ 28 break 29 end if 30 end for 31 end for 32 if$count\ge C_{j,critLevel}$then 33 $S_{i, critLevel}\leftarrow StartTime$ 34 $schedulable\leftarrow 1$ 35 break 36 end if 37 if$delta\ne 0$then 38 $count\leftarrow 0$ 39 $StartTime\leftarrow -1$ 40 else 41 $count\leftarrow count+1$ 42 if$StartTime=-1$then 43 $StartTime\leftarrow t$ 44 end if 45 end if 46 end for 47 if$StartTime=-1$then 48 return$FAILURE$ 49 end if 50 if$schedulable=0$then 51 return$FAILURE$ 52 end if 53 end for 54 return$SUCCESS$

4. P_FENP_MC

4.1. Theoretical Aspects

For mixed criticality multicore systems, we propose an adaptation of the P_FENP which we call P_FENP_MC. The mapping algorithm is similar to that proposed in [28].

P_FENP_MC consists of two phases, namely, an offline phase and an online phase. The task partitioning to processors is carried out offline. A feasibility test is then conducted on each processor, followed by creating the table for that processor. Tasks are scheduled according to the dispatch tables in the online phase. The system starts in Lo-criticality mode; therefore, tasks will be scheduled according to the Lo-criticality dispatch table. Once a job executes beyond its Lo-criticality WCET, the system switches to Hi-criticality mode and tasks will be scheduled in compliance with the Hi-criticality dispatch table. For each processor dispatch table, tasks are sorted in nondecreasing order of their start times. Next, the task with the lowest start time $M_i$ is extracted from the dispatch table and its first instance $J_{i,0}$ is executed. After job $J_{i,0}$ finishes executing, the start time of task $M_i$ is recalculated. $M_i$ is then added to the corresponding dispatch table based on Equation (11), and the task with the lowest start time is again extracted from the sorted list of tasks and executed.

The partitioning algorithm proceeds as follows:

Each processor has a scheduling table associated to it. Tasks from the task set are selected one by one and added in each scheduling table. If the scheduling table was initially not empty, two conditions are verified:

I.

The current processor utilization, which is the sum of utilizations of all the tasks from the scheduling table associated with the corresponding processor and must not exceed 1 [29]:

$$U_{{\mathsf{\Gamma }}_q}\le 1,q=1,\dots ,m$$

(14)

where $q=1,\dots ,m$.

II.

The schedulability test performed for the task subset on the processor must be positive.

If the two conditions are met, the task will remain in the scheduling table, the processor utilization is updated, and the next task is removed from the ready queue and tested. If the scheduling table was initially empty, the task is added without verifying the two conditions and the processor utilization is updated.

If one of the two conditions returns FAILURE, the task is removed from the scheduling table and added in the next processor scheduling list, where the same test is performed.

4.2. Execution Examples

In order to illustrate the task partitioning method described in Section 4.1 we provide an example of six mixed criticality tasks scheduled on a dual-criticality system with two processors. Table 5 contains the timing parameters of the tasks and the processor utilization for each criticality level.

Table 5. Six-task set example.

Task	${\mathit{T}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	${\mathit{L}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{L}\mathit{o}}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{H}\mathit{i}}}$	${\mathit{U}}_{\mathit{i},{\mathit{L}}_{\mathit{L}\mathit{o}}}$	${\mathit{U}}_{\mathit{i},{\mathit{L}}_{\mathit{H}\mathit{i}}}$
$M_1$	24	24	Hi	5	6	0.208	0.25
$M_2$	72	72	Hi	8	9	0.111	0.125
$M_3$	18	18	Hi	3	4	0.167	0.222
$M_4$	8	8	Hi	1	2	0.125	0.25
$M_5$	36	36	Lo	6	-	0.167	-
$M_6$	12	12	Lo	2	-	0.167	-

In this case, P_FENP_MC provides the following results: tasks $M_1$, $M_4$, and $M_6$ are assigned to the first processor ($P_0$) with a Lo-criticality total utilization of 0.5 and a Hi-criticality total utilization of 0.5, while tasks $M_2$, $M_3$, and $M_5$ are partitioned to $P_1$ with a Lo-criticality total utilization of 0.445 and a Hi-criticality total utilization of 0.347. Scheduling for both the Hi- and Lo-criticality modes is illustrated in Figure 5.

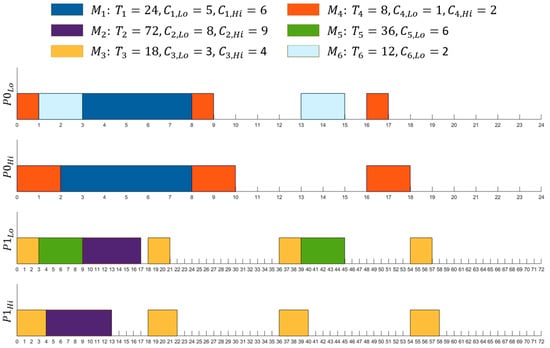
Figure 5. Partitioned Fixed Execution Non-Preemptive Mixed Criticality (P_FENP_MC) scheduling of the six-task set example.

It must be noted that for Condition I and for calculating the total utilization on each processor, we use Hi-criticality total utilization for the Hi-criticality WCET and Lo-criticality total utilization for the Lo-criticality WCET. Therefore, Condition I must be verified for both the Hi-criticality total utilization and the Lo-criticality total utilization. For Condition II, both the Lo-criticality WCET and the Hi-criticality WCET are considered.

4.3. Implementation Guidelines

Next, the two phases of the algorithm are described using diagrams. In the offline phase, the dispatch tables for each processor are created using the mapping function and the feasibility test. A diagram of the P_FENP_MC offline phase is presented in Figure 6.

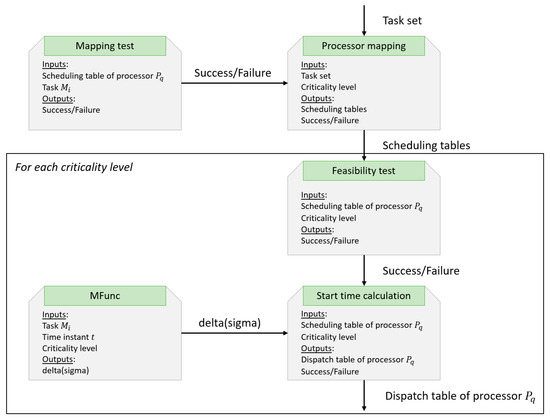
Figure 6. Offline phase execution.

The online phase uses the dispatch tables created in the previous phase and consists of the actual scheduling algorithm. On each processor, its dispatch table is used and updated dynamically. In this table, jobs are sorted in nondecreasing order of their start times and then, one by one, extracted from the set in order to be executed. Once a task instance is executed, the start time of the next instance is calculated using Equation (11) and inserted in the dispatch table so that the table remains sorted by start times. Figure 7 depicts the online phase of the P_FENP_MC algorithm.

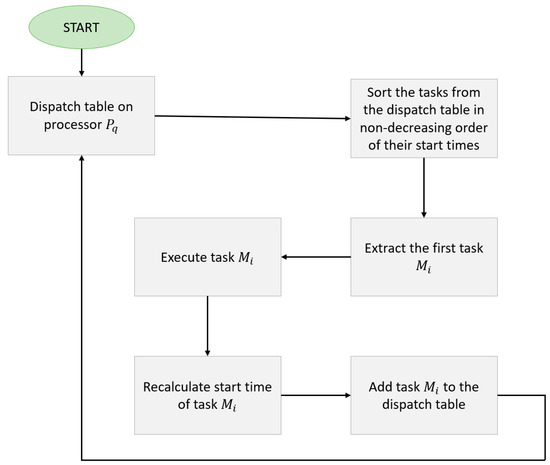
Figure 7. Online phase execution.

The feasibility test conducted on each processor is shown in Algorithm 4, while Algorithm 5 computes the processor dispatch tables.

Algorithm 4 Mapping_test

Input:${\mathsf{\Gamma }}_q \left(the scheduling table of processor q\right), M_i \left(task to be mapped on processor q\right)$ Output:$FAILURE for a negative mapping test, SUCCESS otherwise$ 55 add $M_i$ to ${\mathsf{\Gamma }}_q$ 56 sort ${\mathsf{\Gamma }}_q$ according to $T_i$ in a nondecreasing order 57 for$i=1;i<size of{ \mathsf{\Gamma }}_q;i++$do 58 for$j=0;j<i;j++$do 59 $gcd\leftarrow greatest common divisor of T_i and T_j$ 60 if$C_{i,Lo}+C_{j,Lo}>gcd$then 61 remove $M_i$ from ${\mathsf{\Gamma }}_q$ 62 return$FAILURE$ 63 end if 64 if$L_i=Hi and L_j=Hi and C_{i,Hi}+C_{j,Hi}>gcd$then 65 remove $M_i$ from ${\mathsf{\Gamma }}_q$ 66 return$FAILURE$ 67 end if 68 end for 69 end for 70 return$SUCCESS$

Algorithm 5 P_FENP_MC

Input:$M\in \left\{M_0, M_1, \dots , M_{n-1}\right\},where n\leftarrow number of tasks$

Output:$\mathsf{\Gamma }\in \left\{{\mathsf{\Gamma }}_0, {\mathsf{\Gamma }}_1, \dots , {\mathsf{\Gamma }}_{m-1}\right\},where m\leftarrow number of processors$

$FAILURE if there are not enough processors to execute the task set,$

$SUCCESS otherwise$

1 $q\leftarrow 0$ 2 $UL{o}_{{\mathsf{\Gamma }}_0}\leftarrow 0$ 3 $UH{i}_{{\mathsf{\Gamma }}_0}\leftarrow 0$ 4 for$i=0;i<n;i++$do 5 for$j=0;j\le q;j++$do 6 $tempUtilLo\leftarrow C_{i, Lo}/ T_i$ 7 if$L_i=Hi$ 8 $tempUtilHi\leftarrow C_{i, Hi}/ T_i$ 9 else 10 $tempUtilHi\leftarrow 0$ 11 end if 12 if$UL{o}_{{\mathsf{\Gamma }}_j}\le 1 and UH{i}_{{\mathsf{\Gamma }}_j}\le 1 and mapping\_test\left({\mathsf{\Gamma }}_j, M_i\right)=SUCCESS$then 13 $UL{o}_{{\mathsf{\Gamma }}_j}\leftarrow UL{o}_{{\mathsf{\Gamma }}_j}+tempUtilLo$ 14 $UH{i}_{{\mathsf{\Gamma }}_j}\leftarrow UH{i}_{{\mathsf{\Gamma }}_j}+tempUtilHi$ 15 break 16 ened if 17 end for 18 if$j>q$then 19 if$j+1>m$then 20 return$FAILURE$ 21 end if 22 $q\leftarrow q+1$ 23 $UL{o}_{{\mathsf{\Gamma }}_q}\leftarrow tempUtilLo$ 24 $UH{i}_{{\mathsf{\Gamma }}_q}\leftarrow tempUtilHi$ 25 add $M_i$ to ${\mathsf{\Gamma }}_q$ 26 end if 27 end for 28 return SUCCESS

5. Performance Analysis

5.1. Random Task Set Generation

Our experiments were conducted upon randomly-generated task sets in a dual-criticality system (Lo, Hi). A slight modification of the workload-generation algorithm introduced by Guan et al. [30] was used for the random task set generation process [31]. The parameters for each new task $M_i$ are generated as follows:

• Criticality level: $L_i=Hi$ with probability $P_{Hi}$; otherwise, $L_i=Lo$.
• Period: $T_i$ is drawn using a uniform distribution over $\left[10,50\right].$
• Deadline: $D_i=T_i$ because of the implicit deadline constraint.
• Utilization: $U_{i,L_j}$ is a vector of size l, where l is the number of criticality levels. Five input parameters are considered when generating the utilizations [31]:

  ○

  $U_{bound}$:

  $$\max \left(U_{Lo}\left(M\right),U_{Hi}\left(M\right)\right)=U_{bound}$$

  (15)

  $$U_{Lo}\left(M\right)={\displaystyle \sum }_{M_i\in \pi }{U}_{i,L_{Lo}}$$

  (16)

  $$U_{Hi}\left(M\right)={\displaystyle \sum }_{M_i\in Hi\left(\pi \right)}{U}_{i,L_{Hi}}$$

  (17)

  where π is the task set and Hi(π) is a subset of π that contains only the Hi-criticality tasks.

  ○

  $\left[U_L,U_U\right]$: The range of task utilization, with $0\le U_L\le U_U\le 1$.

  ○

  $\left[Z_L,Z_U\right]$: The range of the ratio between the Hi-criticality utilization of a task and its Lo-criticality utilization, with $0\le Z_L\le Z_U$.

• WCET for criticality level Lo: $C_{i,L_{Lo}}=U_{i,L_{Lo}}·T_i$.
• WCET for criticality level Hi: $C_{i,L_{Hi}}=U_{i,L_{Hi}}·T_i$ if $L_i=Hi$. Otherwise, $C_{i,L_{Hi}}=C_{i,L_{Lo}}$.
• Start time: $S_{i,L_{Lo}}=S_{i,L_{Hi}}=0$.

5.2. Success Ratio

In this section we undertake an experimental evaluation of our algorithm P_FENP_MC by comparing it to another known scheduling method, P-EDF-VD. For the latter, task partitioning is done with regard to Condition (14) under the First-Fit Decreasing (FFD) [32] heuristic with sorting as the period. A non-preemptive version of the EDF-VD method is used. For P_FENP_MC, task mapping is done according to the heuristic described in Section 4.

The parameters used in generating the task sets are provided in the graph caption. Each datapoint was determined by randomly generating 100 task sets. In Figure 8, the task set utilization bound (x-axis) ranges from 0.2 to 0.8 times the number of processors divided by 2, in steps of 0.1, while in Figure 9, the number of processors (x-axis) ranges from 2 to 10 in steps of 2. The number of tasks in a task set will vary according to the task set utilization bound, being at least 3 times and at most 9 times the utilization bound. Thus, a higher value on the x-axis increases the number of tasks in a task set, while a lower value decreases it.

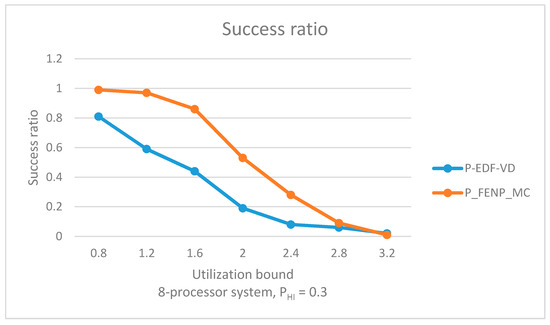
Figure 8. Success ratio by varying the utilization bound. $U_L=0.05, U_U=0.75, Z_L=1, Z_U=4$.

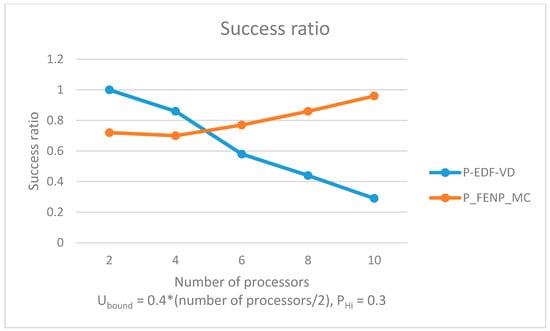
Figure 9. Success ratio by varying the number of processors. $U_L=0.05, U_U=0.75, Z_L=1, Z_U=4$.

As the number of processors increases (see Figure 9), tasks are better scheduled in terms of success ratio when using our proposed algorithm. With more available resources there is a higher chance each task is partitioned on a suitable processor with regard to Conditions I and II (see Section 4.1). The FFD does not run a schedulability test when mapping each task; therefore, if a high number of tasks are partitioned on a single processor, the local scheduling algorithm may return a negative schedulability test.

5.3. Jitterless Execution—Test Case

In order to illustrate the jitterless execution of a task set scheduled with P_FENP_MC and to compare the task execution with that under other scheduling algorithms, we provide an example of three mixed criticality tasks scheduled on a dual-criticality system with one processor. Table 6 contains the timing parameters of the tasks.

Table 6. Task set example.

Task	${\mathit{T}}_{\mathit{i}}$	${\mathit{D}}_{\mathit{i}}$	${\mathit{L}}_{\mathit{i}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{L}\mathit{o}}}$	${\mathit{C}}_{\mathit{i},{\mathit{L}}_{\mathit{H}\mathit{i}}}$
$M_1$	8	8	Hi	2	5
$M_2$	12	12	Lo	1	-
$M_3$	16	16	Lo	2	-

Scheduling for both the Hi- and Lo-criticality modes is illustrated in Figure 10.

Figure 10. Scheduling of the task set example using four methods: Partitioned Fixed Execution Non-Preemptive Mixed Criticality (P_FENP_MC), Partitioned Earliest Deadline First with Virtual Deadlines (P-EDF-VD), a non-preemptive variant, Time-Triggered Merge (TT-Merge), and Energy-efficient Time-Triggered Merge (Energy-efficient TT-Merge).

The jitter of a task is calculated as the difference between the maximum and minimum separation between two consecutive jobs of the same task $M_i$ [33] and is given by (18):

$$Jitter\left(M_i\right)=\underset{k\ge 1}{\max }\left\{\left| J_{i,k}-J_{i,k+1}\right|\right\}-\underset{k\ge 1}{\min }\left\{\left| J_{i,k}-J_{i,k+1}\right|\right\}$$

(18)

where $J_{i,k}$ is the kth job of task $M_i$.

Table 7 contains the jitter values for the task set example scheduled by P_FENP_MC, P-EDF-VD [13] (non-preemptive variant), TT-Merge, and Energy-efficient TT-Merge [12].

Table 7. Jitter values of the task set example scheduled using four algorithms: P_FENP_MC, P-EDF-VD (non-preemptive variant), TT-Merge, and Energy-efficient TT-Merge.

Criticality Mode	Task	Jitter Value
		P_FENP_MC	P-EDF-VD	TT-Merge	Energy-Efficient TT-Merge
Lo	$M_1$	0	0	5	0
	$M_2$	0	4	0	2
	$M_3$	0	1	1	1
Hi	$M_1$	0	0	5	0

As can be seen from the table above, three of the algorithms (P_FENP_MC, P-EDF-VD, and Energy-efficient TT-Merge) provided jitterless execution for the first task ($M_1$), but only P_FENP_MC delivered a scheduling table for jitterless execution of all the tasks in the system.

5.4. Discussion

The jitterless task execution achieved by designing perfectly periodical scheduling for all the criticality levels in an MCS brings advantages in applications regarding message synchronization, signal processing, control applications, or simply different types of certifications. Having jitterless task execution and respecting the time constraints imposed by MCSs, we have full determinism and predictability regarding task execution.

Still, the tradeoff for jitterless scheduling on a uniprocessor is a lower success ratio value compared to using an event-driven method. An algorithm such as EDF-VD can reach up to 80% success ratio for a total utilization factor of 1 for the lowest criticality mode [13]. However, comparative results are harder to obtain with a time-triggered algorithm without using any resource enhancements, such as frequency scaling, for instance [10,12].

For a multiprocessor platform, the success ratio is not only influenced by the scheduling algorithm but also by the function used to map tasks to processors (see Figure 8). If we use a proper partitioned mapping function, we have comparative results between time-triggered and event-driven schedulers in terms of success ratio. As illustrated in Figure 8, our proposed scheduling algorithm obtained better schedulabitily results by using a well-tailored partitioned function in comparison to P-EDF-VD (with an FFD partitioned mapping function).

6. Conclusions and Future Work

As the number and complexity of safety-critical real-time applications increase, special attention needs to be paid to developing suitable and reliable scheduling techniques, especially for safety-critical systems running in time-triggered environments. In this paper we proposed a scheduling method for jitterless execution of hard real-time tasks in mixed criticality systems. Our approach is based on the real-time FENP scheduling algorithm and specifically tailored to MCS requirements. Additionally, feasibility tests were proposed for both uniprocessor and homogenous multiprocessor systems, and the algorithm performance was compared against an event-driven scheduling algorithm in a non-preemptive context, P-EDF-VD.

As future work, we intend to further investigate implementations of this scheduling methodology in RTOSs and to analyze the performance improvements of jitter-sensitive applications scheduled with P_FENP_MC in domains such as system control, robotic systems, and real-time communications.