Investigation on the Mass Flow Rate of a Refrigerator Compressor Based on the p–V Diagram
Abstract
1. Introduction
2. Experimental Setup
2.1. Test Compressor
2.2. Data Acquisition System
3. Method to Calculate the Refrigerant Mass Flow Rate
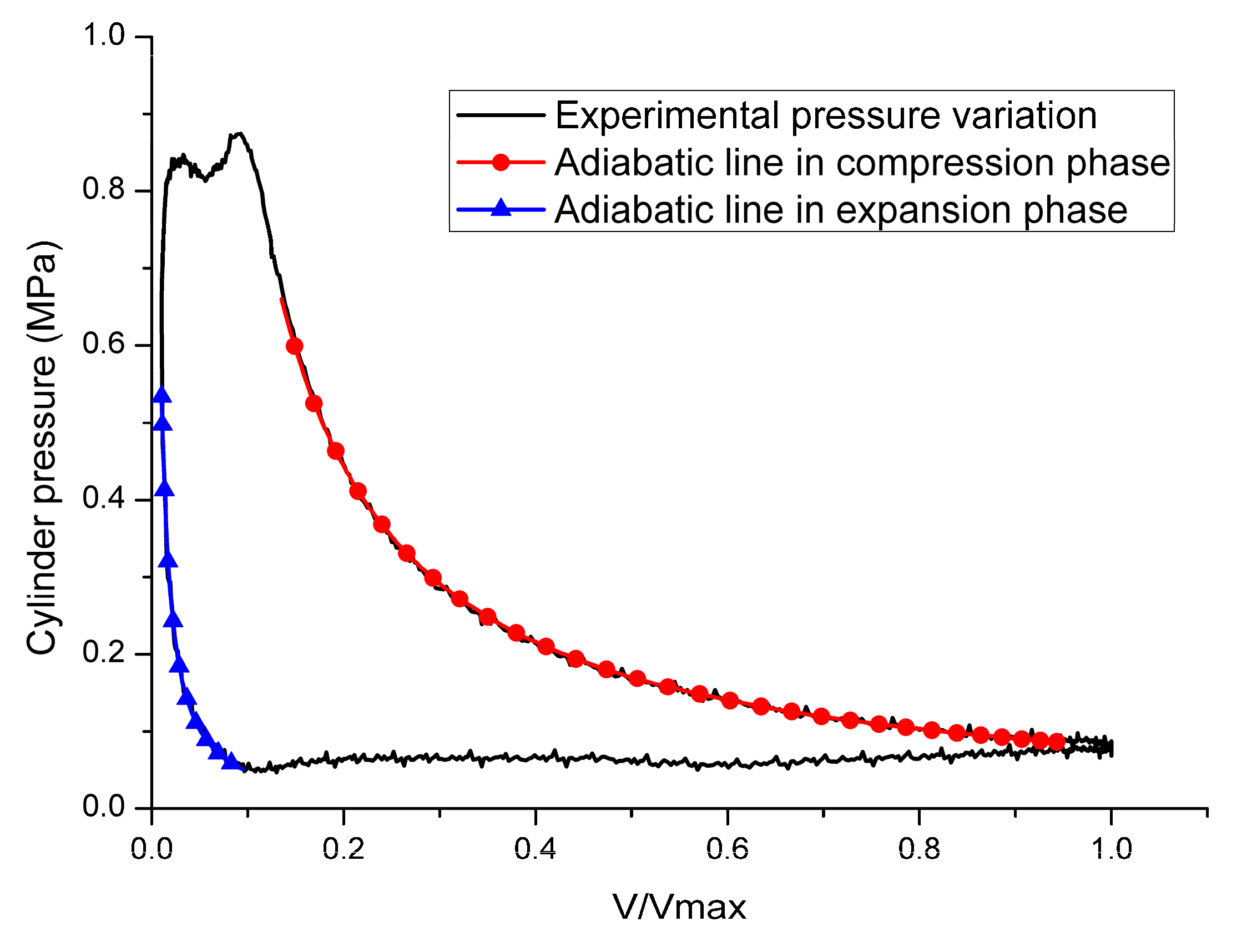
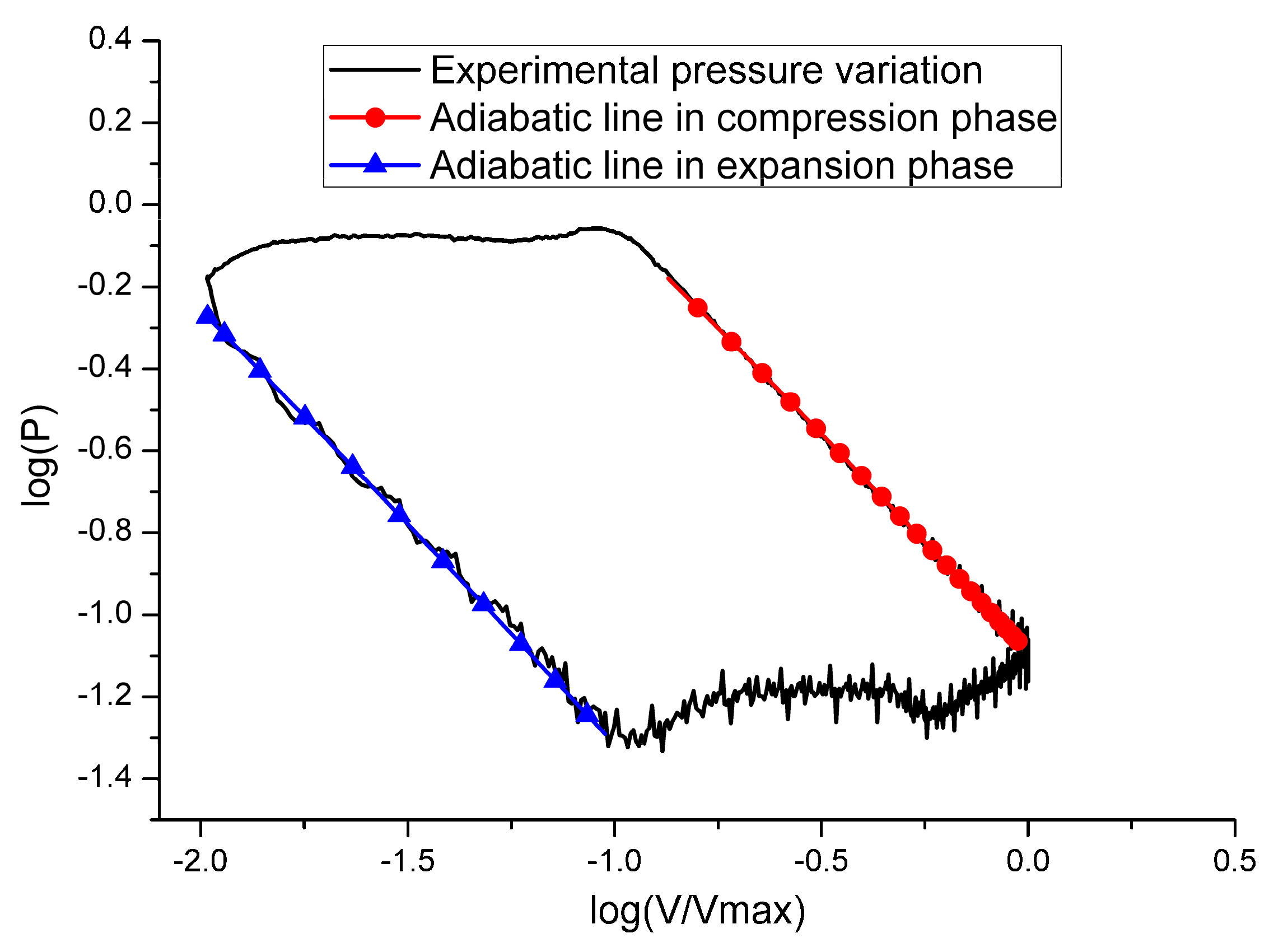
3.1. Validation of Adiabatic Process Hypothesis in the Expansion Phase and Compression Phase
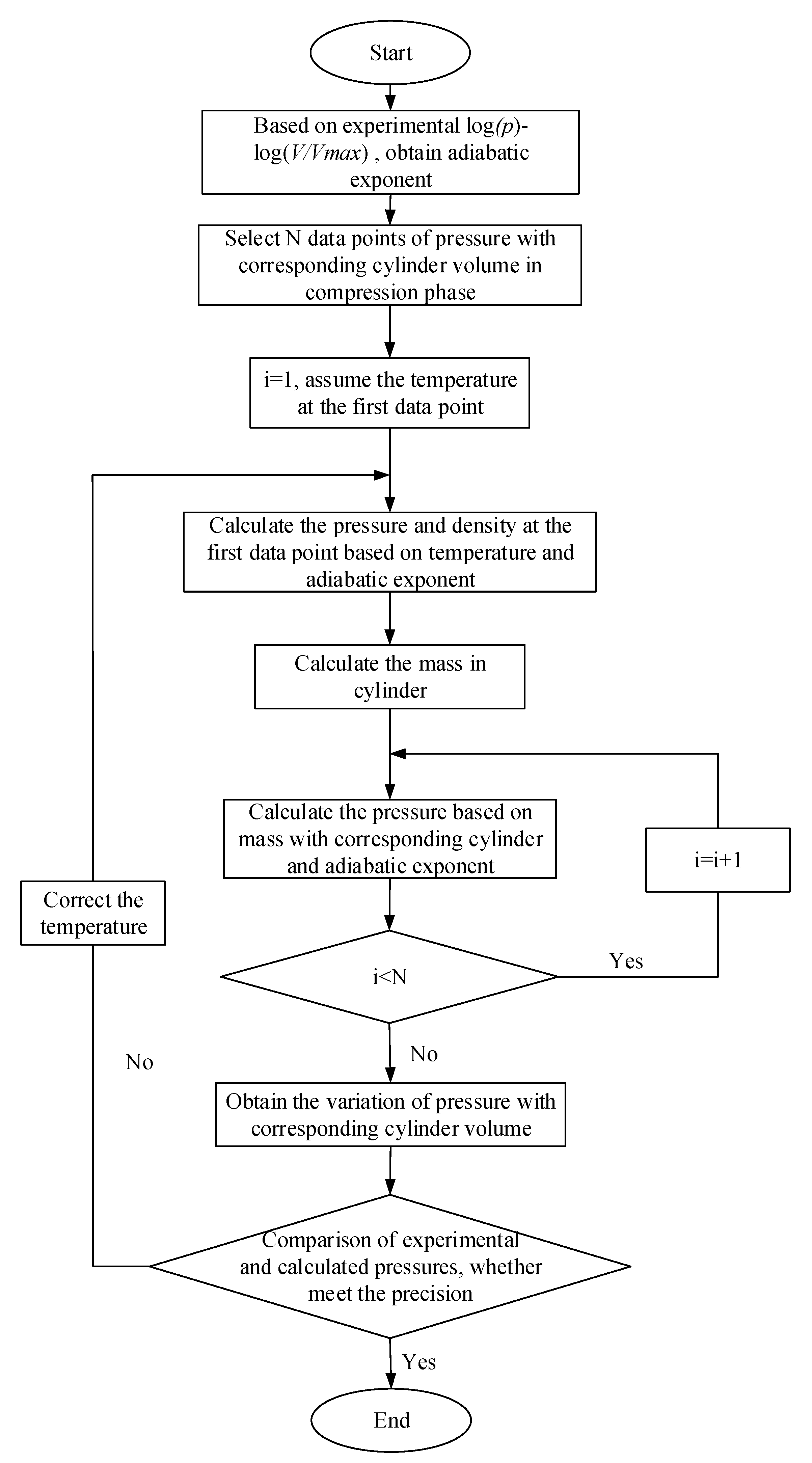
3.2. Calculation Method
4. Results and Discussion
4.1. Verification of Mass Flow Calculation Method
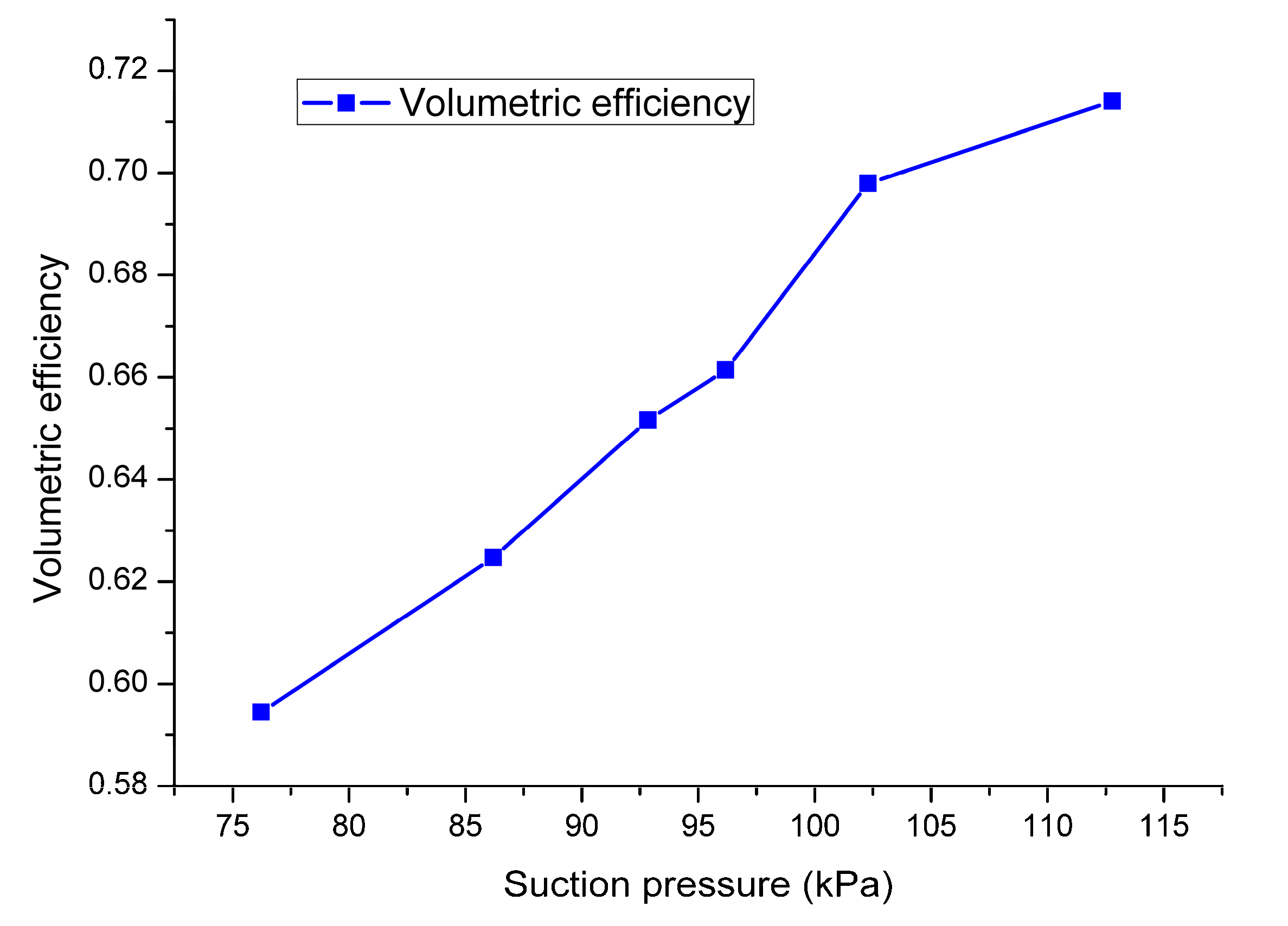
4.2. Effect of Suction Pressure on the Compressor Performance
4.2.1. Effect of Suction Pressure on the Volumetric Efficiency
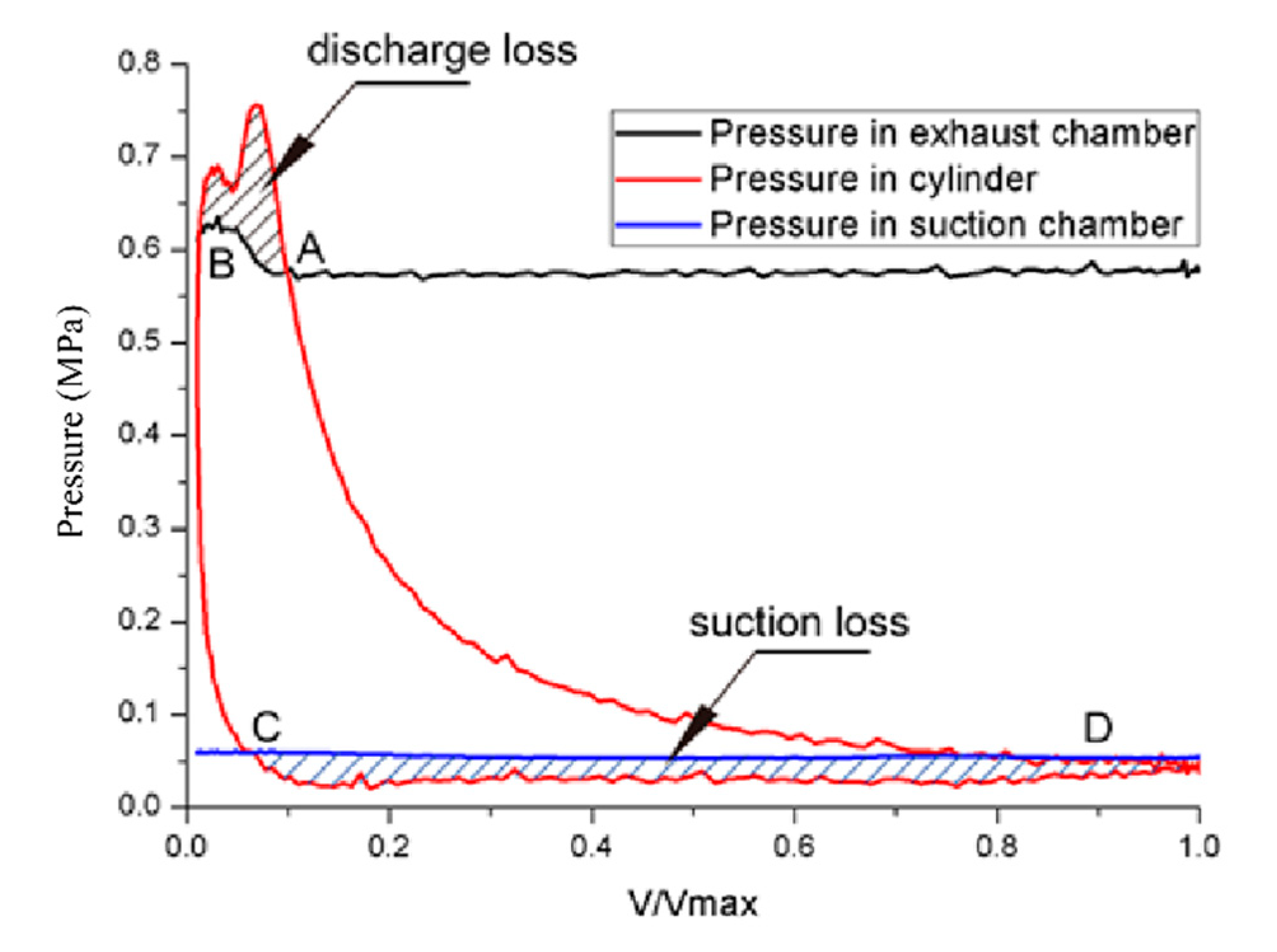
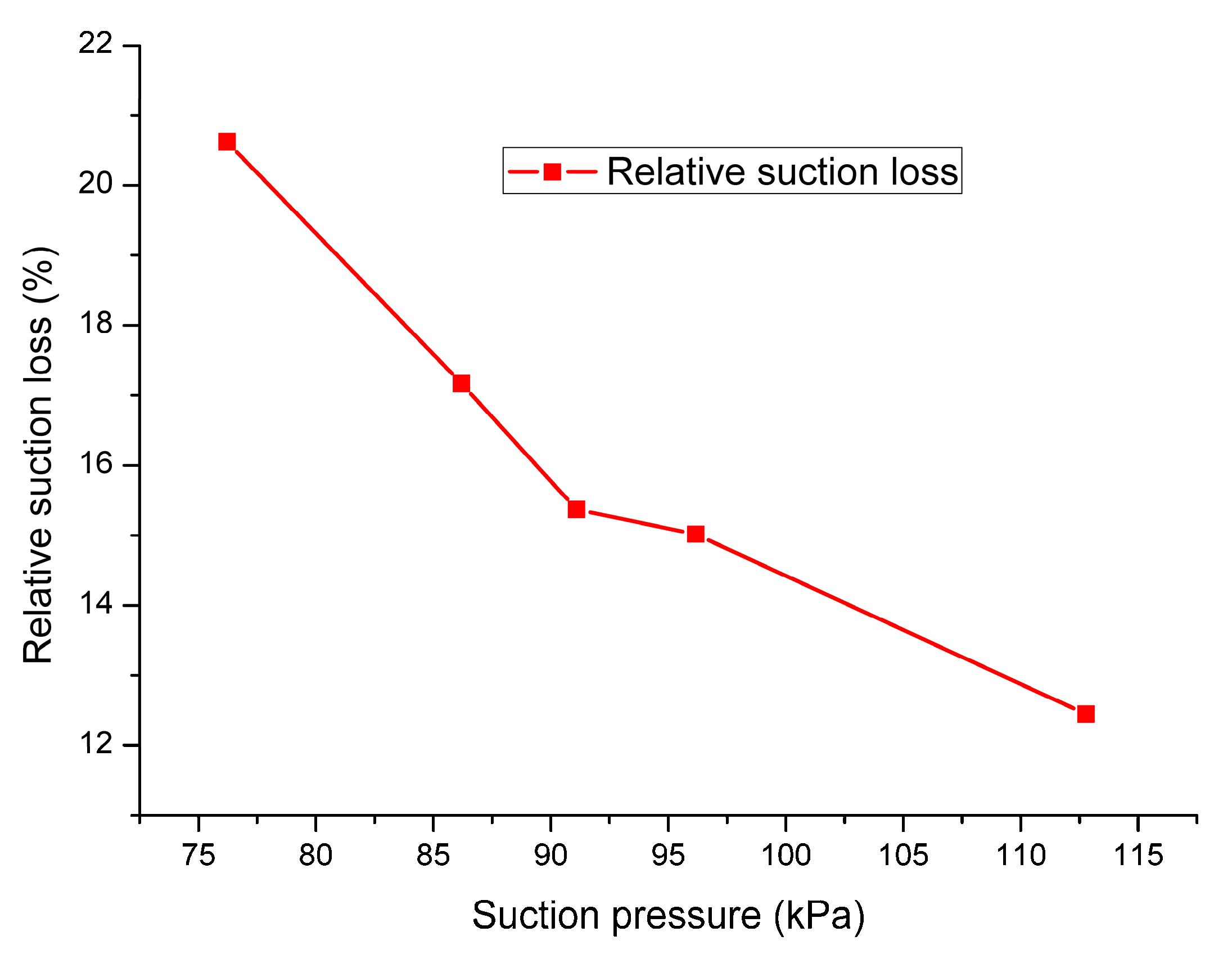
4.2.2. Effect of Suction Pressure on Suction Flow Loss
5. Conclusions
- With the compression and expansion phase approximating the adiabatic process being experimentally verified, a calculation method for the mass flow rate of a compressor is proposed, based on the experimental p–V diagram.
- The accuracy of the calculation method for the mass flow rate of a compressor is directly verified by a mass flow meter. Furthermore, the error of the calculation method is less than 3.13%, which can replace the mass flow meter for most application situations.
- Based on the calculation method, the influence of suction pressure on compressor performance is investigated. Under a constant pressure ratio, the higher suction pressure leads to a higher volumetric efficiency and less suction loss.
- As the measuring equipment is expensive and the calculation method is complex, the proposed method at present is mainly suitable for scientific research. In the future, the authors will focus on reducing the complexity of the method, and based on this method, the mass flow meter of compressor will be manufactured.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cp | Specific heat at constant pressure |
| Cv | Specific heat at constant volume |
| m | Refrigerator mass in the cylinder |
| p | Pressure |
| Vc | The volume of cylinder |
| Vtheo | Theoretical volume of the compressor |
| ρ | Refrigerant density |
| Subscripts | |
| com | Compression phase |
| exp | Expansion phase |
| Inlet | Suction states |
References
- Cao, J.; Wang, Q.; Hu, M.; Ren, X.; Liu, W.; Su, Y.; Pei, G. Investigation on an Improved Household Refrigerator for Energy Saving of Residential Buildings. Appl. Sci. 2020, 10, 4246. [Google Scholar] [CrossRef]
- Zhao, R.; Qiao, L.; Gao, Z.; Huang, D. Effect of Vacuum Insulation Panels on Energy Consumption and Thermal Load Transfer between Compartments in a Three-Temperature Frost-Free Refrigerator. Energies 2020, 13, 1559. [Google Scholar] [CrossRef]
- Zhang, W.; Ji, L.; Xing, Z.; Peng, X. Investigation on the Suction Reed Valve Motion with Sticky Force in a Refrigerator Compressor. Energies 2018, 11, 2897. [Google Scholar] [CrossRef]
- Wang, T.; He, Z.; Guo, J.; Peng, X. Investigation of the Thermodynamic Process of the Refrigerator Compressor Based on the m-θ Diagram. Energies 2017, 10, 1517. [Google Scholar] [CrossRef]
- Fatouh, M. Theoretical investigation of adiabatic capillary tubes working with propane/n-butane/iso-butane blends. Energy Convers. Manag. 2007, 48, 1338–1348. [Google Scholar] [CrossRef]
- Björk, E. A simple technique for refrigerant mass measurement. Appl. Therm. Eng. 2005, 25, 1115–1125. [Google Scholar] [CrossRef]
- Björk, E.; Palm, B. Refrigerant mass charge distribution in a domestic refrigerator, Part I: Transient conditions. Appl. Therm. Eng. 2006, 26, 829–837. [Google Scholar] [CrossRef]
- Björk, E.; Palm, B. Refrigerant mass charge distribution in a domestic refrigerator. Part II: Steady state conditions. Appl. Therm. Eng. 2006, 26, 866–871. [Google Scholar] [CrossRef]
- Possamai, F.C.; Todescat, M.L. A review of household compressor energy performance. In Proceedings of the 17th International Compressor Engineering Conference at Purdue, West Lafayette, IN, USA, 9–12 July 2008. Paper C076. [Google Scholar]
- Ribas, F.A., Jr.; Deschamps, C.J.; Fagotti, F.; Morriesen, A.; Dutra, T. Thermal analysis of reciprocating compressors—A critical review. In Proceedings of the 19th International Compressor Engineering Conference at Purdue (2008), West Lafayette, IN, USA, 14–17 July 2008. Paper 1306. [Google Scholar]
- Morriesen, A.; Deschamps, C.J. Experimental investigation of transient fluid flow and superheating in the suction chamber of a refrigeration reciprocating compressor. Appl. Therm. Eng. 2012, 41, 61–70. [Google Scholar] [CrossRef]
- Stouffs, P.; Tazerout, M.; Wauters, P. Thermodynamic analysis of reciprocating compressors. Int. J. Therm. Sci. 2001, 40, 52–66. [Google Scholar] [CrossRef]
- Ma, Y.; He, Z.; Peng, X.; Xing, Z. Experimental investigation of the discharge valve dynamics in a reciprocating compressor for trans-critical CO2, refrigeration cycle. Appl. Therm. Eng. 2012, 32, 13–21. [Google Scholar] [CrossRef]
- Pérez-Segarra, C.D.; Rigola, J.; Soria, M.; Oliva, A. Detailed thermodynamic characterization of hermetic reciprocating compressors. Int. J. Refrig. 2005, 28, 579–593. [Google Scholar] [CrossRef]
- Longo, G.A.; Gasparella, A. Unsteady state analysis of the compression cycle of a hermetic reciprocating compressor. Int. J. Refrig. 2003, 26, 681–689. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.; Guo, Y.; Peng, X.; Yang, J.; Zhang, Z. The study on mass transport process in the cylinder of CO2 compressor based on p–V diagram. Appl. Therm. Eng. 2020, 174, 115314. [Google Scholar] [CrossRef]
- Tao, W.; Guo, Y.; He, Z.L.; Peng, X.Y. Investigation on the delayed closure of the suction valve in the refrigerator compressor by FSI modeling. Int. J. Refrig. 2018, 91, 111–121. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Crank Radius | 10 mm |
| Connecting Rod Length | 40.5 mm |
| Cylinder Diameter | 31 mm |
| Rated Speed | 2950 r·min−1 |
| Relative Clearance Volume | 2.35% |
| Compression Phase | Expansion Phase | ||||
|---|---|---|---|---|---|
| Experimental Pressure (MPa) | Adiabatic Line (MPa) | Error (%) | Experimental Pressure (MPa) | Adiabatic Line (MPa) | Error (%) |
| 0.088 | 0.086 | 1.86 | 0.529 | 0.504 | 4.64 |
| 0.089 | 0.088 | 1.04 | 0.473 | 0.483 | −2.16 |
| 0.090 | 0.090 | 0.24 | 0.457 | 0.467 | −2.12 |
| 0.091 | 0.092 | −1.73 | 0.449 | 0.450 | −0.23 |
| 0.094 | 0.095 | −1.20 | 0.440 | 0.432 | 1.81 |
| 0.097 | 0.098 | −1.06 | 0.425 | 0.413 | 2.86 |
| 0.099 | 0.101 | −2.10 | 0.390 | 0.384 | 1.53 |
| 0.103 | 0.105 | −1.68 | 0.357 | 0.366 | −2.31 |
| 0.109 | 0.109 | −0.81 | 0.294 | 0.303 | −3.17 |
| 0.114 | 0.114 | 0.00 | 0.292 | 0.287 | 1.50 |
| 0.117 | 0.120 | −1.72 | 0.268 | 0.264 | 1.51 |
| 0.126 | 0.125 | 0.54 | 0.246 | 0.250 | −1.68 |
| 0.130 | 0.132 | −1.45 | 0.230 | 0.236 | −2.59 |
| 0.137 | 0.140 | −1.63 | 0.206 | 0.212 | −2.91 |
| 0.148 | 0.148 | −0.14 | 0.202 | 0.200 | 0.71 |
| 0.154 | 0.158 | −2.50 | 0.195 | 0.190 | 2.65 |
| 0.166 | 0.168 | −1.53 | 0.172 | 0.170 | 0.66 |
| 0.178 | 0.181 | −1.60 | 0.159 | 0.162 | −1.35 |
| 0.190 | 0.194 | −2.01 | 0.151 | 0.153 | −1.41 |
| 0.205 | 0.210 | −2.37 | 0.148 | 0.146 | 1.33 |
| 0.223 | 0.228 | −1.92 | 0.145 | 0.139 | 4.70 |
| 0.242 | 0.248 | −2.72 | 0.121 | 0.120 | 0.86 |
| 0.268 | 0.272 | −1.31 | 0.111 | 0.111 | −0.16 |
| 0.296 | 0.299 | −1.15 | 0.106 | 0.106 | 0.24 |
| 0.325 | 0.331 | −1.74 | 0.094 | 0.091 | 3.97 |
| 0.363 | 0.368 | −1.34 | 0.081 | 0.081 | −0.05 |
| 0.412 | 0.412 | 0.09 | 0.075 | 0.078 | −3.75 |
| 0.461 | 0.463 | −0.53 | 0.068 | 0.066 | 2.77 |
| 0.531 | 0.525 | 1.17 | 0.061 | 0.063 | −2.97 |
| Suction Pressure (MPa) | Suction Temperature (℃) | Discharge Pressure (MPa) | Flow Rate | Error (%) | |
|---|---|---|---|---|---|
| By the p–V Diagram (kg·h−1) | By Flow Meter (kg·h−1) | ||||
| 0.11 | −5.60 | 0.59 | 6.09 | 5.99 | 1.64 |
| 0.12 | −2.50 | 0.75 | 6.91 | 6.72 | 2.75 |
| 0.10 | −0.80 | 0.66 | 5.17 | 5.03 | 2.71 |
| 0.11 | 2.80 | 0.64 | 5.45 | 5.38 | 1.28 |
| 0.08 | 6.40 | 0.60 | 3.51 | 3.40 | 3.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Li, D.; Ji, L.; Wang, X.; Wang, T. Investigation on the Mass Flow Rate of a Refrigerator Compressor Based on the p–V Diagram. Appl. Sci. 2020, 10, 6650. https://doi.org/10.3390/app10196650
He Z, Li D, Ji L, Wang X, Wang T. Investigation on the Mass Flow Rate of a Refrigerator Compressor Based on the p–V Diagram. Applied Sciences. 2020; 10(19):6650. https://doi.org/10.3390/app10196650
Chicago/Turabian StyleHe, Zhilong, Dantong Li, Lantian Ji, Xiaolin Wang, and Tao Wang. 2020. "Investigation on the Mass Flow Rate of a Refrigerator Compressor Based on the p–V Diagram" Applied Sciences 10, no. 19: 6650. https://doi.org/10.3390/app10196650
APA StyleHe, Z., Li, D., Ji, L., Wang, X., & Wang, T. (2020). Investigation on the Mass Flow Rate of a Refrigerator Compressor Based on the p–V Diagram. Applied Sciences, 10(19), 6650. https://doi.org/10.3390/app10196650







